Dissociative Ionization of Molecular CF2Br2 under 800 and 400 nm Intense Femtosecond Laser Fields
Abstract
:1. Introduction
2. Experimental Methods
3. Results and Discussion
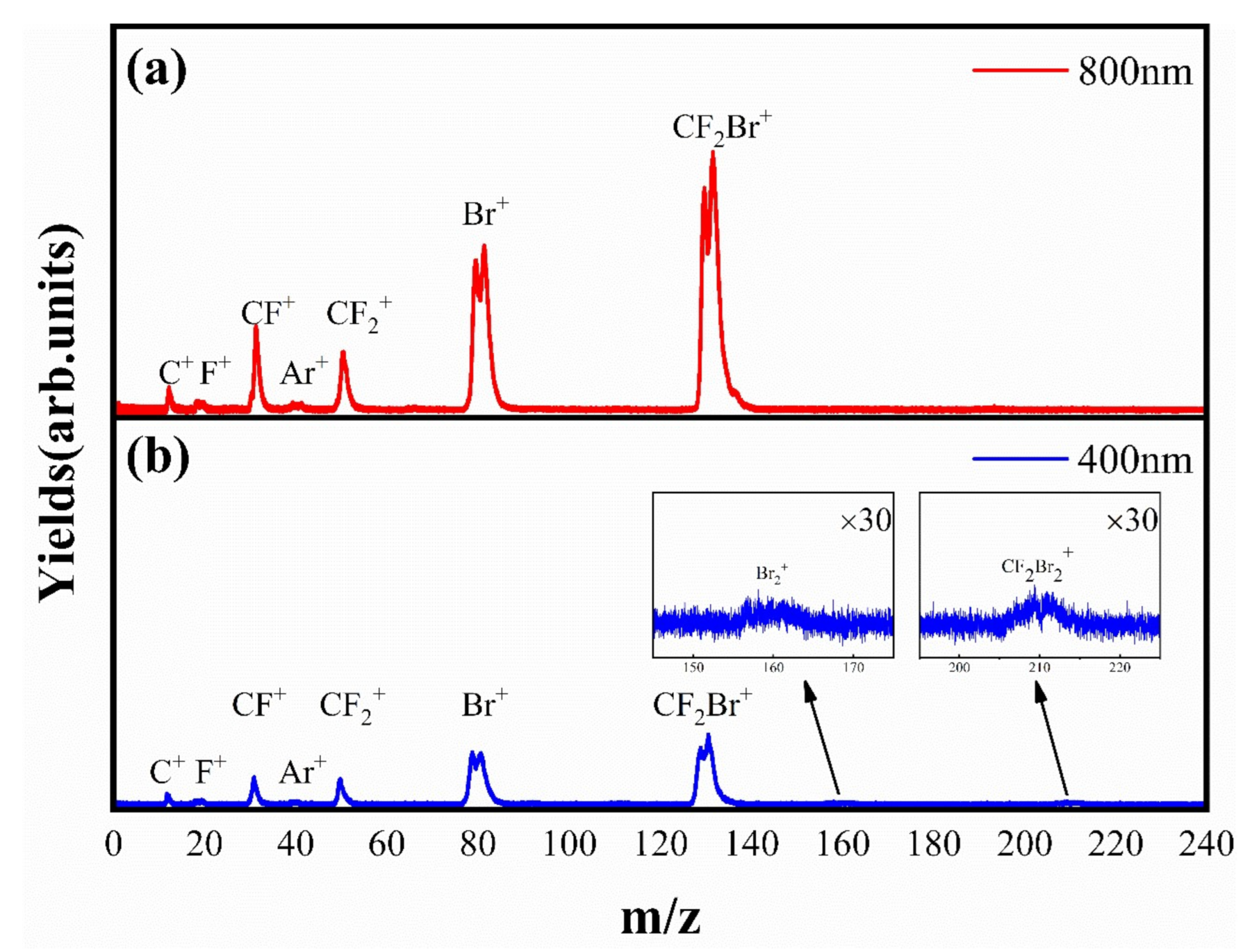
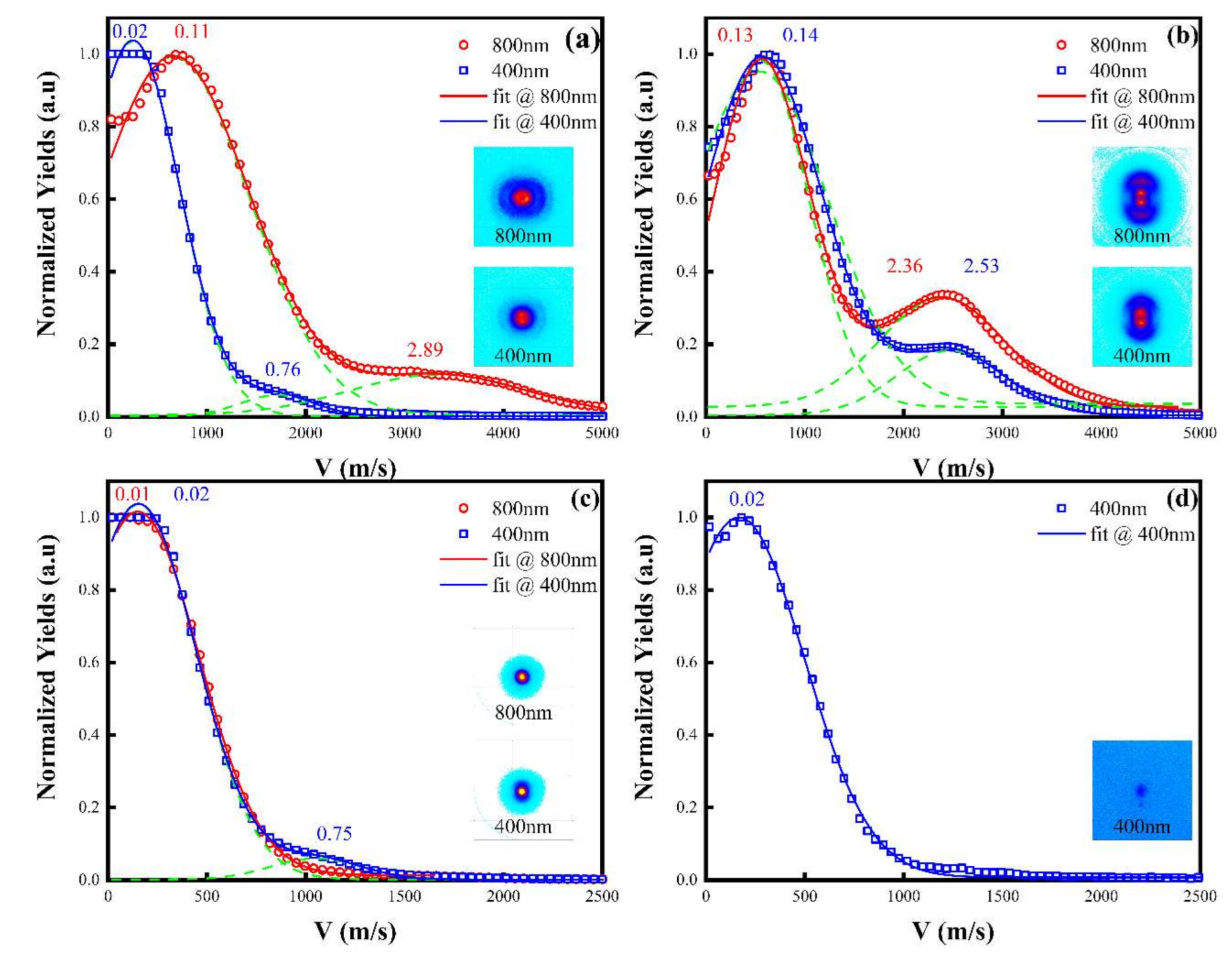
3.1. Time-of-Flight Mass Spectrum and DC-Sliced Images
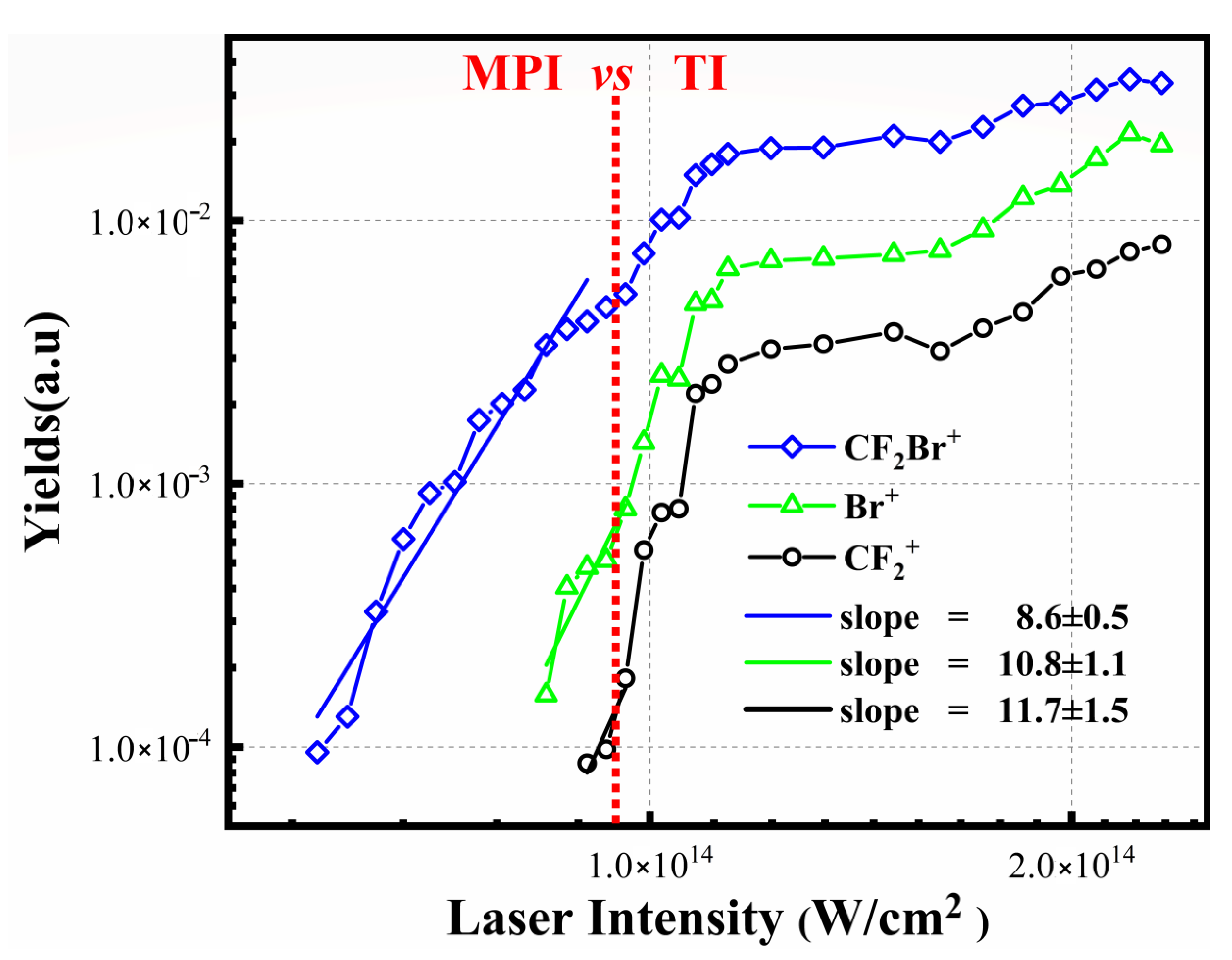
3.2. The Dissociative Ionization of Molecule CF2Br2 in 800 nm Laser Fields
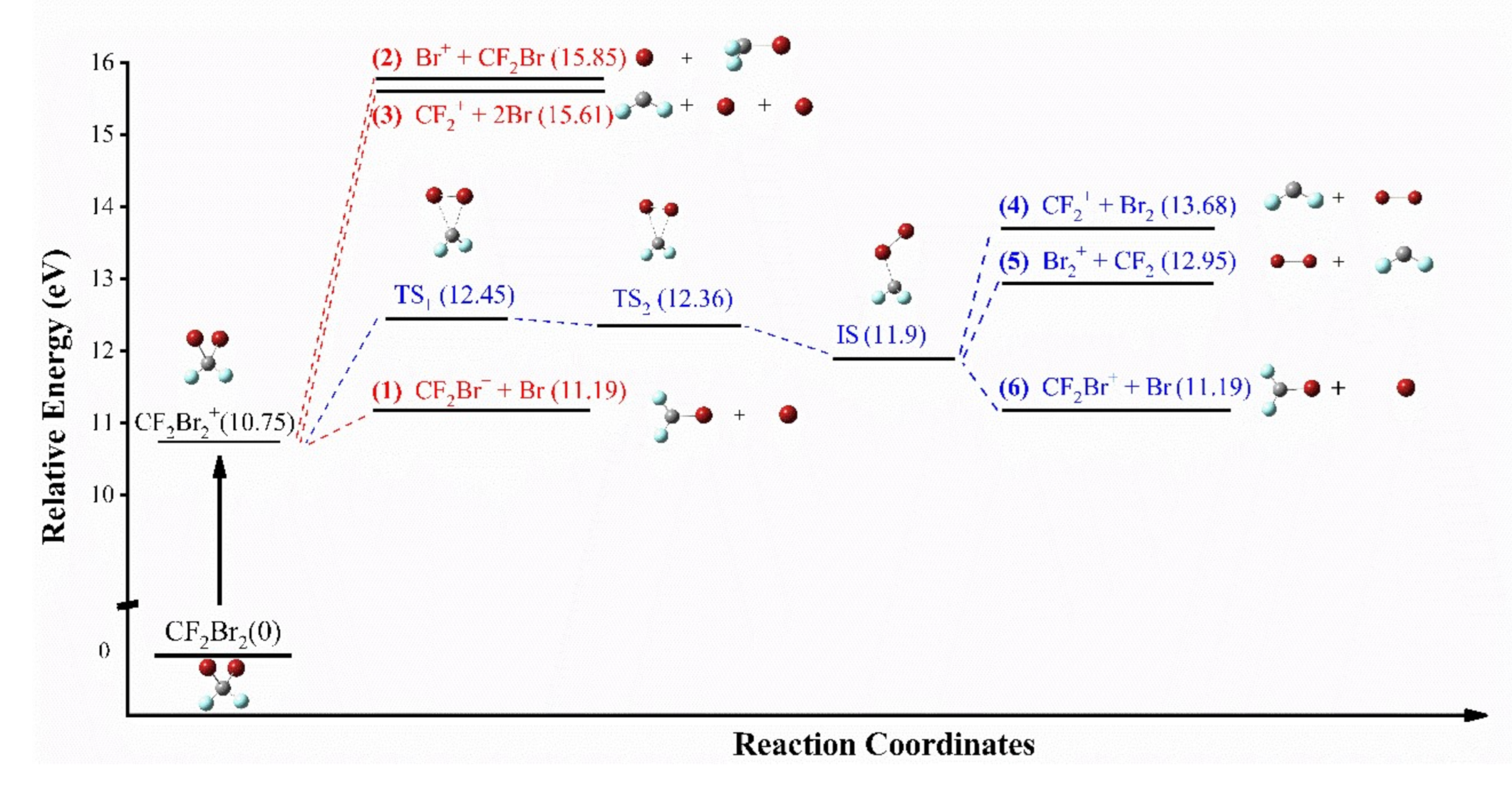
3.3. The Special Dissociation Channels for Singly Ion CF2Br2+ in 400 nm Laser Fields
| Channel | Reaction Path |
| (4) | , |
| (5) | , |
| Channel | Reaction Path |
| (6) |
3.4. The Excited States and Angular Distribution of Fragment Ions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Castillejo, M.; Couris, S.; Koudoumas, E.; Martín, M. Subpicosecond ionization and dissociation of benzene and cyclic alkanes at 800 and 400 nm. Chem. Phys. Lett. 1998, 289, 303–310. [Google Scholar] [CrossRef]
- Agostini, P.; Fabre, F.; Mainfray, G.; Petite, G.; Rahman, N.K. Free-free transitions following six-photon ionization of xenon atoms. Phys. Rev. Lett. 1979, 42, 1127. [Google Scholar] [CrossRef]
- Kornev, A.S.; Zon, B.A. Keldysh theory of tunnel ionization of an atom in a few-cycle laser pulse field. Phys. Rev. A 2012, 85, 035402. [Google Scholar] [CrossRef]
- Vozzi, C.; Calegari, F.; Benedetti, E.; Caumes, J.P.; Sansone, G.; Stagira, S.; Nisoli, M.; Torres, R.; Heesel, E.; Kajumba, N. Controlling two-center interference in molecular high harmonic generation. Phys. Rev. Lett. 2005, 95, 153902. [Google Scholar] [CrossRef] [PubMed]
- Keldysh, L. Ionization in the field of a strong electromagnetic wave. Sov. Phys. Jetp 1965, 20, 1307–1314. [Google Scholar]
- Dewitt, M.J.; Levis, R.J. Calculating the Keldysh adiabaticity parameter for atomic, diatomic, and polyatomic molecules. J. Chem. Phys. 1998, 108, 7739. [Google Scholar] [CrossRef] [Green Version]
- Echt, O.; Morgan, S.; Dao, P.; Stanley, R.; Castleman, A., Jr. Multiphoton ionization of ammonia clusters with a tunable laser. Berichte der Bunsengesellschaft für physikalishe Chemie 1984, 88, 217–219. [Google Scholar] [CrossRef]
- Cao, H.; Evleth, E.; Kassab, E. Some computationally based speculations on the photochemistry of ammonia clusters. J. Chem. Phys. 1984, 81, 1512–1513. [Google Scholar] [CrossRef]
- Levis, R.J.; DeWitt, M.J. Photoexcitation, Ionization, and Dissociation of Molecules Using Intense Near-Infrared Radiation of Femtosecond Duration. J. Phys. Chem. A 1999, 103, 6493–6507. [Google Scholar] [CrossRef]
- Carlson, T.A.; White, R.M. Measurement of the Relative Abundances and Recoil-Energy Spectra of Fragment Ions Produced as the Initial Consequences of X-Ray Interaction with CH3I, HI, and DI. J. Chem. Phys. 1966, 44, 4510–4520. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Li, Z.; Sun, H.; Zhang, S.; Sun, Z. Channel-resolved multiorbital double ionization of molecular Cl2 in an intense femtosecond laser field. Phys. Rev. A 2018, 98, 043402. [Google Scholar] [CrossRef]
- Krajnovich, D.; Zhang, Z.; Butler, L.; Lee, Y.T. Photodissociation of CF2Br2 at 248 nm by the molecular beam method. J. Phys. Chem. 1983, 88, 4561–4566. [Google Scholar] [CrossRef]
- Lee, Y.T. Molecular Beam Studies of Elementary Chemical Processes. Science 1987, 236, 793–798. [Google Scholar] [CrossRef] [Green Version]
- Park, M.S.; Kim, T.K.; Lee, S.H.; Jung, K.H.; Volpp, H.R.; Wolfrum, J. Avoided Curve Crossing between the A 1 and B 1 States in CF 2 Br 2 Photolysis at 234 and 265 nm. J. Phys. Chem. A 2001, 105, 5606–5612. [Google Scholar] [CrossRef]
- Das, S.; Badani, P.M.; Sharma, P.; Vatsa, R.K. Diverse photochemical behavior of dibromodifluoromethane (CF2Br2) monomer and cluster under gigawatt intensity laser fields. Rsc Adv. 2013, 3, 12867–12873. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Y.; Sun, H.; Sun, Z. Dissociative Ionization and Coulomb Explosion of Molecular Bromocyclopropane in an Intense Femtosecond Laser Field. Molecules 2018, 23, 3096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pei, M.; Yang, Y.; Zhang, J.; Sun, Z. Dehydrogenation involved Coulomb explosion of molecular C 2 H 4 FBr in an intense laser field. Chem. Phys. Lett. 2018, 697, 53–60. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef] [PubMed]
- Kállay, M.; Gauss, J. Calculation of excited-state properties using general coupled-cluster and configuration-interaction models. J. Chem. Phys. 2004, 121, 9257–9269. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6–31G* basis set for third-row atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Brandhorst, K.; Grunenberg, J. How strong is it? The interpretation of force and compliance constants as bond strength descriptors. Chem. Soc. Rev. 2008, 37, 1558–1567. [Google Scholar] [CrossRef] [PubMed]
- Doucet, J.; Gilbert, R.; Sauvageau, P.; Sandorfy, C. Photoelectron and far-ultraviolet spectra of CF3Br, CF2BrCl, and CF2Br2. J. Chem. Phys. 1975, 62, 366–369. [Google Scholar] [CrossRef]
- Chelkowski, S.; Foisy, C.; Bandrauk, A.D. Electron-nuclear dynamics of multiphotonH2+dissociative ionization in intense laser fields. Phys. Rev. A 1998, 57, 1176–1185. [Google Scholar] [CrossRef]
- Wu, J.; Kunitski, M.; Pitzer, M.; Trinter, F.; Schmidt, L.P.H.; Jahnke, T.; Magrakvelidze, M.; Madsen, C.B.; Madsen, L.B.; Thumm, U.; et al. Electron-Nuclear Energy Sharing in Above-Threshold Multiphoton Dissociative Ionization of H2. Phys. Rev. Lett. 2013, 111, 023002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riley, S.J.; Wilson, K.R. Excited fragments from excited molecules: Energy partitioning in the photodissociation of alkyl iodides. Faraday Discuss. Chem. Soc. 1972, 53, 132–146. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Li, Z.P.; Sun, Z.R. Dissociative ionization of CH2Br2 in 800 and 400 nm femtosecond laser fields. Chem. Phys. Lett. 2017, 685, 151–156. [Google Scholar] [CrossRef]
- Okino, T.; Furukawa, Y.; Liu, P.; Ichikawa, T.; Itakura, R.; Hoshina, K.; Yamanouchi, K.; Nakano, H. Coincidence momentum imaging of ejection of hydrogen molecular ions from methanol in intense laser fields. Chem. Phys. Lett. 2006, 419, 223–227. [Google Scholar] [CrossRef]
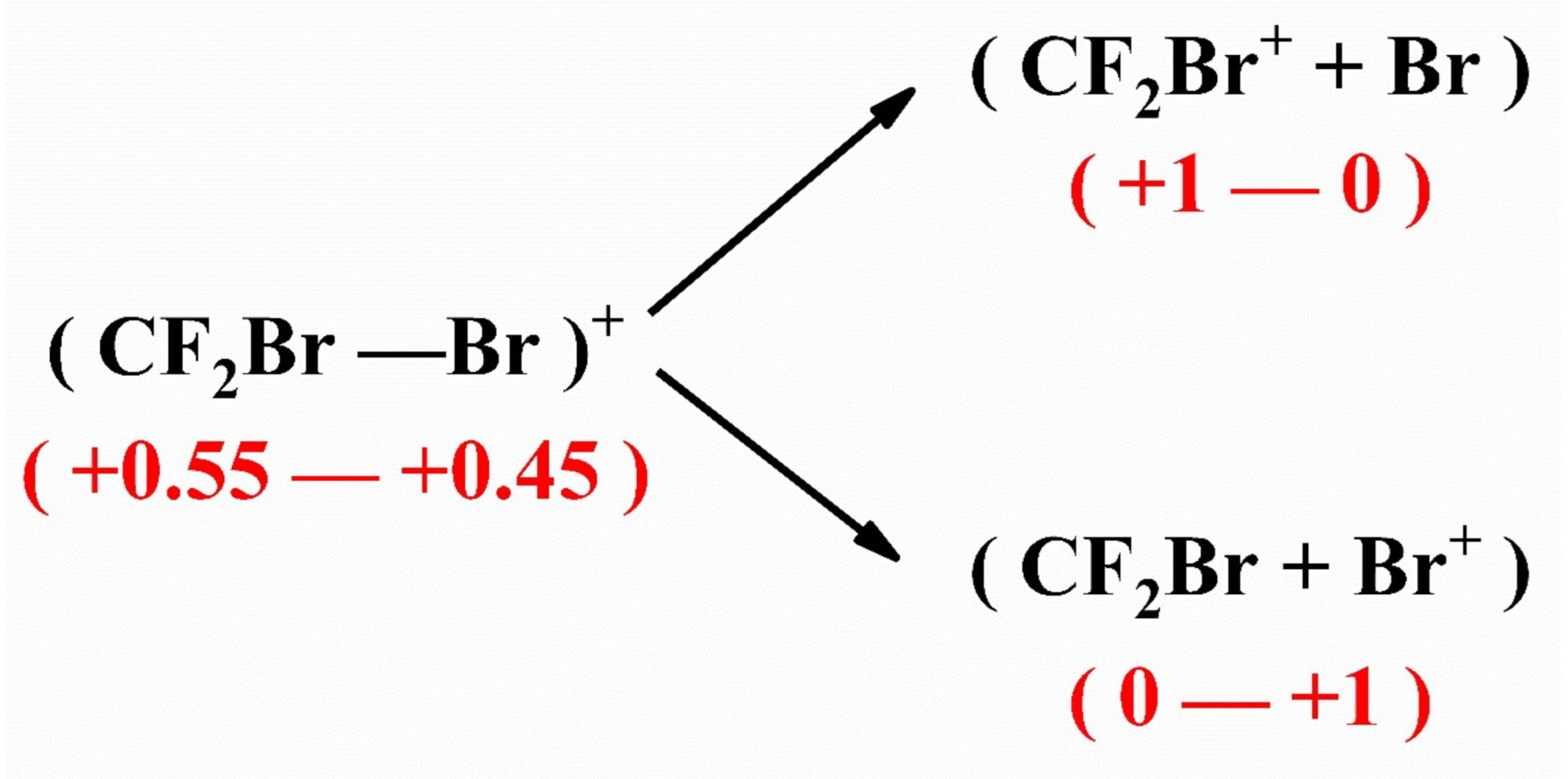
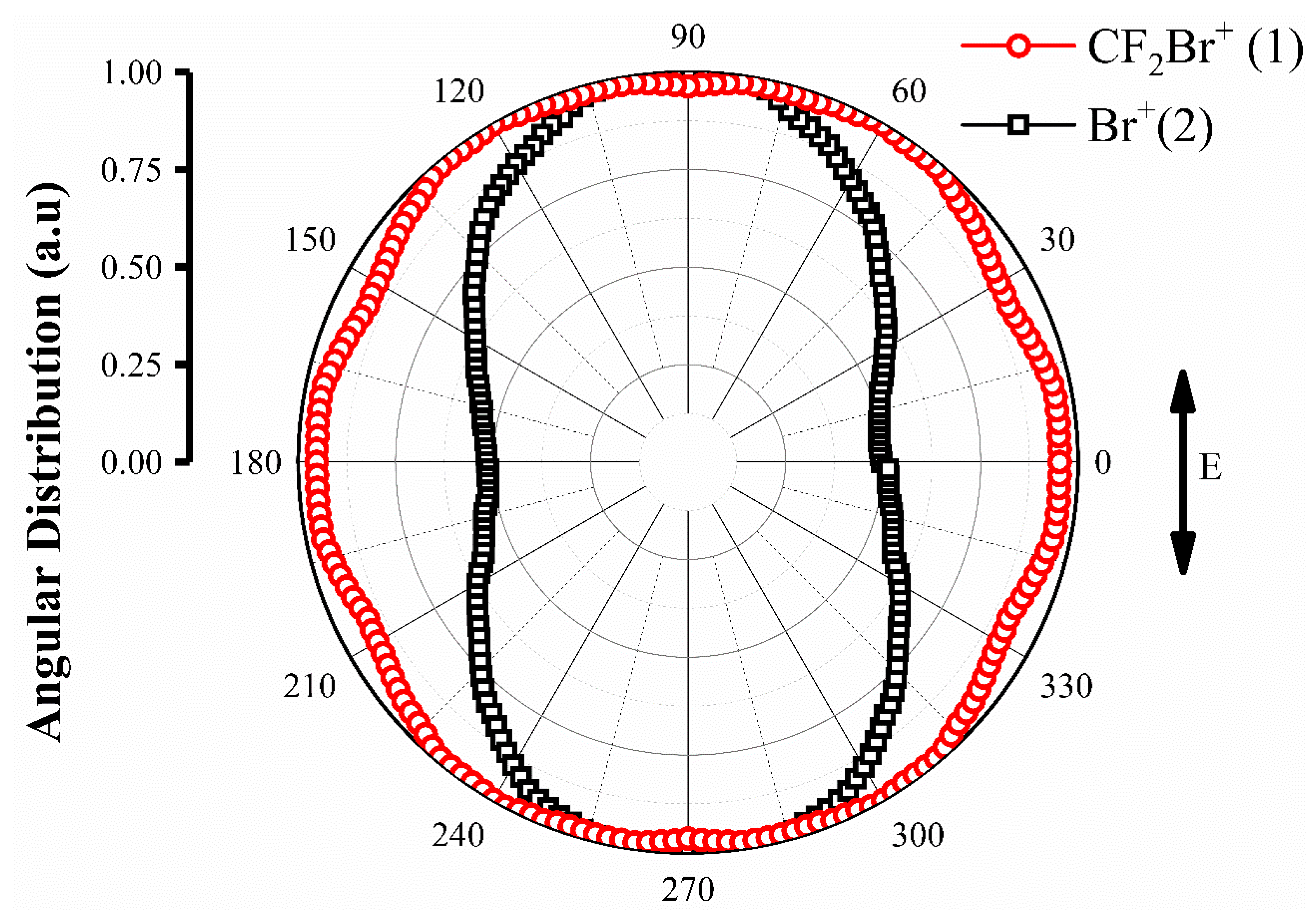
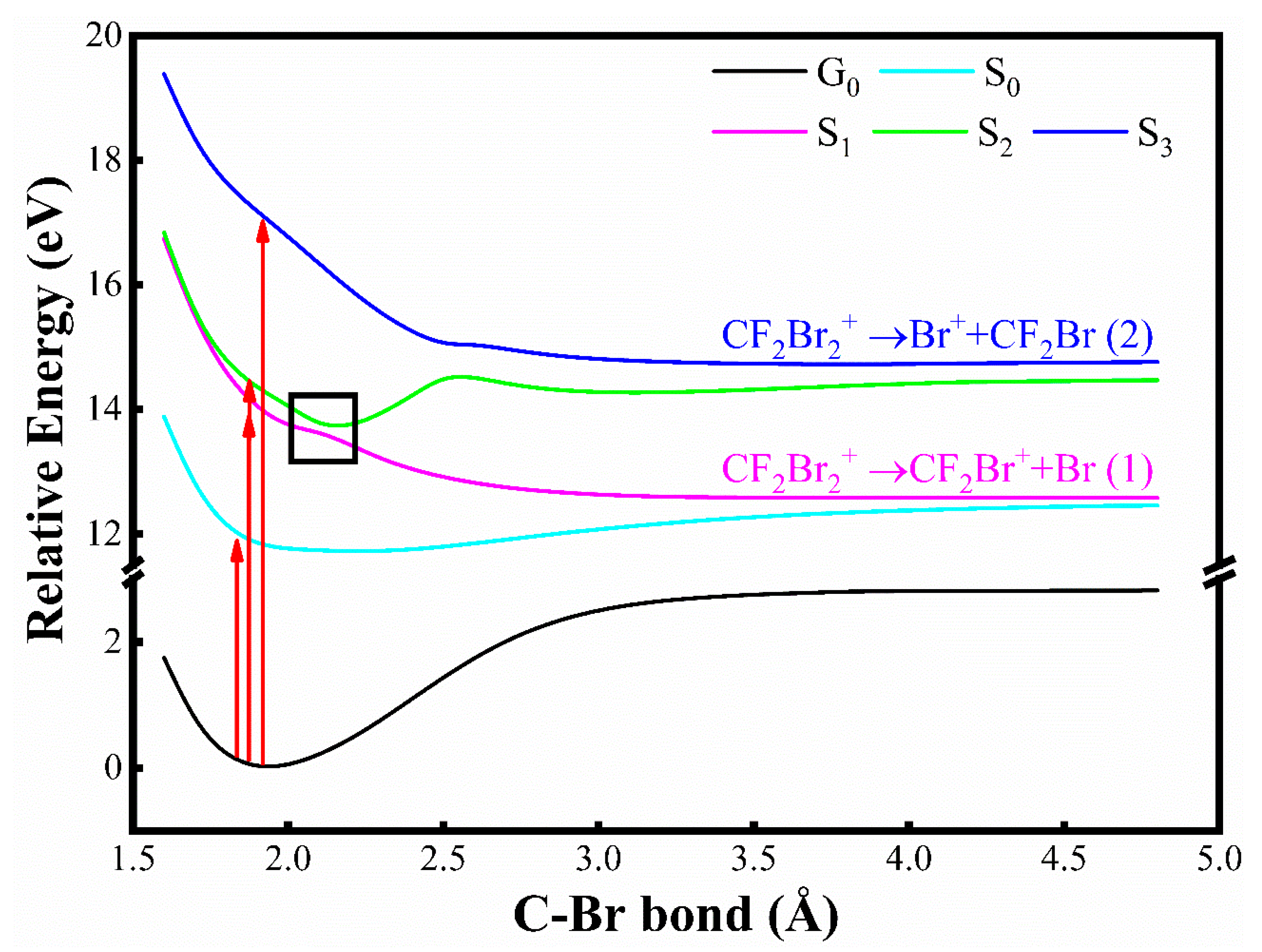
| Channel | Reaction Path | * EAP(eV) |
|---|---|---|
| (1) | , | 11.19 |
| (2) | , | 15.85 |
| (3) | , | 15.61 |
| Channel | EK (eV) | ET (eV) | EAV (eV) |
|---|---|---|---|
| (1) | 0.01 | 0.03 | 1.21 |
| (2) | 0.13 | 0.21 | 1.20 |
| (3) | 0.11 | 0.14 | 1.44 |
| C-Br(4) | C-Br(5) | Br-Br * | ∠Br-C-Br | |
|---|---|---|---|---|
| CF2Br2 | 1.96 | 1.96 | 3.24 | 112.0 |
| CF2Br2+ | 1.99 | 1.99 | 2.86 | 92.0 |
| TS1 | 2.57 | 2.57 | 2.30 | 53.2 |
| TS2 | 2.62 | 2.62 | 2.34 | 53.5 |
| IS | 2.28 | 3.45 | 2.32 | 41.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Li, Z.; Sun, H.; Sun, Z.; Yang, Y. Dissociative Ionization of Molecular CF2Br2 under 800 and 400 nm Intense Femtosecond Laser Fields. Appl. Sci. 2021, 11, 1704. https://doi.org/10.3390/app11041704
Liu B, Li Z, Sun H, Sun Z, Yang Y. Dissociative Ionization of Molecular CF2Br2 under 800 and 400 nm Intense Femtosecond Laser Fields. Applied Sciences. 2021; 11(4):1704. https://doi.org/10.3390/app11041704
Chicago/Turabian StyleLiu, Botong, Zhipeng Li, Haitao Sun, Zhenrong Sun, and Yan Yang. 2021. "Dissociative Ionization of Molecular CF2Br2 under 800 and 400 nm Intense Femtosecond Laser Fields" Applied Sciences 11, no. 4: 1704. https://doi.org/10.3390/app11041704
APA StyleLiu, B., Li, Z., Sun, H., Sun, Z., & Yang, Y. (2021). Dissociative Ionization of Molecular CF2Br2 under 800 and 400 nm Intense Femtosecond Laser Fields. Applied Sciences, 11(4), 1704. https://doi.org/10.3390/app11041704





