Statistical Tolerance Analysis of 3D-Printed Non-Assembly Mechanisms in Motion Using Empirical Predictive Models
Abstract
:1. Introduction and Motivation
2. State-of-the-Art and Related Work
2.1. Tolerance Analysis of Systems in Motion Considering Joint Clearance and Geometric Deviations
2.2. Geometric Part Deviations in FDM
2.3. Investigating Geometric Part Deviations in FDM Using Empirical Predictive Models
2.4. Discussion of the State-of-the-Art
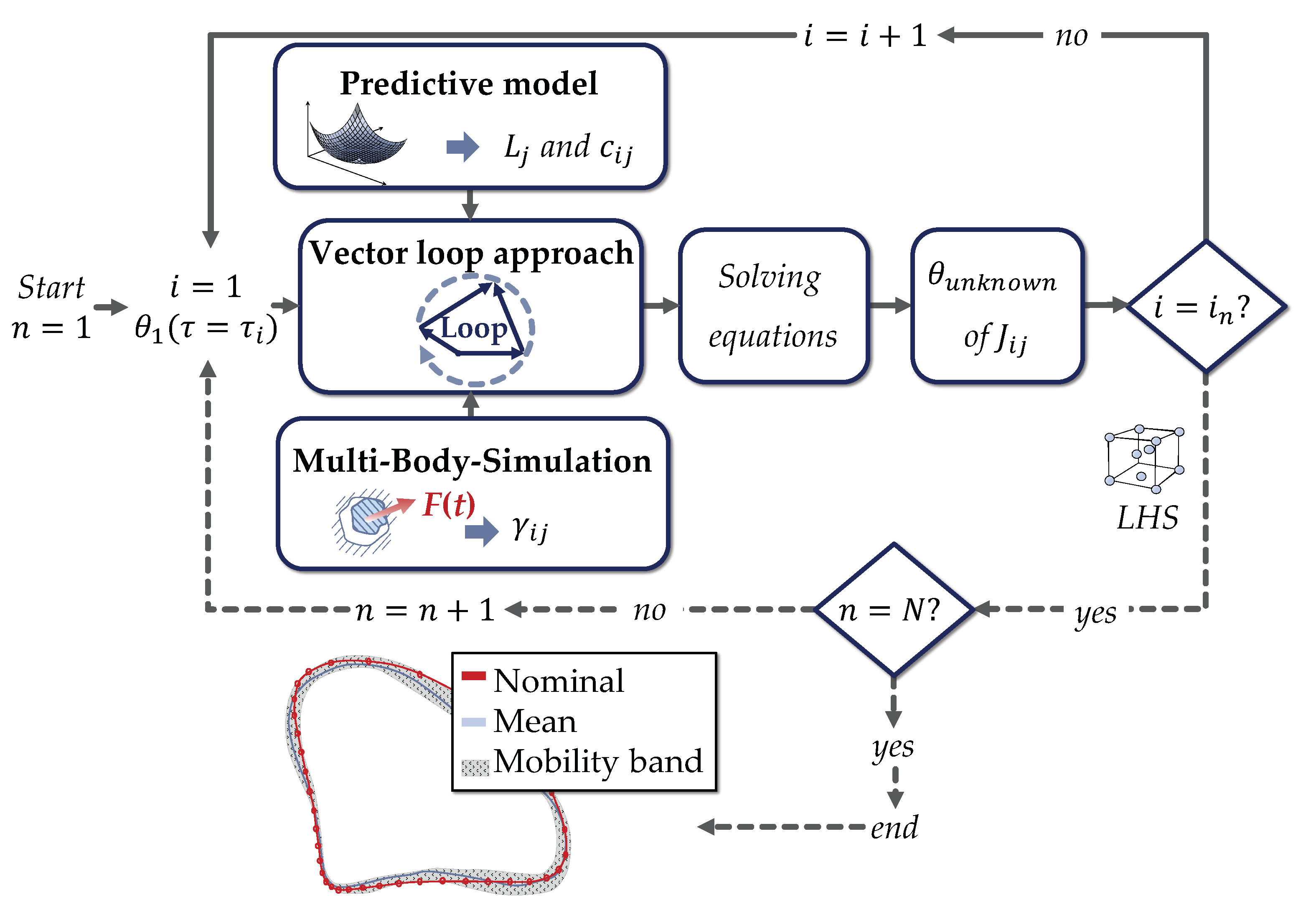
3. Statistical Tolerance Analysis of 3D Printed Non-Assembly Mechanisms in Motion
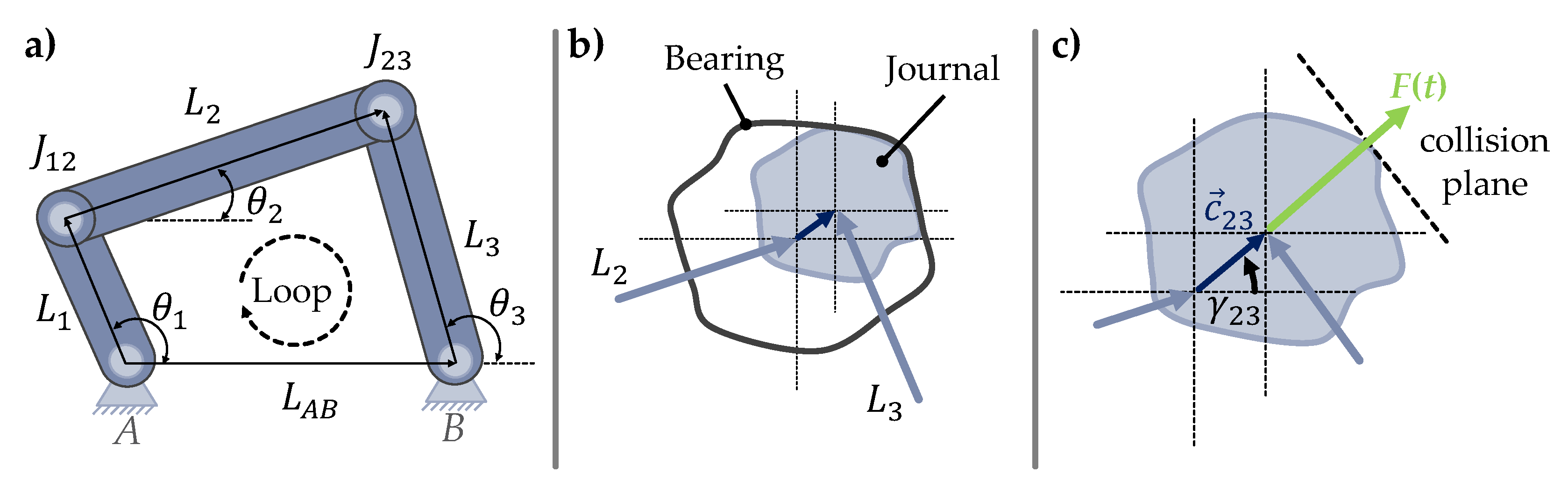
3.1. Tolerance Analysis of Systems in Motion Considering Joint Clearance
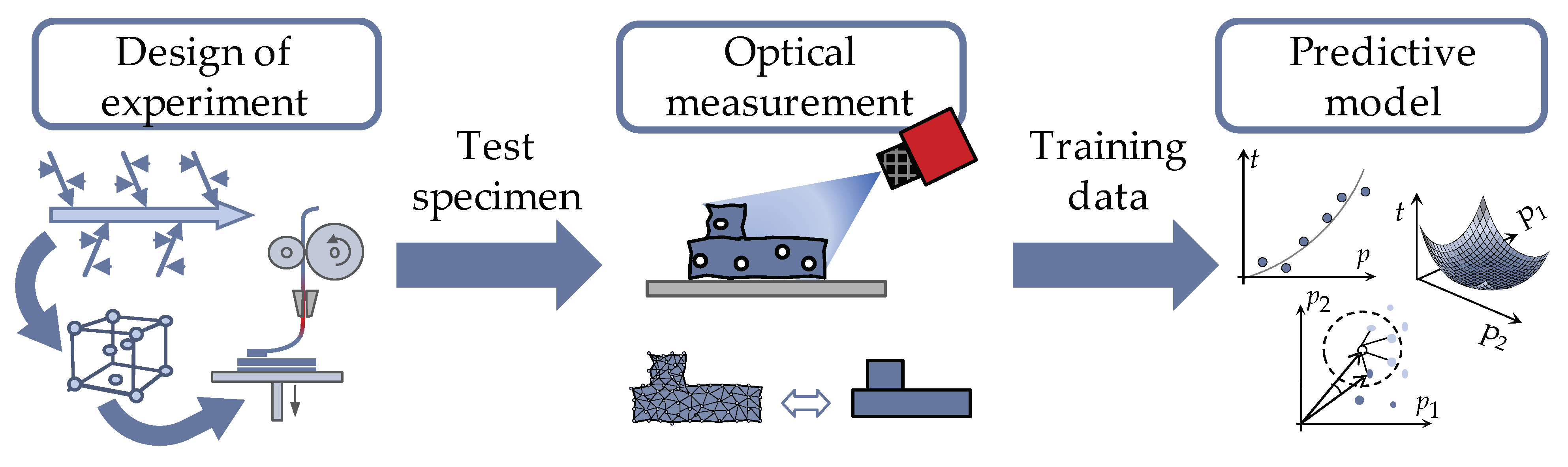
3.2. Determination of Geometric Part Deviations Using Empirical Predictive Models
3.3. Sampling Technique
4. Application
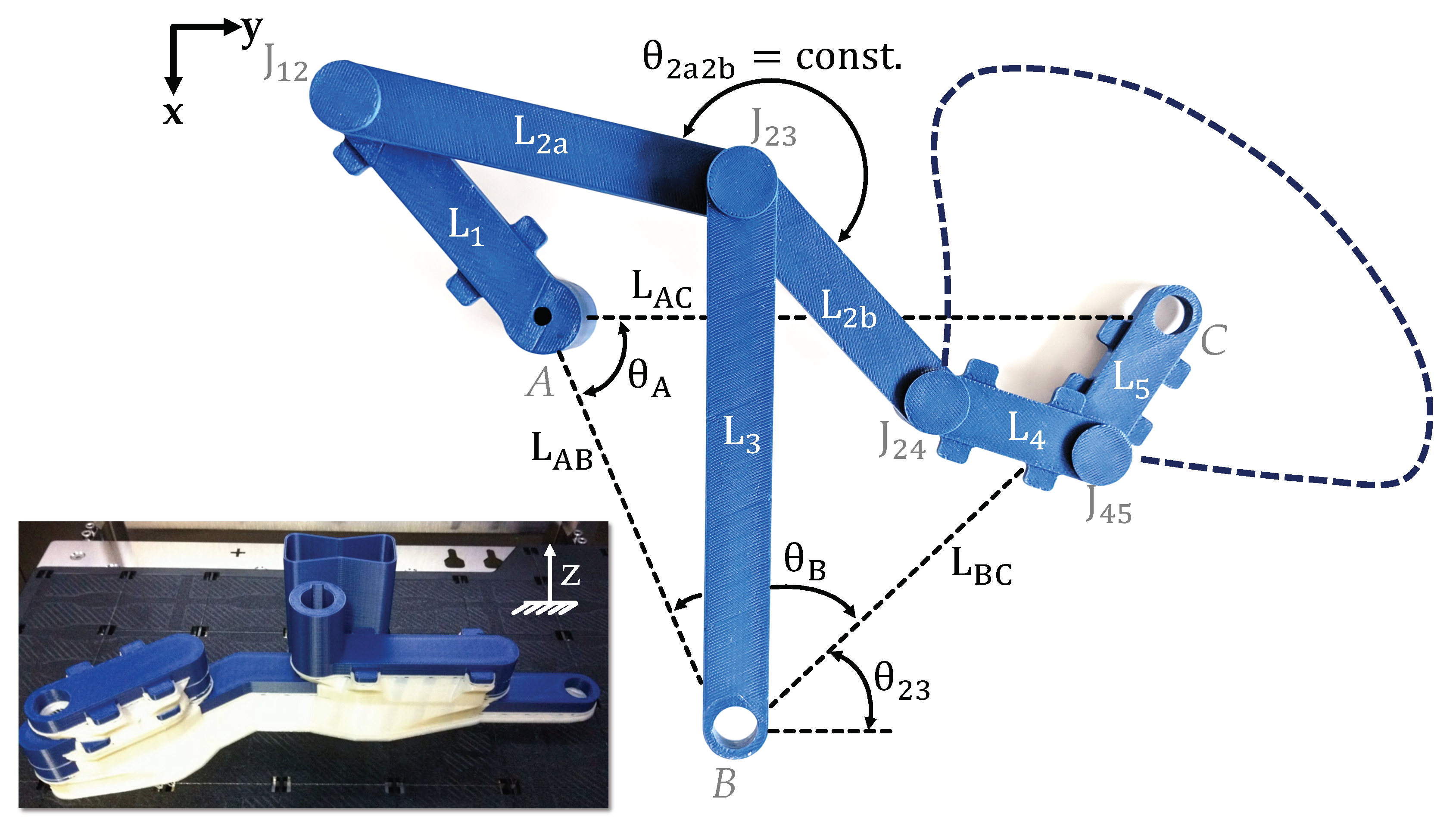
4.1. Presentation of the Case Study
4.2. Tolerance Analysis Model
4.3. Empirical Predictive Models
4.4. Results of the Tolerance Analysis
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile-butadiene-styrene |
| AM | Additive Manufacturing |
| CoP | Coefficient of prognosis |
| DoE | Design of experiment |
| DoF | Degree of Freedom |
| FDM | Fused Deposition modelling |
| FKC | Functional key characteristic |
| MBS | Multi-body-simulation |
| ML | Machine learning |
| SLA | Stereolithography |
| SLM | Selective Laser Melting |
References
- Wohlers, T.; Campbell, R.I.; Diegel, O.; Huff, R.; Kowen, J. Wohlers Report 2020: 3D Printing and Additive Manufacturing State of the Industry; Wohlers Associates: Fort Collins, CO, USA, 2020. [Google Scholar]
- Cuellar, J.S.; Smit, G.; Zadpoor, A.A.; Breedveld, P. Ten guidelines for the design of non-assembly mechanisms: The case of 3d-printed prosthetic hands. Proc. Inst. Mech. Eng. H 2018, 232, 962–971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Culmone, C.; Henselmans, P.W.J.; van Starkenburg, R.I.B.; Breedveld, P. Exploring non-assembly 3d printing for novel compliant surgical devices. PLoS ONE 2020, 15, e0232952. [Google Scholar] [CrossRef] [PubMed]
- Mavroidis, C.; DeLaurentis, K.J.; Won, J.; Alam, M. Fabrication of non-assembly mechanisms and robotic systems using rapid prototyping. J. Mech. 2001, 123, 516–524. [Google Scholar] [CrossRef]
- Zhu, Z.; Anwer, N.; Mathieu, L. Shape transformation perspective for geometric deviation modelling in additive manufacturing. Procedia CIRP 2018, 75, 75–80. [Google Scholar] [CrossRef]
- Schleich, B.; Wartzack, S. A quantitative comparison of tolerance analysis approaches for rigid mechanical assemblies. Procedia CIRP 2016, 43, 172–177. [Google Scholar] [CrossRef] [Green Version]
- Walter, M.; Sprügel, T.; Wartzack, S. Tolerance analysis of systems in motion taking into account interactions between deviations. Proc. Inst. Mech. Eng. Part B J. Eng. 2013, 227, 709–719. [Google Scholar] [CrossRef] [Green Version]
- Hallmann, M.; Schleich, B.; Wartzack, S. Erarbeitung von Gestaltungsrichtlinien für die Konstruktion additiv gefertigter Mechanismen. In Konstruktion für die Additive Fertigung 2018; Lachmayer, R., Lippert, R.B., Kaierle, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 22, pp. 129–143. [Google Scholar] [CrossRef]
- Stuppy, J.; Meerkamm, H. Tolerance analysis of mechanisms taking into account joints with clearance and elastic deformations. In Proceedings of the Design Society: International Conference on Engineering Design, Palo Alto, CA, USA, 24–27 August 2009; pp. 488–500. [Google Scholar]
- Polini, W. To model joints with clearance for tolerance analysis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 1689–1700. [Google Scholar] [CrossRef]
- Schaechtl, P.; Hallmann, M.; Schleich, B.; Wartzack, S. Tolerance analysis of additively manufactured non-assembly mechanisms considering joint clearance. Procedia CIRP 2020, 92, 27–32. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J. Revolute joints with clearance in multibody systems. Comput. Struct. 2004, 82, 1359–1369. [Google Scholar] [CrossRef] [Green Version]
- Lankarani, H.M.; Nikravesh, P. Continuous contact models for impact analysis in multibody systems. Nonlinear Dyn. 1994, 5, 193–207. [Google Scholar]
- Rhyu, J.H.; Kwak, B.M. Optimal stochastic design of four-bar mechanisms for tolerance and clearance. J. Mech. Trans. 1988, 110, 255–262. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modelling process parameters for dimensional accuracy using i-optimality criterion. Measurement 2016, 81, 174–196. [Google Scholar] [CrossRef]
- Wang, T.M.; Xi, J.T.; Jin, Y. A model research for prototype warp deformation in the fdm process. Int. Adv. Manuf. Technol. 2007, 33, 1087–1096. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Improving dimensional accuracy of fused deposition modelling processed part using grey taguchi method. Mater. Des. 2009, 30, 4243–4252. [Google Scholar] [CrossRef]
- Bakar, N.S.A.; Alkahari, M.R.; Boejang, H. Analysis on fused deposition modelling performance. J. Zhejiang-Univ.-Sci. A 2010, 11, 972–977. [Google Scholar] [CrossRef]
- Peng, A.; Xiao, X.; Yue, R. Process parameter optimization for fused deposition modelling using response surface methodology combined with fuzzy inference system. Int. J. Adv. Manuf. Technol. 2014, 73, 87–100. [Google Scholar] [CrossRef]
- Deswal, S.; Narang, R.; Chhabra, D. modelling and parametric optimization of fdm 3d printing process using hybrid techniques for enhancing dimensional preciseness. Int. J. Interact. Des. Manuf. (IJIDeM) 2019, 13, 1197–1214. [Google Scholar] [CrossRef]
- Sheoran, A.J.; Kumar, H. Fused deposition modelling process parameters optimization and effect on mechanical properties and part quality: Review and reflection on present research. Mater. Today Proc. 2020, 21, 1659–1672. [Google Scholar] [CrossRef]
- Mahmood, S.; Qureshi, A.J.; Talamona, D. Taguchi based process optimization for dimension and tolerance control for fused deposition modelling. Addit. Manuf. 2018, 21, 183–190. [Google Scholar] [CrossRef]
- Weichert, D.; Link, P.; Stoll, A.; Rüping, S.; Ihlenfeldt, S.; Wrobel, S. A review of machine learning for the optimization of production processes. Int. J. Adv. Manuf. Technol. 2019, 104, 1889–1902. [Google Scholar] [CrossRef]
- Denkena, B.; Dittrich, M.A.; Uhlich, F. Self-optimizing cutting process using learning process models. Procedia Technol. 2016, 26, 221–226. [Google Scholar] [CrossRef]
- Gupta, A.K.; Guntuku, S.C.; Desu, R.K.; Balu, A. Optimisation of turning parameters by integrating genetic algorithm with support vector regression and artificial neural networks. Int. J. Adv. Manuf. Technol. 2015, 77, 331–339. [Google Scholar] [CrossRef]
- Razvi, S.S.; Feng, S.; Narayanan, A.; Lee, Y.T.T.; Witherell, P. A review of machine learning applications in additive manufacturing. In Proceedings of the 39th Computers and Information in Engineering Conference, American Society of Mechanical Engineers, Anaheim, CA, USA, 18–21 August 2019; Volume 1. [Google Scholar] [CrossRef]
- Huang, Q.; Nouri, H.; Xu, K.; Chen, Y.; Sosina, S.; Dasgupta, T. Predictive modelling of geometric deviations of 3d printed products—A unified modelling approach for cylindrical and polygon shapes. In Proceedings of the 2014 IEEE International Conference on Automation Science and Engineering (CASE), Taipei, Taiwan, 18–22 August 2014; pp. 25–30. [Google Scholar] [CrossRef]
- Sahu, R.K.; Mahapatra, S.S.; Sood, A.K. A study on dimensional accuracy of fused deposition modelling (FDM) processed parts using fuzzy logic. J. Manuf. Sci. Prod. 2013, 13, 183. [Google Scholar] [CrossRef]
- Moroni, G.; Petrò, S.; Polini, W. Geometrical product specification and verification in additive manufacturing. Procedia CIRP 2017, 66, 157–160. [Google Scholar] [CrossRef]
- Noriega, A.; Blanco, D.; Alvarez, B.J.; Garcia, A. Dimensional accuracy improvement of FDM square cross-section parts using artificial neural networks and an optimization algorithm. Int. J. Adv. Manuf. Technol. 2013, 69, 2301–2313. [Google Scholar] [CrossRef]
- Lieneke, T.; Denzer, V.; Adam, G.A.; Zimmer, D. Dimensional tolerances for additive manufacturing: Experimental investigation for fused deposition modelling. Procedia CIRP 2016, 43, 286–291. [Google Scholar] [CrossRef] [Green Version]
- Heling, B.; Oberleiter, T.; Rohrmoser, A.; Kiener, C.; Schleich, B.; Hagenah, H.; Merklein, M.; Willner, K.; Wartzack, S. A concept for process-oriented interdisciplinary tolerance management considering production-specific deviations. Proc. Des. Soc. Int. Conf. Eng. Des. 2019, 1, 3441–3450. [Google Scholar] [CrossRef] [Green Version]
- Erkaya, S.; Uzmay, I. Investigation on effect of joint clearance on dynamics of four-bar mechanism. Nonlinear Dyn. 2009, 58, 179–198. [Google Scholar] [CrossRef]
- Gössner, S. Mechanismentechnik: Vektorielle Analyse Ebener Mechanismen, 3rd ed.; Logos Verlag: Berlin, Germany, 2017. [Google Scholar]
- Polini, W. Geometric Tolerance Analysis. In Geometric Tolerances; Colosimo, B., Senin, N., Eds.; Springer: London, UK, 2011. [Google Scholar] [CrossRef]
- Qi, X.; Chen, G.; Li, Y.; Cheng, X.; Li, C. Applying neural-network-based machine learning to additive manufacturing: Current applications, challenges, and future perspectives. Engineering 2019, 5, 721–729. [Google Scholar] [CrossRef]
- Most, T.; Will, J. Sensitivity analysis using the metamodel of optimal prognosis. In Proceedings Weimarer Optimierungs- und Stochastiktage 8.0; Dynardo: Weimar, Germany, 2011. [Google Scholar]
- Hallmann, M.; Schleich, B.; Wartzack, S. From tolerance allocation to tolerance-cost optimization: A comprehensive literature review. Int. J. Adv. Manuf. Technol. 2020, 107, 4859–4912. [Google Scholar] [CrossRef]
- Hallmann, M.; Schleich, B.; Heling, B.; Aschenbrenner, A.; Wartzack, S. Comparison of different methods for scrap rate estimation in sampling-based tolerance-cost-optimization. Procedia CIRP 2018, 75, 51–56. [Google Scholar] [CrossRef]
- Thornton, A.C. A mathematical framework for the key characteristic process. Res. Eng. Des. 1999, 11, 145–157. [Google Scholar] [CrossRef]
- Taguchi, G.; Chowdhury, S.; Wu, Y.; Taguchi, S.; Yano, H. Taguchi’s Quality Engineering Handbook; John Wiley, & Sons: Hoboken, NI, USA; ASI Consulting Group: Livonia, MI, USA, 2005. [Google Scholar]
- Hain, K. Getriebespiel-Atlas: Eine Zusammenstellung Ungleichförmig übersetzender Getriebe für den Konstrukteur; VDI-Verlag: Düsseldorf, Germany, 1973. [Google Scholar]
- Alafaghani, A.; Qattawi, A. Investigating the effect of fused deposition modelling processing parameters using taguchi design of experiment method. J. Manuf. Process. 2018, 36, 164–174. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. arXiv 2015, arXiv:1506.02142. [Google Scholar]
- Schleich, B.; Wartzack, S. Tolerance analysis of rotating mechanism based on skin model shapes in discrete geometry. Procedia CIRP 2015, 27, 10–15. [Google Scholar] [CrossRef] [Green Version]
- Ahlers, D.; Wasserfall, F.; Hendrich, N.; Zhang, J. 3D printing of nonplanar layers for smooth surface generation. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019. [Google Scholar] [CrossRef]
- Wasserfall, F.; Hendrich, N.; Zhang, J. Adaptive slicing for the FDM process revisited. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017; pp. 49–54. [Google Scholar] [CrossRef]



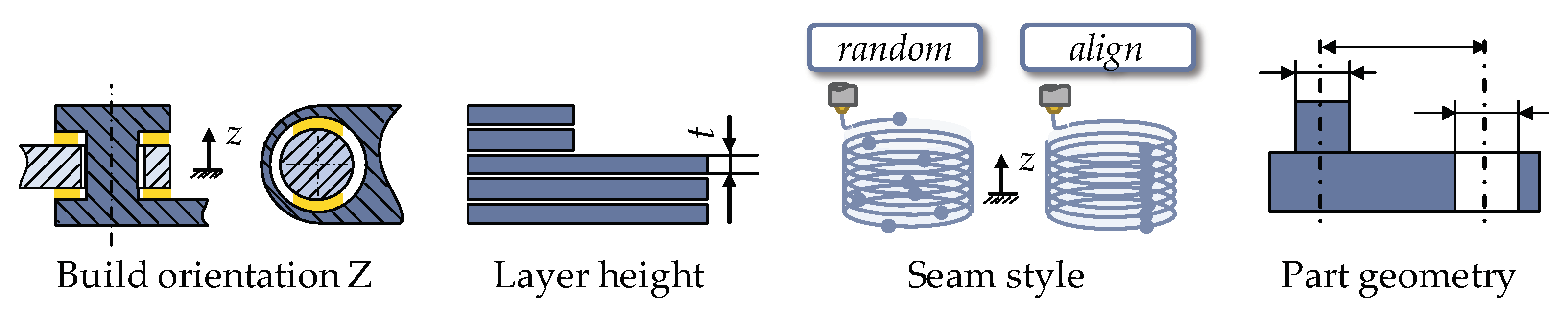

| Definition | Design Parameter | Nominal Value |
|---|---|---|
| Linkage 1 | 81 mm | |
| Linkage 2a | 116 mm | |
| Linkage 2b | 87 mm | |
| Linkage 3 | 161 mm | |
| Linkage 4 | 60 mm | |
| Linkage 5 | 53 mm | |
| Linkage AC | 203.5 mm | |
| Angle | 215° | |
| Radial clearance | 0.4 mm | |
| Planar clearance | 0.2540 mm |
| Parameters | Factor Levels |
|---|---|
| Layer height | 0.1778 mm; 0.2540 mm |
| Seam style | align; random |
| Build orientation Z-direction | 0°; 90° |
| Linkage length | 53 mm; 87 mm; 161 mm |
| Empirical Predictive Model | CoP Value | RMSE Value [mm] |
|---|---|---|
| SVM Joint clearance | 0.9216 | 0.0356 |
| GP Joint clearance | 0.9183 | 0.0362 |
| SVM Tolerance value | 0.8906 | 0.0666 |
| GP Tolerance value | 0.8926 | 0.0653 |
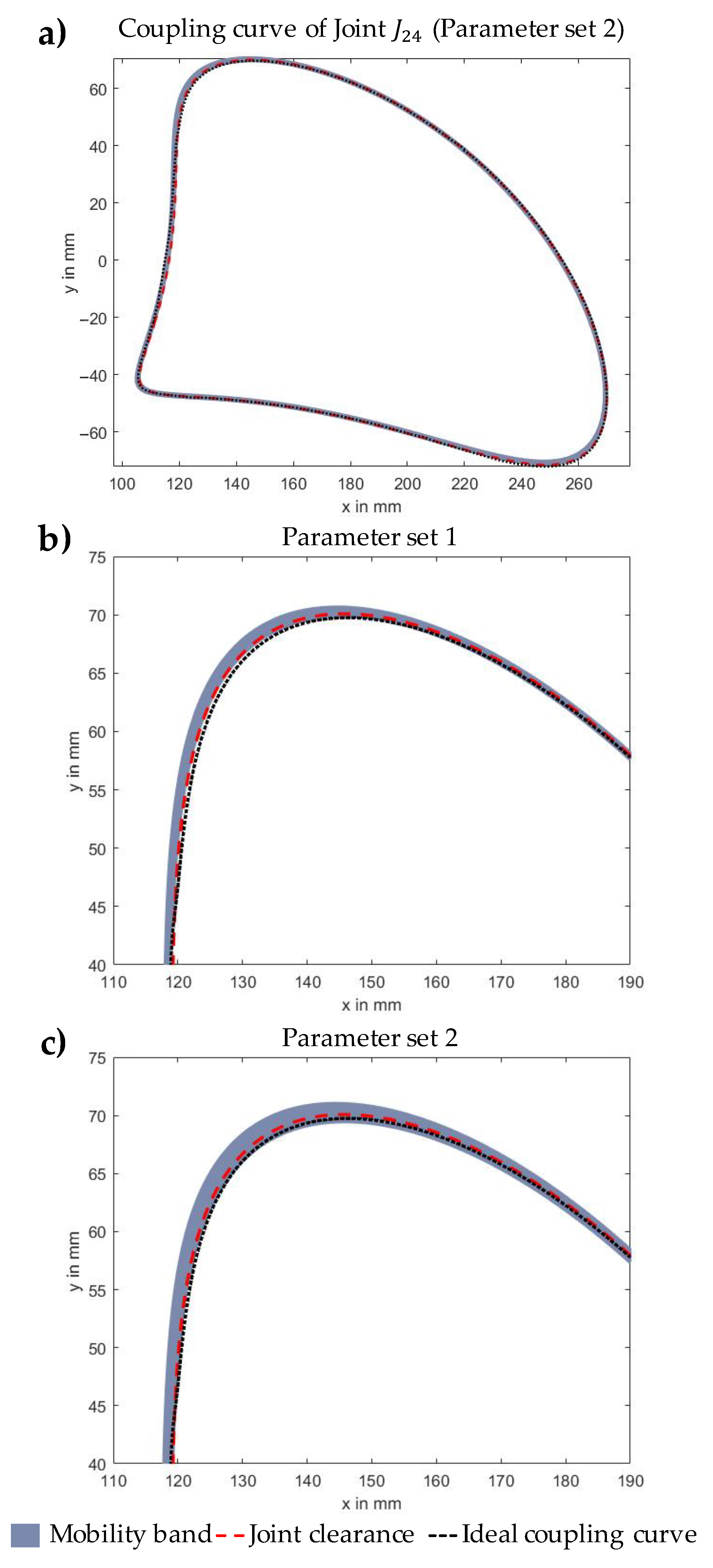
| Parameter Set 1 | Parameter Set 2 | |
|---|---|---|
| Layer height | 0.1778 mm | 0.2540 mm |
| Build orientation Z | 0° | 90° |
| Seam Style | random | align |
| Parameter Set 1 | Parameter Set 2 | |
|---|---|---|
| Predicted tolerance | 0.36 mm | 0.47 mm |
| Predicted deviation of clearance c | 0.04 mm | 0.14 mm |
| Deviation FKC | 2.21 mm | 2.58 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schaechtl, P.; Schleich, B.; Wartzack, S. Statistical Tolerance Analysis of 3D-Printed Non-Assembly Mechanisms in Motion Using Empirical Predictive Models. Appl. Sci. 2021, 11, 1860. https://doi.org/10.3390/app11041860
Schaechtl P, Schleich B, Wartzack S. Statistical Tolerance Analysis of 3D-Printed Non-Assembly Mechanisms in Motion Using Empirical Predictive Models. Applied Sciences. 2021; 11(4):1860. https://doi.org/10.3390/app11041860
Chicago/Turabian StyleSchaechtl, Paul, Benjamin Schleich, and Sandro Wartzack. 2021. "Statistical Tolerance Analysis of 3D-Printed Non-Assembly Mechanisms in Motion Using Empirical Predictive Models" Applied Sciences 11, no. 4: 1860. https://doi.org/10.3390/app11041860
APA StyleSchaechtl, P., Schleich, B., & Wartzack, S. (2021). Statistical Tolerance Analysis of 3D-Printed Non-Assembly Mechanisms in Motion Using Empirical Predictive Models. Applied Sciences, 11(4), 1860. https://doi.org/10.3390/app11041860






