Uncertainty Representation of Natural Frequency for Laminated Composite Cylindrical Shells Considering Probabilistic and Interval Variables
Abstract
1. Introduction
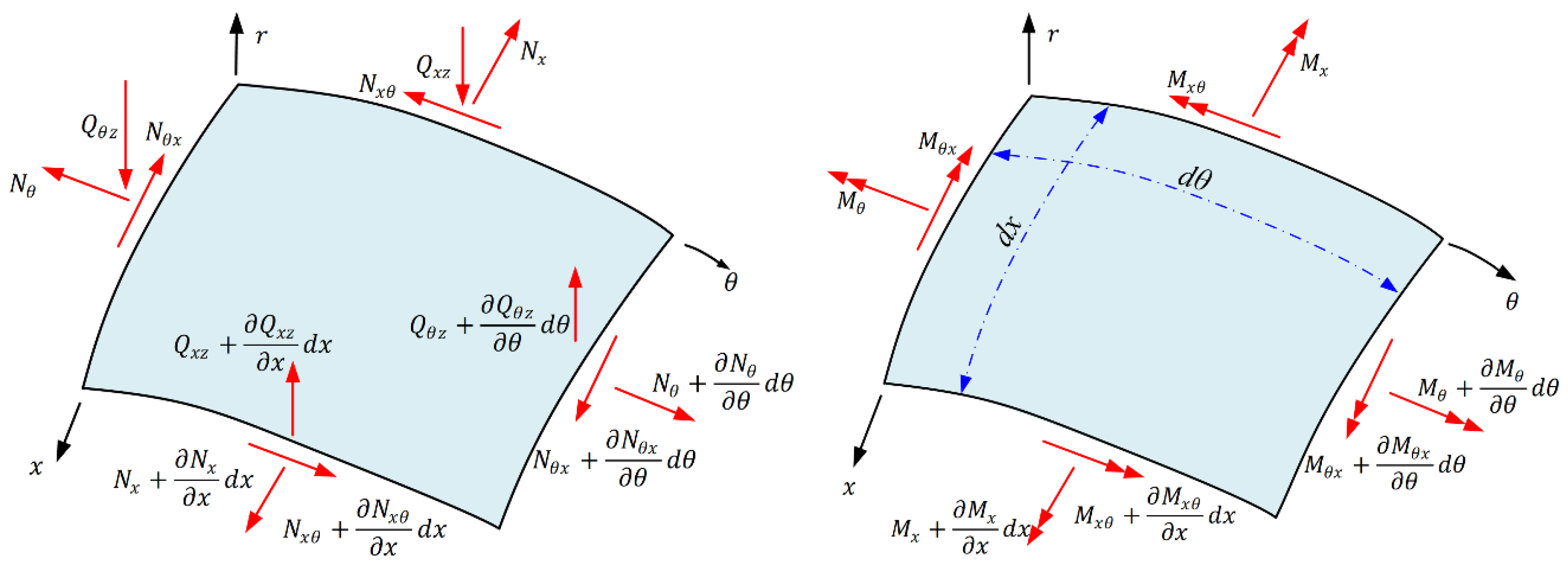
2. Problem Description
3. Interval and Probabilistic Variables Conversion Based on the Four Statistical Moments Method
4. Construction of Accurate Kriging Model Based on Prediction Interval Criterion
4.1. The Basic Principle of Kriging Model
4.2. The Proposed Improved Kriging Model
5. Uncertainty Measurement of Natural Frequency
6. Numerical Examples
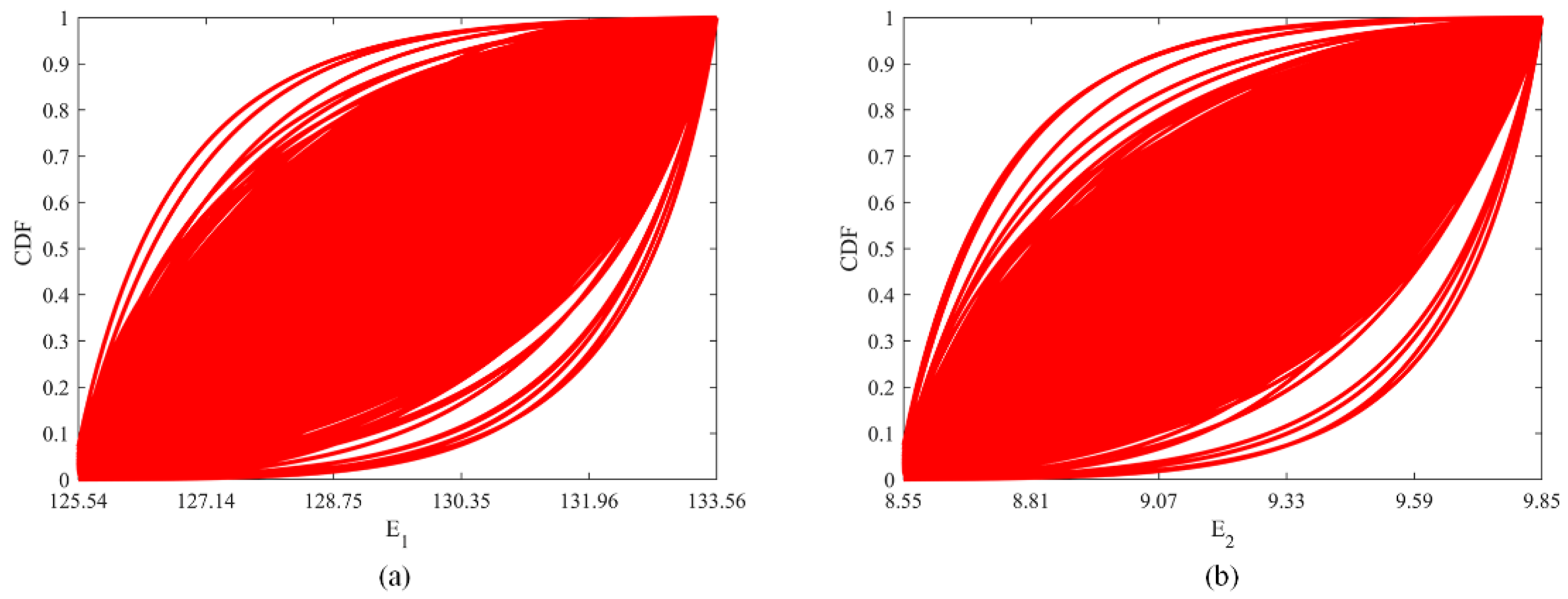
6.1. Construction of Accurate Kriging Model
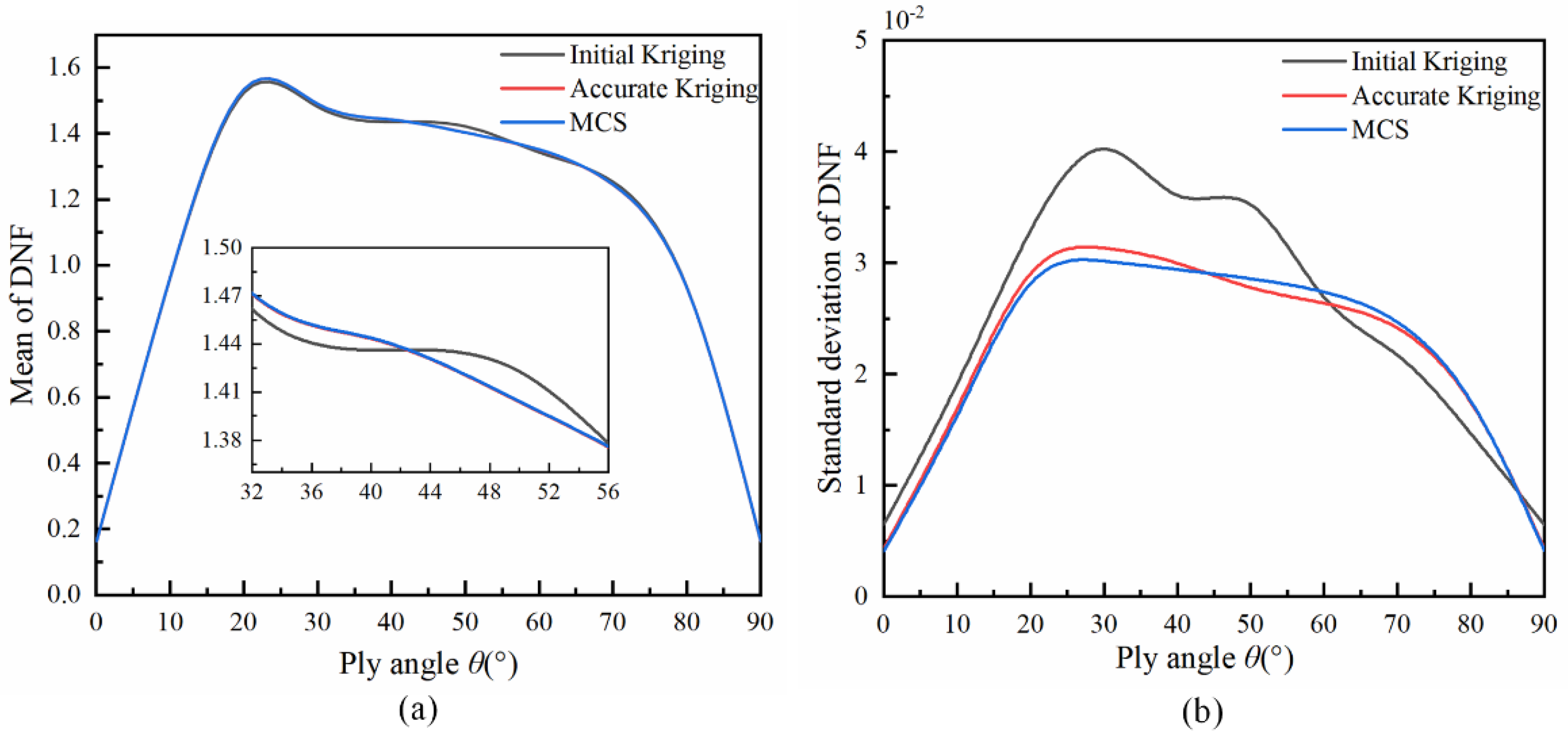
6.2. Three-Layer Laminated Composite Cylindrical Shells
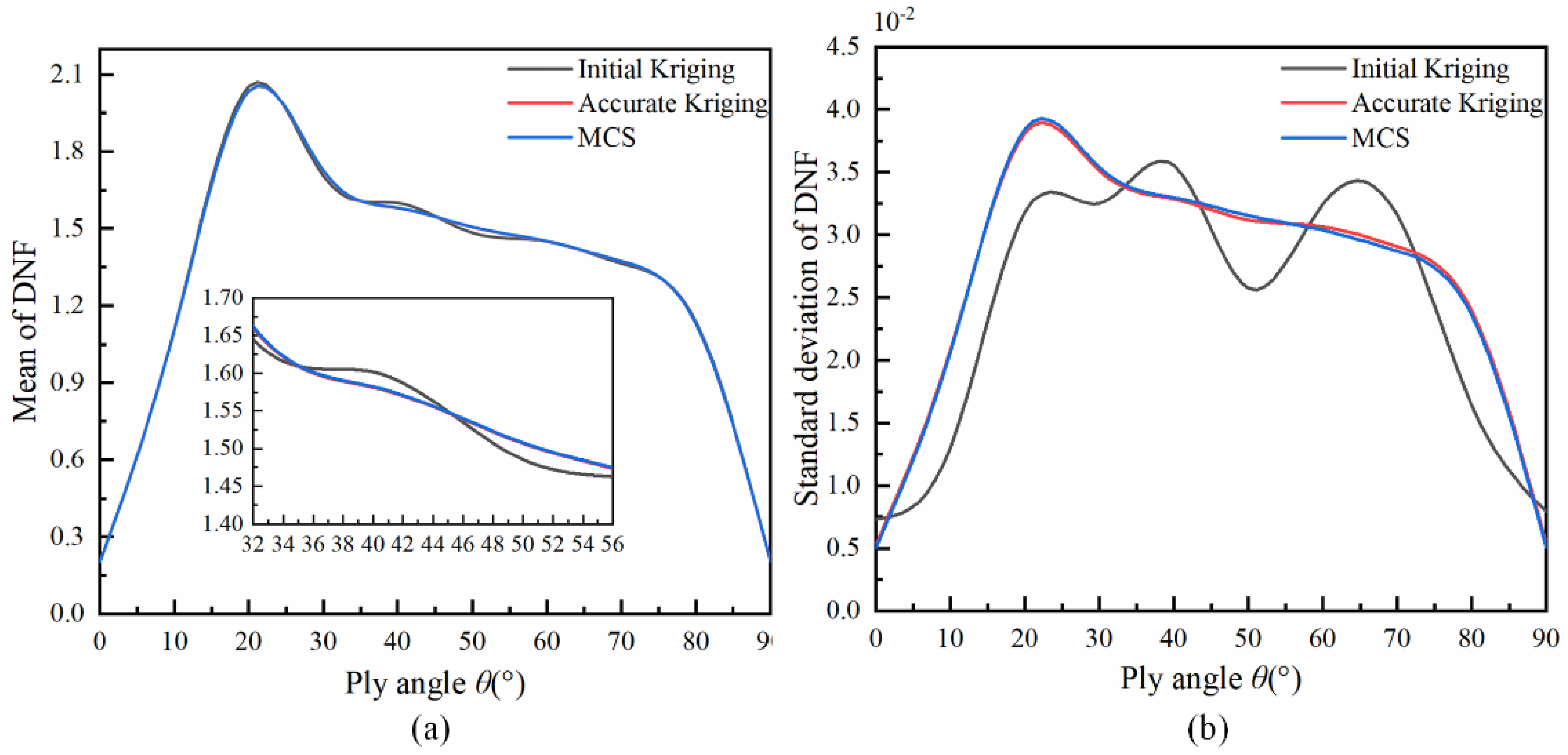
6.3. Five-Layer and Seven-Layer Laminated Composite Cylindrical Shells
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alankaya, V.; Alarcin, F. Using sandwich composite shells for fully pressurized tanks on liquefied petroleum gas carriers. Stroj. Vestn. J. Mech. Eng. 2016, 62, 32–40. [Google Scholar] [CrossRef]
- Cao, X.T.; Ma, C.; Hua, H.X. Acoustic radiation from thick laminated cylindrical shells with sparse cross stiffeners. J. Vib. Acoust. 2013, 135, 031009. [Google Scholar] [CrossRef]
- Qi, H.; Qin, S.K.; Cheng, Z.C.; Teng, Q.; Hong, T.; Yi, X. Towards understanding performance enhancing mechanism of micro-holes on K9 glasses using ultrasonic vibration-assisted abrasive slurry jet. J. Manuf. Process. 2021, in press. [Google Scholar]
- Lam, K.Y.; Qian, W. Free vibration of symmetric angle-ply thick laminated composite cylindrical shells. Compos. Part B Eng. 2000, 31, 145–154. [Google Scholar] [CrossRef]
- Liu, C.C.; Li, F.M.; Huang, W.H. Transient wave propagation and early short time transient responses of laminated composite cylindrical shells. Compos. Struct. 2011, 93, 2587–2597. [Google Scholar] [CrossRef]
- Tomar, S.S.; Zafar, S.; Talha, M.; Gao, W.; Hui, D. State of the art of composite structures in non-deterministic framework: A review. Thin Walled Struct. 2018, 132, 700–716. [Google Scholar] [CrossRef]
- Tan, D.P.; Li, L.; Zhu, Y.L.; Zheng, S.; Yin, Z.C.; Li, D.F. Critical penetration condition and Ekman suction-extraction mechanism of sink vortex. J. Zhejiang Univ. Sci. A 2019, 20, 61–72. [Google Scholar] [CrossRef]
- Peng, X.; Guo, Y.L.; Qiu, C.; Wu, H.P.; Li, J.Q.; Chen, G.H.; Jiang, S.F.; Liu, Z.Y. Reliability optimization design for composite laminated plate considering multiple types of uncertain parameters. Eng. Optimi. 2021, 53, 221–236. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Z.Y.; Tang, M.Y.; Tan, J.R. Robust optimization of uncertain structures based on normalized violation degree of interval constraint. Comput. Struct. 2017, 182, 41–54. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Alvarez, D.A.; Paredes, J.A. Interval reliability analysis under the specification of statistical information on the input variables. Struct. Saf. 2017, 65, 35–48. [Google Scholar] [CrossRef]
- Ben-Haim, Y. A non-probabilistic concept of reliability. Struct. Saf. 1994, 14, 227–245. [Google Scholar] [CrossRef]
- Ni, B.Y.; Jiang, C.; Huang, Z.L. Discussions on non-probabilistic convex modelling for uncertain problems. Appl. Math. Model. 2018, 59, 54–85. [Google Scholar] [CrossRef]
- Shao, S.T.; Zhang, X.H.; Li, Y.; Bo, C.X. Probabilistic single-valued (interval) neutrosophic hesitant fuzzy set and its application in multi-attribute decision making. Symmetry 2018, 10, 419. [Google Scholar] [CrossRef]
- Li, L.; Qi, H.; Yin, Z.C.; Li, D.F.; Zhu, Z.L.; Viboon, T.; Tan, D.P. Investigation on the multiphase sink vortex Ekman pumping effects by CFD-DEM coupling method. Powder Technol. 2020, 360, 462–480. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.Q.; He, Y.Y. Fuzzy interval perturbation method for uncertain heat conduction problem with interval and fuzzy parameters. Int. J. Numer. Methods Eng. 2015, 104, 330–346. [Google Scholar] [CrossRef]
- Zhou, C.C.; Tang, C.H.; Liu, F.C.; Wang, W.X. A probabilistic representation method for interval uncertainty. Int. J. Comp. Meth. Sing. 2018, 15, 1850038. [Google Scholar] [CrossRef]
- Zaman, K.; Rangavajhala, S.; McDonald, M.P.; Mahadevan, S. A probabilistic approach for representation of interval uncertainty. Reliab. Eng. Syst. Saf. 2011, 96, 117–130. [Google Scholar] [CrossRef]
- Peng, X.; Gao, Q.L.; Li, J.Q.; Liu, Z.Y.; Yi, B.; Jian, S.F. Probabilistic representation approach for multiple types of epistemic uncertainties based on cubic normal transformation. Appl. Sci. 2020, 10, 4698. [Google Scholar] [CrossRef]
- Li, L.; Lu, J.F.; Fang, H.; Yin, Z.C.; Wang, T.; Wang, R.H.; Fan, X.H.; Zhao, L.J.; Tan, D.P.; Wan, Y.H. Lattice Boltzmann method for fluid-thermal systems: Status, hotspots, trends and outlook. IEEE Access 2020, 8, 27649–27675. [Google Scholar] [CrossRef]
- Lu, J.F.; Wang, T.; Li, L.; Yin, Z.C.; Wang, R.H.; Fan, X.H.; Tan, D.P. Dynamic characteristics and wall effects of bubble bursting in gas-liquid-solid three-phase particle flow. Processes 2020, 8, 760. [Google Scholar] [CrossRef]
- Peng, X.; Li, D.H.; Wu, H.P.; Liu, Z.Y.; Li, J.Q.; Jiang, S.F.; Tan, J.R. Uncertainty analysis of composite laminated plate with data-driven polynomial chaos expansion method under insufficient input data of uncertain parameters. Comput. Struct. 2019, 209, 625–633. [Google Scholar] [CrossRef]
- Yin, Z.C.; Lu, J.F.; Li, L.; Wang, T.; Wang, R.H.; Fan, X.H.; Lin, H.K.; Huang, Y.S.; Tan, D.P. Optimized scheme for accelerating the slagging reaction and slag-metal-gas emulsification in a basic oxygen furnace. Appl. Sci. 2020, 10, 5101. [Google Scholar] [CrossRef]
- Hu, X.X.; Xu, F.; Wang, R.H.; Tan, D.P. Synchronous sampling-based direct current estimation method for self-sensing active magnetic bearings. Sensors 2020, 20, 3497. [Google Scholar] [CrossRef]
- Ma, P.; Zhou, P.C.; Shang, X.B.; Yang, M. Firing accuracy evaluation of electromagnetic railgun based on multicriteria optimal Latin hypercube design. IEEE Trans. Plasma Sci. 2017, 45, 1503–1511. [Google Scholar] [CrossRef]
- Wang, J.X.; Tan, D.P.; Cao, B.; Fan, J.; Deep, S. An independent path-based process recommendation algorithm for improving biomedical process modeling. Electron. Lett. 2020, 56, 531–533. [Google Scholar] [CrossRef]
- Wang, J.X.; Cao, B.; Zheng, X.; Tan, D.P.; Fan, J. Detecting difference between process models using edge network. IEEE Access 2019, 7, 142916–142925. [Google Scholar] [CrossRef]
- Buyukada, M. Probabilistic uncertainty analysis based on Monte Carlo simulations of co-combustion of hazelnut hull and coal blends: Data-Driven modeling and response surface optimization. Bioresour. Technol. 2017, 225, 106–112. [Google Scholar] [CrossRef]
- Yadav, R.N. A hybrid approach of Taguchi-Response surface methodology for modeling and optimization of duplex turning process. Measurement 2017, 100, 131–138. [Google Scholar] [CrossRef]
- Tan, D.P.; Li, L.; Zhu, Y.L.; Zheng, S.; Ruan, H.J.; Jiang, X.X. An embedded cloud database service method for distributed industry monitoring. IEEE Trans. Ind. Inform. 2018, 14, 2881–2893. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Bacciocchi, M.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. Radial basis functions based on differential quadrature method for the free vibration analysis of laminated composite arbitrarily shaped plates. Compos. Part B Eng. 2015, 78, 65–78. [Google Scholar] [CrossRef]
- Freier, L.; Wiechert, W.; von Lieres, E. Kriging with trend functions nonlinear in their parameters: Theory and application in enzyme kinetics. Eng. Life Sci. 2017, 17, 916–922. [Google Scholar] [CrossRef]
- Tan, D.P.; Li, L.; Yin, Z.C.; Li, D.F.; Zhu, Y.L.; Zheng, S. Ekman boundary layer mass transfer mechanism of free sink vortex. Int. J. Heat Mass Trans. 2020, 150, 119250. [Google Scholar] [CrossRef]
- Wang, J.Y.; Zhang, C. Software reliability prediction using a deep learning model based on the RNN encoder-decoder. Reliab. Eng. Syst. Saf. 2018, 170, 73–82. [Google Scholar] [CrossRef]
- Zhang, X.W.; Liu, J.X.; Chen, X.F.; Cao, H.R. Neural network based multi-objective active vibration optimization method for shell structure. Chin. J. Mech. Eng. Engl. 2016, 52, 56–64. [Google Scholar] [CrossRef]
- Abibullaev, B.; An, J.; Jin, S.-H.; Lee, S.H.; Moon, J. Minimizing inter-subject variability in fNIRS-based brain-computer interfaces via multiple-kernel support vector learning. Med. Eng. Phys. 2013, 35, 1811–1818. [Google Scholar] [CrossRef]
- Mukhopadhyay, T.; Chakraborty, S.; Dey, S.; Adhikari, S.; Chowdhury, R. A critical assessment of Kriging model variants for high-fidelity uncertainty quantification in dynamics of composite shells. Arch. Comput. Methods Eng. 2017, 24, 495–518. [Google Scholar] [CrossRef]
- Tan, D.P.; Zhang, L.B.; Ai, Q.L. An embedded self-adapting network service framework for networked manufacturing system. J. Intell. Manuf. 2019, 30, 539–556. [Google Scholar] [CrossRef]
- Dey, S.; Mukhopadhyay, T.; Adhikari, S. Stochastic free vibration analyses of composite shallow doubly curved Shells—A Kriging model approach. Compos. Part B Eng. 2015, 70, 99–112. [Google Scholar] [CrossRef]
- Behrooz, K.; Trung, N.; Tam, T.; Zhu, S.P. Optimization of buckling load for composite laminated plates using adaptive Kriging-improved PSO: A novel hybrid intelligent method. Def. Technol. 2021, 17, 85–99. [Google Scholar]
- Sakata, S.; Ashida, F.; Zako, M. Kriging-Based approximate stochastic homogenization analysis for composite materials. Comput. Methods Appl. Mech. 2007, 197, 1953–1964. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, S.M.; Tan, D.P. Cavitation based soft abrasive flow processing method. Int. J. Adv. Manuf. Technol. 2020, 109, 2587–2602. [Google Scholar] [CrossRef]
- Eldho, J.J.; Arjun, S.; Menon, N.; Biju, N. Implementation of kriging surrogate models for delamination detection in composite structures. Adv. Compos. Lett. 2018, 27, 220–231. [Google Scholar]
- Jiang, Q.S.; Tan, D.P.; Li, Y.B.; Ji, S.M.; Cai, C.P.; Zheng, Q.M. Object detection and classification of metal polishing shaft surface defects based on convolutional neural network deep learning. Appl. Sci. 2020, 10, 87. [Google Scholar] [CrossRef]
- Yang, J.H.; Fu, Y.M. Analysis of dynamic stability for composite laminated cylindrical shells with delaminations. Comput. Struct. 2007, 78, 209–315. [Google Scholar] [CrossRef]
- Ge, J.Q.; Li, C.; Gao, Z.Y.; Ren, Y.L.; Xu, X.S.; Li, C.; Xie, Y. Softness abrasive flow polishing method using constrained boundary vibration. Powder Technol. 2021, 382, 173–187. [Google Scholar] [CrossRef]
- Lam, K.Y.; Loy, C.T. Analysis of rotating laminated cylindrical shells by different thin shell theories. J. Sound Vib. 1995, 196, 23–35. [Google Scholar] [CrossRef]
- Wu, M.G.; Lu, C.D.; Tan, D.P.; Hong, T.; Chen, G.H.; Wen, D.H. Effects of metal buffer layer for amorphous carbon film of 304 stainless steel bipolar plate. Thin Solid Films 2016, 616, 507–514. [Google Scholar]
- Tan, D.P.; Ni, Y.S.; Zhang, L.B. Two-Phase sink vortex suction mechanism and penetration dynamic characteristics in ladle teeming process. J. Iron Steel Res. Int. 2017, 24, 669–677. [Google Scholar] [CrossRef]
- Li, L.; Tan, D.P.; Wang, T.; Yin, Z.C.; Fan, X.H.; Wang, R.H. Multiphase coupling mechanism of free surface vortex and the vibration-based sensing method. Energy 2021, 216, 119136. [Google Scholar] [CrossRef]
- Zhang, X.M. Vibration analysis of cross-ply laminated composite cylindrical shells using the wave propagation approach. Appl. Acoust. 2001, 62, 1221–1228. [Google Scholar] [CrossRef]
- Zheng, S.H.; Yu, Y.K.; Qiu, M.Z.; Wang, L.M.; Tan, D.P. A modal analysis of vibration response of a cracked fluid-filled cylindrical shell. Appl. Math. Model. 2021, 91, 934–958. [Google Scholar] [CrossRef]
- Tan, D.P.; Zhang, L.B. A WP-Based nonlinear vibration sensing method for invisible liquid steel slag detection. Sens. Actuators B Chem. 2014, 202, 1257–1269. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Lu, Z.H. Applicable range of the fourth-moment method for structural reliability. J. Asian Archit. Build. 2007, 6, 151–158. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Zhang, X.Y.; Zhao, H.L. Complete monotonic expression of the fourth-moment normal transformation for structural reliability. Comput. Struct. 2018, 196, 186–199. [Google Scholar] [CrossRef]
- Jansson, N.; Wakeman, W.D.; Manson, J.A.E. Optimization of hybrid thermoplastic composite structures using surrogate models and genetic algorithms. Comput. Struct. 2007, 80, 21–31. [Google Scholar] [CrossRef]
- Oudjene, M.; Ben-Ayed, L.; Delameziere, A.; Batoz, J.L. Shape optimization of clinching tools using the response surface methodology with moving least-square approximation. J. Mater. Process. Technol. 2009, 209, 289–296. [Google Scholar] [CrossRef]
- Goggin, P.R. The elastic constants of carbon-fiber composites. J. Mater. Sci. 1973, 8, 233–244. [Google Scholar] [CrossRef]
- Zhang, J.F.; Yong, D. A method to determine basic probability assignment in the open world and its application in data fusion and classification. Appl. Intell. 2017, 46, 934–951. [Google Scholar] [CrossRef]


| Boundary Condition | |
|---|---|
| Free–free | |
| Clamped–clamped | |
| Free–clamped | |
| Free–Supported | |
| Clamped–supported | |
| Supported–supported |
| Parameter Value | The Range of x | Type | |||
|---|---|---|---|---|---|
| IV | |||||
| II | |||||
| III | |||||
| I | |||||
| V | |||||
| VI | |||||
| NO. | ||||
|---|---|---|---|---|
| 1 | 130.63 | 9.08 | 0.33 | 5.16 |
| 2 | 132.19 | 9.07 | 0.3 | 4.85 |
| 3 | 132 | 9.73 | 0.35 | 5 |
| 4 | 130.39 | 9.21 | 0.34 | 5.34 |
| 5 | 128.28 | 8.67 | 0.33 | 4.98 |
| 6 | 135.3 | 9.18 | 0.32 | 5.13 |
| 7 | 137.33 | 9.28 | 0.33 | 5.25 |
| 8 | 126.91 | 9.39 | 0.33 | 5.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Wang, T.; Lu, C.; Yang, Y.; Li, L.; Yin, Z.; Peng, X. Uncertainty Representation of Natural Frequency for Laminated Composite Cylindrical Shells Considering Probabilistic and Interval Variables. Appl. Sci. 2021, 11, 1883. https://doi.org/10.3390/app11041883
Chen G, Wang T, Lu C, Yang Y, Li L, Yin Z, Peng X. Uncertainty Representation of Natural Frequency for Laminated Composite Cylindrical Shells Considering Probabilistic and Interval Variables. Applied Sciences. 2021; 11(4):1883. https://doi.org/10.3390/app11041883
Chicago/Turabian StyleChen, Guohai, Tong Wang, Congda Lu, Yuanshan Yang, Lin Li, Zichao Yin, and Xiang Peng. 2021. "Uncertainty Representation of Natural Frequency for Laminated Composite Cylindrical Shells Considering Probabilistic and Interval Variables" Applied Sciences 11, no. 4: 1883. https://doi.org/10.3390/app11041883
APA StyleChen, G., Wang, T., Lu, C., Yang, Y., Li, L., Yin, Z., & Peng, X. (2021). Uncertainty Representation of Natural Frequency for Laminated Composite Cylindrical Shells Considering Probabilistic and Interval Variables. Applied Sciences, 11(4), 1883. https://doi.org/10.3390/app11041883







