Establishment of a Rolling-Sliding Test Bench to Analyze Abrasive Wear Propagation of Different Bearing Materials for Knee Implants
Abstract
:1. Introduction
2. Materials and Methods
2.1. Construction of the Rolling-Sliding Test Bench
2.2. Test Samples
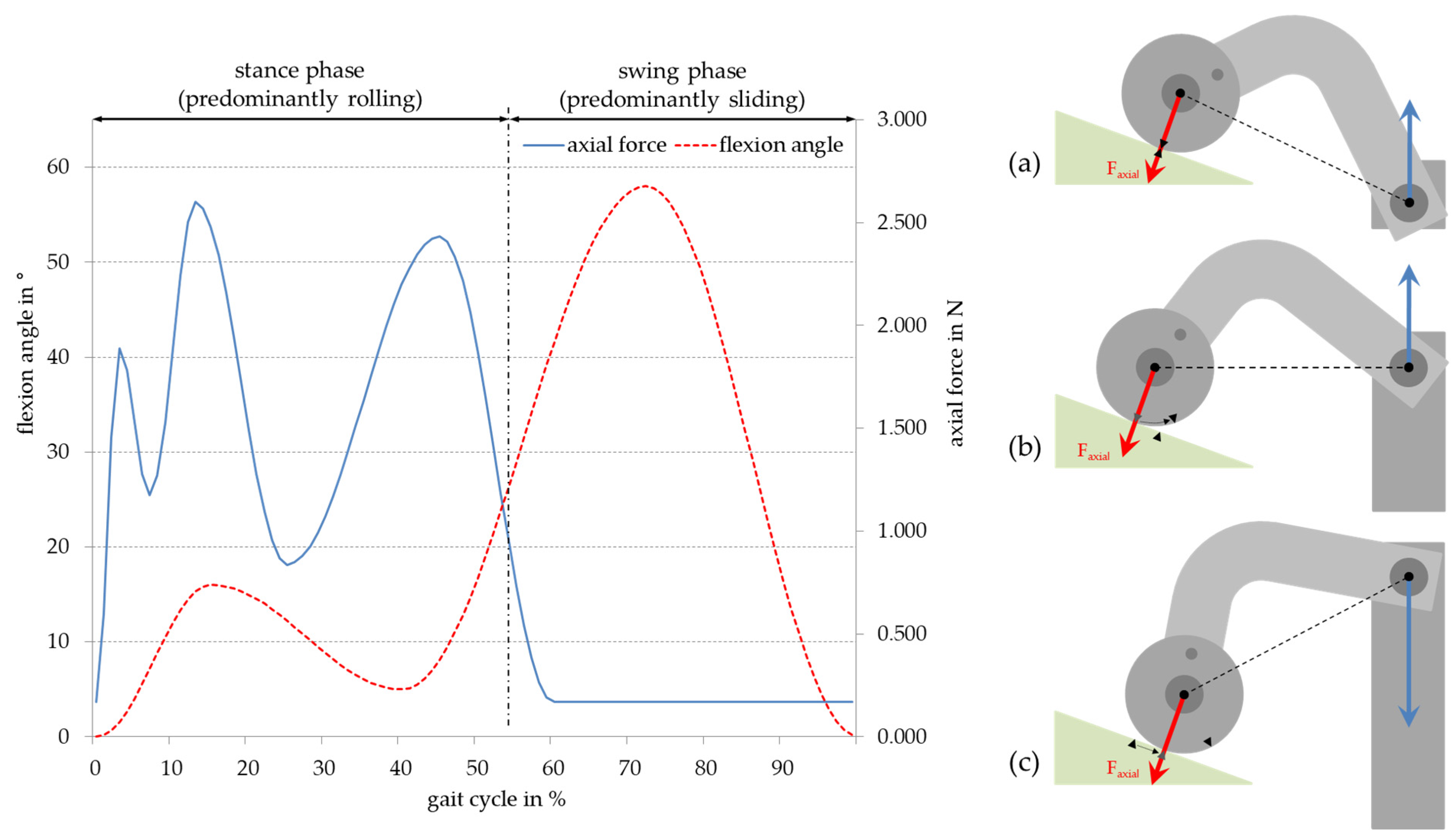
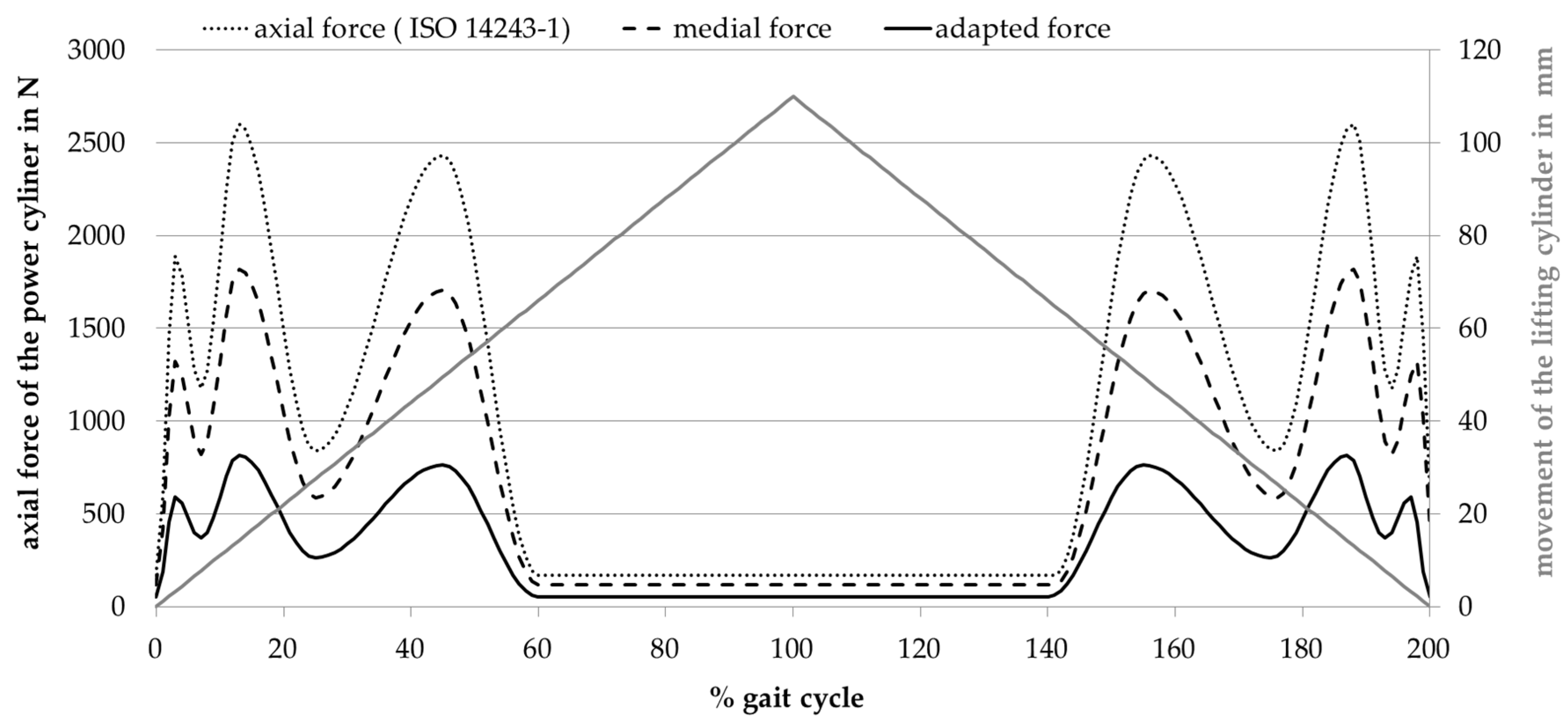
2.3. Adjustment of Load Pattern
2.4. Shape Analysis for Parameter Detection
2.5. Abrasive Wear Measurement
2.6. Surface Analysis and Roughness Measurement
3. Results
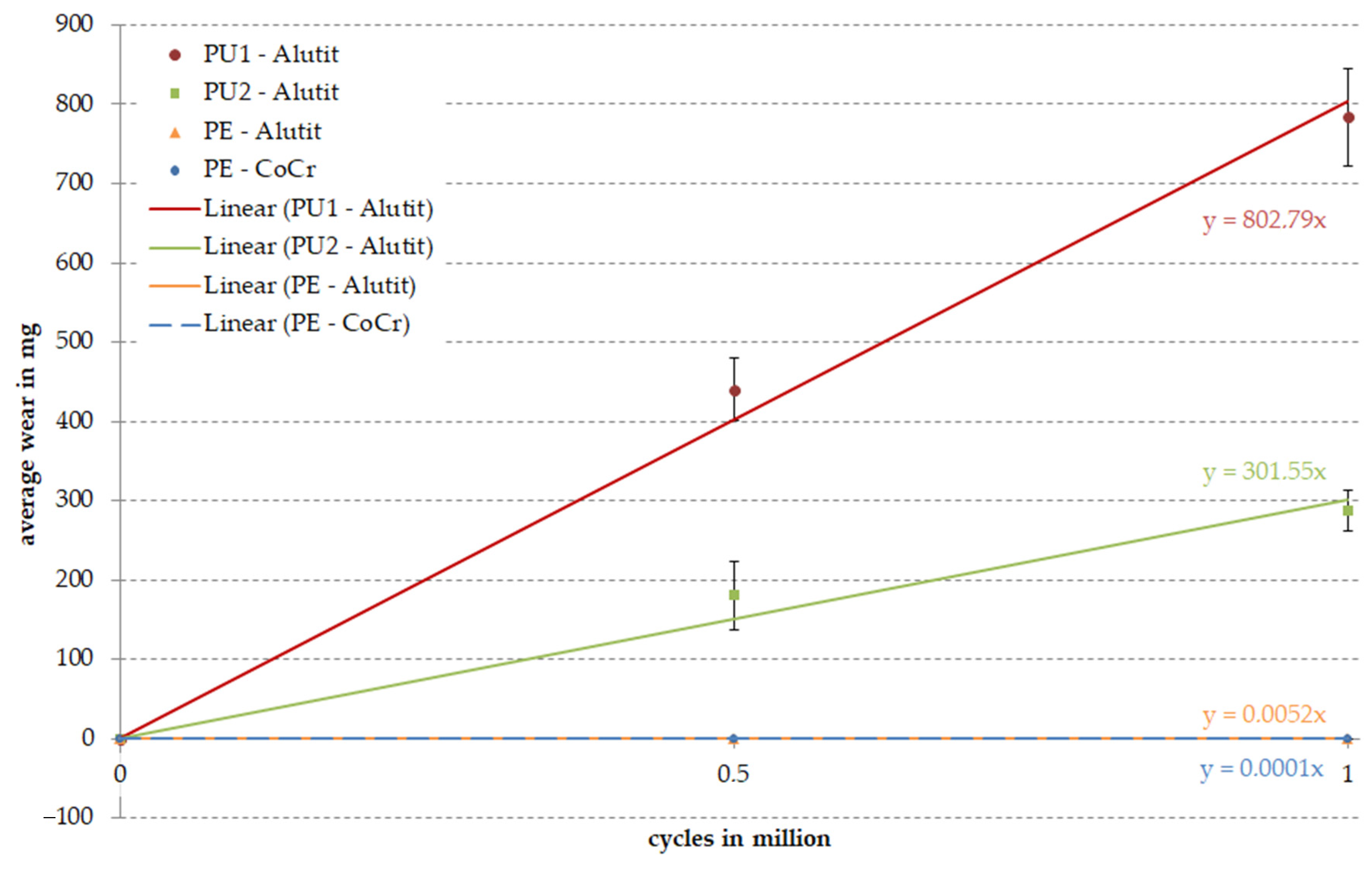
3.1. Amount of Wear
3.2. Surface Analysis and Roughness Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Drake, R.L.; Vogl, W.; Mitchell, A.W.M. Drake, Gray’s Anatomie SC; Elsevier, Urban&FischerVerlag: Munich, Germany, 2007; ISBN 978-3-437-41231-8. [Google Scholar]
- Krukemeyer, M.G.; Möllenhoff, G. Endoprothetik: Ein Leitfaden für den Praktiker, 3rd ed.; De Gruyter: Berlin, Germany, 2013; ISBN 978-3-11-028261-0. [Google Scholar]
- Faller, A.; Schünke, M. Der Körper des Menschen: Einführung in Bau und Funktion; Georg Thieme Verlag: Stuttgart, Germany, 2016; ISBN 978-3-13-151957-3. [Google Scholar]
- Nägerl, H.; Frosch, K.H.; Wachowski, M.M.; Dumont, C.; Abicht, C.; Adam, P.; Kubein-Meesenburg, D. A novel total knee replacement by rolling articulating surfaces. In vivo functional measurements and tests. Acta Bioeng. Biomech. 2008, 10, 55–60. [Google Scholar]
- Abicht, C. Artifical Knee Joints Following the Principle of a Four-Bar Linkage—Concept, Design and Tribological Properties of a New Natural Shaped Knee Endoprosthesis; Ernst-Moritz-Arndt-Universität, Medizinische Fakultät: Greifswald, Germany, 2006. [Google Scholar]
- Kapandji, I.A.; Koebke, J. Funktionelle Anatomie der Gelenke: Obere Extremität—Untere Extremität—Rumpf und Wirbelsäule, 5th ed.; Georg Thieme Verlag: Stuttgart, Germany, 2009; ISBN 978-3-13-142215-6. [Google Scholar]
- Goebel, P.; Zietz, C.; Bieck, R.; Kluess, D.; Bader, R. A novel method for tribological evaluation of bearing materials in total knee replacements. Biomed. Tech. Eng. 2012, 57. [Google Scholar] [CrossRef]
- Robertsson, O.; Lidgren, L.; Sundberg, M.; W-Dahl, A. The Swedish Knee Arthroplasty Register—Annual Report 2018; Lund University Department of Clinical Sciences, Orthopedics Skåne University Hospital: Holmgrens, Malmö, Sweden, 2019. [Google Scholar]
- Abu-Amer, Y.; Darwech, I.; Clohisy, J.C. Aseptic loosening of total joint replacements: Mechanisms underlying osteolysis and potential therapies. Arthritis Res. Ther. 2007, 9, S6. [Google Scholar] [CrossRef] [Green Version]
- Kretzer, J.; Zietz, C.; Schröder, C.; Reinders, J.; Middelborg, L.; Paulus, A.; Sonntag, R.; Bader, R.; Utzschneider, S. Grundlagen zur tribologischen Analyse von Endoprothesen. Der Orthopäde 2012, 41, 844–852. [Google Scholar] [CrossRef]
- I Richter, B.; Ostermeier, S.; Turger, A.; Denkena, B.; Hurschler, C. A rolling-gliding wear simulator for the investigation of tribological material pairings for application in total knee arthroplasty. Biomed. Eng. Online 2010, 9, 24. [Google Scholar] [CrossRef] [Green Version]
- Van Citters, D.W.; Kennedy, F.E.; Currier, J.H.; Collier, J.P.; Nichols, T.D. A Multi-Station Rolling/Sliding Tribotester for Knee Bearing Materials. J. Tribol. 2004, 126, 380–385. [Google Scholar] [CrossRef]
- Van Citters, D.W.; Kennedy, F.E.; Collier, J.P. Rolling sliding wear of UHMWPE for knee bearing applications. Wear 2007, 263, 1087–1094. [Google Scholar] [CrossRef]
- Wieser, J. Testung Unterschiedlicher Polyethylene im Roll-Gleit-Prüfstand. Text. Ph.D. Thesis, Ludwig-Maximilians-Universität München, Munich, Germany, 2014. [Google Scholar]
- ISO 14243-1:2009 Implants for Surgery—Wear of Total Knee-Joint Prostheses—Part 1: Loading and Displacement Parameters for Wear-Testing Machines with Load Control and Corresponding Environmental Conditions for Test. Available online: https://www.iso.org/cms/render/live/en/sites/isoorg/contents/data/standard/04/42/44262.html (accessed on 18 June 2020).
- Schwitalle, M.; Just, A.; Mark, T.; Bodem, F.; Schwitalle, E.; Koller, S. Kinematische Analyse vor und nach bikondylaerem Oberflaechenersatz des Kniegelenks. Der Orthopäde 2003, 32, 266–273. [Google Scholar] [CrossRef]
- Kutuzova, L.; Athanasopulu, K.; Schneider, M.; Kandelbauer, A.; Lorenz, G.; Kemkemer, R. In vitro bio-stability screening of novel implantable polyurethane elastomers. Curr. Dir. Biomed. Eng. 2018, 4, 535–538. [Google Scholar] [CrossRef]
- Athanasopulu, K.; Kutuzova, L.; Thiel, J.; Lorenz, G.; Kemkemer, R. Enhancing the biocompatibility of siliconepolycarbonate urethane based implant materials. Curr. Dir. Biomed. Eng. 2019, 5, 453–455. [Google Scholar] [CrossRef]
- Heller, M.O.; Taylor, W.R.; Perka, C.; Duda, G.N. The influence of alignment on the musculo-skeletal loading conditions at the knee. Langenbeck’s Arch. Surg. 2003, 388, 291–297. [Google Scholar] [CrossRef] [PubMed]
- Hayes, W.C.; Mockros, L.F. Viscoelastic properties of human articular cartilage. J. Appl. Physiol. 1971, 31, 562–568. [Google Scholar] [CrossRef]
- Adams, J.; McaLindon, T.; Dimasi, M.; Carey, J.; Eustace, S. Contribution of meniscal extrusion and cartilage loss to joint space narrowing in osteoarthritis. Clin. Radiol. 1999, 54, 502–506. [Google Scholar] [CrossRef]
- Ambellan, F.; Tack, A.; Ehlke, M.; Zachow, S. Automated segmentation of knee bone and cartilage combining statistical shape knowledge and convolutional neural networks: Data from the Osteoarthritis Initiative. Med Image Anal. 2019, 52, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Ambellan, F.; Lamecker, H.; Von Tycowicz, C.; Zachow, S. Statistical Shape Models: Understanding and Mastering Variation in Anatomy. In Advances in Experimental Medicine and Biology; Springer International Publishing: Basel, Switzerland, 2019; Volume 1156, pp. 67–84. [Google Scholar]
- Howell, S.M.; Howell, S.J.; Hull, M.L. Assessment of the Radii of the Medial and Lateral Femoral Condyles in Varus and Valgus Knees with Osteoarthritis. J. Bone Jt. Surg.-Am. Vol. 2010, 92, 98–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sancisi, N.; Parenti-Castelli, V. A sequentially-defined stiffness model of the knee. Mech. Mach. Theory 2011, 46, 1920–1928. [Google Scholar] [CrossRef]
- Schultze, C.; Klüss, D.; Martin, H.; Hingst, V.; Mittelmeier, W.; Schmitz, K.-P.; Bader, R. Finite-Elemente-Analyse einer zementierten, keramischen Femurkomponente unter Berücksichtigung der Einbausituation bei künstlichem Kniegelenkersatz/Finite element analysis of a cemented ceramic femoral component for the assembly situation in total knee arthroplasty. Biomed. Tech. Eng. 2007, 52, 301–307. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F.; Piccigallo, B.; Ciulli, E. Lubrication and wear modelling of artificial hip joints: A review. Tribol. Int. 2011, 44, 532–549. [Google Scholar] [CrossRef]
- Kluess, D.; Martin, H.; Mittelmeier, W.; Schmitz, K.-P.; Bader, R. Influence of femoral head size on impingement, dislocation and stress distribution in total hip replacement. Med Eng. Phys. 2007, 29, 465–471. [Google Scholar] [CrossRef]
- Eichmiller, F.; Tesk, J.A.; Croarkin, C.M. Mechanical Properties of Ultra High Molecular Weight Polyethylene NIST Reference Material RM 8456. Soc. Biomater. 2001, 22, 6. [Google Scholar]
- ISO 14243-2:2009 Implants for Surgery—Wear of Total Knee-Joint Prostheses—Part 2: Methods of Measurement. Available online: https://www.iso.org/standard/69851.html (accessed on 18 June 2020).
- DIN EN ISO 4288:1998 Geometrische Produktspezifikation (GPS)—Oberflächenbeschaffenheit: Tastschnittverfahren—Regeln und Verfahren für die Beurteilung der Oberflächenbeschaffenheit (ISO 4288:1996); Beuth Verlag: Berlin, Germany, 1998. [CrossRef]
- DIN EN ISO 3274:1998 Geometrische Produktspezifikationen (GPS)—Oberflächenbeschaffenheit: Tastschnittverfahren—Nenneigenschaften von Tastschnittgeräten (ISO 3274:1996); Beuth Verlag: Berlin, Germany, 1998. [CrossRef]
- Jin, Z.; Fisher, J. Tribology in joint replacement*Note: This chapter is an updated version of Chapter 2, from the first edition of Joint replacement technology, edited by P. A. Revell and published by Woodhead Publishing, 2008*. Jt. Replace. Technol. 2014, 31–61. [Google Scholar] [CrossRef]
- Sivananthan, S.; Goodman, S.; Burke, M. Failure mechanisms in joint replacement**Note: This chapter is an updated version of Chapter 12, from the first edition of Joint replacement technology, edited by P. A. Revell and published by Woodhead Publishing, 2008. Jt. Replace. Technol. 2014, 370–400. [Google Scholar] [CrossRef]
- Taylor, W.R.; Heller, M.O.; Bergmann, G.; Duda, G.N. Tibio-femoral loading during human gait and stair climbing. J. Orthop. Res. 2004, 22, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Madeti, B.K.; Rao, C.S.; Rao, B.S.S. Failure analysis of ACL and Hertz contact stress in human knee. Int. J. Biomed. Eng. Technol. 2014, 16, 317. [Google Scholar] [CrossRef]
- Machado, M.; Flores, P.; Claro, J.C.P.; Ambrósio, J.; Silva, M.; Completo, A.; Lankarani, H.M. Development of a planar multibody model of the human knee joint. Nonlinear Dyn. 2010, 60, 459–478. [Google Scholar] [CrossRef]
- Khoshgoftar, M.; Vrancken, A.; Van Tienen, T.; Buma, P.; Janssen, D.; Verdonschot, N. The sensitivity of cartilage contact pressures in the knee joint to the size and shape of an anatomically shaped meniscal implant. J. Biomech. 2015, 48, 1427–1435. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, C.J.; Bahadur, S. Development and testing of a novel joint wear simulator and investigation of the viability of an elastomeric polyurethane for total-joint arthroplasty devices. Wear 2007, 262, 331–339. [Google Scholar] [CrossRef]





| Parameter | Value | Meaning |
|---|---|---|
| F | 0.17 to 2.6 kN | Axial force according to ISO 14243–1 [15] |
| Fmedial | 0.12 to 1.82 kN | Axial force that is transmitted via the medial condyle (Fmedial = 70% F [19]) |
| rmedial | 20.584 mm | Cylinder radius/radius of the condyle |
| lmedial | 25.29 mm | Length of contact of the cylinder with the plane/cartilage surface |
| EA = Ecortical bone | 17,000 N/mm2 | Young’s modulus of cortical bone [26] |
| υA = υcortical bone | 0.3 | Poisson’s ratio of cortical bone [26] |
| EB = Ecartilage | 12 N/mm2 | Young’s modulus of cartilage [20] |
| υB = υcartilage | 0.42 | Poisson’s ratio of cartilage [20] |
| Parameter | Bearing Material Pair 1 | Bearing Material Pair 2 | Bearing Material Pair 3 | |||
|---|---|---|---|---|---|---|
| Alutit T 1 | PU | CoCr [27] | PE [28,29] | Alutit T | PE | |
| Ecylinder in N/mm2 | 17,000 | - | 230,000 | - | 17,000 | - |
| υcylinder | 0.22 | - | 0.3 | - | 0.22 | - |
| Eplane in N/mm2 | - | 18.9 | - | 945 | - | 945 |
| υplane | - | 0.4 | - | 0.45 | - | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hembus, J.; Ambellan, F.; Zachow, S.; Bader, R. Establishment of a Rolling-Sliding Test Bench to Analyze Abrasive Wear Propagation of Different Bearing Materials for Knee Implants. Appl. Sci. 2021, 11, 1886. https://doi.org/10.3390/app11041886
Hembus J, Ambellan F, Zachow S, Bader R. Establishment of a Rolling-Sliding Test Bench to Analyze Abrasive Wear Propagation of Different Bearing Materials for Knee Implants. Applied Sciences. 2021; 11(4):1886. https://doi.org/10.3390/app11041886
Chicago/Turabian StyleHembus, Jessica, Felix Ambellan, Stefan Zachow, and Rainer Bader. 2021. "Establishment of a Rolling-Sliding Test Bench to Analyze Abrasive Wear Propagation of Different Bearing Materials for Knee Implants" Applied Sciences 11, no. 4: 1886. https://doi.org/10.3390/app11041886
APA StyleHembus, J., Ambellan, F., Zachow, S., & Bader, R. (2021). Establishment of a Rolling-Sliding Test Bench to Analyze Abrasive Wear Propagation of Different Bearing Materials for Knee Implants. Applied Sciences, 11(4), 1886. https://doi.org/10.3390/app11041886







