A Novel Structure of Rubber Ring for Hydraulic Buffer Seal Based on Numerical Simulation
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Structure
2.1. Material
2.2. Structure
3. Modeling
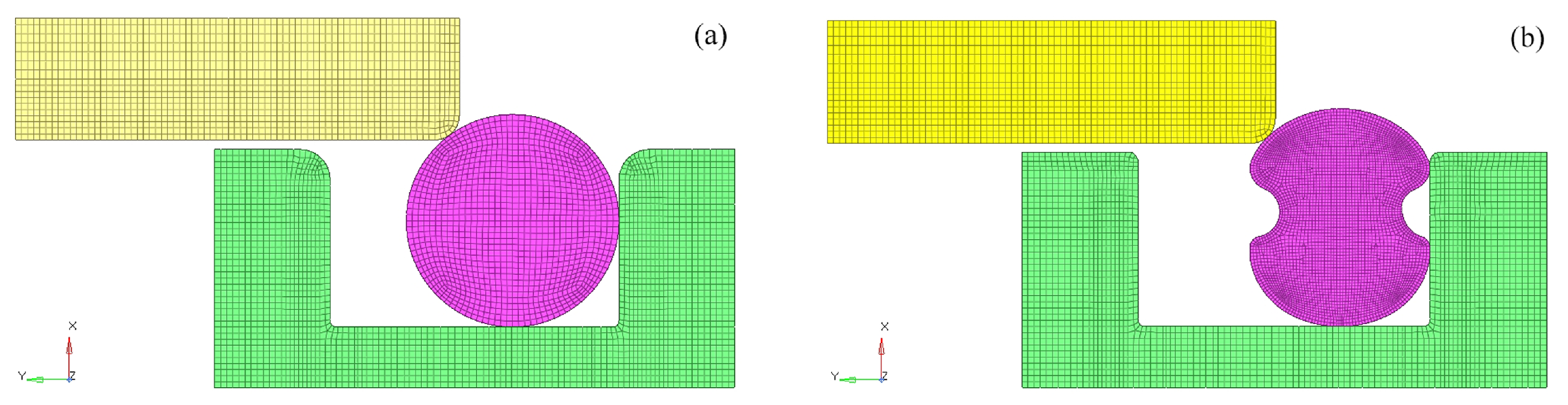
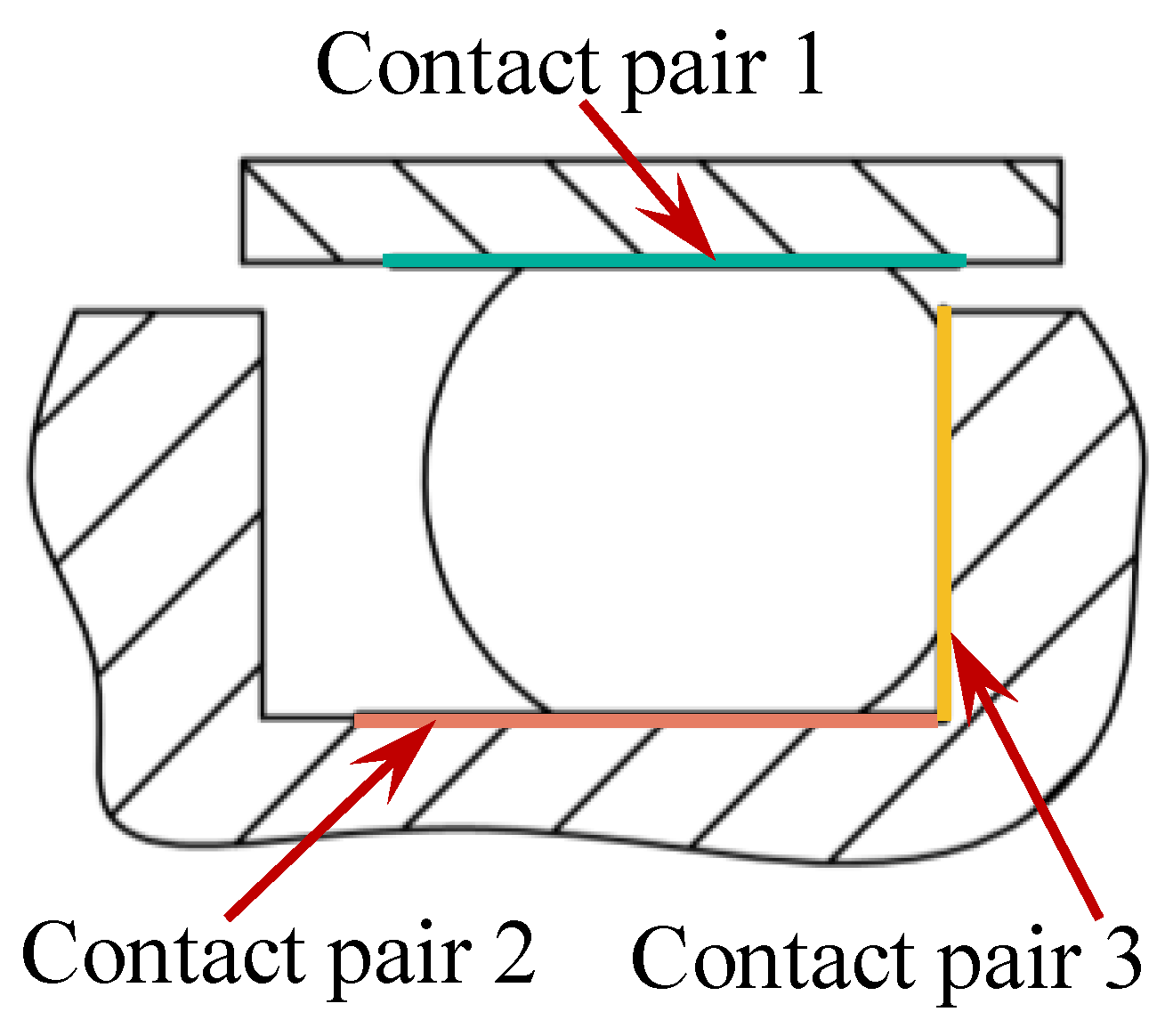
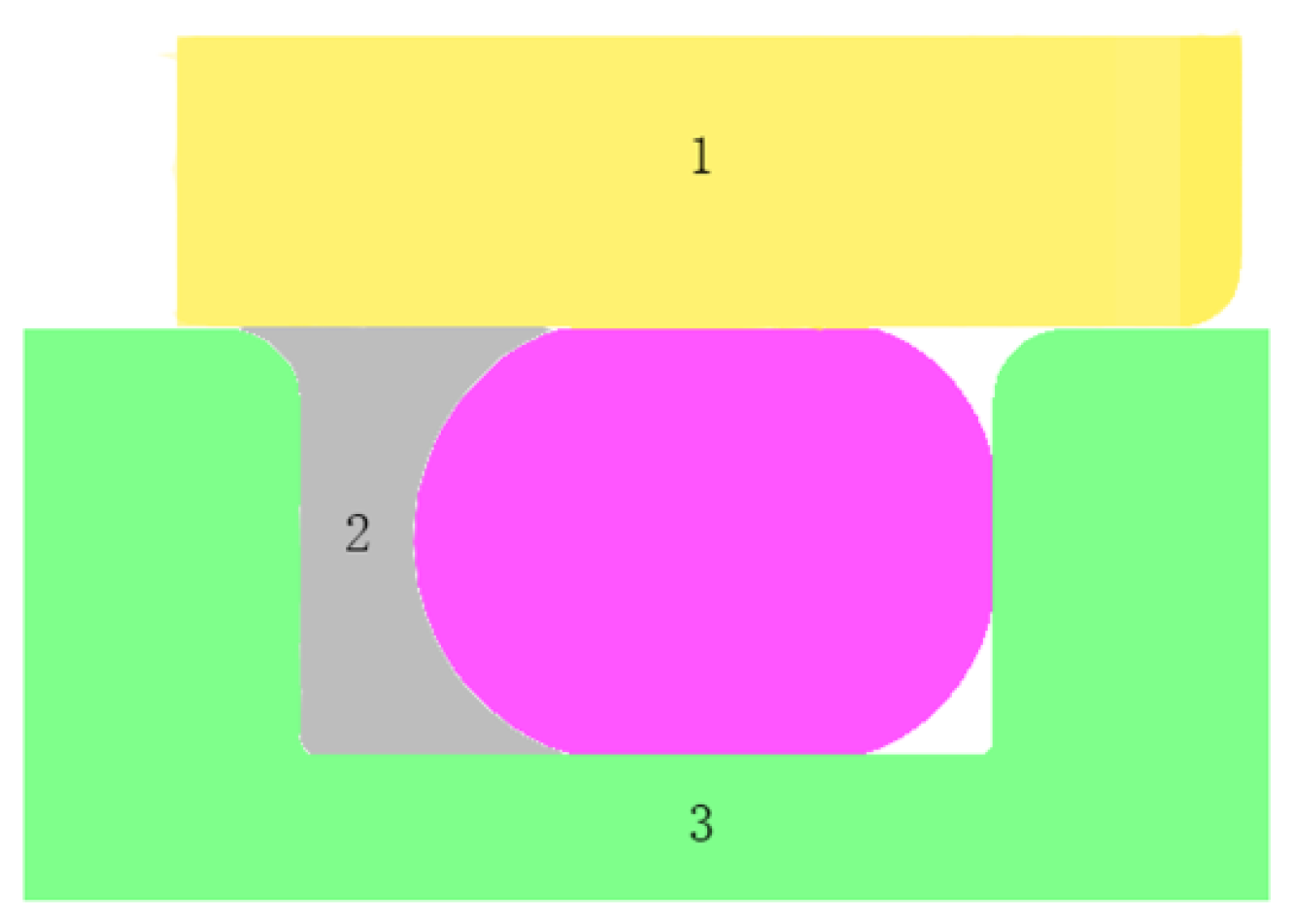
3.1. Finite Element Model
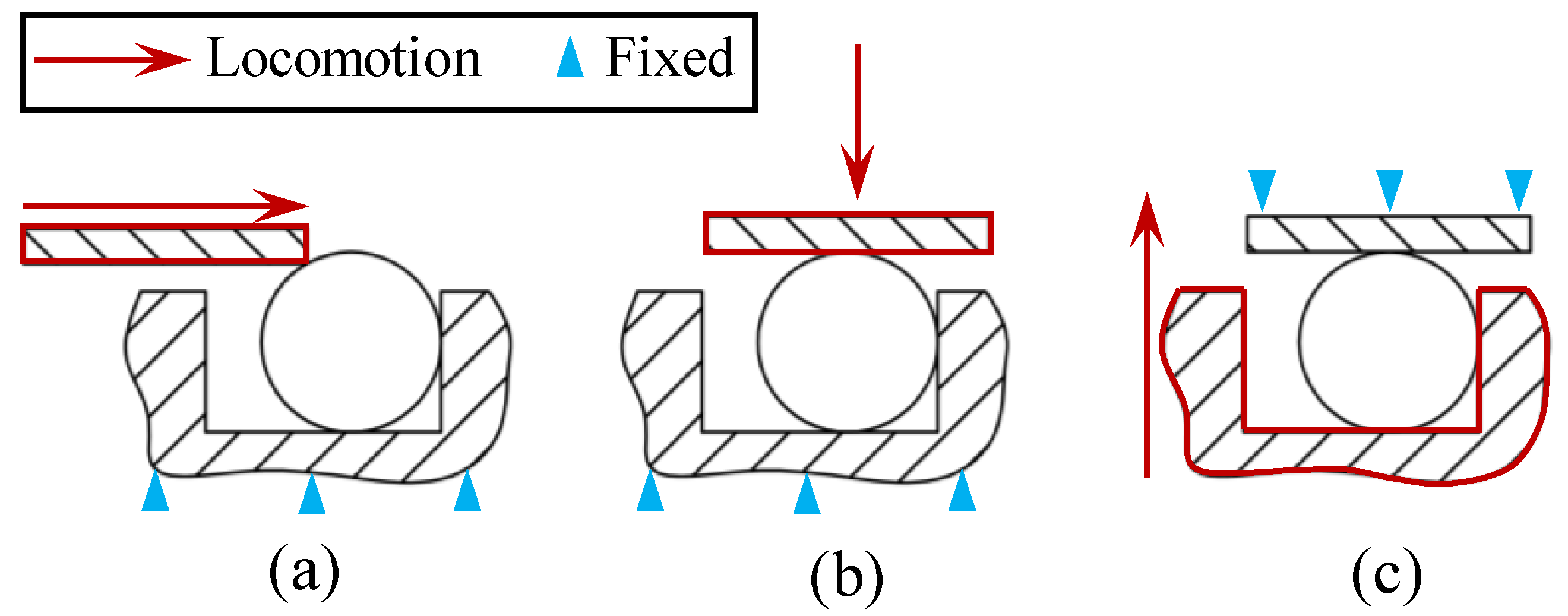
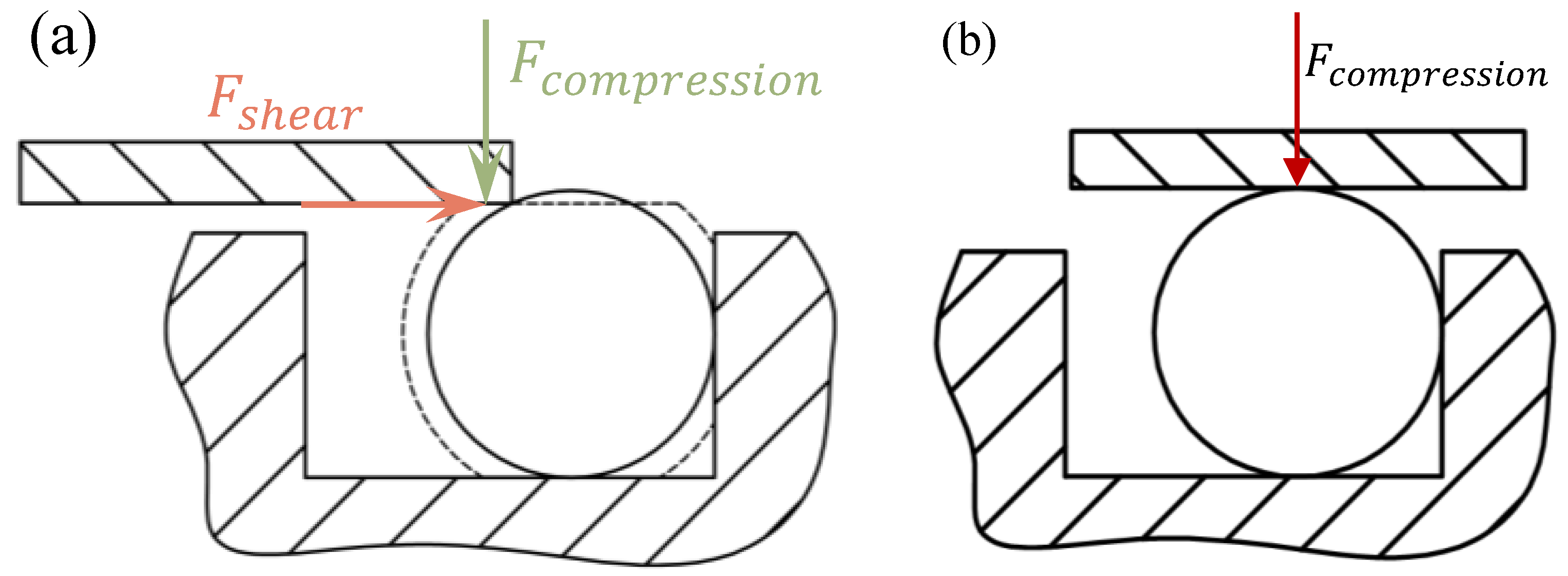
3.2. Installation Mode
3.3. Working Mode
4. Results
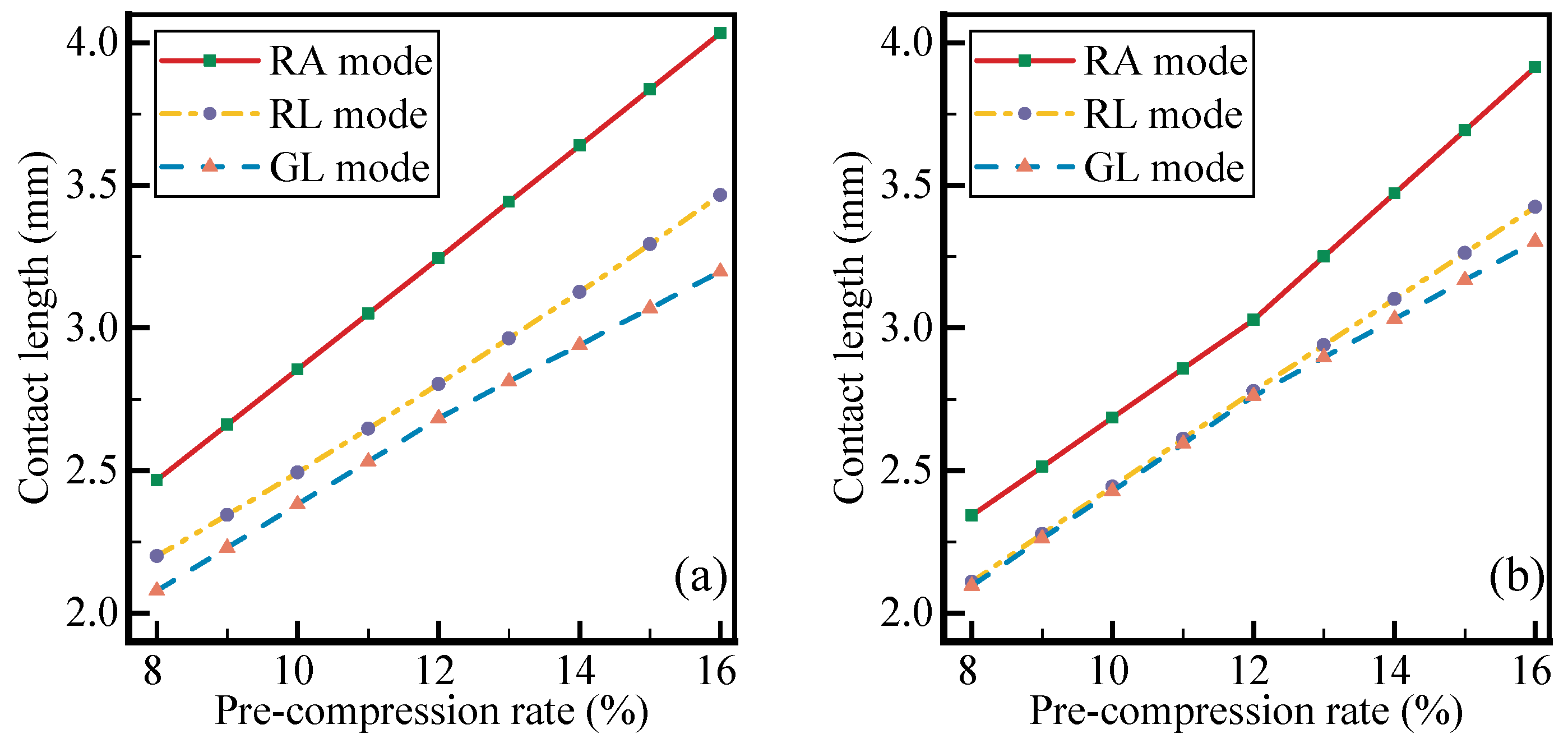
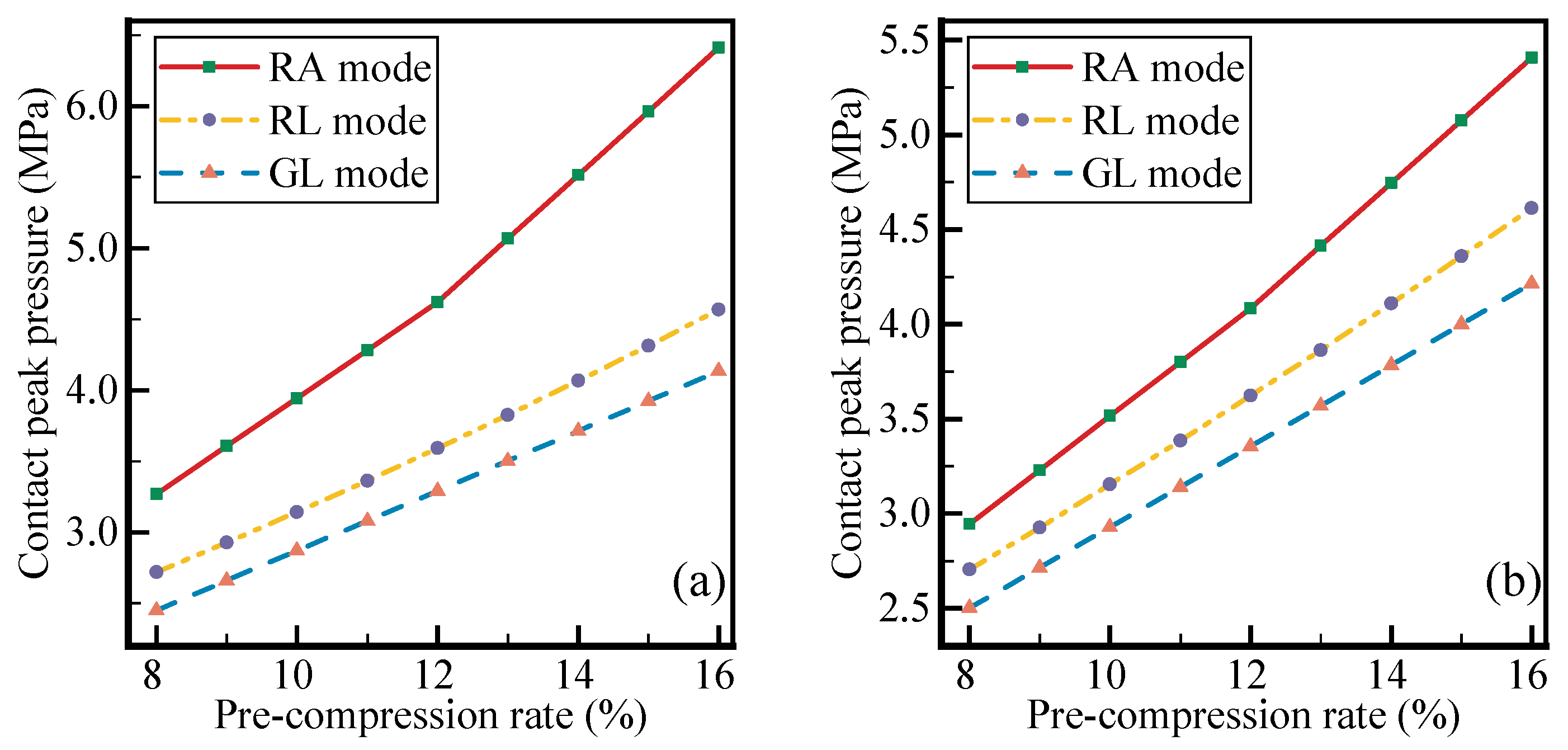
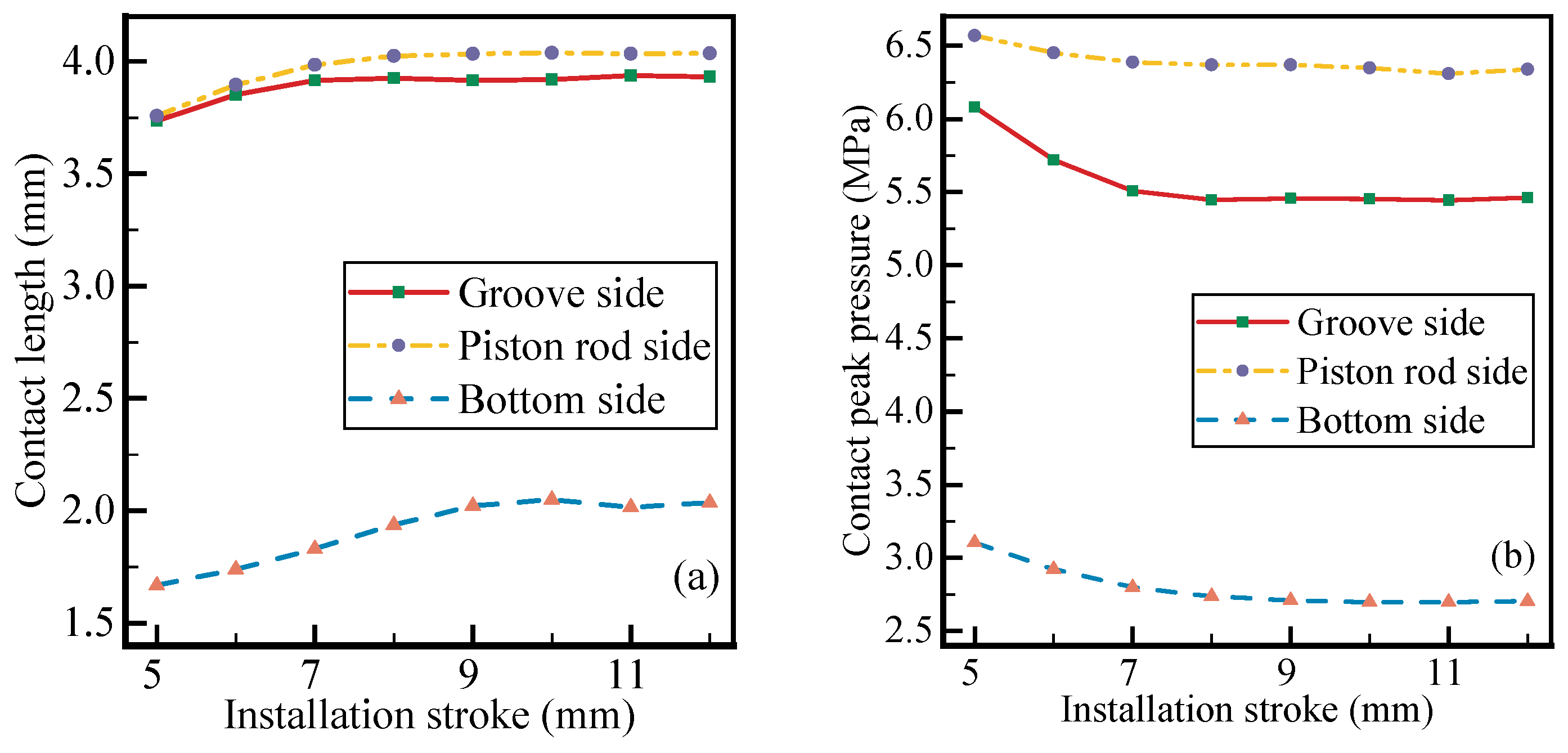
4.1. Influence of Installation Mode
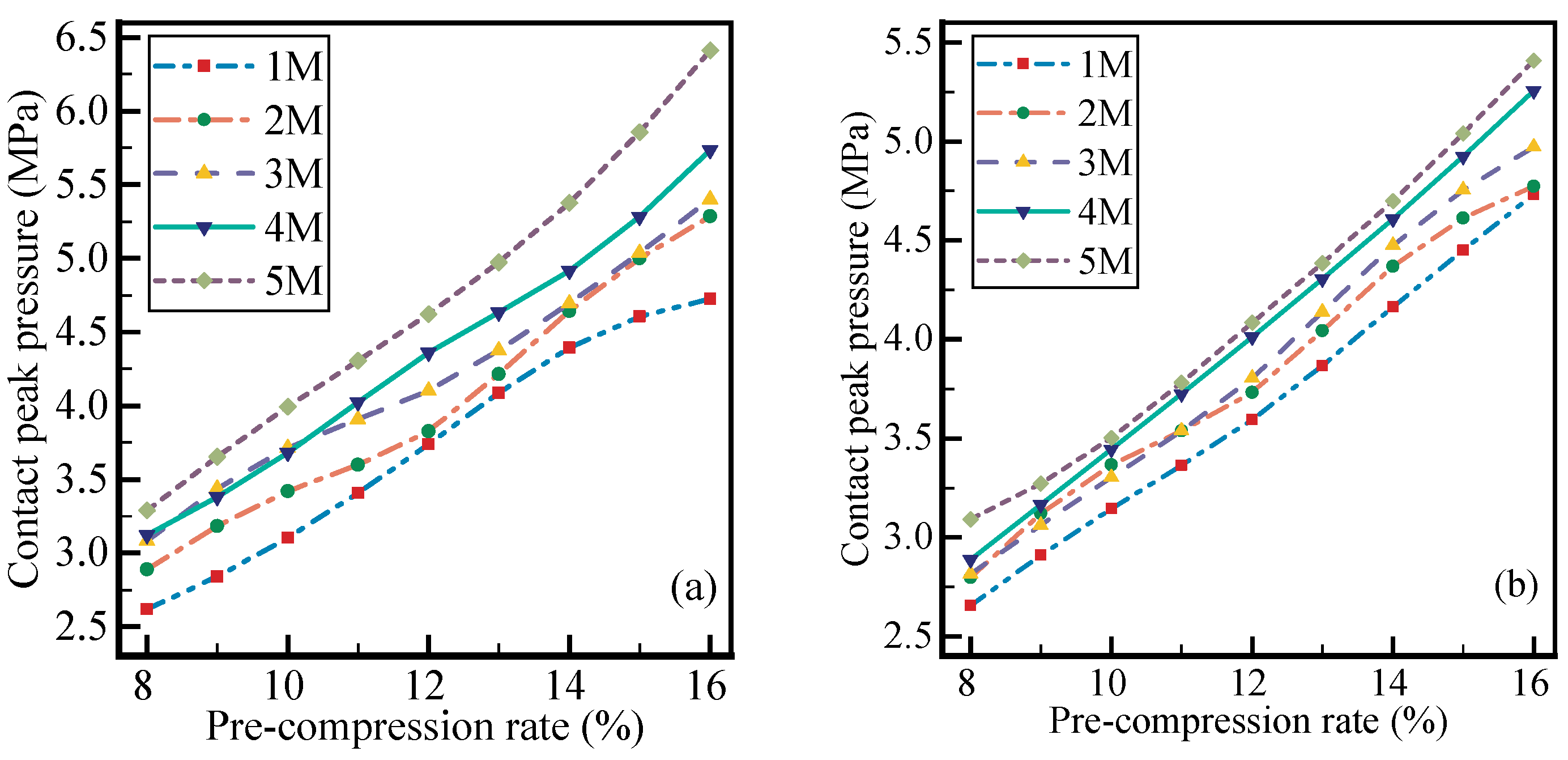
4.2. Influence of Pre-Compression Rate
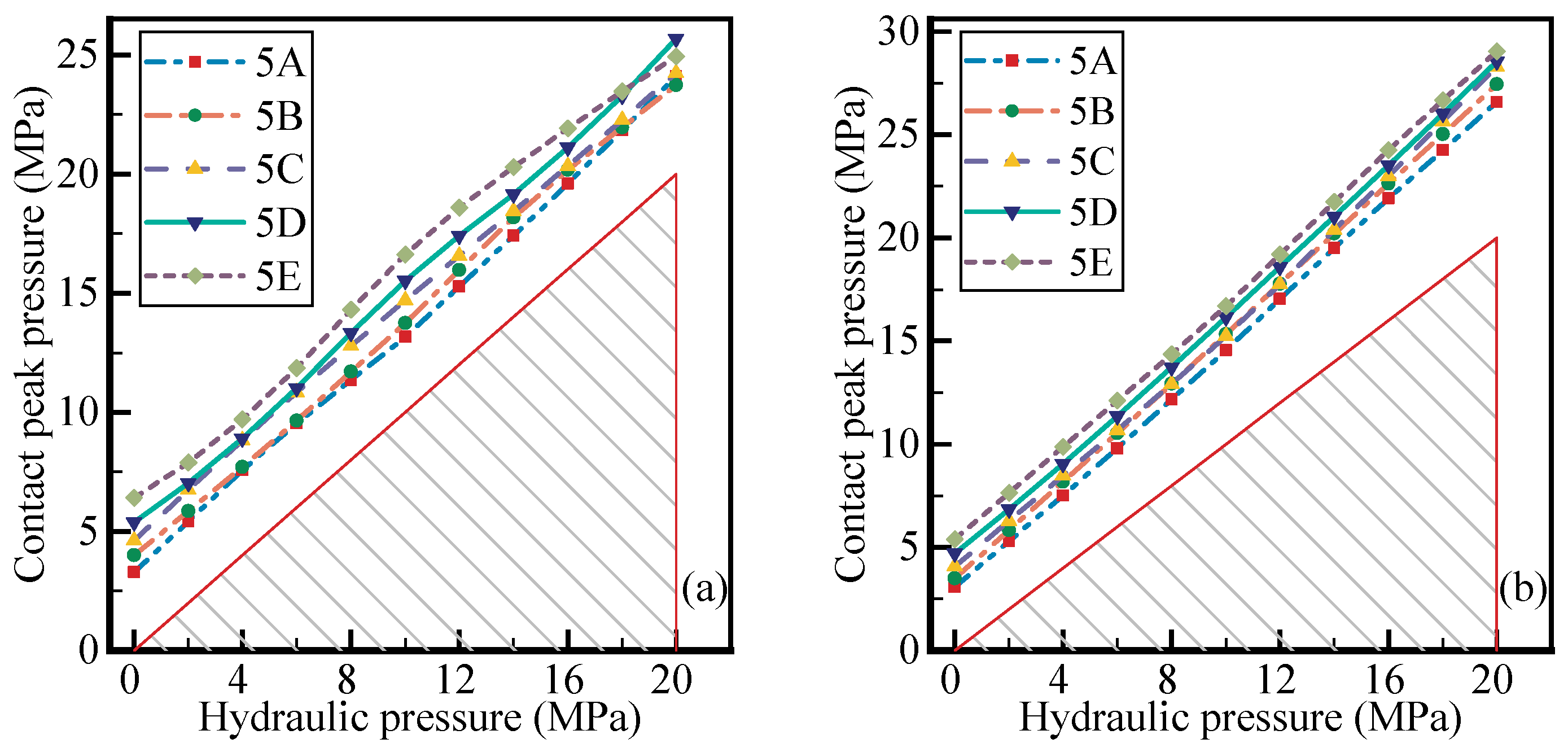
4.3. Influence of Hydraulic Pressure
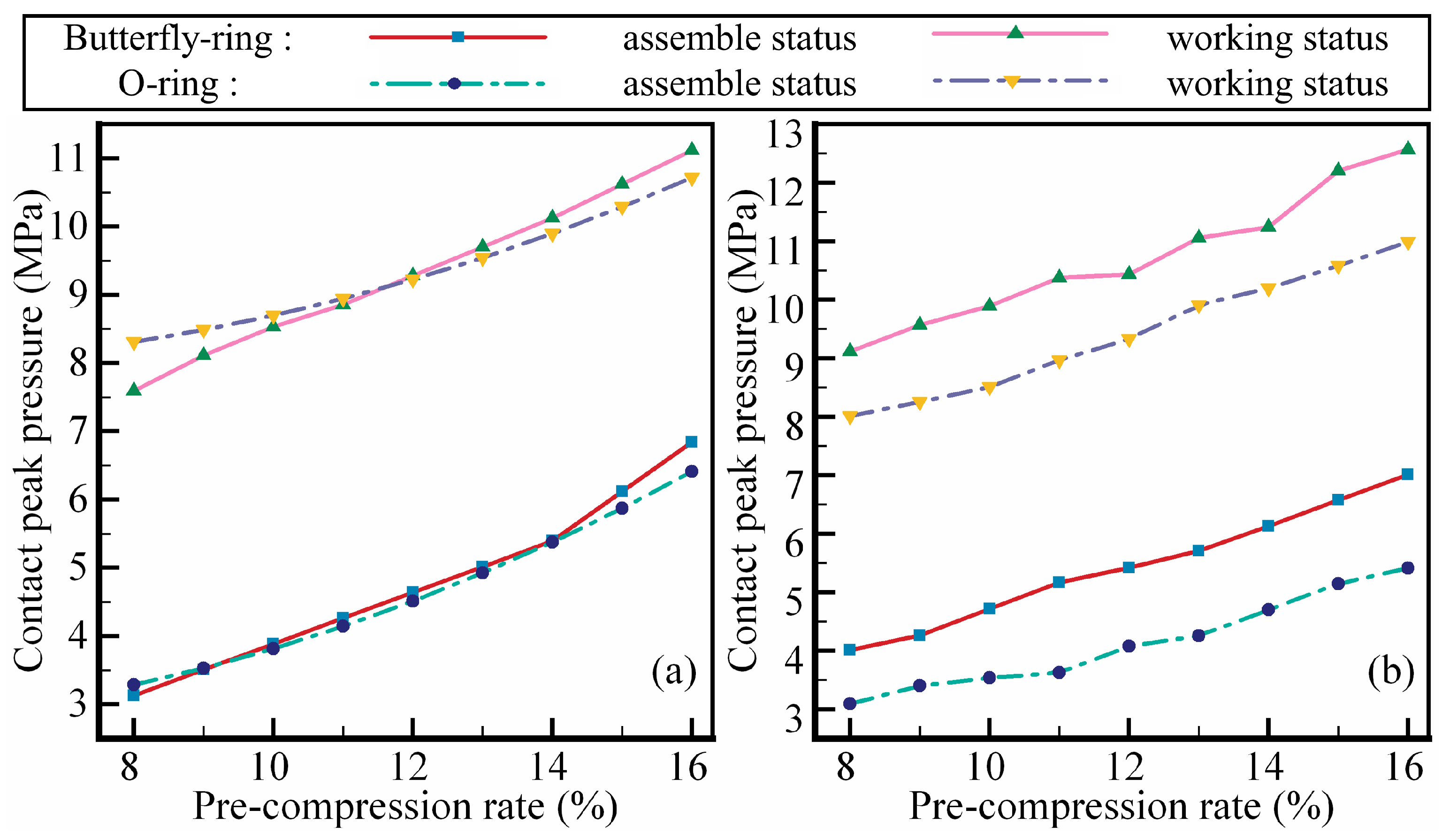
4.4. Sealing Performance of Butterfly-Ring
5. Discussion
5.1. Evaluation of Installation Mode
5.2. Evaluation of Pre-Compression Rate and Hydraulic Pressure
5.3. Evaluation of Butterfly-Ring on Sealing Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FEA | Finite element analysis |
| M-R | Mooney–Rivlin |
| NBR | Nitrile rubber |
| RA | Piston rod axial displacement |
| RL | Piston rod lateral displacement |
| GL | Groove lateral displacement |
| W | Strain–energy function |
| I | Invariant of the Cauchy–Green strain tensor |
| Three invariants of the Green deformation tensor | |
| Three principal stretches ratios | |
| Cauchy stress tensor | |
| Three principal Cauchy stresses | |
| Poisson ratio | |
| First material parameter of M-R model | |
| Second material parameter of M-R model |
Appendix A. Parameter and Design of Installation Mode Simulation
| Installation Mode | Direction | Pre-Compression Rate (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RA | Negative of Y | ||||||||||
| RL | Negative of X | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| GL | Positive of X | ||||||||||
| Project | Label | Basic Parameter | Installation Stroke (mm) |
|---|---|---|---|
| 5EM | 5EM3 | Section diameter: 7 mm | 3 |
| 5EM5 | 5 | ||
| 5EM6 | 6 | ||
| 5EM7 | 7 | ||
| 5EM8 | Pre-compression: 16% | 8 | |
| 5EM9 | 9 | ||
| 5EM10 | 10 | ||
| 5EM11 | 11 | ||
| 5EM12 | 12 |
Appendix B. Parameter and Design of Pre-Compression Rate Simulation
| Project | Label | Section Diameter | Pre-Compression Rate (%) |
|---|---|---|---|
| 1M | 1AM | 1.8 mm | 8 |
| 1BM | 9 | ||
| 1CM | 10 | ||
| 1DM | 11 | ||
| 1EM | 12 | ||
| 1FM | 13 | ||
| 1GM | 14 | ||
| 1HM | 15 | ||
| 1KM | 16 |
Appendix C. Parameter and Design of Hydraulic Pressure Simulation
| Project | Label | Pre-Compression Rate | Hydraulic Pressure (MPa) |
|---|---|---|---|
| 5A | 5AM | 8% | 0 |
| 5AN | 2 | ||
| 5AO | 4 | ||
| 5AP | 6 | ||
| 5AQ | 8 | ||
| 5AR | 10 | ||
| 5AS | 12 | ||
| 5AT | 14 | ||
| 5AU | 16 | ||
| 5AV | 18 | ||
| 5AW | 20 |
References
- Nikas, G.K. Eighty years of research on hydraulic reciprocating seals: Review of tribological studies and related topics since the 1930s. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 1–23. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, G.; Xiao, S.; Hua, Z.; Gu, C. Study on fretting behavior of rubber O-ring seal in high-pressure gaseous hydrogen. Int. J. Hydrogen Energy 2019, 44, 22569–22575. [Google Scholar] [CrossRef]
- Zeng, D.; He, Q.; Li, T.; Hu, J.; Shi, T.; Zhang, Z.; Yu, Z.; Liu, R. Corrosion mechanism of hydrogenated nitrile butadiene rubber O-ring under simulated wellbore conditions. Corros. Sci. 2016, 107, 145–154. [Google Scholar] [CrossRef]
- Kömmling, A.; Jaunich, M.; Pourmand, P.; Wolff, D.; Hedenqvist, M. Analysis of O-Ring Seal Failure under Static Conditions and Determination of End-of-Lifetime Criterion. Polymers 2019, 11, 1251. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Hosseini, M.; Sahari, B.B. A Review of Constitutive Models for Rubber-Like Materials. Am. J. Eng. Appl. Sci. 2010, 3, 232–239. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Li, G. Optimization of cone bit bearing seal based on failure analysis. Adv. Mech. Eng. 2018, 10, 168781401876748. [Google Scholar] [CrossRef]
- Hao, S.; Yang, J. A Novel Quality Requirement Design Method for the Quality Characteristic of Rubber Products Based on the Reliability Constraint. IEEE Access 2018, 6, 17887–17895. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Z.; Tan, L.; Ma, Y.; Qiu, C.; Zhang, F.; Yuan, Y.; Sun, C.; Guo, L. Cone bit bearing seal failure analysis based on the finite element analysis. Eng. Fail. Anal. 2014, 45, 292–299. [Google Scholar] [CrossRef]
- Yildiz, Y.; Duzgun, M. Stress analysis of ventilated brake discs using the finite element method. Int. J. Automot. Technol. 2010, 11, 133–138. [Google Scholar] [CrossRef]
- Jeang, A.; Chung, C.P.; Ko, C.P. Parameters decision for an assembly under mechanical structure deformation via probabilistic optimization. Adv. Mech. Eng. 2019, 11, 168781401987924. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Chen, G.; Liu, P. Finite Element Analysis of Sealing Performance of Rubber D-Ring Seal in High-Pressure Hydrogen Storage Vessel. J. Fail. Anal. Prev. 2018, 18, 846–855. [Google Scholar] [CrossRef]
- Mose, B.R.; Hawong, J.S.; Nam, J.H. Stress analysis of a stepped rounded D-ring with a ratio of H1/H2 = 3.0 under uniform squeeze rate and internal pressure by photoelastic experimental hybrid method. Mater. Und Werkst. 2013, 44, 861–878. [Google Scholar] [CrossRef]
- Shin, D.C.; Hawong, J.S.; Lee, S.W.; Bernard, A.O.; Lim, H.S. Contact behavior analysis of X-ring under internal pressure and uniform squeeze rate using photoelastic experimental hybrid method. J. Mech. Sci. Technol. 2014, 28, 4063–4073. [Google Scholar] [CrossRef]
- Bernard, A.O.; Hawong, J.S.; Shin, D.C.; Dong, B. Contact behavior analysis of elastomeric x-ring under uniform squeeze rate and internal pressure before and after forcing-out using the photoelastic experimental hybrid method. J. Mech. Sci. Technol. 2015, 29, 2157–2168. [Google Scholar] [CrossRef]
- Cui, K.B.; Qin, J.Q.; Di, C.C.; Yang, Y.F. Finite Element Analysis and Simulation of the Sealing Performance of Y-Ring Rubber Seal. Appl. Mech. Mater. 2013, 444–445, 1379–1383. [Google Scholar] [CrossRef]
- Zhang, S.X.; Wang, J.J.; Gao, G.; Parke, K.; Ma, J.X. Pigment epithelium-derived factor downregulates vascular endothelial growth factor (VEGF) expression and inhibits VEGF-VEGF receptor 2 binding in diabetic retinopathy. J. Mol. Endocrinol. 2006, 37, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Mirza, J. Joint seals for hydraulic structure in sever climates. J. Civ. Eng. Manag. 2014, 20, 38–46. [Google Scholar] [CrossRef]
- Yamabe, J.; Nishimura, S. Tensile Properties and Swelling Behavior of Sealing Rubber Materials Exposed to High-Pressure Hydrogen Gas. J. Solid Mech. Mater. Eng. 2012, 6, 466–477. [Google Scholar] [CrossRef] [Green Version]
- Orzechowski, G.; Frączek, J. Nearly incompressible nonlinear material models in the large deformation analysis of beams using ANCF. Nonlinear Dyn. 2015, 82, 451–464. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Sin, F.; Zhu, Y.; Barbič, J. Nonlinear material design using principal stretches. ACM Trans. Graph. 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Yang, H.; Yao, X.F.; Ke, Y.C.; Ma, Y.J.; Liu, Y.H. Constitutive behaviors and mechanical characterizations of fabric reinforced rubber composites. Compos. Struct. 2016, 152, 117–123. [Google Scholar] [CrossRef]
- Maureira, N.; de La Llera, J.; Oyarzo, C.; Miranda, S. A nonlinear model for multilayered rubber isolators based on a co-rotational formulation. Eng. Struct. 2017, 131, 1–13. [Google Scholar] [CrossRef]
- Yaya, K.; Bechir, H. A new hyper-elastic model for predicting multi-axial behaviour of rubber-like materials: Formulation and computational aspects. Mech. Time-Depend. Mater. 2018, 22, 167–186. [Google Scholar] [CrossRef]
- Tiwari, A.; Dorogin, L.; Tahir, M.; Stöckelhuber, K.W.; Heinrich, G.; Espallargas, N.; Persson, B.N.J. Rubber contact mechanics: Adhesion, friction and leakage of seals. Soft Matter 2017, 13, 9103–9121. [Google Scholar] [CrossRef] [PubMed]
- Sanjaya, D.P.; Fidkowski, K.J. Improving High-Order Finite Element Approximation Through Geometrical Warping. AIAA J. 2016, 54, 3994–4010. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.R.; Jeong, H.Y. Development of Headform Impactor Finite Element Model Considering the Hyperelastic and Viscoelastic Responses of Rubber. Int. J. Automot. Technol. 2018, 19, 523–534. [Google Scholar] [CrossRef]
- Adams, G.G.; Nosonovsky, M. Contact modeling—Forces. Tribol. Int. 2000, 33, 431–442. [Google Scholar] [CrossRef]
- Belhocine, A.; Duzgun, M.; Ghazaly, N.M.; Abdullah, O.I. RETRACTED ARTICLE: Structural and contact analysis of a three-dimensional disc-pad model with and without thermal effects. Friction 2015. [Google Scholar] [CrossRef] [Green Version]
- Kawasaki, S.; Tada, T.; Persson, B.N.J. Adhesion and friction between glass and rubber in the dry state and in water: Role of contact hydrophobicity. Soft Matter 2018, 14, 5428–5441. [Google Scholar] [CrossRef]
- Shimanovsky, A.O.; Abdulkader, M.H.; Kuzniatsova, M.G. Finite Element Modelling of Contact Interaction between Spherical Indenter and Elastic-Plastic Body. Appl. Mech. Mater. 2015, 797, 307–313. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J. Static and Dynamic Sealing Performance Analysis of Rubber D-Ring Based on FEM. J. Fail. Anal. Prev. 2016, 16, 165–172. [Google Scholar] [CrossRef]
- Yamabe, J.; Nishimura, S. Influence of fillers on hydrogen penetration properties and blister fracture of rubber composites for O-ring exposed to high-pressure hydrogen gas. Int. J. Hydrogen Energy 2009, 34, 1977–1989. [Google Scholar] [CrossRef]
- Yamabe, J.; Koga, A.; Nishimura, S. Failure behavior of rubber O-ring under cyclic exposure to high-pressure hydrogen gas. Eng. Fail. Anal. 2013, 35, 193–205. [Google Scholar] [CrossRef]
- Jana, T.; Mitra, A.; Sahoo, P. Dynamic analysis of elastically and plastically graded spherical and cylindrical contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1712–1728. [Google Scholar] [CrossRef]
- Yeoh, O.H.; Pinter, G.A.; Banks, H.T. Compression of Bonded Rubber Blocks. Rubber Chem. Technol. 2002, 75, 549–562. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y.; Etsion, I. The effect of contact conditions and material properties on the elasticity terminus of a spherical contact. Int. J. Solids Struct. 2006, 43, 5736–5749. [Google Scholar] [CrossRef] [Green Version]
- Belhocine, A.; Omar, W.Z.W. Three-dimensional finite element modeling and analysis of the mechanical behavior of dry contact slipping between the disc and the brake pads. Int. J. Adv. Manuf. Technol. 2017, 88, 1035–1051. [Google Scholar] [CrossRef]
- Kožar, I.; Rukavina, T. The effect of material density on load rate sensitivity in nonlinear viscoelastic material models. Arch. Appl. Mech. 2019, 89, 873–883. [Google Scholar] [CrossRef]

| Variable | Number | Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Section diameter | Code | 1 | 2 | 3 | 4 | 5 | ||||||
| Value (mm) | 1.8 | 2.7 | 3.6 | 5.3 | 7 | |||||||
| Pre-compression | Code | A | B | C | D | E | F | G | H | K | ||
| Value (%) | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| Hydraulic pressure | Code | M | N | O | P | Q | R | S | T | U | V | W |
| Value (MPa) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wei, X. A Novel Structure of Rubber Ring for Hydraulic Buffer Seal Based on Numerical Simulation. Appl. Sci. 2021, 11, 2036. https://doi.org/10.3390/app11052036
Zhang L, Wei X. A Novel Structure of Rubber Ring for Hydraulic Buffer Seal Based on Numerical Simulation. Applied Sciences. 2021; 11(5):2036. https://doi.org/10.3390/app11052036
Chicago/Turabian StyleZhang, Lin, and Xiaohui Wei. 2021. "A Novel Structure of Rubber Ring for Hydraulic Buffer Seal Based on Numerical Simulation" Applied Sciences 11, no. 5: 2036. https://doi.org/10.3390/app11052036
APA StyleZhang, L., & Wei, X. (2021). A Novel Structure of Rubber Ring for Hydraulic Buffer Seal Based on Numerical Simulation. Applied Sciences, 11(5), 2036. https://doi.org/10.3390/app11052036






