A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful
Abstract
:1. Introduction
2. Motivation for Modeling
“FDA recognizes the public health benefits offered by modeling and simulation, including those in the area of in silico clinical trials (using individualized computer simulation in development and or regulatory evaluation of medical products, medical devices, or medical interventions).” [59]
3. Challenges to Progress
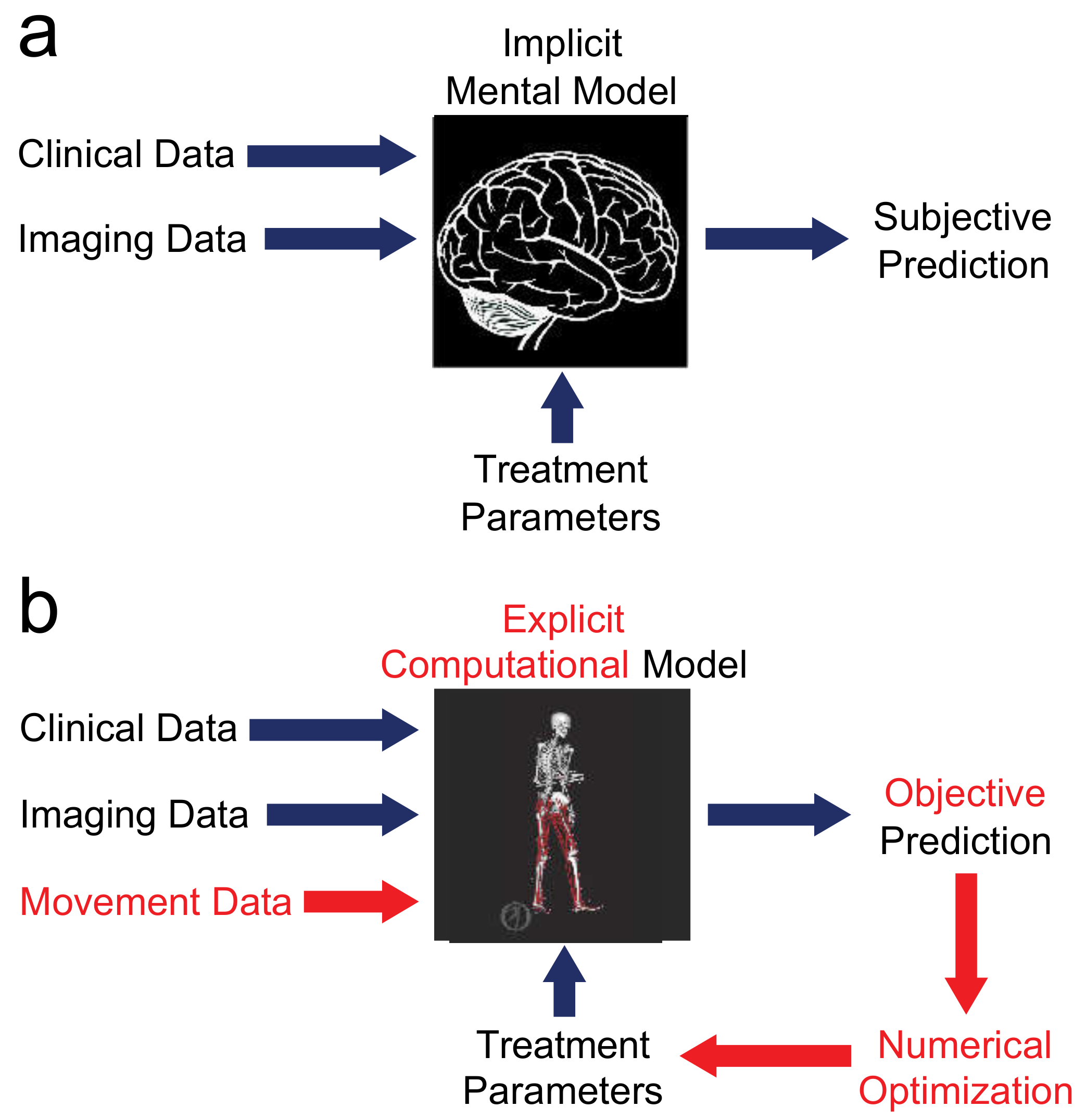
3.1. Movement Data Alone Do Not Provide the Answer
3.2. Every Patient Is Unique
3.3. People Change over Time
3.4. Validation Is Often Weak
3.5. Prediction of Post-Treatment Function Is Difficult
4. Description of Needs
4.1. Clinical Needs
4.2. Technical Needs
4.3. Collaboration Needs
4.4. Practical Needs
5. Opportunities for Enhancement
5.1. Enhanced Model Fidelity
5.2. Enhanced Model Personalization
5.3. Enhanced Model Utilization
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hatze, H. A comprehensive model for human motion simulation and its application to the take-off phase of the long jump. J. Biomech. 1981, 14, 135–142. [Google Scholar] [CrossRef]
- Mena, D.; Mansour, J.M.; Simon, S.R. Analysis and synthesis of human swing leg motion during gait and its clinical applications. J. Biomech. 1981, 14, 823–832. [Google Scholar] [CrossRef]
- Zajac, F.E.; Wicke, R.W.; Levine, W.S. Dependence of jumping performance on muscle properties when humans use only calf muscles for propulsion. J. Biomech. 1984, 17, 513–523. [Google Scholar] [CrossRef]
- Delp, S.L.; Loan, J.P.; Hoy, M.G.; Zajac, F.E.; Topp, E.L.; Rosen, J.M. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans. Biomed. Eng. 1990, 37, 757–767. [Google Scholar] [CrossRef] [PubMed]
- Audu, M.L.; Davy, D.T. The influence of muscle model complexity in musculoskeletal motion modeling. J. Biomech. Eng. 1985, 107, 147–157. [Google Scholar] [CrossRef]
- Hoy, M.G.; Zajac, F.E.; Gordon, M.E. A musculoskeletal model of the human lower extremity: The effect of muscle, tendon, and moment arm on the moment-angle relationship of musculotendon actuators at the hip, knee, and ankle. J. Biomech. 1990, 23, 157–169. [Google Scholar] [CrossRef]
- Yamaguchi, G.T.; Zajac, F.E. A planar model of the knee joint to characterize the knee extensor mechanism. J. Biomech. 1989, 22, 1–10. [Google Scholar] [CrossRef]
- Pandy, M.G.; Zajac, F.E.; Sim, E.; Levine, W.S. An optimal control model for maximum-height human jumping. J. Biomech. 1990, 23, 1185–1198. [Google Scholar] [CrossRef]
- Gerritsen, K.G.; van den Bogert, A.J.; Hulliger, M.; Zernicke, R.F. Intrinsic muscle properties facilitate locomotor control—A computer simulation study. Mot. Control 1998, 2, 206–220. [Google Scholar] [CrossRef]
- Blankevoort, L.; Kuiper, J.H.; Huiskes, R.; Grootenboer, H.J. Articular contact in a three-dimensional model of the knee. J. Biomech. 1991, 24, 1019–1031. [Google Scholar] [CrossRef] [Green Version]
- Fregly, B.J.; Zajac, F.E. A state-space analysis of mechanical energy generation, absorption, and transfer during pedaling. J. Biomech. 1996, 29, 81–90. [Google Scholar] [CrossRef]
- Neptune, R.R.; Hull, M.L. A theoretical analysis of preferred pedaling rate selection in endurance cycling. J. Biomech. 1999, 32, 409–415. [Google Scholar] [CrossRef]
- Raasch, C.C.; Zajac, F.E.; Ma, B.; Levine, W.S. Muscle coordination of maximum-speed pedaling. J. Biomech. 1997, 30, 595–602. [Google Scholar] [CrossRef]
- Hubbard, M. Computer simulation in sport and industry. J. Biomech. 1993, 26 (Suppl. S1), 53–61. [Google Scholar] [CrossRef]
- Van Soest, A.J.; Huijing, P.A.; Solomonow, M. The effect of tendon on muscle force in dynamic isometric contractions: A simulation study. J. Biomech. 1995, 28, 801–807. [Google Scholar] [CrossRef]
- Yeadon, M.R.; Atha, J.; Hales, F.D. The simulation of aerial movement--IV A computer simulation model. J. Biomech. 1990, 23, 85–89. [Google Scholar] [CrossRef] [Green Version]
- Fregly, B.J.; Reinbolt, J.A.; Rooney, K.L.; Mitchell, K.H.; Chmielewski, T.L. Design of patient-specific gait modifications for knee osteoarthritis rehabilitation. IEEE Trans. Biomed. Eng. 2007, 54, 1687–1695. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, A.; Kidziński, Ł.; McGlaughlin, A.; Hicks, J.; Delp, S.; Schwartz, M. Pre-operative gastrocnemius lengths in gait predict outcomes following gastrocnemius lengthening surgery in children with cerebral palsy. PLoS ONE 2020, 15, e0233706. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef] [PubMed]
- Fregly, B.J.; Boninger, M.L.; Reinkensmeyer, D.J. Personalized neuromusculoskeletal modeling to improve treatment of mobility impairments: A perspective from European research sites. J. Neuroeng. Rehabil. 2012, 9, 18. [Google Scholar] [CrossRef] [Green Version]
- McMorland, A.J.C.; Runnalls, K.D.; Byblow, W.D. A neuroanatomical framework for upper limb synergies after stroke. Front. Hum. Neurosci. 2015, 9, 82. [Google Scholar] [CrossRef]
- Song, S.; Geyer, H. Predictive neuromechanical simulations indicate why walking performance declines with ageing. J. Physiol. 2018, 596, 1199–1210. [Google Scholar] [CrossRef]
- Thelen, D.G.; Chumanov, E.S.; Sherry, M.A.; Heiderscheit, B.C. Neuromusculoskeletal models provide insights into the mechanisms and rehabilitation of hamstring strains. Exerc. Sport Sci. Rev. 2006, 34, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Butler, D. Crossing the valley of death. Nature 2008, 453, 840–842. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.J.; Eskinazi, I.; Jackson, J.N.; Rao, A.V.; Patten, C.; Fregly, B.J. Muscle synergies facilitate computational prediction of subject-specific walking motions. Front. Bioeng. Biotechnol. 2016, 4, 77. [Google Scholar] [CrossRef] [Green Version]
- Sauder, N.R.; Meyer, A.J.; Allen, J.L.; Ting, L.H.; Kesar, T.M.; Fregly, B.J. Computational design of FastFES treatment to improve propulsive force symmetry during post-stroke gait: A feasibility study. Front. Neurorobotics 2019, 13, 80. [Google Scholar] [CrossRef]
- Pitto, L.; Kainz, H.; Falisse, A.; Wesseling, M.; van Rossom, S.; Hoang, H.; Papageorgiou, E.; Hallemans, A.; Desloovere, K.; Molenaers, G.; et al. SimCP: A simulation platform to predict gait performance following orthopedic intervention in children with cerebral palsy. Front. Neurorobotics 2019, 13, 54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harve Bennett Productions, Silverton Productions, and Universal Television. The Six Million Dollar Man; Harve Bennett Productions, Silverton Productions, and Universal Television: Los Angeles, CA, USA, 1974. [Google Scholar]
- Ma, V.Y.; Chan, L.; Carruthers, K.J. Incidence, prevalence, costs, and impact on disability of common conditions requiring rehabilitation in the United States: Stroke, spinal cord injury, traumatic brain injury, multiple sclerosis, osteoarthritis, rheumatoid arthritis, limb loss, and back pa. Arch. Phys. Med. Rehabil. 2014, 95, 986–995. [Google Scholar] [CrossRef] [Green Version]
- Ovbiagele, B.; Goldstein, L.B.; Higashida, R.T.; Howard, V.J.; Johnston, S.C.; Khavjou, O.A.; Lackland, D.T.; Lichtman, J.H.; Mohl, S.; Sacco, R.L.; et al. Forecasting the future of stroke in the United States: A policy statement from the American Heart Association and American Stroke Association. Stroke 2013, 44, 2361–2375. [Google Scholar] [CrossRef] [Green Version]
- Theis, K.A.; Roblin, D.W.; Helmick, C.G.; Luo, R. Prevalence and causes of work disability among working-age US adults, 2011-2013, NHIS. Disabil. Health J. 2018, 11, 108–115. [Google Scholar] [CrossRef]
- Praemer, A.; Furner, S.; Rice, D.P. Musculoskeletal Conditions in the United States; American Academy of Orthopaedic Surgeons: Rosemont, IL, USA, 1999. [Google Scholar]
- Proietti, T.; Crocher, V.; Roby-Brami, A.; Jarrasse, N. Upper-limb robotic exoskeletons for neurorehabilitation: A review on control strategies. IEEE Rev. Biomed. Eng. 2016, 9, 4–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allen, J.L.; Ting, L.H.; Kesar, T.M. Gait rehabilitation using functional electrical stimulation induces changes in ankle muscle coordination in stroke survivors: A preliminary study. Front. Neurol. 2018, 9, 1127. [Google Scholar] [CrossRef] [PubMed]
- Barbour, K.E.; Helmick, C.G.; Boring, M.; Brady, T.J. Vital signs: Prevalence of doctor-diagnosed arthritis and arthritis-attributable activity limitation-United States, 2013-2015. Mmwr Morb. Mortal. Wkly. Rep. 2017, 66, 246–253. [Google Scholar] [CrossRef]
- Dunbar, M.J.; Richardson, G.; Robertsson, O. I can’t get no satisfaction after my total knee replacement: Rhymes and reasons. Bone Joint J. 2013, 95-B, 148–152. [Google Scholar] [CrossRef] [Green Version]
- Brandstater, M.E.; de Bruin, H.; Gowland, C.; Clark, B.M. Hemiplegic gait: Analysis of temporal variables. Arch. Phys. Med. Rehabil. 1983, 64, 583–587. [Google Scholar]
- Chen, G.; Patten, C.; Kothari, D.H.; Zajac, F.E. Gait differences between individuals with post-stroke hemiparesis and non-disabled controls at matched speeds. Gait Posture 2005, 22, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Patten, C.; Kothari, D.H.; Zajac, F.E. Gait deviations associated with post-stroke hemiparesis: Improvement during treadmill walking using weight support, speed, support stiffness, and handrail hold. Gait Posture 2005, 22, 57–62. [Google Scholar] [CrossRef] [PubMed]
- Olney, S.J.; Monga, T.N.; Costigan, P.A. Mechanical energy of walking of stroke patients. Arch. Phys. Med. Rehabil. 1986, 67, 92–98. [Google Scholar] [CrossRef]
- Duncan, P.W.; Sullivan, K.J.; Behrman, A.L.; Azen, S.P.; Wu, S.S.; Nadeau, S.E.; Dobkin, B.H.; Rose, D.K.; Tilson, J.K.; Cen, S.; et al. Body-weight–supported treadmill rehabilitation after stroke. N. Engl. J. Med. 2011, 364, 2026–2036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baars, E.C.; Schrier, E.; Dijkstra, P.U.; Geertzen, J.H.B. Prosthesis satisfaction in lower limb amputees: A systematic review of associated factors and questionnaires. Medicine 2018, 97, e12296. [Google Scholar] [CrossRef] [PubMed]
- Gerrand, C.H.; Bell, R.S.; Griffin, A.M.; Wunder, J.S. Instability after major tumor resection: Prevention and treatment. Orthop. Clin. N. Am. 2001, 32, 697–710. [Google Scholar] [CrossRef]
- Lewis, V.O. Internal hemipelvectomies: Resection and reconstructive options. Oper. Tech. Orthop. 2014, 24, 74–78. [Google Scholar] [CrossRef]
- Heaven, D. The Designer Changing the Way Aircraft are Built. BBC Future. 2018. Available online: https://www.bbc.com/future/article/20181129-the-ai-transforming-the-way-aircraft-are-built (accessed on 29 December 2020).
- Koebler, J. SpaceX is Using These Simulations to Design the Rocket That’ll Take us to Mars. Vice. 2015. Available online: https://www.vice.com/en_us/article/ezv79w/spacex-i (accessed on 29 December 2020).
- Alexander, C. A Brief History of Computing in Formula 1. McLaren Website. 2016. Available online: https://www.mclaren.com/racing/team/a-brief-history-of-computing-in-F1-1052199/ (accessed on 29 December 2020).
- Niccolai, J. The America’s Cup: Nerves, Skill, and Computer Design. PCWorld. 2013. Available online: https://www.pcworld.com/article/2049820/the-americas-cup-nerves-skill-and-a-lot-of-computers.html (accessed on 29 December 2020).
- Dandy, G.; Daniell, T.; Foley, B.; Warner, R. Planning and Design of Engineering Systems, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gualdrón, C.-I.L.; Ibarra, E.-R.B.; Bohórquez, A.-P.; Bohórquez, M.I.G. Present and future for technologies to develop patient-specific medical devices: A systematic review approach. Med. Devices Evid. Res. 2019, 12, 253–273. [Google Scholar] [CrossRef] [Green Version]
- Sharma, K.J.; Bowonder, B. The making of the Boeing 777: A case study in concurrent engineering. Int. J. Manuf. Technol. Manag. 2004, 6, 254–264. [Google Scholar] [CrossRef]
- Zhang, B. The glorious history of the best plane Boeing has ever built. Business Insider. 2018. Available online: https://www.businessinsider.nl/boeing-777-history-2017-6/ (accessed on 29 December 2020).
- Weiss, S.I.; Amir, A.R. Aerospace Industry-Design Methods. In Encyclopædia Britannica; Encyclopædia Britannica Inc.: Chicago, IL, USA, 2019. [Google Scholar]
- Petroski, H. Engineering: The Boeing 777. Am. Sci. 1995, 83, 519–522. [Google Scholar]
- Vishwas, M.; Vinyas, M.; Puneeth, K. Application of computer aided engineering in reducing the product development life cycle. Int. J. Innov. Res. Sci. Technol. 2016, 2, 19–22. [Google Scholar]
- Miller, L. Product innovation through computational prototypes and supercomputing. IEEE Comput. Sci. Eng. 2017, 19, 9–17. [Google Scholar] [CrossRef]
- Morrison, T.M.; Pathmanathan, P.; Adwan, M.; Margerrison, E. Advancing regulatory science with computational modeling for medical devices at the FDA’s Office of Science and Engineering Laboratories. Front. Med. 2018, 5, 241. [Google Scholar] [CrossRef] [Green Version]
- James, G. Using Simulation in Medical Device Design-Image-Based Modeling and Simulation are Becoming Increasingly Common for Device Design. Orthopedic Design & Technology. 2015. Available online: https://www.odtmag.com/issues/2015-11-01/view_features/using-simulation-in-medical-device-design (accessed on 29 December 2020).
- Morrison, T. How Simulation Can Transform Regulatory Pathways. In Food and Drug Administration; U.S. Food & Drug Administration; 2018. Available online: https://www.fda.gov/science-research/about-science-research-fda/how-simulation-can-transform-regulatory-pathways (accessed on 29 December 2020).
- Mehrotra, D.; Howlader, D.; Singh, P.K.; Gupta, S. Patient specific three-dimensional implant for reconstruction of complex mandibular defect. J. Craniofacial Surg. 2019, 30, e308–e311. [Google Scholar]
- Sutradhar, A.; Park, J.; Carrau, D.; Miller, M.J. Experimental validation of 3D printed patient-specific implants using digital image correlation and finite element analysis. Comput. Biol. Med. 2014, 52, 8–17. [Google Scholar] [CrossRef]
- Pinheiro, M.; Alves, J.L. The feasibility of a custom-made endoprosthesis in mandibular reconstruction: Implant design and finite element analysis. J. Cranio Maxillo Facial Surg. 2015, 43, 2116–2128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anonymous. HeartFlow. HeartFlow Website. 2020. Available online: https://www.heartflow.com/ (accessed on 29 December 2020).
- Gray, R.A.; Pathmanathan, P. Patient-specific cardiovascular computational modeling: Diversity of personalization and challenges. J. Cardiovasc. Transl. Res. 2018, 11, 80–88. [Google Scholar] [CrossRef] [Green Version]
- Hlatky, M.A.; de Bruyne, B.; Pontone, G.; Patel, M.R.; Norgaard, B.L.; Byrne, R.A.; Curzen, N.; Purcell, I.; Gutberlet, M.; Rioufol, G.; et al. Quality-of-life and economic outcomes of assessing fractional flow reserve with computed tomography angiography: PLATFORM. J. Am. Coll. Cardiol. 2015, 66, 2315–2323. [Google Scholar] [CrossRef] [Green Version]
- Douglas, P.S.; Pontone, G.; Hlatky, M.A.; Patel, M.R.; Norgaard, B.L.; Byrne, R.A.; Curzen, N.; Purcell, I.; Gutberlet, M.; Rioufol, G.; et al. Clinical outcomes of fractional flow reserve by computed tomographic angiography-guided diagnostic strategies vs usual care in patients with suspected coronary artery disease: The prospective longitudinal trial of FFR(CT): Outcome and resource impacts st. Eur. Heart J. 2015, 36, 3359–3367. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.S.; Goyal, P.; Li, C.; Zhao, K. Computational fluid dynamics to evaluate the effectiveness of inferior turbinate reduction techniques to improve nasal airflow. JAMA Facial Plast. Surg. 2018, 20, 263–270. [Google Scholar] [CrossRef] [Green Version]
- Boyle, P.M.; Zghaib, T.; Zahid, S.; Ali, R.L.; Deng, D.; Franceschi, W.H.; Hakim, J.B.; Murphy, M.J.; Prakosa, A.; Zimmerman, S.L.; et al. Computationally guided personalized targeted ablation of persistent atrial fibrillation. Nat. Biomed. Eng. 2019, 3, 870–879. [Google Scholar] [CrossRef]
- Uchida, T.; Delp, S. Biomechanics of Movement: Science of Sports, Robotics, and Rehabiliation; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Fregly, B.J.; D’Lima, D.D.; Colwell, C.W. Effective gait patterns for offloading the medial compartment of the knee. J. Orthop. Res. 2009, 27, 1016–1021. [Google Scholar] [CrossRef] [Green Version]
- Gerbrands, T.A.; Pisters, M.F.; Theeven, P.J.R.; Verschueren, S.; Vanwanseele, B. Lateral trunk lean and medializing the knee as gait strategies for knee osteoarthritis. Gait Posture 2017, 51, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Ferrigno, C.; Wimmer, M.A.; Trombley, R.M.; Lundberg, H.J.; Shakoor, N.; Thorp, L.E. A reduction in the knee adduction moment with medial thrust gait is associated with a medial shift in center of plantar pressure. Med. Eng. Phys. 2016, 38, 615–621. [Google Scholar] [CrossRef] [PubMed]
- Gerbrands, T.A.; Pisters, M.F.; Vanwanseele, B. Individual selection of gait retraining strategies is essential to optimally reduce medial knee load during gait. Clin. Biomech. 2014, 29, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, L.K.; Laubach, L.L.; Barrios, J.A. Effect of specific gait modifications on medial knee loading, metabolic cost and perception of task difficulty. Clin. Biomech. 2013, 28, 649–654. [Google Scholar] [CrossRef]
- Shull, P.B.; Lurie, K.L.; Cutkosky, M.R.; Besier, T.F. Training multi-parameter gaits to reduce the knee adduction moment with data-driven models and haptic feedback. J. Biomech. 2011, 44, 1605–1609. [Google Scholar] [CrossRef]
- Barrios, J.A.; Crossley, K.M.; Davis, I.S. Gait retraining to reduce the knee adduction moment through real-time visual feedback of dynamic knee alignment. J. Biomech. 2010, 43, 2208–2213. [Google Scholar] [CrossRef] [Green Version]
- Dowling, A.V.; Fisher, D.S.; Andriacchi, T.P. Gait modification via verbal instruction and an active feedback system to reduce peak knee adduction moment. J. Biomech. Eng. 2010, 132, 071007. [Google Scholar] [CrossRef]
- Schwartz, R.P.; Heath, A.L. The pneumographic method of recording gait. J. Bone Jt. Surg. (Am.) 1932, 14, 783–794. [Google Scholar]
- Lofterød, B.; Terjesen, T.; Skaaret, I.; Huse, A.; Jahnsen, R. Preoperative gait analysis has a substantial effect on orthopedic decision making in children with cerebral palsy: Comparison between clinical evaluation and gait analysis in 60 patients. Acta Orthop. 2007, 78, 74–80. [Google Scholar] [CrossRef]
- Lofterød, B.; Terjesen, T. Results of treatment when orthopaedic surgeons follow gait-analysis recommendations in children with CP. Dev. Med. Child Neurol. 2008, 50, 503–509. [Google Scholar] [CrossRef]
- Ferrari, A.; Brunner, R.; Faccioli, S.; Reverberi, S.; Benedetti, M. Gait analysis contribution to problems identification and surgical planning in CP patients: An agreement study. Eur. J. Phys. Rehabil. Med. 2015, 51, 39–48. [Google Scholar] [PubMed]
- Brand, R.A. Locomotion analysis. In Oxford Textbook of Orthopaedics and Trauma, 1st ed.; Bulstrode, C., Buckwalter, J.J., Carr, A., Marsh, L., Fairbank, J., Wilson-MacDonald, J., Bowden, G., Eds.; Oxford University Press: New York, NY, USA, 2002; pp. 439–454. [Google Scholar]
- Zajac, F.E. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 1989, 17, 359–411. [Google Scholar]
- Hatem, S.M.; Saussez, G.; della Faille, M.; Prist, V.; Zhang, X.; Dispa, D.; Bleyenheuft, Y. Rehabilitation of motor function after stroke: A multiple systematic review focused on techniques to stimulate upper extremity recovery. Front. Hum. Neurosci. 2016, 10, 442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akhras, M.A.; Bortoletto, R.; Madehkhaksar, F.; Tagliapietra, L. Neural and musculoskeletal modeling: Its role in neurorehabilitation. In Emerging Therapies in Neurorehabilitation II (Biosystems & Biorobotics), 1st ed.; Pons, J.L., Raya, R., González, J., Eds.; Springer: New York, NY, USA, 2016; pp. 109–144. [Google Scholar]
- Serrancoli, G.; Kinney, A.L.; Fregly, B.J.; Font-Llagunes, J.M. Neuromusculoskeletal model calibration significantly affects predicted knee contact forces for walking. J. Biomech. Eng. 2016, 138, 081001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Żuk, M.; Syczewska, M.; Pezowicz, C. Influence of uncertainty in selected musculoskeletal model parameters on muscle forces estimated in inverse dynamics-based static optimization and hybrid approach. J. Biomech. Eng. 2018, 140, 121001. [Google Scholar] [CrossRef]
- Lloyd, D.G.; Besier, T.F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Manal, K.; Buchanan, T.S. Use of an EMG-driven biomechanical model to study virtual injuries. Med. Sci. Sports Exerc. 2005, 37, 1917–1923. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.J.; Patten, C.; Fregly, B.J. Lower extremity EMG-driven modeling of walking with automated adjustment of musculoskeletal geometry. PLoS ONE 2017, 12, e0179698. [Google Scholar] [CrossRef] [PubMed]
- Reinbolt, J.A.; Haftka, R.T.; Chmielewski, T.L.; Fregly, B.J. Are patient-specific joint and inertial parameters necessary for accurate inverse dynamics analyses of gait? IEEE Trans. Biomed. Eng. 2007, 54, 782–793. [Google Scholar] [CrossRef] [Green Version]
- Moissenet, F.; Modenese, L.; Dumas, R. Alterations of musculoskeletal models for a more accurate estimation of lower limb joint contact forces during normal gait: A systematic review. J. Biomech. 2017, 63, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Arones, M.; Shourijeh, M.S.; Patten, C.; Fregly, B.J. Musculoskeletal model personalization affects metabolic cost estimates for walking. Front. Bioeng. Biotechnol. 2020, in press. [Google Scholar] [CrossRef]
- Gerus, P.; Sartori, M.; Besier, T.F.; Fregly, B.J.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’Lima, D.D.; Lloyd, D.G. Subject-specific knee joint geometry improves predictions of medial tibiofemoral contact forces. J. Biomech. 2013, 46, 2778–2786. [Google Scholar] [CrossRef] [Green Version]
- National Academy of Engineering, Engineering Better Medicines. 2010. Available online: http://www.engineeringchallenges.org/challenges/medicines.aspx (accessed on 29 December 2020).
- Carter, D.R.; Vasu, R.; Harris, W.H. Stress changes in the femoral head due to porous ingrowth surface replacement arthroplasty. J. Biomech. 1984, 17, 737–747. [Google Scholar] [CrossRef]
- Fyhrie, D.P.; Schaffler, M.B. The adaptation of bone apparent density to applied load. J. Biomech. 1995, 28, 135–146. [Google Scholar] [CrossRef]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An approach for time-dependent bone modeling and remodeling-application: A preliminary remodeling simulation. J. Orthop. Res. 1990, 8, 662–670. [Google Scholar] [CrossRef]
- Ruimerman, R.; Hilbers, P.; van Rietbergen, B.; Huiskes, R. A theoretical framework for strain-related trabecular bone maintenance and adaptation. J. Biomech. 2005, 38, 931–941. [Google Scholar] [CrossRef]
- Jacobs, C.R.; Levenston, M.E.; Beaupré, G.S.; Simo, J.C.; Carter, D.R. Numerical instabilities in bone remodeling simulations: The advantages of a node-based finite element approach. J. Biomech. 1995, 28, 449–459. [Google Scholar] [CrossRef] [Green Version]
- Siffert, R.S.; Luo, G.M.; Cowin, S.C.; Kaufman, J.J. Dynamic relationships of trabecular bone density, architecture, and strength in a computational model of osteopenia. Bone 1996, 18, 197–206. [Google Scholar] [CrossRef]
- Martin, K.S.; Virgilio, K.M.; Peirce, S.M.; Blemker, S.S. Computational modeling of muscle regeneration and adaptation to advance muscle tissue regeneration strategies. Cells Tissues Organs 2016, 202, 250–266. [Google Scholar] [CrossRef]
- Brand, R.A. Biomechanics or necromechanics? Or how to interpret biomechanical studies. Iowa Orthop. J. 2002, 22, 110–115. [Google Scholar] [PubMed]
- Reinkensmeyer, D.J.; Burdet, E.; Casadio, M.; Krakauer, J.W.; Kwakkel, G.; Lang, C.E.; Swinnen, S.P.; Ward, N.S.; Schweighofer, N. Computational neurorehabilitation: Modeling plasticity and learning to predict recovery. J. Neuroeng. Rehabil. 2016, 13, 42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hicks, J.L.; Uchida, T.K.; Seth, A.; Rajagopal, A.; Delp, S.L. Is my model good enough? Best practices for verification and validation of musculoskeletal models and simulations of movement. J. Biomech. Eng. 2015, 137, 020905. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, D.R.; Brand, R.A.; Cheng, C.; Arora, J.S. Direct comparison of muscle force predictions using linear and nonlinear programming. J. Biomech. Eng. 1987, 109, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, K.R.; An, K.W.; Litchy, W.J.; Chao, E.Y. Physiological prediction of muscle forces--I Theoretical formulation. Neuroscience 1991, 40, 781–792. [Google Scholar] [CrossRef]
- Li, G.; Kaufman, K.R.; Chao, E.Y.; Rubash, H.E. Prediction of antagonistic muscle forces using inverse dynamic optimization during flexion/extension of the knee. J. Biomech. Eng. 1999, 121, 316–322. [Google Scholar] [CrossRef]
- Jinha, A.; Ait-Haddou, R.; Binding, P.; Herzog, W. Antagonistic activity of one-joint muscles in three-dimensions using non-linear optimisation. Math. Biosci. 2006, 202, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R.; Heller, M.O.; Bergmann, G.; Duda, G.N. Tibio-femoral loading during human gait and stair climbing. J. Orthop. Res. 2004, 22, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, G.; Deuretzbacher, G.; Heller, M.; Graichen, F.; Rohlmann, A.; Strauss, J.; Duda, G.N. Hip contact forces and gait patterns from routine activities. J. Biomech. 2001, 34, 859–871. [Google Scholar] [CrossRef]
- Brand, R.A.; Pedersen, D.R.; Davy, D.T.; Kotzar, G.M.; Heiple, K.G.; Goldberg, V.M. Comparison of hip force calculations and measurements in the same patient. J. Arthroplast. 1994, 9, 45–51. [Google Scholar] [CrossRef]
- Graichen, F.; Bergmann, G. Four-channel telemetry system for in vivo measurement of hip joint forces. J. Biomed. Eng. 1991, 13, 370–374. [Google Scholar] [CrossRef]
- Heller, M.O.; Bergmann, G.; Deuretzbacher, G.; Dürselen, L.; Pohl, M.; Claes, L.; Haas, N.P.; Duda, G.N. Musculo-skeletal loading conditions at the hip during walking and stair climbing. J. Biomech. 2001, 34, 883–893. [Google Scholar] [CrossRef]
- Rohlmann, A.; Graichen, F.; Bender, A.; Kayser, R.; Bergmann, G. Loads on a telemeterized vertebral body replacement measured in three patients within the first postoperative month. Clin. Biomech. 2008, 23, 147–158. [Google Scholar] [CrossRef]
- Stansfield, B.W.; Nicol, A.C.; Paul, J.P.; Kelly, I.G.; Graichen, F.; Bergmann, G. Direct comparison of calculated hip joint contact forces with those measured using instrumented implants An evaluation of a three-dimensional mathematical model of the lower limb. J. Biomech. 2003, 36, 929–936. [Google Scholar] [CrossRef]
- Kaufman, K.R.; Kovacevic, N.; Irby, S.E.; Colwell, C.W. Instrumented implant for measuring tibiofemoral forces. J. Biomech. 1996, 29, 667–671. [Google Scholar] [CrossRef]
- D’Lima, D.D.; Patil, S.; Steklov, N.; Slamin, J.E.; Colwell, C.W. The Chitranjan Ranawat Award: In vivo knee forces after total knee arthroplasty. Clin. Orthop. Relat. Res. 2005, 440, 45–49. [Google Scholar] [CrossRef]
- D’Lima, D.D.; Steklov, N.; Patil, S.; Colwell, C.W. The Mark Coventry Award: In vivo knee forces during recreation and exercise after knee arthroplasty. Clin. Orthop. Relat. Res. 2008, 466, 2605–2611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Lima, D.D.; Townsend, C.P.; Arms, S.W.; Morris, B.A.; Colwell, C.W. An implantable telemetry device to measure intra-articular tibial forces. J. Biomech. 2005, 38, 299–304. [Google Scholar] [CrossRef]
- Fregly, B.J.; Besier, T.F.; Lloyd, D.G.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’Lima, D.D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, R.; Schütz, P.; Bergmann, G.; List, R.; Postolka, B.; Hitz, M.; Dymke, J.; Damm, P.; Duda, G.; Gerber, H.; et al. A comprehensive assessment of the musculoskeletal system: The CAMS-Knee data set. J. Biomech. 2017, 65, 32–39. [Google Scholar] [CrossRef]
- Anonymous. Orthoload. OrthoLoad—Loading of Orthopaedic Implants Website. 2020. Available online: https://orthoload.com/ (accessed on 29 December 2020).
- Finni, T.; Komi, P.V.; Lukkariniemi, J. Achilles tendon loading during walking: Application of a novel optic fiber technique. Eur. J. Appl. Physiol. Occup. Physiol. 1998, 77, 289–291. [Google Scholar] [CrossRef] [PubMed]
- Komi, P.V.; Fukashiro, S.; Järvinen, M. Biomechanical loading of Achilles tendon during normal locomotion. Clin. Sports Med. 1992, 11, 521–531. [Google Scholar] [CrossRef]
- Ishikawa, M.; Komi, P.V.; Grey, M.J.; Lepola, V.; Bruggemann, G.P. Muscle-tendon interaction and elastic energy usage in human walking. J. Appl. Physiol. 2005, 99, 603–608. [Google Scholar] [CrossRef] [Green Version]
- Dennerlein, J.T.; Diao, E.; Mote, C.D.; Rempel, D.M. Tensions of the flexor digitorum superficialis are higher than a current model predicts. J. Biomech. 1998, 31, 295–301. [Google Scholar] [CrossRef]
- Schuind, F.; Garcia-Elias, M.; Cooney, W.P.; An, K.N. Flexor tendon forces: In vivo measurements. J. Hand Surg. 1992, 17, 291–298. [Google Scholar] [CrossRef]
- Gregor, R.J.; Komi, P.V.; Järvinen, M. Achilles tendon forces during cycling. Int. J. Sports Med. 1987, 8 (Suppl. S1), 9–14. [Google Scholar] [CrossRef]
- Martin, J.A.; Brandon, S.C.E.; Keuler, E.M.; Hermus, J.R.; Ehlers, A.C.; Segalman, D.J.; Allen, M.S.; Thelen, D.G. Gauging force by tapping tendons. Nat. Commun. 2018, 9, 1592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Acuña, S.A.; Ebrahimi, A.; Pomeroy, R.L.; Martin, J.A.; Thelen, D.G. Achilles tendon shear wave speed tracks the dynamic modulation of standing balance. Physiol. Rep. 2019, 7, e14298. [Google Scholar] [CrossRef]
- Fregly, B.J.; D’Lima, D.D.; Besier, T.F. SimTK: Grand Challenge Competition to Predict In Vivo Knee Loads: Project Home. SimTK.org Project. 2021. Available online: https://simtk.org/projects/kneeloads (accessed on 8 February 2021).
- Erdemir, A.; Hunter, P.J.; Holzapfel, G.A.; Loew, L.M.; Middleton, J.; Jacobs, C.R.; Nithiarasu, P.; Löhner, R.; Wei, G.; Winkelstein, B.A.; et al. Perspectives on sharing models and related resources in computational biomechanics research. J. Biomech. Eng. 2018, 140, 0247011. [Google Scholar] [CrossRef] [Green Version]
- Anderson, F.C.; Pandy, M.G. Dynamic optimization of human walking. J. Biomech. Eng. 2001, 123, 381–390. [Google Scholar] [CrossRef] [Green Version]
- Falisse, A.; Serrancolí, G.; Dembia, C.L.; Gillis, J.; Jonkers, I.; de Groote, F. Rapid predictive simulations with complex musculoskeletal models suggest that diverse healthy and pathological human gaits can emerge from similar control strategies. J. R. Soc. Interface 2019, 16, 20190402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falisse, A.; Pitto, L.; Kainz, H.; Hoang, H.; Wesseling, M.; van Rossom, S.; Papageorgiou, E.; Bar-On, L.; Hallemans, A.; Desloovere, K.; et al. Physics-based simulations to predict the differential effects of motor control and musculoskeletal deficits on gait dysfunction in cerebral palsy: A retrospective case study. Front. Hum. Neurosci. 2020, 14, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allen, J.L.; Kautz, S.A.; Neptune, R.R. The influence of merged muscle excitation modules on post-stroke hemiparetic walking performance. Clin. Biomech. 2013, 28, 697–704. [Google Scholar] [CrossRef] [Green Version]
- Miller, R.H. A comparison of muscle energy models for simulating human walking in three dimensions. J. Biomech. 2014, 47, 1373–1381. [Google Scholar] [CrossRef]
- Miller, R.H.; Esterson, A.Y.; Shim, J.K. Joint contact forces when minimizing the external knee adduction moment by gait modification: A computer simulation study. Knee 2015, 22, 481–489. [Google Scholar] [CrossRef]
- John, C.T.; Anderson, F.C.; Higginson, J.S.; Delp, S.L. Stabilisation of walking by intrinsic muscle properties revealed in a three-dimensional muscle-driven simulation. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 452–462. [Google Scholar] [CrossRef] [Green Version]
- Steele, K.M.; van der Krogt, M.M.; Schwartz, M.H.; Delp, S.L. How much muscle strength is required to walk in a crouch gait? J. Biomech. 2012, 45, 2564–2569. [Google Scholar] [CrossRef] [Green Version]
- Hamner, S.R.; Seth, A.; Delp, S.L. Muscle contributions to propulsion and support during running. J. Biomech. 2010, 43, 2709–2716. [Google Scholar] [CrossRef] [Green Version]
- Knarr, B.A.; Reisman, D.S.; Binder-Macleod, S.A.; Higginson, J.S. Understanding compensatory strategies for muscle weakness during gait by simulating activation deficits seen post-stroke. Gait Posture 2013, 38, 270–275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pitto, L.; van Rossom, S.; Desloovere, K.; Molenaers, G.; Huenaerts, C.; de Groote, F.; Jonkers, I. Pre-treatment EMG can be used to model post-treatment muscle coordination during walking in children with cerebral palsy. PLoS ONE 2020, 15, e0228851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogihara, N.; Yamazaki, N. Generation of human bipedal locomotion by a bio-mimetic neuro-musculo-skeletal model. Biol. Cybern. 2001, 84, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Van Soest, A.J.; Haenen, W.P.; Rozendaal, L.A. Stability of bipedal stance: The contribution of cocontraction and spindle feedback. Biol. Cybern. 2003, 88, 293–301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jo, S.; Massaquoi, S.G. A model of cerebrocerebello-spinomuscular interaction in the sagittal control of human walking. Biol. Cybern. 2007, 96, 279–307. [Google Scholar] [CrossRef]
- Jo, S. A neurobiological model of the recovery strategies from perturbed walking. Biosystems 2007, 90, 750–768. [Google Scholar] [CrossRef]
- Geyer, H.; Herr, H. A muscle-reflex model that encodes principles of legged mechanics produces human walking dynamics and muscle activities. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 263–273. [Google Scholar] [CrossRef]
- Kistemaker, D.A.; van Soest, A.J.K.; Wong, J.D.; Kurtzer, I.; Gribble, P.L. Control of position and movement is simplified by combined muscle spindle and Golgi tendon organ feedback. J. Neurophysiol. 2013, 109, 1126–1139. [Google Scholar] [CrossRef] [Green Version]
- Tsianos, G.A.; Goodner, J.; Loeb, G.E. Useful properties of spinal circuits for learning and performing planar reaches. J. Neural Eng. 2014, 11, 056006. [Google Scholar] [CrossRef] [PubMed]
- Byadarhaly, K.V.; Perdoor, M.C.; Minai, A.A. A modular neural model of motor synergies. Neural Netw. 2012, 32, 96–108. [Google Scholar] [CrossRef]
- Sreenivasa, M.; Ayusawa, K.; Nakamura, Y. Modeling and identification of a realistic spiking neural network and musculoskeletal model of the human arm, and an application to the stretch reflex. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 591–602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hardesty, R.L.; Boots, M.T.; Yakovenko, S.; Gritsenko, V. Computational evidence for nonlinear feedforward modulation of fusimotor drive to antagonistic co-contracting muscles. Sci. Rep. 2020, 10, 10625. [Google Scholar] [CrossRef] [PubMed]
- Aoi, S.; Ohashi, T.; Bamba, R.; Fujiki, S.; Tamura, D.; Funato, T.; Senda, K.; Ivanenko, Y.; Tsuchiya, K. Neuromusculoskeletal model that walks and runs across a speed range with a few motor control parameter changes based on the muscle synergy hypothesis. Sci. Rep. 2019, 9, 369. [Google Scholar] [CrossRef] [Green Version]
- Dzeladini, F.; van den Kieboom, J.; Ijspeert, A. The contribution of a central pattern generator in a reflex-based neuromuscular model. Front. Hum. Neurosci. 2014, 8, 371. [Google Scholar] [CrossRef] [Green Version]
- Markin, S.N.; Klishko, A.N.; Shevtsova, N.A.; Lemay, M.A.; Prilutsky, B.I.; Rybak, I.A. Afferent control of locomotor CPG: Insights from a simple neuromechanical model. Ann. N. Y. Acad. Sci. 2010, 1198, 21–34. [Google Scholar] [CrossRef]
- Endo, K.; Herr, H. A model of muscle-tendon function in human walking at self-selected speed. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 352–362. [Google Scholar] [CrossRef]
- Franklin, D.W.; Burdet, E.; Tee, K.P.; Osu, R.; Chew, C.-M.; Milner, T.E.; Kawato, M. CNS learns stable, accurate, and efficient movements using a simple algorithm. J. Neurosci. 2008, 28, 11165–11173. [Google Scholar] [CrossRef] [PubMed]
- McKay, J.L.; Ting, L.H. Optimization of muscle activity for task-level goals predicts complex changes in limb forces across biomechanical contexts. PLoS Comput. Biol. 2012, 8, e1002465. [Google Scholar] [CrossRef] [PubMed]
- Sartori, M.; Gizzi, L.; Lloyd, D.G.; Farina, D. A musculoskeletal model of human locomotion driven by a low dimensional set of impulsive excitation primitives. Front. Comput. Neurosci. 2013, 7, 79. [Google Scholar] [CrossRef] [Green Version]
- Razavian, R.S.; Ghannadi, B.; McPhee, J. A synergy-based motor control framework for the fast feedback control of musculoskeletal systems. J. Biomech. Eng. 2018, 141, 031009. [Google Scholar] [CrossRef]
- Al Borno, M.; Hicks, J.L.; Delp, S.L. The effects of motor modularity on performance, learning and generalizability in upper-extremity reaching: A computational analysis. J. R. Soc. Interface 2020, 17, 20200011. [Google Scholar] [CrossRef]
- Williams, I.; Constandinou, T.G. Computationally efficient modeling of proprioceptive signals in the upper limb for prostheses: A simulation study. Front. Neurosci. 2014, 8, 181. [Google Scholar] [CrossRef] [Green Version]
- Falisse, A.; Bar-On, L.; Desloovere, K.; Jonkers, I.; de Groote, F. A spasticity model based on feedback from muscle force explains muscle activity during passive stretches and gait in children with cerebral palsy. PLoS ONE 2018, 13, e0208811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Groote, F.; Blum, K.P.; Horslen, B.C.; Ting, L.H. Interaction between muscle tone, short-range stiffness and increased sensory feedback gains explains key kinematic features of the pendulum test in spastic cerebral palsy: A simulation study. PLoS ONE 2018, 13, e0205763. [Google Scholar] [CrossRef]
- Miyazaki, T.; Wada, M.; Kawahara, H.; Sato, M.; Baba, H.; Shimada, S. Dynamic load at baseline can predict radiographic disease progression in medial compartment knee osteoarthritis. Ann. Rheum. Dis. 2002, 61, 617–622. [Google Scholar] [CrossRef]
- Prodromos, C.C.; Andriacchi, T.P.; Galante, J.O. A relationship between gait and clinical changes following high tibial osteotomy. J. Bone Jt. Surg. Am. Vol. 1985, 67, 1188–1194. [Google Scholar] [CrossRef]
- Wada, M.; Imura, S.; Nagatani, K.; Baba, H.; Shimada, S.; Sasaki, S. Relationship between gait and clinical results after high tibial osteotomy. Clin. Orthop. Relat. Res. 1998, 354, 180–188. [Google Scholar] [CrossRef]
- Van den Bogert, A.J.; Smith, G.D.; Nigg, B.M. In vivo determination of the anatomical axes of the ankle joint complex: An optimization approach. J. Biomech. 1994, 27, 1477–1488. [Google Scholar] [CrossRef]
- Charlton, I.W.; Tate, P.; Smyth, P.; Roren, L. Repeatability of an optimised lower body model. Gait Posture 2004, 20, 213–221. [Google Scholar] [CrossRef]
- Reinbolt, J.A.; Schutte, J.F.; Fregly, B.J.; Koh, B.I.; Haftka, R.T.; George, A.D.; Mitchell, K.H. Determination of patient-specific multi-joint kinematic models through two-level optimization. J. Biomech. 2005, 38, 621–626. [Google Scholar] [CrossRef] [PubMed]
- Reinbolt, J.A.; Haftka, R.T.; Chmielewski, T.L.; Fregly, B.J. A computational framework to predict post-treatment outcome for gait-related disorders. Med. Eng. Phys. 2008, 30, 434–443. [Google Scholar] [CrossRef]
- Piazza, S.J.; Okita, N.; Cavanagh, P.R. Accuracy of the functional method of hip joint center location: Effects of limited motion and varied implementation. J. Biomech. 2001, 34, 967–973. [Google Scholar] [CrossRef]
- Piazza, S.J.; Erdemir, A.; Okita, N.; Cavanagh, P.R. Assessment of the functional method of hip joint center location subject to reduced range of hip motion. J. Biomech. 2004, 37, 349–356. [Google Scholar] [CrossRef]
- Besier, T.F.; Sturnieks, D.L.; Alderson, J.A.; Lloyd, D.G. Repeatability of gait data using a functional hip joint centre and a mean helical knee axis. J. Biomech. 2003, 36, 1159–1168. [Google Scholar] [CrossRef]
- Millard, M.; Uchida, T.; Seth, A.; Delp, S.L. Flexing computational muscle: Modeling and simulation of musculotendon dynamics. J. Biomech. Eng. 2013, 135, 021005. [Google Scholar] [CrossRef] [PubMed]
- Bogey, R.A.; Perry, J.; Gitter, A.J. An EMG-to-force processing approach for determining ankle muscle forces during normal human gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 302–310. [Google Scholar] [CrossRef]
- Buchanan, T.S.; Lloyd, D.G.; Manal, K.; Besier, T.F. Estimation of muscle forces and joint moments using a forward-inverse dynamics model. Med. Sci. Sports Exerc. 2005, 37, 1911–1916. [Google Scholar] [CrossRef] [Green Version]
- Winby, C.R.; Lloyd, D.G.; Besier, T.F.; Kirk, T.B. Muscle and external load contribution to knee joint contact loads during normal gait. J. Biomech. 2009, 42, 2294–2300. [Google Scholar] [CrossRef]
- Gerus, P.; Rao, G.; Buchanan, T.S.; Berton, E. A clinically applicable model to estimate the opposing muscle groups contributions to isometric and dynamic tasks. Ann. Biomed. Eng. 2010, 38, 2406–2417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, D.; Rudolph, K.S.; Manal, K.T. EMG-driven modeling approach to muscle force and joint load estimations: Case study in knee osteoarthritis. J. Orthop. Res. 2012, 30, 377–383. [Google Scholar] [CrossRef] [Green Version]
- Sartori, M.; Reggiani, M.; Farina, D.; Lloyd, D.G. EMG-driven forward-dynamic estimation of muscle force and joint moment about multiple degrees of freedom in the human lower extremity. PLoS ONE 2012, 7, e52618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gardinier, E.S.; Manal, K.; Buchanan, T.S.; Snyder-Mackler, L. Minimum detectable change for knee joint contact force estimates using an EMG-driven model. Gait Posture 2013, 38, 1051–1053. [Google Scholar] [CrossRef] [Green Version]
- Menegaldo, L.L.; Fleury, A.d.; Weber, H.I. Moment arms and musculotendon lengths estimation for a three-dimensional lower-limb model. J. Biomech. 2004, 37, 1447–1453. [Google Scholar] [CrossRef] [PubMed]
- Sartori, M.; Reggiani, M.; van den Bogert, A.J.; Lloyd, D.G. Estimation of musculotendon kinematics in large musculoskeletal models using multidimensional B-splines. J. Biomech. 2012, 45, 595–601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jackson, J.N.; Hass, C.J.; Fregly, B.J. Development of a subject-specific foot-ground contact model for walking. J. Biomech. Eng. 2016, 138, 091002. [Google Scholar] [CrossRef] [Green Version]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [Green Version]
- Damsgaard, M.; Rasmussen, J.; Christensen, S.T.; Surma, E.; de Zee, M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Van den Bogert, A.J.; Blana, D.; Heinrich, D. Implicit methods for efficient musculoskeletal simulation and optimal control. Procedia Iutam 2011, 2, 297–316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ackermann, M.; van den Bogert, A.J. Optimality principles for model-based prediction of human gait. J. Biomech. 2010, 43, 1055–1060. [Google Scholar] [CrossRef] [Green Version]
- Halloran, J.P.; Erdemir, A.; van den Bogert, A.J. Adaptive surrogate modeling for efficient coupling of musculoskeletal control and tissue deformation models. J. Biomech. Eng. 2009, 131, 011014. [Google Scholar] [CrossRef] [Green Version]
- Ackermann, M.; van den Bogert, A.J. Predictive simulation of gait at low gravity reveals skipping as the preferred locomotion strategy. J. Biomech. 2012, 45, 1293–1298. [Google Scholar] [CrossRef] [Green Version]
- McLean, S.G.; Su, A.; van den Bogert, A.J. Development and validation of a 3-D model to predict knee joint loading during dynamic movement. J. Biomech. Eng. 2003, 125, 864–874. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koelewijn, A.D.; Dorschky, E.; van den Bogert, A.J. A metabolic energy expenditure model with a continuous first derivative and its application to predictive simulations of gait. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 521–531. [Google Scholar] [CrossRef]
- Van den Bogert, A.J.; Samorezov, S.; Davis, B.L.; Smith, W.A. Modeling and optimal control of an energy-storing prosthetic knee. J. Biomech. Eng. 2012, 134, 051007. [Google Scholar] [CrossRef] [Green Version]
- Koelewijn, A.D.; van den Bogert, A.J. Joint contact forces can be reduced by improving joint moment symmetry in below-knee amputee gait simulations. Gait Posture 2016, 49, 219–225. [Google Scholar] [CrossRef] [Green Version]
- Buchanan, T.S.; Lloyd, D.G.; Manal, K.; Besier, T.F. Neuromusculoskeletal modeling: Estimation of muscle forces and joint moments and movements from measurements of neural command. J. Appl. Biomech. 2004, 20, 367–395. [Google Scholar] [CrossRef] [Green Version]
- Rao, G.; Berton, E.; Amarantini, D.; Vigouroux, L.; Buchanan, T.S. An EMG-driven biomechanical model that accounts for the decrease in moment generation capacity during a dynamic fatigued condition. J. Biomech. Eng. 2010, 132, 071003. [Google Scholar] [CrossRef]
- Shao, Q.; Bassett, D.N.; Manal, K.; Buchanan, T.S. An EMG-driven model to estimate muscle forces and joint moments in stroke patients. Comput. Biol. Med. 2009, 39, 1083–1088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manal, K.; Buchanan, T.S. An electromyogram-driven musculoskeletal model of the knee to predict in vivo joint contact forces during normal and novel gait patterns. J. Biomech. Eng. 2013, 135, 021014. [Google Scholar] [CrossRef]
- Manal, K.; Gravare-Silbernagel, K.; Buchanan, T.S. A real-time EMG-driven musculoskeletal model of the ankle. Multibody Syst. Dyn. 2012, 28, 169–180. [Google Scholar] [CrossRef] [Green Version]
- Pàmies-Vilà, R.; Font-Llagunes, J.M.; Lugris, U.; Cuadrado, J. Parameter identification method for a three-dimensional foot-ground contact model. Mech. Mach. Theory 2014, 75, 107–116. [Google Scholar] [CrossRef]
- Higginson, J.S.; Zajac, F.E.; Neptune, R.R.; Kautz, S.A.; Delp, S.L. Muscle contributions to support during gait in an individual with post-stroke hemiparesis. J. Biomech. 2006, 39, 1769–1777. [Google Scholar] [CrossRef]
- Liu, M.Q.; Anderson, F.C.; Pandy, M.G.; Delp, S.L. Muscles that support the body also modulate forward progression during walking. J. Biomech. 2006, 39, 2623–2630. [Google Scholar] [CrossRef]
- Arnold, A.S.; Anderson, F.C.; Pandy, M.G.; Delp, S.L. Muscular contributions to hip and knee extension during the single limb stance phase of normal gait: A framework for investigating the causes of crouch gait. J. Biomech. 2005, 38, 2181–2189. [Google Scholar] [CrossRef]
- Goldberg, S.R.; Anderson, F.C.; Pandy, M.G.; Delp, S.L. Muscles that influence knee flexion velocity in double support: Implications for stiff-knee gait. J. Biomech. 2004, 37, 1189–1196. [Google Scholar] [CrossRef] [PubMed]
- Piazza, S.J.; Delp, S.L. Three-dimensional dynamic simulation of total knee replacement motion during a step-up task. J. Biomech. Eng. 2001, 123, 599–606. [Google Scholar] [CrossRef]
- Ong, C.F.; Hicks, J.L.; Delp, S.L. Simulation-based design for wearable robotic systems: An optimization framework for enhancing a standing long jump. IEEE Trans. Biomed. Eng. 2016, 63, 894–903. [Google Scholar] [CrossRef] [Green Version]
- Sartori, M.; Llyod, D.G.; Farina, D. Neural data-driven musculoskeletal modeling for personalized neurorehabilitation technologies. IEEE Trans. Biomed. Eng. 2016, 63, 879–893. [Google Scholar] [CrossRef] [Green Version]
- Sartori, M.; Farina, D.; Lloyd, D.G. Hybrid neuromusculoskeletal modeling to best track joint moments using a balance between muscle excitations derived from electromyograms and optimization. J. Biomech. 2014, 47, 3613–3621. [Google Scholar] [CrossRef]
- Gonzalez-Vargas, J.; Sartori, M.; Dosen, S.; Torricelli, D.; Pons, J.L.; Farina, D. A predictive model of muscle excitations based on muscle modularity for a large repertoire of human locomotion conditions. Front. Comput. Neurosci. 2015, 9, 114. [Google Scholar] [CrossRef] [Green Version]
- Febrer-Nafría, M.; Pallarès-López, R.; Fregly, B.J.; Font-Llagunes, J.M. Comparison of different optimal control formulations for generating dynamically consistent orthosis-assisted crutch walking simulations. Mech. Mach. Theory 2020, 154, 104031. [Google Scholar] [CrossRef]
- Febrer-Nafría, M.; Pallarès-López, R.; Fregly, B.J.; Font-Llagunes, J.M. Prediction of three-dimensional crutch walking patterns using a torque-driven model. Multibody Syst. Dyn. 2021, 51, 1–19. [Google Scholar] [CrossRef]
- Ao, D.; Shourijeh, M.S.; Patten, C.; Fregly, B.J. Evaluation of synergy extrapolation for predicting unmeasured muscle excitations from measured muscle synergies. Front. Comput. Neurosci. 2020, 14, 588943. [Google Scholar] [CrossRef] [PubMed]
- Walter, J.P.; Kinney, A.L.; Banks, S.A.; D’Lima, D.D.; Besier, T.F.; Lloyd, D.G.; Fregly, B.J. Muscle synergies may improve optimization prediction of knee contact forces during walking. J. Biomech. Eng. 2014, 136, 021031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fregly, B.J.; Reinbolt, J.A.; Chmielewski, T.L. Evaluation of a patient-specific cost function to predict the influence of foot path on the knee adduction torque during gait. Comput. Methods Biomech. Biomed. Eng. 2008, 11, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Fregly, B.J. Computational assessment of combinations of gait modifications for knee osteoarthritis rehabilitation. IEEE Trans. Biomed. Eng. 2008, 55, 2104–2106. [Google Scholar] [CrossRef] [Green Version]
- Koh, B.-I.; Reinbolt, J.A.; George, A.D.; Haftka, R.T.; Fregly, B.J. Limitations of parallel global optimization for large-scale human movement problems. Med. Eng. Phys. 2009, 31, 515–521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eskinazi, I.; Fregly, B.J. A computational framework for simultaneous estimation of muscle and joint contact forces and body motion using optimization and surrogate modeling. Med. Eng. Phys. 2018, 54, 56–64. [Google Scholar] [CrossRef]
- Falisse, A.; van Rossom, S.; Jonkers, I.; de Groote, F. EMG-driven optimal estimation of subject-specific Hill model muscle-tendon parameters of the knee joint actuators. IEEE Trans. Biomed. Eng. 2017, 64, 2253–2262. [Google Scholar]
- Jansen, K.; de Groote, F.; Aerts, W.; de Schutter, J.; Duysens, J.; Jonkers, I. Altering length and velocity feedback during a neuro-musculoskeletal simulation of normal gait contributes to hemiparetic gait characteristics. J. Neuroeng. Rehabil. 2014, 11, 78. [Google Scholar] [CrossRef] [Green Version]
- Jonkers, I.; Spaepen, A.; Papaioannou, G.; Stewart, C. An EMG-based, muscle driven forward simulation of single support phase of gait. J. Biomech. 2002, 35, 609–619. [Google Scholar] [CrossRef]
- Hoang, H.X.; Pizzolato, C.; Diamond, L.E.; Lloyd, D.G. Subject-specific calibration of neuromuscular parameters enables neuromusculoskeletal models to estimate physiologically plausible hip joint contact forces in healthy adults. J. Biomech. 2018, 80, 111–120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Millard, M.; McPhee, J.; Kubica, E. Multi-step forward dynamic gait simulation. In Multibody Dynamics: Computational Methods and Applications; Bottasso, C., Ed.; Springer: Amsterdam, The Netherlands, 2009; pp. 25–43. [Google Scholar]
- Shourijeh, M.S.; McPhee, J. Foot–ground contact modeling within human gait simulations: From Kelvin–Voigt to hyper-volumetric models. Multibody Syst. Dyn. 2015, 35, 393–407. [Google Scholar] [CrossRef] [Green Version]
- Brown, P.; McPhee, J. A 3D ellipsoidal volumetric foot-ground contact model for forward dynamics. Multibody Syst. Dyn. 2018, 42, 447–467. [Google Scholar] [CrossRef]
- Razavian, R.S.; Mehrabi, N.; McPhee, J. A model-based approach to predict muscle synergies using optimization: Application to feedback control. Front. Comput. Neurosci. 2015, 9, 121. [Google Scholar]
- Shourijeh, M.S.; McPhee, J. Forward dynamic optimization of human gait simulations: A global parameterization approach. J. Comput. Nonlinear Dyn. 2014, 9, 31018. [Google Scholar] [CrossRef]
- Mehrabi, N.; Razavian, R.S.; McPhee, J. A physics-based musculoskeletal driver model to study steering tasks. J. Comput. Nonlinear Dyn. 2015, 10, 21012. [Google Scholar] [CrossRef]
- Mehrabi, N.; Razavian, R.S.; Ghannadi, B.; McPhee, J. Predictive simulation of reaching moving targets using nonlinear model predictive control. Front. Comput. Neurosci. 2017, 10, 143. [Google Scholar] [CrossRef] [Green Version]
- Umberger, B.R.; Miller, R.H. Optimal control modeling of human movement. In Handbook of Human Motion; Müller, B., Ed.; Springer: New York, NY, USA, 2018; pp. 1–22. [Google Scholar]
- Miller, R.H.; Hamill, J. Optimal footfall patterns for cost minimization in running. J. Biomech. 2015, 48, 2858–2864. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.L.; Neptune, R.R. Three-dimensional modular control of human walking. J. Biomech. 2012, 45, 2157–2163. [Google Scholar] [CrossRef] [Green Version]
- McGowan, C.P.; Neptune, R.R.; Clark, D.J.; Kautz, S.A. Modular control of human walking: Adaptations to altered mechanical demands. J. Biomech. 2010, 43, 412–419. [Google Scholar] [CrossRef] [Green Version]
- Neptune, R.R.; Clark, D.J.; Kautz, S.A. Modular control of human walking: A simulation study. J. Biomech. 2009, 42, 1282–1287. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, K.; Neptune, R.R. Differences in muscle function during walking and running at the same speed. J. Biomech. 2006, 39, 2005–2013. [Google Scholar] [CrossRef] [PubMed]
- Neptune, R.R. Optimization algorithm performance in determining optimal controls in human movement analyses. J. Biomech. Eng. 1999, 121, 249–252. [Google Scholar] [CrossRef] [PubMed]
- Pandy, M.G.; Anderson, F.C.; Hull, D.G. A parameter optimization approach for the optimal control of large-scale musculoskeletal systems. J. Biomech. Eng. 1992, 114, 450–460. [Google Scholar] [CrossRef] [PubMed]
- Anderson, F.C.; Pandy, M.G. A dynamic optimization solution for vertical jumping in three dimensions. Comput. Methods Biomech. Biomed. Eng. 1999, 2, 201–231. [Google Scholar] [CrossRef]
- Dorn, T.W.; Lin, Y.-C.; Pandy, M.G. Estimates of muscle function in human gait depend on how foot-ground contact is modelled. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 657–668. [Google Scholar] [CrossRef] [PubMed]
- Porsa, S.; Lin, Y.-C.; Pandy, M.G. Direct methods for predicting movement biomechanics based upon optimal control theory with implementation in OpenSim. Ann. Biomed. Eng. 2016, 44, 2542–2557. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.-F.; Umberger, B.R. Generating optimal control simulations of musculoskeletal movement using OpenSim and MATLAB. PeerJ 2016, 4, e1638. [Google Scholar] [CrossRef] [PubMed]
- Gidley, A.D.; Marsh, A.P.; Umberger, B.R. Performance criteria for generating predictive optimal control simulations of bicycle pedaling. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 11–20. [Google Scholar] [CrossRef]
- Nguyen, V.Q.; Johnson, R.T.; Sup, F.C.; Umberger, B.R. Bilevel optimization for cost function determination in dynamic simulation of human gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1426–1435. [Google Scholar] [CrossRef] [PubMed]
- Pandy, M.G.; Zajac, F.E. Optimal muscular coordination strategies for jumping. J. Biomech. 1991, 24, 1–10. [Google Scholar] [CrossRef]
- Rohani, F.; Richter, H.; van den Bogert, A.J. Optimal design and control of an electromechanical transfemoral prosthesis with energy regeneration. PLoS ONE 2017, 12, e0188266. [Google Scholar]
- Dembia, C.L.; Bianco, N.A.; Falisse, A.; Hicks, J.L.; Delp, S.L. OpenSim Moco: Musculoskeletal optimal control. PLoS Comput. Biol. 2020, 16, e1008493. [Google Scholar] [CrossRef]
- Wang, H.; van den Bogert, A. Identification of postural controllers in human standing balance. J. Biomech. Eng. 2021, 143, 041001. [Google Scholar] [CrossRef]
- Lin, Y.C.; Pandy, M.G. Three-dimensional data-tracking dynamic optimization simulations of human locomotion generated by direct collocation. J. Biomech. 2017, 59, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.C.; Walter, J.P.; Pandy, M.G. Predictive simulations of neuromuscular coordination and joint-contact loading in human gait. Ann. Biomed. Eng. 2018, 46, 1216–1227. [Google Scholar] [CrossRef] [PubMed]
- Killen, B.A.; Falisse, A.; de Groote, F.; Jonkers, I. In silico-enhanced treatment and rehabilitation planning for patients with musculoskeletal disorders: Can musculoskeletalm and dynamic simulations really impact current clinical practice? Appl. Sci. 2020, 10, 7255. [Google Scholar] [CrossRef]
- Blemker, S.S.; Pinsky, P.M.; Delp, S.L. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J. Biomech. 2005, 38, 657–665. [Google Scholar] [CrossRef] [PubMed]
- Fiorentino, N.M.; Blemker, S.S. Musculotendon variability influences tissue strains experienced by the biceps femoris long head muscle during high-speed running. J. Biomech. 2014, 47, 3325–3333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Virgilio, K.M.; Martin, K.S.; Peirce, S.M.; Blemker, S.S. Multiscale models of skeletal muscle reveal the complex effects of muscular dystrophy on tissue mechanics and damage susceptibility. Interface Focus 2015, 5, 20140080. [Google Scholar] [CrossRef]
- Navacchia, A.; Hume, D.R.; Rullkoetter, P.J.; Shelburne, K.B. A computationally efficient strategy to estimate muscle forces in a finite element musculoskeletal model of the lower limb. J. Biomech. 2019, 84, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Hume, D.R.; Rullkoetter, P.J.; Shelburne, K.B. ReadySim: A computational framework for building explicit finite element musculoskeletal simulations directly from motion laboratory data. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3396. [Google Scholar] [CrossRef] [PubMed]
- Perillo-Marcone, A.; Taylor, M. Effect of varus/valgus malalignment on bone strains in the proximal tibia after TKR: An explicit finite element study. J. Biomech. Eng. 2007, 129, 1–11. [Google Scholar] [CrossRef]
- Maas, S.A.; Ateshian, G.A.; Weiss, J.A. FEBio: History and advances. Annu. Rev. Biomed. Eng. 2017, 19, 279–299. [Google Scholar] [CrossRef]
- Anderson, A.E.; Peters, C.L.; Tuttle, B.D.; Weiss, J.A. Subject-specific finite element model of the pelvis: Development, validation and sensitivity studies. J. Biomech. Eng. 2005, 127, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Pegg, E.C.; Walter, J.; Mellon, S.J.; Pandit, H.G.; Murray, D.W.; D’Lima, D.D.; Fregly, B.J.; Gill, H.S. Evaluation of factors affecting tibial bone strain after unicompartmental knee replacement. J. Orthop. Res. 2013, 31, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, A. Open Knee: Open source modeling and simulation in knee biomechanics. J. Knee Surg. 2016, 29, 107–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, W.; Pandy, M. Direct validation of human knee-joint contact mechanics derived from subject-specific finite-element models of the tibiofemoral and patellofemoral joints. J. Biomech. Eng. 2020, 142, 071001. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Patil, S.; Steklov, N.; Bae, W.; D’Lima, D.D.; Sah, R.L.; Fregly, B.J. Finite element modelling of in vitro articular cartilage wear in the patellofemoral joint. In Proceedings of the 2012 ASME Summer Bioengineering Conference, Fajardo, PR, USA, 20–23 June 2012; pp. 163–164. [Google Scholar]
- Knight, L.A.; Pal, S.; Coleman, J.C.; Bronson, F.; Haider, H.; Levine, D.L.; Taylor, M.; Rullkoetter, P.J. Comparison of long-term numerical and experimental total knee replacement wear during simulated gait loading. J. Biomech. 2007, 40, 1550–1558. [Google Scholar] [CrossRef]
- Zhao, D.; Sakoda, H.; Sawyer, W.G.; Banks, S.A.; Fregly, B.J. Predicting knee replacement damage in a simulator machine using a computational model with a consistent wear factor. J. Biomech. Eng. 2008, 130, 011004. [Google Scholar] [CrossRef] [Green Version]
- Valente, G.; Crimi, G.; Vanella, N.; Schileo, E.; Taddei, F. nmsBuilder: Freeware to create subject-specific musculoskeletal models for OpenSim. Comput. Methods Programs Biomed. 2017, 152, 85–92. [Google Scholar] [CrossRef]
- Killen, B.A.; da Luz, S.B.; Lloyd, D.G.; Carleton, A.D.; Zhang, J.; Besier, T.F.; Saxby, D.J. Automated creation and tuning of personalised muscle paths for OpenSim musculoskeletal models of the knee joint. Biomech. Model. Mechanobiol. 2021. Online ahead of print.. [Google Scholar]
- Modenese, L.; Renault, J.-B. Automatic generation of personalised skeletal models of the lower limb from three-dimensional bone geometries. J. Biomech. 2021, 116, 110186. [Google Scholar] [CrossRef] [PubMed]
- Modenese, L.; Renault, J.-B. What are the differences between the STAPLE toolbox, NMSBuilder and the MAP Client for generating OpenSim models? 2021. Available online: https://github.com/modenaxe/msk-STAPLE (accessed on 14 February 2021).
- Modenese, L.; Montefiori, E.; Wang, A.; Wesarg, S.; Viceconti, M.; Mazzà, C. Investigation of the dependence of joint contact forces on musculotendon parameters using a codified workflow for image-based modelling. J. Biomech. 2018, 73, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Myers, C.A.; Laz, P.J.; Shelburne, K.B.; Davidson, B.S. A probabilistic approach to quantify the impact of uncertainty propagation in musculoskeletal simulations. Ann. Biomed. Eng. 2015, 43, 1098–1111. [Google Scholar] [CrossRef] [Green Version]
- Valente, G.; Pitto, L.; Testi, D.; Seth, A.; Delp, S.L.; Stagni, R.; Viceconti, M.; Taddei, F. Are subject-specific musculoskeletal models robust to the uncertainties in parameter identification? PLoS ONE 2014, 9, e112625. [Google Scholar] [CrossRef]
- Ackland, D.C.; Lin, Y.-C.; Pandy, M.G. Sensitivity of model predictions of muscle function to changes in moment arms and muscle-tendon properties: A Monte-Carlo analysis. J. Biomech. 2012, 45, 1463–1471. [Google Scholar] [CrossRef] [PubMed]
- Navacchia, A.; Myers, C.A.; Rullkoetter, P.J.; Shelburne, K.B. Prediction of in vivo knee joint loads using a global probabilistic analysis. J. Biomech. Eng. 2016, 138, 4032379. [Google Scholar] [CrossRef] [Green Version]
- Bujalski, P.; Martins, J.; Stirling, L. A Monte Carlo analysis of muscle force estimation sensitivity to muscle-tendon properties using a Hill-based muscle model. J. Biomech. 2018, 79, 67–77. [Google Scholar] [CrossRef]
- Bosmans, L.; Valente, G.; Wesseling, M.; van Campen, A.; de Groote, F.; de Schutter, J.; Jonkers, I. Sensitivity of predicted muscle forces during gait to anatomical variability in musculotendon geometry. J. Biomech. 2015, 48, 2116–2123. [Google Scholar] [CrossRef] [PubMed]
- Handsfield, G.G.; Meyer, C.H.; Hart, J.M.; Abel, M.F.; Blemker, S.S. Relationships of 35 lower limb muscles to height and body mass quantified using MRI. J. Biomech. 2014, 47, 631–638. [Google Scholar] [CrossRef] [PubMed]
- Lansdown, D.A.; Ding, Z.; Wadington, M.; Hornberger, J.L.; Damon, B.M. Quantitative diffusion tensor MRI-based fiber tracking of human skeletal muscle. J. Appl. Physiol. 2007, 103, 673–681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scheel, M.; von Roth, P.; Winkler, T.; Arampatzis, A.; Prokscha, T.; Hamm, B.; Diederichs, G. Fiber type characterization in skeletal muscle by diffusion tensor imaging. Nmr Biomed. 2013, 26, 1220–1224. [Google Scholar] [CrossRef]
- Gerus, P.; Rao, G.; Berton, E. Ultrasound-based subject-specific parameters improve fascicle behaviour estimation in Hill-type muscle model. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 116–123. [Google Scholar] [CrossRef]
- Li, L.; Tong, K.Y.; Hu, X.L.; Hung, L.K.; Koo, T.K.K. Incorporating ultrasound-measured musculotendon parameters to subject-specific EMG-driven model to simulate voluntary elbow flexion for persons after stroke. Clin. Biomech. 2009, 24, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Bohm, S.; Marzilger, R.; Mersmann, F.; Santuz, A.; Arampatzis, A. Operating length and velocity of human vastus lateralis muscle during walking and running. Sci. Rep. 2018, 8, 5066. [Google Scholar] [CrossRef] [Green Version]
- Saxby, D.J.; Killen, B.A.; Pizzolato, C.; Carty, C.P.; Diamond, L.E.; Modenese, L.; Fernandez, J.; Davico, G.; Barzan, M.; Lenton, G.; et al. Machine learning methods to support personalized neuromusculoskeletal modelling. Biomech. Model. Mechanobiol. 2020, 19, 1169–1185. [Google Scholar] [CrossRef]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathana, R.; Tuckerb, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Ziaeipoor, H.; Martelli, S.; Pandy, M.; Taylor, M. Efficacy and efficiency of multivariate linear regression for rapid prediction of femoral strain fields during activity. Med. Eng. Phys. 2019, 63, 88–92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.-C.; Farr, J.; Carter, K.; Fregly, B.J. Response surface optimization for joint contact model evaluation. J. Appl. Biomech. 2006, 22, 120–130. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-C.; Haftka, R.T.; Queipo, N.V.; Fregly, B.J. Two-dimensional surrogate contact modeling for computationally efficient dynamic simulation of total knee replacements. J. Biomech. Eng. 2009, 131, 041010. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-C.; Haftka, R.T.; Queipo, N.V.; Fregly, B.J. Surrogate articular contact models for computationally efficient multibody dynamic simulations. Med. Eng. Phys. 2010, 32, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Eskinazi, I.; Fregly, B.J. Surrogate modeling of deformable joint contact using artificial neural networks. Med. Eng. Phys. 2015, 37, 885–891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eskinazi, I.; Fregly, B.J. An open-source toolbox for surrogate modeling of joint contact mechanics. IEEE Trans. Biomed. Eng. 2016, 63, 269–277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marra, M.A.; Andersen, M.S.; Damsgaard, M.; Koopman, B.F.J.M.; Janssen, D.; Verdonschot, N. Evaluation of a surrogate contact model in force-dependent kinematic simulations of total knee replacement. J. Biomech. Eng. 2017, 139, 081001. [Google Scholar] [CrossRef] [Green Version]
- O’Rourke, D.; Martelli, S.; Bottema, M.; Taylor, M. A computational efficient method to assess the sensitivity of finite-element models: An illustration with the hemipelvis. J. Biomech. Eng. 2016, 138, 121008. [Google Scholar] [CrossRef] [PubMed]
| Model Personalization | |||||
|---|---|---|---|---|---|
| Researchers | Joint Structure | Muscle-Tendon | Foot-Ground Contact | Neural Control | Motion Prediction |
| Ton van den Bogert | [170] | [190,191,192,193,194,195,196,197] | |||
| Tom Buchanan/Kurt Manal | [89,179,184,198,199,200,201,202] | ||||
| Javier Cuadrado | [203] | ||||
| Scott Delp | [204,205,206,207,208,209] | ||||
| Dario Farina/Massimo Sartori | [161,183,210,211,212] | ||||
| Josep Font-Llagunes | [213,214] | ||||
| B.J. Fregly | [17,91,172,173] | [25,90] | [25,187,215] | [25,26,216] | [17,25,26,173,217,218,219,220] |
| Ilse Jonkers/Friedl De Groote | [27,221] | [27] | [135,136,222,223,27] | ||
| David Lloyd/Thor Besier | [161,179,183,210,211,224] | ||||
| John McPhee | [225,226,227] | [225,228,229,230,231] | |||
| Ross Miller | [138,139,232,233] | ||||
| Rick Neptune | [137,234,235,236] | [12,137,204,234,235,236,237,238] | |||
| Marcus Pandy | [8,134,205,206,207,239,240,241,242] | ||||
| Brian Umberger | [232,243,244,245] | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fregly, B.J. A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful. Appl. Sci. 2021, 11, 2037. https://doi.org/10.3390/app11052037
Fregly BJ. A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful. Applied Sciences. 2021; 11(5):2037. https://doi.org/10.3390/app11052037
Chicago/Turabian StyleFregly, Benjamin J. 2021. "A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful" Applied Sciences 11, no. 5: 2037. https://doi.org/10.3390/app11052037
APA StyleFregly, B. J. (2021). A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful. Applied Sciences, 11(5), 2037. https://doi.org/10.3390/app11052037






