Robust Analysis and Laser Stripe Center Extraction for Rail Images
Abstract
1. Introduction
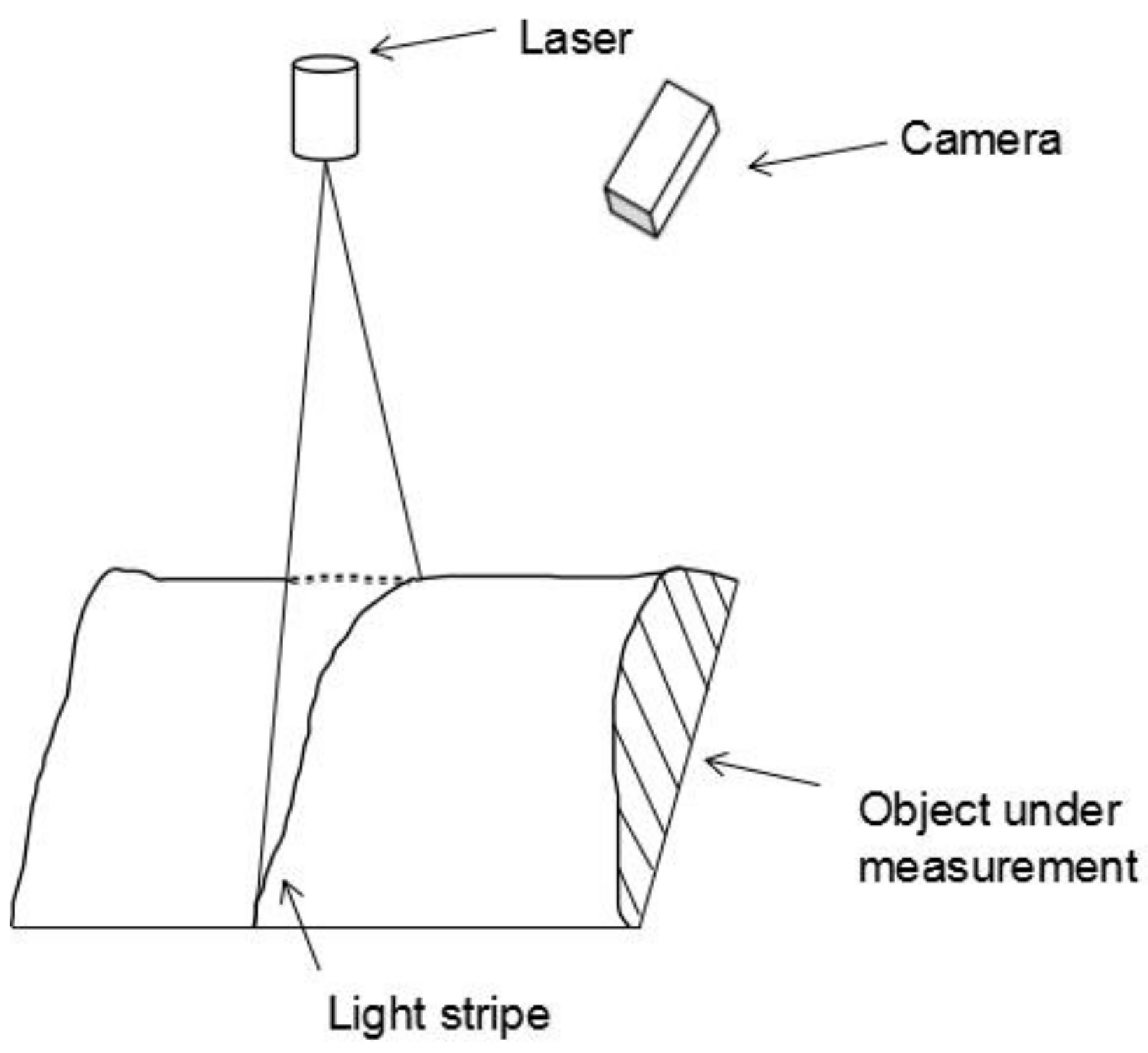
2. Laser Stripe Center Extraction for Rail Images
2.1. Light Stripe Preprocessing
2.2. Light Stripe Extraction
3. Experiments
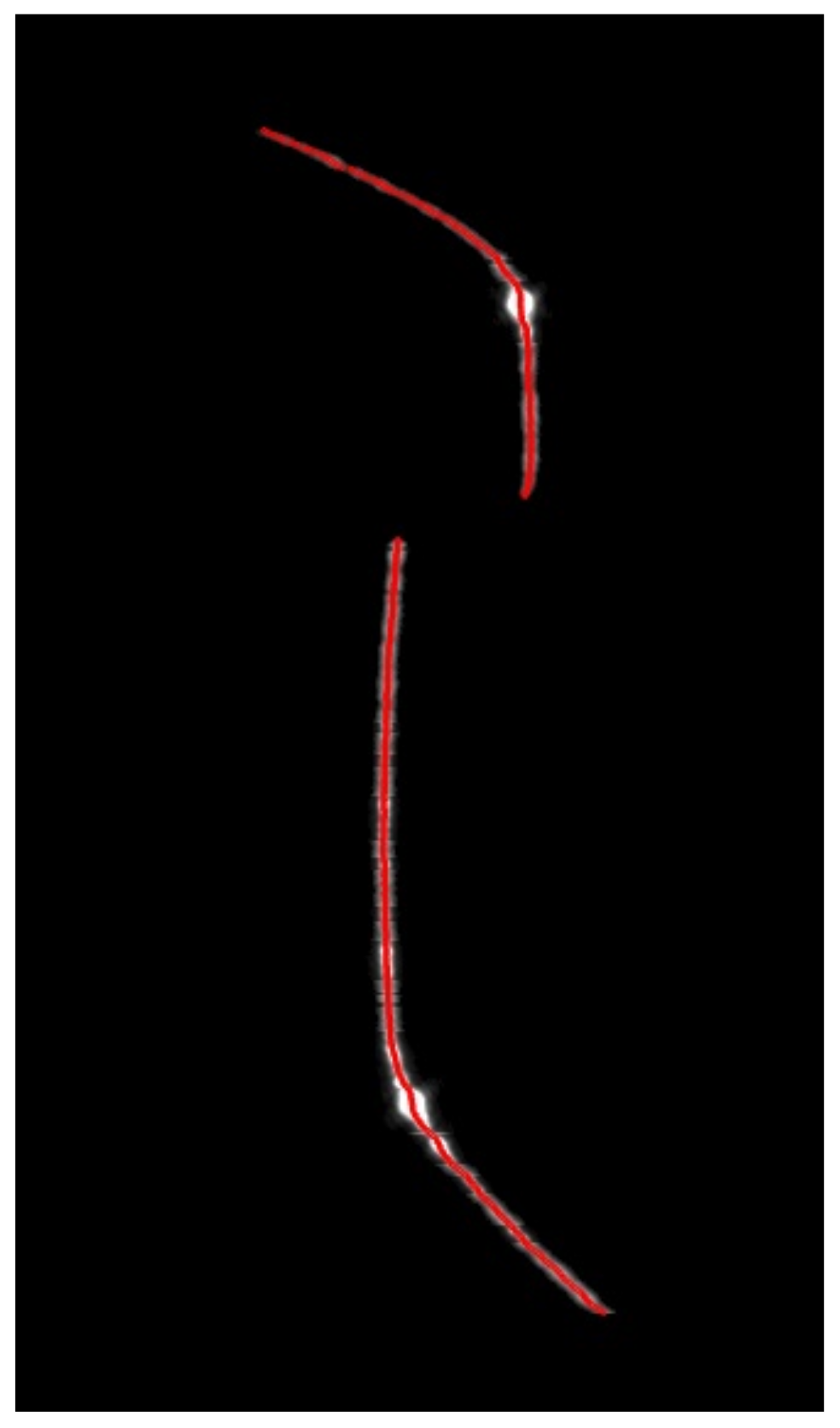
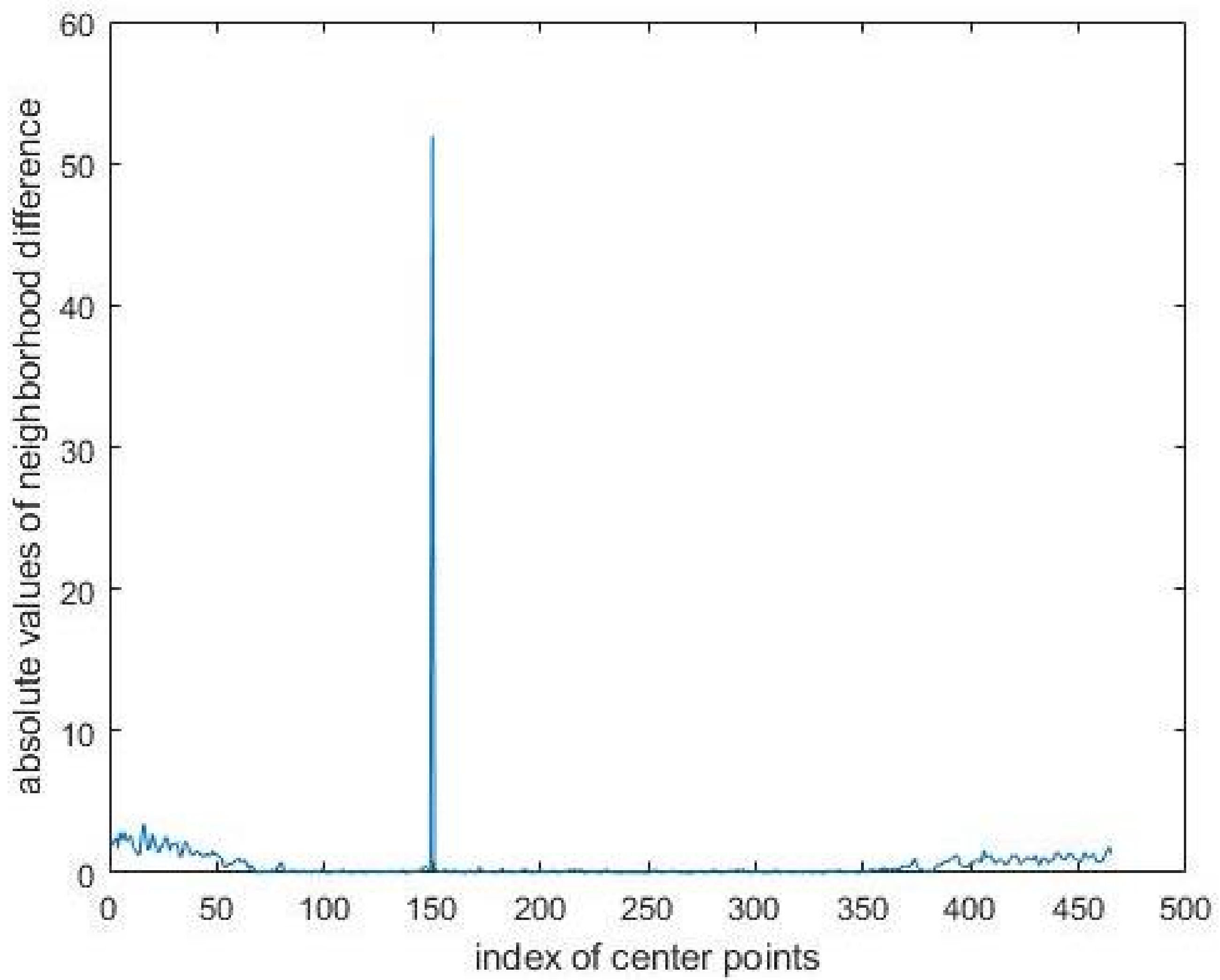
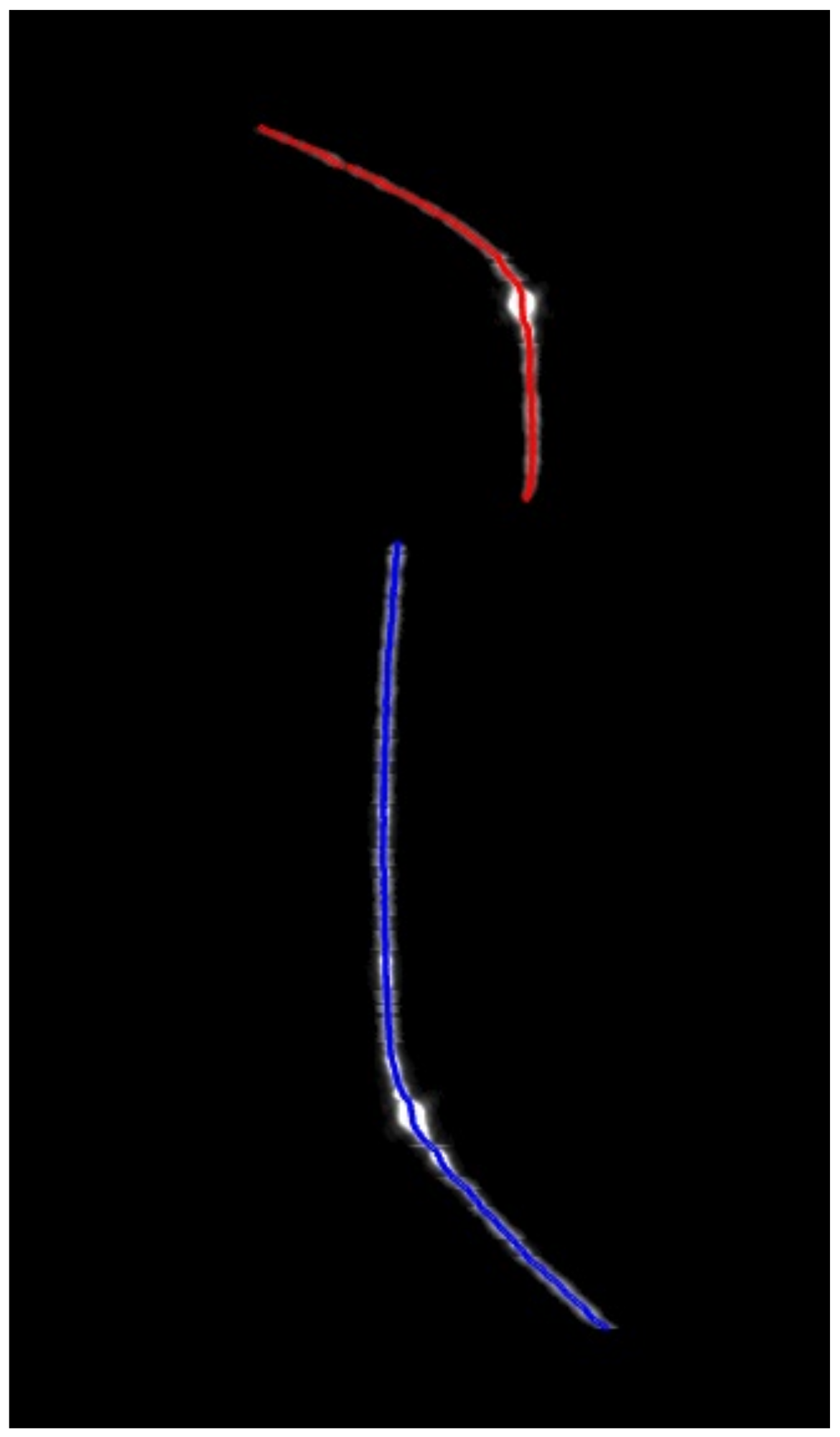
3.1. Robustness
3.2. Efficiency
3.3. Accuracy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, P.; Xu, K.; Wang, D.D. Rail profile measurement based on line-structured light vision. IEEE Access 2018, 6, 16423–16431. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, J.H.; Wang, H.; Zhang, G.J. Simple and fast rail wear measurement method based on structured light. Opt. Lasers Eng. 2011, 49, 1343–1351. [Google Scholar] [CrossRef]
- Molleda, J.; Usamentiaga, R.; Millara, Á.F.; García, D.F.; Manso, P.; Suárez, C.M.; García, I. A profile measurement system for rail quality assessment during manufacturing. IEEE Trans. Ind. Appl. 2016, 52, 2684–2692. [Google Scholar] [CrossRef]
- Bouguet, J. Camera Calibration Toolbox for Matlab. Available online: c://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 2 October 2019).
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.F.; Ma, Z.J.; Zeng, J.Z.; Jin, T.; Liu, H.L. Distortion rectifying for dynamically measuring rail profile based on self-calibration of multiline structured light. IEEE Trans. Instrum. Meas. 2018, 67, 678–689. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.J.; Yin, Y. On-site calibration of line-structured light vision sensor in complex light environments. Opt. Express 2015, 23, 29896–29911. [Google Scholar] [CrossRef] [PubMed]
- Steger, C. An unbiased detector of curvilinear structures. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 113–125. [Google Scholar] [CrossRef]
- Steger, C. Unbiased extraction of lines with parabolic and Gaussian profiles. Comput. Vis. Image Underst. 2013, 117, 97–112. [Google Scholar] [CrossRef]
- Fisher, R.; Naidu, D. A comparison of algorithms for subpixel peak detection. In Image Technology; Springer: Berlin/Heidelberg, Germany, 1996; pp. 385–404. [Google Scholar]
- Haug, K.; Pritschow, G. Robust laser-stripe sensor for automated weld-seam-tracking in the shipbuilding industry. In Proceedings of the 24th Annual Conference of the IEEE Industrial Electronics Society (Cat. No. 98CH36200), Aachen, Germany, 31 August–4 September 1998; Volume 2, pp. 1236–1241. [Google Scholar]
- Yang, Z.D.; Wang, P.; Li, X.H.; Sun, C.K. 3D laser scanner system using high dynamic range imaging. Opt. Lasers Eng. 2014, 54, 31–41. [Google Scholar]
- Usamentiaga, R.; Molleda, J.; García, D.F. Fast and robust laser stripe extraction for 3D reconstruction in industrial environments. Mach. Vis. Appl. 2012, 23, 179–196. [Google Scholar] [CrossRef]
- Yin, X.Q.; Tao, W.; Feng, Y.Y.; Gao, Q.; He, Q.Z.; Zhao, H. Laser stripe extraction method in industrial environments utilizing self-adaptive convolution technique. Appl. Opt. 2017, 56, 2653–2660. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Xiong, W.; Chen, W.Y.; Cheng, J.R.; Wang, Y.; Gu, Y.; Chia, S.C. Robust laser stripe extraction using ridge segmentation and region ranking for 3D reconstruction of reflective and uneven surface. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec, QC, Canada, 27–30 September 2015; pp. 4912–4916. [Google Scholar]
- Liu, S.Y.; Bao, H.J.; Zhang, Y.H.; Lian, F.H.; Zhang, Z.H.; Tan, Q.C. Research on image enhancement of light stripe based on template matching. EURASIP J. Image Video Process. 2018, 2018, 124. [Google Scholar] [CrossRef]
- Pan, X.; Liu, Z. High dynamic stripe image enhancement for reliable center extraction in complex environment. In Proceedings of the International Conference on Video and Image Processing, Singapore, 27–29 December 2017; pp. 135–139. [Google Scholar]
- Wang, W.H.; Sun, J.H.; Liu, Z.; Zhang, G.J. Stripe center extrication algorithm for structured-light in rail wear dynamic measurement. Laser Infrared 2010, 40, 87–90. [Google Scholar]
- Sun, J.H.; Wang, H.; Liu, Z.; Zhang, G.J. Rapid extraction algorithm of laser stripe center in rail wear dynamic measurement. Opt. Precis. Eng. 2011, 19, 690–696. [Google Scholar]
- Wang, S.C.; Han, Q.; Wang, H.; Zhao, X.X.; Dai, P. Laser Stripe Center Extraction Method of Rail Profile in Train-Running Environment. Acta Opt. Sin. 2019, 39, 0212004. [Google Scholar] [CrossRef]
- Bracewell, R.N.; Bracewell, R.N. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1986; Volume 31999. [Google Scholar]
- Walnut, D.F. An Introduction to Wavelet Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay smoothing filters. Comput. Phys. 1990, 4, 669–672. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Hanmandlu, M.; Verma, O.P.; Kumar, N.K.; Kulkarni, M. A novel optimal fuzzy system for color image enhancement using bacterial foraging. IEEE Trans. Instrum. Meas. 2009, 58, 2867–2879. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/products/matlab.html (accessed on 2 October 2019).







| Noise Parameter | UM | Steger | The Proposed Method |
|---|---|---|---|
| 0.1 | 0.0045 | 0.4230 | 0.0009 |
| 0.15 | 0.0051 | 0.4231 | 0.0015 |
| 0.2 | 0.0057 | 0.4230 | 0.0019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Xu, G. Robust Analysis and Laser Stripe Center Extraction for Rail Images. Appl. Sci. 2021, 11, 2038. https://doi.org/10.3390/app11052038
Gao H, Xu G. Robust Analysis and Laser Stripe Center Extraction for Rail Images. Applied Sciences. 2021; 11(5):2038. https://doi.org/10.3390/app11052038
Chicago/Turabian StyleGao, Huiping, and Guili Xu. 2021. "Robust Analysis and Laser Stripe Center Extraction for Rail Images" Applied Sciences 11, no. 5: 2038. https://doi.org/10.3390/app11052038
APA StyleGao, H., & Xu, G. (2021). Robust Analysis and Laser Stripe Center Extraction for Rail Images. Applied Sciences, 11(5), 2038. https://doi.org/10.3390/app11052038





