Abstract
Featured Application
This optimization algorithm can be implemented in a smart grid for reconfiguration purpose.
Abstract
The distribution systems operate radially with meshed topologies thanks to tie-switches and sectionalizing switches consisting of the systems. The power distribution systems are undergoing evolutions strongly toward active distribution systems for reliability and quality of service enhancements through reconfiguration. The distributed generations are also one effective solution for the above objectives. A consumption time is one of the considerable issues that many existing methods have not been achieved for reconfiguration purpose. This paper brings an adaptive solution called modified sequential switch opening and exchange (MSSOE), which is carried out with MATLAB and MATPOWER tool, to overcome these issues. The fundamental loop has been proposed for the MSSOE method to reduce search space in the iteration process. In each step of the searching process, MSSOE observes that if any switches within the same loop of the selected tie-switch are deleted to avoid opening those switches in the next iteration. The process of MSSOE is done when the radial topology is given. The proposed method is tested with the standard IEEE 33-bus, IEEE 69-bus, and IEEE 119-bus distribution systems to observe the effectiveness of the MSSOE algorithm. Comparison to existing algorithms in terms of global solution and computation time conclude that the MSSOE is the best method.
1. Introduction
The power distribution systems generally operate radially with meshed topologies thanks to normally open switches and normally closed switches consisting in the systems []. In addition, the electrical power distribution network reconfiguration problem is recently becoming more interesting towards active distribution networks with and without distributed generations. Many research papers in the literature review have investigated to search for the switches which are optimal tie-switches and sectionalizing switches in the distribution systems.
Regarding network reconfiguration issues, many strategies and algorithms are developed to get power loss reduction, increase power quality, and maintain radial distribution system topology. The modern network technique for reconfiguration is provided in []; this paper investigated the problem formation included in multi-objective function, which considered in minimizing the number of switches operation, voltage constraints, and loading limits of feeder and transformer. The fundamental loop concept has been introduced into the reconfiguration of distribution system problem and tested on many evolutionary algorithms (EA), which proved to be good integration solving power distribution system problem with fast convergence []. In [], the authors proposed a new technique called the sequential switch opening and exchange (SSOE) method, which provides an accurate result and converges to optimum solution by considering to open any sectionalizing switch with the minimum value of power loss; this proposed method can solve the issue of large-scale systems and obtain an accuracy of the result, unlike other EA, which has a different optimum solution with a different running time. The power losses reduction through the distribution system reconfiguration have been provided using different algorithms such as Johnson’s algorithm [], Ant Colony [], Expended invasive weed optimization [], Cuckoo search [], Opposition learning genetic algorithm [], Genetic algorithm [], Grasshopper optimization [], Augmented grey wolf optimization [], Vector shift operation [], Salp swarm optimization [], Particle swarm optimization [], Improved fireworks [], and Backpropagation neural network []. Furthermore, the authors in [] had implemented the selective firefly algorithm and search space reduction for the complex problem of distribution system reconfiguration; a set of switches for opening based on mesh analysis is initially provided and eliminated from the switches possibility as search space based on lowest active power of branch. The distribution system reconfiguration using qualified binary particle swarm optimization is authorized by []; two different power flows have been compared to perform the optimal reconfiguration. An optimal reconfiguration with multi-objective of reduced active power and reactive power losses as well as reliability improvement are studied in []; the authors had also applied particle swarm optimization to search for that optimal reconfiguration. This multi-objective is also investigated in [] using an evolutionary algorithm. Moreover, to tackle with huge search space for reconfiguration, recent researchers have implemented novel techniques for reconfiguration. Two-stage optimizations as a fast optimal system reconfiguration have been provided in []; the authors have proposed a method to simplify the system into a simplified system graph, and this is applied for initializations and generations guiding of the algorithm, and it is implemented with firefly algorithm. A sequential switch opening method is implemented in [] to aim at searching for feeder reconfiguration; this paper is based on minimum active power flow due to replacing impedances by resistances in the branches. The sequential opening of branches has been developed in [] to search for optimal distribution topology in the real system; the authors had compared the simulation and experiment based on the active distribution system testbed for research and teaching. Three steps of a switch opening and exchange method have been also implemented in [] to cope with distributions system reconfiguration; this method is based on sequentially opening the switches and exchange from a looped system to obtain the optimal radial distribution system.
Besides, distributed generation (DG) is one factor that overcomes the issue of under-voltage and power loss in the power distribution system. The sitting and sizing of DGs were described in detail in [,,,] and presented a particular algorithm that results to get the best sitting and sizing of each studied system. The authors in [] have proposed a method of DG placement and reconfiguration simultaneously to address the issue of not only power loss and voltage profile but also system in critical condition like tripping distributed transformer and control increasing short circuit level; they have also studied on real topology 33 bus of the city in Iran. In [,], the authors have presented separately case studies focusing on DG injection into the grid system before, during, and after reconfiguration with the objective of loss reduction and voltage profile improvement. The planning of a distribution system with integration of renewable energy source (RES) and energy storage (ES) has been studied in [,]; the optimal capital and operation costs of components (i.e., line, RES, and ES) as the development cost over a 1-year time horizon based on its sizing, allocation, and curtailment is provided using mixed-integer linear programming (MILP) model.
However, a huge search space, time consumption, and obtaining optimal solution are still a big challenge to solve in large systems with these existing methods. In addition, this existing algorithm development has been attracted the current authors to propose a modified method based on search space reduction for each iteration process. This research paper proposes to modify the existing sequential opening switch and exchange in [] for optimal reconfiguration challenges in comparison to an optimal solution and computation time.
2. Materials and Methods
This paper purposes to develop a modified method for optimal reconfiguration in distribution systems with and without integrated distributed generations.
2.1. Problem Formulation
This part aims at minimizing the power losses through distribution system reconfiguration. The following equation expresses the objective function of the reconfiguration.
where Nbr is the total branches’ number, Ri is the branch resistance i, Vi is the voltage at sending end node of ith branch, and Pi and Qi are the active and reactive power at the sending end node of ith branch.
Subject to the following constraints:
- Voltage constraint
- Current constraint
- Radial topology constraint
The topology of distribution systems must be a radial configuration and there is no isolated node in the system. The radial topology constraint expresses as follows.
where Nnode is the number of nodes in the system.
2.2. Methodology
In this part, the proposed method to achieve the research objectives on distribution system reconfiguration using a modified sequential switch opening and exchange (MSSOE) is presented. The comparison between a proposed method and existing methods is also discussed to figure out the contribution of the research paper. Two sequential steps of the MSSOE method were implemented to achieve the objectives.
2.2.1. Sequential Switch Opening and Exchange (SSOE)
The SSOE method works by searching switch in a topology to open to be a tie-switch in the system. From one iteration to another, there was a repeating switch that was in the same loop as the opened switch. It is necessary to open just a switch in a loop to reach the radial system. However, loops of the switch were integrated into this problem to avoid this repeating process. A novel proposed method in the paper called as a modified switch opening and exchange (MSSOE) method found a tie switch in the first iteration by considering the smallest power loss. Once we got the tie switch, we started to check in the loop in which the tie-switch was in and deleted all switches within the same loop of that tie. By doing this, any switches in the same loop of the tie did not appear in the search space for the next iteration.
2.2.2. Procedure of Step 1 for MSSOE
A flowchart presenting the several steps of the proposed method based on the sequential switch opening technique is provided in Figure 1. First, all switches were closed to perform a meshed system. Then, the power losses in the system for each open switch were determined. Next, we selected a switch with the smallest power loss as a first tie-switch. The rest tie-switches were selected respectively based also on the smallest power loss and maintained radial system. With this proposed method, all switches in the same loop of the previous tie-switches were completely removed from the search space of possible switches to be tie-switches for further iterations. However, all switches in the same loops were not removed from possible tie-switches in the existing method. An optimal radial topology was finally provided.
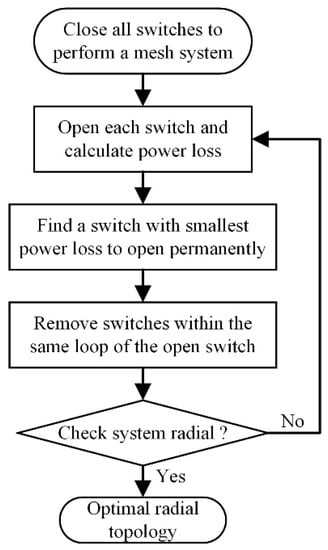
Figure 1.
Flowchart of step 1 for modified sequential switch opening and exchange (MSSOE).
Moreover, the detailed procedure of step 1 for MSSOE is described as follows:
Step 1-1: Read the data of the system.
Step 1-2: Close all ties switches and find out all the switches in loops.
Step 1-3: Open a switch in a loop of topology and calculate power loss.
Step 1-4: Check the opened switch in the loop based on minimum loss and delete all switches in the loop.
Step 1-5: Repeat steps 1–3.
Step 1-6: Find minimum loss satisfied objective function in Equation (1)
Step 1-7: Repeat steps 1–2 to 1–5 until Equation (4) is satisfied.
2.2.3. Procedure of Step 2 for MSSOE
To get more accurate solution, step 2 was proposed to searches for an optimal topology based on the solution obtained in step 1. To do so, it needed to change a sectionalizing switch in the initial topology to a tie-switch, and step 1 was run to get a different topology. Moreover, three excluded switch types were presented (Type-1 switch, Type-2 switch, and Type-3 switch). The different switch types were defined as follows:
Type-1 switch: Any switch whose shortest path was close to the substation node.
Type-2 switch: Any switch whose shortest path was placed at upstream of ending node.
Type-3 switch: Any switch that consisted of the substation node.
The flowchart of step 2 for MSSOE is figured out in Figure 2.
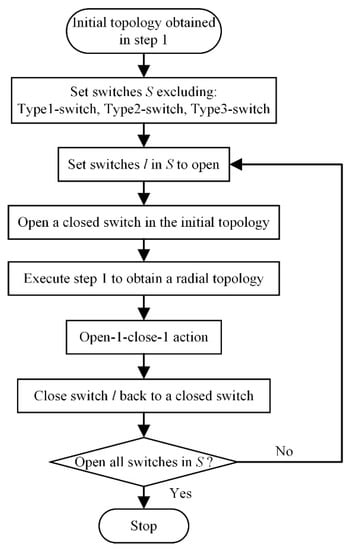
Figure 2.
Flowchart of step 2 for MSSOE.
Moreover, the detailed procedure of step 2 for MSSOE is provided as follows:
Step 2-1: Let S be set of all close-switches obtained in step 1 topology and l is the switch in set S to open.
Step 2-2: Excluded type-1, type-2, and type-3 from S.
Step 2-3: Set switch l open to be a tie-switch.
Step 2-4: Execute step 1 to obtain radial topology and store topology and power loss.
Step 2-5: Close switch l back to a closed switch.
Step 2-6: Repeat steps 2–3 to 2–5 for each switch in S.
Then, the next process of MSSOE were executed by obtaining radial topology given from sub-steps as initialization, which focused on the type-2 switch but not on type-1 and type-3. Switches close to the ending node were set to open and then close a tie switch called open-1-close-1 action [].
2.2.4. Distributed Generation Integration
The restoration with distributed generations (DGs) integration was proposed to reduce system power loss and to improve the voltage profile in the system. The distribution system already existed DGs on a specific bus [] as a hypothesis in this paper, i.e., when the reconfiguration is performed, DG starts injecting its power into the grid then the reconfiguration algorithm will be employed.
3. Simulation Results and Discussion
In this part, the simulation results and discussion of the proposed method for optimal reconfiguration with and with distributed generations with selected test systems are provided. The optimal result of the standard distribution systems of the Institute of Electrical and Electronics Engineers (IEEE) of IEEE 33 [], IEEE 69 [], and IEEE 119 [], are performed in MATLAB R2018a on a Dell PC XPS 8930, Intel Core i7-9700, 3 GHz processor with 16 GB RAM and manufactured by Dell in Texas, U.S.
3.1. Reconfiguration without DGs
3.1.1. Standard IEEE 33-Bus Distribution System
The initial configuration of the standard IEEE 33-bus system is shown in Figure 3 followed by the performance results in Table 1. The initial active power loss of the system is 202.69 kW and the minimum voltage node is 18 with 0.9131 pu. After reconfiguration based on SFS [], SSOE [], and MSSOE, the power loss for all algorithms is reduced to 139.55 kW with a minimum voltage of 0.9378 pu. Regarding time consumption, MSSOE has shown the fastest speed but we notice that it is not much different (i.e., 0.0166 s) for 33 bus system (0.2496 and 0.2330 s). The voltage profiles of the base case and after the reconfiguration are provided in Figure 4. As seen in the figure, the voltage profile of the system is improved with reconfiguration.
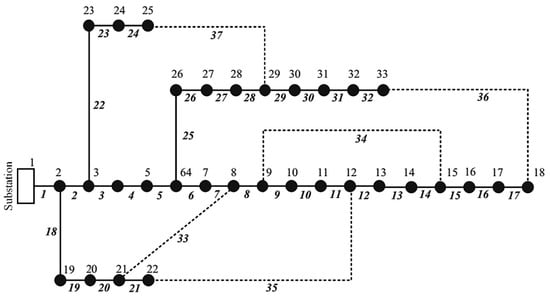
Figure 3.
Single-line diagram of IEEE 33-bus distribution system.

Table 1.
Simulation result of reconfiguration for IEEE 33-bus without the integration of distributed generations (DGs).
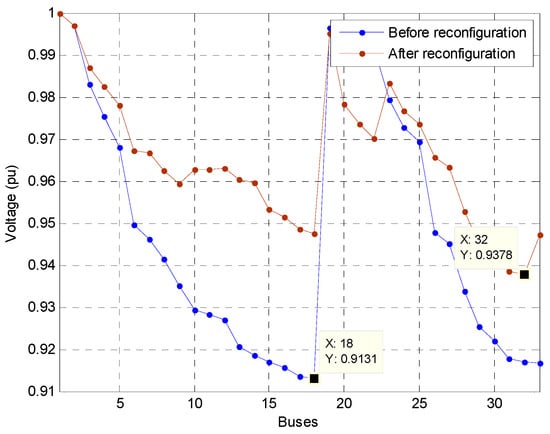
Figure 4.
Voltage profile of IEEE 33 bus before and after the reconfiguration without distributed generations (DGs).
3.1.2. Standard IEEE 69-Bus Distribution System
The initial configuration of the standard IEEE 69-bus system is provided in Figure 5 followed by the performance indicator listed in Table 2. For IEEE 69-bus system, both SSOE and MSSOE has found the same result but different computation time; the MSSOE is the fastest one. The initial active power loss is 224.95 kW and the minimum voltage node is 65 with 0.9092 pu. After reconfiguration, the power loss is reduced to 99.69 kW and the minimum voltage node is 61 with 0.9428 pu. The voltage profile is also improved with the reconfiguration as provided in Figure 6.
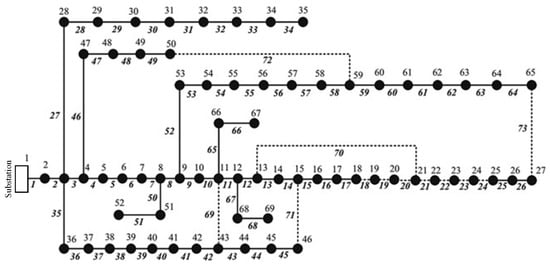
Figure 5.
Single-line diagram of IEEE 69-bus distribution system.

Table 2.
Simulation result of reconfiguration for IEEE 69-bus without DGs.
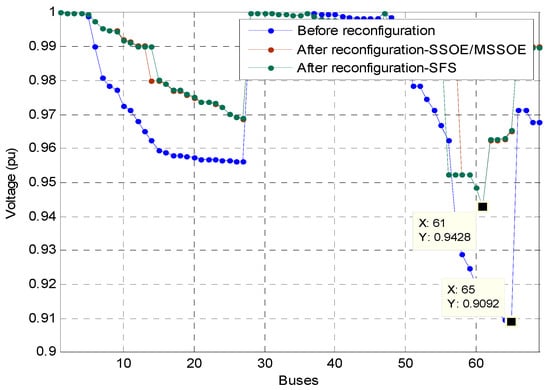
Figure 6.
Voltage profile of IEEE 69-bus before and after the reconfiguration without DGs.
3.1.3. Standard IEEE 119-Bus Distribution System
Figure 7 shows the standard IEEE 119-bus distribution systems. The power loss and minimum voltages are 1296.57 kW and 0.8688 pu, respectively, at the initial configuration. As seen in Table 3, all the three algorithms have given power loss of 853.6, 853.6, and 854.03 kW after system reconfiguration, respectively. Regarding SSOE and MSSOE, it can be noticed that the computation time is reduced from 4.0328 to 2.5256 s. Refer to the voltage profile, the performance is increased considerably with reconfiguration. Figure 8 illustrates the voltage profile before and after the reconfiguration.
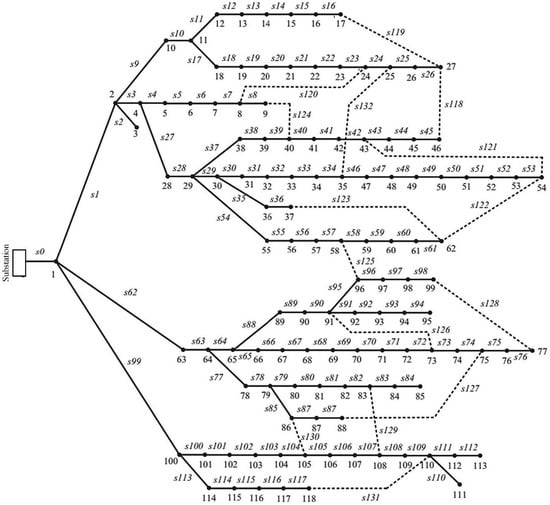
Figure 7.
Single-line diagram of IEEE 119-bus distribution system.

Table 3.
Simulation result of reconfiguration for IEEE 119-bus without DGs.
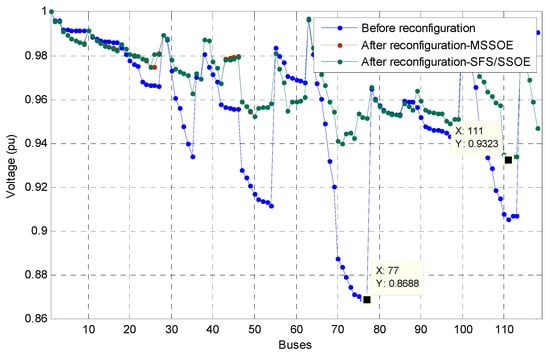
Figure 8.
Voltage profile of IEEE 119-bus before and after the reconfiguration with DGs.
3.2. Reconfiguration with DGs
In this part, we presented the reconfiguration with DG integration into the test systems obtained in [] with its size and location.
3.2.1. Standard IEEE 33-Bus Distribution System
Three distributed generations at buses of 14, 24, and 30 are proposed to integrate into the standard test system before the reconfiguration. The initial configuration of the system provides a power loss of 71.46 kW with a minimum voltage of 0.9687 pu. After the reconfiguration using three different methods, it can be noticed that the topologies are slightly different with increased minimum voltage (i.e., 0.9774 pu). Additionally, the computation time of MSSOE is faster compared to the existing method as seen in Table 4. The voltage profile of the system is shown in Figure 9. Regarding power loss, it has been reduced dramatically to 57.7 kW due to the reconfiguration.

Table 4.
Simulation result of reconfiguration for IEEE 33-bus with DGs.
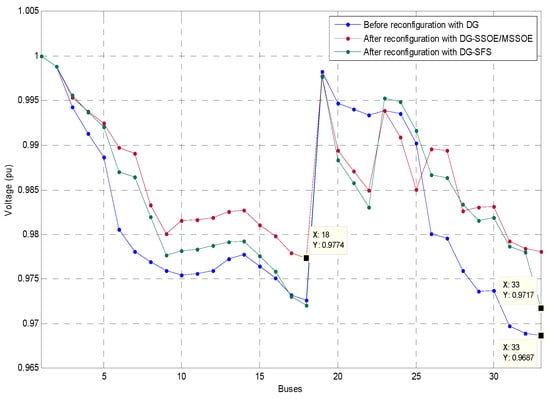
Figure 9.
Voltage profile of IEEE 33-bus before and after the reconfiguration with DGs.
3.2.2. Standard IEEE 69-Bus Distribution System
This standard test system is also proposed to have the three distributed generations in the systems which are at 11, 18, and 61 with the sizing as provided in Table 5. We observe that the voltage profile before reconfiguration (i.e., 0.9793) is higher than reconfiguration (i.e., 0.9690 pu). However, the power loss is dramatically reduced to 39.64, which equals to 42.88 % reduction compared to the base case as seen in the table. In addition, the MSSOE is computed fastest compared to SSOE, i.e., it is 0.1291 s faster. Figure 10 shows the voltage profile before and after the reconfiguration with integrated distributed generations.

Table 5.
Simulation result of reconfiguration for IEEE 69-bus with DGs.
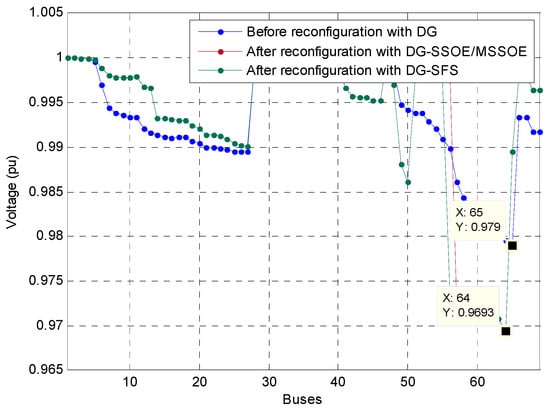
Figure 10.
Voltage profile of IEEE 69-bus before and after the reconfiguration with DGs.
3.2.3. Standard IEEE 119-Bus Distribution System
The distributed generations at buses of 50, 71, and 109 with the capacities of 2.88, 2.97, and 3.11 MW are proposed to be integrated into the standard IEEE 119-bus distribution system, respectively. The minimum voltages for before and after reconfiguration based on three methods are slightly different (i.e., 0.9545 pu vs. 0.9549 pu). The voltage profiles of the system before and after the reconfiguration are illustrated in Figure 11. However, the power losses are reduced considerably from 666.04 to 620.65 kW (SFS), 617.9 kW (SSOE), and 616.8 kW (MSSOE), respectively. The result in Table 6 shows that the power loss reduction is not much different, however, the time consumption of the proposed method is less compared to the existing method. The computation time of MSSOE is 1.2727 s faster than SSOE as provided in the Table 6. Therefore, distributed generators into the system are the key solution for loss reduction in the power system network.
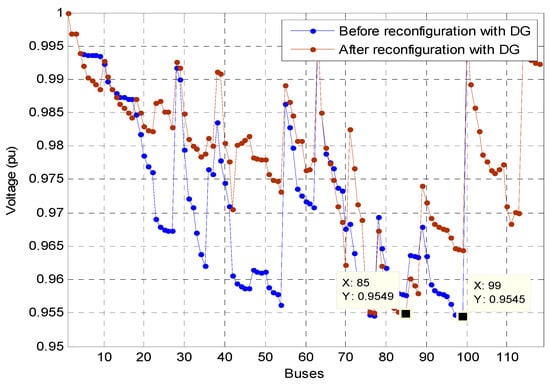
Figure 11.
Voltage profile of IEEE 119-bus before and after the reconfiguration.

Table 6.
Simulation result of reconfiguration for IEEE 119-bus with DGs.
4. Conclusions and Future Work
In this research paper, the modified sequential switch opening and exchange (MSSOE) has been developed for reducing power losses through distribution system reconfiguration with and without the integration of distributed generations. The novel approach is based on the existing method in which the search space for each iteration process is modified for reconfiguration thanks to predefined individual loops of the distribution systems. The simulation results of selected three different standards of IEEE 33-bus, IEEE 69-bus, and 119-bus systems provide the effectiveness of the proposed method over the existing methods. Moreover, the more the large systems, more is the difference of computation time; this is compared to the proposed method. The global optimization solution and fast computation time compared to existing methods are also a challenge in this research paper. It can be concluded that the proposed method based on MSSOE is the fastest algorithm compared to existing methods. To extend the implementation of the proposed method, the integration of distribution generations and load demand uncertainties over various times will be investigated. In addition, the challenge of allocation and sizing of distributed generations including its maximum penetration with the proposed reconfiguration technique will be considered. A prototype development at the laboratory to narrow a gap between simulation and experiment is also considered in the future work.
Author Contributions
Conceptualization, V.V. and S.E.; methodology, V.V.; software, R.L. and S.S.; validation, R.L., S.S., and V.V.; formal analysis, V.V.; investigation, R.L., S.S., and V.V.; resources, R.L., S.S., and S.E.; data curation, R.L., S.S., and S.E.; writing—original draft preparation, V.V.; writing—review and editing, V.V., S.E., R.L., S.S., C.C., and L.B.; visualization, S.S., C.C., and L.B.; supervision, V.V., S.E., and L.B.; project administration, C.C., V.V., and L.B.; funding acquisition, V.V. and L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Japan International Cooperation Agency (JICA) through Laboratory-based education (LBE) in the Department of Electrical and Energy Engineering at the Institute of Technology of Cambodia (ITC), CAMBODIA.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, T.; Wang, C.; Luo, F.; Li, P.; Yao, L. Optimal design of the sectional switch and tie line for the distribution network based on the fault incidence matrix. IEEE Trans. Power Syst. 2019, 34, 4869–4879. [Google Scholar] [CrossRef]
- Ahmed, E.B.A.; Salama, M.M.A.; Khaled, B.S. Modern network reconfiguration techniques for service restoration in distribution systems: A step to a smarter grid. Alex. Eng. J. 2018, 57, 3959–3967. [Google Scholar]
- Darko, S.; Predrag, S. Reconfiguration of distribution system with distributed generation using an adaptive loop approach. J. Electr. Eng. 2019, 70, 345–357. [Google Scholar]
- Zhan, J.; Liu, W.; Chung, C.Y.; Yang, J. Switch opening and exchange method for stochastic distribution network reconfiguration. IEEE Trans. Smart Grid 2020, 11, 2995–3007. [Google Scholar] [CrossRef]
- Anitha, S.; Ramesh, M.B. Network reconfiguration for loss minimization by using Johnson’s algorithm. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 680–684. [Google Scholar]
- Daud, J.G.; Kondoj, M.; Patabo, M. Reconfiguration distribution network with ant colony. In Proceedings of the 2018 International Conference on Applied Science and Technology (iCAST), Manado, Indonesia, 26–27 October 2018; pp. 349–353. [Google Scholar]
- Diaaeldin, I.M.; Aleem, S.H.E.A.; El-rafei, A.; Abdelaziz, A.Y. A novel reconfiguration methodology of radial distribution systems for power loss minimization using expanded invasive weed optimization. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 119–124. [Google Scholar]
- Fuad, N.A.A.; Azlin, A.A.N.; Zahari, M.F.D.; Hanifah, M.S.A. Power distribution loss reduction using cuckoo search. In Proceedings of the 2018 7th International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 19–20 September 2018; pp. 333–337. [Google Scholar]
- Guo, Z.; Li, X.; Geng, J.; Wu, B. Distribution network reconfiguration based on opposition learning genetic algorithm. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGTAsia), Singapore, 22–25 May 2018; pp. 345–349. [Google Scholar]
- Hamioud, A.; Sebaa, P.K. Genetic algorithms for the reconfiguration of electrical distribution networks. In Proceedings of the 2019 International Conference on Advanced Electrical Engineering (ICAEE), Algiers, Algeria, 19–21 November 2019; pp. 1–6. [Google Scholar]
- Hamour, H.; Kamel, S.; Abdel-mawgoud, H.; Korashy, A.; Jurado, F.F. Distribution network reconfiguration using grasshopper optimization algorithm for power loss minimization. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–5. [Google Scholar]
- Hamour, H.; Kamel, S.; Nasrat, L.; Yu, J.J. Distribution network reconfiguration using augmented grey wolf optimization algorithm for power loss minimization. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 450–454. [Google Scholar]
- Ji, X.; Liu, Q.; Yu, Y.; Fan, S.; Wu, N. Distribution network reconfiguration based on vector shift operation. IET Gener. Transm. Distrib. Res. 2018, 12, 3339–3345. [Google Scholar] [CrossRef]
- Kamel, S.; Nasrat, L.; Yu, J.; Xie, K.; Khasanov, M. Radial distribution system reconfiguration for real power losses reduction by using salp swarm optimization algorithm. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Asia Radial, Chengdu, China, 21–24 May 2019; pp. 720–725. [Google Scholar]
- Sellami, R.; Neji, F.; Bouktir, T. Enhancing radial distribution network performance by optimal reconfiguration with PSO algorithm. In Proceedings of the 2019 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 21–24 March 2019; pp. 180–186. [Google Scholar]
- Shi, Y.; Yan, Y.; Liu, Y. Research on optimized reconfiguration of distribution network based on improved fireworks algorithm. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 70–74. [Google Scholar]
- Tang, H.; Zhu, J.; Chen, C.; Zhang, Z.; Zhang, D. Distribution network reconfiguration based on back propagation neural networks. In Proceedings of the IEEE conference on Energy Internet and Energy System Integration, Changsha, China, 8–10 November 2019; pp. 2578–2582. [Google Scholar]
- Gerez, C.; Silva, L.I.; Belati, E.A.; Filho, A.J.S.; Costa, E.C.M. Distribution network reconfiguration using selective firefly algorithm and a load flow analysis criterion for reducing the search space. IEEE Access 2019, 7, 67874–67888. [Google Scholar] [CrossRef]
- Hussain, A.N.; Al-Jubori, W.K.; Kadom, H.F. Optimal distribution system reconfiguration using qualified binary particle swarm optimization algorithm. In Proceedings of the 2019 4th Scientific International Conference Najaf (SICN), Al-Najaf, Iraq, 29–30 April 2019; pp. 64–69. [Google Scholar]
- Kumar, B.; Saw, B.K.S.; Bohre, A.K. Optimal distribution network reconfiguration to improve the system performances using PSO with multiple-objectives. In Proceedings of the IEEE International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Odisha, India, 23–25 April 2020; pp. 1–6. [Google Scholar]
- Landeros, A.; Koziel, S.; Abdel-fattah, M.F. Distribution network reconfiguration using feasibility-preserving evolutionary optimization. J. Mod. Power Syst. Clean Energy 2019, 7, 589–598. [Google Scholar] [CrossRef]
- Samman, M.A.; Mokhlis, H.; Mansor, N.N.; Suyono, H.; Sapari, N. Fast optimal network reconfiguration with guided initialization based on a simplified network approach. IEEE Access 2020, 8, 11948–11963. [Google Scholar] [CrossRef]
- Singh, S.P.; Raju, G.S.; Rao, G.K.; Afsari, M. A heuristic method for feeder reconfiguration and service restoration in distribution networks. Int. J. Electr. Power Energy Syst. 2009, 31, 309–314. [Google Scholar] [CrossRef]
- Alvarez-Herault, M.C.; Labonne, A.; Toure, S.; Braconnier, T.; Debusschere, V.; Caire, R.; Hadjsaid, N. An original smart-grids test bed to teach feeder automation functions in a distribution grid. IEEE Trans. Power Syst. 2017, 33, 373–385. [Google Scholar] [CrossRef]
- Priyadarshini, R.; Kori, S.; Rekha, C.M. Cuckoo search algorithm based multiple dg placement and voltage profile improvement in a radial distribution system. In Proceedings of the 2017 International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 22–24 February 2017; pp. 1–6. [Google Scholar]
- Vatani, M.; Alkaran, D.S.; Sanjari, M.J.; Gharehpetian, G.B. Multiple distributed generation units allocation in distribution network for loss reduction based on a combination of analytical and genetic algorithm methods. IET Gener. Transmiss. Distrib. 2016, 10, 66–72. [Google Scholar] [CrossRef]
- Rajaram, R.; Kumar, K.S.; Rajasekar, N.N. Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with distributed generation (DG). Energy Rep. 2015, 1, 116–122. [Google Scholar] [CrossRef]
- Lalitha, M.P.; Babu, P.S.; Adivesh, B. SOS algorithm for DG placement for loss minimization considering reverse power flow in the distribution systems. In Proceedings of the 2016 International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 25–27 May 2016; pp. 443–448. [Google Scholar]
- Moarrefi, H.; Nematollahi, M.; Tadayon, M. Reconfiguration and distributed generation (DG) placement considering critical system condition. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED), Stockholm, Sweden, 10–13 June 2013; pp. 1–5. [Google Scholar]
- Tran, T.T.; Truong, K.H.; Vo, D.N. Stochastic fractal search algorithm for reconfiguration of distribution networks with distributed generations. Ain Shams Eng. J. 2020, 11, 389–407. [Google Scholar] [CrossRef]
- Siahbalaee, J.; Rezanejad, N.; Gharehpetian, G.B. Reconfiguration and DG sizing and placement using improved shuffled frog leaping algorithm. Elec. Power Comp. Syst. 2019, 47, 1475–1488. [Google Scholar] [CrossRef]
- Andrychowicz, M. RES and ES integration in combination with distribution grid development using MILP. Energies 2021, 14, 383. [Google Scholar] [CrossRef]
- Andrychowicz, M. Comparison of the use of energy storages and energy curtailment as an addition to the allocation of renewable energy in the distribution system in order to minimize development costs. Energies 2020, 13, 3746. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Savier, J.S.; Das, D. Impact of network reconfiguration on loss allocation of radial distribution systems. IEEE Trans. Power Deliv. 2007, 22, 2473–2480. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).