Aerodynamics of Cycling Skinsuits Focused on the Surface Shape of the Arms
Abstract
:1. Introduction
2. Methods
2.1. Wind-Tunnel Experiment
2.2. CFD Analysis
3. Results and Discussion
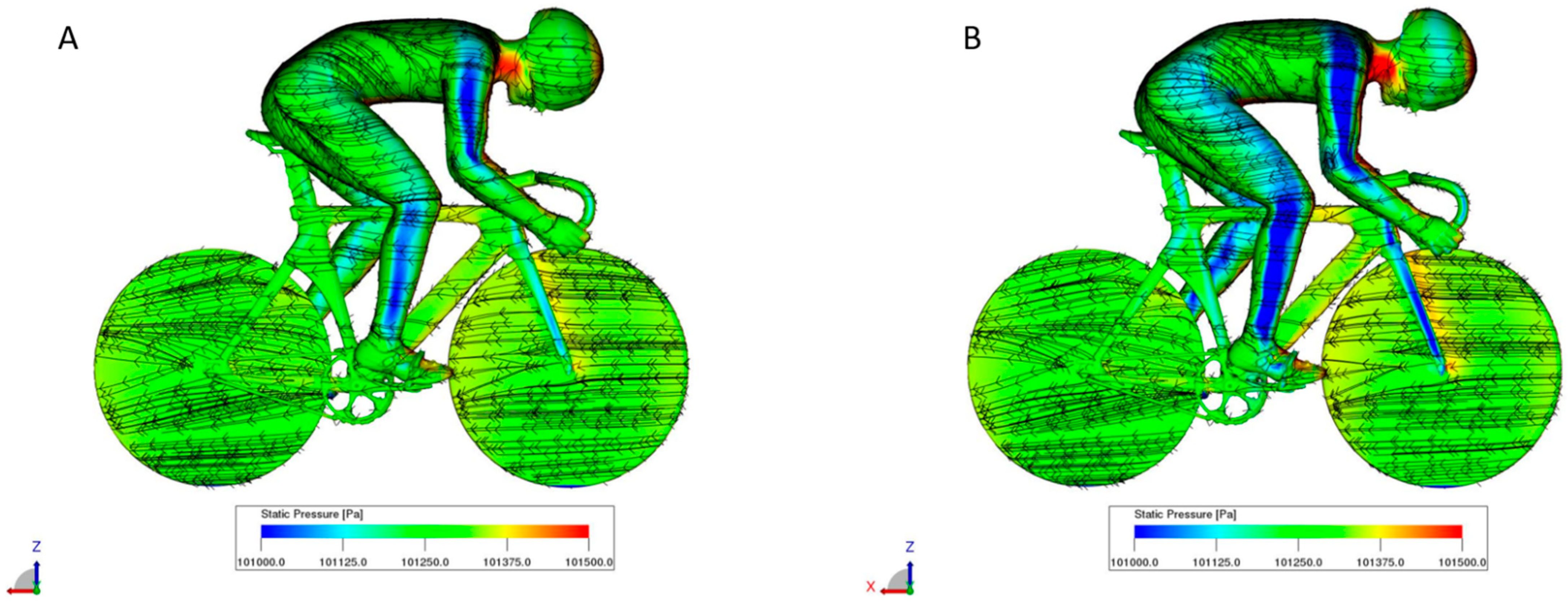
3.1. Visualization Results Using CFD
3.2. Wind Tunnel Experiment Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kyle, C.R.; Burke, E. Improving the racing bicycle. Mech. Eng. 1984, 106, 34–45. [Google Scholar]
- Crouch, T.N.; Burton, D.; Brown, N.A.T.; Thompson, M.C.; Sheridan, J. Flow topology in the wake of a cyclist and its effect on aerodynamic drag. J. Fluid Mech. 2014, 748, 5–35. [Google Scholar] [CrossRef]
- Crouch, T.N.; Burton, D.; Thompson, M.C.; Brown, N.A.T.; Sheridan, J. Dynamic leg motion and its effect on the aerodynamic performance of cyclists. J. Fluids Struct. 2016, 65, 121–137. [Google Scholar] [CrossRef]
- Blocken, B.; van Druenen, T.; Toparlar, Y.; Andrianne, T. Aerodynamic analysis of different cyclist hill descent positions. J. Wind Eng. Ind. Aerodyn. 2018, 181, 27–45. [Google Scholar] [CrossRef]
- Chen, J.; Miau, J.; Chen, Y.; Tseng, C. Flow over a complex buffy body: Investigation of flow around the cyclist. In Proceedings of the International Symposium on Advanced Science and Technology in Experimental Mechanics (FL-425(1-5)), Tsukuba, Japan, 9–11 July 2019. [Google Scholar]
- Crouch, T.N.; Burton, D.; Venning, J.A.; Thompson, M.C.; Brown, N.A.T.; Sheridan, J. A comparison of the wake structures of scale and full-scale pedaling cycling models. Procedia Eng. 2016, 147, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Miau, J.; Li, S.; Tsai, Z.; Phung, M.V.; Lin, S. On the aerodynamic flow around a cyclist model at the hoods position. J. Vis. 2020, 23, 35–47. [Google Scholar] [CrossRef] [Green Version]
- Griffith, M.D.; Crouch, T.N.; Thompson, M.C.; Burton, D.; Sheridan, J.; Brown, N.A. Computational fluid dynamics study of the effect of leg position on cyclist aerodynamic drag. J. Fluids Eng. 2014, 136, 101–105. [Google Scholar] [CrossRef] [Green Version]
- Debraux, P.; Grappe, F.; Manolova, A.V.; Bertucci, W. Aerodynamic drag in cycling: Methods of assessment. Sports Biomech. 2011, 10, 197–218. [Google Scholar] [CrossRef] [PubMed]
- Godo, M.N.; Corson, D.; Legensky, S.M. Comparative aerodynamic study of commercial bicycle wheels using CFD. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; pp. 2010–2143. [Google Scholar] [CrossRef] [Green Version]
- Crouch, T.N.; Burton, D.; LaBry, Z.A.; Blair, K.B. Riding against the wind: A review of competition cycling aerodynamic. Sports Eng. 2017, 20, 81–110. [Google Scholar] [CrossRef]
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Carmeliet, J. Computational fluid dynamics analysis of cyclist aerodynamics: Performance of different turbulence-modelling and boundary-layer modelling approaches. J. Biomech. 2010, 43, 2281–2287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Carmeliet, J. Computational fluid dynamics analysis of drag and convective heat transfer of individual body segments for different cyclist positions. J. Biomech. 2011, 44, 1695–1701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Verboven, P.; Nicolai, B.; Carmeliet, J. Cyclist drag in team pursuit: Influence of cyclist sequence, stature, and arm spacing. J. Biomech. Eng. Trans. ASME 2014, 136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gibertini, G.; Grassi, D. Cycling aerodynamics. In Sport Aerodynamics; Nørstrud, H., Ed.; Springer: Vienna, Austria, 2008; Volume 56, pp. 23–47. [Google Scholar]
- Zdravkovich, M.M.; Ashcroft, M.W.; Chisholm, S.J.; Hicks, N. Effect of cyclists’ posture and vicinity of another cyclist on aerodynamic drag. Eng. Sport 1996, 1, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Malizia, F.; Blocken, B. Bicycle aerodynamics: History, state-of-the-art and future perspectives. J. Wind Eng. Ind. Aerodyn. 2020, 200, 104134. [Google Scholar] [CrossRef]
- Chen, H. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept. Phys. Rev. E 1998, 58, 3955–3963. [Google Scholar] [CrossRef]
- Liu, Q.; Feng, X.; He, Y.L.; Lu, C.; Gu, Q. Three-dimensional multiple-relaxation-time lattice Boltzmann models for single-phase and solid-liquid phase-change heat transfer in porous media at the REV scale. Appl. Therm. Eng. 2019, 152, 319–337. [Google Scholar] [CrossRef]
- Kotapati, R.; Keating, A.; Kandasamy, S.; Duncan, B.; Shock, R.; Chen, H. The lattice-Boltzmann-VLES method for automotive dynamics simulation, a review. SAE Tech. Pap. 2009, 26, 57. [Google Scholar] [CrossRef]
- Peng, Y.; Shu, C.; Chew, Y. A 3D incompressible thermal lattice Boltzmann model and its application to simulate natural convection in a cubic cavity. J. Comput. Phys. 2003, 193, 260–274. [Google Scholar] [CrossRef]









| Item | Values | |
|---|---|---|
| Turbulence model | VLES (analyzed with Powerflow 5.5) | |
| Representative pressure [Pa] | 101,325 | |
| Representative temperature [°C] | 20.0 | |
| Representative density [kg/m3] | 1.204 | |
| Representative kinematic viscosity [m2/s] | 1.49 × 10−5 | |
| Calculated physical time [sec] | 1.27 (case 1; 16 m/s) | 1.40 (case 2; 20 m/s) |
| Minimum voxel size [mm] | 1.25 | |
| Total voxels | 191.20 million | |
| Fine Equivalent Voxels (FEV) | 100.61 million | |
| Total surfels | 7.09 million | |
| FES (fine equivalent surfels) | 6.85 million | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.; Asai, T. Aerodynamics of Cycling Skinsuits Focused on the Surface Shape of the Arms. Appl. Sci. 2021, 11, 2200. https://doi.org/10.3390/app11052200
Hong S, Asai T. Aerodynamics of Cycling Skinsuits Focused on the Surface Shape of the Arms. Applied Sciences. 2021; 11(5):2200. https://doi.org/10.3390/app11052200
Chicago/Turabian StyleHong, Sungchan, and Takeshi Asai. 2021. "Aerodynamics of Cycling Skinsuits Focused on the Surface Shape of the Arms" Applied Sciences 11, no. 5: 2200. https://doi.org/10.3390/app11052200
APA StyleHong, S., & Asai, T. (2021). Aerodynamics of Cycling Skinsuits Focused on the Surface Shape of the Arms. Applied Sciences, 11(5), 2200. https://doi.org/10.3390/app11052200







