Parasitic-Based Active Gate Driver Improving the Turn-On Process of 1.7 kV SiC Power MOSFET
Abstract
:1. Introduction
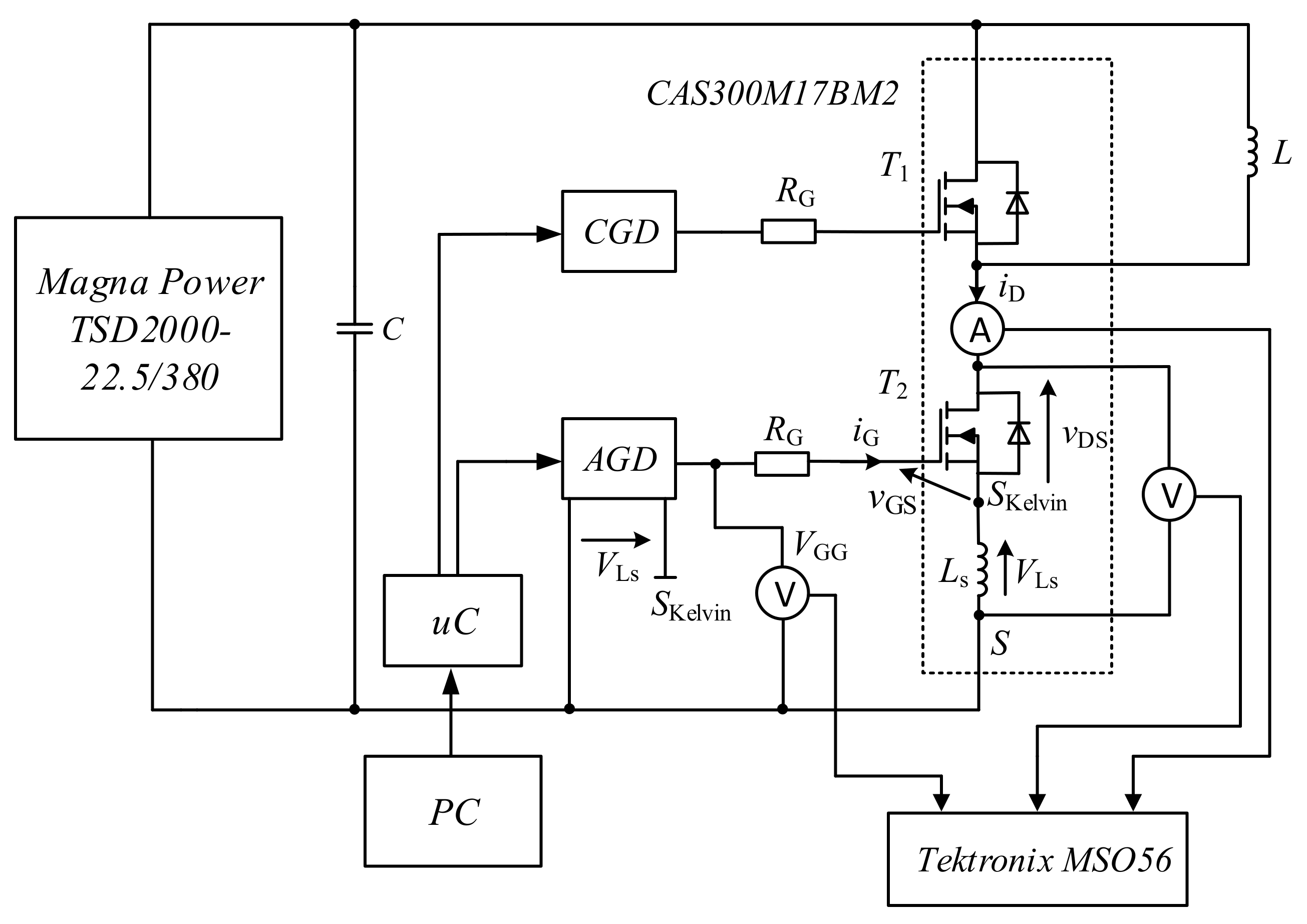
2. The Active Gate Driver
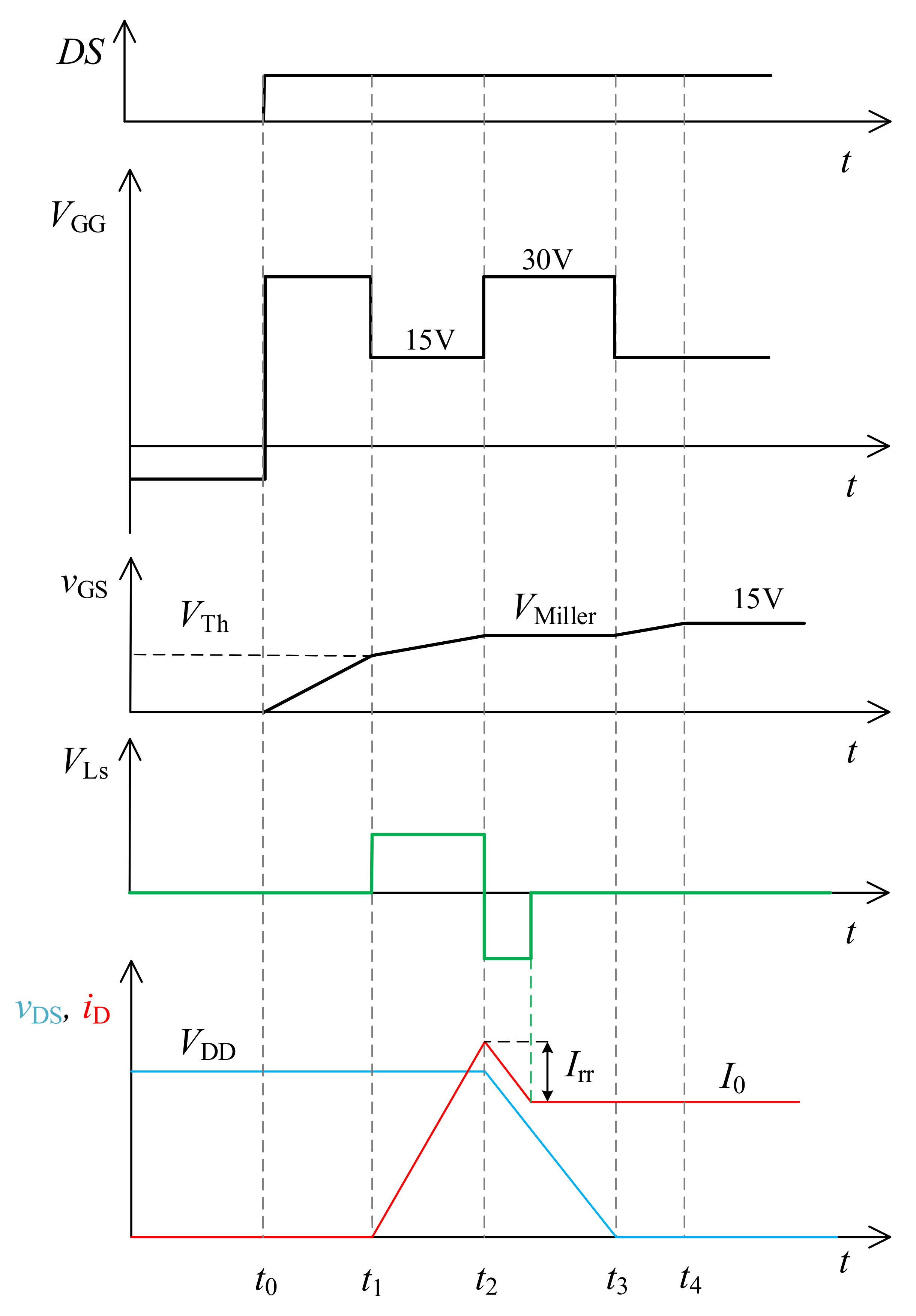
Gate Voltage Manipulation for the Turn-On Cycle Improvment
3. Simulation Study
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mishra, P.; Maheshwari, R. Evaluation of All SiC MOSFET Based Voltage Source Inverter with Open Loop Induction Motor. In Proceedings of the 2017 14th IEEE India Council International Conference (INDICON), Roorkee, India, 15–17 December 2017; pp. 1–6. [Google Scholar]
- Sayed, H.; Surf, A.; Zhang, J. Investigation of the effects of load parasitic inductance on SC MOSFETs switching performance. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 125–129. [Google Scholar]
- Nayak, P.; Hague, K. Modeling of switching behavior of 1200 V sick MOSFET in presence of layout parasitic inductance. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; pp. 1–6. [Google Scholar]
- Sugihara, Y.; Nanamori, K.; Ishiwaki, S.; Hayashi, Y.; Aikawa, K.; Umetani, K.; Hiraki, E.; Yamamoto, M. Analytical investigation on design to avoid oscillatory false triggering of fast switching SiC-MOSFETs. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5113–5118. [Google Scholar]
- Dalal, D.N.; Christensen, N.; Jørgensen, A.B.; Jørgensen, J.K.; Bęczkowski, S.; Munk-Nielsen, S.; Uhrenfeldt, C. Impact of Power Module Parasitic Capacitances on Medium-Voltage SiC MOSFETs Switching Transients. IEEE J. Emerg. Sel. Top. Power Instr. Electron. 2020, 8, 298–310. [Google Scholar] [CrossRef]
- Rasoanarivo, I.; Dell’Isola, D. Improvements of switching energy of SiC transistor with respect of chip integrity and EMC standards. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar]
- Kim, T.; Feng, D.; Jang, M.; Agelidis, V.G. Common Mode Noise Analysis for Cascaded Boost Converter with Silicon Carbide Devices. IEEE Trans. Power Electron. 2017, 32, 1917–1926. [Google Scholar] [CrossRef]
- Han, Y.; Lu, H.; Li, Y.; Chai, J. Open-Loop Gate Control for Optimizing the Turn-ON Transition of SiC MOSFETs. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1126–1136. [Google Scholar] [CrossRef]
- Li, H.; Jiang, Y.; Feng, C.; Yang, Z. A Voltage-injected Active Gate Driver for Improving the Dynamic Performance of SiC MOSFET. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6943–6948. [Google Scholar]
- Paredes, A.; Fernandez, E.; Sala, V.; Ghorbani, H.; Romeral, L. Switching trajectory improvement of SiC MOSFET devices using a feedback gate driver. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 19–22 February 2018; pp. 847–852. [Google Scholar]
- Nayak, P.; Hatua, K. Active gate driving technique for a 1200 V SiC MOSFET to minimize detrimental effects of parasitic inductance in the converter layout. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]
- Wang, J.; Shen, Z.; DiMarino, C.; Burgos, R.; Boroyevich, D. Gate driver design for 1.7 kV SiC MOSFET module with Rogowski current sensor for shortcircuit protection. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 516–523. [Google Scholar]
- Marzoughi, A.; Burgos, R.; Boroyevich, D. Active Gate-Driver with dv/dt Controller for Dynamic Voltage Balancing in Series-Connected SiC MOSFETs. IEEE Trans. Ind. Electron. 2019, 66, 2488–2498. [Google Scholar] [CrossRef]
- Krishna, M.V.; Hatua, K. Closed loop analog active gate driver for fast switching and active damping of SiC MOSFET. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 3017–3021. [Google Scholar]
- Yang, Y.; Wen, Y.; Gao, Y. A Novel Active Gate Driver for Improving Switching Performance of High-Power SiC MOSFET Modules. IEEE Trans. Power Electron. 2019, 34, 7775–7787. [Google Scholar] [CrossRef]
- Sobieski, R.; Trochimiuk, P.; Skoneczny, H.; Rąbkowski, J. Impact of a gate drive on performance of three-phase inverters based on 3.3 kV SiC MOSFETs. In Proceedings of the 2020 Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 21–26 June 2020; pp. 1–7. [Google Scholar]
- Li, X.; Zhang, L.; Guo, S.; Lei, Y.; Huang, A.Q.; Zhang, B. Understanding switching losses in SiC MOSFET: Toward lossless switching. In Proceedings of the 2015 IEEE 3rd Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Blacksburg, VA, USA, 2–4 November 2015; pp. 257–262. [Google Scholar]
- Zeng, Y.; Yi, Y.; Liu, P. An Improved Investigation into the Effects of the Temperature-Dependent Parasitic Elements on the Losses of SiC MOSFETs. Appl. Sci. 2020, 10, 7192. [Google Scholar] [CrossRef]
- Wolfspeed CAS300M17BM2 Datasheet. Available online: https://www.wolfspeed.com/downloads/dl/file/id/185/product/102/cas300m17bm2.pdf (accessed on 2 March 2021).
- Rashid, M.H. Power Electronics Handbook, 1st ed.; Academic Press: San Diego, CA, USA, 2001; pp. 86–88. [Google Scholar]










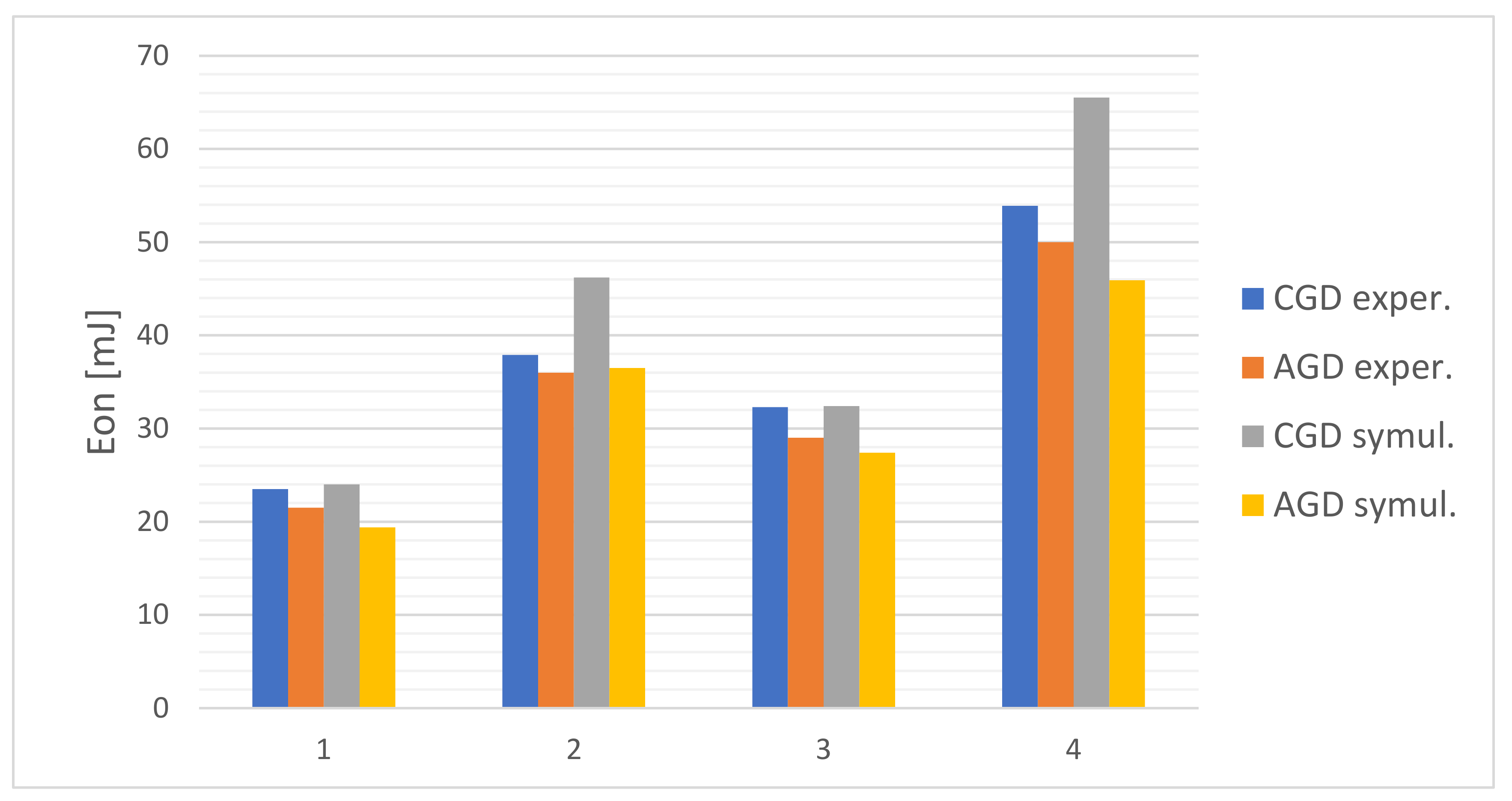
| VDD | I0 | Eon CGD | Eon AGD |
|---|---|---|---|
| 700 V | 170 A | 24.0 mJ | 19.4 mJ |
| 700 V | 270 A | 46.2 mJ | 36.5 mJ |
| 900 V | 170 A | 32.4 mJ | 27.4 mJ |
| 900 V | 270 A | 65.5 mJ | 45.9 mJ |
| VDD | I0 | Eon CGD | Eon AGD |
|---|---|---|---|
| 700 (±14) V | 170 (±3.4) A | 23.5 (±0.94) mJ | 21.5 (±0.86) mJ |
| 700 (±14) V | 270 (±5.4) A | 37.9 (±1.52) mJ | 36.0 (±1.44) mJ |
| 900 (±18) V | 170 (±3.4) A | 32.3 (±1.29) mJ | 29.0 (±1.16) mJ |
| 900 (±18) V | 270 (±5.4) A | 53.9 (±2.16) mJ | 50.0 (±2.0) mJ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lasek, B.; Trochimiuk, P.; Kopacz, R.; Rąbkowski, J. Parasitic-Based Active Gate Driver Improving the Turn-On Process of 1.7 kV SiC Power MOSFET. Appl. Sci. 2021, 11, 2210. https://doi.org/10.3390/app11052210
Lasek B, Trochimiuk P, Kopacz R, Rąbkowski J. Parasitic-Based Active Gate Driver Improving the Turn-On Process of 1.7 kV SiC Power MOSFET. Applied Sciences. 2021; 11(5):2210. https://doi.org/10.3390/app11052210
Chicago/Turabian StyleLasek, Bartosz, Przemysław Trochimiuk, Rafał Kopacz, and Jacek Rąbkowski. 2021. "Parasitic-Based Active Gate Driver Improving the Turn-On Process of 1.7 kV SiC Power MOSFET" Applied Sciences 11, no. 5: 2210. https://doi.org/10.3390/app11052210
APA StyleLasek, B., Trochimiuk, P., Kopacz, R., & Rąbkowski, J. (2021). Parasitic-Based Active Gate Driver Improving the Turn-On Process of 1.7 kV SiC Power MOSFET. Applied Sciences, 11(5), 2210. https://doi.org/10.3390/app11052210






