Multifunctional Hyperelastic Structured Surface for Tunable and Switchable Transparency
Abstract
:1. Introduction
2. Materials and Methods
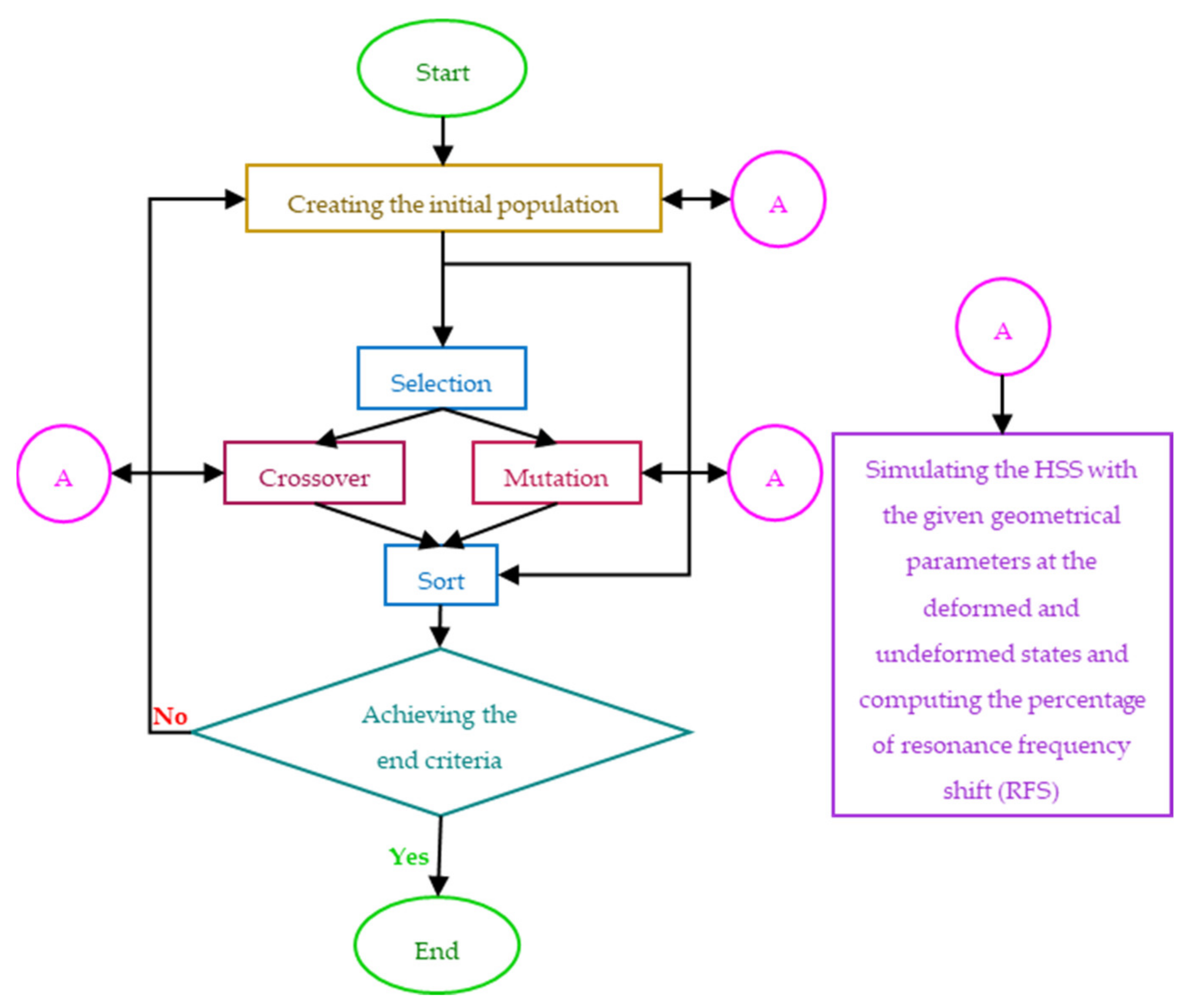
2.1. Analysis and Design
2.2. Experimental Section
2.2.1. Material
2.2.2. Fabrication Process
2.2.3. Measurements and Characterization
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bukhari, S.S.; Vardaxoglou, J.Y.; Whittow, W. A metasurfaces review: Definitions and applications. Appl. Sci. 2019, 9, 2727. [Google Scholar] [CrossRef] [Green Version]
- Ziolkowski, R.W.; Jin, P.; Lin, C.C. Metamaterial-inspired engineering of antennas. Proc. IEEE 2010, 99, 1720–1731. [Google Scholar] [CrossRef]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub–diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, Y.; Kim, S.J.; Park, H.; Lee, B. Metamaterials and metasurfaces for sensor applications. Sensors 2017, 17, 1726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burch, J.; Di Falco, A. Surface topology specific metasurface holograms. ACS Photonics 2018, 5, 1762–1766. [Google Scholar] [CrossRef]
- Butt, H.; Montelongo, Y.; Butler, T.; Rajesekharan, R.; Dai, Q.; Shiva-Reddy, S.G.; Wilkinson, T.D.; Amaratunga, G.A. Carbon nanotube based high resolution holograms. Adv. Mater. 2012, 24, OP331–OP336. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [Green Version]
- Rajasekharan Unnithan, R.; Sun, M.; He, X.; Balaur, E.; Minovich, A.; Neshev, D.N.; Skafidas, E.; Roberts, A. Plasmonic colour filters based on coaxial holes in aluminium. Materials 2017, 10, 383. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Liu, Y.; Ganesan, K.; Ahnood, A.; Beckett, P.; Eftekhari, F.; Smith, D.; Uddin, M.H.; Skafidas, E.; Nirmalathas, A.; et al. A single sensor based multispectral imaging camera using a narrow spectral band color mosaic integrated on the monochrome CMOS image sensor. APL Photonics 2020, 5, 046104. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.; Chen, H.T. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [Green Version]
- Cure, D.; Weller, T.M.; Miranda, F.A. Study of a low-profile 2.4-GHz planar dipole antenna using a high-impedance surface with 1-D varactor tuning. IEEE Trans. Antennas Propag. 2012, 61, 506–515. [Google Scholar] [CrossRef]
- Kim, M.; Kim, I.; Jang, J.; Lee, D.; Nam, K.T.; Rho, J. Active color control in a metasurface by polarization rotation. Appl. Sci. 2018, 8, 982. [Google Scholar] [CrossRef] [Green Version]
- Pryce, I.M.; Aydin, K.; Kelaita, Y.A.; Briggs, R.M.; Atwater, H.A. Highly strained compliant optical metamaterials with large frequency tunability. Nano Lett. 2010, 10, 4222–4227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, H.; Zhu, B.O.; Feng, Y. A frequency and bandwidth tunable metamaterial absorber in x-band. J. Appl. Phys. 2015, 117, 173103. [Google Scholar] [CrossRef]
- Li, Y.; Lin, J.; Guo, H.; Sun, W.; Xiao, S.; Zhou, L. A tunable metasurface with switchable functionalities: From perfect transparency to perfect absorption. Adv. Opt. Mater. 2020, 8, 1901548. [Google Scholar] [CrossRef]
- Ren, Z.; Chang, Y.; Ma, Y.; Shih, K.; Dong, B.; Lee, C. Leveraging of MEMS technologies for optical metamaterials applications. Adv. Opt. Mater. 2020, 8, 1900653. [Google Scholar] [CrossRef]
- Sharma, M.; Hendler, N.; Ellenbogen, T. Electrically switchable color tags based on active liquid-crystal plasmonic metasurface platform. Adv. Opt. Mater. 2020, 8, 1901182. [Google Scholar] [CrossRef]
- Lu, F.; Liu, B.; Shen, S. Infrared wavefront control based on graphene metasurfaces. Adv. Opt. Mater. 2014, 2, 794–799. [Google Scholar] [CrossRef]
- Ding, L.; Luo, X.; Cheng, L.; Thway, M.; Song, J.; Chua, S.J.; Chia, E.E.; Teng, J. Electrically and thermally tunable smooth silicon metasurfaces for broadband terahertz antireflection. Adv. Opt. Mater. 2018, 6, 1800928. [Google Scholar] [CrossRef]
- Gao, B.; Yuen, M.M.; Ye, T. Ferrite film loaded frequency selective metamaterials for sub-GHz applications. Materials 2016, 9, 1009. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Jing, L.; Yao, K.; Yang, Y.; Zheng, B.; Soukoulis, C.M.; Chen, H.; Liu, Y. Origami-based reconfigurable metamaterials for tunable chirality. Adv. Mater. 2017, 29, 1700412. [Google Scholar] [CrossRef] [PubMed]
- Nauroze, S.A.; Novelino, L.S.; Tentzeris, M.M.; Paulino, G.H. Continuous-range tunable multilayer frequency-selective surfaces using origami and inkjet printing. Proc. Natl. Acad. Sci. USA 2018, 115, 13210–13215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Azemi, S.N.; Ghorbani, K.; Rowe, W.S. A reconfigurable FSS using a spring resonator element. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 781–784. [Google Scholar] [CrossRef]
- Arritt, B.; Adomanis, B.; Khraishi, T.; Smith, D. Parametric analysis of the strain-dependent behavior of a metamaterial electric resonator. Appl. Phys. Lett. 2010, 97, 191907. [Google Scholar] [CrossRef] [Green Version]
- Arritt, B.J.; Smith, D.R.; Khraishi, T. Equivalent circuit analysis of metamaterial strain-dependent effective medium parameters. J. Appl. Phys. 2011, 109, 073512. [Google Scholar] [CrossRef] [Green Version]
- Karimi Mahabadi, R.; Goudarzi, T.; Fleury, R.; Sohrabpour, S.; Naghdabadi, R. Challenges in finite element analysis of a deformable metasurface unit cell using COMSOL Multiphysics. Presented at the Iberian COMSOL Multiphysics Conference, Malaga, Spain, 28 June 2019. [Google Scholar]
- COMSOL Multiphysics®; v.5.4. 2020; COMSOL EPFL: Lausanne, Switzerland, 2020; Available online: www.comsol.com.
- Smith, D.R.; Pendry, J.B. Homogenization of metamaterials by field averaging. J. Opt. Soc. Am. B 2006, 23, 391–403. [Google Scholar] [CrossRef]
- Hollister, S.J.; Kikuchi, N. A comparison of homogenization and standard mechanics analyses for periodic porous composites. Comput. Mech. 1992, 10, 73–95. [Google Scholar] [CrossRef] [Green Version]
- Ogden, R.W. Non-Linear Elastic Deformations, 1st ed.; Dover Publication Inc.: Mineola, NY, USA, 1997. [Google Scholar]
- Li, J.; Shah, C.M.; Withayachumnankul, W.; Ung, B.S.Y.; Mitchell, A.; Sriram, S.; Bhaskaran, M.; Chang, S.; Abbott, D. Mechanically tunable terahertz metamaterials. Appl. Phys. Lett. 2013, 102, 121101. [Google Scholar] [CrossRef] [Green Version]
- Aksu, S.; Huang, M.; Artar, A.; Yanik, A.A.; Selvarasah, S.; Dokmeci, M.R.; Altug, H. Flexible plasmonics: Flexible plasmonics on unconventional and nonplanar substrates (Adv. Mater. 38/2011). Adv. Mater. 2011, 23, 4421. [Google Scholar] [CrossRef]
- Liu, N.; Guo, H.; Fu, L.; Kaiser, S.; Schweizer, H.; Giessen, H. Three-dimensional photonic metamaterials at optical frequencies. Nat. Mater. 2008, 7, 31–37. [Google Scholar] [CrossRef]
- Han, N.R.; Chen, Z.C.; Lim, C.S.; Ng, B.; Hong, M.H. Broadband multi-layer terahertz metamaterials fabrication and characterization on flexible substrates. Opt. Express 2011, 19, 6990–6998. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.; Strikwerda, A.C.; Zhang, X.; Averitt, R.D. Three-dimensional broadband tunable terahertz metamaterials. Phys. Rev. B 2013, 87, 161104. [Google Scholar] [CrossRef] [Green Version]
- Bückmann, T.; Stenger, N.; Kadic, M.; Kaschke, J.; Frölich, A.; Kennerknecht, T.; Eberl, C.; Thiel, M.; Wegener, M. Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography. Adv. Mater. 2012, 24, 2710–2714. [Google Scholar] [CrossRef] [PubMed]
- Walia, S.; Shah, C.M.; Gutruf, P.; Nili, H.; Chowdhury, D.R.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Flexible metasurfaces and metamaterials: A review of materials and fabrication processes at micro-and nano-scales. Appl. Phys. Rev. 2015, 2, 011303. [Google Scholar] [CrossRef]
- Befahy, S.; Lipnik, P.; Pardoen, T.; Nascimento, C.; Patris, B.; Bertrand, P.; Yunus, S. Thickness and elastic modulus of plasma treated PDMS silica-like surface layer. Langmuir 2010, 26, 3372–3375. [Google Scholar] [CrossRef]
- Ohishi, T.; Noda, H.; Matsui, T.S.; Jile, H.; Deguchi, S. Tensile strength of oxygen plasma-created surface layer of PDMS. J. Micromech. Microeng. 2016, 27, 015015. [Google Scholar] [CrossRef]

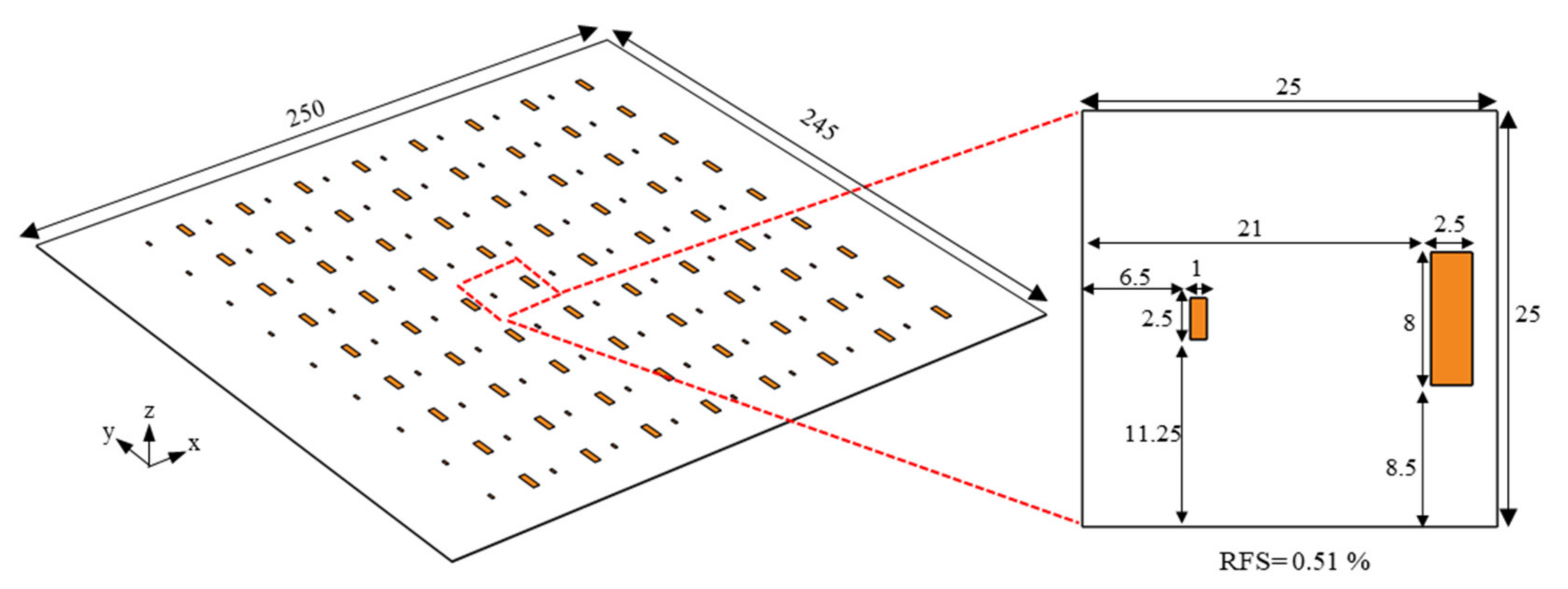
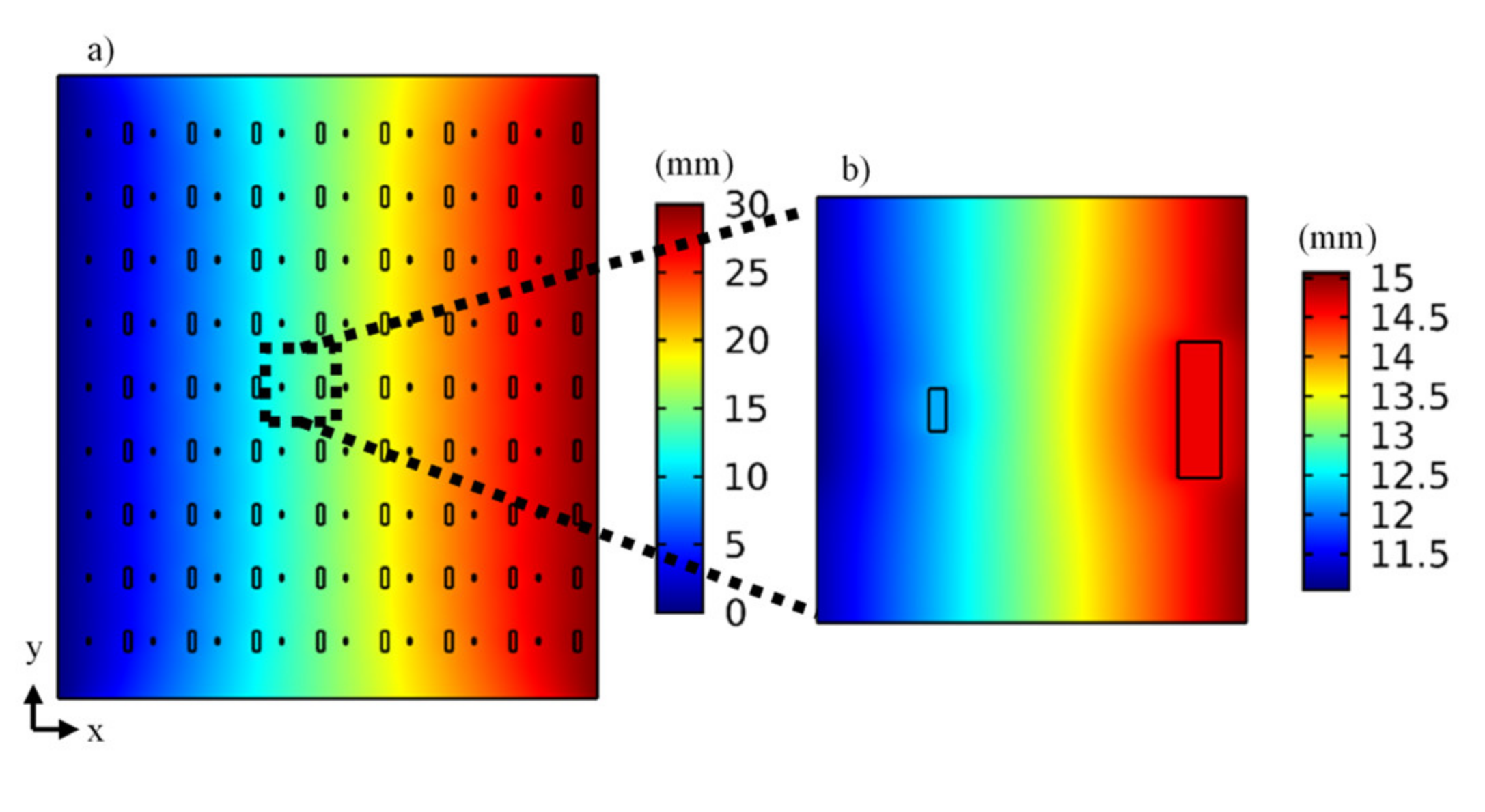



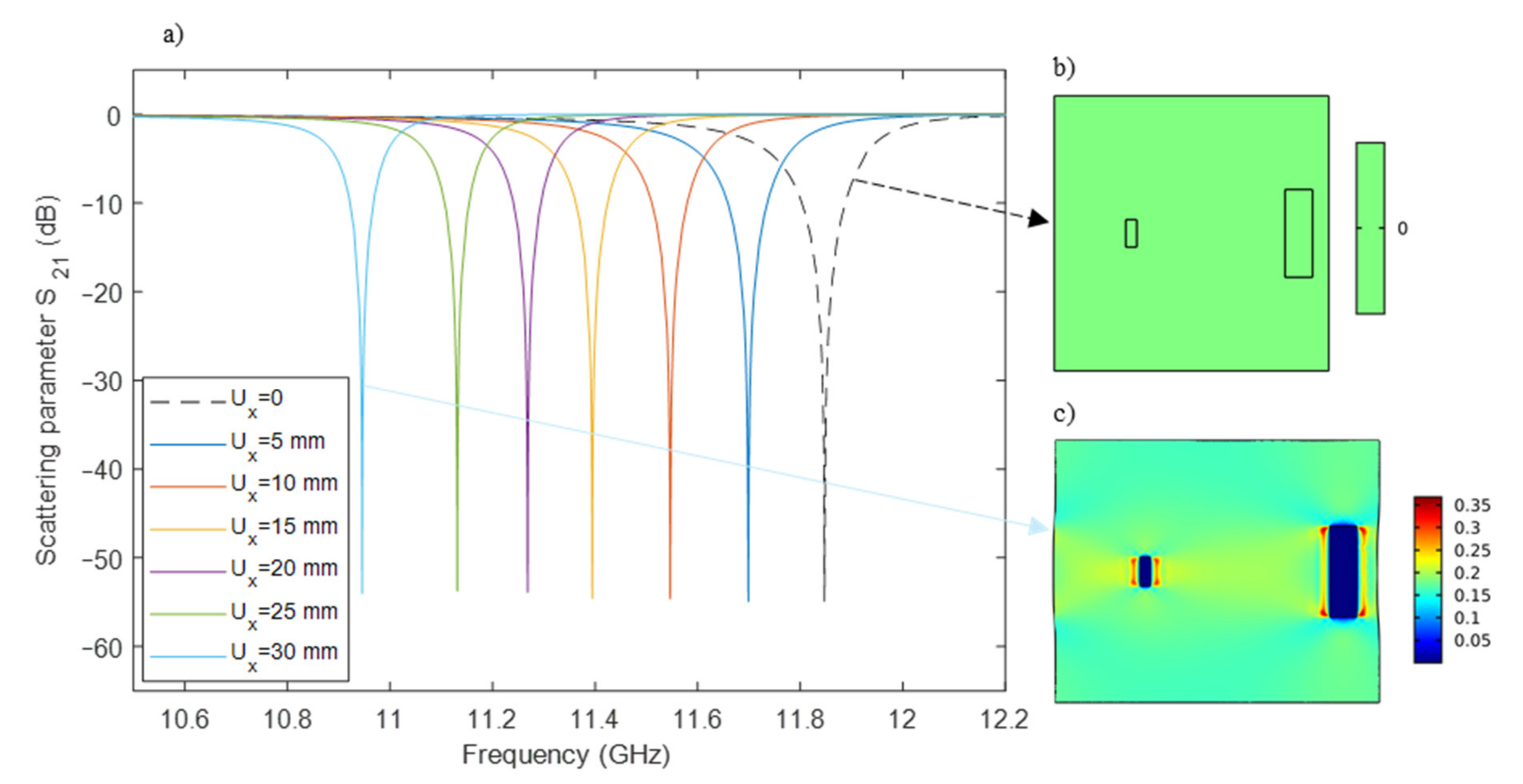
(mm) | (%) | (GHz) | RFS (GHz) | (%) | (dB) | (dB) |
|---|---|---|---|---|---|---|
| 5 | 2.66 | 11.69 | −0.16 | 1.35 | 46.5 | −49.3 |
| 10 | 5.36 | 11.55 | −0.30 | 2.53 | 47.8 | −45.1 |
| 15 | 8.10 | 11.39 | −0.46 | 3.88 | 48.0 | −45.6 |
| 20 | 10.88 | 11.27 | −0.58 | 4.89 | 48.0 | −43.6 |
| 25 | 13.70 | 11.13 | −0.72 | 6.08 | 48.0 | −45.8 |
| 30 | 16.79 | 10.95 | −0.90 | 7.59 | 48.0 | −49.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi Mahabadi, R.; Goudarzi, T.; Fleury, R.; Naghdabadi, R. Multifunctional Hyperelastic Structured Surface for Tunable and Switchable Transparency. Appl. Sci. 2021, 11, 2255. https://doi.org/10.3390/app11052255
Karimi Mahabadi R, Goudarzi T, Fleury R, Naghdabadi R. Multifunctional Hyperelastic Structured Surface for Tunable and Switchable Transparency. Applied Sciences. 2021; 11(5):2255. https://doi.org/10.3390/app11052255
Chicago/Turabian StyleKarimi Mahabadi, Rayehe, Taha Goudarzi, Romain Fleury, and Reza Naghdabadi. 2021. "Multifunctional Hyperelastic Structured Surface for Tunable and Switchable Transparency" Applied Sciences 11, no. 5: 2255. https://doi.org/10.3390/app11052255
APA StyleKarimi Mahabadi, R., Goudarzi, T., Fleury, R., & Naghdabadi, R. (2021). Multifunctional Hyperelastic Structured Surface for Tunable and Switchable Transparency. Applied Sciences, 11(5), 2255. https://doi.org/10.3390/app11052255





