Uncertainties in the Seismic Assessment of Historical Masonry Buildings
Abstract
1. Introduction
2. Case Studies
2.1. Holsteiner Hof
2.2. Lausanne Malley
2.3. Modelling Approach
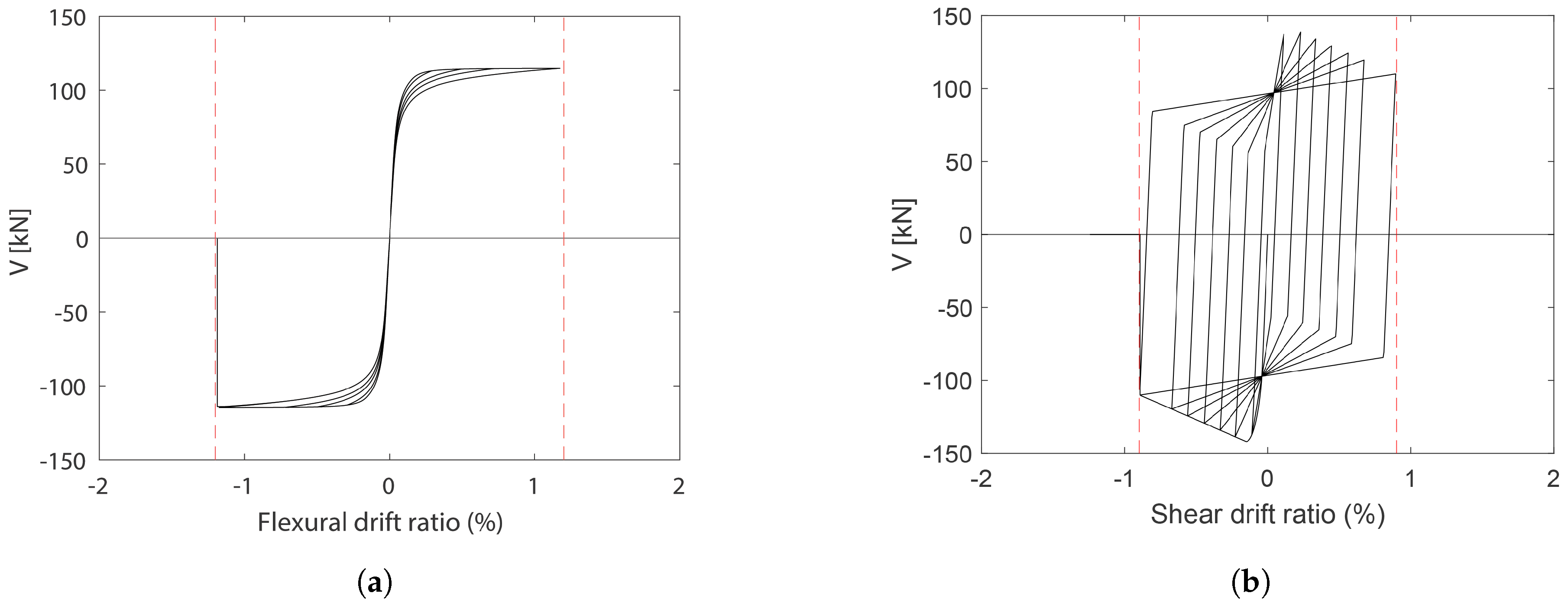
2.4. Material and Modelling Parameters
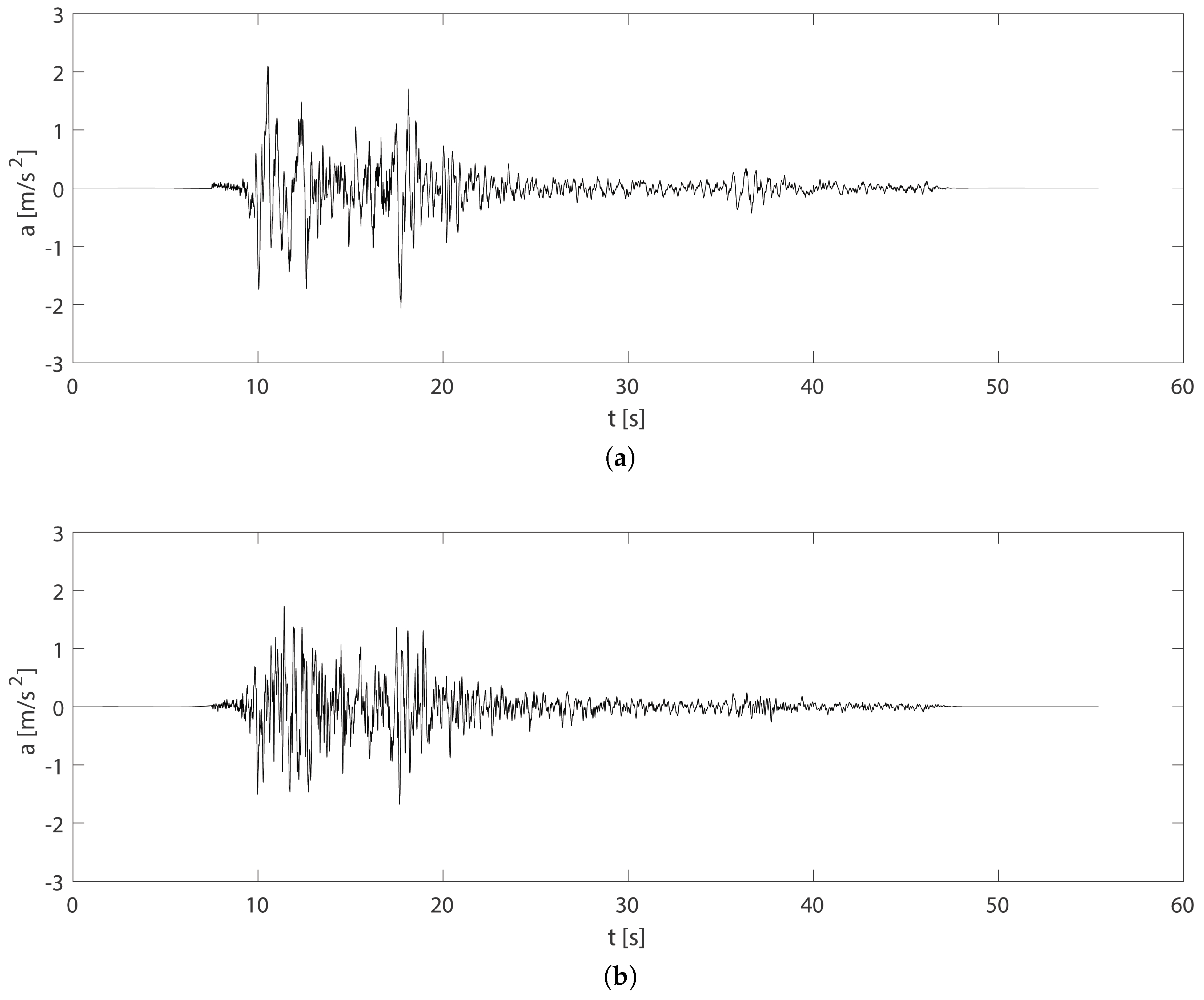
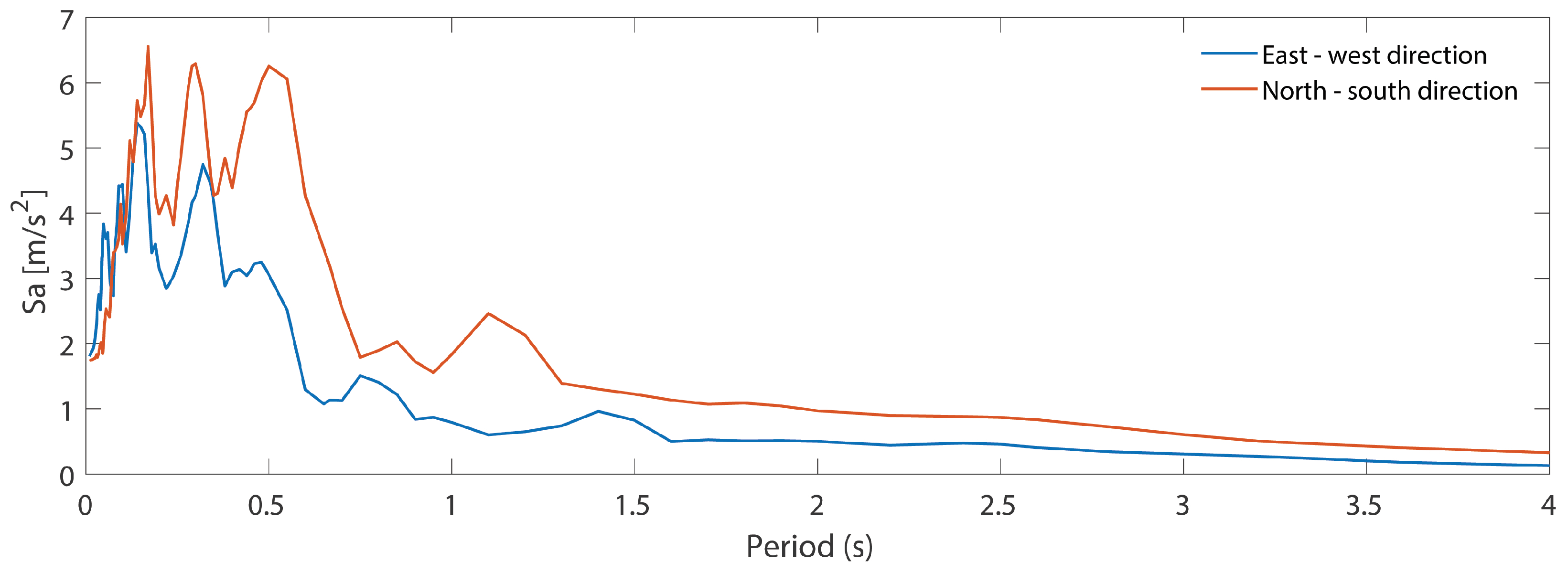
2.5. Earthquake Record
3. Methodology
3.1. Seismic Response Parameters
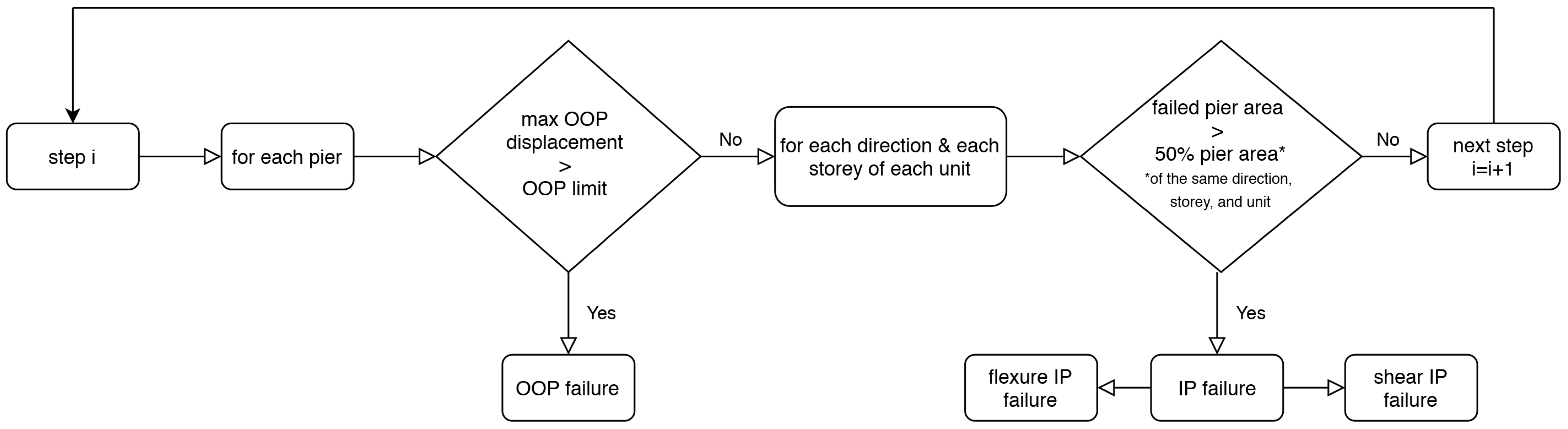
3.2. Failure Criterion
4. Results
4.1. Holsteiner Hof
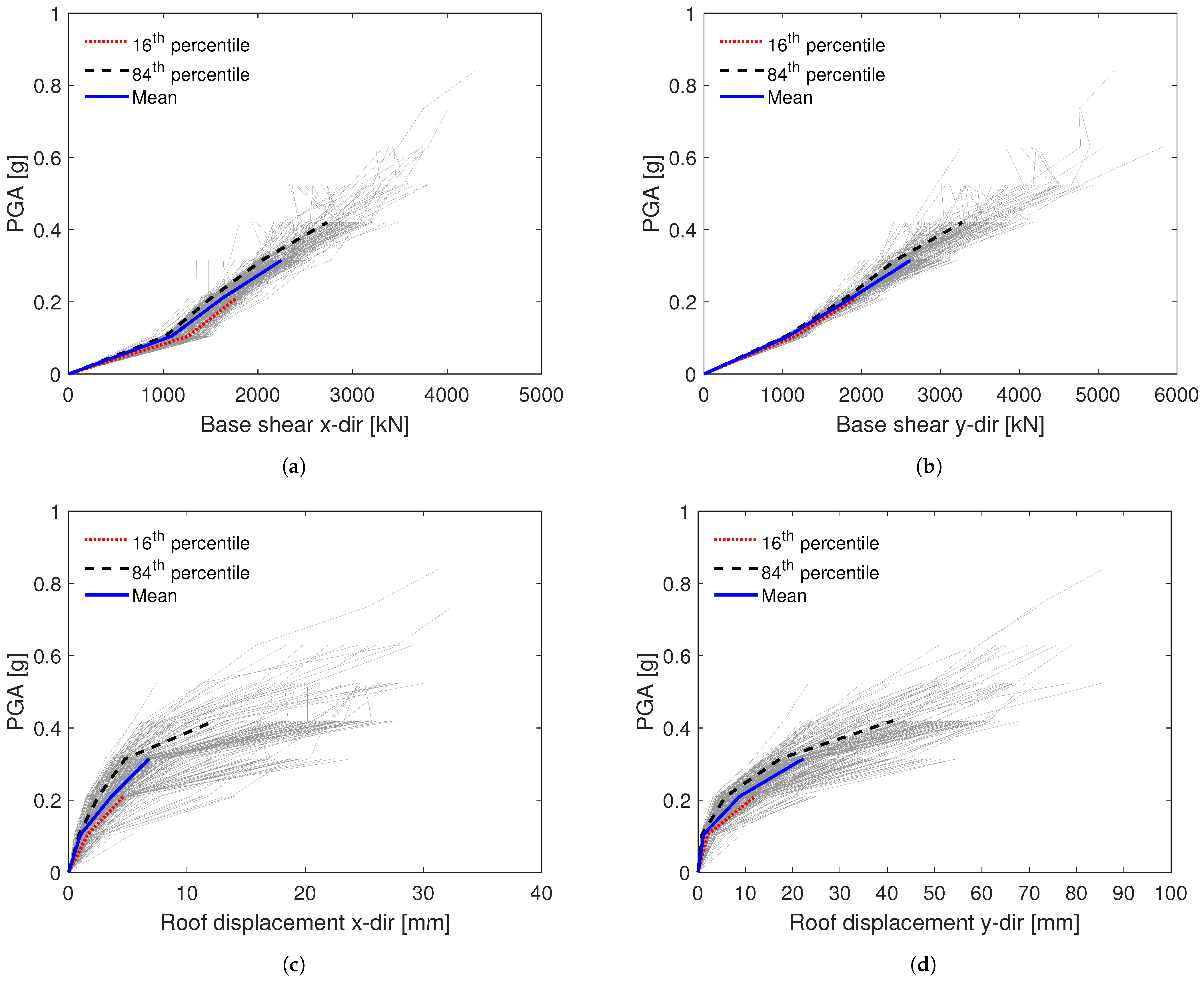
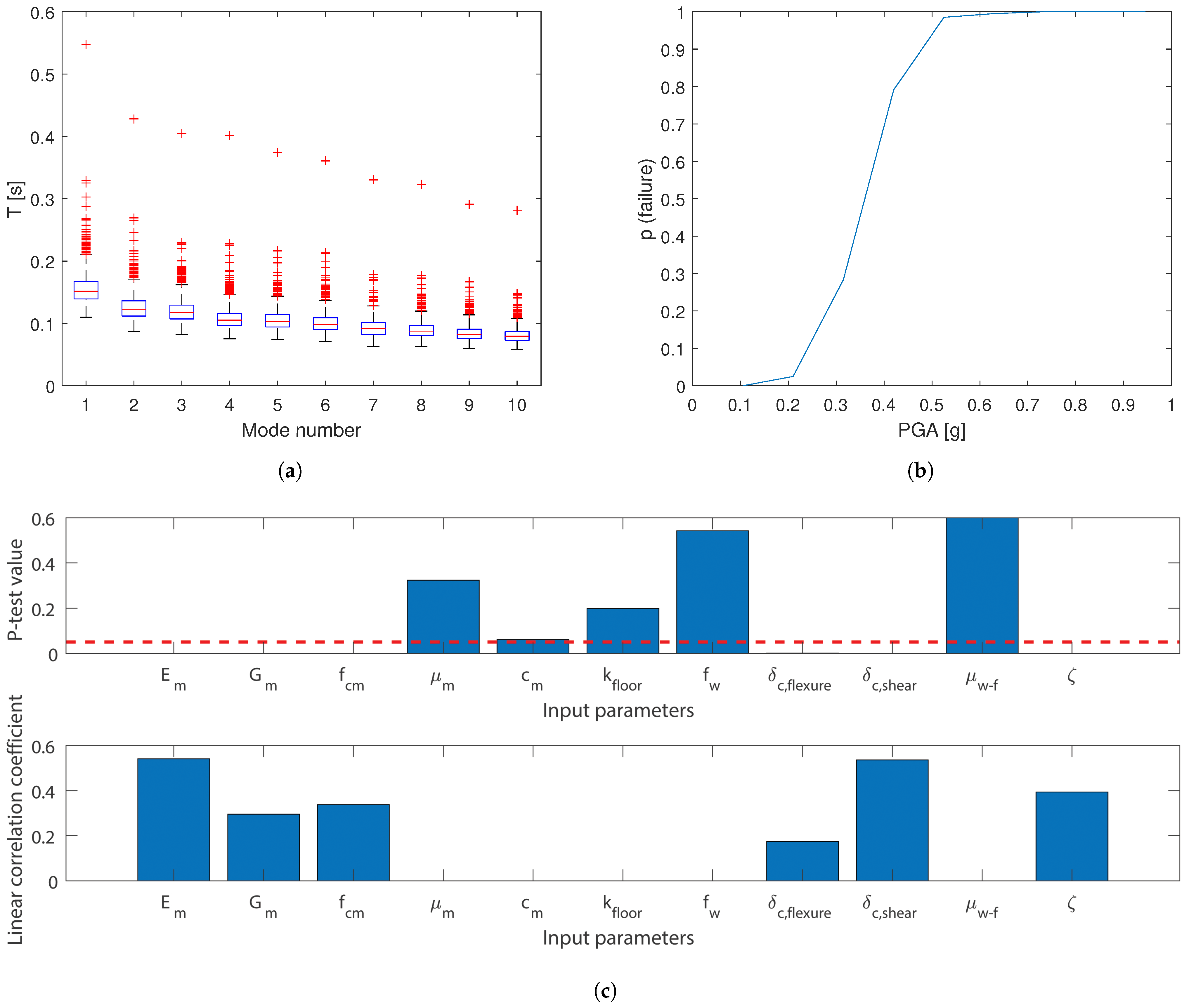
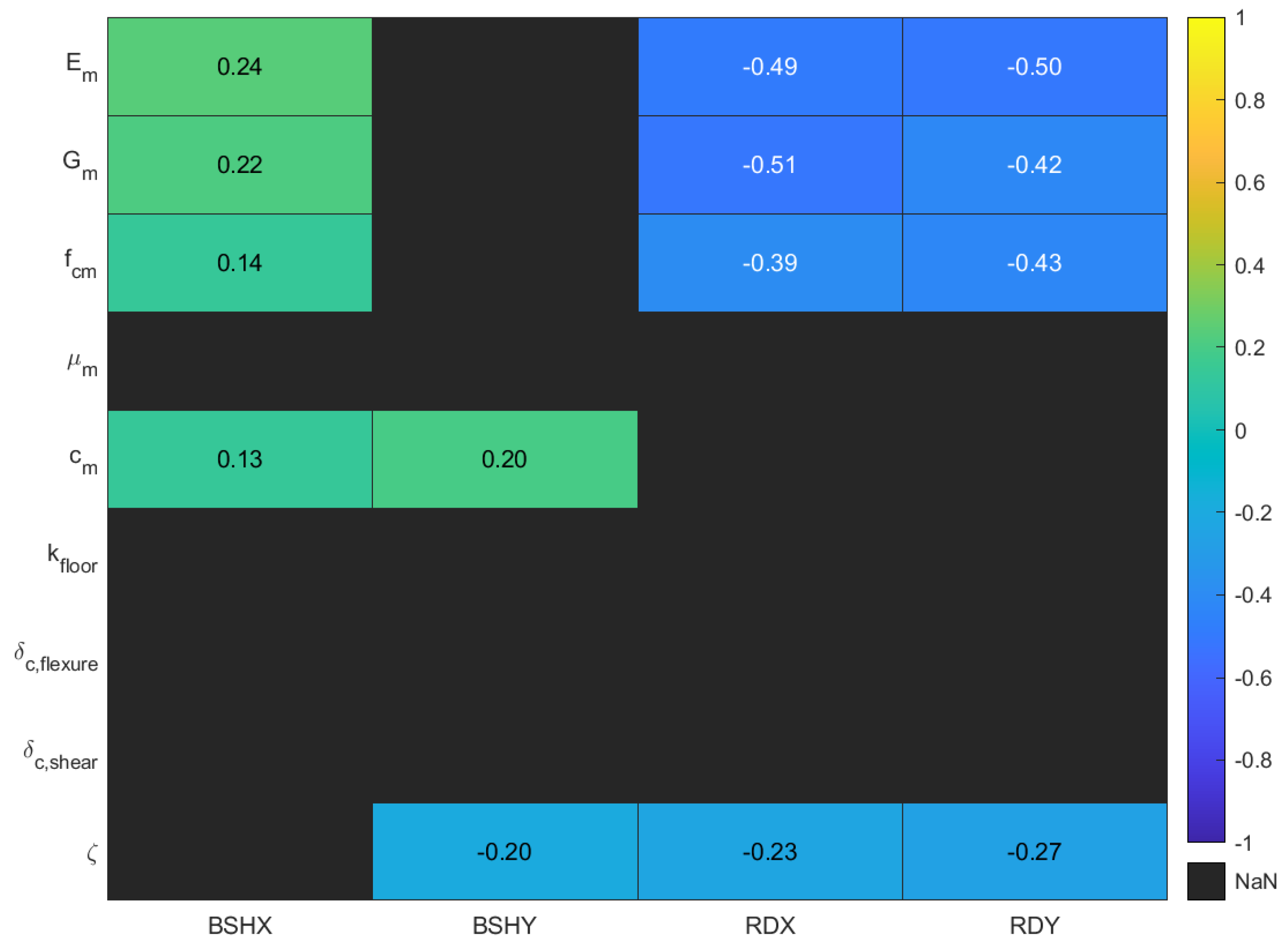
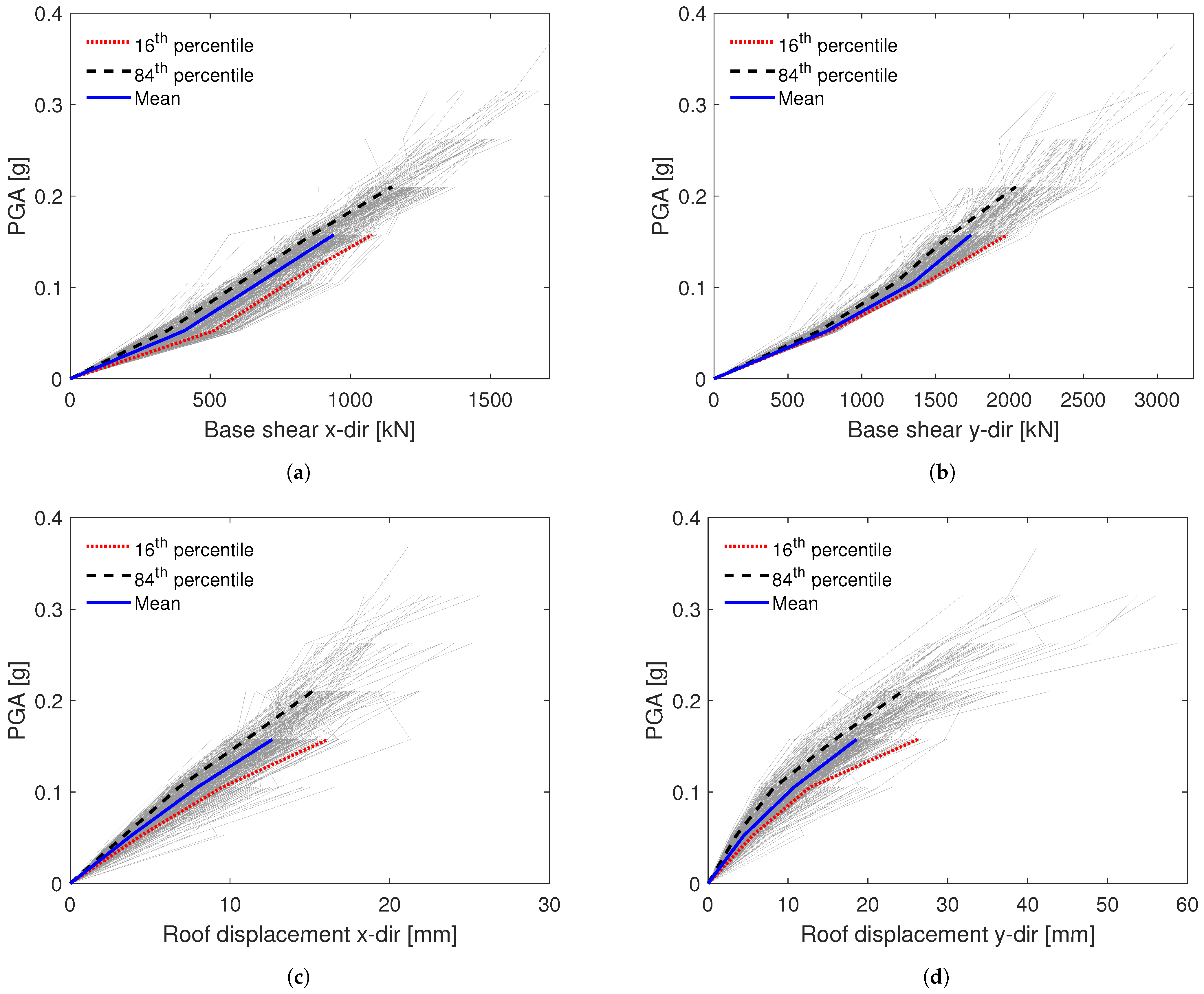
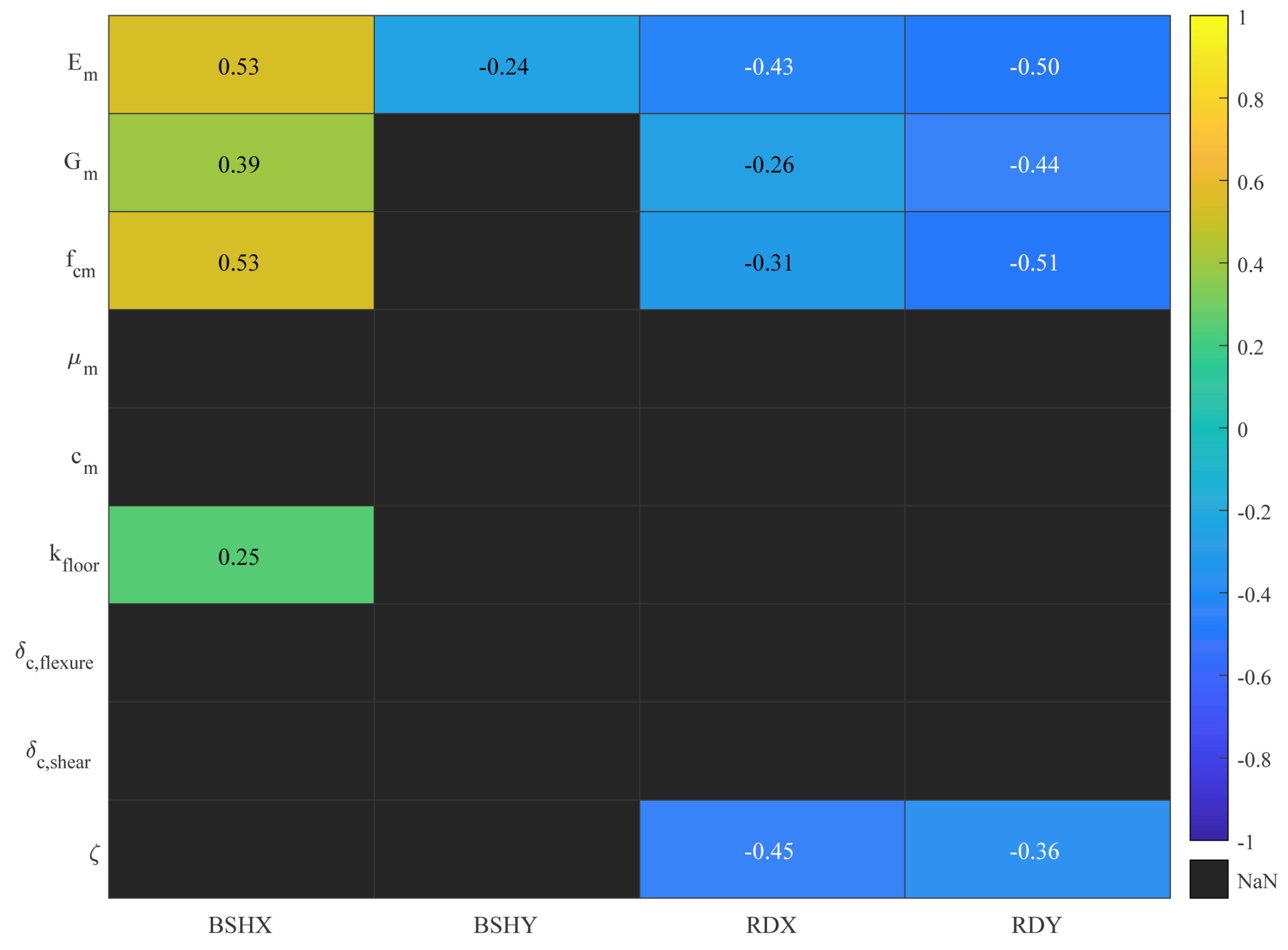
4.1.1. Seismic Response Parameters
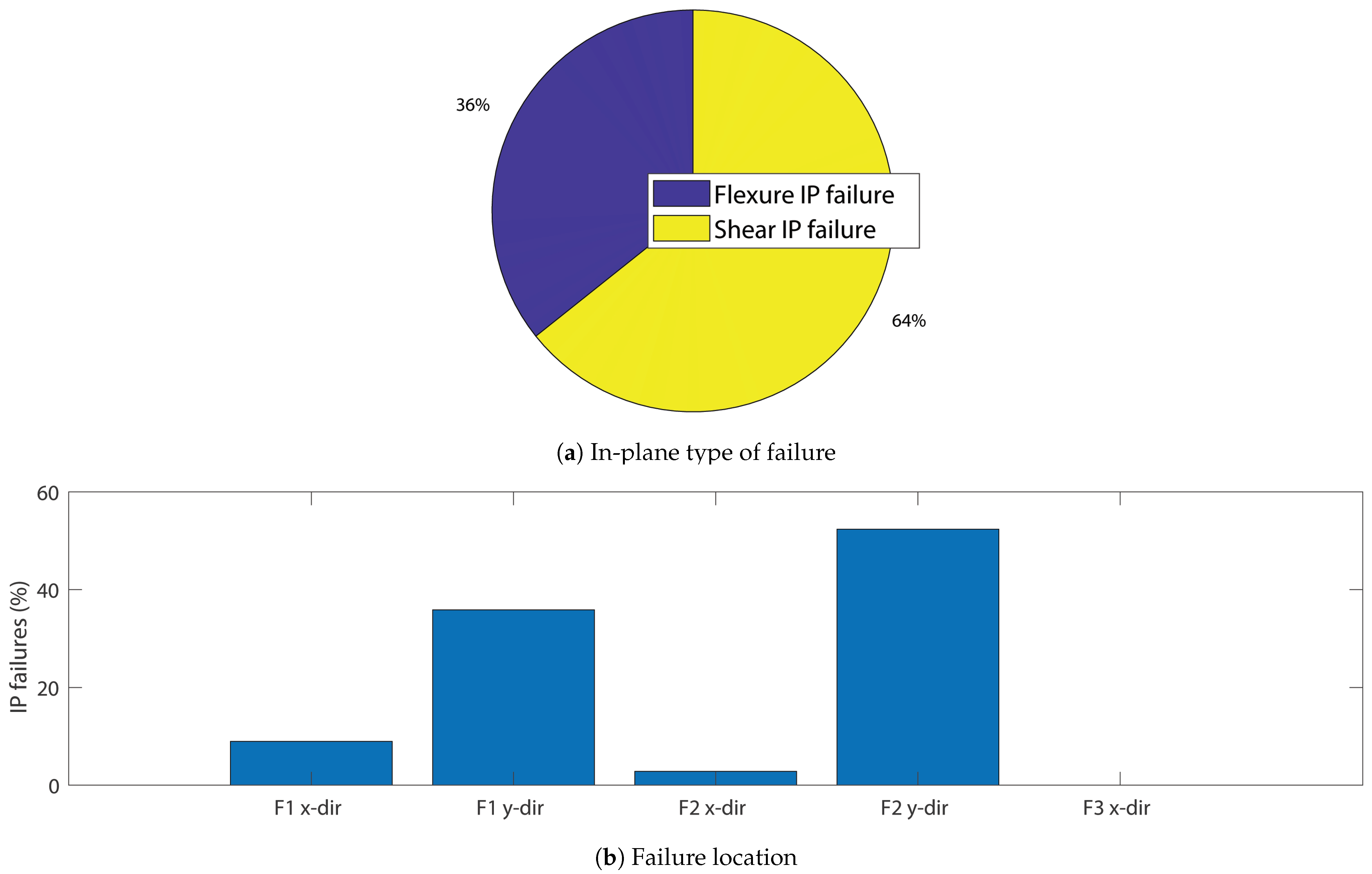
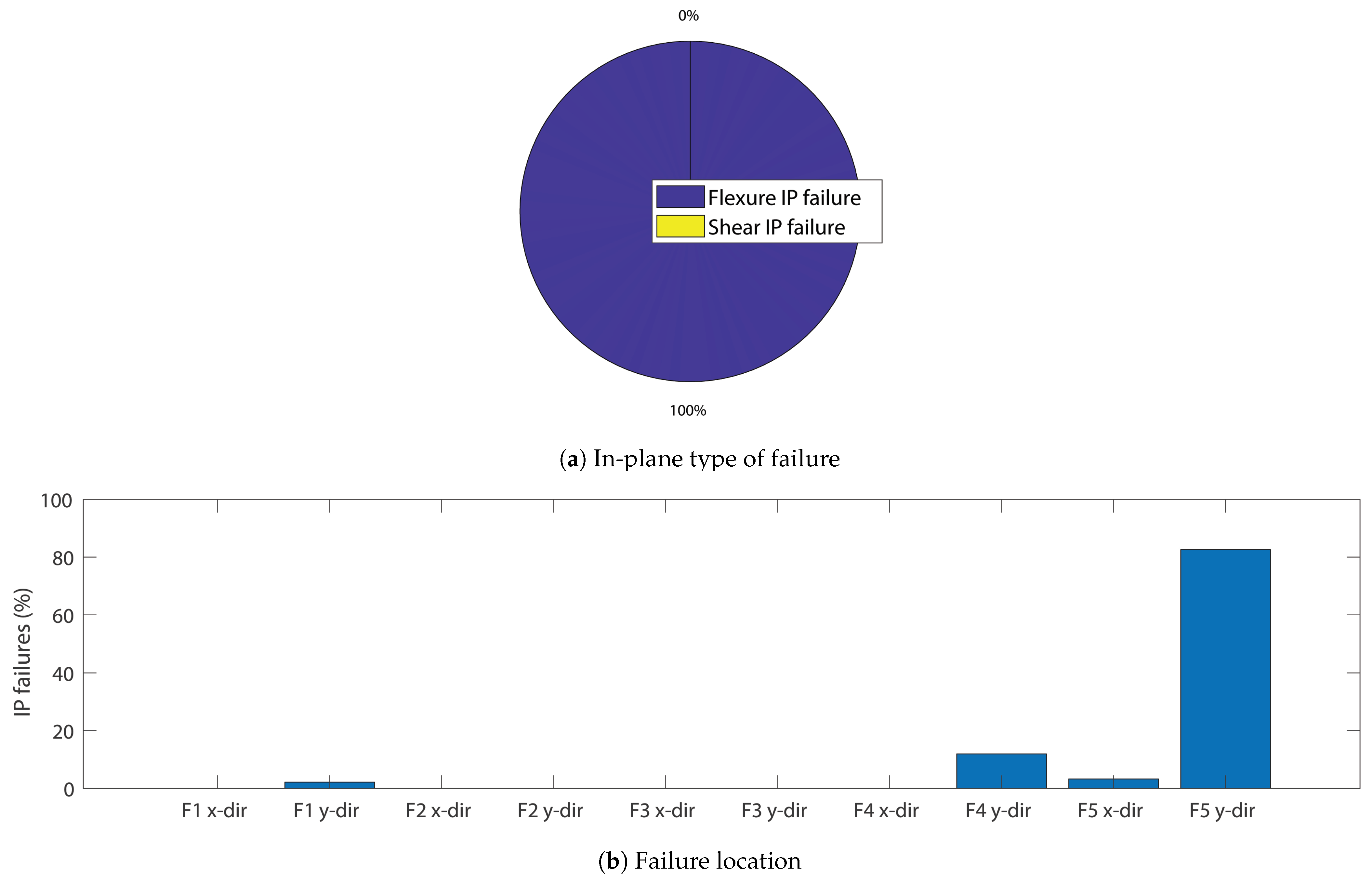
4.1.2. Failure Analysis
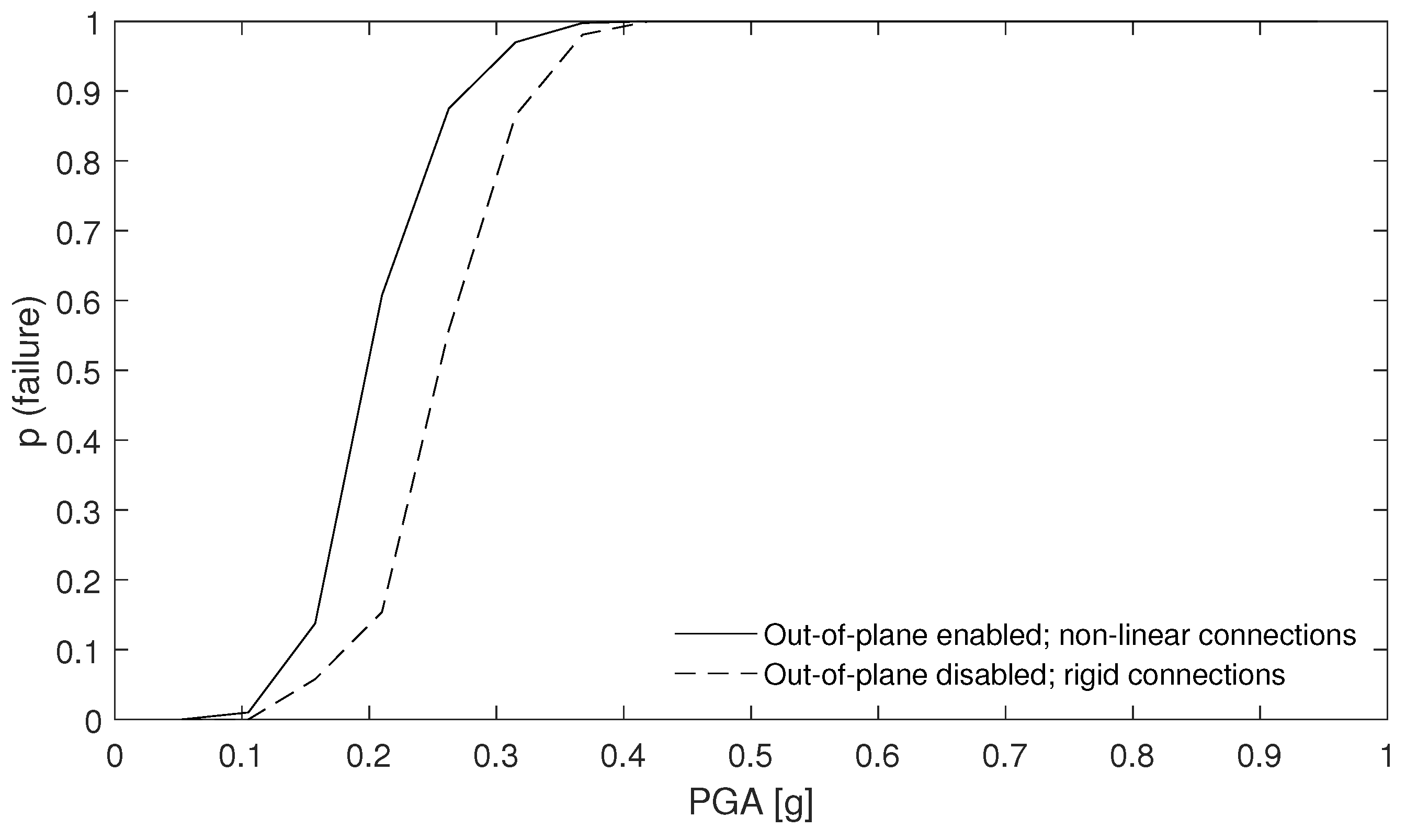
4.2. Holsteiner Hof-Out-of-Plane Disabled and Rigid Connections
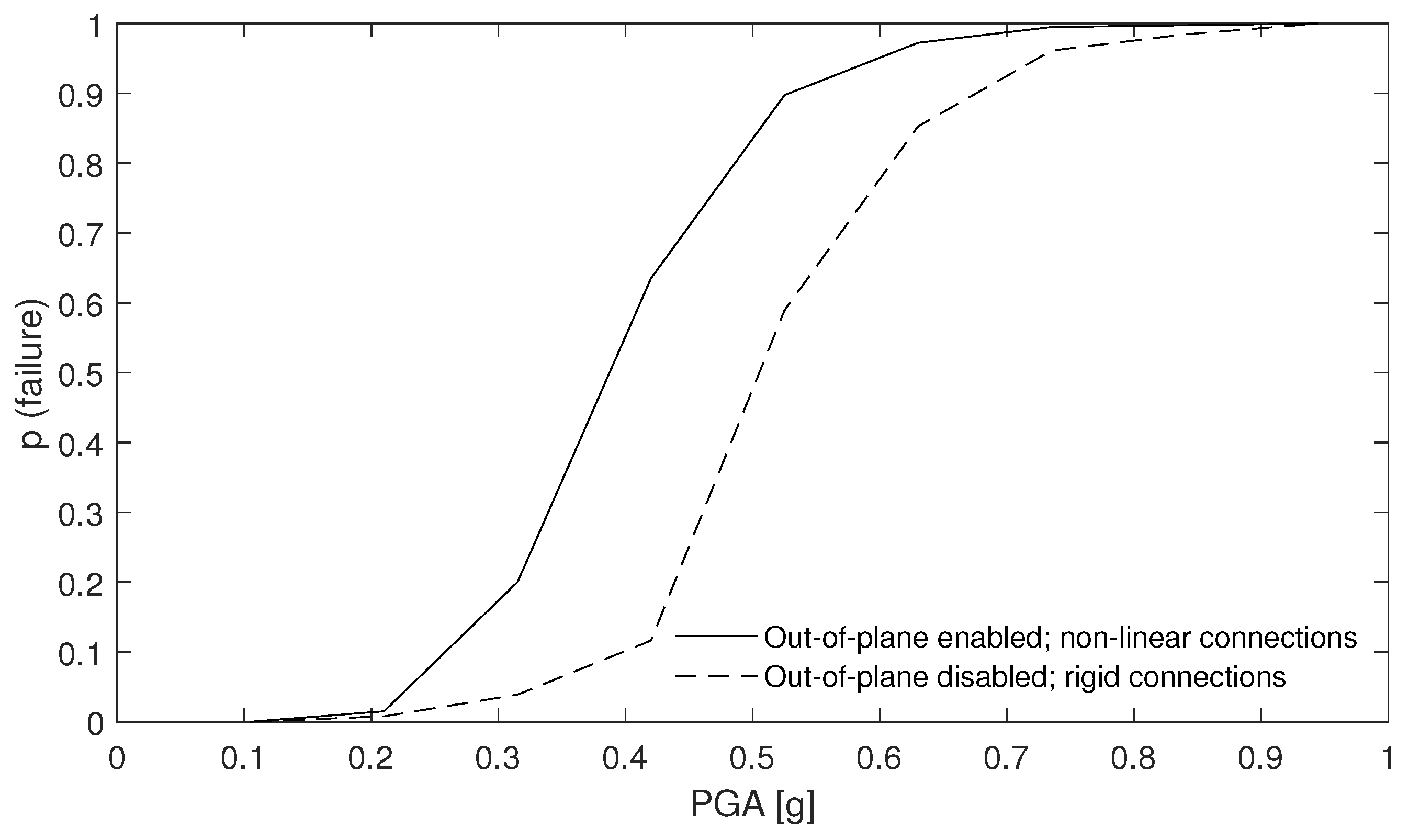
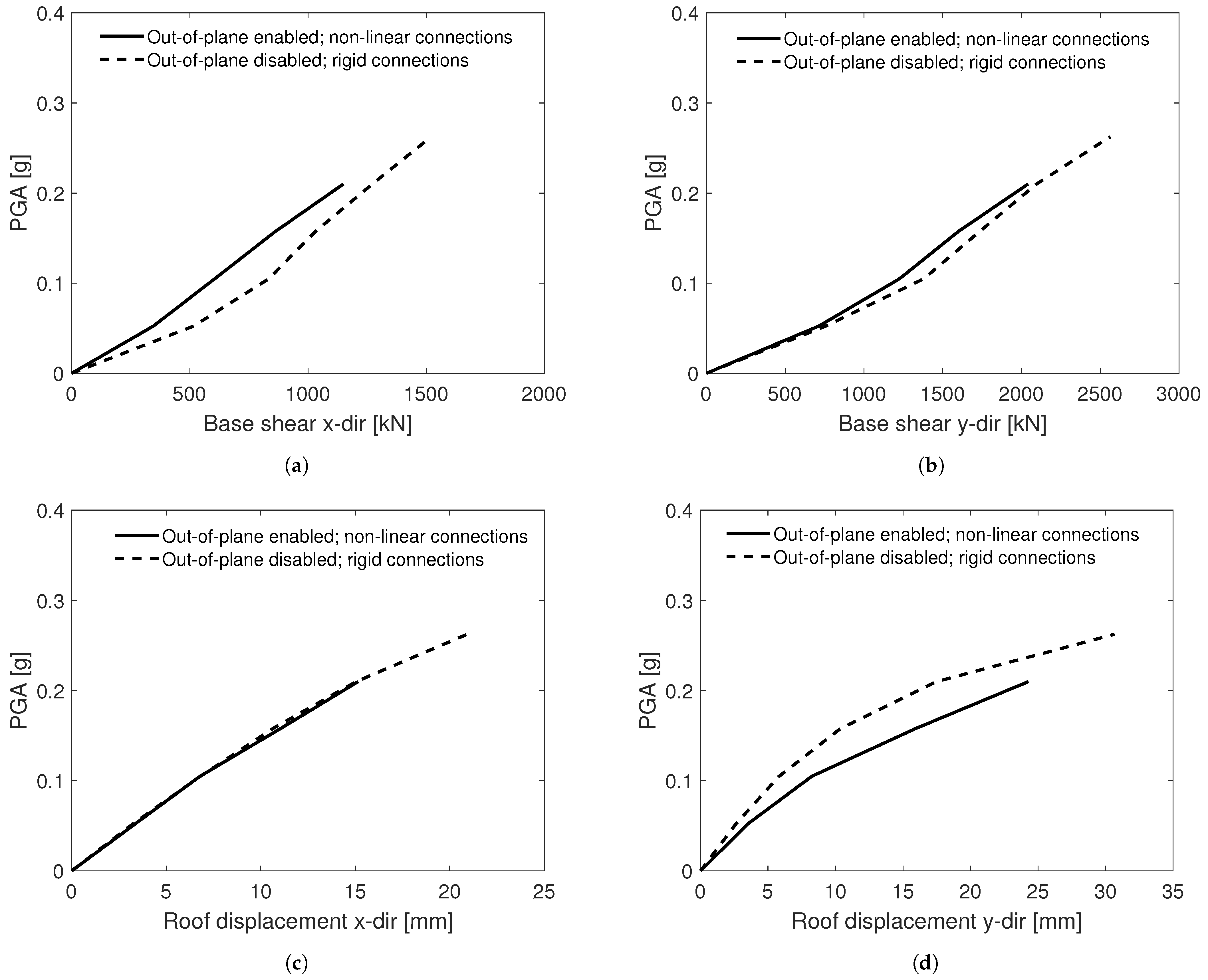
4.2.1. Seismic Response Parameters
4.2.2. Failure Analysis
4.3. Lausanne Malley
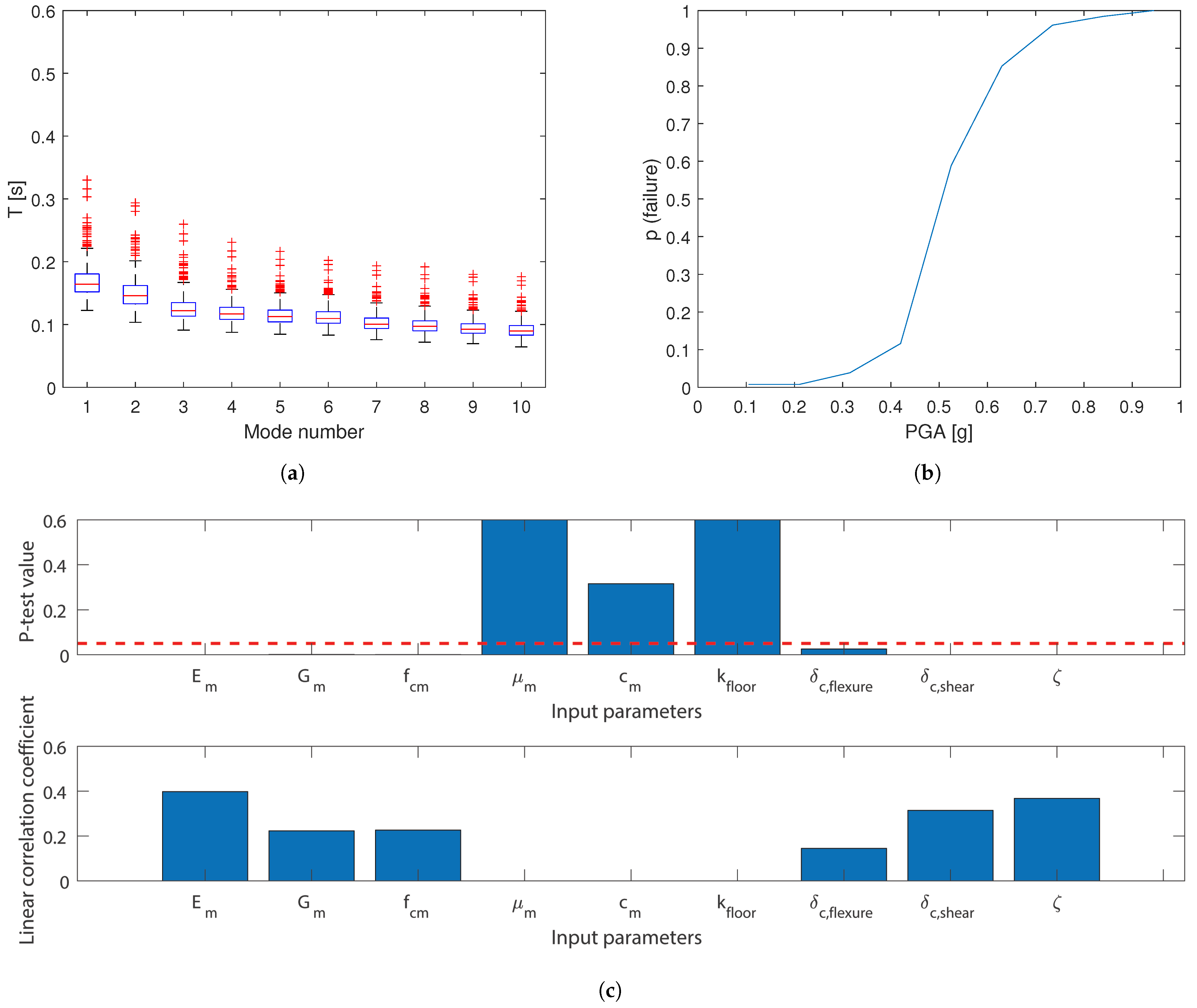
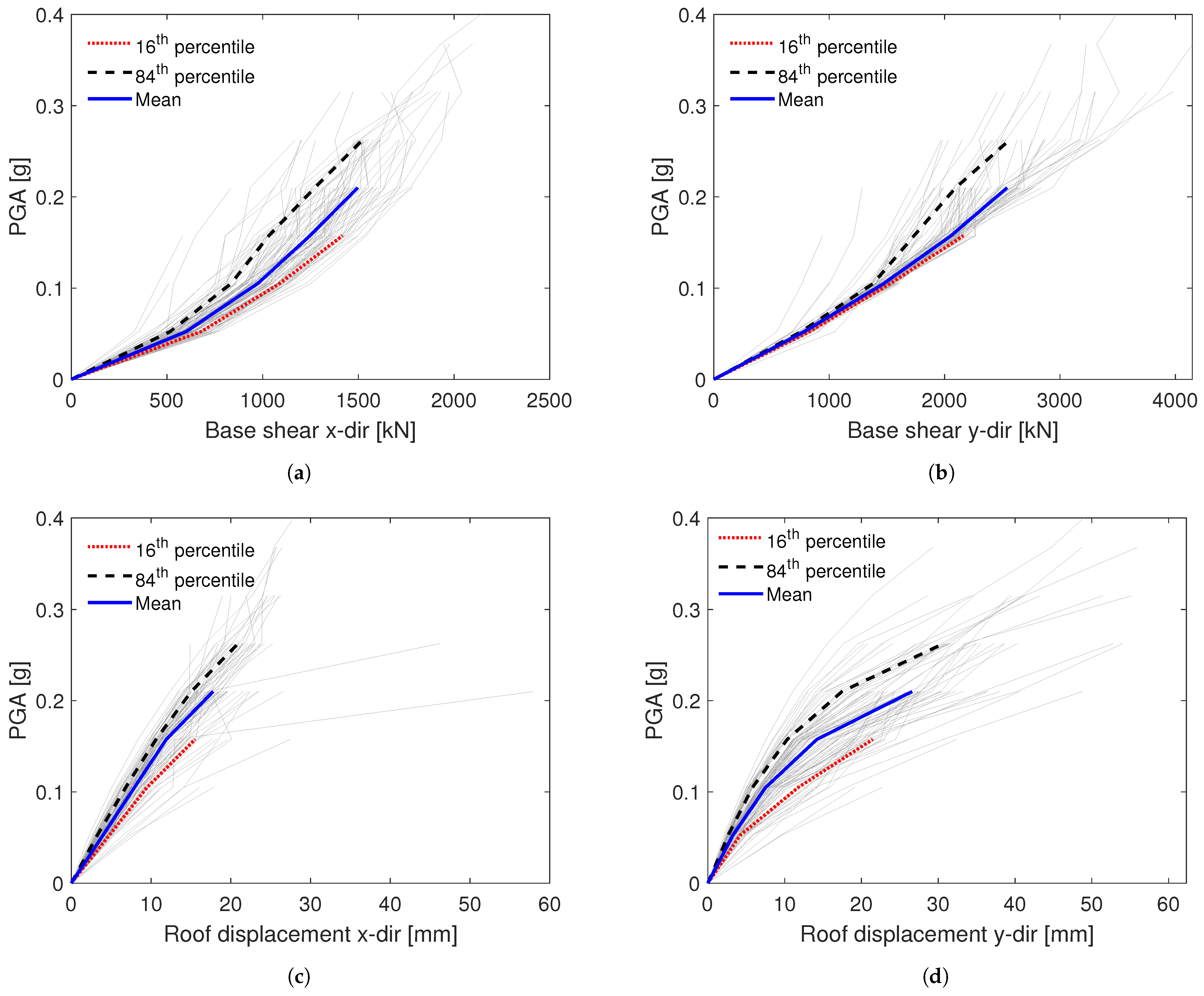
4.3.1. Seismic Response Parameters
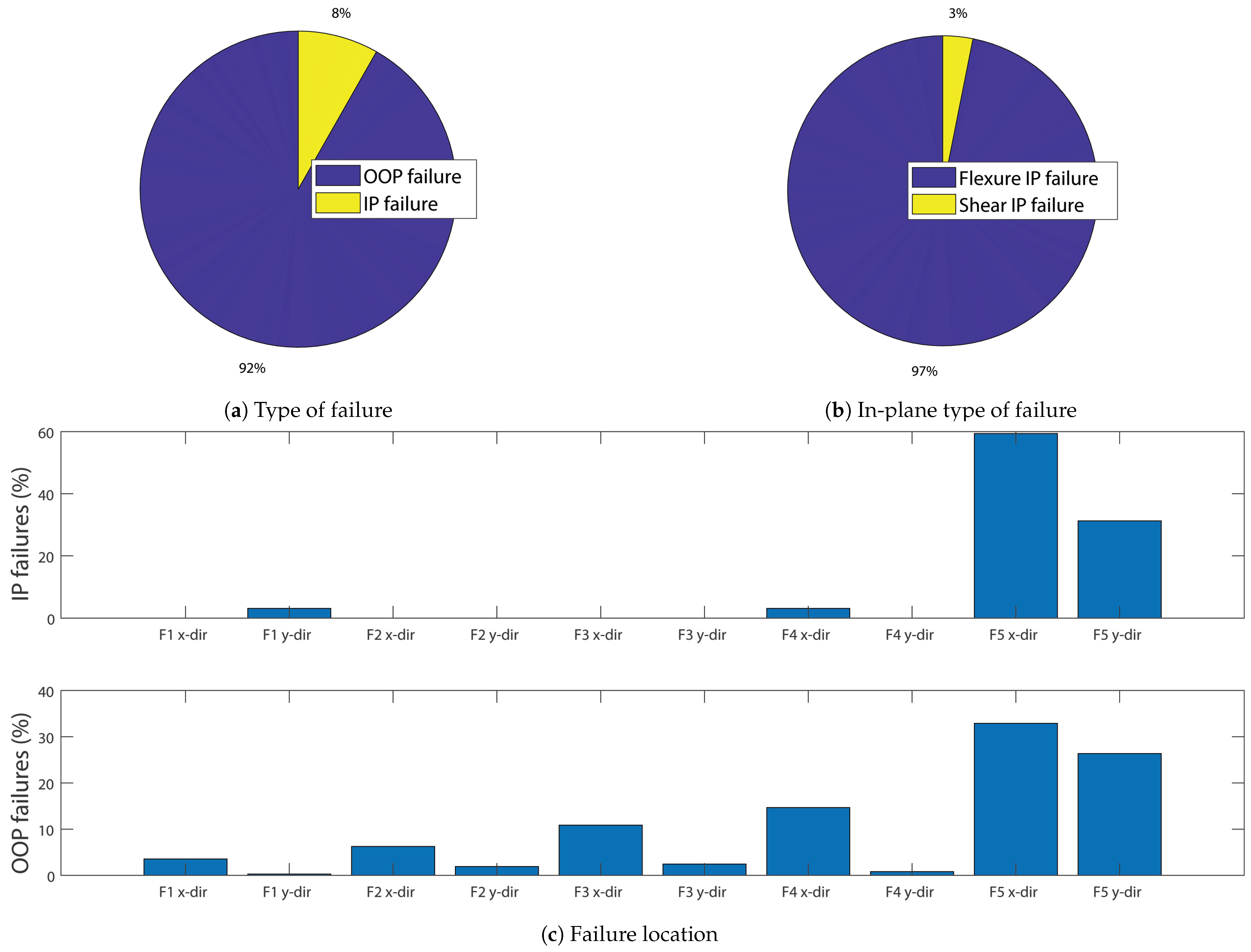
4.3.2. Failure Analysis
4.4. Lausanne Malley-Out-of-Plane Disabled and Rigid Connections
4.4.1. Seismic Response Parameters
4.4.2. Failure Analysis
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Zuccaro, G.; Perelli, F.; De Gregorio, D.; Cacace, F. Empirical vulnerability curves for Italian mansory buildings: Evolution of vulnerability model from the DPM to curves as a function of acceleration. Bull. Earthq. Eng. 2020. [Google Scholar] [CrossRef]
- Ruggieri, S.; Tosto, C.; Rosati, G.; Uva, G.; Ferro, G.A. Seismic Vulnerability Analysis of Masonry Churches in Piemonte after 2003 Valle Scrivia Earthquake: Post-event Screening and Situation 17 Years Later. Int. J. Arch. Herit. 2020, 1–29. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
- Roca, P.; Cervera, M.; Gariup, G.; Pela, L. Structural analysis of masonry historical constructions. Classical and advanced approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef]
- Fragiadakis, M.; Vamvatsikos, D. Fast performance uncertainty estimation via pushover and approximate IDA. Earthq. Eng. Struct. Dyn. 2010, 39, 683–703. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Fragiadakis, M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty. Earthq. Eng. Struct. Dyn. 2010, 39, 141–163. [Google Scholar] [CrossRef]
- Dolsek, M. Incremental dynamic analysis with consideration of modeling uncertainties. Earthq. Eng. Struct. Dyn. 2009, 38, 805–825. [Google Scholar] [CrossRef]
- Rota, M.; Penna, A.; Magenes, G. A framework for the seismic assessment of existing masonry buildings accounting for different sources of uncertainty. Earthq. Eng. Struct. Dyn. 2014, 43, 1045–1066. [Google Scholar] [CrossRef]
- EN 1998-3. Eurocode 8: Design of structures for earthquake resistance-Part 3: Assessment and retrofitting of buildings. Eur. Comm. Stand. Brux. Belgium 2005, 1, 1–91. [Google Scholar]
- Saloustros, S.; Pelà, L.; Contrafatto, F.R.; Roca, P.; Petromichelakis, I. Analytical derivation of seismic fragility curves for historical masonry structures based on stochastic analysis of uncertain material parameters. Int. J. Arch. Herit. 2019, 13, 1142–1164. [Google Scholar] [CrossRef]
- Vanin, F.; Beyer, K. Application of a point estimate method for incorporating the epistemic uncertainty in the seismic assessment of a masonry building. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Vanin, F.; Penna, A.; Beyer, K. A three-dimensional macroelement for modelling the in-plane and out-of-plane response of masonry walls. Earthq. Eng. Struct. Dyn. 2020, 49, 1365–1387. [Google Scholar] [CrossRef]
- Michel, C.; Karbassi, A.; Lestuzzi, P. Evaluation of the seismic retrofitting of an unreinforced masonry building using numerical modeling and ambient vibration measurements. Eng. Struct. 2018, 158, 124–135. [Google Scholar] [CrossRef]
- Quagliarini, E.; Maracchini, G.; Clementi, F. Uses and limits of the Equivalent Frame Model on existing unreinforced masonry buildings for assessing their seismic risk: A review. J. Build. Eng. 2017, 10, 166–182. [Google Scholar] [CrossRef]
- Penna, A.; Lagomarsino, S.; Galasco, A. A nonlinear macroelement model for the seismic analysis of masonry buildings. Earthq. Eng. Struct. Dyn. 2014, 43, 159–179. [Google Scholar] [CrossRef]
- Vanin, F.; Penna, A.; Beyer, K. Equivalent-frame modeling of two shaking table tests of masonry buildings accounting for their out-of-plane response. Front. Built Environ. 2020, 6, 42. [Google Scholar] [CrossRef]
- McKenna, F.; Fenves, G.; Scott, M.; Jeremic, B. Open System for Earthquake Engineering Simulation (OpenSees); Technical Report; University of California: Berkeley, CA, USA, 2000. [Google Scholar]
- Guerrini, G.; Senaldi, I.; Scherini, S.; Morganti, S.; Magenes, G. Material characterization for the shaking-table test of the scaled prototype of a stone masonry building aggregate. In Proceedings of the XVII Convegno ANIDIS L’ingegneria Sismica, Pistoia, Italy, 17–21 September 2017; pp. 105–115. [Google Scholar]
- Guerrini, G.; Senaldi, I.; Graziotti, F.; Magenes, G.; Beyer, K.; Penna, A. Shake-table test of a strengthened stone masonry building aggregate with flexible diaphragms. Int. J. Arch. Herit. 2019, 13, 1078–1097. [Google Scholar] [CrossRef]
- Senaldi, I.; Guerrini, G.; Scherini, S.; Morganti, S.; Magenes, G.; Beyer, K.; Penna, A. Natural stone masonry characterization for the shaking-table test of a scaled building specimen. In Proceedings of the 10th International Masonry Conference, Milan, Italy, 9–11 July 2018; pp. 9–11. [Google Scholar]
- Senaldi, I.E.; Guerrini, G.; Comini, P.; Graziotti, F.; Penna, A.; Beyer, K.; Magenes, G. Experimental seismic performance of a half-scale stone masonry building aggregate. Bull. Earthq. Eng. 2020, 18, 609–643. [Google Scholar] [CrossRef]
- Brignola, A.; Podesta, S.; Pampanin, S. In-plane stiffness of wooden floor. In Proceedings of the New Zealand Society of Earthquake Engineering (NZSEE) Conference, Wairakei, New Zealand, 11–13 April 2008. [Google Scholar]
- Brignola, A.; Pampanin, S.; Podestà, S. Experimental evaluation of the in-plane stiffness of timber diaphragms. Earthq. Spect. 2012, 28, 1687–1709. [Google Scholar] [CrossRef]
- POLIMI. Critical Review of Methodologies and Tools for Assessment of Failure Mechanisms and Interventions, Deliverable 3.3, Workpackage 3: Damage Based Selection Of Technologies; Technical Report; NIKER Project: Padova, Italy, 2010. [Google Scholar]
- Almeida, J.P.; Beyer, K.; Brunner, R.; Wenk, T. Characterization of mortar–timber and timber–timber cyclic friction in timber floor connections of masonry buildings. Mater. Struct. 2020, 53, 51. [Google Scholar] [CrossRef]
- Vanin, F.; Zaganelli, D.; Penna, A.; Beyer, K. Estimates for the stiffness, strength and drift capacity of stone masonry walls based on 123 quasi-static cyclic tests reported in the literature. Bull. Earthq. Eng. 2017, 15, 5435–5479. [Google Scholar] [CrossRef]
- Luzi, L.; Lanzano, G.; Felicetta, C.; D’Amico, M.C.; Russo, E.; Sgobba, S.; Pacor, F.; ORFEUS Working Group 5. Engineering Strong Motion Database (ESM) (Version 2.0); Technical Report; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2020. [Google Scholar] [CrossRef]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Vořechovskỳ, M.; Novák, D. Statistical correlation in stratified sampling. In Proceedings of the 9th International Conferences on Applications of Statistics and Probability in Civil Engineering–ICASP, Citeseer, San Francisco, CA, USA, 6–9 July 2003; Volume 9, pp. 119–124. [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Penna, A.; Rota, M.; Mouyiannou, A.; Magenes, G. Issues on the use of time-history analysis for the design and assessment of masonry structures. In Proceedings of the 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Kos Island, Greece, 12–14 June 2013. [Google Scholar]










| Parameter | Unit | Distribution | Mean | Lognormal Mean | Standard Deviation | Reference |
| Pa | Normal | 3.5 × | - | 1.0 × | [18,20] | |
| Pa | Normal | 1.3 × 10 | - | 0.35 × 10 | [18,20] | |
| - | Normal | 0.02 | - | 0.005 | [16] | |
| Parameter | Unit | Distribution | Median | Lognormal Mean | Standard Deviation | Reference |
| Pa | Lognormal | 1.5 × 10 | 21.13 | 0.5 | [18,20] | |
| Pa | Lognormal | 0.233 × 10 | 12.36 | 0.5 | [18,20] | |
| - | Lognormal | 0.25 | −1.39 | 0.3 | [18,20] | |
| - | Lognormal | 1 | 0 | 0.5 | [22,23] | |
| - | Lognormal | 1 | 0 | 0.3 | [24] | |
| - | Lognormal | 1 | 0 | 0.3 | [16,25] | |
| - | Lognormal | 0.01035 | −4.57 | 0.2 | [26] | |
| - | Lognormal | 0.007 | −4.96 | 0.2 | [26] |
| Correlated Parameters | Correlation Coefficient | Strength of Correlation |
|---|---|---|
| E, G, f | 0.7 | Strong |
| , | 0.5 | Moderate |
| BSHX | Base shear in x-direction |
| BSHY | Base shear in y-direction |
| RDX | Average roof displacement in x-direction |
| RDY | Average roof displacement in y-direction |
| F1 x-dir | 1st floor in x-direction |
| F1 y-dir | 1st floor in y-direction |
| F2 x-dir | 2nd floor in x-direction |
| F2 y-dir | 2nd floor in y-direction |
| F3 x-dir | 3rd floor in x-direction |
| F3 y-dir | 3rd floor in y-direction |
| F4 x-dir | 4th floor in x-direction |
| F4 y-dir | 4th floor in y-direction |
| F5 x-dir | 5th floor in x-direction |
| F5 y-dir | 5th floor in y-direction |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomić, I.; Vanin, F.; Beyer, K. Uncertainties in the Seismic Assessment of Historical Masonry Buildings. Appl. Sci. 2021, 11, 2280. https://doi.org/10.3390/app11052280
Tomić I, Vanin F, Beyer K. Uncertainties in the Seismic Assessment of Historical Masonry Buildings. Applied Sciences. 2021; 11(5):2280. https://doi.org/10.3390/app11052280
Chicago/Turabian StyleTomić, Igor, Francesco Vanin, and Katrin Beyer. 2021. "Uncertainties in the Seismic Assessment of Historical Masonry Buildings" Applied Sciences 11, no. 5: 2280. https://doi.org/10.3390/app11052280
APA StyleTomić, I., Vanin, F., & Beyer, K. (2021). Uncertainties in the Seismic Assessment of Historical Masonry Buildings. Applied Sciences, 11(5), 2280. https://doi.org/10.3390/app11052280







