Theoretical Prediction of P-Triphenylene-Graphdiyne as an Excellent Anode Material for Li, Na, K, Mg, and Ca Batteries
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
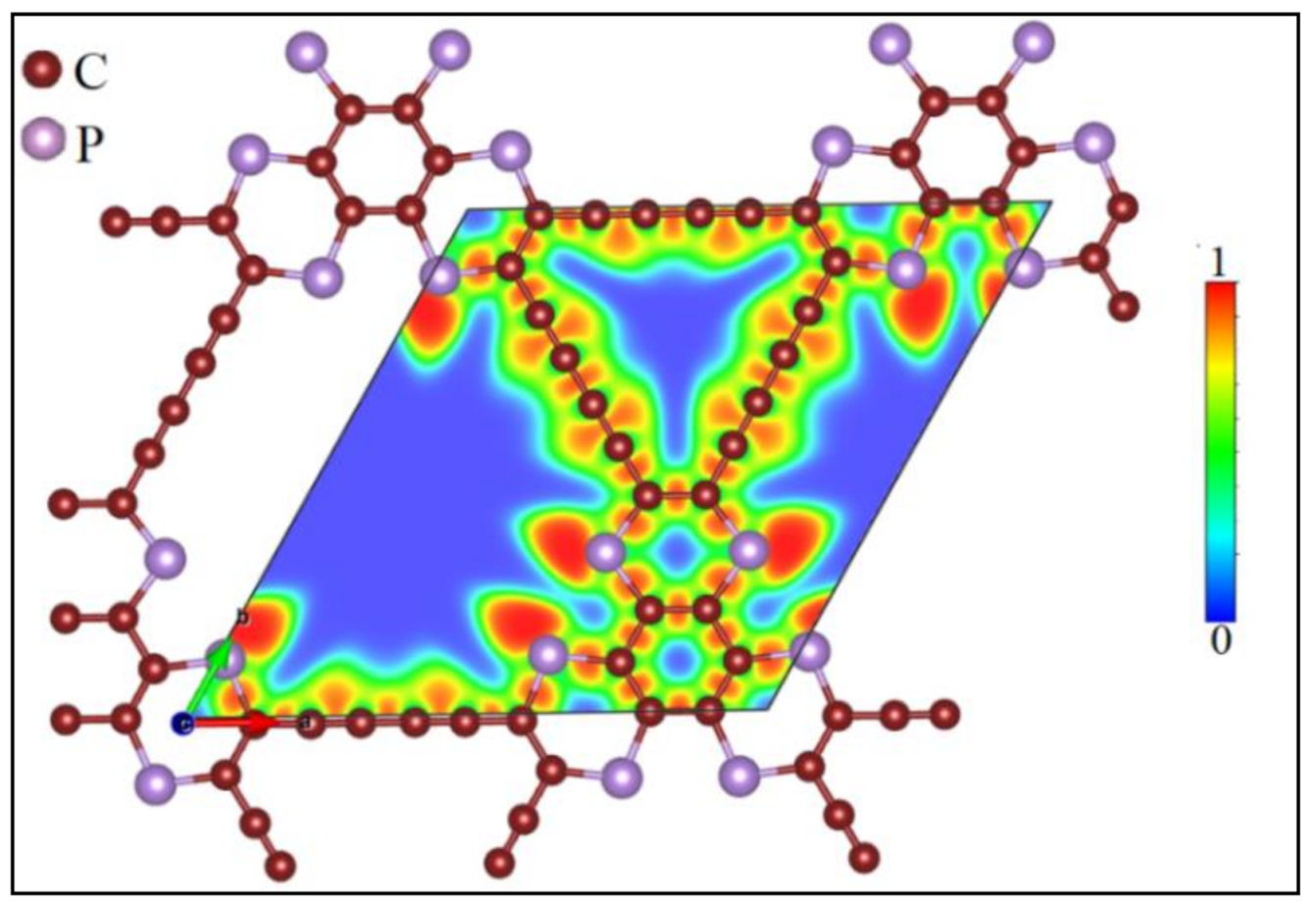
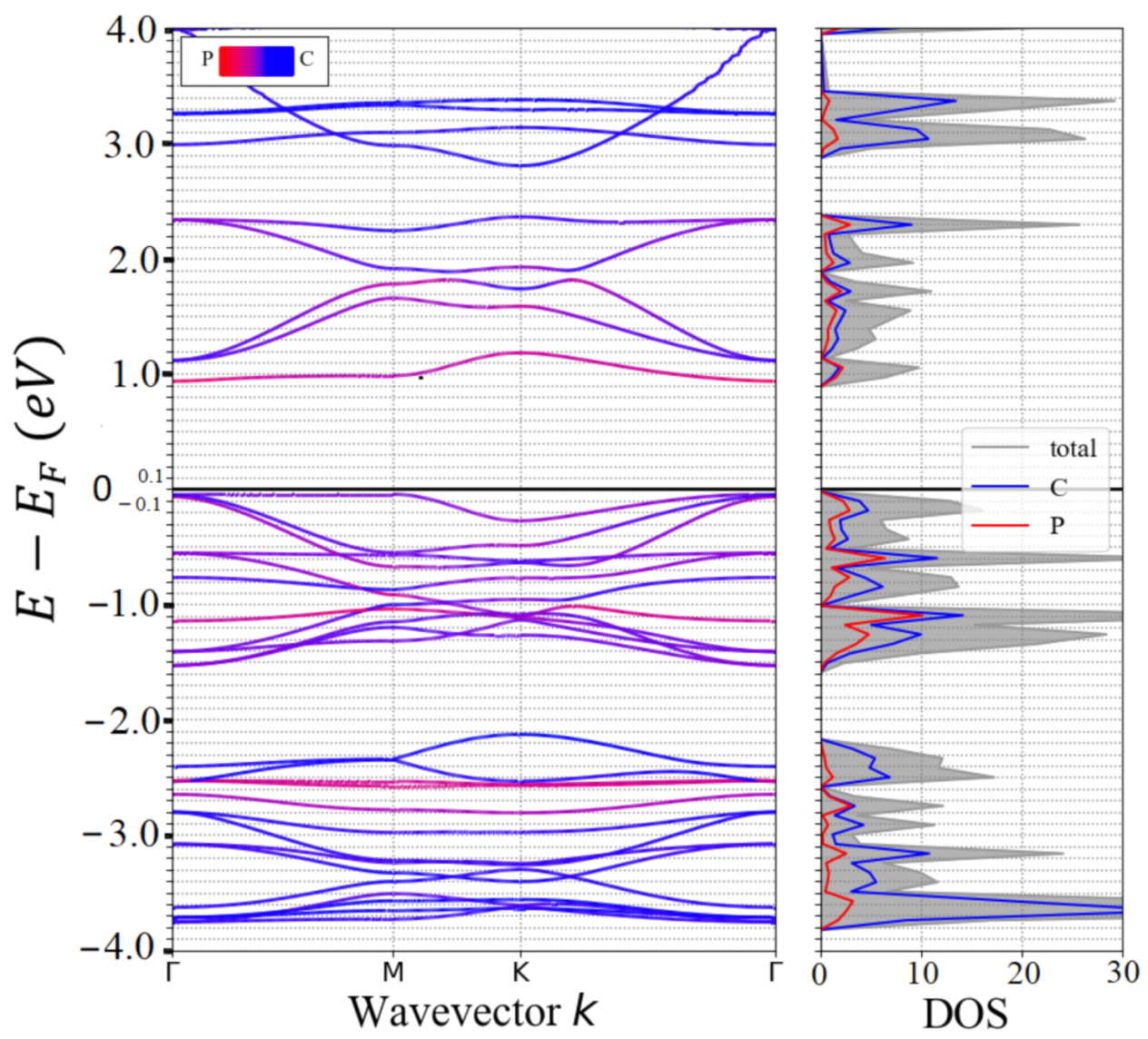
3.1. Lattice Structure and Electronic Properties
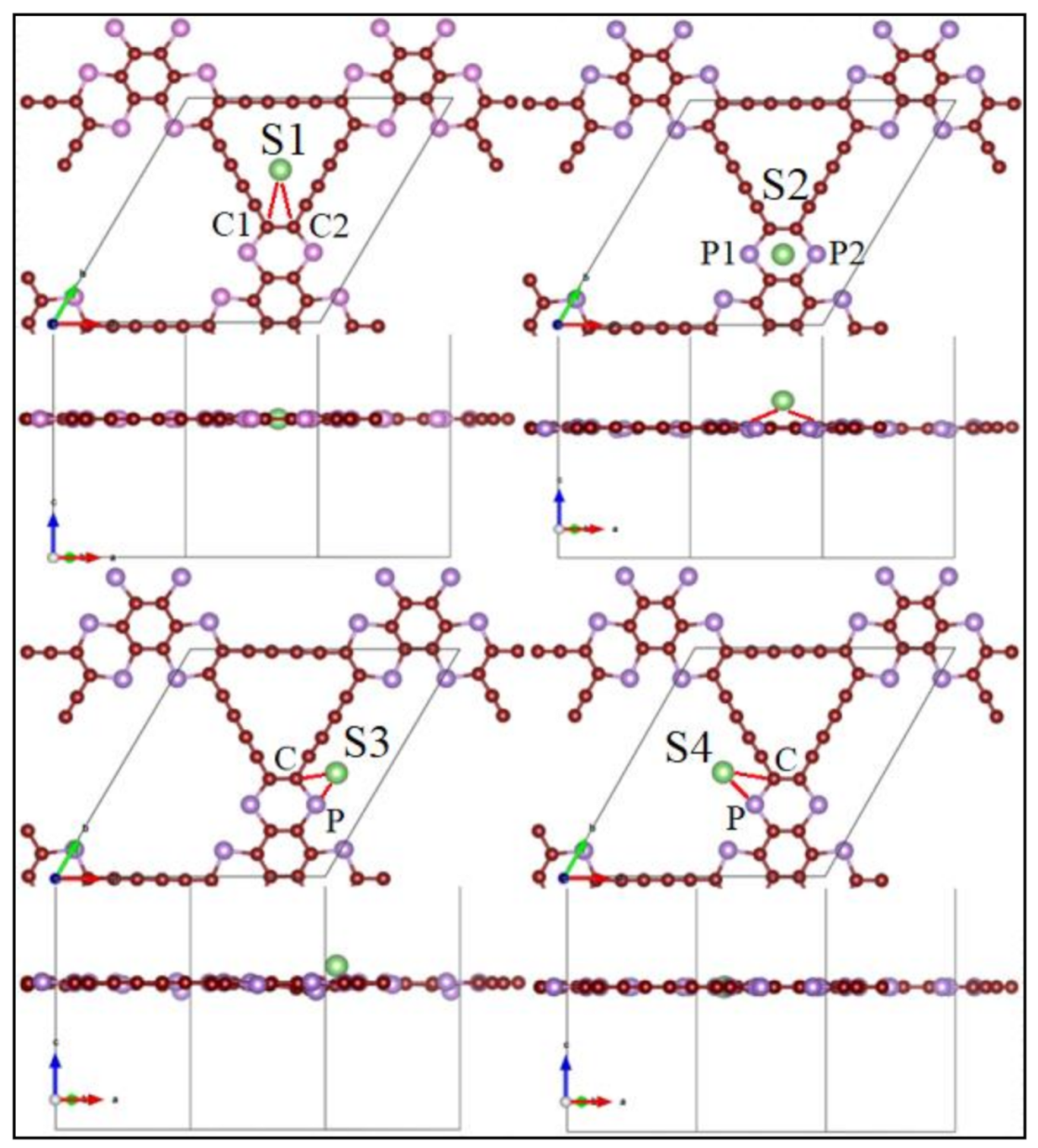
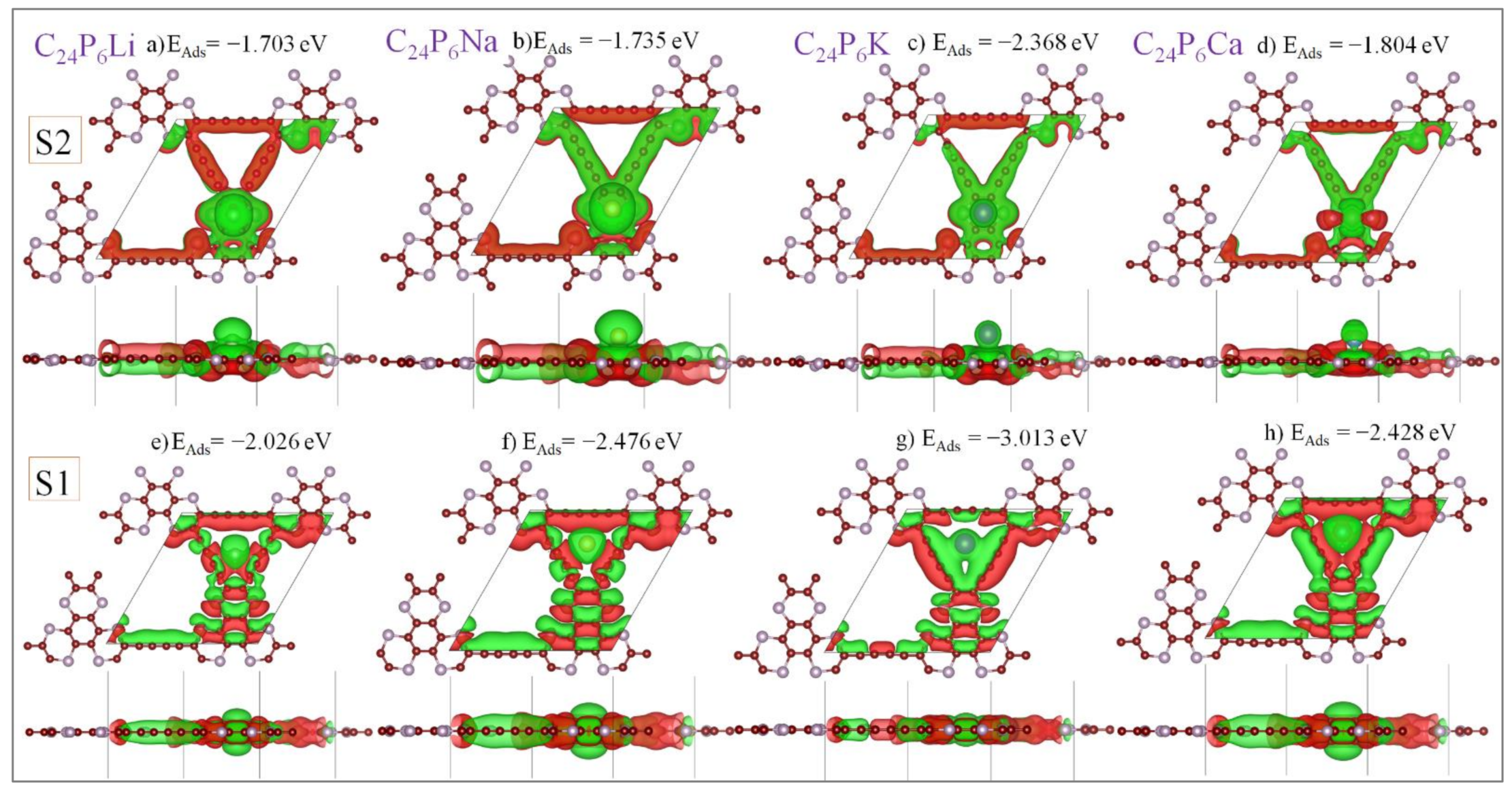
3.2. Application as Anode Materials for Li, Na, K, Mg and Ca-Ions Batteries
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, W.; Zhang, J.; Li, H. Batteries with high theoretical energy densities. Energy Storage Mater. 2020, 26, 46–55. [Google Scholar] [CrossRef]
- Zhu, K.; Li, Q.; Xue, Z.; Yu, Q.; Liu, X.; Shan, Z.; Liu, K. Mesoporous TiO2 Spheres as Advanced Anodes for Low-Cost, Safe, and High-Areal-Capacity Lithium-Ion Full Batteries. ACS Appl. Nano Mater. 2020. [CrossRef]
- Goodenough, J.B.; Kim, Y. Challenges for Rechargeable Li Batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.K.; Novoselov, K.S.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Huskinson, B.; Marshak, M.P.; Suh, C.; Er, S.; Gerhardt, M.R.; Galvin, C.J.; Chen, X.; Aspuru-Guzik, A.; Gordon, R.G.; Aziz, M.J. A metal-free organic-inorganic aqueous flow battery. Nature 2014, 505, 195–198. [Google Scholar] [CrossRef]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef]
- Magasinski, A.; Dixon, P.; Hertzberg, B.; Kvit, A.; Ayala, J.; Yushin, G. High-performance lithium-ion anodes using a hierarchical bottom-up approach. Nat. Mater. 2010, 9. [Google Scholar] [CrossRef] [PubMed]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, H.B.; Madhavi, S.; Hng, H.H.; Lou, X.W. Formation of Fe 2O 3 microboxes with hierarchical shell structures from metal-organic frameworks and their lithium storage properties. J. Am. Chem. Soc. 2012, 134, 17388–17391. [Google Scholar] [CrossRef]
- Han, D.; Zhang, J.; Weng, Z.; Kong, D.; Tao, Y.; Ding, F.; Ruan, D.; Yang, Q.H. Two-dimensional materials for lithium/sodium-ion capacitors. Mater. Today Energy 2019, 11, 30–45. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, N.; Cui, Y. Promises and challenges of nanomaterials for lithium-based rechargeable batteries. Nat. Energy 2016, 1. [Google Scholar] [CrossRef]
- Pramudita, J.C.; Sehrawat, D.; Goonetilleke, D.; Sharma, N. An Initial Review of the Status of Electrode Materials for Potassium-Ion Batteries. Adv. Energy Mater. 2017, 7, 1602911. [Google Scholar] [CrossRef]
- Schmuch, R.; Wagner, R.; Hörpel, G.; Placke, T.; Winter, M. Performance and cost of materials for lithium-based rechargeable automotive batteries. Nat. Energy 2018, 3, 267–278. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research development on sodium-ion batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, Z.; Zhou, Z. MXene-based materials for electrochemical energy storage. J. Energy Chem. 2018, 27, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Su, D.S.; Centi, G. A perspective on carbon materials for future energy application. J. Energy Chem. 2013, 22, 151–173. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, Y.; Lian, R.; Yang, D.; Zhang, D.; Meng, X.; Liu, Y.; Wei, Y.; Chen, G. Atomic insight into the structural transformation and anionic/cationic redox reactions of VS2 nanosheets in sodium-ion batteries. J. Mater. Chem. A 2018, 6, 15985–15992. [Google Scholar] [CrossRef]
- Xie, Y.; Dall’Agnese, Y.; Naguib, M.; Gogotsi, Y.; Barsoum, M.W.; Zhuang, H.L.; Kent, P.R.C. Prediction and characterization of mxene nanosheet anodes for non-lithium-ion batteries. ACS Nano 2014, 8, 9606–9615. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Zhao, M.Q.; Anasori, B.; Maleski, K.; Ren, C.E.; Li, J.; Byles, B.W.; Pomerantseva, E.; Wang, G.; Gogotsi, Y. Porous heterostructured MXene/carbon nanotube composite paper with high volumetric capacity for sodium-based energy storage devices. Nano Energy 2016, 26, 513–523. [Google Scholar] [CrossRef]
- Salavati, M.; Rabczuk, T. Application of highly stretchable and conductive two-dimensional 1T VS2 and VSe2 as anode materials for Li-, Na- and Ca-ion storage. Comput. Mater. Sci. 2019, 160, 360–367. [Google Scholar] [CrossRef]
- Wu, Y.; Nie, P.; Jiang, J.; Ding, B.; Dou, H.; Zhang, X. MoS 2 -Nanosheet-Decorated 2D Titanium Carbide (MXene) as High-Performance Anodes for Sodium-Ion Batteries. ChemElectroChem 2017, 4, 1560–1565. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, D.; Yang, D.; Wei, L.; Liu, B.; Wang, X.; Chen, G.; Wei, Y. Superior Mg2+ storage properties of VS2 nanosheets by using an APC-PP14Cl/THF electrolyte. Energy Storage Mater. 2019, 23, 749–756. [Google Scholar] [CrossRef]
- Mortazavi, B.; Makaremi, M.; Shahrokhi, M.; Raeisi, M.; Singh, C.V.; Rabczuk, T.; Pereira, L.F.C. Borophene hydride: A stiff 2D material with high thermal conductivity and attractive optical and electronic properties. Nanoscale 2018, 10, 3759–3768. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salavati, M.; Alajlan, N.; Rabczuk, T. Super-stretchability in two-dimensional RuCl3 and RuBr3 confirmed by first-principles simulations. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 113. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Zhang, S.; Liu, H.; Li, Y.; Cui, G.; Li, Y. Graphdiyne for high capacity and long-life lithium storage. Nano Energy 2015, 11, 481–489. [Google Scholar] [CrossRef]
- Mortazavi, B.; Dianat, A.; Rahaman, O.; Cuniberti, G.; Rabczuk, T. Borophene as an anode material for Ca, Mg, Na or Li ion storage: A first-principle study. J. Power Sources 2016, 329, 456–461. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zuo, Z.; Shang, H.; Wang, F.; Li, Y. In-situ constructing 3D graphdiyne as all-carbon binder for high-performance silicon anode. Nano Energy 2018, 53, 135–143. [Google Scholar] [CrossRef]
- Kuang, P.; Zhu, B.; Li, Y.; Liu, H.; Yu, J.; Fan, K. Graphdiyne: A superior carbon additive to boost the activity of water oxidation catalysts. Nanoscale Horiz. 2018, 3, 317–326. [Google Scholar] [CrossRef]
- Shang, H.; Zuo, Z.; Li, L.; Wang, F.; Liu, H.; Li, Y.; Li, Y. Ultrathin Graphdiyne Nanosheets Grown In Situ on Copper Nanowires and Their Performance as Lithium-Ion Battery Anodes. Angew. Chemie Int. Ed. 2017, 57, 774–778. [Google Scholar] [CrossRef] [PubMed]
- Shang, H.; Zuo, Z.; Yu, L.; Wang, F.; He, F.; Li, Y. Low-Temperature Growth of All-Carbon Graphdiyne on a Silicon Anode for High-Performance Lithium-Ion Batteries. Adv. Mater. 2018, 30, 1801459. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, R.; Toyoda, R.; Shiotsuki, R.; Fukui, N.; Wada, K.; Maeda, H.; Sakamoto, R.; Sasaki, S.; Masunaga, H.; Nagashio, K.; et al. Expansion of the Graphdiyne Family: A Triphenylene-Cored Analogue. ACS Appl. Mater. Interfaces 2019, 11, 2730–2733. [Google Scholar] [CrossRef]
- Matsuoka, R.; Sakamoto, R.; Hoshiko, K.; Sasaki, S.; Masunaga, H.; Nagashio, K.; Nishihara, H. Crystalline Graphdiyne Nanosheets Produced at a Gas/Liquid or Liquid/Liquid Interface. J. Am. Chem. Soc. 2017, 139, 3145–3152. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.T.; Lee, S.; Park, S.; Lee, C.Y. Graphene chemiresistors modified with functionalized triphenylene for highly sensitive and selective detection of dimethyl methylphosphonate. RSC Adv. 2019, 9, 33976–33980. [Google Scholar] [CrossRef] [Green Version]
- Taghilou, H.; Fathi, D. Spin related transport in two pyrene and Triphenylene graphene nanodisks using NEGF method. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 101, 208–211. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Madjet, M.E.; Makaremi, M.; Ahzi, S.; Rabczuk, T. N-, P-, As-triphenylene-graphdiyne: Strong and stable 2D semiconductors with outstanding capacities as anodes for Li-ion batteries. Carbon 2019, 141, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Srinivasu, K.; Ghosh, S.K. Graphyne and graphdiyne: Promising materials for nanoelectronics and energy storage applications. J. Phys. Chem. C 2012, 116, 5951–5956. [Google Scholar] [CrossRef]
- Li, X.; Wang, N.; He, J.; Yang, Z.; Tu, Z.; Zhao, F.; Wang, K.; Yi, Y.; Huang, C. Designing the efficient lithium diffusion and storage channels based on graphdiyne. Carbon N. Y. 2020, 162, 579–585. [Google Scholar] [CrossRef]
- Jia, Z.; Li, Y.; Zuo, Z.; Liu, H.; Huang, C.; Li, Y. Synthesis and Properties of 2D Carbon - Graphdiyne. Acc. Chem. Res. 2017, 50, 2470–2478. [Google Scholar] [CrossRef]
- Sun, C.; Searles, D.J. Lithium storage on graphdiyne predicted by DFT calculations. J. Phys. Chem. C 2012, 116, 26222–26226. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liu, H.; Guo, Y.; Li, Y.; Zhu, D. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256–3258. [Google Scholar] [CrossRef]
- Baughman, R.H.; Eckhardt, H.; Kertesz, M. Structure-property predictions for new planar forms of carbon: Layered phases containing sp 2 and sp atoms. J. Chem. Phys. 1987, 87, 6687–6699. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Liu, H.; Li, Y. Graphdiyne and graphyne: From theoretical predictions to practical construction. Chem. Soc. Rev. 2014, 43, 2572–2586. [Google Scholar] [CrossRef]
- Long, M.; Tang, L.; Wang, D.; Li, Y.; Shuai, Z. Electronic structure and carrier mobility in graphdiyne sheet and nanoribbons: Theoretical predictions. ACS Nano 2011, 5, 2593–2600. [Google Scholar] [CrossRef]
- Pan, L.D.; Zhang, L.Z.; Song, B.Q.; Du, S.X.; Gao, H.J. Graphyne- and graphdiyne-based nanoribbons: Density functional theory calculations of electronic structures. Appl. Phys. Lett. 2011, 98, 173102. [Google Scholar] [CrossRef] [Green Version]
- Mortazavi, B.; Makaremi, M.; Shahrokhi, M.; Fan, Z.; Rabczuk, T. N-graphdiyne two-dimensional nanomaterials: Semiconductors with low thermal conductivity and high stretchability. Carbon N. Y. 2018, 137, 57–67. [Google Scholar] [CrossRef] [Green Version]
- Mortazavi, B.; Shahrokhi, M.; Zhuang, X.; Rabczuk, T. Boron-graphdiyne: A superstretchable semiconductor with low thermal conductivity and ultrahigh capacity for Li, Na and Ca ion storage. J. Mater. Chem. A 2018, 6, 11022–11036. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Li, X.; Tu, Z.; Zhao, F.; He, J.; Guan, Z.; Huang, C.; Yi, Y.; Li, Y. Synthesis and Electronic Structure of Boron-Graphdiyne with an sp-Hybridized Carbon Skeleton and Its Application in Sodium Storage. Angew. Chemie Int. Ed. 2018, 57, 3968–3973. [Google Scholar] [CrossRef]
- Lu, C.; Yang, Y.; Wang, J.; Fu, R.; Zhao, X.; Zhao, L.; Ming, Y.; Hu, Y.; Lin, H.; Tao, X.; et al. High-performance graphdiyne-based electrochemical actuators. Nat. Commun. 2018, 9, 752. [Google Scholar] [CrossRef]
- Zhao, Y.; Wan, J.; Yao, H.; Zhang, L.; Lin, K.; Wang, L.; Yang, N.; Liu, D.; Song, L.; Zhu, J.; et al. Few-layer graphdiyne doped with sp-hybridized nitrogen atoms at acetylenic sites for oxygen reduction electrocatalysis. Nat. Chem. 2018, 10, 924–931. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Madjet, M.E.; Hussain, T.; Zhuang, X.; Rabczuk, T. N-, B-, P-, Al-, As-, and Ga-graphdiyne/Graphyne Lattices: First-Principles Investigation of Mechanical, Optical and Electronic Properties. Available online: https://pubs.rsc.org/en/content/articlelanding/2019/tc/c9tc00082h/unauth#!divAbstract (accessed on 8 February 2019).
- Salavati, M.; Rabczuk, T. First-principles investigation of N-triphenylene-graphdiyne nanosheets as an anode material for Na, K, Mg and Ca storage. Comput. Mater. Sci. 2019, 169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Mortazavi, B.; Dianat, A.; Cuniberti, G.; Rabczuk, T. Application of silicene, germanene and stanene for Na or Li ion storage: A theoretical investigation. Electrochim. Acta 2016, 213, 865–870. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Scheffler, M.; Stampfl, C. Chapter 5 Theory of adsorption on metal substrates. Handb. Surf. Sci. 2000, 2, 285–356. [Google Scholar] [CrossRef] [Green Version]
- Aydinol, M.; Kohan, A.; Ceder, G.; Cho, K.; Joannopoulos, J. Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 56, 1354–1365. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Jang, B.; Koo, J.; Park, M.; Lee, H.; Nam, J.; Kwon, Y. Graphdiyne as a high-capacity lithium ion battery anode material. Appl. Phys. Lett. 2013, 103, 263904. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Jiu, T.; Chen, S.; Liu, L.; Yao, Q.; Bi, F.; Zhao, C.; Wang, Z.; Zhao, M.; Zhang, G.; et al. Graphdiyne as a Host Active Material for Perovskite Solar Cell Application. Nano Lett. 2018, 18, 6941–6947. [Google Scholar] [CrossRef] [PubMed]
- Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
- Pollak, E.; Geng, B.; Jeon, K.J.; Lucas, I.T.; Richardson, T.J.; Wang, F.; Kostecki, R. The interaction of Li+ with single-layer and few-layer graphene. Nano Lett. 2010, 10, 3386–3388. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Hassanein, A. Kinetic Monte Carlo simulation of hydrogen diffusion on tungsten reconstructed (0 0 1) surface. Fusion Eng. Des. 2014, 89, 2545–2549. [Google Scholar] [CrossRef]
- Moon, J.; Lee, B.; Cho, M.; Cho, K. Ab initio and kinetic Monte Carlo simulation study of lithiation in crystalline and amorphous silicon. J. Power Sources 2014, 272, 1010–1017. [Google Scholar] [CrossRef]
- Zhong, K.; Hu, R.; Xu, G.; Yang, Y.; Zhang, J.M.; Huang, Z. Adsorption and ultrafast diffusion of lithium in bilayer graphene: Ab initio and kinetic Monte Carlo simulation study. Phys. Rev. B 2019, 99, 155403. [Google Scholar] [CrossRef] [Green Version]
- Hu, R.; Xu, G.; Yang, Y.; Zhang, J.M.; Zhong, K.; Huang, Z. Effect of stacking structure on lithium adsorption and diffusion in bilayer black phosphorene. Phys. Rev. B 2019, 100, 085422. [Google Scholar] [CrossRef]
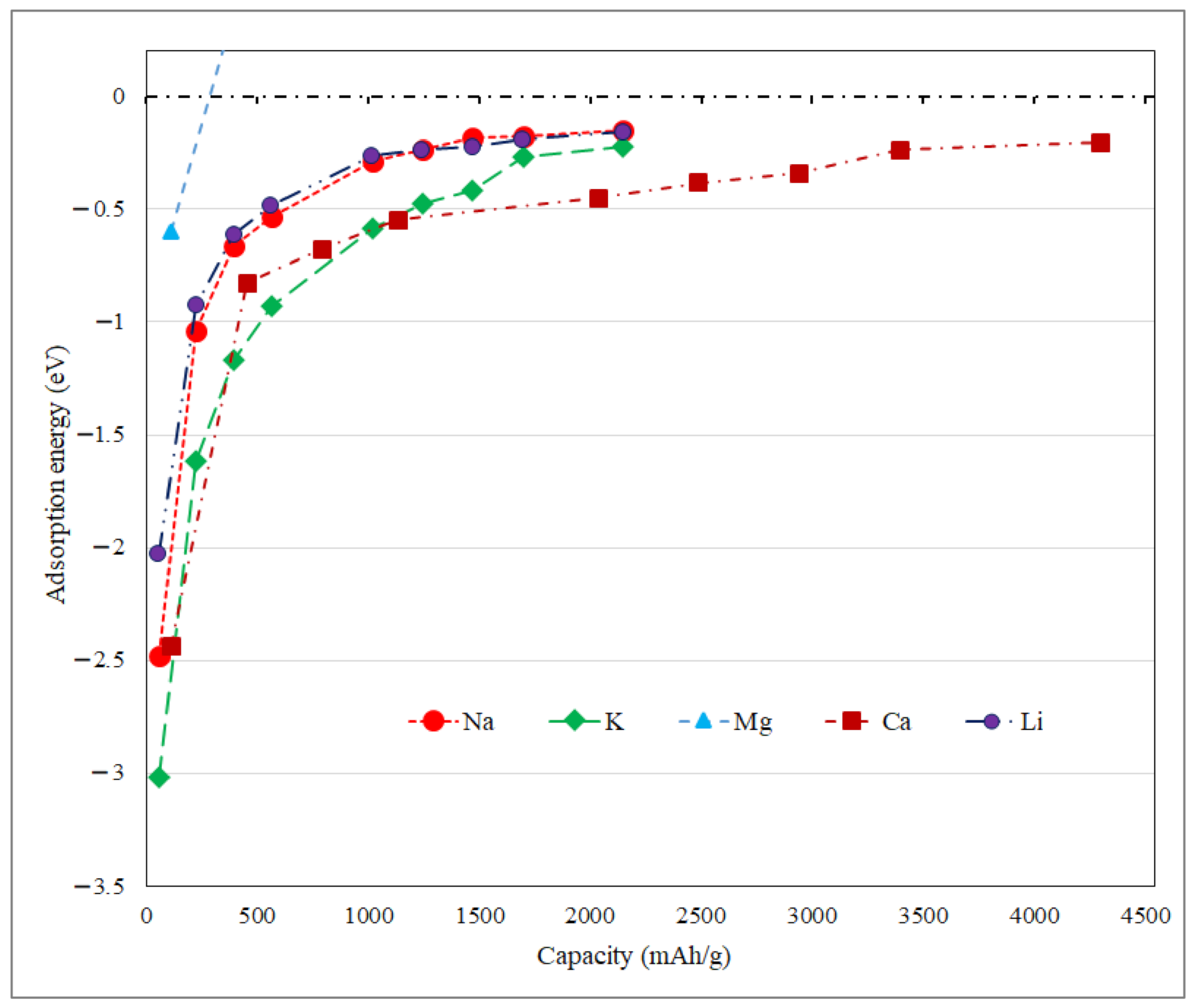
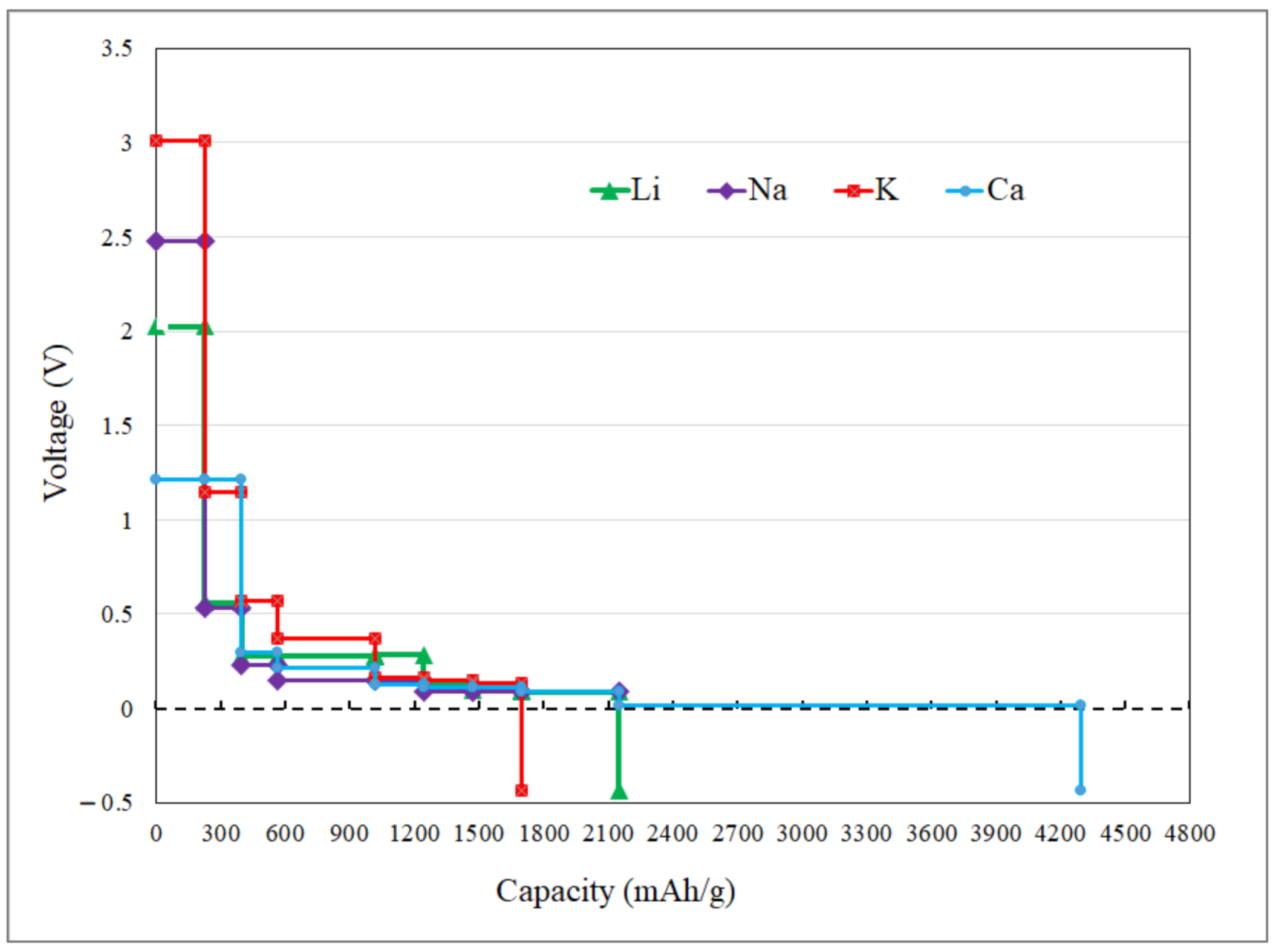

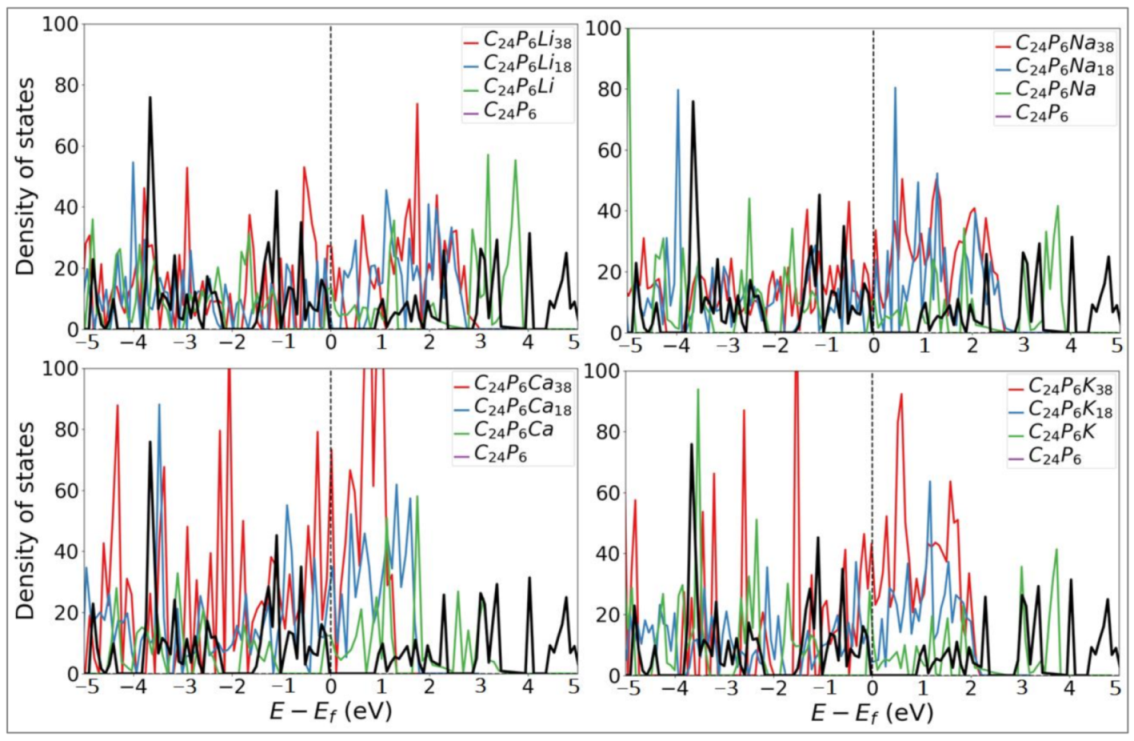
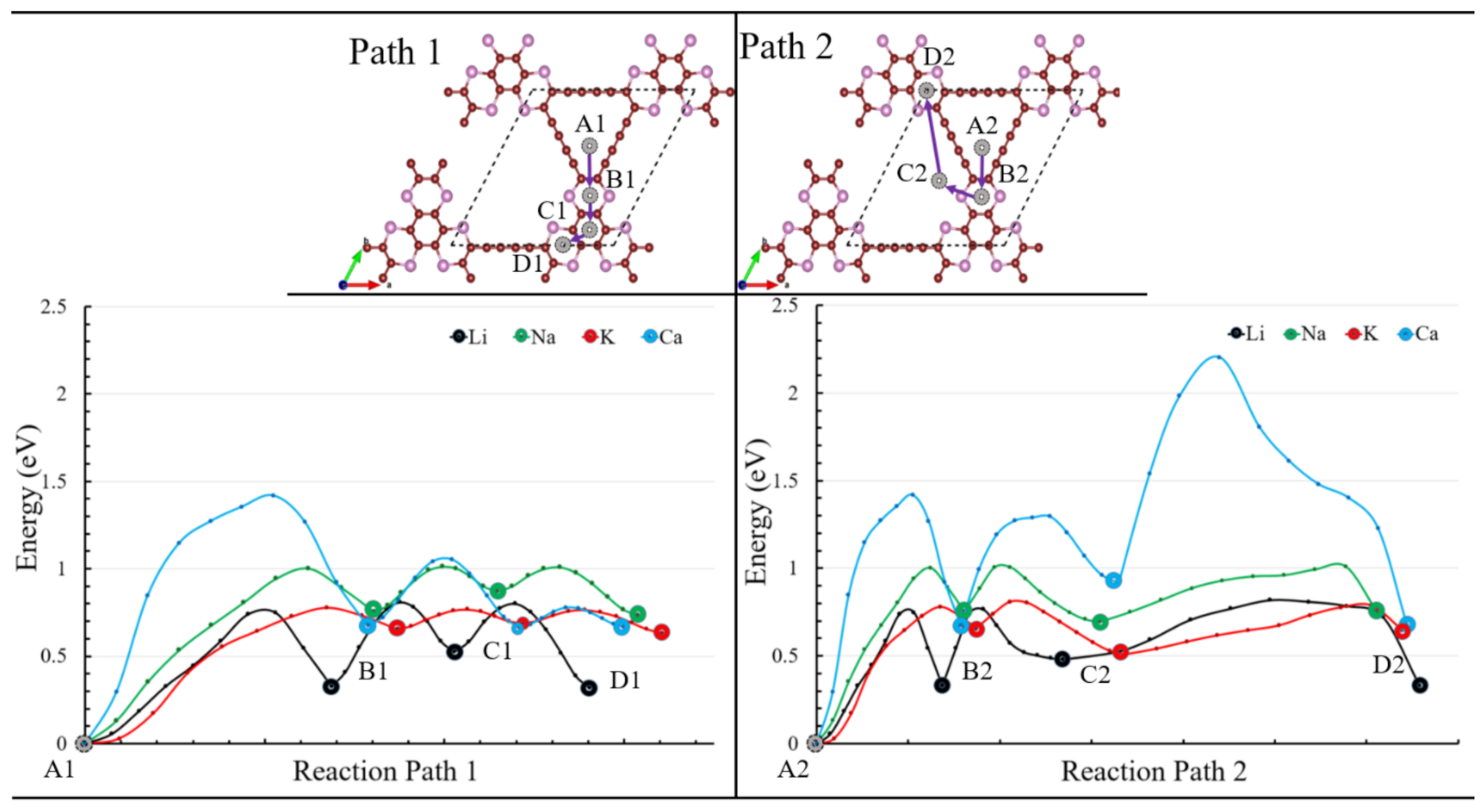
| Li | Na | K | Ca | ||
|---|---|---|---|---|---|
| Most stable adsorption sites | S1 | EAds = −2.026 eV | EAds = −2.476 eV | EAds = −3.013 eV | EAds = −2.428 eV |
| LC1-Li = 3.280 Å | LC1-Na = 4.263 Å | LC1-K = 4.260 Å | LC1-Ca = 4.226 Å | ||
| LC2-Li = 3.279 Å | LC2-Na = 4.263 Å | LC2-K = 4.260Å | LC2-Ca = 4.226 Å | ||
| LZ = 0 Å | LZ = 0 Å | LZ = 0 Å | LZ = 0 Å | ||
| ΔQ = 0.995 |e| | ΔQ = 0.996 |e| | ΔQ = 0.850 |e| | ΔQ = 1.620 |e| | ||
| S2 | EAds = −1.703eV | EAds = −1.735eV | EAds = −2.368 eV | EAds = −1.804 eV | |
| LP1-Li = 2.558 Å | LP1-Na = 2.901 Å | LP1-K = 3.297 Å | LP1-Ca = 2.734 Å | ||
| LP2-Li = 2.559 Å | LP2-Na = 2.900 Å | LP2-K = 3.302 Å | LP2-Ca = 2.733 Å | ||
| LZ = 1.678 Å | LZ = 2.163 Å | LZ = 2.514 Å | LZ = 2.027 Å | ||
| ΔQ = 0.993 |e| | ΔQ = 0.991 |e| | ΔQ = 0.932 |e| | ΔQ = 1.510 |e| | ||
| S3 | EAds = −1.567eV | EAds = −1.794eV | EAds = −2.284 eV | EAds = −1.712 eV | |
| LC-Li = 2.505 Å | LC-Na = 3.255 Å | LC-K = 2.965 Å | LC-Ca = 2.408 Å | ||
| LP-Li = 2.482 Å | LP-Na = 2.819 Å | LP-K = 3.399 Å | LP-Ca = 2.882 Å | ||
| LZ = 1.024 Å | LZ = 0.216 Å | LZ = 2.397 Å | LZ = 1.819 Å | ||
| ΔQ = 0.994 |e| | ΔQ = 0.993 |e| | ΔQ = 0.912 |e| | ΔQ = 1.615 |e| | ||
| S4 | EAds = −1.551 eV | EAds = −1.793 eV | EAds = −2.513 eV | EAds = −1.560 eV | |
| LC-Li = 2.840 Å | LC-Na = 3.239 Å | LC-K = 3.729 Å | LC-Ca = 2.631 Å | ||
| LP-Li = 2.487 Å | LP-Na = 2.807 Å | LP-K = 3.214 Å | LP-Ca = 2.647 Å | ||
| LZ = 0 Å | LZ = 0 Å | LZ = 0 Å | LZ = 0 Å | ||
| ΔQ = 0.993 |e| | ΔQ = 0.992 |e| | ΔQ = 0.910 |e| | ΔQ = 1.625 |e| |
| Maximum Barrier Energy | ||
|---|---|---|
| Ions | Path 1 | Path 2 |
| Li | 0.75 | 0.75 |
| 0.44 | 0.48 | |
| 0.34 | 0.28 | |
| Na | 1.00 | 1.00 |
| 0.25 | 0.26 | |
| 0.32 | 0.14 | |
| K | 0.78 | 0.78 |
| 0.15 | 0.11 | |
| 0.28 | 0.08 | |
| Ca | 1.42 | 1.42 |
| 0.62 | 0.38 | |
| 1.29 | 0.11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salavati, M.; Alajlan, N.; Rabczuk, T. Theoretical Prediction of P-Triphenylene-Graphdiyne as an Excellent Anode Material for Li, Na, K, Mg, and Ca Batteries. Appl. Sci. 2021, 11, 2308. https://doi.org/10.3390/app11052308
Salavati M, Alajlan N, Rabczuk T. Theoretical Prediction of P-Triphenylene-Graphdiyne as an Excellent Anode Material for Li, Na, K, Mg, and Ca Batteries. Applied Sciences. 2021; 11(5):2308. https://doi.org/10.3390/app11052308
Chicago/Turabian StyleSalavati, Mohammad, Naif Alajlan, and Timon Rabczuk. 2021. "Theoretical Prediction of P-Triphenylene-Graphdiyne as an Excellent Anode Material for Li, Na, K, Mg, and Ca Batteries" Applied Sciences 11, no. 5: 2308. https://doi.org/10.3390/app11052308
APA StyleSalavati, M., Alajlan, N., & Rabczuk, T. (2021). Theoretical Prediction of P-Triphenylene-Graphdiyne as an Excellent Anode Material for Li, Na, K, Mg, and Ca Batteries. Applied Sciences, 11(5), 2308. https://doi.org/10.3390/app11052308







