Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data
Abstract
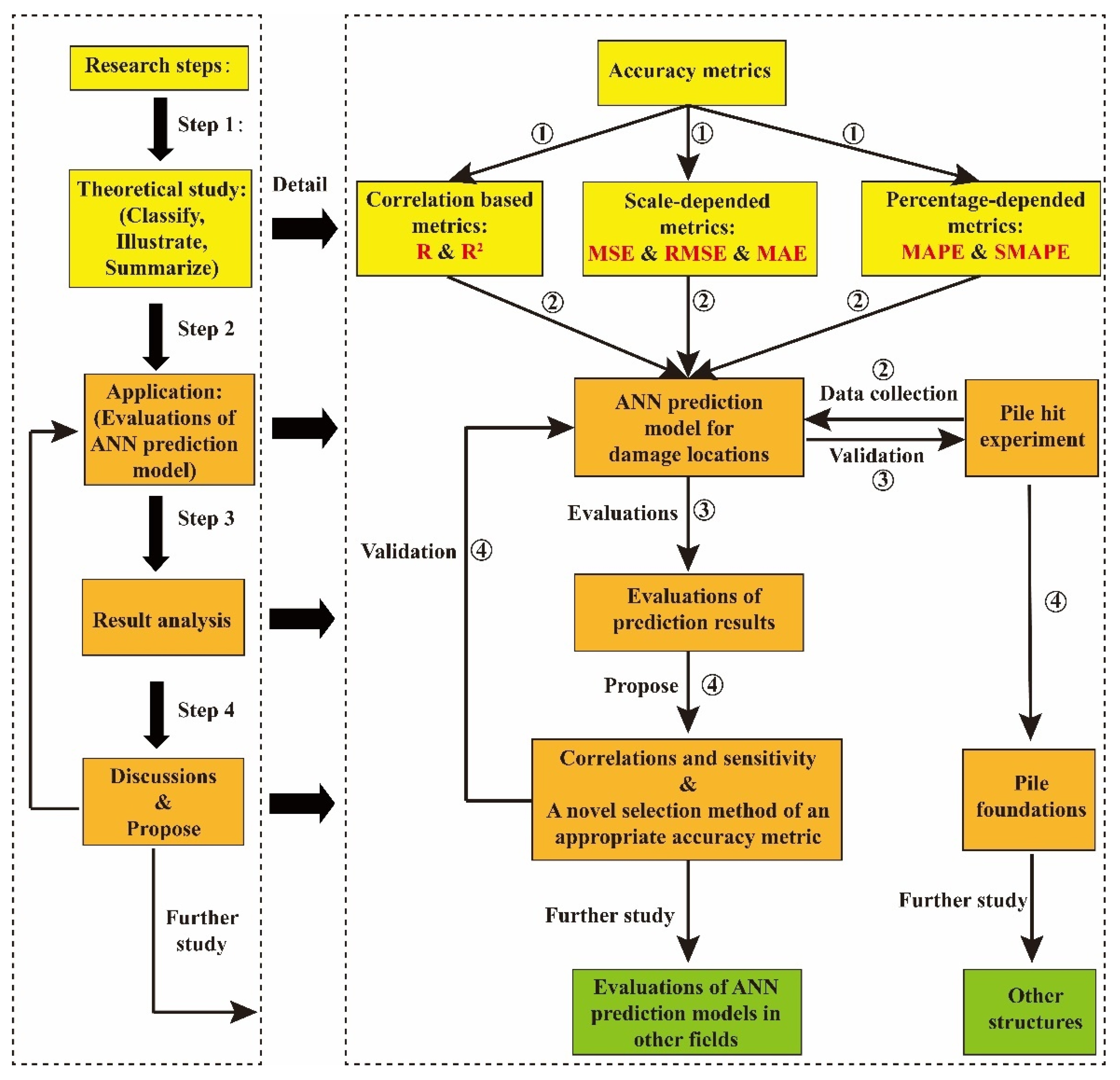
:1. Introduction
2. Accuracy Metrics
2.1. Correlation-Based Metrics
2.2. Scale-Dependent Metrics
2.3. Percentage-Dependent Metrics
3. Damage Location Prediction Model Using AE Signal Data
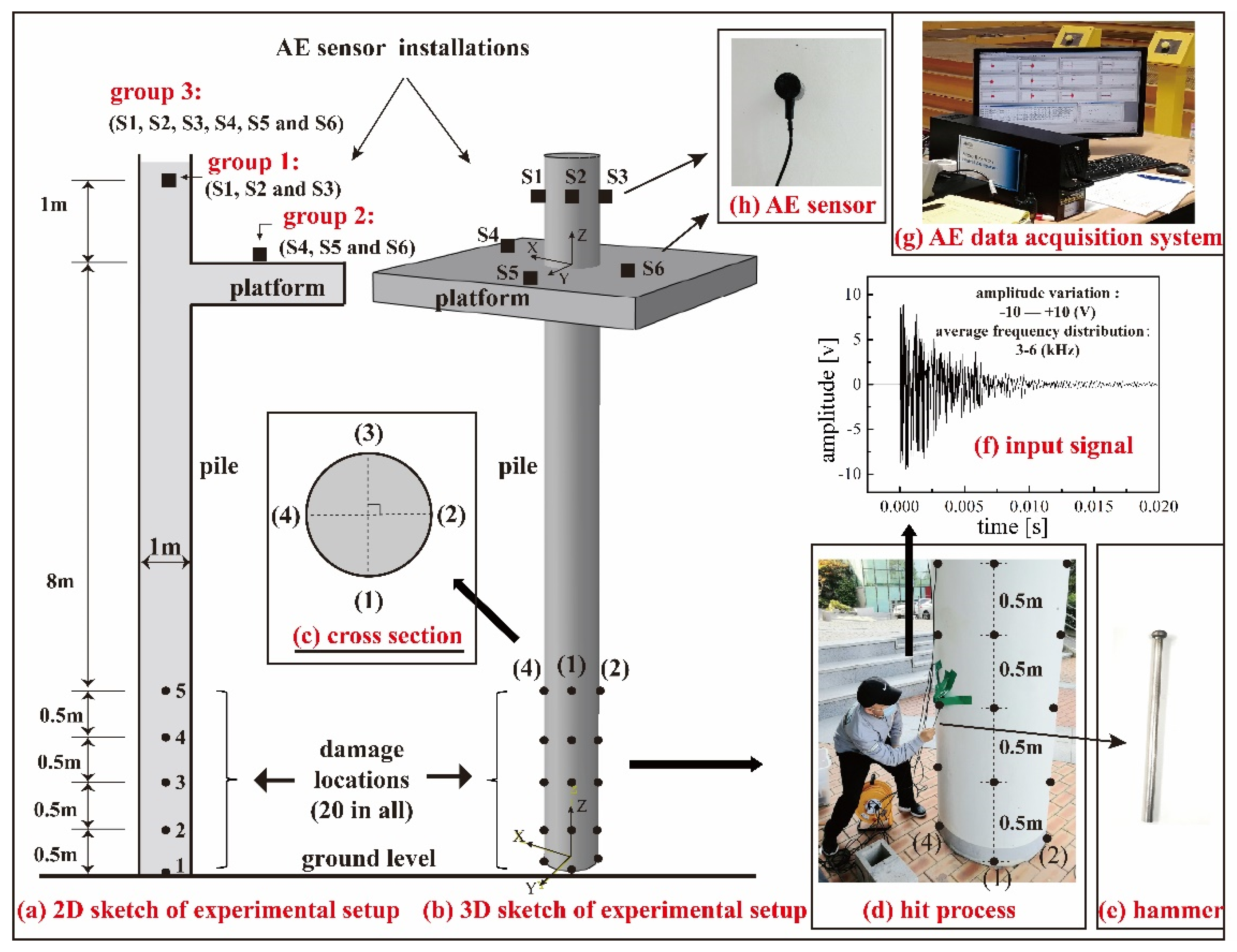
3.1. Experimental Setup of Pile Hit Test
3.2. Data Collection of AE Signals
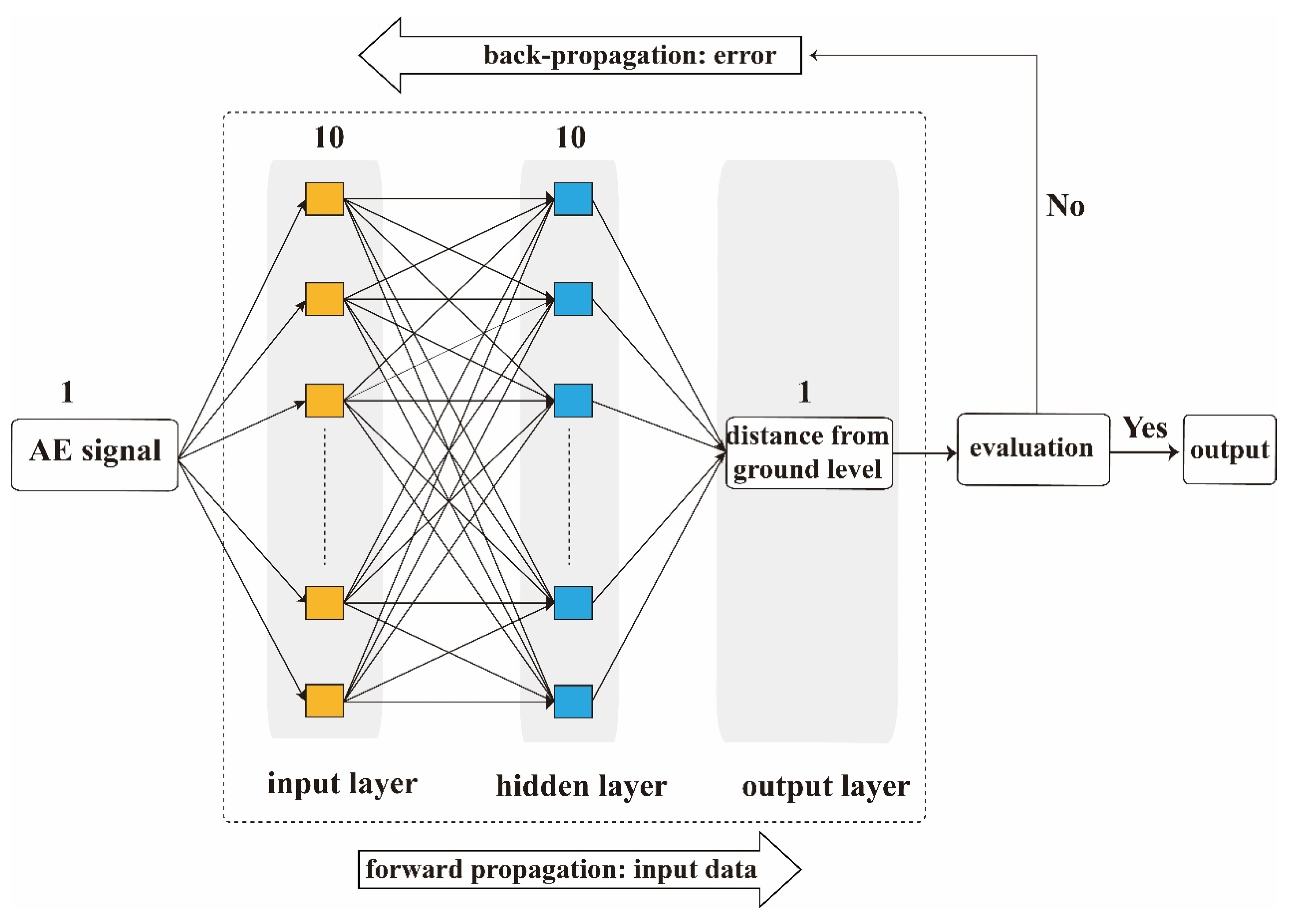
3.3. ANN Prediction Model
4. Evaluations of Prediction Results Using Accuracy Metrics
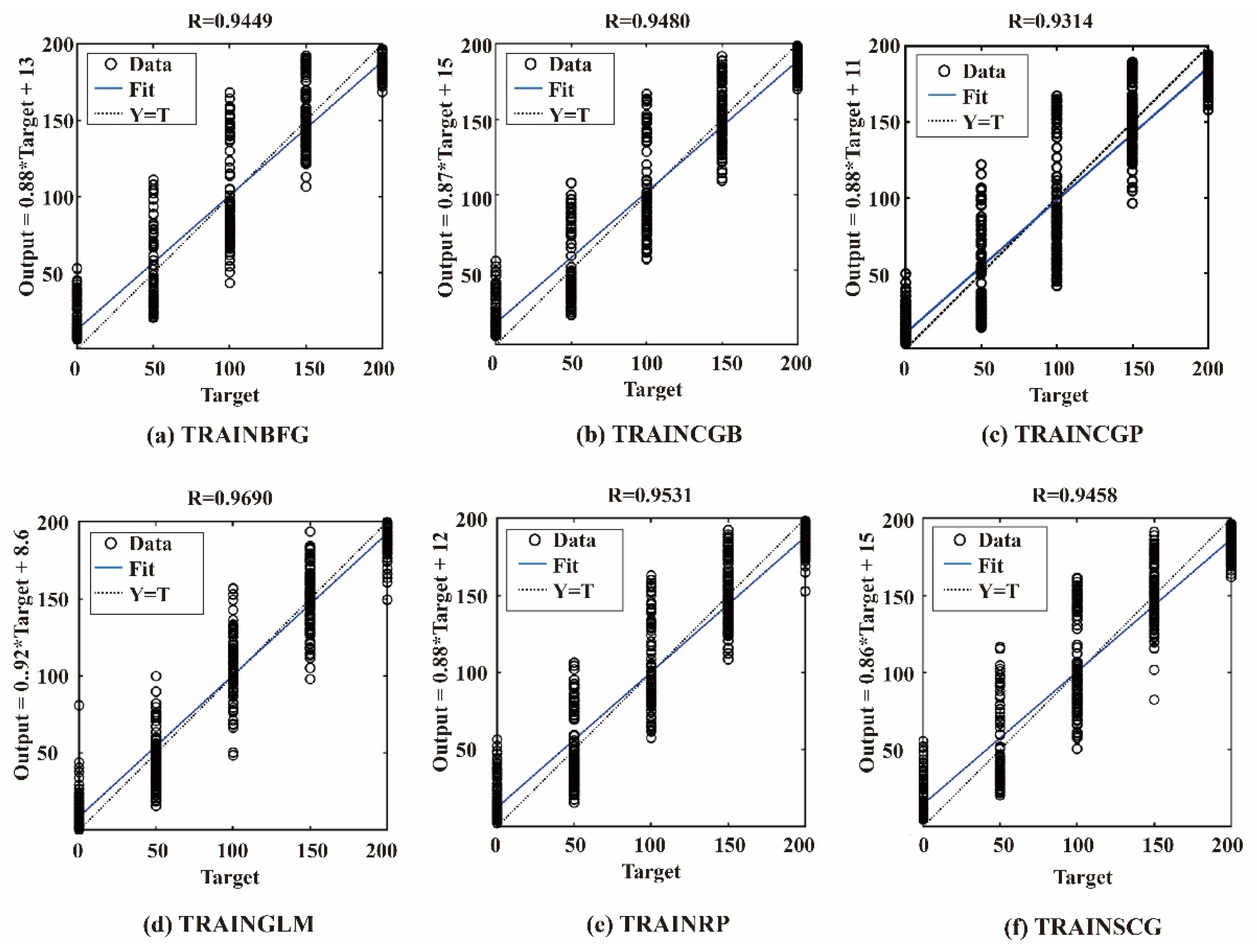
4.1. Evaluations of Performance of Different Training Algorithms
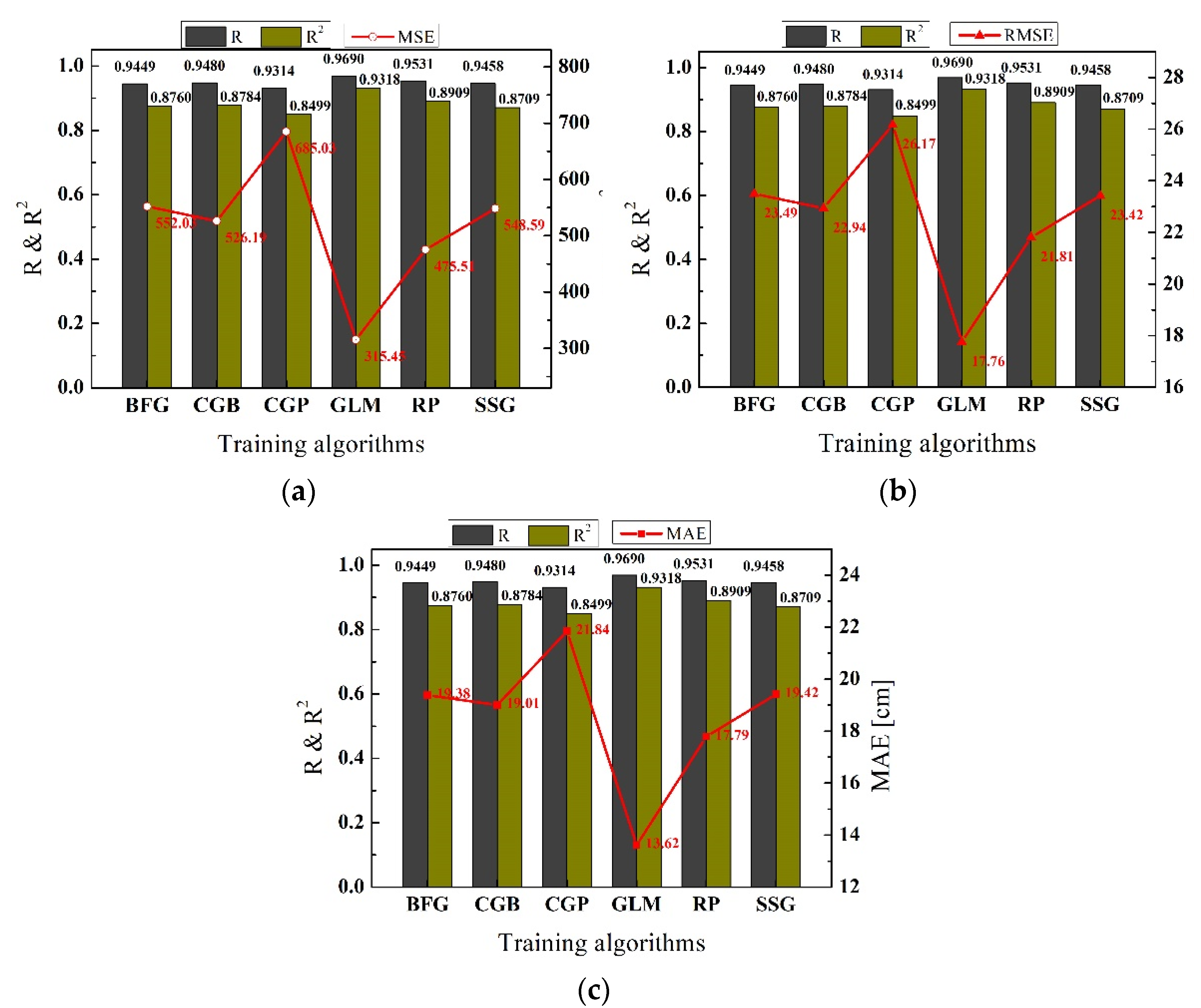
4.1.1. Evaluations of Performance Using Scale-Dependent Metrics
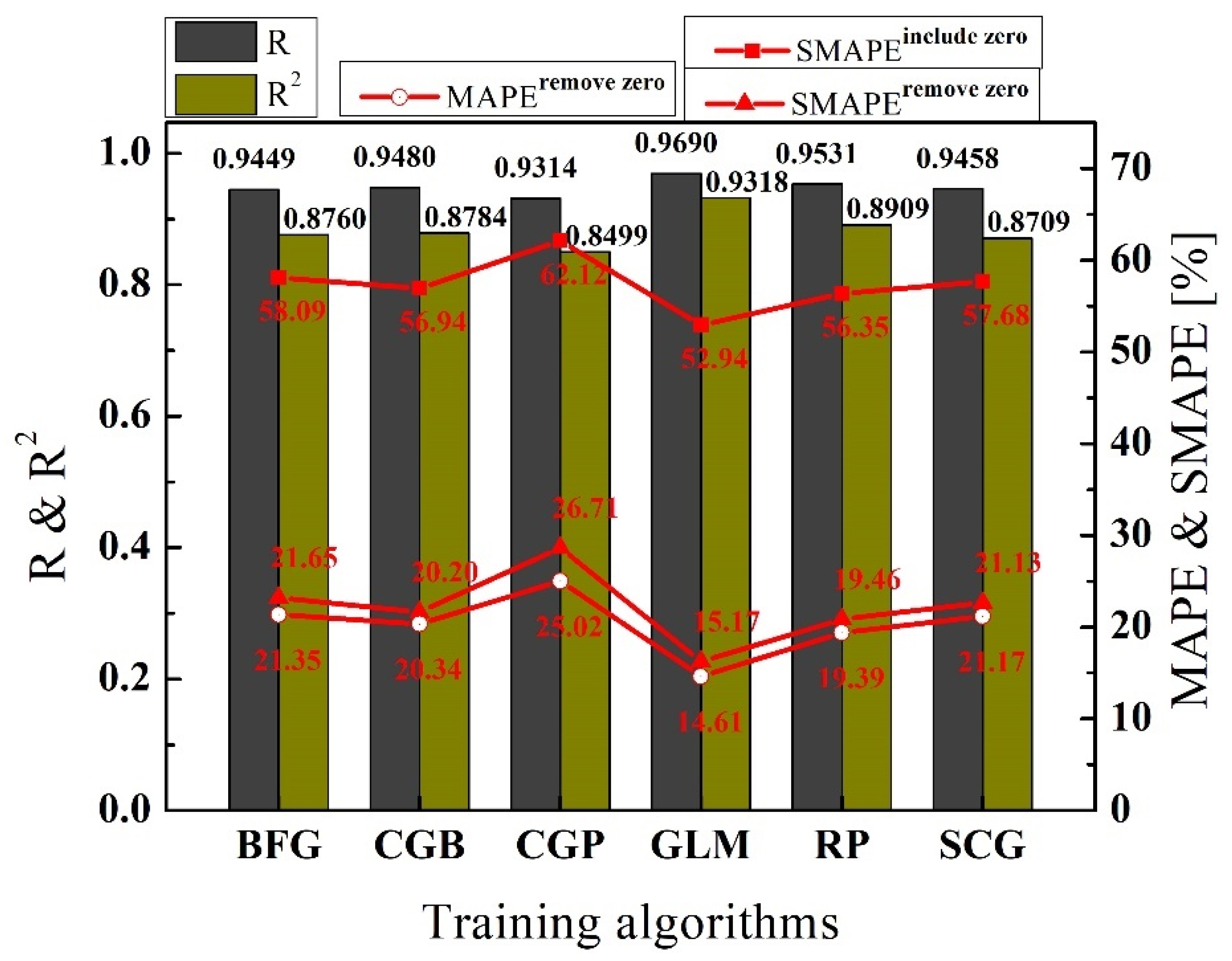
4.1.2. Evaluations of Performance Using Percentage-Dependent Metrics
4.2. Evaluations of Prediction Accuracy of Different Training Datasets
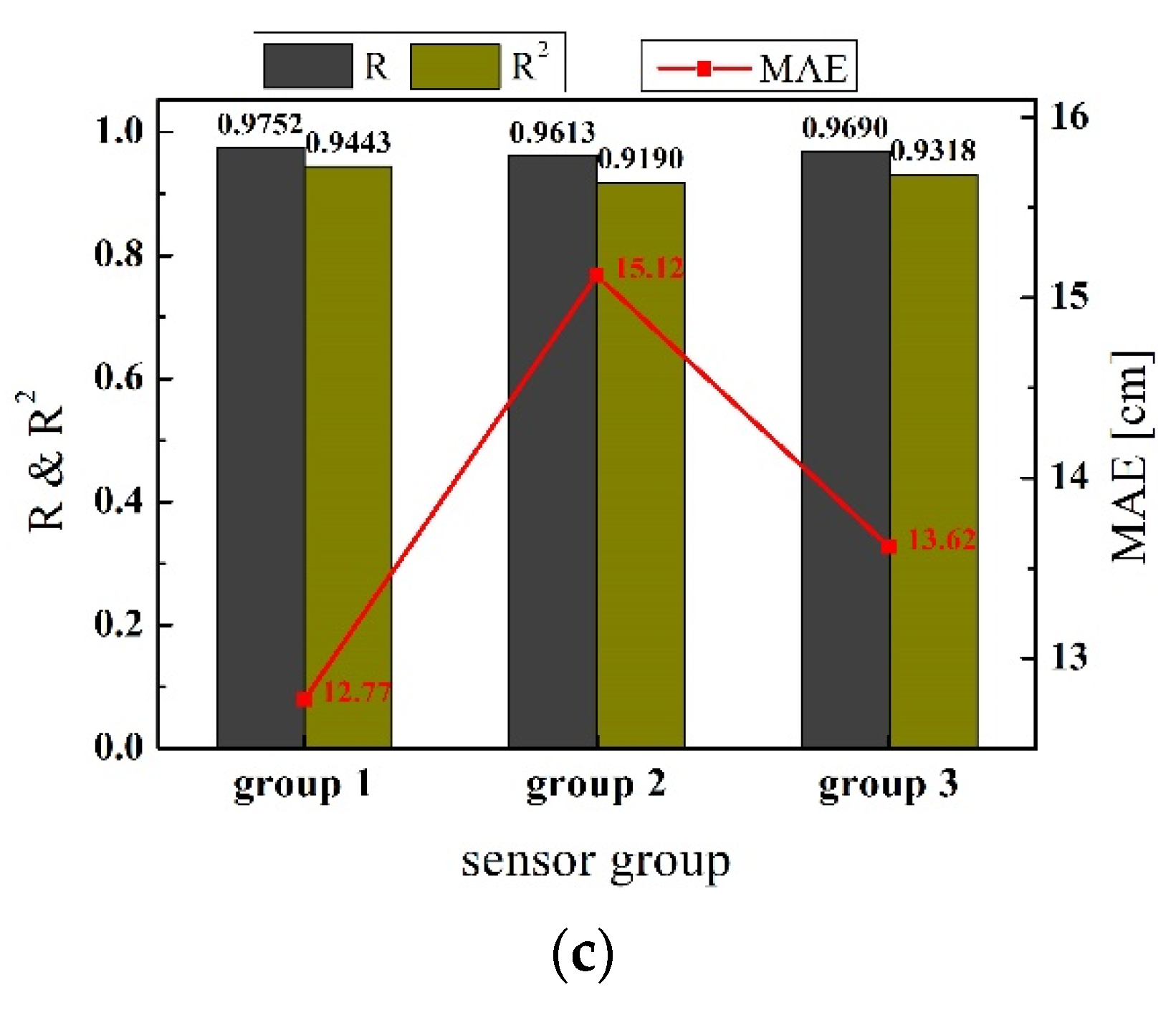
4.2.1. Evaluations of Prediction Accuracy Using Scale-Dependent Metrics
4.2.2. Evaluations of Prediction Accuracy Using Percentage-Dependent Metrics
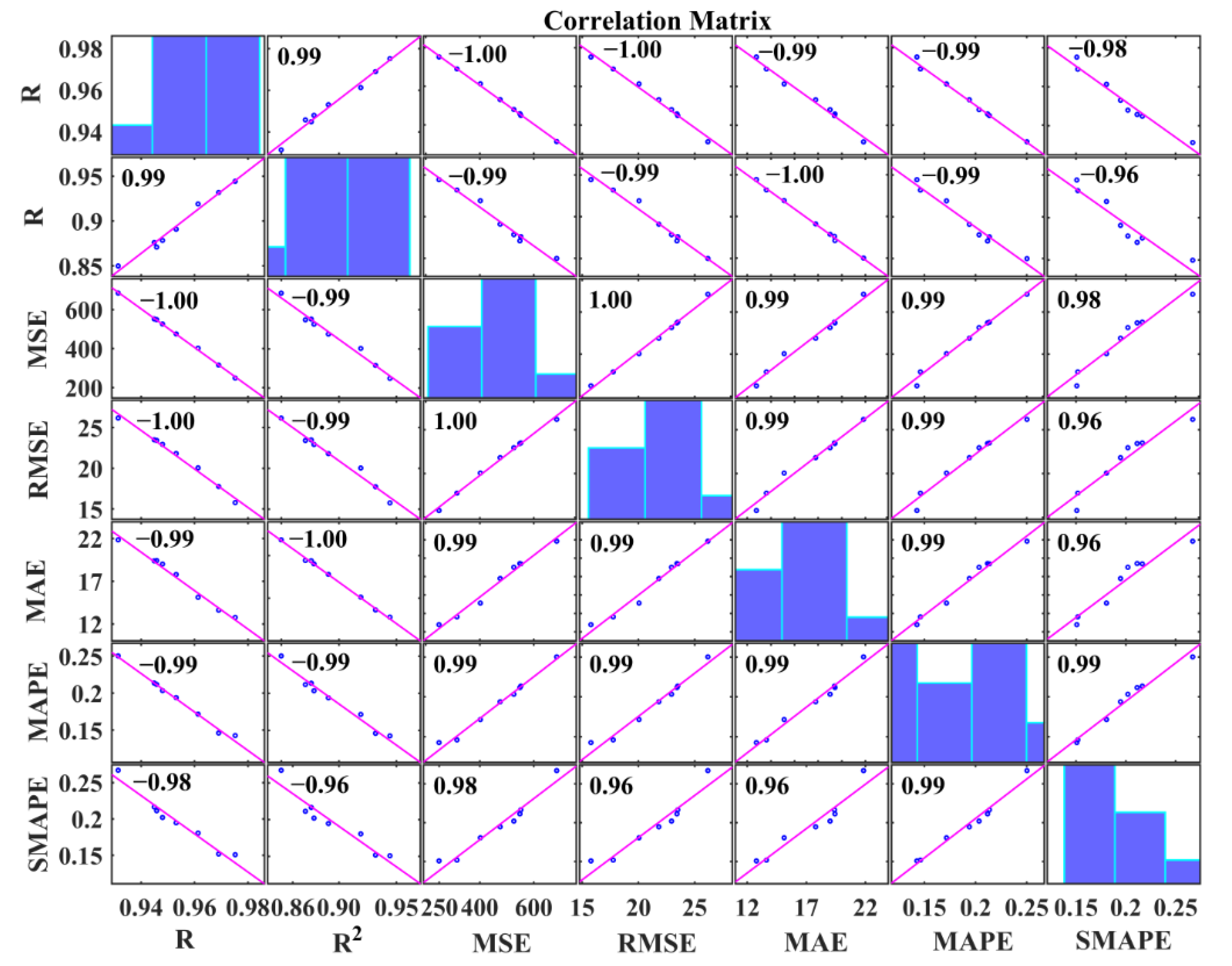
5. Discussion
6. Conclusions
- Among the six training algorithms studied in this paper, the training algorithm of “TRAINGLM” has the best performance for training the ANN model for predicting damage locations in deep piles.
- The prediction accuracies of three sensor installation groups can be ranked as follows: group 1 (pile body-installation group) > group 3 (mix-installation group) > group 2 (platform-installation group). This result can lead engineers to decide that when detecting the damages of deep piles using the AE technique, the priority AE sensor installation option is pile body-installation, the second option is mix-installation (pile body and platform), and the last option is platform-installation.
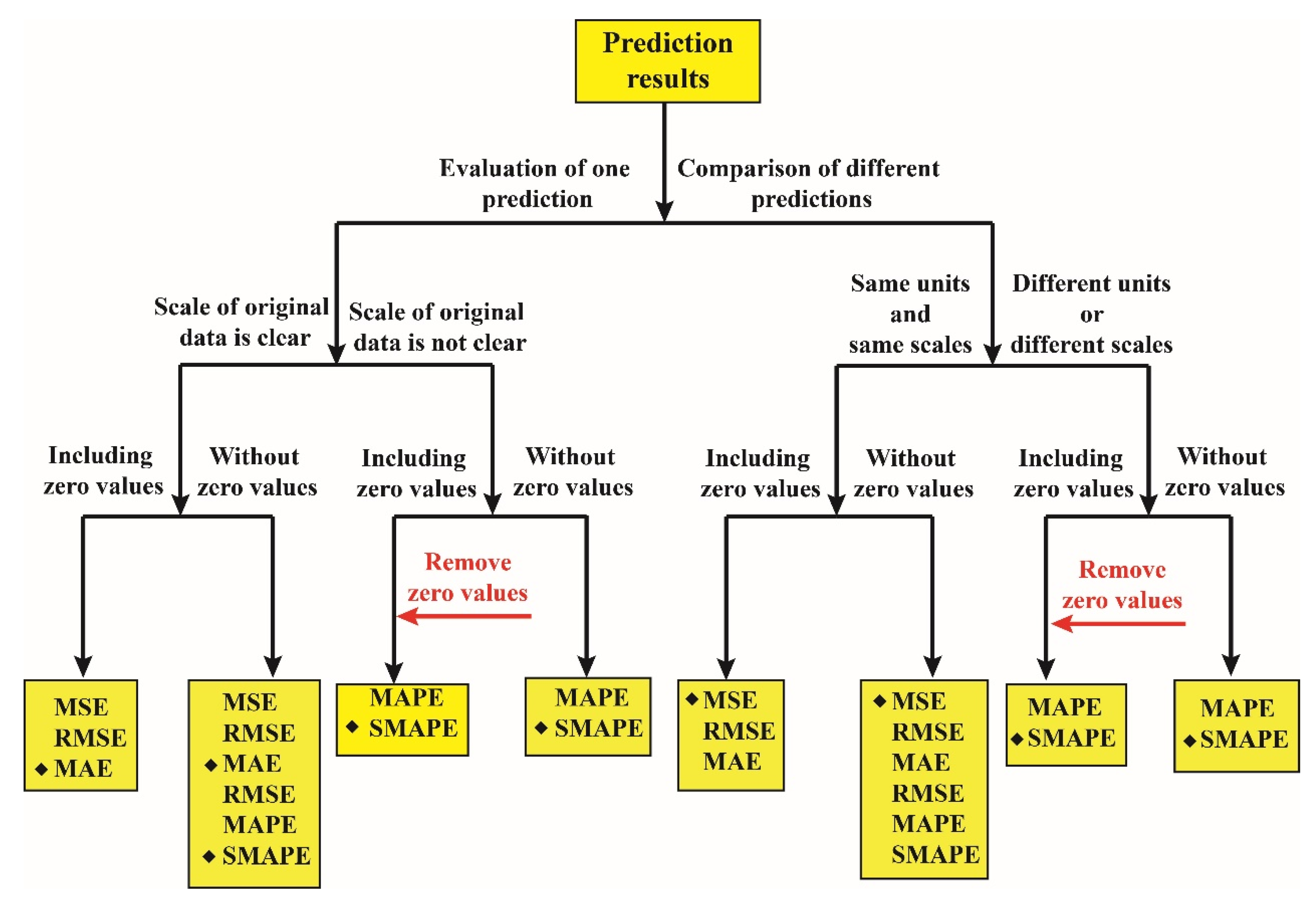
- The existence of zero values in actual values makes the MAPE infinite, and zero values can maximize the evaluation results of the SMAPE. Thus, when evaluating the accuracy of predictions using the MAPE and SMAPE, the zero values should be removed from the actual values. The result is suitable for every prediction.
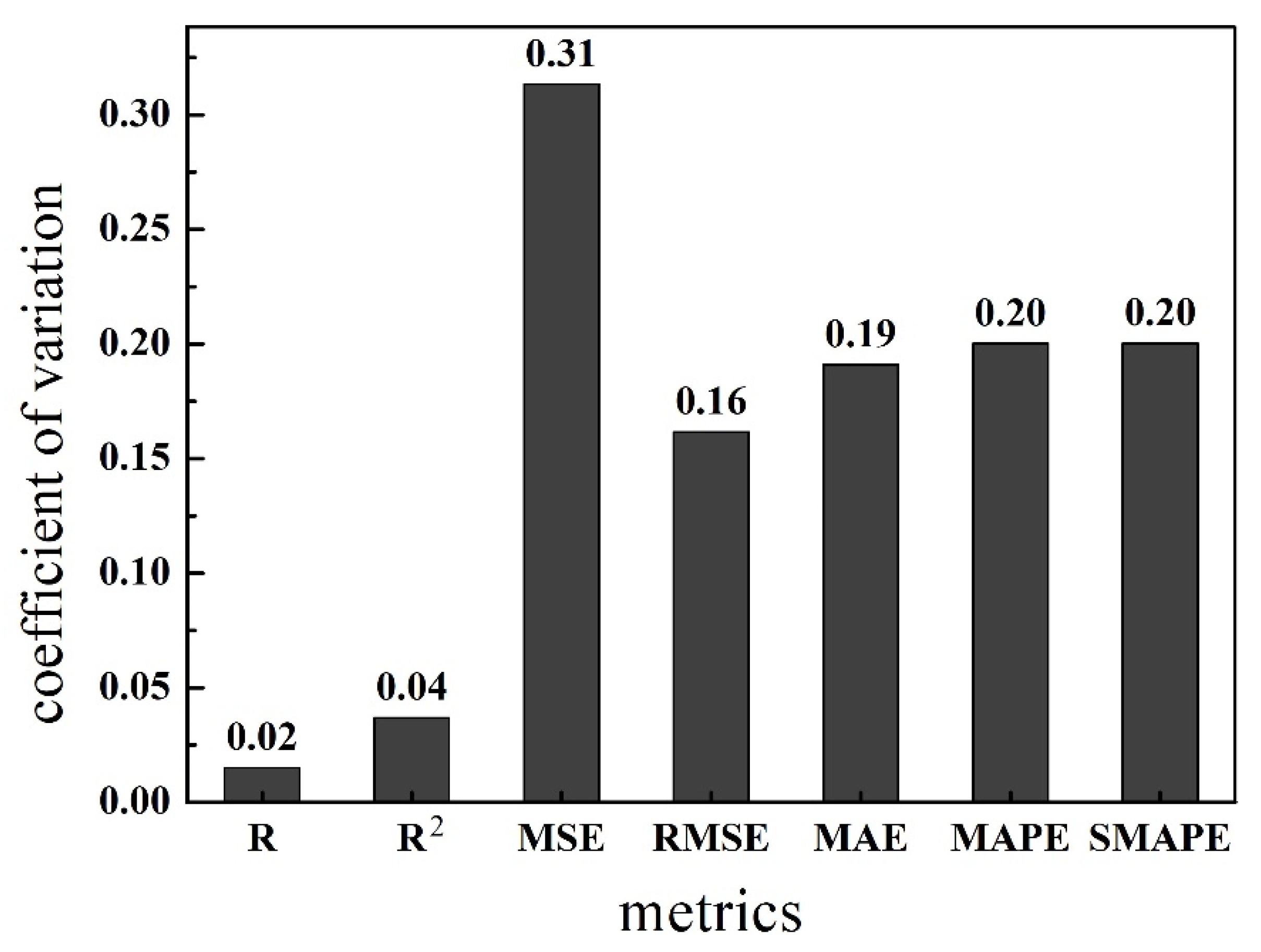
- The sensitivity of the seven accuracy metrics can be ranked as follows: MSE > SMAPE = MAPE > MAE > RMSE > R2 > R. The more sensitive the metric is, the more suitable it is for comparing the accuracy of different predictions. The result is suitable for every prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mao, W.; Aoyama, S.; Towhata, I. Feasibility study of using acoustic emission signals for investigation of pile spacing effect on group pile behavior. Appl. Acoust. 2018, 139, 189–202. [Google Scholar] [CrossRef]
- Mao, W.W.; Towhata, I.; Aoyama, S.; Goto, S. Grain Crushing under Pile Tip Explored by Acoustic Emission. Geotech. Eng. 2016, 47, 164–175. [Google Scholar]
- Vélez, W.; Matta, F.; Ziehl, P. Acoustic emission monitoring of early corrosion in prestressed concrete piles. Struct. Control Health Monit. 2015, 22, 873–887. [Google Scholar] [CrossRef]
- Kumar, K.V.; Saravanan, T.J.; Sreekala, R.; Gopalakrishnan, N.; Mini, K.M. Structural damage detection through longitudinal wave propagation using spectral finite element method. Geomech. Eng. 2017, 12, 161–183. [Google Scholar] [CrossRef]
- Mao, W.; Yang, Y.; Lin, W. An acoustic emission characterization of the failure process of shallow foundation resting on sandy soils. Ultrasonics 2019, 93, 107–111. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Li, S.; Wang, D.; Zhao, G. Damage monitoring of masonry structure under in-situ uniaxial compression test using acoustic emission parameters. Constr. Build. Mater. 2019, 215, 812–822. [Google Scholar] [CrossRef]
- Kim, Y.-M.; Han, G.; Kim, H.; Oh, T.-M.; Kim, J.-S.; Kwon, T.-H. An Integrated Approach to Real-Time Acoustic Emission Damage Source Localization in Piled Raft Foundations. Appl. Sci. 2020, 10, 8727. [Google Scholar] [CrossRef]
- Grosse, C.; Ohtsu, M. Acoustic Emission Testing: Basics for Research-Applications in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Wang, S.; Huang, R.; Ni, P.; Pathegama Gamage, R.; Zhang, M. Fracture Behavior of Intact Rock Using Acoustic Emission: Experimental Observation and Realistic Modeling. Geotech. Test. J. 2013, 36, 903–914. [Google Scholar] [CrossRef] [Green Version]
- Cortés, G.; Suarez Vargas, E.; Gallego, A.; Benavent-Climent, A. Health monitoring of reinforced concrete structures with hysteretic dampers subjected to dynamical loads by means of the acoustic emission energy. Struct. Health Monit. 2018, 18. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic fault analysis of three commutator motors. Mech. Syst. Signal Process. 2019, 133, 106226. [Google Scholar] [CrossRef]
- Arakawa, K.; Matsuo, T. Acoustic Emission Pattern Recognition Method Utilizing Elastic Wave Simulation. Mater. Trans. 2017, 58, 1411–1417. [Google Scholar] [CrossRef]
- Gelman, L.; Kırlangıç, A.S. Novel vibration structural health monitoring technology for deep foundation piles by non-stationary higher order frequency response function. Struct. Control Health Monit. 2020, 27, e2526. [Google Scholar] [CrossRef]
- Zhou, G.; Ji, Y.C.; Chen, X.D.; Zhang, F.F. Artificial Neural Networks and the Mass Appraisal of Real Estate. Int. J. Online Eng. 2018, 14, 180–187. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.-c.; Feng, J.-w. Development and Application of Artificial Neural Network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Anitescu, C.; Atroshchenko, E.; Alajlan, N.; Rabczuk, T. Artificial Neural Network Methods for the Solution of Second Order Boundary Value Problems. Comput. Mater. Contin. 2019, 59, 345–359. [Google Scholar] [CrossRef] [Green Version]
- Benzer, R. Population dynamics forecasting using artificial neural networks. Fresenius Environ. Bull. 2015, 12, 14–26. [Google Scholar]
- Al-Jumaili, S.K.; Pearson, M.R.; Holford, K.M.; Eaton, M.J.; Pullin, R. Acoustic emission source location in complex structures using full automatic delta T mapping technique. Mech. Syst. Signal Process. 2016, 72–73, 513–524. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Dubuc, B.; Salamone, S. A generalizable deep learning framework for localizing and characterizing acoustic emission sources in riveted metallic panels. Mech. Syst. Signal Process. 2019, 130, 248–272. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. Single-Sensor Acoustic Emission Source Localization in Plate-Like Structures Using Deep Learning. Aerospace 2018, 5, 50. [Google Scholar] [CrossRef] [Green Version]
- Hussain, D.; Khan, A.A. Machine learning techniques for monthly river flow forecasting of Hunza River, Pakistan. Earth Sci. Inform. 2020, 13, 939–949. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Polat, K.; Alghoson, A.; Alshdadi, A.A.; Abd El-Latif, A.A. Gaussian process regression (GPR) based non-invasive continuous blood pressure prediction method from cuff oscillometric signals. Appl. Acoust. 2020, 164. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Polat, K.; Alghoson, A.; Alshdadi, A.A.; Abd El-Latif, A.A. A novel blood pressure estimation method based on the classification of oscillometric waveforms using machine-learning methods. Appl. Acoust. 2020, 164. [Google Scholar] [CrossRef]
- Nandy, A. Statistical methods for analysis of Parkinson’s disease gait pattern and classification. Multimed. Tools Appl. 2019, 78, 19697–19734. [Google Scholar] [CrossRef]
- Naz, A.; Javed, M.U.; Javaid, N.; Saba, T.; Alhussein, M.; Aurangzeb, K. Short-Term Electric Load and Price Forecasting Using Enhanced Extreme Learning Machine Optimization in Smart Grids. Energies 2019, 12, 866. [Google Scholar] [CrossRef] [Green Version]
- Qiu, G.Q.; Gu, Y.K.; Chen, J.J. Selective health indicator for bearings ensemble remaining useful life prediction with genetic algorithm and Weibull proportional hazards model. Measurement 2020, 150. [Google Scholar] [CrossRef]
- Popoola, S.I.; Jefia, A.; Atayero, A.A.; Kingsley, O.; Faruk, N.; Oseni, O.F.; Abolade, R. Determination of Neural Network Parameters for Path Loss Prediction in Very High Frequency Wireless Channel. IEEE Access 2019, 7, 150462–150483. [Google Scholar] [CrossRef]
- Kvålseth, T.O. Cautionary Note about R 2. Am. Stat. 1985, 39, 279–285. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Cheng, C.T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef] [Green Version]
- Jamei, M.; Ahmadianfar, I.; Chu, X.F.; Yaseen, Z.M. Prediction of surface water total dissolved solids using hybridized wavelet-multigene genetic programming: New approach. J. Hydrol. 2020, 589. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Deo, R.C. Near real-time significant wave height forecasting with hybridized multiple linear regression algorithms. Renew. Sustain. Energy Rev. 2020, 132, 110003. [Google Scholar] [CrossRef]
- Bucchianico, A.D. Coefficient of Determination (R2). In Encyclopedia of Statistics in Quality and Reliability; John Wiley & Sons, Ltd: New Jersey, NY, USA, 2008. [Google Scholar] [CrossRef]
- Kim, S.; Alizamir, M.; Zounemat-Kermani, M.; Kisi, O.; Singh, V.P. Assessing the biochemical oxygen demand using neural networks and ensemble tree approaches in South Korea. J. Environ. Manag. 2020, 270. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J. Another Look at Forecast Accuracy Metrics for Intermittent Demand. Foresight Int. J. Appl. Forecast. 2006, 4, 43–46. [Google Scholar]
- Sanders, N.R. Measuring forecast accuracy: Some practical suggestions. Prod. Inventory Manag. J. 1997, 38, 43–46. [Google Scholar]
- Flores, B.E. A pragmatic view of accuracy measurement in forecasting. Omega 1986, 14, 93–98. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, Y.C. Application of Artificial Neural Network Over Nickel-Based Catalyst for Combined Steam-Carbon Dioxide of Methane Reforming (CSDRM). J. Nanoence Nanotechnol. 2020, 20, 5716–5719. [Google Scholar] [CrossRef] [PubMed]
- Rakićević, Z.; Vujosevic, M. Focus forecasting in supply chain: The Case study of fast moving consumer goods company in Serbia. Serb. J. Manag. 2014, 10. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, J.S.; Collopy, F. Error measures for generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Khac Le, H.; Kim, S. Machine Learning Based Energy-Efficient Design Approach for Interconnects in Circuits and Systems. Appl. Sci. 2021, 11, 915. [Google Scholar] [CrossRef]
- Wu, P.; Che, A. Spatiotemporal Monitoring and Evaluation Method for Sand-Filling of Immersed Tube Tunnel Foundation. Appl. Sci. 2021, 11, 1084. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J.; Liu, Y.; Ma, D.; Li, M.; Xiang, B. Comparison of GA-BP and PSO-BP neural network models with initial BP model for rainfall-induced landslides risk assessment in regional scale: A case study in Sichuan, China. Nat. Hazards J. Int. Soc. Prev. Mitig. Nat. Hazards 2020, 100, 173–204. [Google Scholar] [CrossRef]
- Silitonga, P.; Bustamam, A.; Muradi, H.; Mangunwardoyo, W.; Dewi, B.E. Comparison of Dengue Predictive Models Developed Using Artificial Neural Network and Discriminant Analysis with Small Dataset. Appl. Sci. 2021, 11, 943. [Google Scholar] [CrossRef]
- Pimentel-Mendoza, A.B.; Rico-Pérez, L.; Rosel-Solis, M.J.; Villarreal-Gómez, L.J.; Vega, Y.; Dávalos-Ramírez, J.O. Application of Inverse Neural Networks for Optimal Pretension of Absorbable Mini Plate and Screw System. Appl. Sci. 2021, 11, 1350. [Google Scholar] [CrossRef]
- Pandey, S.; Hindoliya, D.A.; Mod, R. Artificial neural networks for predicting indoor temperature using roof passive cooling techniques in buildings in different climatic conditions. Appl. Soft Comput. 2012, 12, 1214–1226. [Google Scholar] [CrossRef]



| Operating Specifications | Value | |
|---|---|---|
| Dynamic | Peak Sensitivity, Ref V(m/s) | 124 dB |
| Operating Frequency Range | 1–30 kHz | |
| Resonant Frequency, Ref V(m/s) | 20 kHz | |
| Environmental | Temperature Range | −35 °C–−75 °C |
| Shock Limit | 500 g | |
| Physical | Dimensions | 28.6 mm OD × 50 mm H |
| Weight | 121 g | |
| Electrical | Gain | 40 dB |
| Power requirements | 20–30 VDC @ 25 mA | |
| Dynamic Range | >87 dB | |
| Algorithm | Description |
|---|---|
| TRAINBFG | It is a network training algorithm that updates weight and bias values in terms of the BFGS quasi-Newton method. |
| TRAINCGB | It is a network training algorithm that updates weight and bias values in terms of the conjugate gradient backpropagation with Powell-Beale restarts. |
| TRAINCGP | It is a network training algorithm that updates weight and bias values in terms of conjugate gradient backpropagation with Polak-Ribiére updates. |
| TRAINGLM | It is a network training algorithm that updates weight and bias values in terms of Levenberg-Marquardt optimization. |
| TRAINRP | It is a network training algorithm that updates weight and bias values in terms of the resilient backpropagation algorithm (Rprop). |
| TRAINSCG | It is a network training algorithm that updates weight and bias values in terms of the scaled conjugate gradient method. |
| Algorithm | R | R2 | MSE (cm2) | RMSE (cm) | MAE (cm) |
|---|---|---|---|---|---|
| TRAINBFG | 0.9449 | 0.8760 | 552.03 | 23.49 | 19.38 |
| TRAINCGB | 0.9480 | 0.8784 | 526.19 | 22.94 | 19.01 |
| TRAINCGP | 0.9314 | 0.8499 | 685.03 | 26.17 | 21.84 |
| TRAINGLM | 0.9690 | 0.9318 | 315.45 | 17.76 | 13.62 |
| TRAINRP | 0.9531 | 0.8909 | 475.50 | 21.81 | 17.79 |
| TRAINSCG | 0.9458 | 0.8709 | 548.59 | 23.42 | 19.42 |
| Group | R | R2 | MPAE (Include Zero Values) | MAPE (Remove Zero Values) | SMAPE (Include Zero Values) | SMAPE (Remove Zero Values) |
|---|---|---|---|---|---|---|
| TRAINBFG | 0.9449 | 0.8760 | Infinite | 21.35 % | 58.09 % | 21.65 % |
| TRAINCGB | 0.9480 | 0.8784 | Infinite | 20.34 % | 56.94 % | 20.20 % |
| TRAINCGP | 0.9314 | 0.8499 | Infinite | 25.02 % | 62.12 % | 26.71 % |
| TRAINGLM | 0.9690 | 0.9318 | Infinite | 14.61 % | 52.94 % | 15.17 % |
| TRAINRP | 0.9531 | 0.8909 | Infinite | 19.39 % | 56.35 % | 19.46 % |
| TRAINSCG | 0.9458 | 0.8709 | Infinite | 21.17 % | 57.68 % | 21.13 % |
| Group | R | R2 | MSE (cm2) | RMSE (cm) | MAE (cm) |
|---|---|---|---|---|---|
| Group 1 | 0.9752 | 0.9443 | 249.02 | 15.78 | 12.77 |
| Group 2 | 0.9613 | 0.9190 | 402.15 | 20.05 | 15.12 |
| Group 3 | 0.9690 | 0.9318 | 315.45 | 17.76 | 13.62 |
| Group | R | R2 | MAPE (Including Zero Values) | MAPE (Remove Zero Values) | SMAPE (Including Zero Values) | SMAPE (Remove Zero Values) |
|---|---|---|---|---|---|---|
| Group 1 | 0.9752 | 0.9443 | Infinite | 14.27% | 52.02% | 15.07% |
| Group 2 | 0.9613 | 0.9190 | Infinite | 17.16% | 56.17% | 18.05% |
| Group 3 | 0.9690 | 0.9318 | Infinite | 14.61% | 52.94% | 15.17% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jierula, A.; Wang, S.; OH, T.-M.; Wang, P. Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Appl. Sci. 2021, 11, 2314. https://doi.org/10.3390/app11052314
Jierula A, Wang S, OH T-M, Wang P. Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Applied Sciences. 2021; 11(5):2314. https://doi.org/10.3390/app11052314
Chicago/Turabian StyleJierula, Alipujiang, Shuhong Wang, Tae-Min OH, and Pengyu Wang. 2021. "Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data" Applied Sciences 11, no. 5: 2314. https://doi.org/10.3390/app11052314
APA StyleJierula, A., Wang, S., OH, T.-M., & Wang, P. (2021). Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Applied Sciences, 11(5), 2314. https://doi.org/10.3390/app11052314







