Multiple-Criteria Fuzzy Optimization of the Heat Treatment Processes for Two Steel Rolled Products
Abstract
:1. Introduction
- Aggregated presentation of local criteria under different types of uncertainty.Local criteria can be built based on measured parameters, such as technological ones, or with the use of expert subjective estimations, e.g., a verbal assessment of the investment project’s scientific or innovative levels. The known property of people’s thinking is that experts usually try to provide estimates at the verbal level of consideration, avoiding quantitative ones, as they their opinions are unreliable. Therefore, the problem of the synthesized treatment of local criteria characterized by different types of uncertainty becomes actual [1,2,3,4].However, people’s experience and intuition are very important in the formulation of optimization tasks, and should not be lost in analysis. Of course, uncertainty is an inevitable component of such types of information, which should not be ignored; on the contrary, it should be studied carefully, evaluated and included in the optimization process. This uncertainty is of subjective nature. Therefore, it cannot adequately be presented by means of a traditional probabilistic approach. Therefore, a justified methodology, providing an opportunity for synthesized assessments of uncertainty factors, that makes it possible to design comparable local criteria based on measurable quantitative parameters as well as verbal assessments, is needed.To solve this problem, the methods of the fuzzy set theory, developed for dealing with uncertainties of a subjective origin, may be used with great efficiency. Therefore, in real-world optimization problems, we deal with two groups of local criteria: objective criteria based on measured parameters, and subjective criteria based on the verbal expert assessments. Therefore, we have a problem in the development of an appropriate common quantitative scale for representing objective and subjective criteria;
- Generalization of experts opinions.In the formulation of especially important fuzzy optimization tasks, groups of experts from corresponding fields are often involved in defining the membership functions of the local criteria used, and their relative importance (weights). To aggregate experts’ opinions, the methods developed in the framework of the Group Multiple-Criteria Decision-Making group (MCDM) [5,6,7] may successfully be applied. These methods provide a compromise between expert assessments, including the cases when they are presented in a verbal form. The modern methods of the hesitant fuzzy set theory [8] may be applied when different numbers of experts can be invited to define the local criteria or their weights [9];
- Local criteria aggregation.The real-world optimization problems can involve broad sets of local criteria that need to be analyzed simultaneously in each step of an optimization process. It is clear that the corresponding optimizing algorithm should somewhat reflect human possibilities to make this analysis. Unfortunately, a person’s ability to carry out such an analysis is severely limited by the well-known, strict, experimentally justified law of applied psychology, according to which a person can discern no more than 7 or minus 2 classes or grades on any scale of characteristics. If the number of classes is greater than this, neighboring classes begin to merge and cannot confidently be distinguished [10,11]. To solve this problem, an appropriate method for the aggregation of local criteria, taking their weights into account, can be applied to build a generalized criterion. Therefore, the problem of choosing a relevant aggregation method is of continuing interest, since it is directly related to the practical optimization problems. The most-used aggregation method is the weighted sum. This is used in many known optimization models as it is the simplest (linear) approach, but, regrettably, is often used often without any previous critical analysis.On the other hand, in some areas, e.g., environmental modeling, the weighted sum aggregation is forbidden from use [12]. The reason for this is that, in practice, there are cases when, if any of the local criteria are completely unsatisfied, the alternative in question may be excluded from consideration altogether, although the values of other criteria may be great enough to recompensate the zero value of the single criterion. Therefore, when solving a complex problem with a large number of local criteria, it seems justified to use all possible aggregating modes that are relevant to the problem at hand. If the results obtained using different aggregation methods are similar, then this fact can be considered as a good confirmation of their optimality. Otherwise, an additional analysis of local criteria and their ranking should be carried out;
- Local criteria weights’ establishment.First, based on our experience, we can say that if an expert considers local criteria to be of equal importance, this usually only means that he/she is not competent enough. In cases when we are dealing with a small number (2 or 3) of local criteria, their weights can be direcly established by an expert based on his/her experience and intuition, but if we have more criteria, then, due to the abovementioned psychological law, an expert begins to experience serious difficulties in determining the weights of the criteria. Therefore, the methods based on linguistic pairwise comparison matrices are currently used to obtain the real-valued [13,14] or fuzzy weights of local criteria [15,16];
- Generalization of aggregation modes.A natural consequence of problem 3 is the growing interest in methods for generalization (convolution) aggregating operators [17]. For this purpose, the use of the theory of possibilities [18], the weighted sum aggregation of aggregating modes [19] and the methods of soft sets’ theory are proposed [20]. In [21], a critical analysis of the known approaches to the aggregation of aggregating modes is provided and a new method, based on the synthesis of type 2 and level 2 fuzzy sets, which is free of the revealed drawbacks of existing approaches, is developed. This method was successfully used for the solution of the fuzzy multiple-objective optimization problem in logistic [22];
- Comparing the fuzzy values.
2. Informal Presentation of the Problem
3. Fuzzy Multiple-Criteria Optimization of Heat-Technological Processes in the Rolled Steel Production
- Creating a mathematical model of a process, with parameters characterizing the process quality as outputs, and inputs which are technological parameters defining the process quality. If the values of all input and output parameters can be directly measured, such a model can be obtained using the data of a passive production experiment, i.e., recording data continuously coming from the automatic control system and the factory laboratory. Then, these data are used to obtain, by statistical methods, a regression model defining the dependencies of output parameters on input ones.In many cases, the parameters that determine the quality cannot be directly measured, such as, for example, the temperature in the center of the heated ingot or the thermal stresses in it. To estimate the values of such parameters, complex systems of non-stationary differential equations in finite differences solved by numerical methods are used. Usually, the values of some important parameters of such models, such as, for example, the coefficients of heat exchange with the external environment, are not known in advance. However, their values can be found by parametric identification, i.e., by determining the values that minimize the discrepancies between the calculated data and the data of the industrial experiment. Note that industrial experiments are usually very expensive, but they are easily paid off after the setting of optimal technological modes.Nevertheless, even the “precise” mathematical model obtained after identification, based on a complex system of differential equations in finite differences, is not very convenient for the frequent solution of optimization problems due to the too-high machine-time expenses needed for calculations by the model. To reduce expenses for optimization, the initial “precise” model is considered to be a real process, and a certain number of numerical experiments (calculations made for predefined different values of input parameters) are provided according to the defined plan of the numerical experiment. Based on the obtained results and using statistical methods, the simple polynomial regression model representing the dependence of the output parameters on the input ones is finally inferred. This model is simple enough to be used for optimization;
- Establishment of the membership functions of local criteria based on actual technological instructions, as well as on the experience and intuition of technologists;
- Calculation of the local criteria’s relative importance (weights) based on the linguistic pairwise comparisons matrix using the method developed in [29];
- Choice of an appropriate method for the local criteria aggregation or a set of relevant methods to build a compromise general criterion;
- Solution of the optimization task based on the maximization of a general criterion.This methodology can be applied to the optimization of a wide range of technologies, not only to those based on heat transfer processes.
3.1. The Simulation, Parametric Identification and Fuzzy Multiple-Criteria Optimization of the Heating Steel Ingots for the Rolling Process
- Two-dimensional nonlinear equation of the non-stationary heat transfer in partial derivatives with boundary conditions of the third and fourth kind;
- equation for calculating the thickness of the formed scale;
- The system of equations for calculating thermal stresses.
3.2. Fuzzy Multiple-Criteria Optimization of the Wire Rod Heat Treatment Process
- Relative water consumption in water-cooling sections , , , measured as a percentage of the maximum flow rate when the injectors are fully engaged;
- Speed of movement of turns on the conveyor ;
- The relative amount of air pumped by the fans and measured in fractions of the maximum possible amount;
- The degree of cooling , equal to the proportion of closed thermal insulation covers.
- Tensile strength ;
- The relative narrowing ;
- Relative elongation ;
- Grain size d;
- The relative thickness of the decarburized layer .
4. Conclusions
- Creating a mathematical model of a process, with parameters characterizing the process quality as outputs, and inputs which are technological parameters defining the process quality. If the values of all input and output parameters can be directly measured, such a model can be obtained using the data of the passive production experiment, i.e., recording data continuously coming from the automatic control system and the factory laboratory. Then, these data are used to obtain, by means of statistical methods, a regression model defining the dependencies of output parameters on input ones.In many cases, the parameters that determine quality cannot be directly measured, such as, for example, the temperature in the center of the heated ingot or the thermal stresses in it. To estimate the values of such parameters, complex systems of non-stationary differential equations in finite differences solved by numerical methods are used. Usually, the values of some important parameters of such models, e.g., the coefficients of heat exchange with the external environment, are not known in advance. However, these values can be found by parametric identification, i.e., by determining the values that minimize the discrepancies between the calculated data and the data of the industrial experiment;
- Establishment of the membership functions of local criteria based on actual technological instructions as well as on the experience and intuition of technologists;
- Calculation of the local criterias relative importance (weights) based on the linguistic pairwise comparisons matrix;
- Choice of an appropriate method for the local criteria aggregation or a set of relevant methods to build a compromise general criterion;
- Solution to the optimization task based on the maximization of a general criterion.The effectiveness of this methodology is illustrated by the solutions of two different fuzzy multiple-criteria optimization problems concerned with the heat-treatment processes for two steel-rolled products. These processes are components of the overall technological chain in the “Belorussian Metallurgical Mini Plant”.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bamber, N.; Turner, I.; Arulnathan, V.; Li, Y.; Zargar Ershadi, S.; Smart, A.; Pelletier, N. Comparing sources and analysis of uncertainty in consequential and attributional life cycle assessment: Review of current practice and recommendations. Int. J. Life Cycle Assess. 2020, 25, 168–180. [Google Scholar] [CrossRef] [Green Version]
- Uusitalo, L.; Lehikoinen, A.; Helle, I.; Myrberg, K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environ. Model. Softw. 2015, 63, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Toth, W.; Vacik, H. A comprehensive uncertainty analysis of the analytic hierarchy process methodology applied in the context of environmental decision making. J. Multi Criteria Decis. Anal. 2018, 25, 142–161. [Google Scholar] [CrossRef]
- Super, I.; Dellaert, S.N.C.; Visschedijk, A.J.H.; Denier van der Gon, H.A.C. Uncertainty analysis of a European high-resolution emission inventory of CO2 and CO to support inverse modelling and network design. Atmos. Chem. Phys. 2020, 20, 1795–1816. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.S.; Nepal, M.P.; Skitmore, M. Modified fuzzy group decision-making approach to cost overrun risk assessment of power plant projects. J. Constr. Eng. Manag. 2019, 145, 04018126. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Yeh, C.-H.; Chang, Y.-W. A new method selection approach for fuzzy group multicriteria decision making. Appl. Soft Comput. 2013, 13, 2179–2187. [Google Scholar] [CrossRef]
- Wang, Y.; Chu, J.; Liu, Y. Multi-Criteria Pythagorean Fuzzy Group Decision Approach Based on Social Network Analysis. Symmetry 2020, 12, 255. [Google Scholar] [CrossRef] [Green Version]
- Sevastjanov, P.; Dymova, L. Generalised operations on hesitant fuzzy values in the framework of Dempster-Shafer theory. Inf. Sci. 2015, 311, 39–58. [Google Scholar] [CrossRef]
- Meng, F.; Chen, S.-M.; Zhang, S. Group decision making based on acceptable consistency analysis of interval linguistic hesitant fuzzy preference relations. Inf. Sci. 2020, 530, 66–84. [Google Scholar] [CrossRef]
- Miller, G.A. The magical number seven plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cowan, N. George Miller’s magical number of immediate memory in retrospect: Observations on the faltering progression of science. Psychol. Rev. 2015, 122, 536–541. [Google Scholar] [CrossRef]
- Silvert, W. Ecological impact classification with fuzzy sets. Ecol. Model. 1997, 96, 1–10. [Google Scholar] [CrossRef]
- Aragon, T.J. Deriving Criteria Weights for Health Decision Making: A Brief Tutorial; UC Berkeley, School of Public Health: Berkeley, CA, USA, 2017. [Google Scholar]
- Ramík, J. Pairwise Comparisons Method. Theory and Applications in Decision Making; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Entani, T. Estimating fuzzy weight vector from interval pairwise comparison matrix with various processed matrices. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Yuen, K.K.F. The fuzzy cognitive pairwise comparisons for ranking and grade clustering to build a recommender system: An application of smartphone recommendation. Eng. Appl. Artif. Intell. 2017, 61, 136–151. [Google Scholar] [CrossRef] [Green Version]
- Roubens, M. Fuzzy sets and decision analysis. Fuzzy Sets Syst. 1997, 90, 199–206. [Google Scholar] [CrossRef]
- Dubois, D.; Koenig, J.L. Social choice axioms for fuzzy set aggregation. Fuzzy Sets Syst. 1991, 43, 257–274. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Xiao, Z.; Kuang, T.; Rong, T. The Aggregation of Aggregating Methods in MCDM Based on the Fuzzy Soft Sets. In Proceedings of the 2010 Second WRI Global Congress on Intelligent Systems, Wuhan, China, 16–17 December 2010; pp. 135–138. [Google Scholar]
- Sevastjanov, P.; Figat, P. Aggregation of aggregating modes in MCDM: Synthesis of Type 2 and Level 2 fuzzy sets. Omega 2007, 35, 505–523. [Google Scholar] [CrossRef]
- Kaczmarek, K.; Dymova, L.; Sevastjanov, P. A two phase method for solving the distribution problem in a fuzzy setting. Entropy 2019, 21, 1214. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Kerre, E.E. Reasonable properties for the ordering of fuzzy quantities (I) (II). Fuzzy Sets Syst. 2001, 112, 387–405. [Google Scholar] [CrossRef]
- Wang, Y.M.; Yang, J.B.; Xu, D.L. A preference aggregation method through the estimation of utility intervals. Comput. Oper. Res. 2005, 32, 2027–2049. [Google Scholar] [CrossRef]
- Yager, R.R.; Detyniecki, M. Ranking fuzzy numbers using a-weighted valuations international journal of uncertainty. Fuzziness Knowl. Based Syst. 2000, 8, 573–591. [Google Scholar]
- Sevastjanov, P. Numerical methods for interval and fuzzy number comparison based on the probabilistic approach and Dempster-Shafer theory. Inf. Sci. 2007, 177, 4645–4661. [Google Scholar] [CrossRef]
- Harington, J. The Desirability Function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Zadeh, L. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Chu, A.; Kalaba, R.; Springarn, R. A comparison of two methods for determining the weights of belonging to fuzzy sets. J. Optim. Theory Appl. 1979, 27, 531–538. [Google Scholar] [CrossRef]
- Dymova, L.; Kaczmarek, K.; Sevastjanov, P.; Kulawik, J. A fuzzy multiple criteria decision making approach with a complete user friendly computer implementation. Entropy 2021, 23, 203. [Google Scholar] [CrossRef] [PubMed]
- Dymova, L.; Kaczmarek, K.; Sevastjanov, P.; Sułkowski, Ł.; Przybyszewski, K. An approach to generalization of the intuitionistic fuzzy TOPSIS method in the framework of evidence theory. J. Artif. Intell. Soft Comput. Res. 2021, 11, 157–175. [Google Scholar] [CrossRef]
- Dymova, L.; Sewastianow, P.; Sewastianow, D. MCDM in a fuzzy setting: Investment projects assessment application. Int. J. Prod. Econ. 2006, 100, 10–29. [Google Scholar] [CrossRef]
- Törn, A.; Žilinskas, A. Global optimization. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1989; Volume 350. [Google Scholar]
- Ali, M.M.; Törn, A. Population set-based global algorithms: Some modifications and numerical studies. Comput. Oper. Res. 2004, 31, 1703–1725. [Google Scholar] [CrossRef] [Green Version]


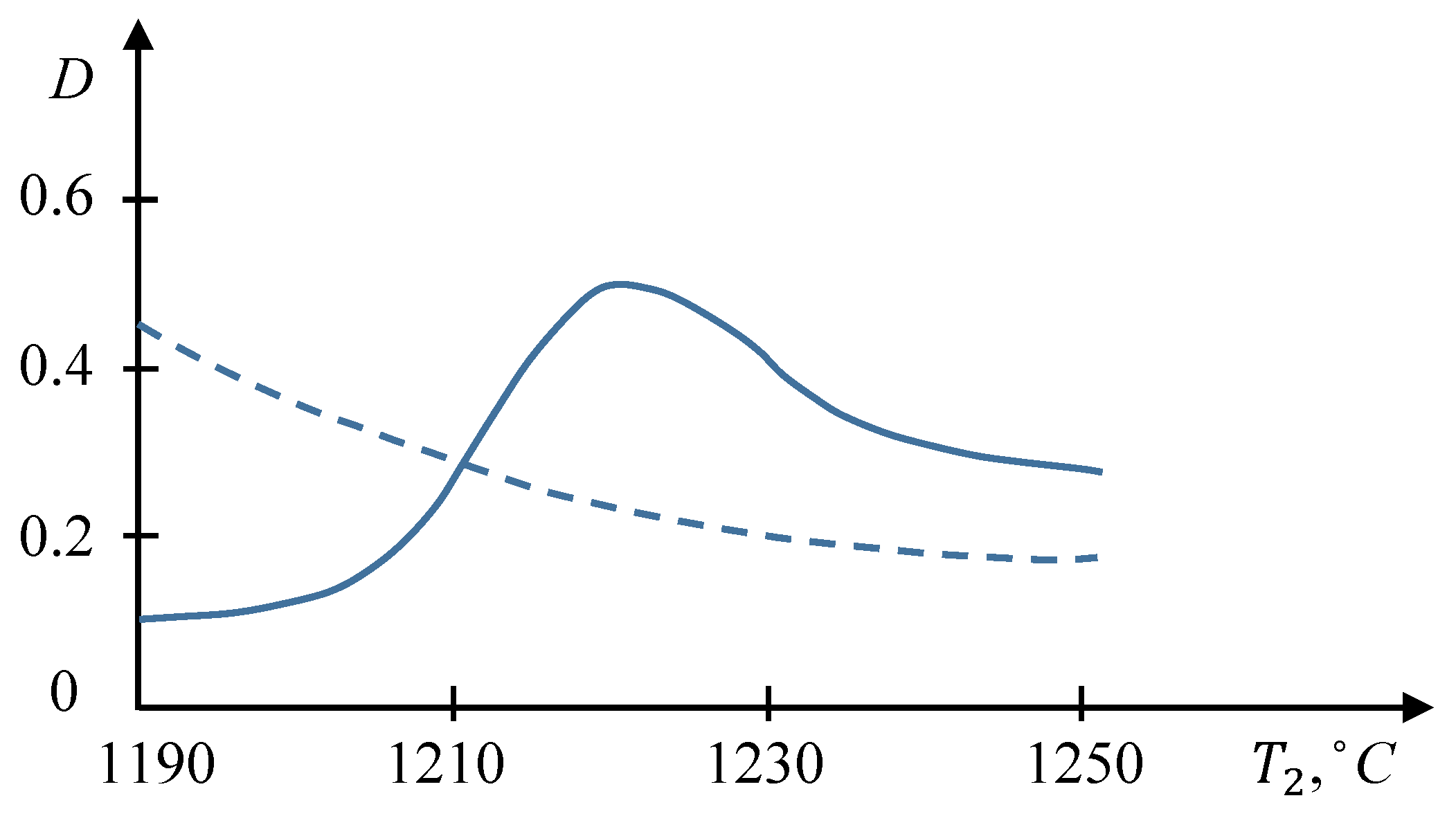
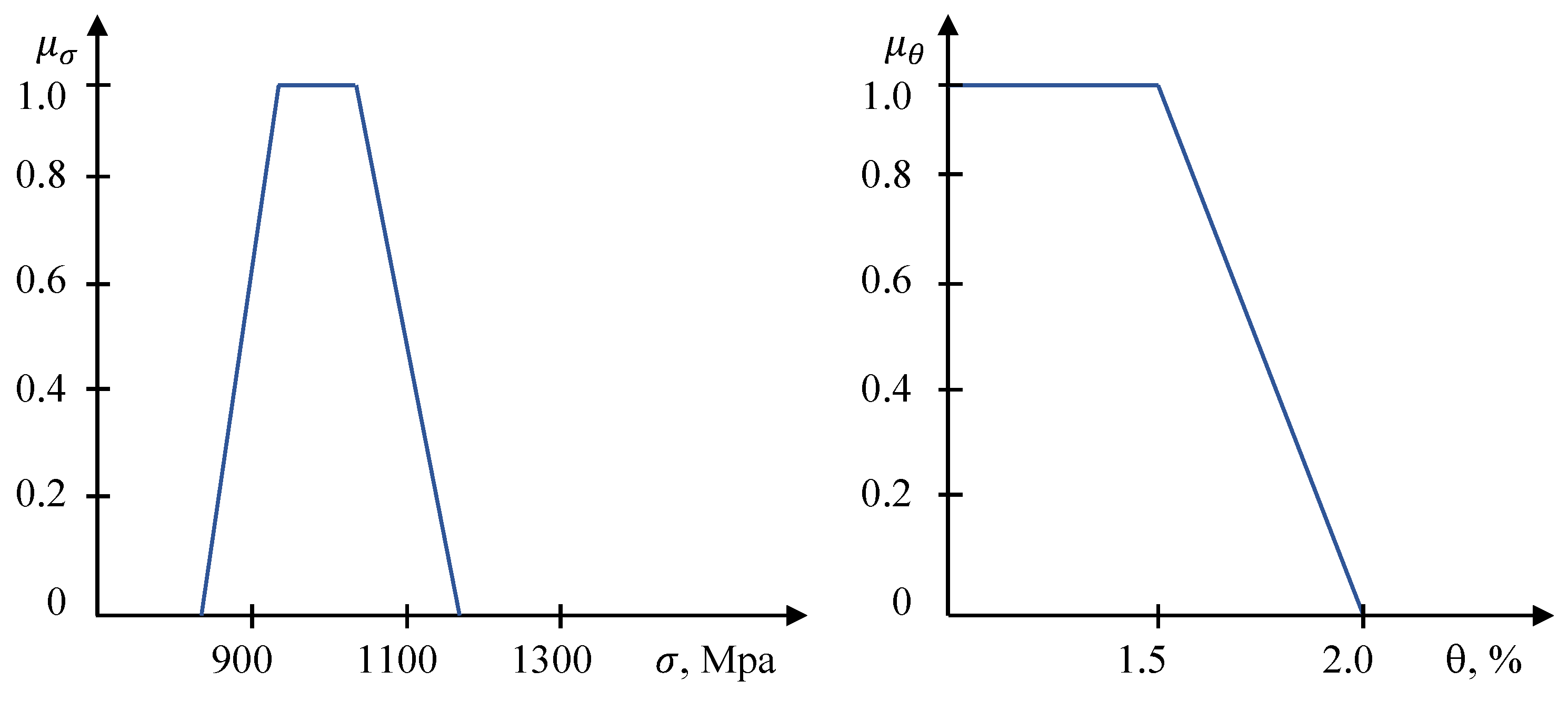
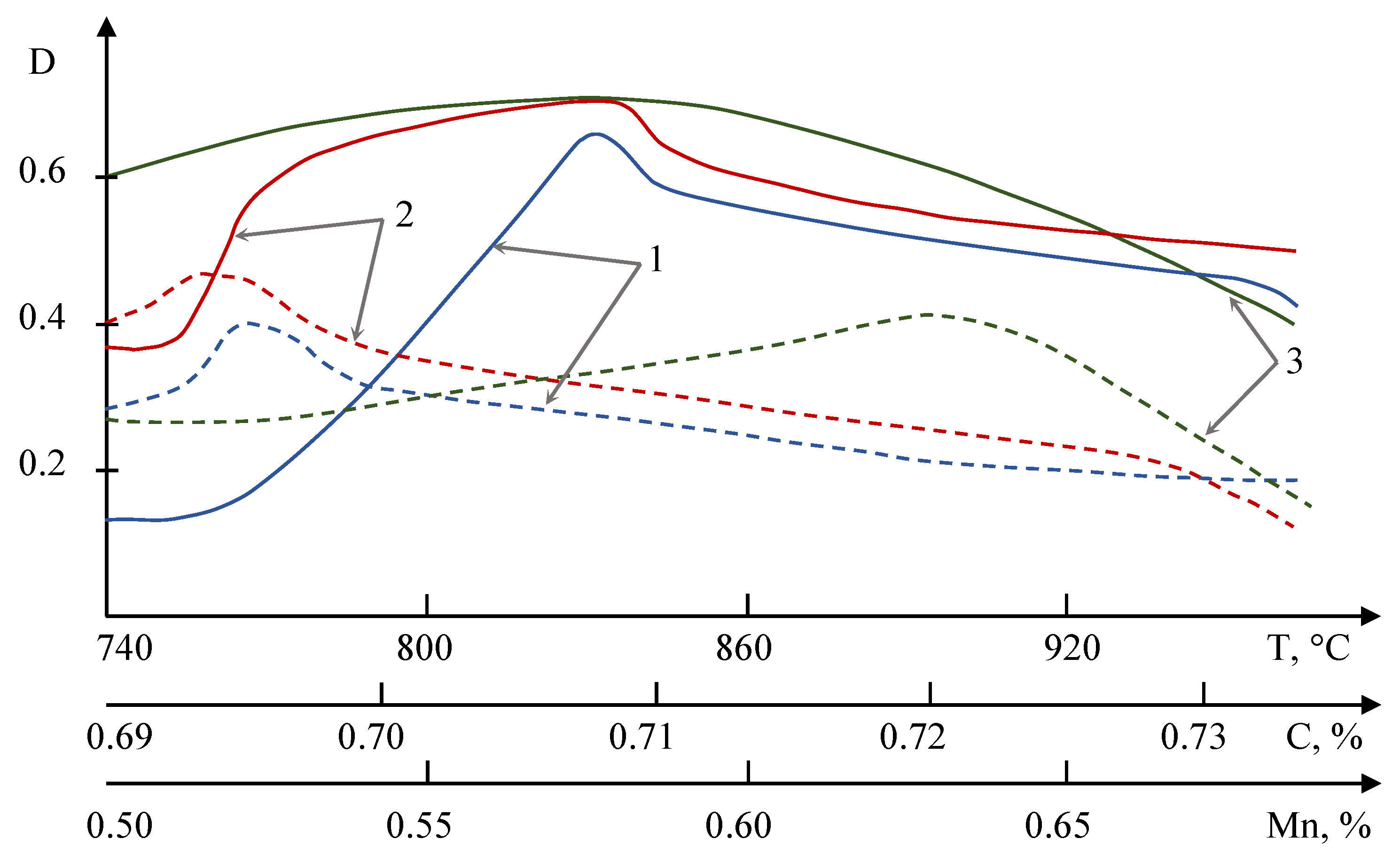

| P, t/h | , °C | , °C | , °C | , MM | T, °C | , °C | D | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 60 | 100 | 1194 | 1242 | 1.33 | 1206 | 9.41 | 0.91 | 0.85 | 0.56 | 0.46 |
| 200 | 1134 | 1257 | 1.46 | 1207 | 9.29 | 0.82 | 0.82 | 0.56 | 0.46 | |
| 300 | 976 | 1249 | 1.63 | 1193 | 1.64 | 0.69 | 1 | 0.97 | 0.46 | |
| 400 | 1011 | 1221 | 1.71 | 1189 | 1.22 | 0.63 | 0.99 | 0.99 | 0.48 | |
| 80 | 100 | 1245 | 1260 | 1.34 | 1204 | 4.44 | 0.90 | 0.89 | 0.82 | 0.98 |
| 200 | 1299 | 1236 | 1.39 | 1203 | 2.63 | 0.85 | 0.92 | 0.91 | 0.92 | |
| 300 | 1076 | 1275 | 1.76 | 1193 | 1.45 | 0.59 | 1 | 0.48 | 0.47 | |
| 400 | 1072 | 1262 | 1.66 | 1189 | 0.62 | 0.67 | 0.98 | 1 | 0.76 |
| Criterium | d | C | Mn | ||||
|---|---|---|---|---|---|---|---|
| 2.64 | 1.65 | 1.00 | 0.69 | 0.45 | 0.32 | 0.25 | |
| 1.00 | 0.76 | 0.76 | 0.73 | 0.37 | 0.76 | 0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dymova, L.; Kaczmarek, K.; Sevastjanov, P. Multiple-Criteria Fuzzy Optimization of the Heat Treatment Processes for Two Steel Rolled Products. Appl. Sci. 2021, 11, 2324. https://doi.org/10.3390/app11052324
Dymova L, Kaczmarek K, Sevastjanov P. Multiple-Criteria Fuzzy Optimization of the Heat Treatment Processes for Two Steel Rolled Products. Applied Sciences. 2021; 11(5):2324. https://doi.org/10.3390/app11052324
Chicago/Turabian StyleDymova, Ludmila, Krzysztof Kaczmarek, and Pavel Sevastjanov. 2021. "Multiple-Criteria Fuzzy Optimization of the Heat Treatment Processes for Two Steel Rolled Products" Applied Sciences 11, no. 5: 2324. https://doi.org/10.3390/app11052324








