Modeling the Dynamic Behavior of a Pilot-Operated Solenoid Valve for an Ultra-High Pressure Vessel
Abstract
:1. Introduction
2. Modeling the Solenoid Motion
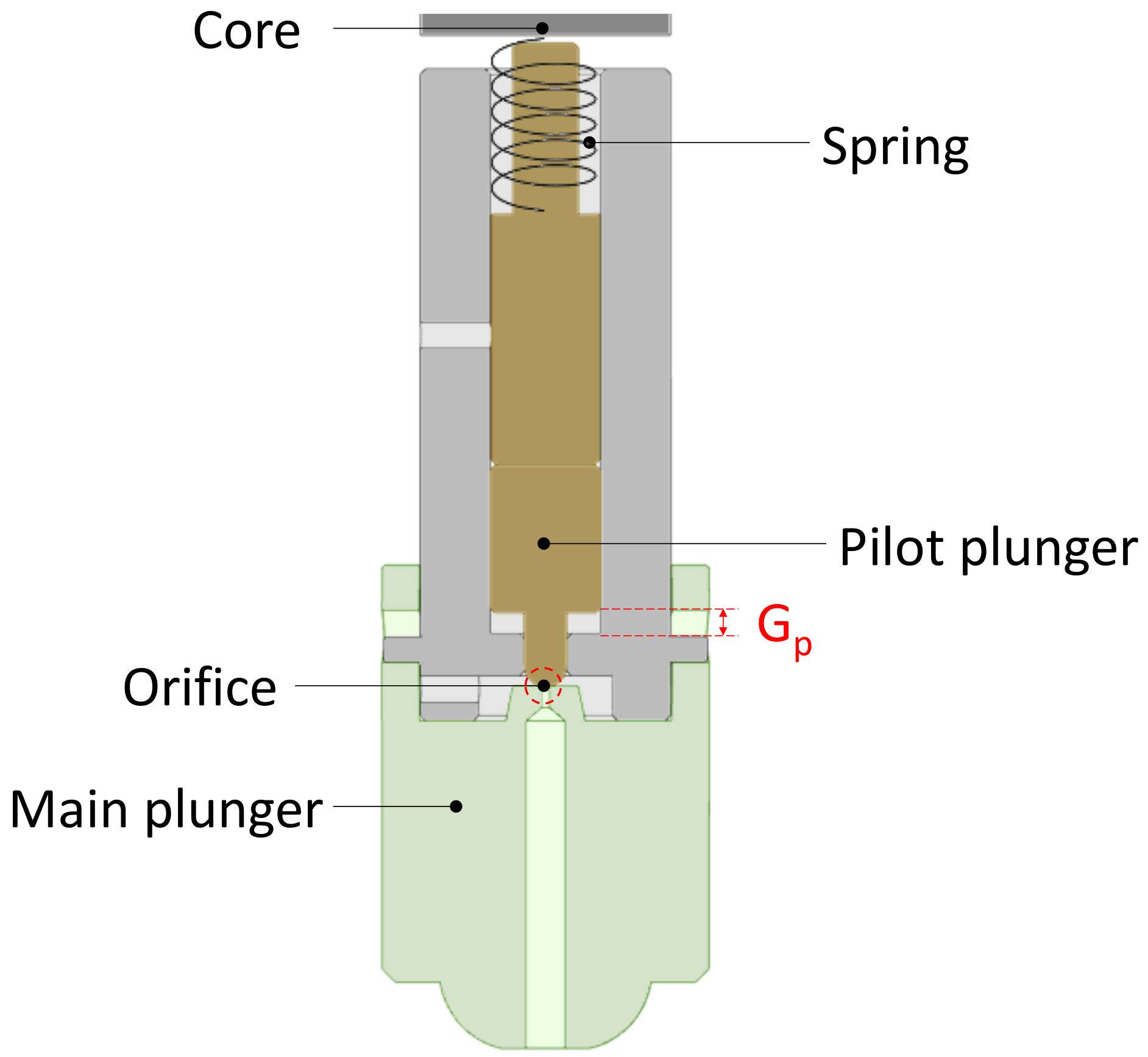
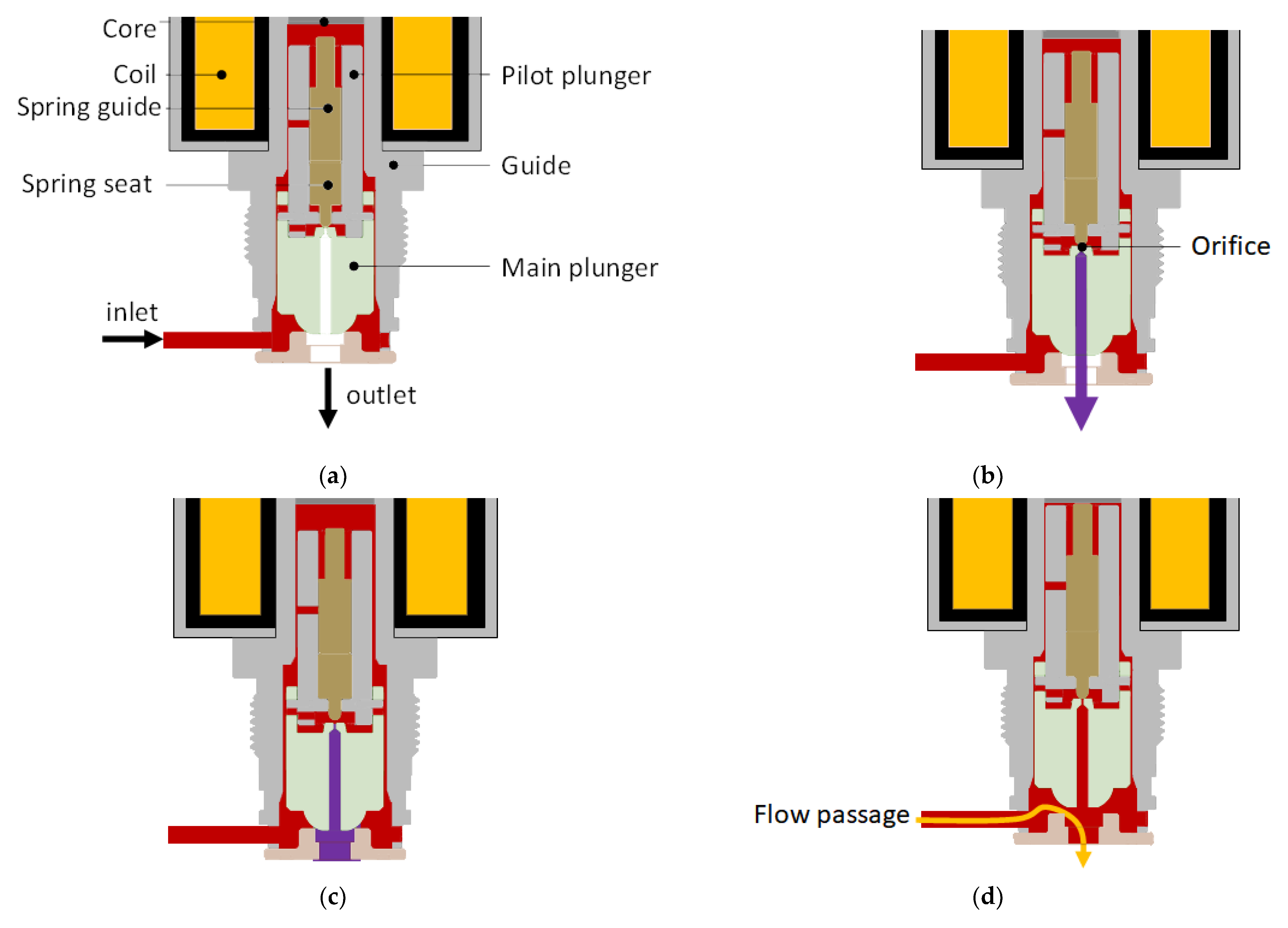
2.1. Structure of the Pilot-Operated Solenoid Valve
2.2. Multi-Step of the Pilot-Operated Solenoid Valve
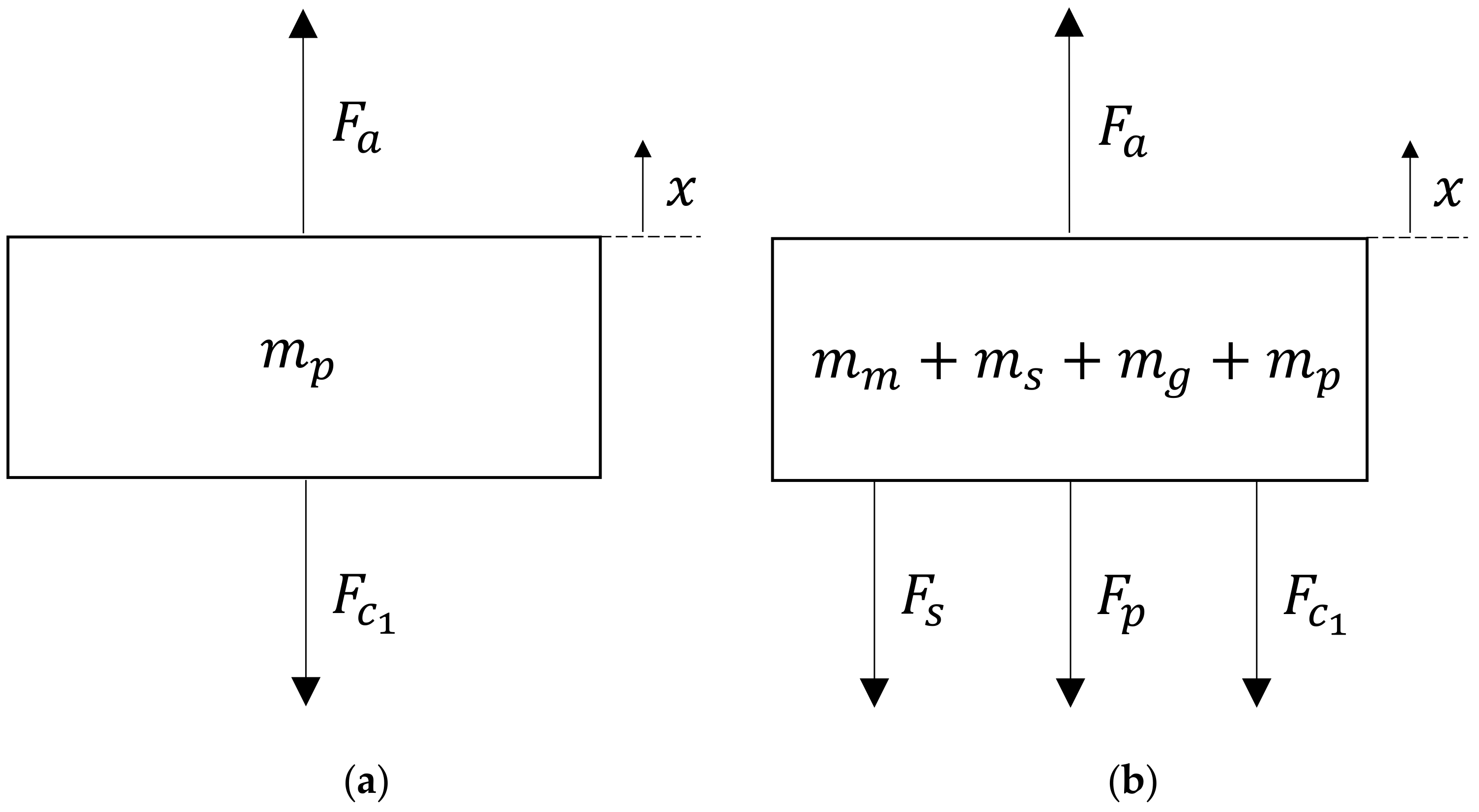
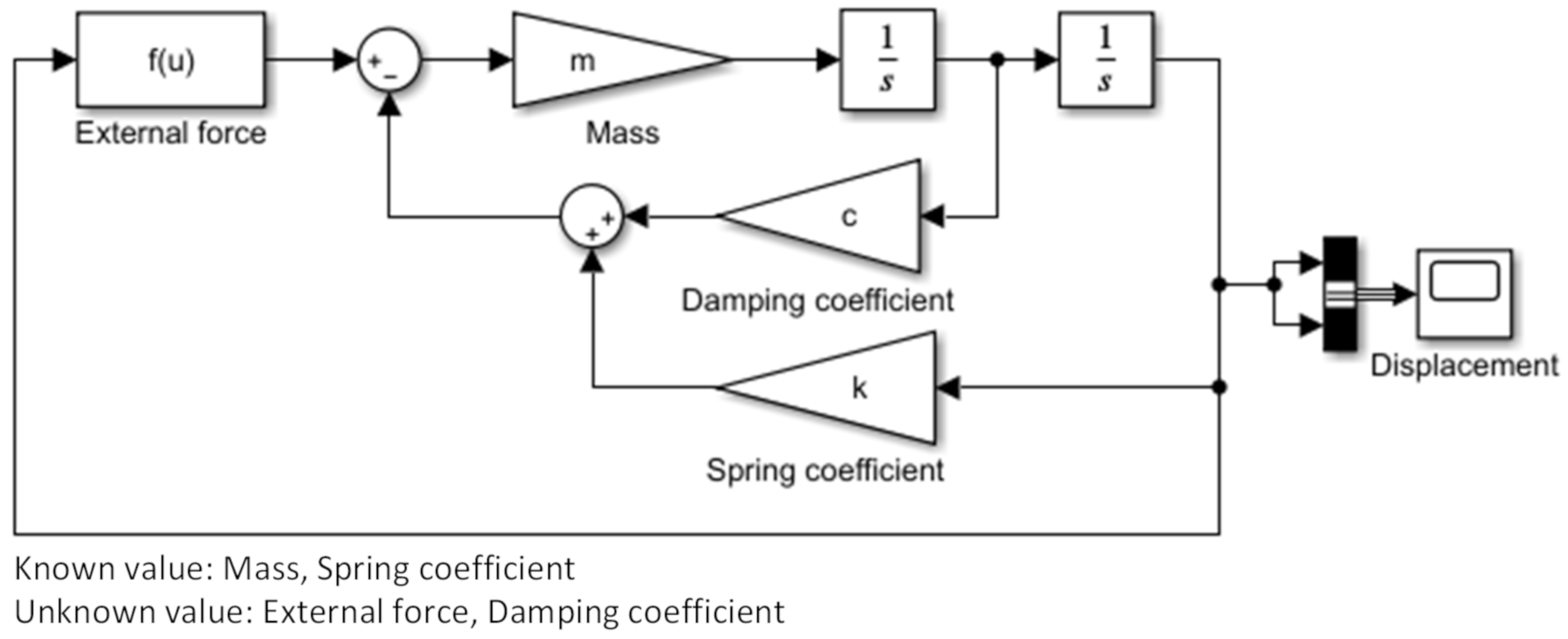
2.3. Modeling the Motion Equation by Phase
3. Experiments on the Plunger Movement
3.1. Configuration of the Experiments
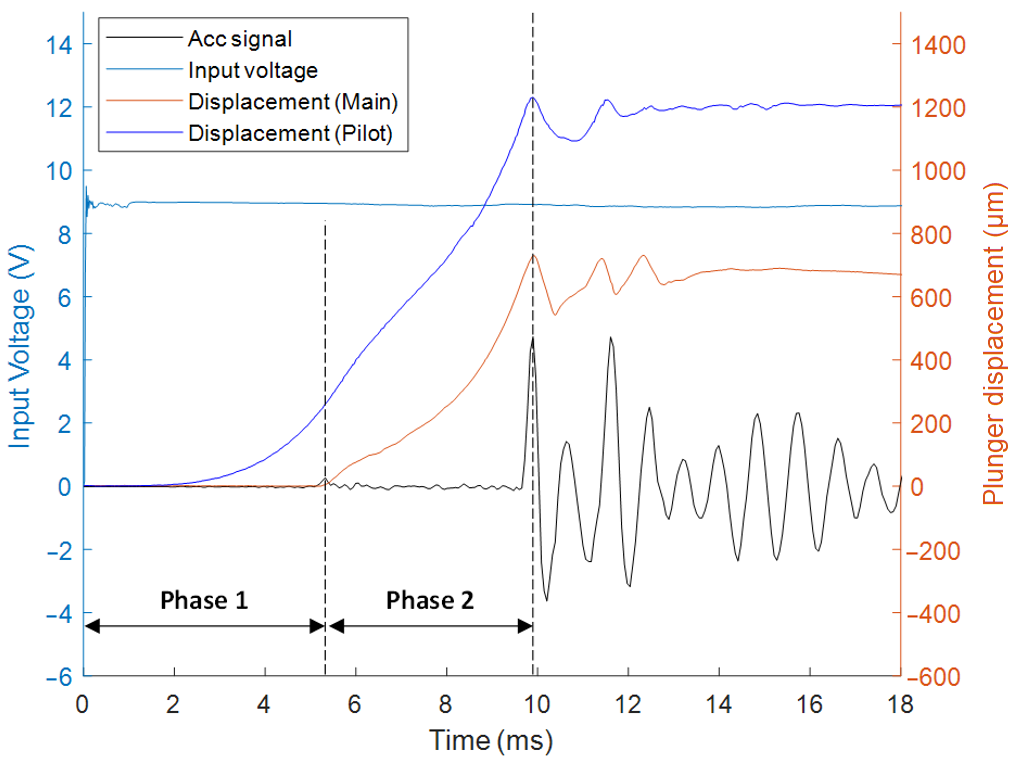
3.2. Experimental Results
4. System Identification through Simulations
4.1. Overview of System Identification
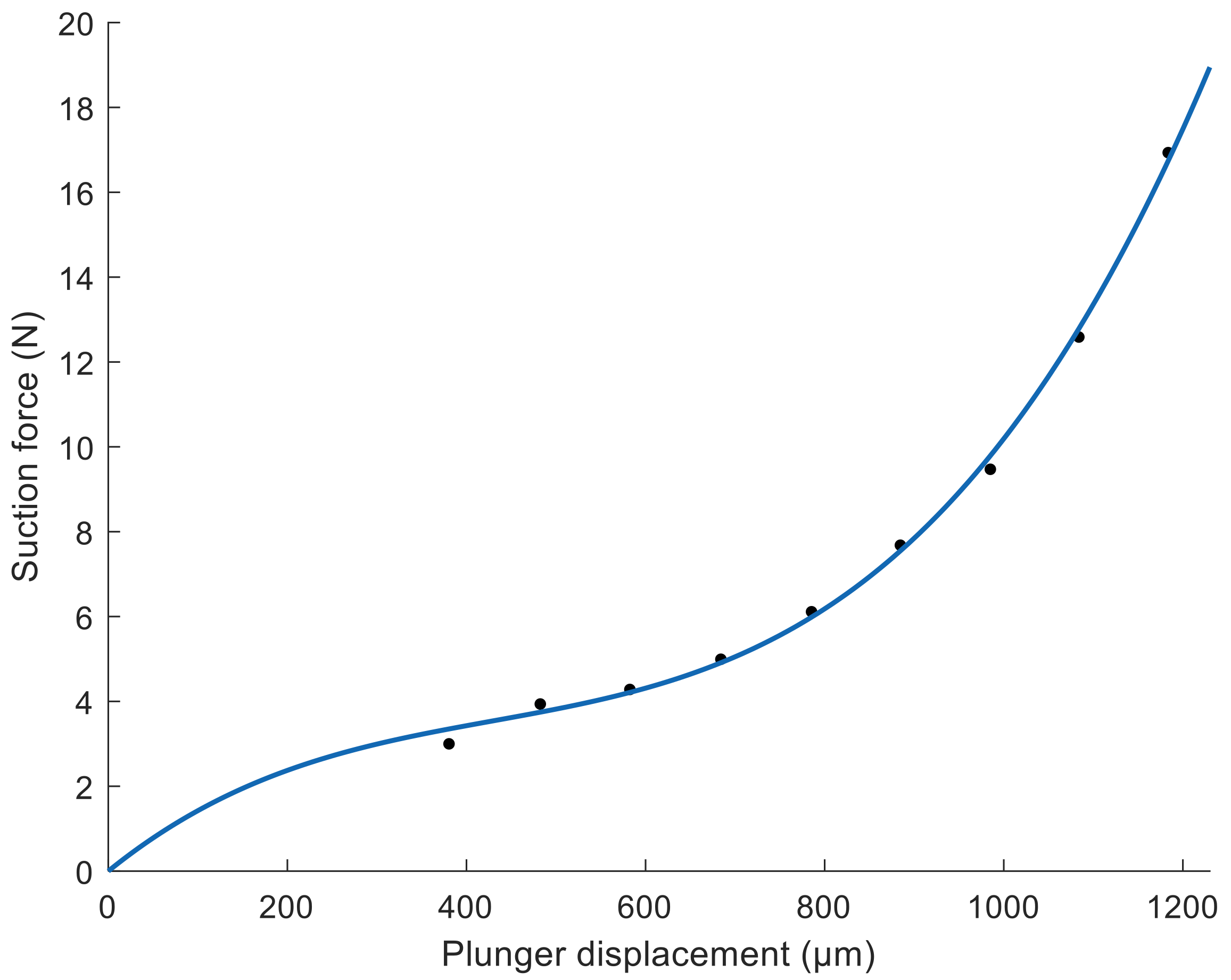
4.2. Attraction Force of Solenoid Valve
4.3. Estimation of the Damping Coefficient
4.4. Motion Equation for the Pilot-Operated Solenoid Valve
5. Conclusions
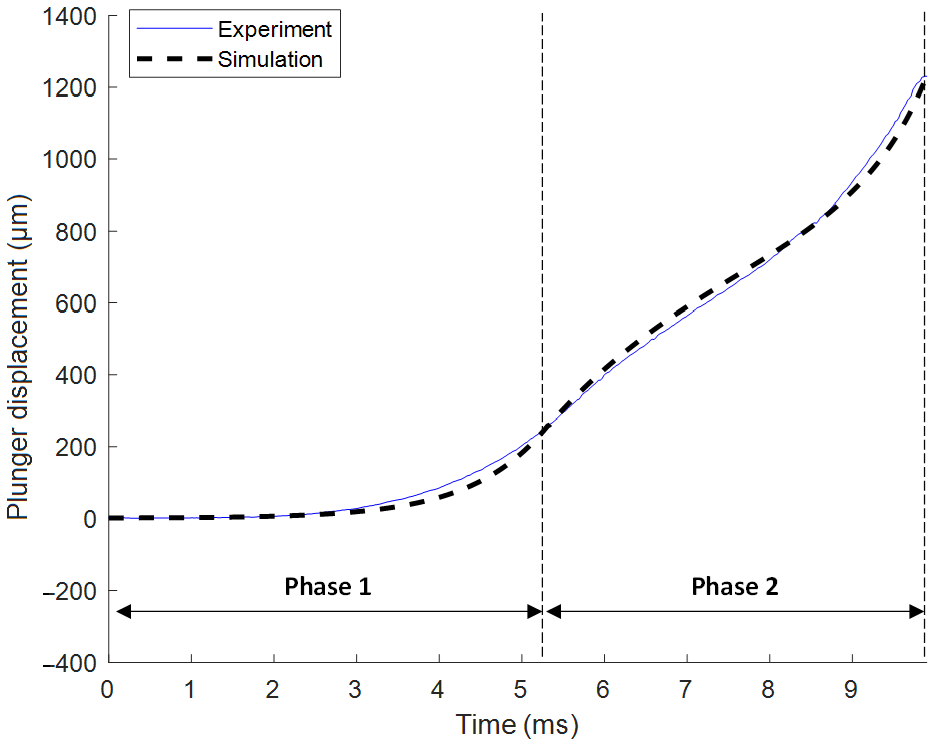
- The driving unit motion consists of two sequential movements. In Phase 1, only pilot plunger moves, and in Phase 2, pilot plunger and main plunger move together. The mathematical models for the driving unit are constructed.
- Phase 1 has a displacement of 260 µm over 5.3 ms, with an average velocity of 49.1 mm/s. Phase 2 has a displacement of 970 µm over 4.6 ms, with an average velocity of 210.9 mm/s. Although Phase 2 has a large mass and high damping coefficient, the average velocity is four times faster, so the influence of the attraction force is dominant.
- The damping coefficient of each phase is estimated 0.001 N ∙ s/mm at Phase 1, 0.004 N ∙ s/mm at Phase 2 by comparing the experimental results and the simulation results through Matlab Simulink.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahn, B.K. Development trend of the Clean Tech Fuel Cell Vehicles. Korean Soc. Mech. Eng. 2012, 52, 34–38. [Google Scholar]
- Li, M.; Bai, Y.; Zhang, C.; Song, Y.; Jiang, S.; Grouset, D.; Zhang, M. Review on the Research of Hydrogen Storage System Fast Refueling in Fuel Cell Vehicle. Int. J. Hydrog. Energy 2019, 44, 10677–10693. [Google Scholar] [CrossRef] [Green Version]
- Asano, S.; Ozaki, H.; Kato, K.; Wada, M. Development of In-Tank Solenoid Valve Compatible with 70 MPa High-Pressure Hydrogen Storage and Supply System for FCV. Honda R&D Tech. Rev. 2016, 28, 8–14. [Google Scholar]
- Lansky, Z.J. Industrial Pneumatic Control; CRC Press: Boca Raton, FL, USA, 1986; pp. 54–62. [Google Scholar]
- Kajima, T.; Kawamura, Y. Development of a High-Speed Solenoid Valve: Investigation of Solenoids. IEEE Trans. Ind. Electron. 1995, 42, 1–8. [Google Scholar] [CrossRef]
- Piron, M.; Sangha, P.; Reid, G.; Miller, T.J.E.; Ionel, D.M. Rapid Computer-Aided Design Method for Fast-Acting Solenoid Actuators. IEEE Trans. Ind. Applicat. 1999, 35, 991–999. [Google Scholar] [CrossRef]
- Liu, Q.; Bo, H.; Qin, B. Experimental Study and Numerical Analysis on Electromagnetic Force of Direct Action Solenoid Valve. Nucl. Eng. Des. 2010, 240, 4031–4036. [Google Scholar] [CrossRef]
- Xufeng, F.; Changbin, G.; Zhenxing, W. Dynamic Performance Analysis of a Pilot Operated Solenoid Valve in a Divert Engine for Spacecrafts. In Proceedings of the 2019 IEEE 8th International Conference on Fluid Power and Mechatronics (FPM), Wuhan, China, 10–13 April 2019; pp. 575–578. [Google Scholar]
- Rahman, M.F.; Cheung, N.C.; Lim, K.W. Position Estimation in Solenoid Actuators. IEEE Trans. Ind. Applicat. 1996, 32, 552–559. [Google Scholar] [CrossRef]
- Dai Jia, H.M.; Yong, Y.; Hengwei, Z.; Jiaqing, M. Simulation on the Dynamic Response Characteristics of Solenoid Valve. J. Rocket Propuls. 2007, 1, 40–48. [Google Scholar]
- Lee, H.R.; Ahn, J.H.; Kim, H.Y. Design of a solenoid actuator for a cylinder valve in a fuel cell vehicle. Appl. Sci. 2016, 6, 288. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.R.; Ahn, J.H.; Shin, J.O.; Kim, H.Y. Design of Solenoid Actuator for FCV Cylinder Valve Considering Structural Safety. J. Korean Soc. Manuf. Technol. Eng. 2016, 25, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Roters, H.C. Electromagnetic Devices; Wiley: New York, NY, USA, 1941; pp. 130–149. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The matlab ode suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]


| Equipment | Parameter | Value |
|---|---|---|
| Laser sensor (LK-G30, KISTLER) | Measuring range | ±5 mm |
| Repeatability | 0.05 μm | |
| Accelerometer (8762A10, KISTLER) | Acc. Range | ±10 G |
| Freq. response | 0.5–6000 Hz |
| Equipment | Parameter | Value |
|---|---|---|
| Laser sensor (LK-G30, KISTLER) | Measuring range | ±5 mm |
| Repeatability | 0.05 μm | |
| Load cell (LCM300, FUTEK) | Rated Output | 2 mV/V |
| Non-repeatability | ±0.25% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Ahn, J.H.; Kim, H.Y. Modeling the Dynamic Behavior of a Pilot-Operated Solenoid Valve for an Ultra-High Pressure Vessel. Appl. Sci. 2021, 11, 2329. https://doi.org/10.3390/app11052329
Choi J, Ahn JH, Kim HY. Modeling the Dynamic Behavior of a Pilot-Operated Solenoid Valve for an Ultra-High Pressure Vessel. Applied Sciences. 2021; 11(5):2329. https://doi.org/10.3390/app11052329
Chicago/Turabian StyleChoi, Jaeseong, Jung Hwan Ahn, and Hwa Young Kim. 2021. "Modeling the Dynamic Behavior of a Pilot-Operated Solenoid Valve for an Ultra-High Pressure Vessel" Applied Sciences 11, no. 5: 2329. https://doi.org/10.3390/app11052329
APA StyleChoi, J., Ahn, J. H., & Kim, H. Y. (2021). Modeling the Dynamic Behavior of a Pilot-Operated Solenoid Valve for an Ultra-High Pressure Vessel. Applied Sciences, 11(5), 2329. https://doi.org/10.3390/app11052329





