Analysis of Vertical Stiffness Characteristics Based on Spoke Shape of Non-Pneumatic Tire
Abstract
:1. Introduction
2. Numerical Model and Analysis Conditions of Non-Pneumatic Tire
2.1. Development of Finite Element Analysis Model
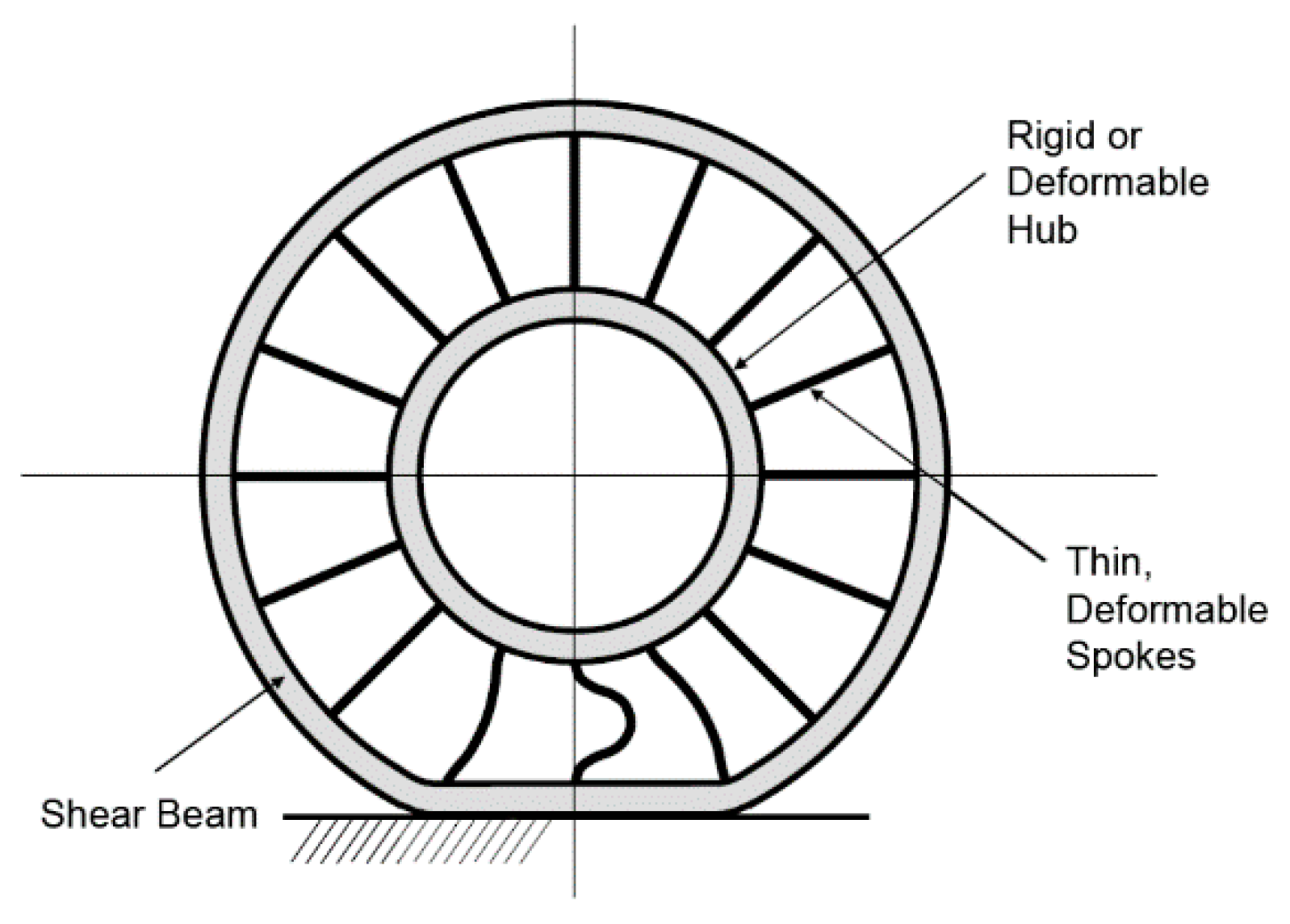
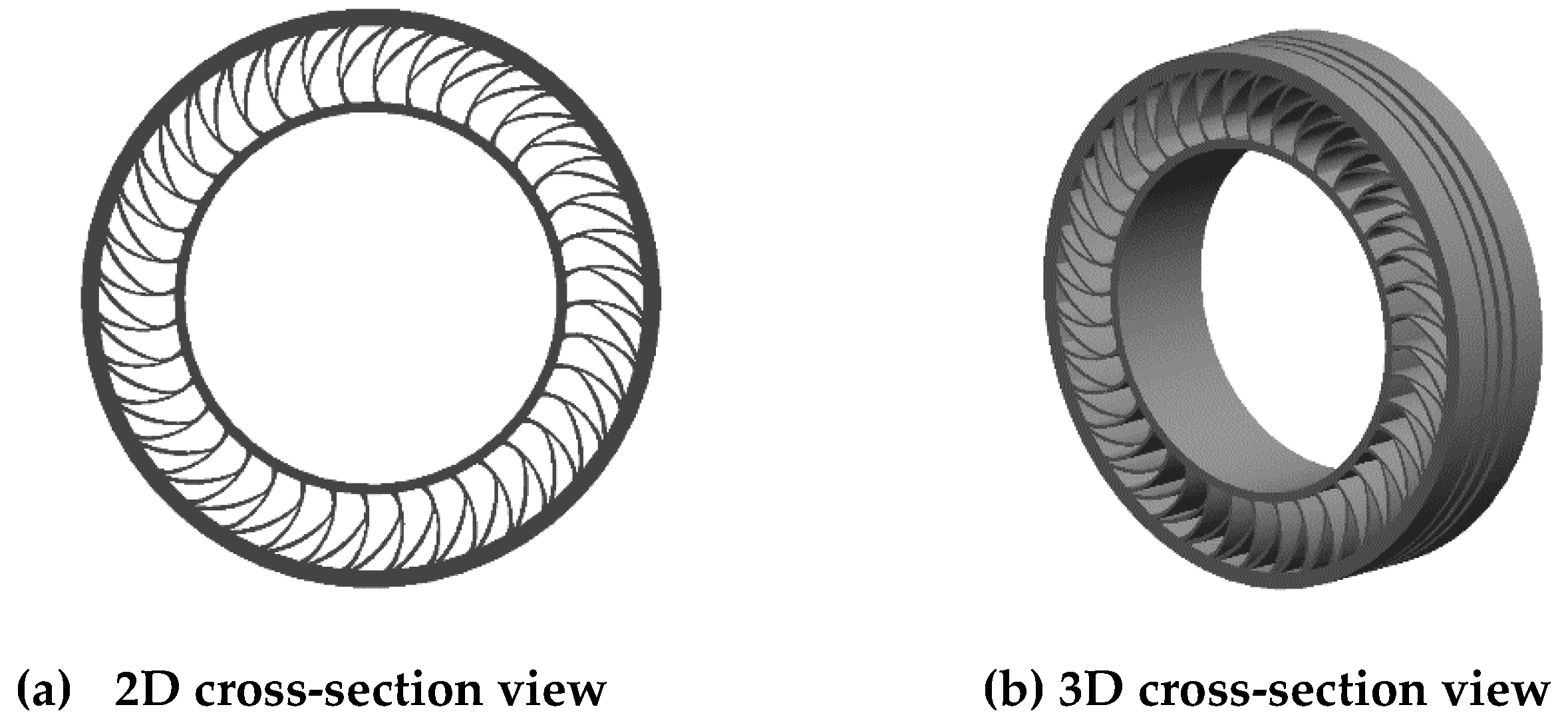
2.1.1. Base Model of Non-Pneumatic Tire
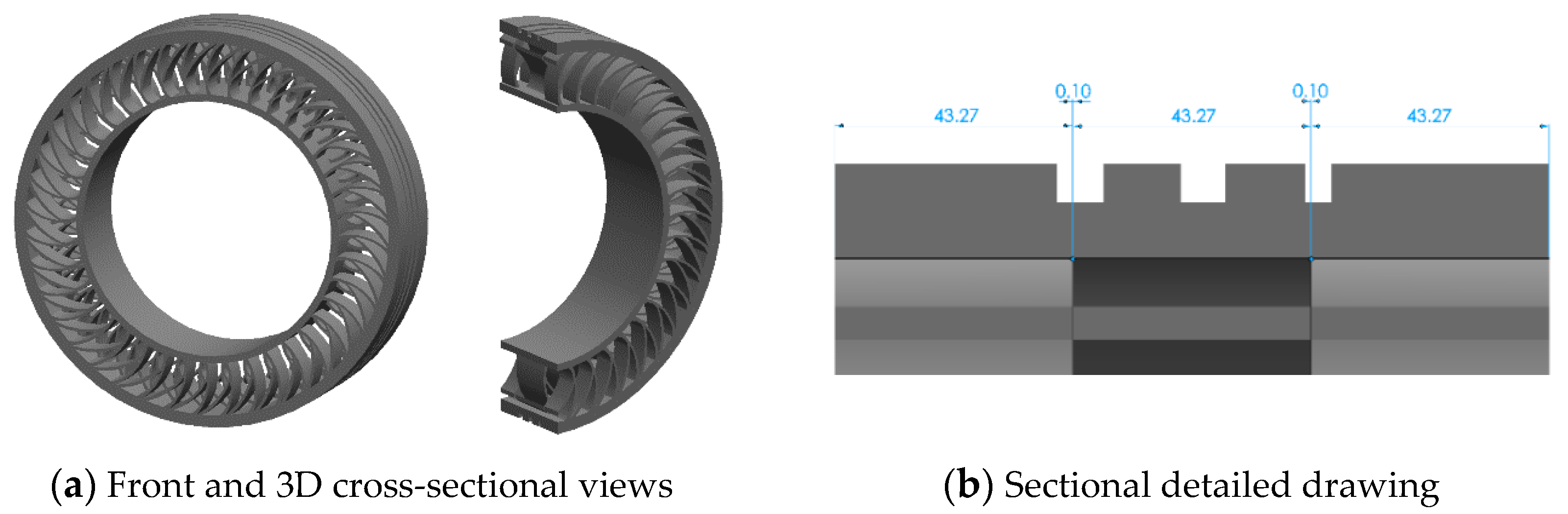
2.1.2. Modeling of Spoke Deformation of Non-Pneumatic Tire
- (1)
- Fillet-applied model of spoke
- (2)
- Asymmetric-spoke division model
- (3)
- Symmetric-spoke division model
2.2. Set-Up of Finite Element Analysis
2.2.1. Geometry Set-Up
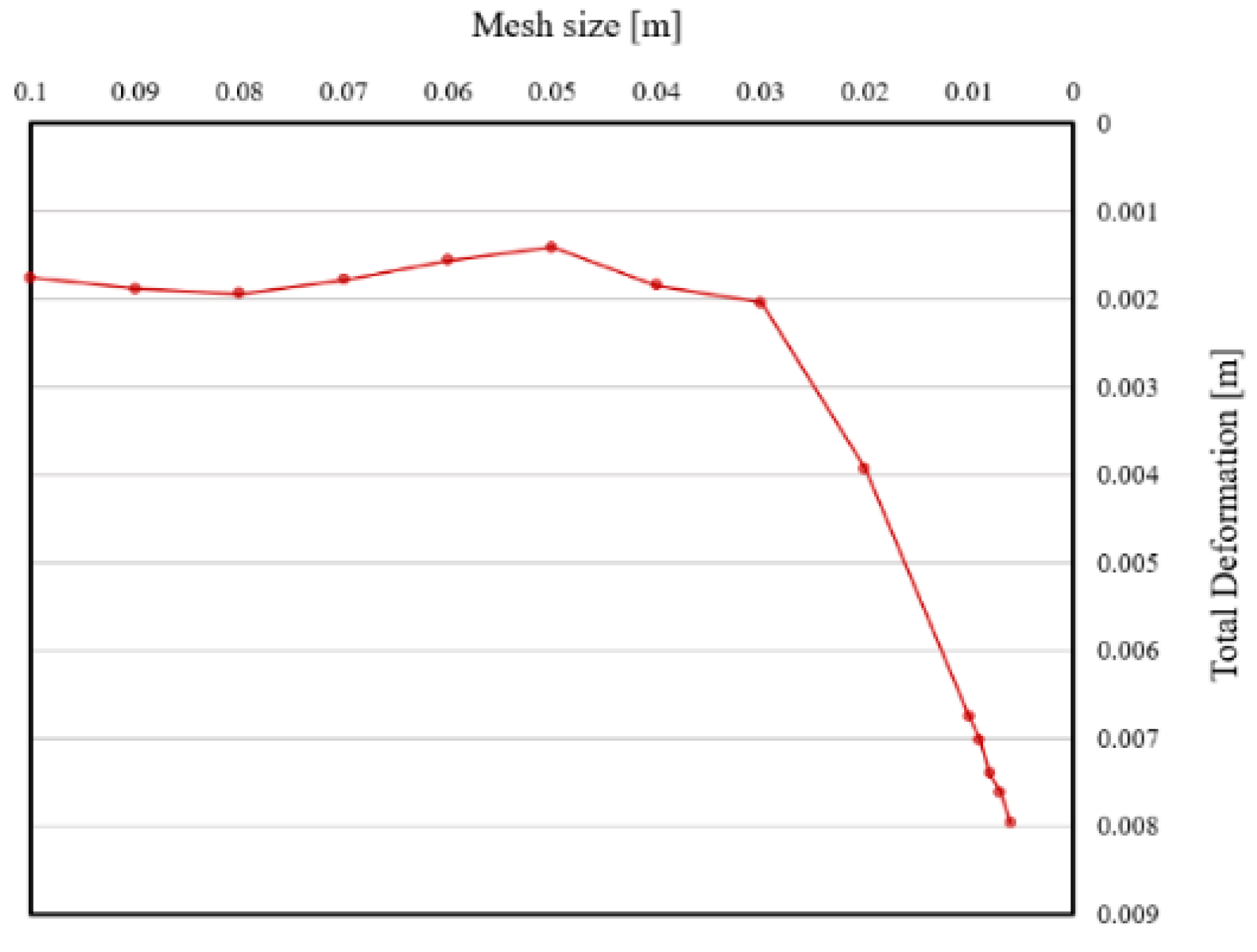
2.2.2. Mesh Set-Up
2.2.3. Boundary Condition Set-Up
3. Results and Discussion
3.1. Validation of Non-Pneumatic Tire Analysis Model
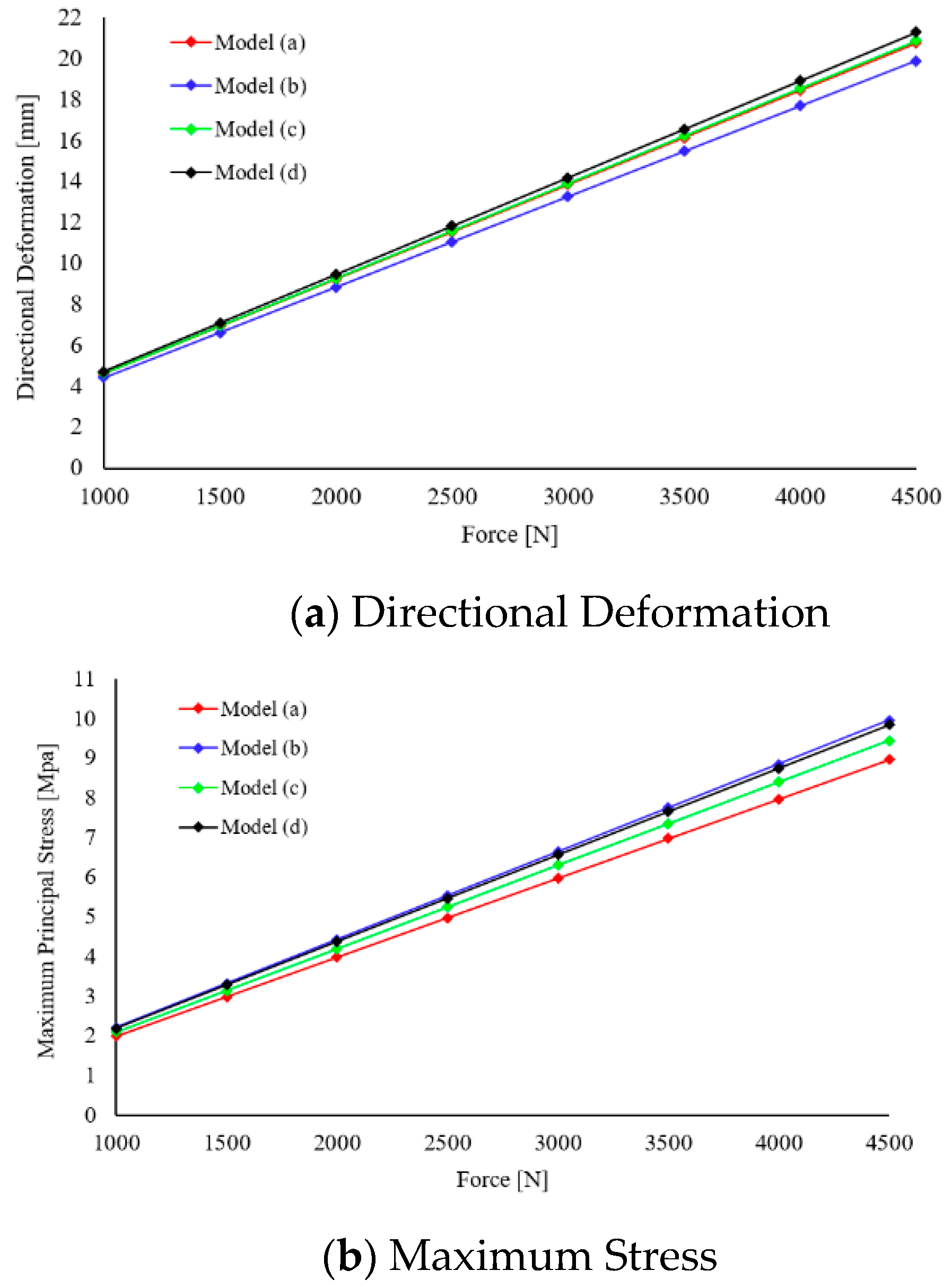
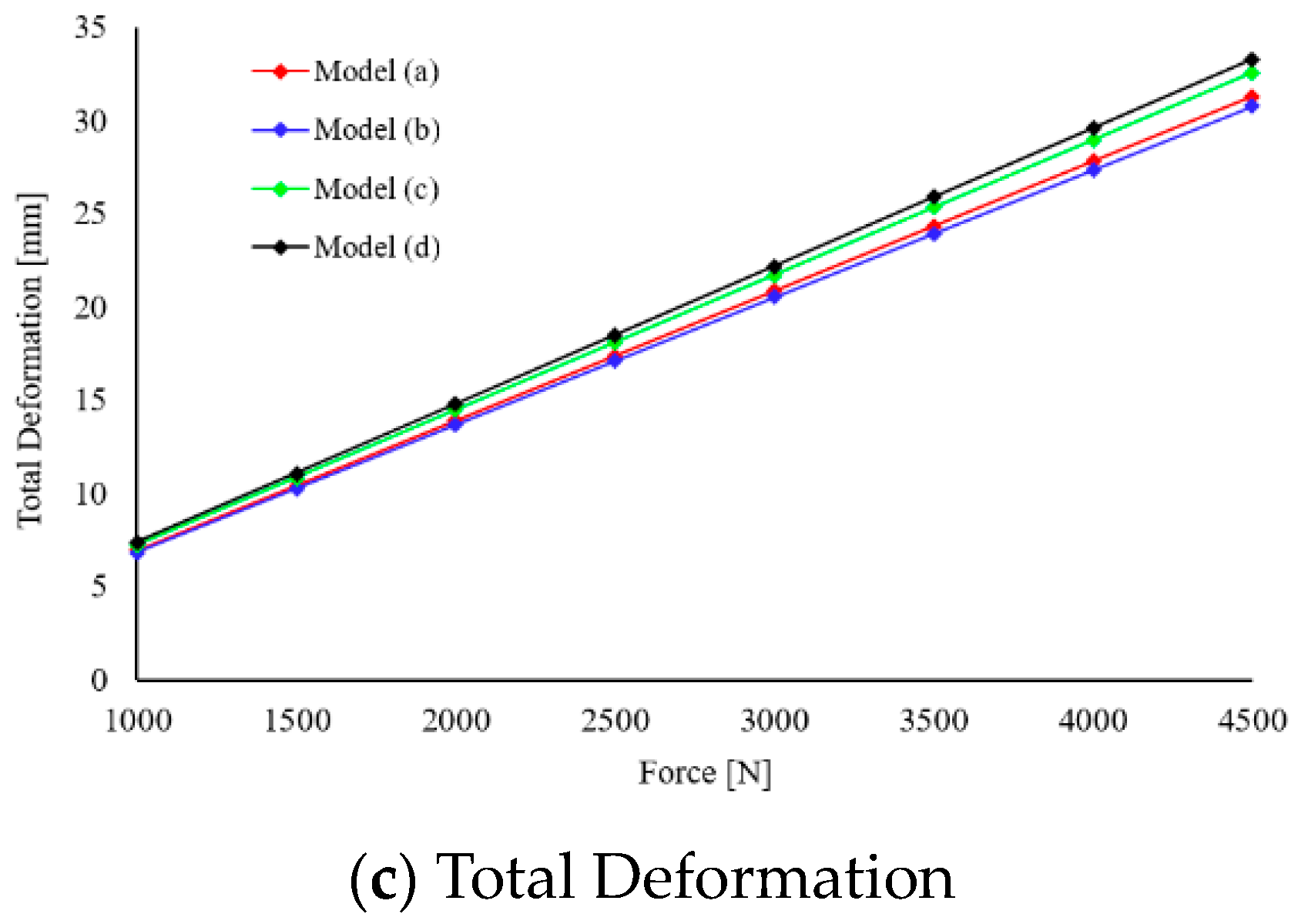
3.2. Effect of Change in Spoke Shape on Total Deformation
3.3. Effect of Change in Spoke Shape on Maximum Principal Stress
3.4. Effect of Change in Spoke Shape on Directional Deformation
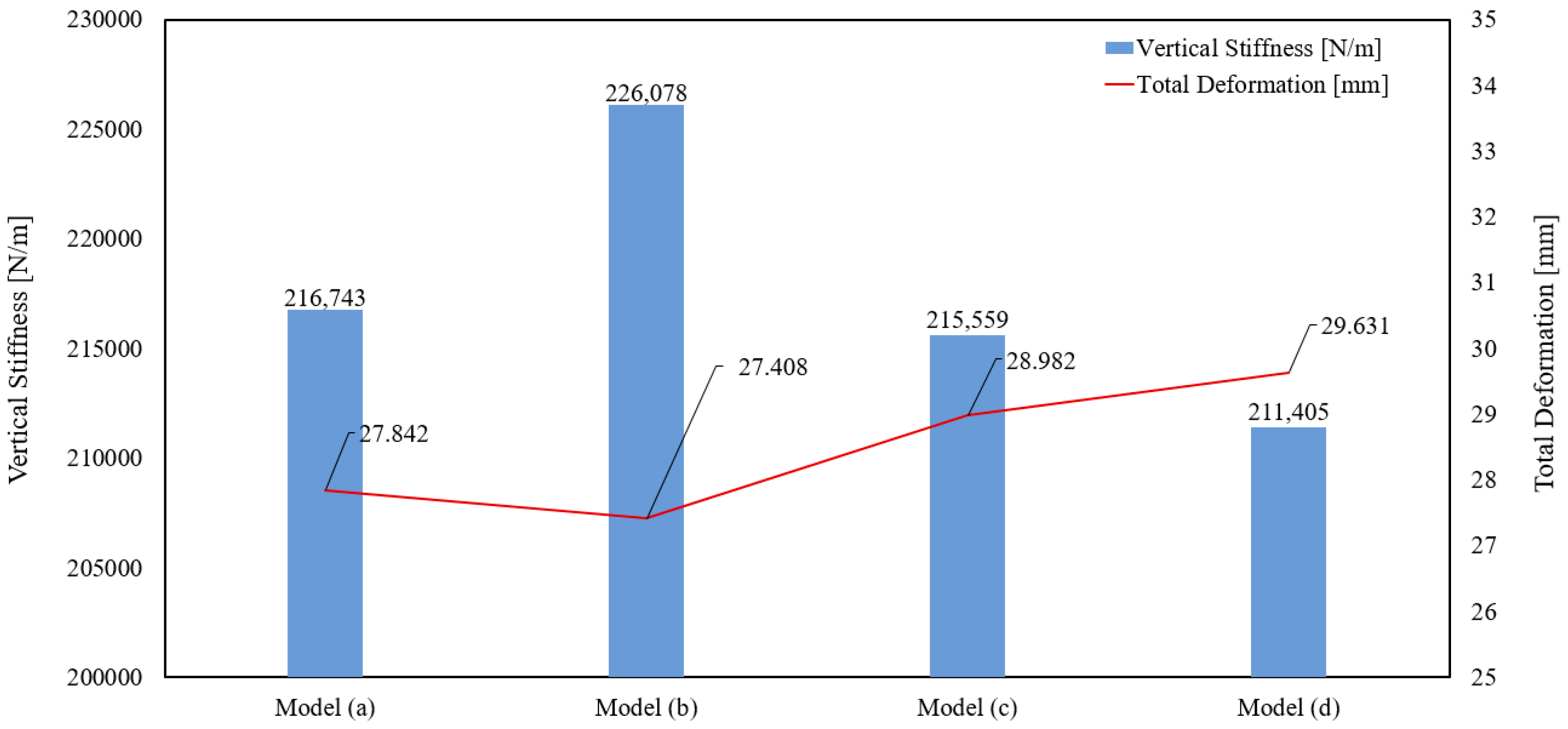
3.5. Vertical Stiffness Characteristics for Each Spoke Shape
4. Conclusions
- (1)
- Compared with the reference model, the total deformation was lower by approximately 1.56% for the fillet-applied model, higher by 4.09% for the asymmetric-spoke division model, and higher by approximately 6.43% for the symmetric-spoke division model.
- (2)
- Compared with the reference model, the maximum principal stress was higher by approximately 11.13% for the fillet-applied model, 5.34% for the asymmetric-spoke division model, and 9.81% for the symmetric-spoke division model.
- (3)
- Compared with the reference model, the directional deformation was lower by approximately 4.13% for the fillet-applied model, higher by 0.53% for the asymmetric-spoke division model, and higher by 2.53% for the symmetric-spoke division model.
- (4)
- The fillet-applied model with the smallest deformation indicated the highest vertical stiffness at 226,078 N/m, whereas the symmetric-spoke division model with the greatest deformation indicated the lowest vertical stiffness at 211,405 N/m.
- (5)
- When applying the fillet, the maximum principal stress was relatively large but the directional deformation decreased. Consequently, the vertical stiffness of the non-pneumatic tire increased.
- (6)
- When the spoke was divided, the resistance against the load in the longitudinal direction decreased, deformation increased, vertical stiffness decreased, and the stress acting on the spoke increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, K.W.; Kwark, C.W. Introduction to Technology Trends, Problems and Solutions of Non-Pneumatic. J. Korean Soc. Automot. Eng. 2019, 41, 26–31. [Google Scholar]
- Jung, S.P.; Park, J.H.; Mah, K.U.; Jeong, J.S. Study on Improving the Vibration Characteristics of Non-Pneumatic Tires. Trans. Korean Soc. Mech. Eng. A 2019, 46, 427–433. [Google Scholar] [CrossRef]
- Aboul-Yazid, A.M.; Emam, M.A.A.; Shaaban, A.; El-shar, M.A. Effect of Spokes Structures on Characteristics Performance of Non-pneumatic Tires. Int. J. Automot. Mech. Eng. 2015, 11, 2212–2223. [Google Scholar] [CrossRef]
- Meng, F.; Lu, D.; Yu, J. Flexible Cellular Structures of a Non-Pneumatic Tire. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. DETC2016-59124. [Google Scholar]
- Jina, X.; Houa, C.; Fana, X.; Sunb, Y.; Lvc, J.; Lu, C. Investigation on the static and dynamic behaviors of non-pneumatic tires with honeycomb spokes. Compos. Struct. 2018, 187, 27–35. [Google Scholar] [CrossRef]
- Jang, I.G.; Sung, Y.H.; Yoo, E.J.; Kwak, B.M. Pattern Design of a Non-Pneumatic Tyre for Stiffness Using Topology Optimization. Eng. Optim. 2007, 2007, 569–570. [Google Scholar] [CrossRef]
- Gasmi, A.; Joseph, P.F.; Rhyne, T.B.; Cron, S.M. Development of a two-dimensional model of a compliant non-pneumatic tire. Compos. Struct. 2012, 49, 1723–1740. [Google Scholar] [CrossRef] [Green Version]
- Ju, J.H.; Kim, D.M.; Kim, K.W. Flexible cellular solid spokes of a non-pneumatic tire. Compos. Struct. 2012, 94, 2285–2295. [Google Scholar] [CrossRef]
- Rugsai, R.; Suvanjumrat, C. Proper Radial Spokes of Non-pneumatic Tire for Vertical Load Supporting by Finite Element Analysis. Int. J. Automot. Technol. 2019, 20, 801–812. [Google Scholar] [CrossRef]
- Umesh, G.C.; Amith Kumar, S.N. Design and Analysis of Non-Pneumatic Tyre (NPT) With Honeycomb Spokes Structure. Int. J. Eng. Sci. Comput. 2016, 6, 2136–2140. [Google Scholar]
- Wu, T.; Li, M.; Zhu, X.L.; Lu, X.F. Research on non-pneumatic tire with gradient anti-tetrachiral structures. Mech. Adv. Mater. Struct. 2020, 1–9. [Google Scholar] [CrossRef]
- Rugsai, R.; Suvanjumrat, C. Study of geometric effects on nonpneumatic tire spoke structures using finite element method. Mech. Based Des. Struct. Mach. 2020, 1–21. [Google Scholar] [CrossRef]
- Evangelia, G.P.; Panagiotis, C.Z.; Wang, X. The Influence of the Honeycomb Design Parameters on the Mechanical Behavior of Non-Pneumatic Tires. Int. J. Appl. Mech. 2020, 12, 2050024. [Google Scholar]
- Zhang, Z.f.; Fu, H.X.; Liang, X.M.; Chen, X.X.; Tan, D. Comparative Analysis of Static and Dynamic Performance of Non-pneumatic Tire with Flexible Spoke Structure. J. Mech. Eng. 2020, 66, 458–466. [Google Scholar] [CrossRef]
- Kim, K.W.; Kim, D.M.; Ju, J.H.; Kim, S.H. Contact Pressure of a Non-Pneumatic Tire With Three-Dimensional Cellular Spokes. In Proceedings of the ASME 2011 International Mechanical Engineering Conference & Exposition, Denver, CO, USA, 11–17 November 2011. DRAFT: IMECE2011-6423. [Google Scholar]
- Rajam, L.; Ayyanar, C.; Shobith, N.; Verma, A.; Subhash Raj, S. Design and Comparative Analysis of Non-Pneumatic Tires for a Tractor. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 8, 301–307. [Google Scholar]
- Taylor, R.K.; Bashford, L.L.; Schrock, M.D. Methods for Measuring Vertical Tire Stiffness. Trans. Am. Soc. Agric. Eng. 2000, 43, 1415–1419. [Google Scholar] [CrossRef]
- Wang, S.; Chester, S.A. Experimental characterization and continuum modeling of inelasticity in filled rubber-like materials. Int. J. Solids Struct. 2018, 136–137, 25–136. [Google Scholar] [CrossRef]
- Wang, S.; Chester, S.A. Modeling thermal recovery of the Mullins effect. Mech. Mater. 2018, 126, 88–98. [Google Scholar] [CrossRef]
- Wang, S.; Decker, M.; Henann, D.L.; Chester, S.A. Modeling of dielectric viscoelastomers with application to electromechanical instabilities. J. Mech. Phys. Solids 2016, 95, 213–229. [Google Scholar] [CrossRef] [Green Version]






| Properties | Unit | Value |
|---|---|---|
| Density | kg/m3 | 1210 |
| Elastic modulus | MPa | 35.0 |
| Poisson’s ratio | - | 0.48 |
| Yield strength | MPa | 145 |
| Shear modulus | MPa | 11.8 |
| Non-Pneumatic Tire Models | Nodes | Elements |
|---|---|---|
| Model type (a) | 326,781 | 181,737 |
| Model type (b) | 342,969 | 191,189 |
| Model type (c) | 339,744 | 187,092 |
| Model type (d) | 335,785 | 193,463 |
| Force (N) | Directional Deformation (mm) | Vertical Stiffness (N/m) |
|---|---|---|
| 1000 | 4.614 | 216,746 |
| 1500 | 6.924 | 216,744 |
| 2000 | 9.228 | 216,743 |
| 2500 | 11.534 | 216,750 |
| 3000 | 13.841 | 216,747 |
| 3500 | 16.148 | 216,745 |
| 4000 | 18.455 | 216,743 |
| 4500 | 20.762 | 216,742 |
| Average | 216,745 | |
| Model Type | Total Deformation (mm) | Maximum Principal Stress (MPa) | Directional Deformation (mm) |
|---|---|---|---|
| (a) |  |  | 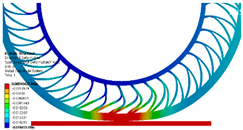 |
| (b) |  | 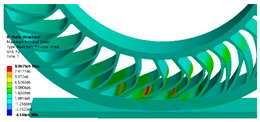 |  |
| (c) |  | 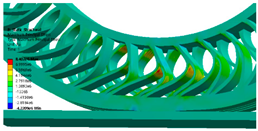 | 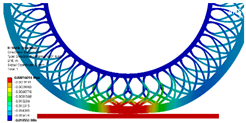 |
| (d) |  | 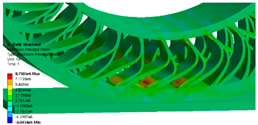 | 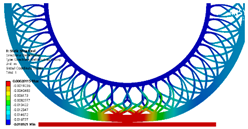 |
| Model Type | Maximum Principal Stress (MPa) | Total Deformation (mm) | Vertical Stiffness (N/m) |
|---|---|---|---|
| (a) | 7.976 | 27.842 | 216,743 |
| (b) | 8.864 | 27.408 | 226,078 |
| (c) | 8.402 | 28.982 | 215,599 |
| (d) | 8.758 | 29.631 | 211,405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, J.; Hong, J.; Cho, I.; Lee, J. Analysis of Vertical Stiffness Characteristics Based on Spoke Shape of Non-Pneumatic Tire. Appl. Sci. 2021, 11, 2369. https://doi.org/10.3390/app11052369
Sim J, Hong J, Cho I, Lee J. Analysis of Vertical Stiffness Characteristics Based on Spoke Shape of Non-Pneumatic Tire. Applied Sciences. 2021; 11(5):2369. https://doi.org/10.3390/app11052369
Chicago/Turabian StyleSim, Jongkeun, Jiyeon Hong, Insu Cho, and Jinwook Lee. 2021. "Analysis of Vertical Stiffness Characteristics Based on Spoke Shape of Non-Pneumatic Tire" Applied Sciences 11, no. 5: 2369. https://doi.org/10.3390/app11052369
APA StyleSim, J., Hong, J., Cho, I., & Lee, J. (2021). Analysis of Vertical Stiffness Characteristics Based on Spoke Shape of Non-Pneumatic Tire. Applied Sciences, 11(5), 2369. https://doi.org/10.3390/app11052369






