Experimental Study and Development of Design Formula for Estimating the Ultimate Strength of Curved Plates
Abstract
:1. Introduction
2. Experimental Preparations
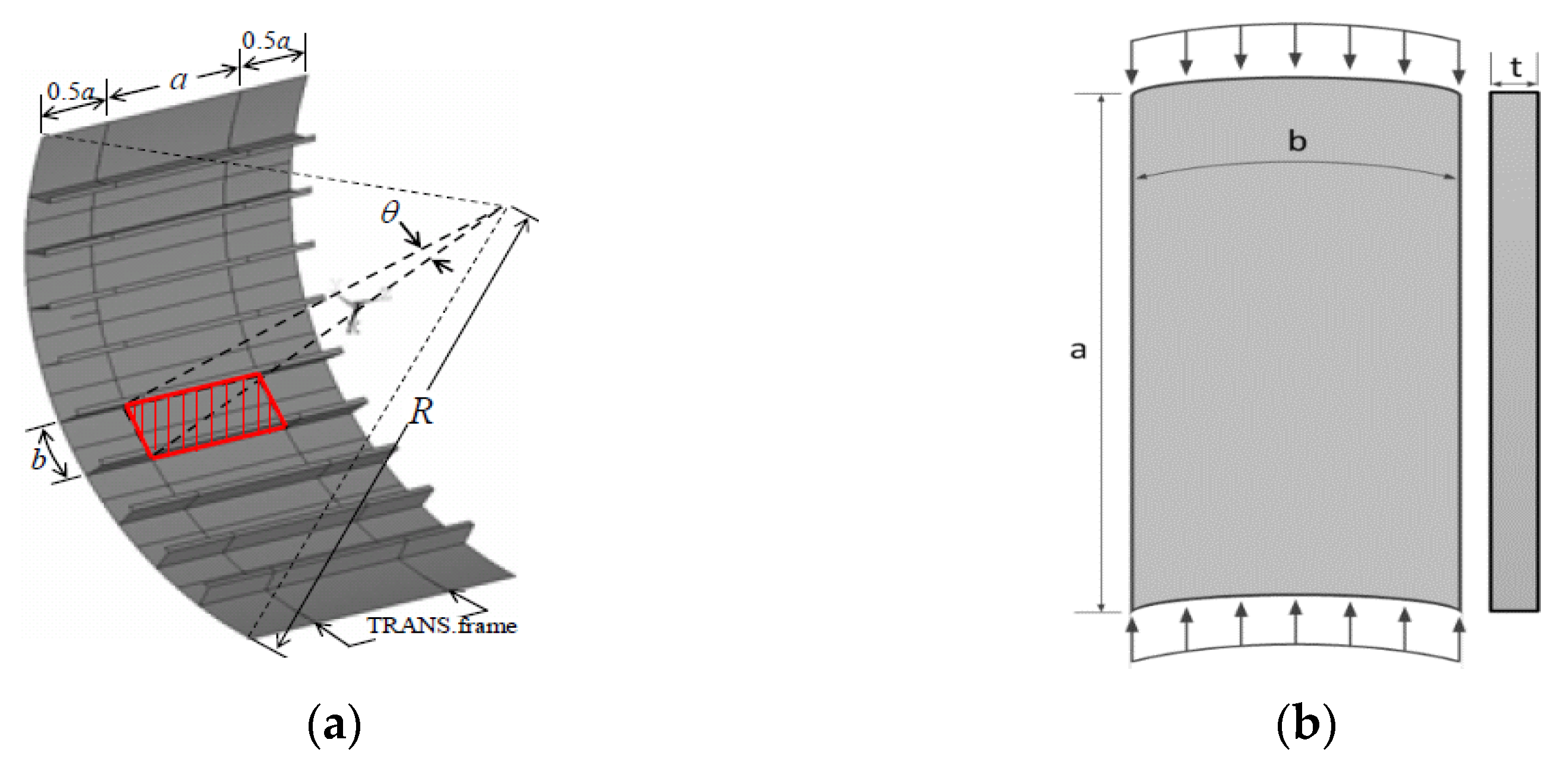
2.1. Test Specimen and Scenario
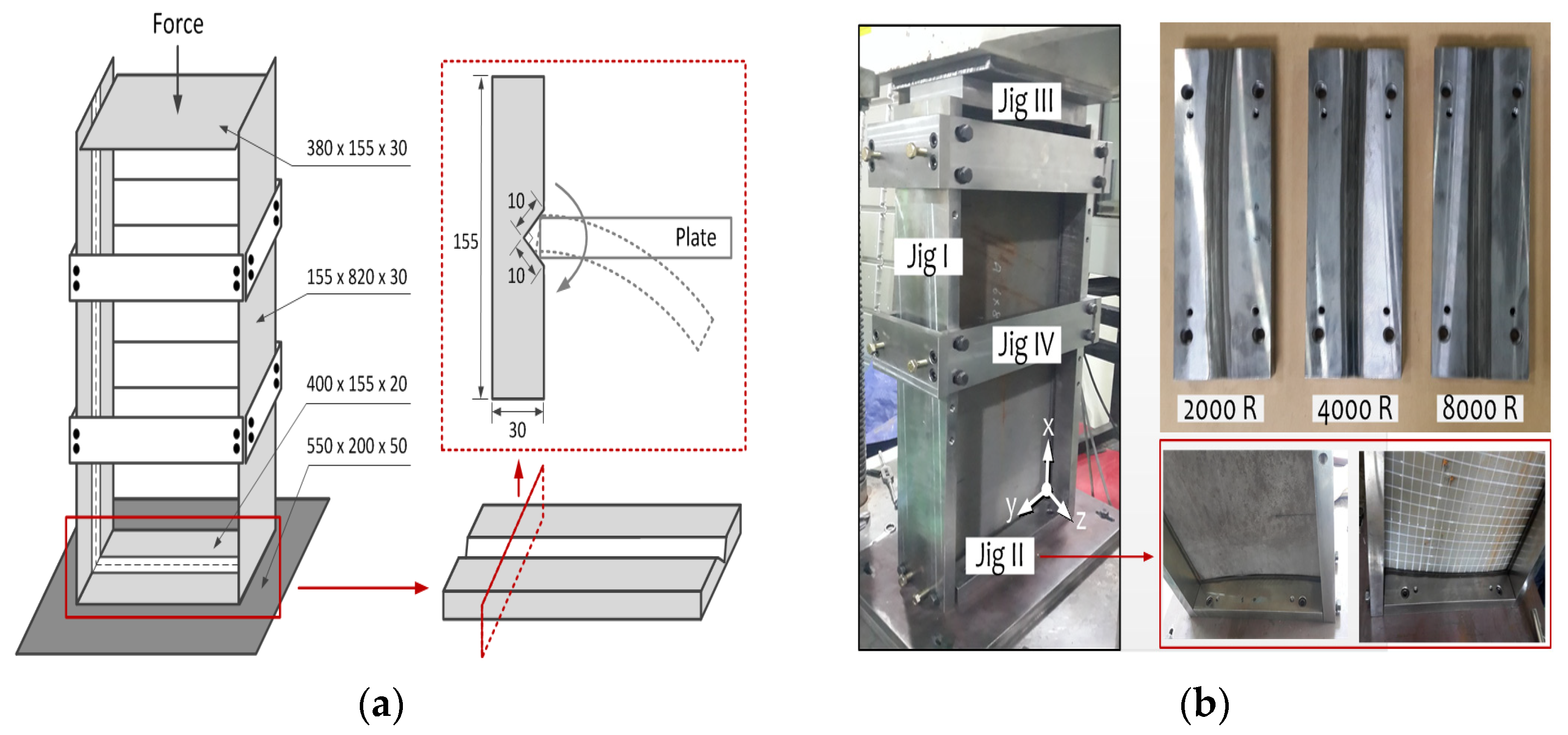
2.2. Apparatus
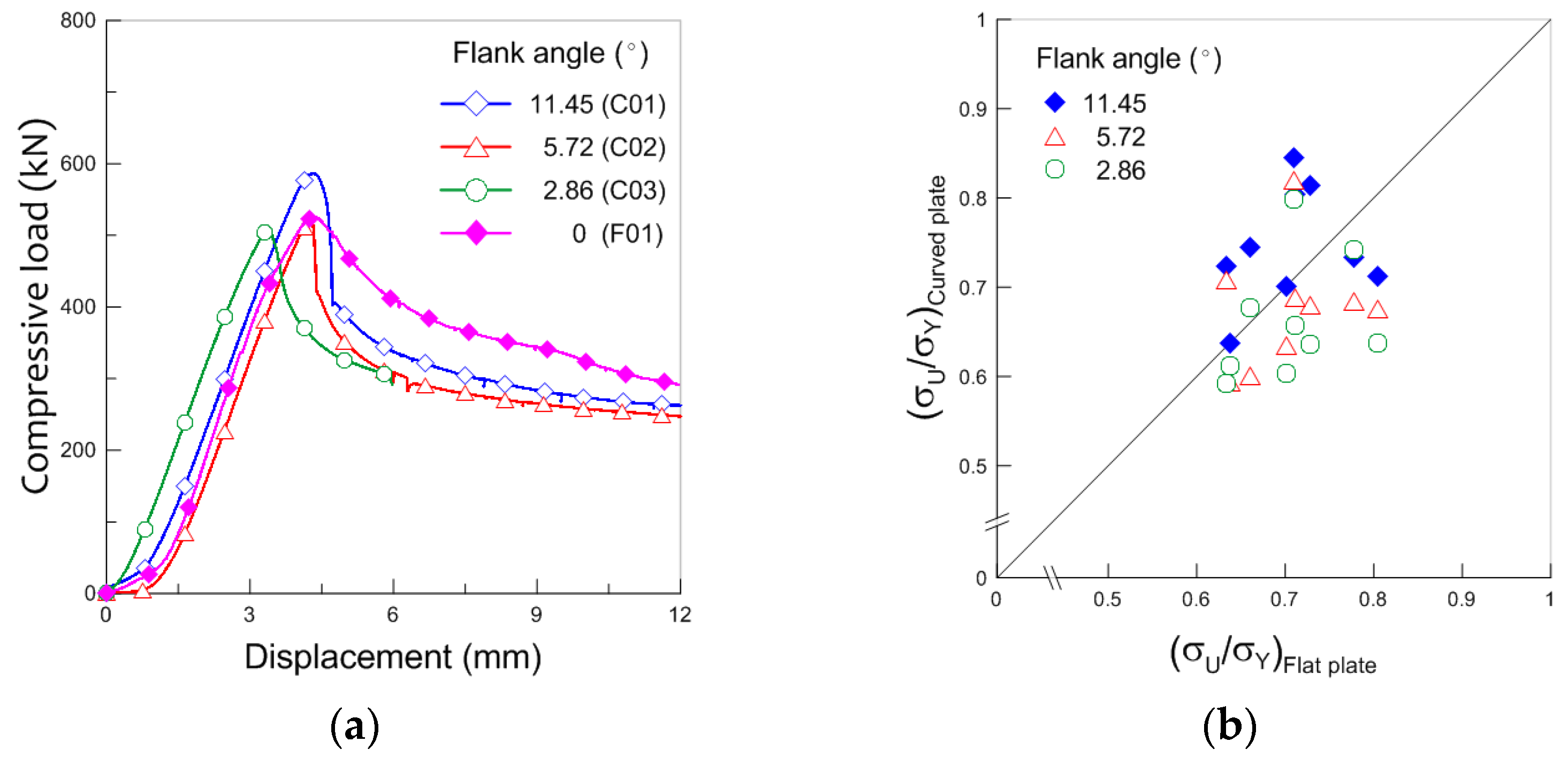
2.3. Experimental Results
3. Design Formula
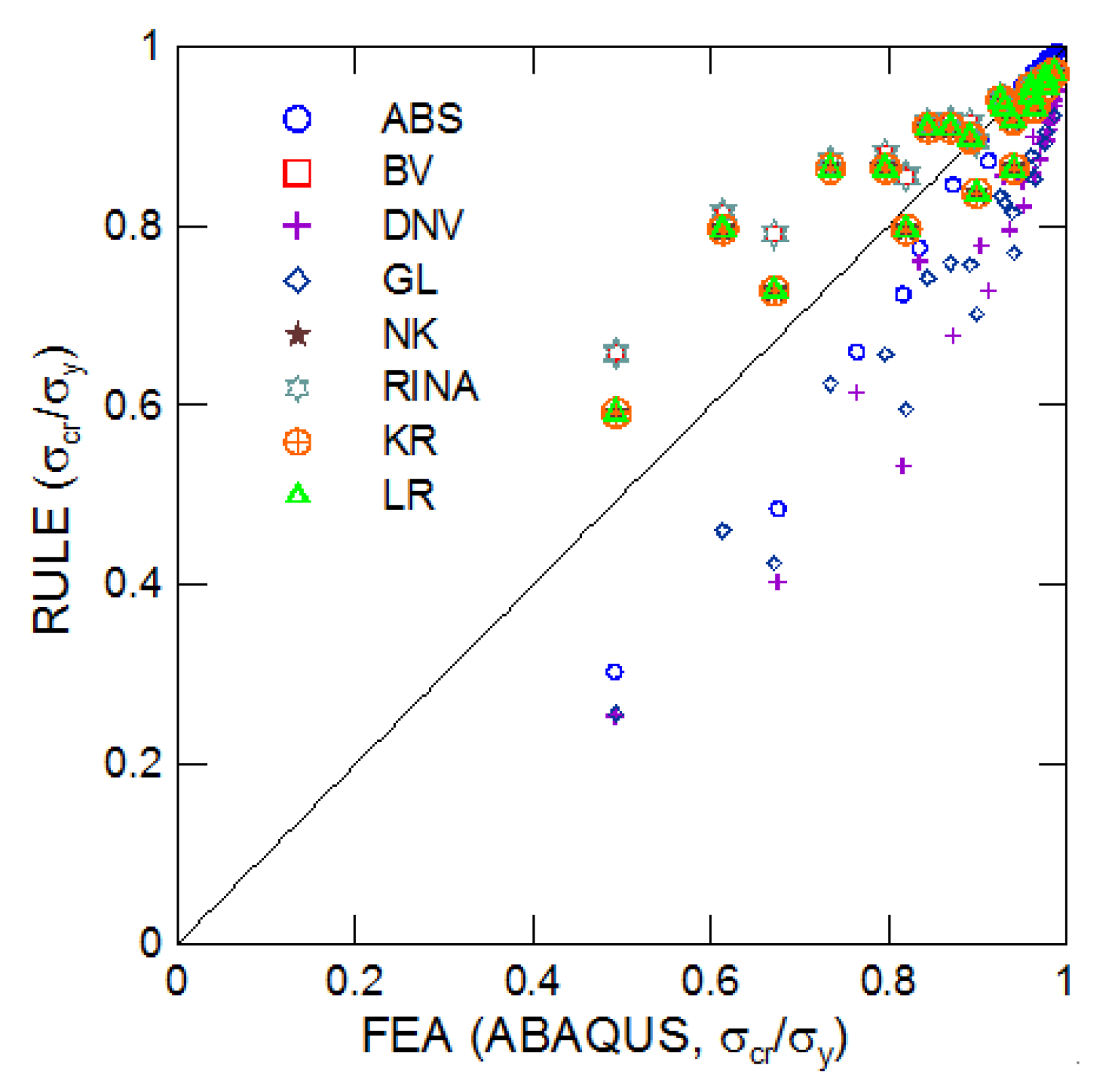
3.1. Investigation for Classification Rule
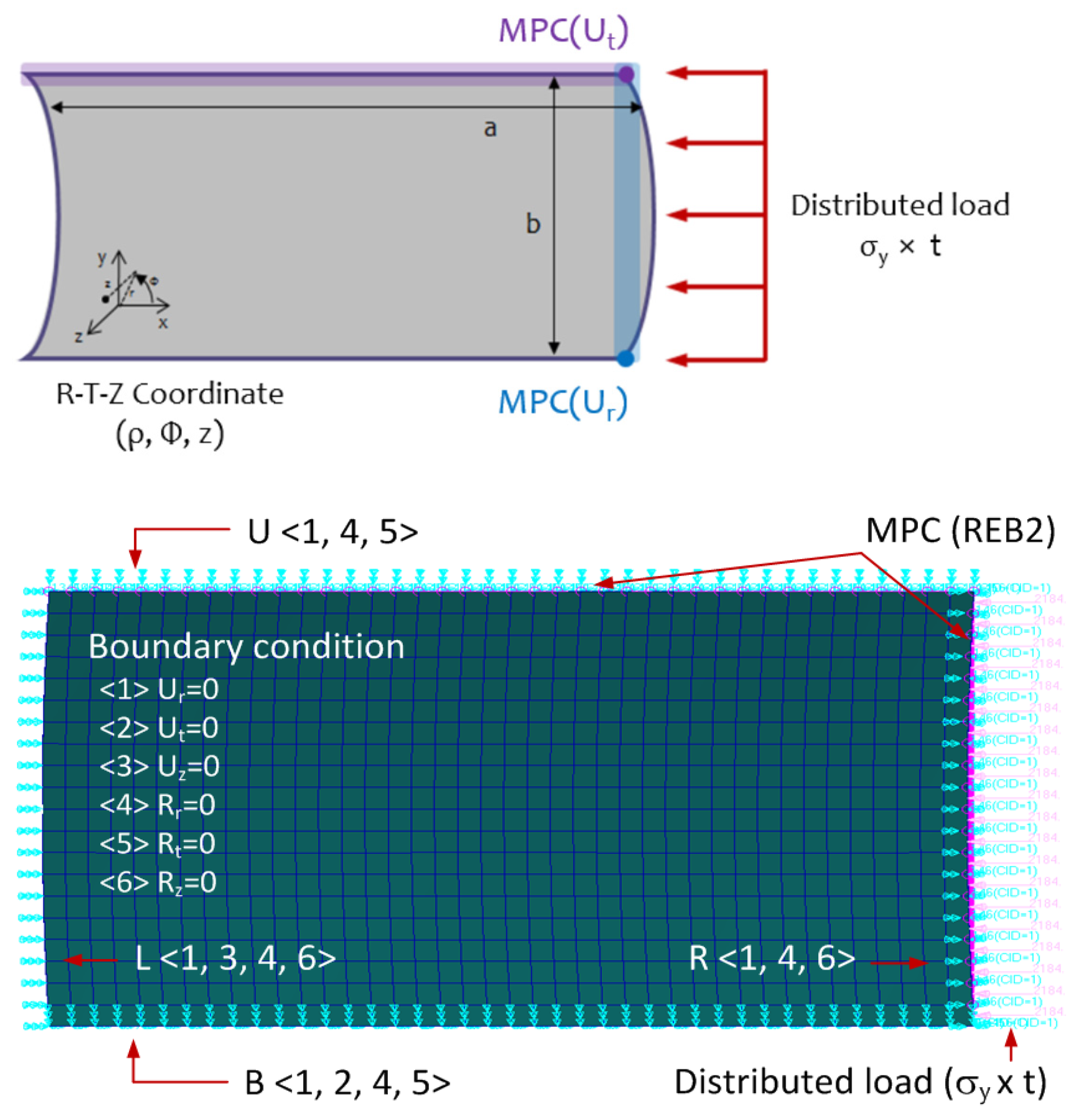
3.2. FE Analysis
4. Comparison with Experimental Results
4.1. Buckling Mode
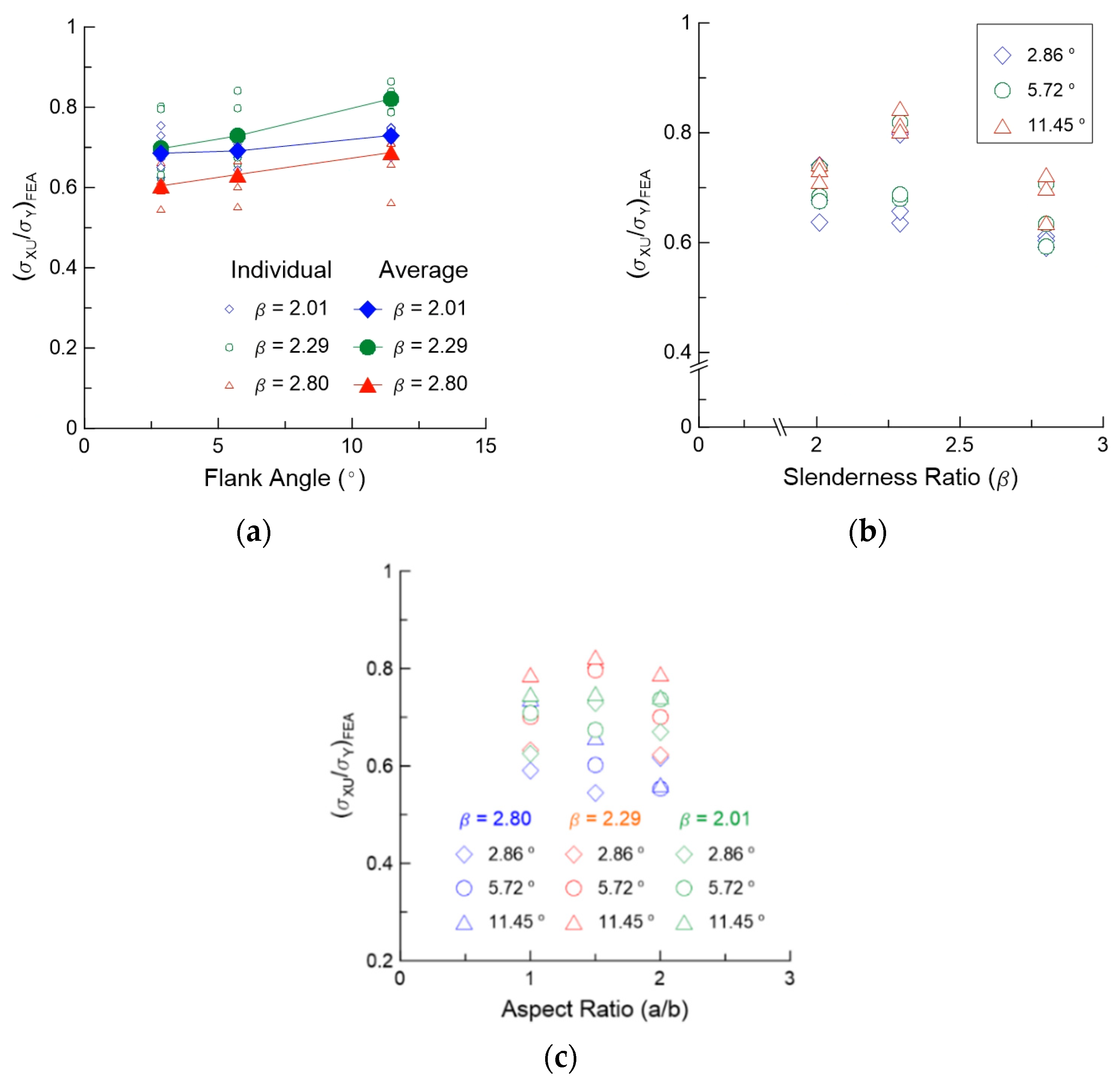
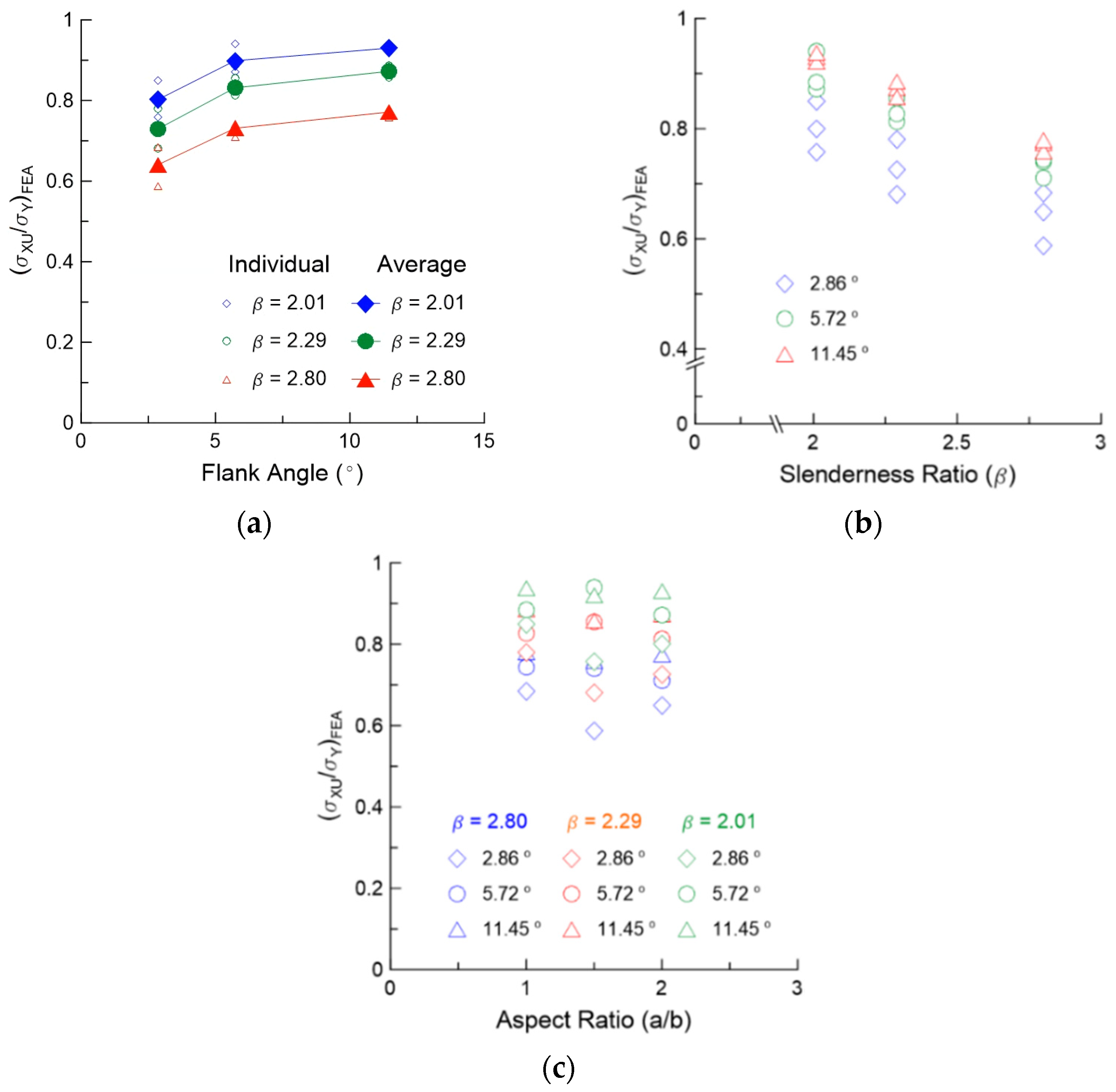
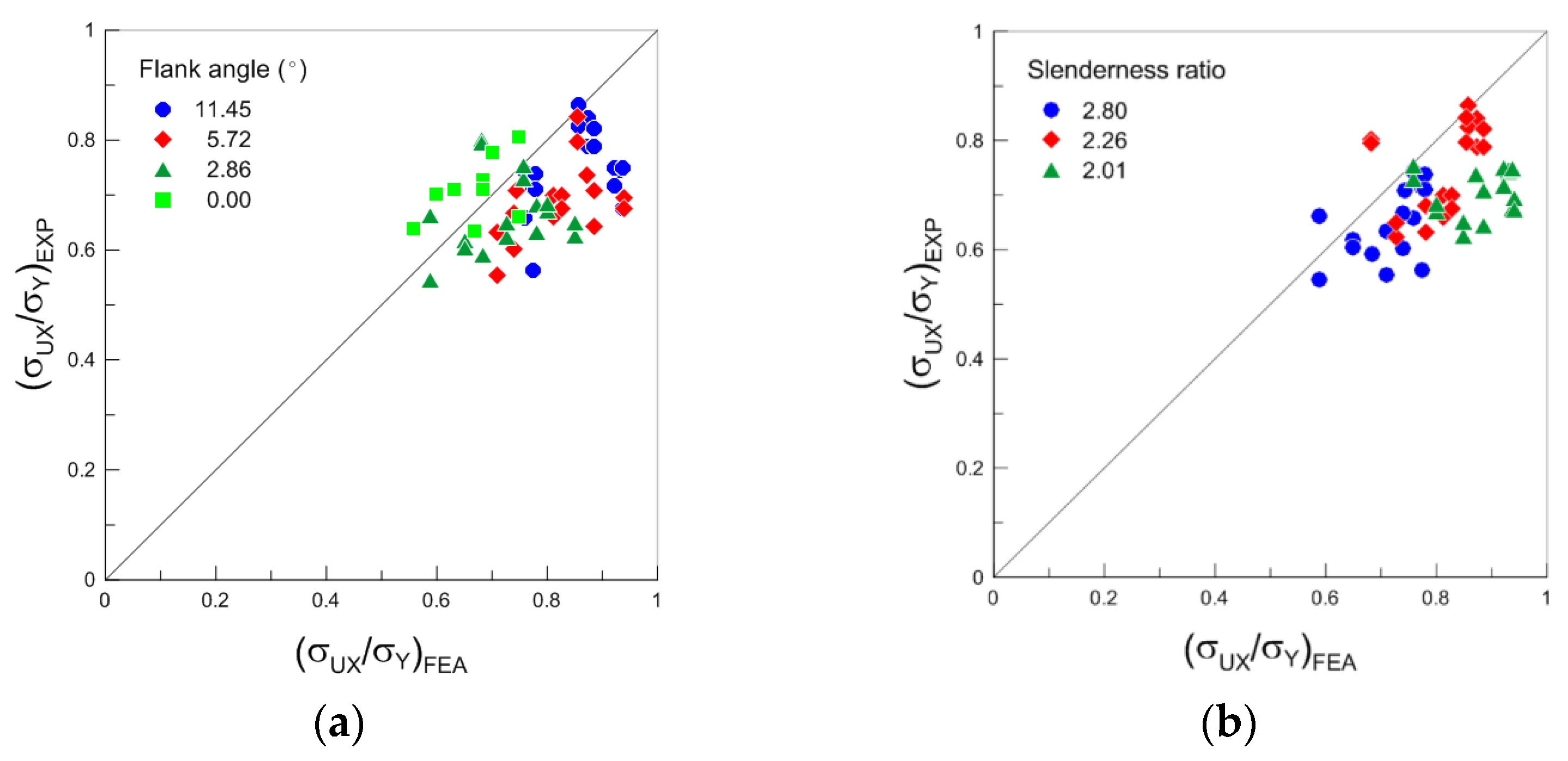
4.2. Ultimate Strength
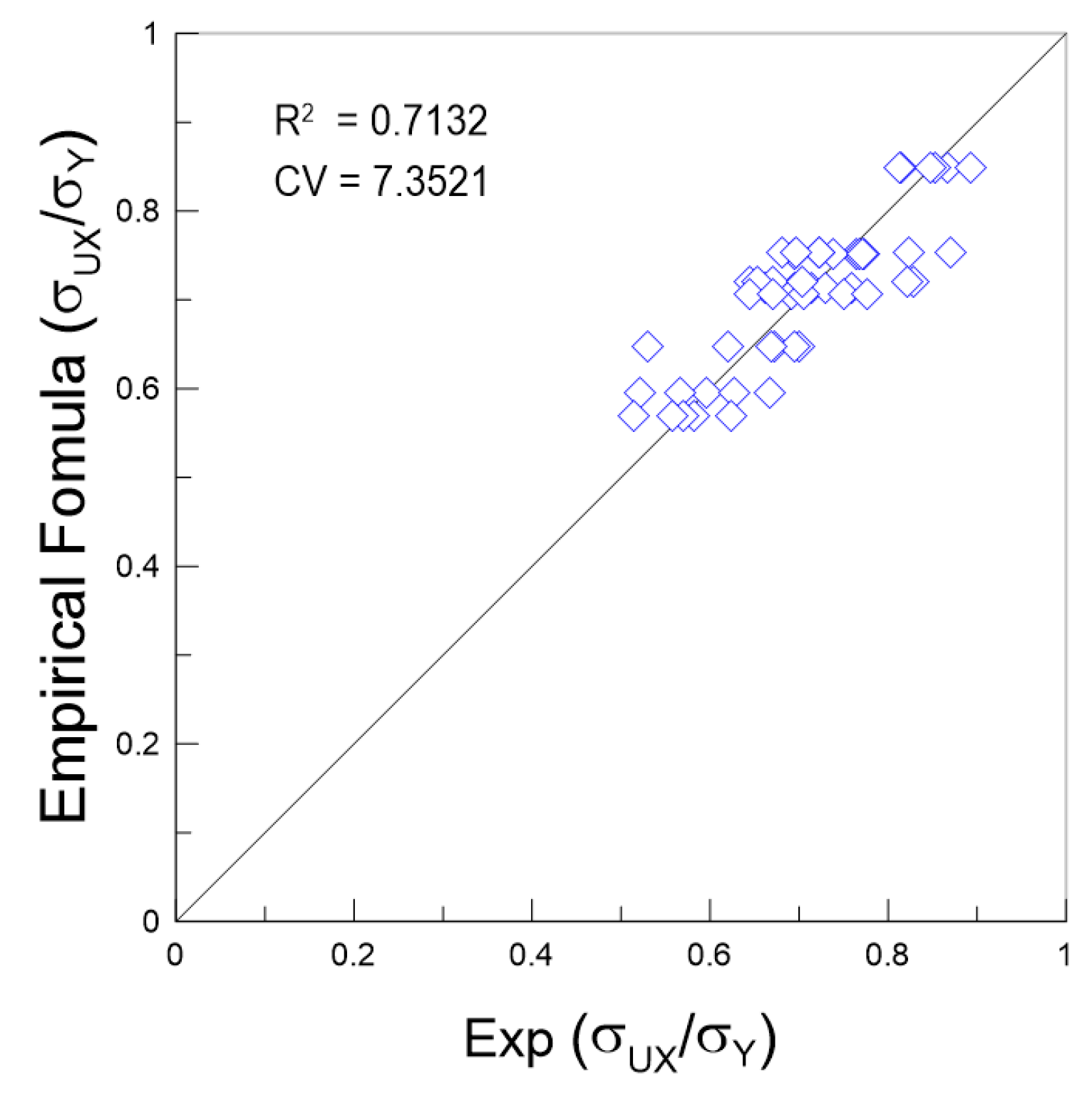
4.3. Suggestion for Design Formula
5. Conclusions
- The ultimate strength of a simply supported curved plate increases with the increase in the flank angle and thickness. In addition, the ultimate strength of a curved plate is significantly low when the slenderness ratio is 2.01 because of special phenomenon such as secondary buckling.
- As the flank angle increases, an additional membrane stress, which is generated in the longitudinal direction at the central part of the curved plate, can restrain the lateral deflection and improve the strength of the curved plate.
- As the flank angle increases, the buckling mode of a simply supported curved plate sequentially changes in the order of two half-wave, three half-wave, and one half-wave under longitudinal compressive loads when aspect ratio is 2. The buckling mode are similar to those of the flat plates as the aspect ratio decreases.
- The difference in the ultimate strengths obtained from the FE analysis and experiment increased with the increase in flank angle, as well as with the decrease in slenderness ratio.
- Improved empirical formulae were derived based on the quantitative experimental database for predicting the ultimate strength of a curved plate. In addition, the result of correlation shows good agreement between the experimental results and the new design formulae. The results can be helpful as a reference in the design of curved plates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.H.; Park, J.S.; Lee, K.H.; Kim, J.H.; Kim, M.H.; Lee, J.M. Computational analysis and design formula development for the design of curved plates for ships and offshore structures. Struct. Eng. Mech. 2014, 49, 705–726. [Google Scholar] [CrossRef]
- Lian, V.T.; Shanmugam, N.E. Opening in horizontally curved plate girder webs. Thin Wall Struct. 2003, 41, 245–269. [Google Scholar] [CrossRef]
- Zhang, N.; Fu, C.C.; Che, H. Experiment and numerical modeling of prestressed concrete curved slab with spatial unbonded tendons. Eng. Struct. 2011, 33, 747–756. [Google Scholar] [CrossRef]
- Wang, J.; Yin, X.; Murakawa, H. Experimental and computational analysis of residual buckling distortion of bead-on-plate welded joint. J. Mater. Process. Technol. 2013, 213, 1447–1458. [Google Scholar] [CrossRef]
- Seifi, R.; Khoda-yari, N. Experimental and numerical studies on buckling of cracked thin-plates under full and partial compression edge loading. Thin Wall Struct. 2011, 49, 1504–1516. [Google Scholar] [CrossRef]
- Gordo, J.M.; Soares, C.G. Compressive tests on stiffened panels of intermediate slenderness. Thin Wall Struct. 2011, 49, 782–794. [Google Scholar] [CrossRef]
- Kwon, Y.B.; Park, H.S. Compression tests of longitudinally stiffened plates undergoing distortional buckling. J. Constr. Steel Res. 2011, 67, 1212–1224. [Google Scholar] [CrossRef]
- Tran, K.L.; Douthe, C.; Sab, K.; Dallot, J.; Davaine, L. Buckling of stiffened curved panels under uniform axial compression. J. Constr. Steel Res. 2014, 103, 140–147. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H.; Jeon, J.H.; Park, J.S.; Seo, H.D.; Ahn, H.J.; Lee, J.M. Effect of reinforcement on buckling and ultimate strength of perforated plates. Int. J. Mech. Sci. 2015, 92, 194–205. [Google Scholar] [CrossRef]
- Memon, B.A.; Su, X.Z. Arc-length technique for nonlinear finite element analysis. J. Zhejiang Univ. Sci. 2004, 5, 618–628. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.S.; Davidson, P.C.; Chapman, J.C.; Dowling, P.J. Strength and stiffness of ships’ plating under in-plane compression and tension. Trans. RINA 1988, 130, 227–296. [Google Scholar]
- Mateus, A.F.; Witz, J.A. A parametric study of the post-buckling behavior of steel plates. Eng. Struct. 2001, 23, 172–185. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, A. Pre- and postbuckling response of curved, thin, composite panels with cutouts under compression. Int. J. Number Method Eng. 1994, 37, 1499–1510. [Google Scholar] [CrossRef]
- Byklum, E.; Amdahl, J. A simplified method for elastic large deflection analysis of plates and stiffened panels due to local buckling. Thin Wall Struct. 2002, 40, 925–953. [Google Scholar] [CrossRef]
- Faulkner, D. A review of effective plating to be used in the analysis of stiffened plating in bending and compression. J. Ship Res. 1975, 19, 1–17. [Google Scholar] [CrossRef]
- Guedes Soares, C. Design equation for the compressive strength of unstiffened plate elements with initial imperfections. J. Constr. Steel Res. 1988, 9, 287–310. [Google Scholar] [CrossRef]






| Test Model | a/b (b = 400 mm) | t (mm) | R (mm) |
|---|---|---|---|
| F01 | 2.0 | 6 | 0 |
| C01 | 2000 | ||
| C02 | 4000 | ||
| C03 | 8000 | ||
| F02 | 2.0 | 7 | 0 |
| C04 | 2000 | ||
| C05 | 4000 | ||
| C06 | 8000 | ||
| F03 | 2.0 | 8 | 0 |
| C07 | 2000 | ||
| C08 | 4000 | ||
| C09 | 8000 | ||
| F04 | 1.5 | 6 | 0 |
| C10 | 2000 | ||
| C11 | 4000 | ||
| C12 | 8000 | ||
| F05 | 1.5 | 7 | 0 |
| C13 | 2000 | ||
| C14 | 4000 | ||
| C15 | 8000 | ||
| F06 | 1.5 | 8 | 0 |
| C16 | 2000 | ||
| C17 | 4000 | ||
| C18 | 8000 | ||
| F07 | 1.0 | 6 | 0 |
| C19 | 2000 | ||
| C20 | 4000 | ||
| C21 | 8000 | ||
| F08 | 1.0 | 7 | 0 |
| C22 | 2000 | ||
| C23 | 4000 | ||
| C24 | 8000 | ||
| F09 | 1.0 | 8 | 0 |
| C25 | 2000 | ||
| C26 | 4000 | ||
| C27 | 8000 |
| Ingredient List | C | Si | Mn | P | S | Ni | Cr |
|---|---|---|---|---|---|---|---|
| Component content (%) | 0.150 | 0.220 | 0.900 | 0.010 | 0.004 | 0.010 | 0.020 |
| No. | Thickness | Yield Strength | Tensile Strength | Elongation |
|---|---|---|---|---|
| 1 | 6 mm | 364 MPa | 491 MPa | 32% |
| 2 | 6 mm | 345 MPa | 478 MPa | 35% |
| 3 | 7 mm | 332 MPa | 475 MPa | 37% |
| 4 | 7 mm | 342 MPa | 475 MPa | 36% |
| 5 | 8 mm | 333 MPa | 464 MPa | 37% |
| 6 | 8 mm | 343 MPa | 476 MPa | 35% |
| Average | 343 MPa | 477 MPa | 35% | |
| Test Model | β | b/R (rad.) | Ultimate Strength (MPa) | FEA/Exp. | |
|---|---|---|---|---|---|
| Experiment | FEA | ||||
| F01 | 2.80 | 0.00 | 218.98 | 190.97 | 0.8720 |
| C01 | 0.20 | 218.65 | 265.84 | 1.2158 | |
| C02 | 0.10 | 203.46 | 243.53 | 1.1969 | |
| C03 | 0.05 | 209.63 | 222.90 | 1.0633 | |
| F02 | 2.29 | 0.00 | 249.63 | 234.26 | 0.9384 |
| C04 | 0.20 | 279.29 | 299.71 | 1.0731 | |
| C05 | 0.10 | 233.11 | 278.64 | 1.1953 | |
| C06 | 0.05 | 218.15 | 249.21 | 1.1424 | |
| F03 | 2.01 | 0.00 | 226.42 | 257.06 | 1.1352 |
| C07 | 0.20 | 255.18 | 319.30 | 1.2513 | |
| C08 | 0.10 | 206.13 | 298.95 | 1.4503 | |
| C09 | 0.05 | 232.34 | 274.48 | 1.1813 | |
| F04 | 2.80 | 0.00 | 240.68 | 205.32 | 0.8530 |
| C10 | 0.20 | 240.28 | 271.73 | 1.1309 | |
| C11 | 0.10 | 217.47 | 253.84 | 1.1673 | |
| C12 | 0.05 | 207.13 | 201.67 | 0.9736 | |
| F05 | 2.29 | 0.00 | 243.40 | 216.51 | 0.8895 |
| C13 | 0.20 | 289.76 | 294.15 | 1.0151 | |
| C14 | 0.10 | 281.00 | 293.15 | 1.0433 | |
| C15 | 0.05 | 273.79 | 233.82 | 0.8540 | |
| F06 | 2.01 | 0.00 | 266.54 | 240.20 | 0.9011 |
| C16 | 0.20 | 251.66 | 315.99 | 1.2556 | |
| C17 | 0.10 | 234.66 | 322.47 | 1.3742 | |
| C18 | 0.05 | 254.34 | 259.92 | 1.0219 | |
| F07 | 2.80 | 0.00 | 217.27 | 228.90 | 1.0535 |
| C19 | 0.20 | 248.25 | 267.43 | 1.0772 | |
| C20 | 0.10 | 242.86 | 254.98 | 1.0499 | |
| C21 | 0.05 | 202.86 | 234.73 | 1.1571 | |
| F08 | 2.29 | 0.00 | 243.87 | 234.26 | 0.9606 |
| C22 | 0.20 | 275.95 | 303.82 | 1.1010 | |
| C23 | 0.10 | 235.86 | 283.76 | 1.2031 | |
| C24 | 0.05 | 225.30 | 267.77 | 1.1885 | |
| F09 | 2.01 | 0.00 | 276.15 | 257.06 | 0.9308 |
| C25 | 0.20 | 244.03 | 321.62 | 1.3180 | |
| C26 | 0.10 | 231.83 | 303.46 | 1.3090 | |
| C27 | 0.05 | 218.75 | 291.36 | 1.3319 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-H.; Park, D.-H.; Kim, S.-K.; Kim, M.-S.; Lee, J.-M. Experimental Study and Development of Design Formula for Estimating the Ultimate Strength of Curved Plates. Appl. Sci. 2021, 11, 2379. https://doi.org/10.3390/app11052379
Kim J-H, Park D-H, Kim S-K, Kim M-S, Lee J-M. Experimental Study and Development of Design Formula for Estimating the Ultimate Strength of Curved Plates. Applied Sciences. 2021; 11(5):2379. https://doi.org/10.3390/app11052379
Chicago/Turabian StyleKim, Jeong-Hyeon, Doo-Hwan Park, Seul-Kee Kim, Myung-Sung Kim, and Jae-Myung Lee. 2021. "Experimental Study and Development of Design Formula for Estimating the Ultimate Strength of Curved Plates" Applied Sciences 11, no. 5: 2379. https://doi.org/10.3390/app11052379
APA StyleKim, J.-H., Park, D.-H., Kim, S.-K., Kim, M.-S., & Lee, J.-M. (2021). Experimental Study and Development of Design Formula for Estimating the Ultimate Strength of Curved Plates. Applied Sciences, 11(5), 2379. https://doi.org/10.3390/app11052379






