Integrated Design of a Morphing Winglet for Active Load Control and Alleviation of Turboprop Regional Aircraft
Abstract
:1. Introduction
2. Regional Aircraft AG2-Natural Laminar Flow Wing
2.1. Reference Aircraft
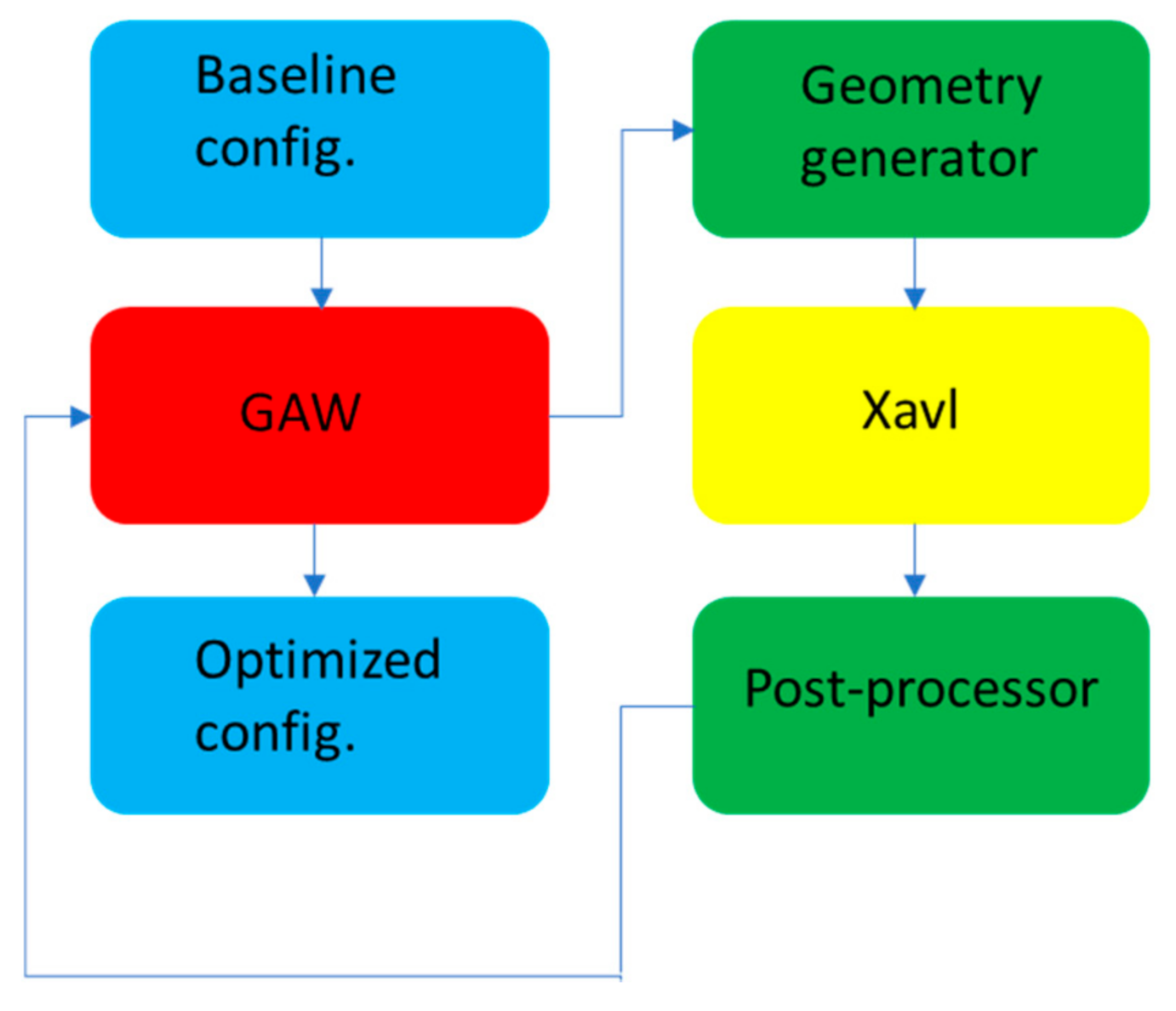
2.2. Numerical Methods Used for Aerodynamic Performance Evaluation
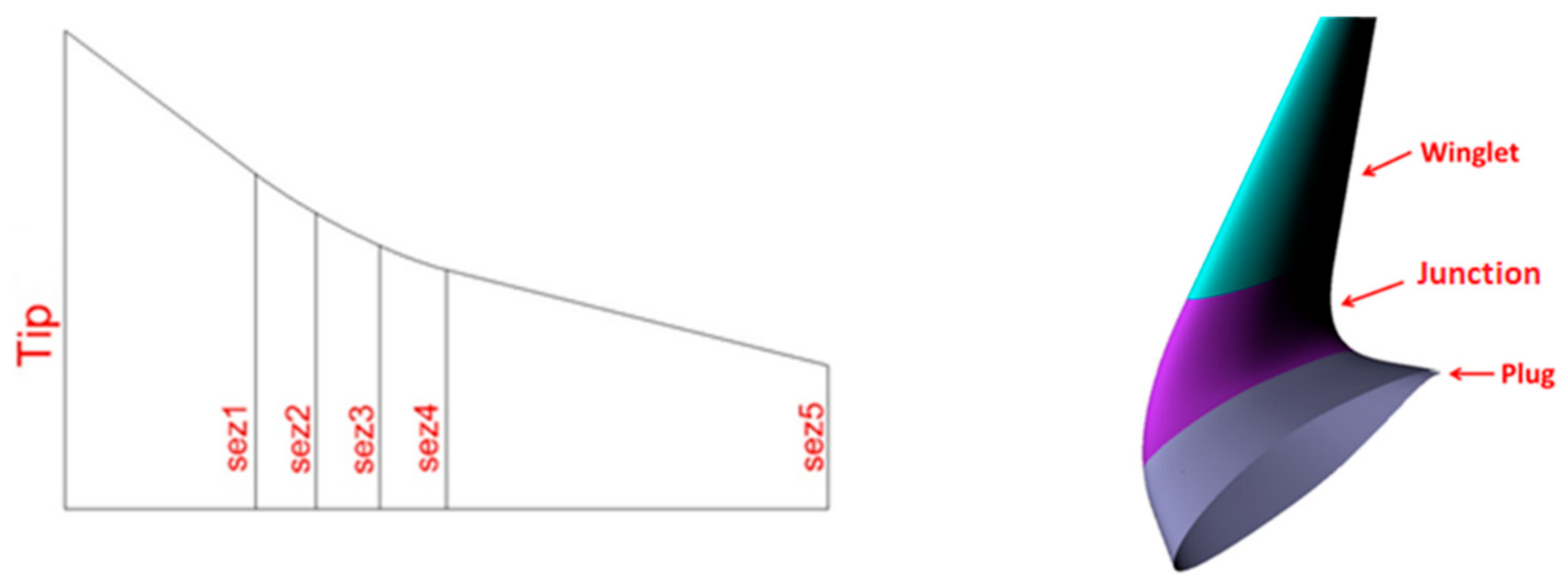
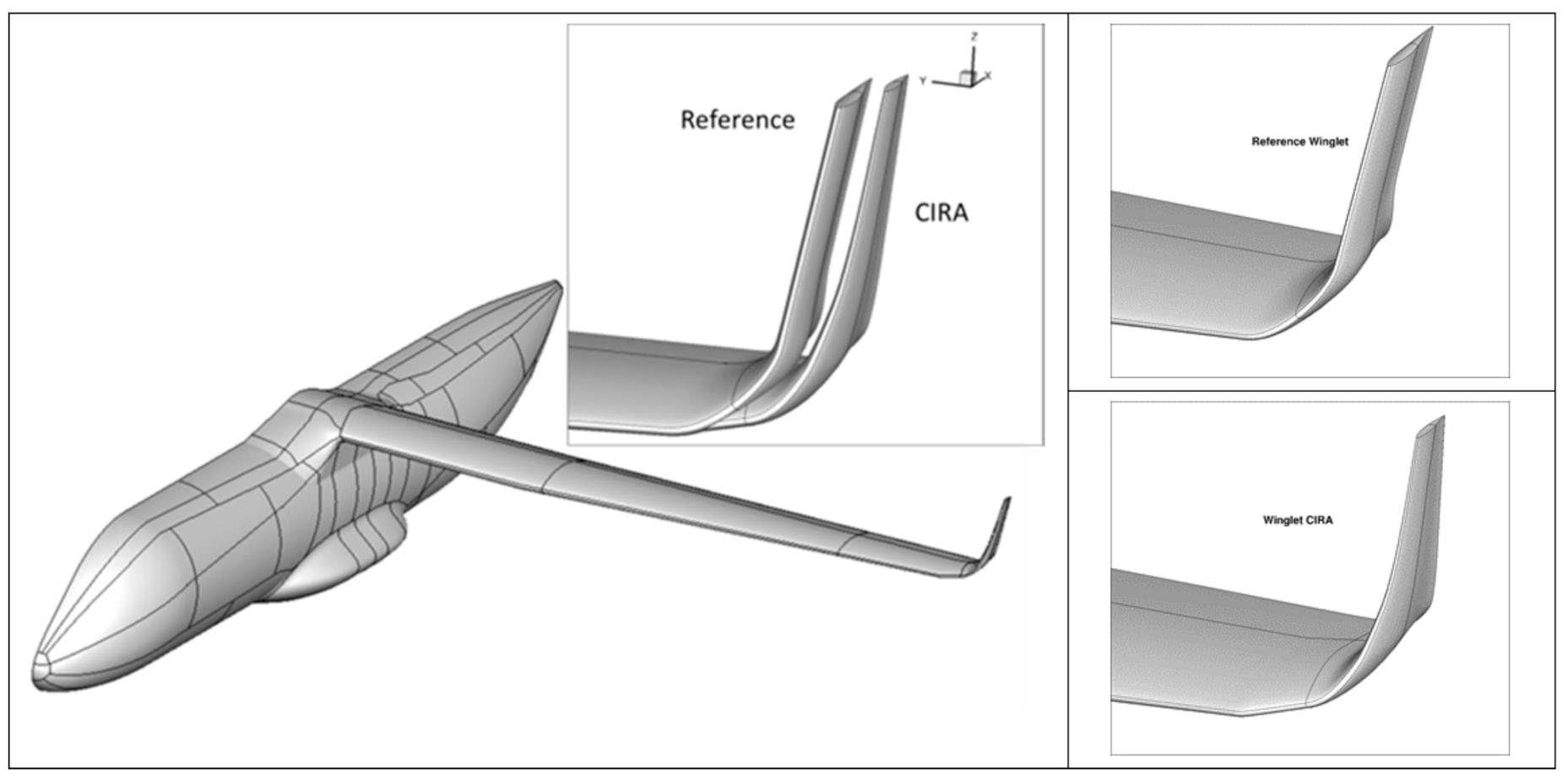
2.3. AG2-NLF Wing Equipped with Reference Winglets
2.4. A/C Aero-Structural Model
2.4.1. Structural Model
2.4.2. Aerodynamic Model
3. Aerodynamic Design and Performance of the Morphing Winglet
3.1. Morphing Winglet Concept
3.2. Low-Fidelity Simulations
3.3. High Fidelity CFD Results and Performance Comparison at Design Points
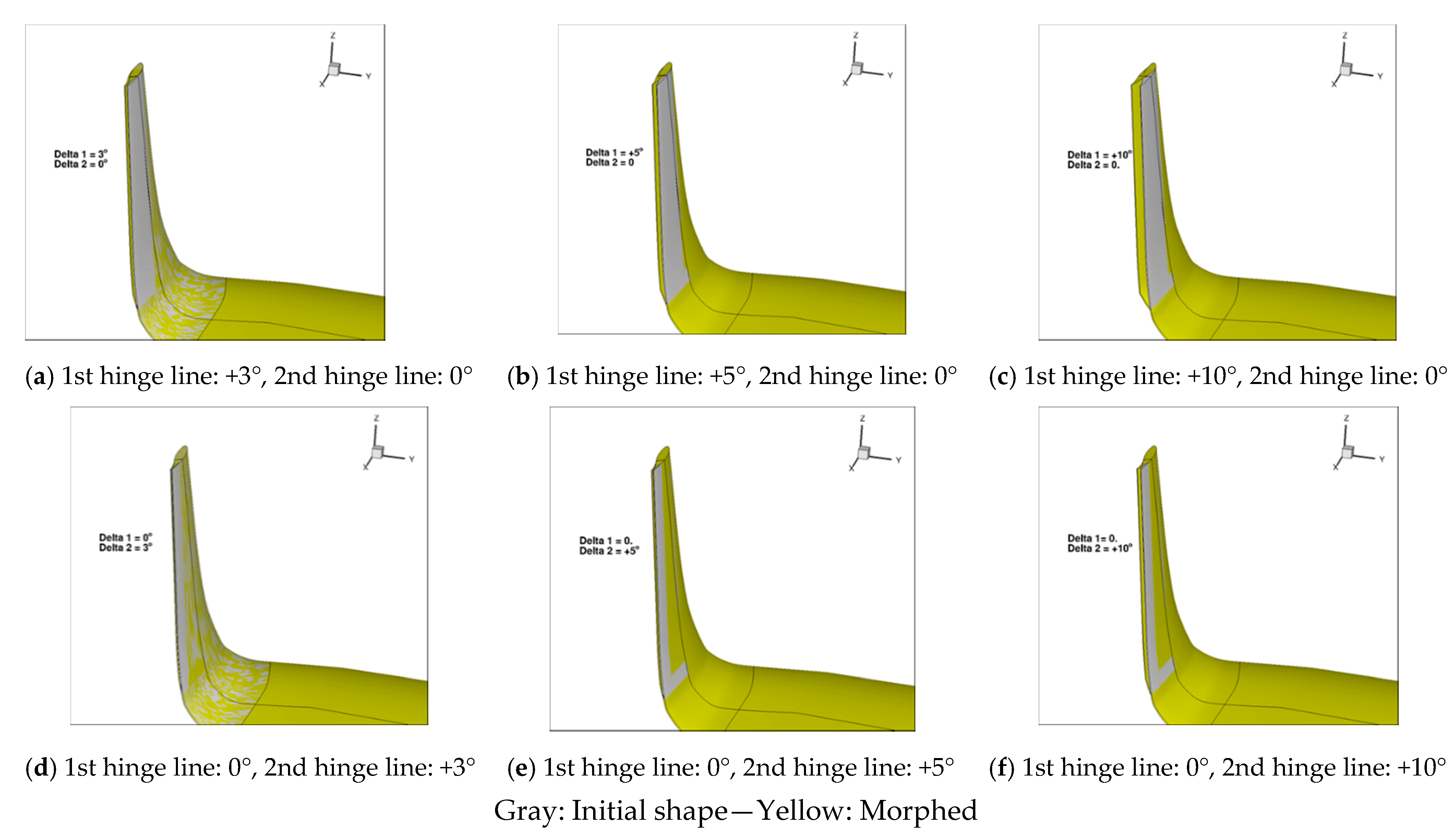
3.4. Study of Morphing Winglet Configurations
4. Active Load Alleviation Performance
4.1. Static Aeroelastic Analysis
4.1.1. Model Definition
4.1.2. Controller Definition
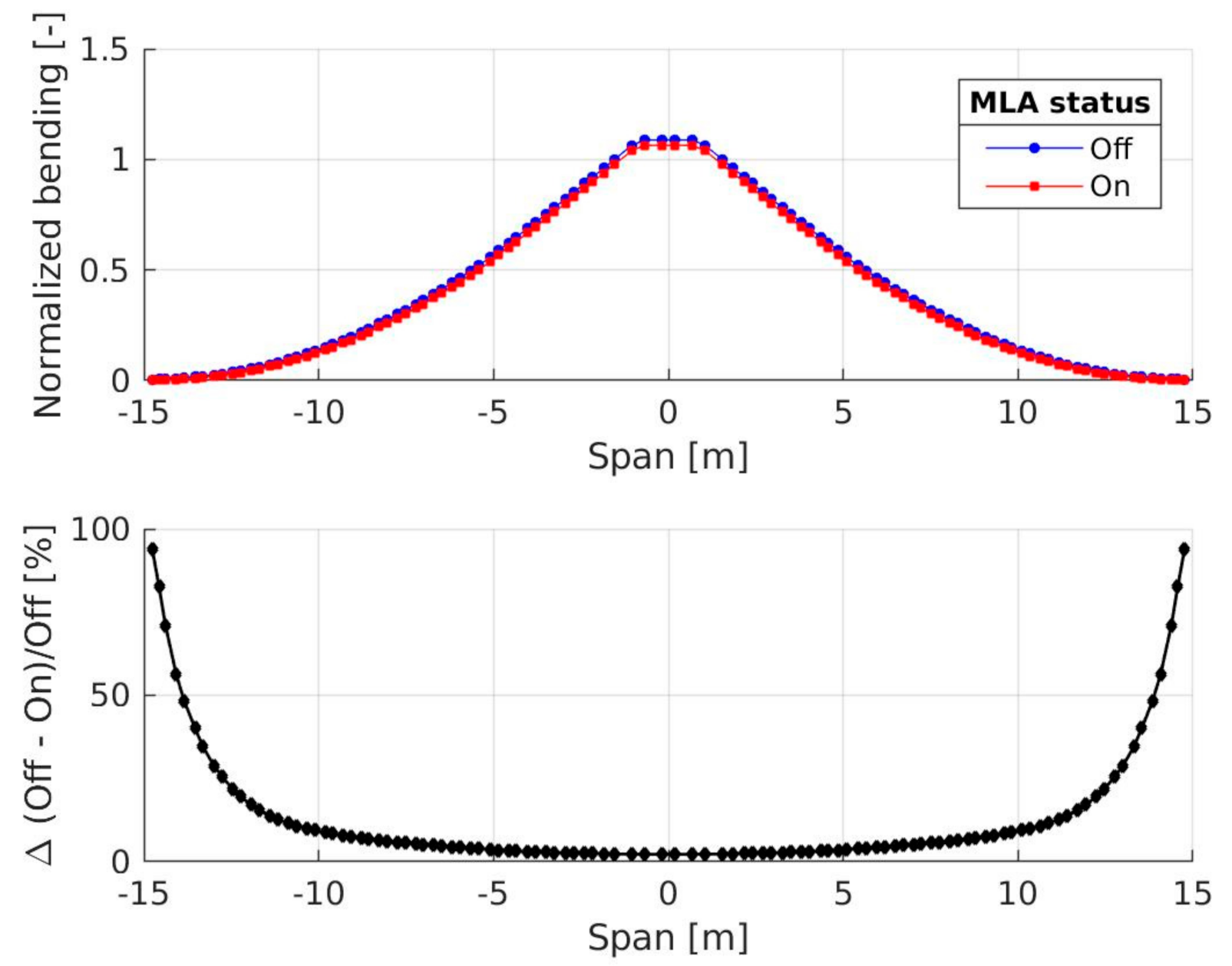
4.1.3. Simulation Results
4.2. Aeroelastic State-Space Model of the A/C
4.3. Winglet Actuation Model
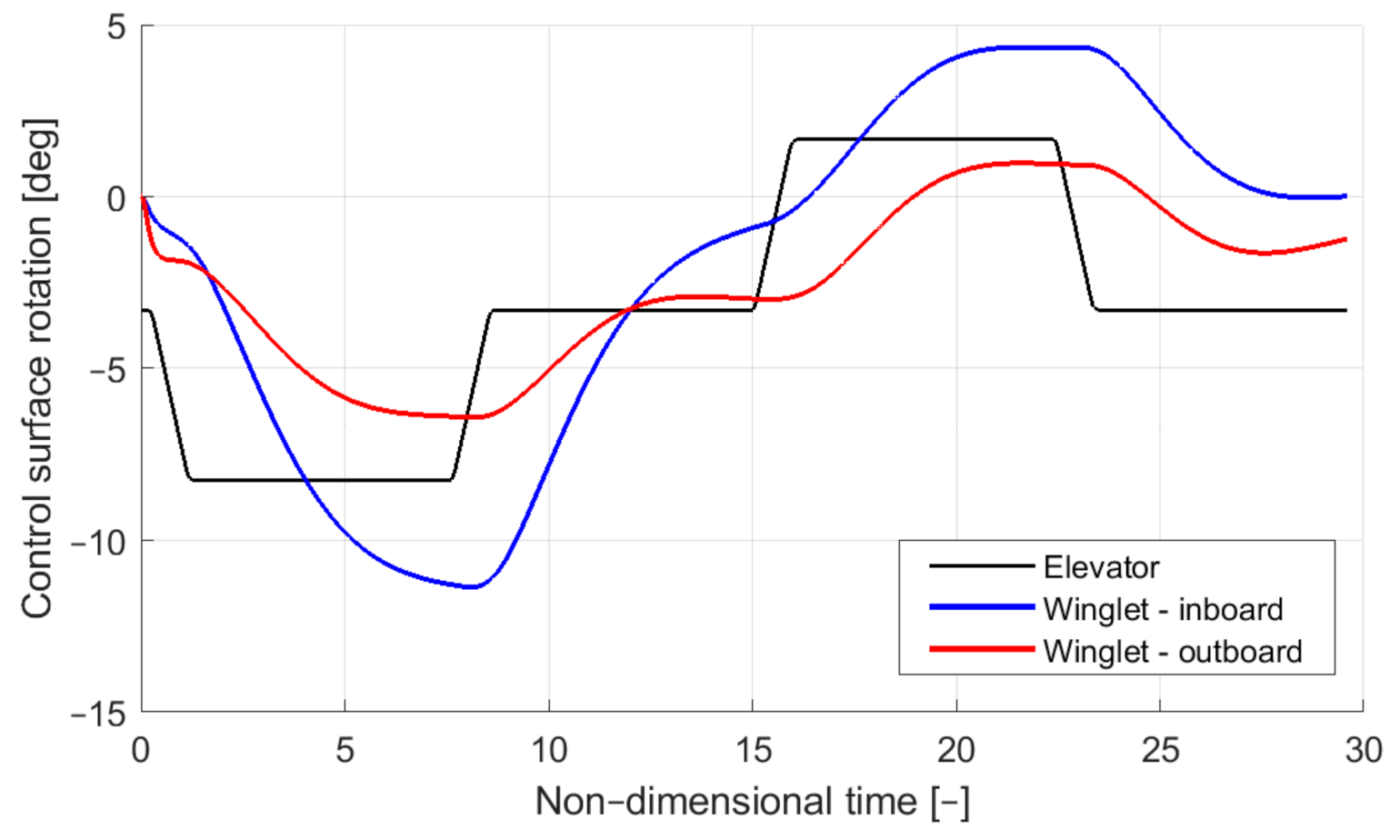
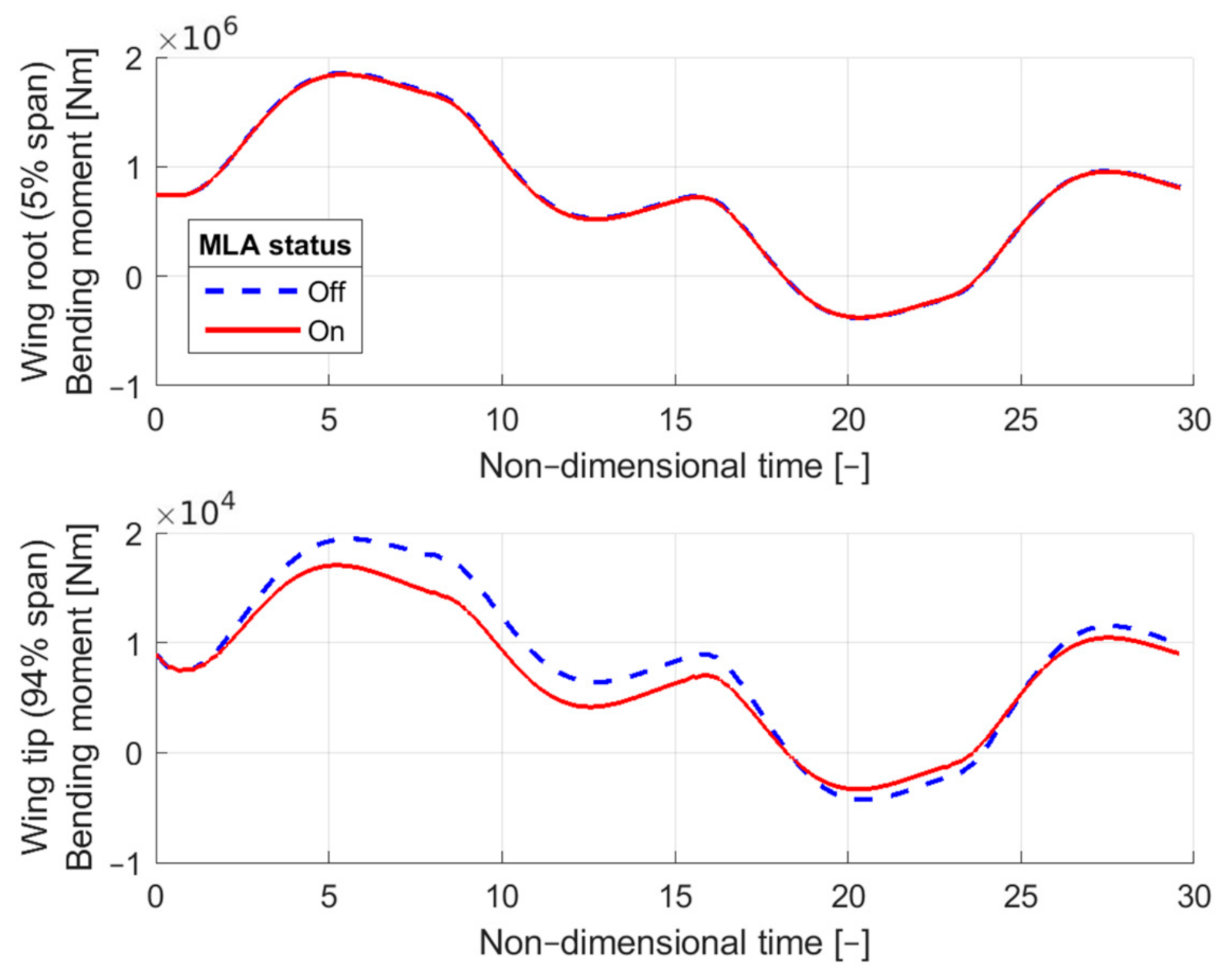
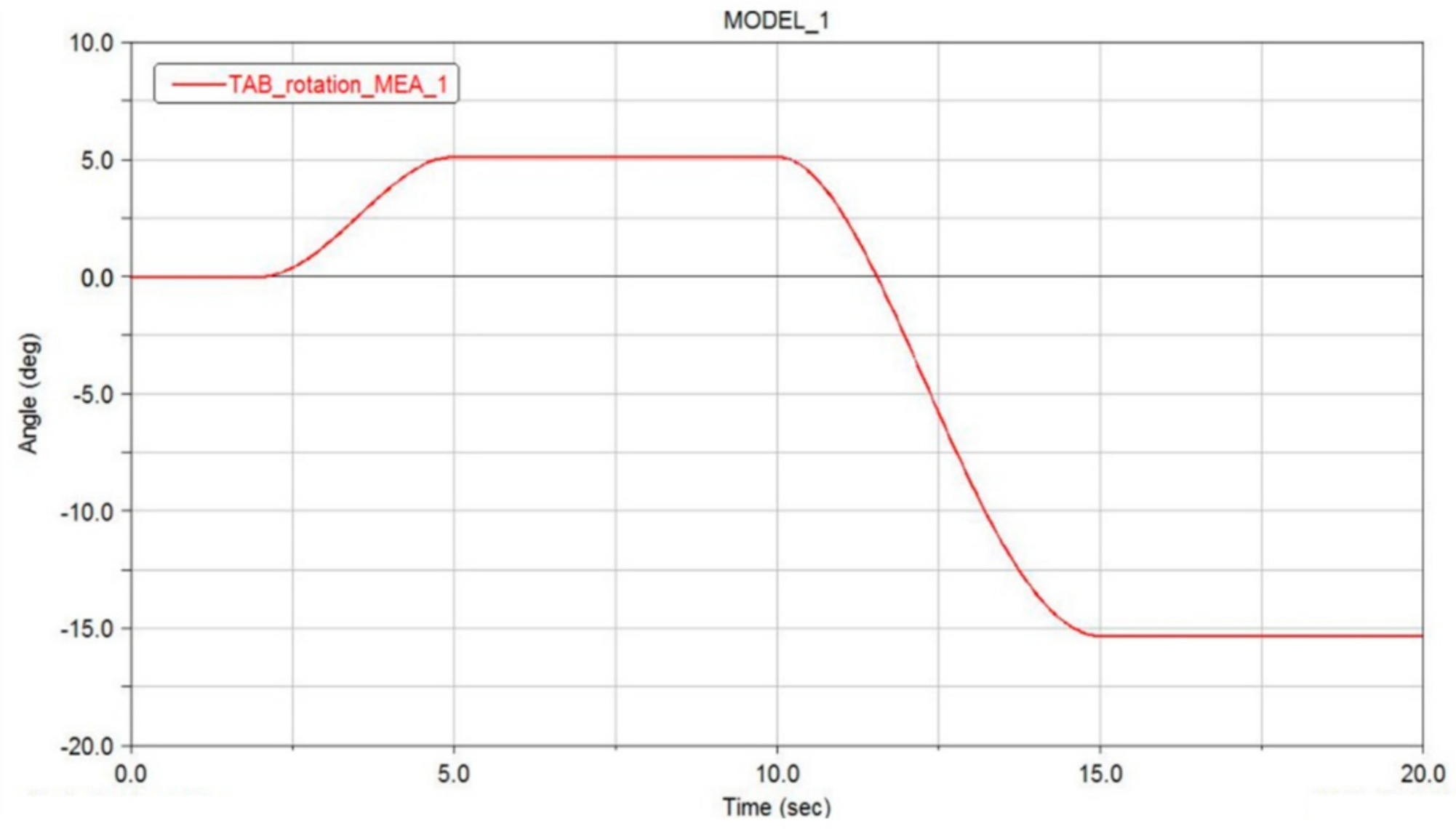
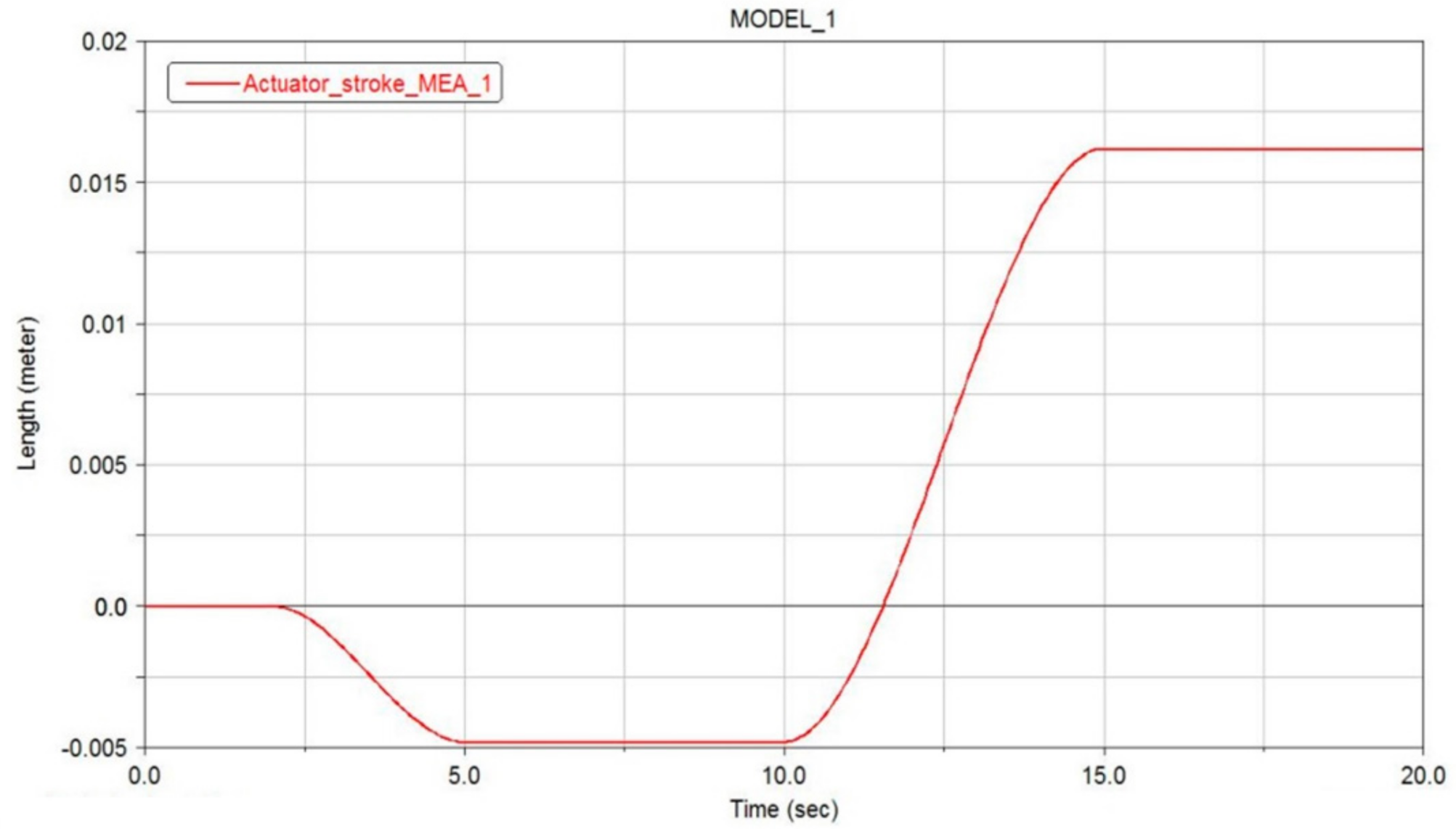
4.4. Time Simulation Results
5. Structural Design and Systems Integration
5.1. Preliminary Structural Layout
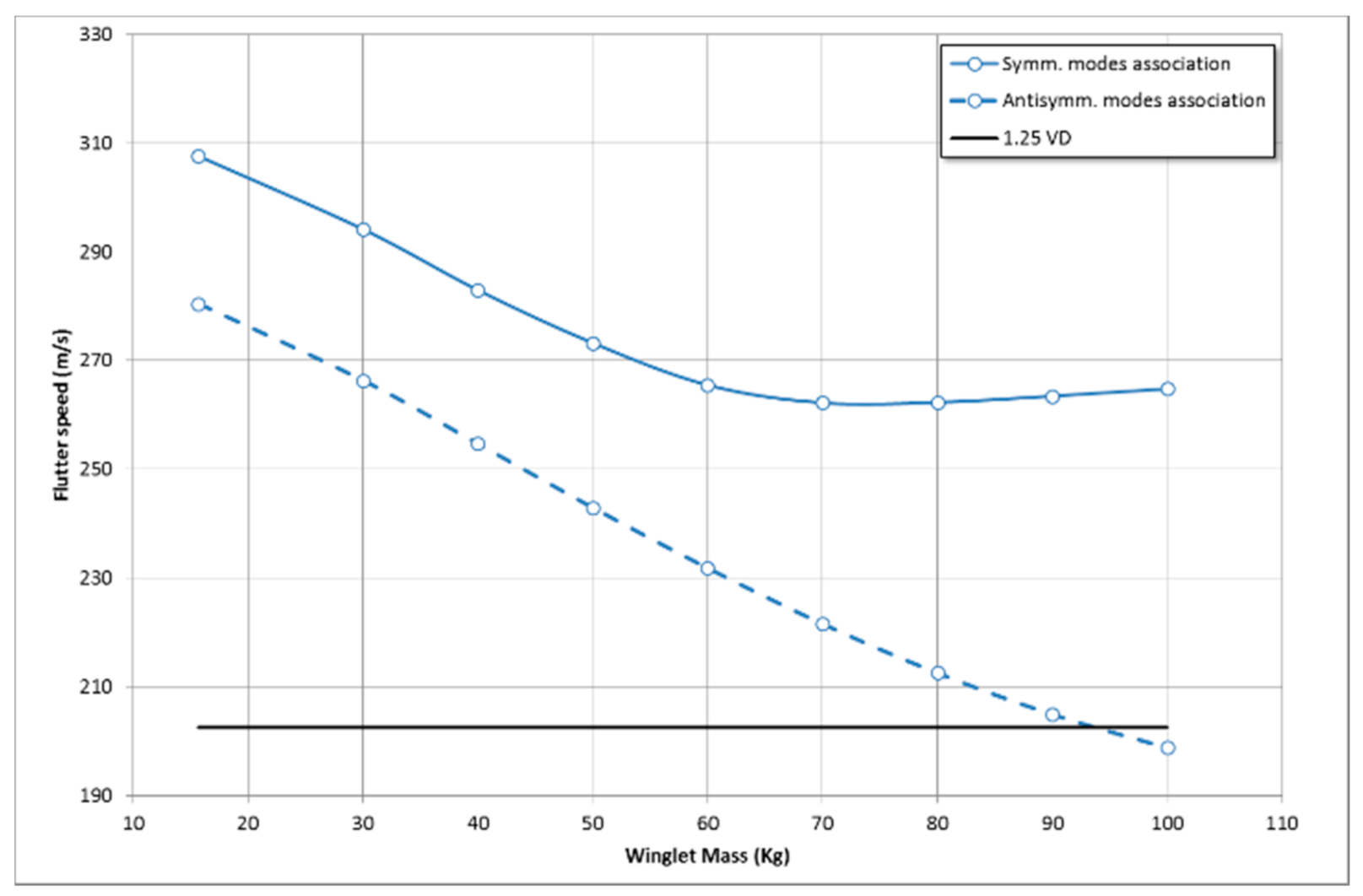
5.2. Aeroelastic Trade-Off
- Association of the theoretical elastic modes up to 60 Hz;
- Modal damping conservatively set to 1.5% for all the elastic modes;
- All moveable surfaces in control-fixed attitude;
- Sea-level flight altitude;
- Flight speed range: (0: 200 m/s) 200 m/s being equal to 1.25*VD as for certification requirements.
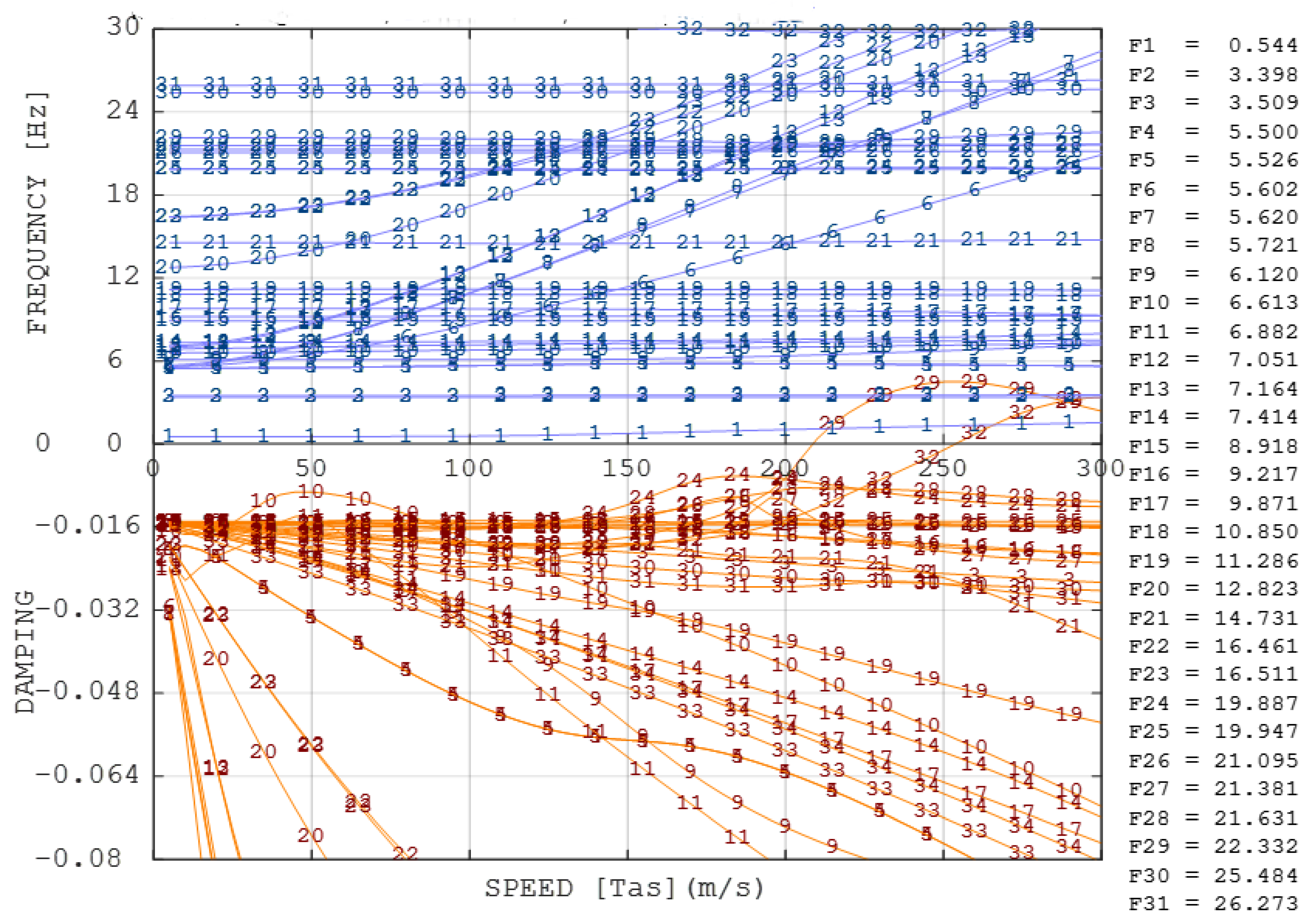
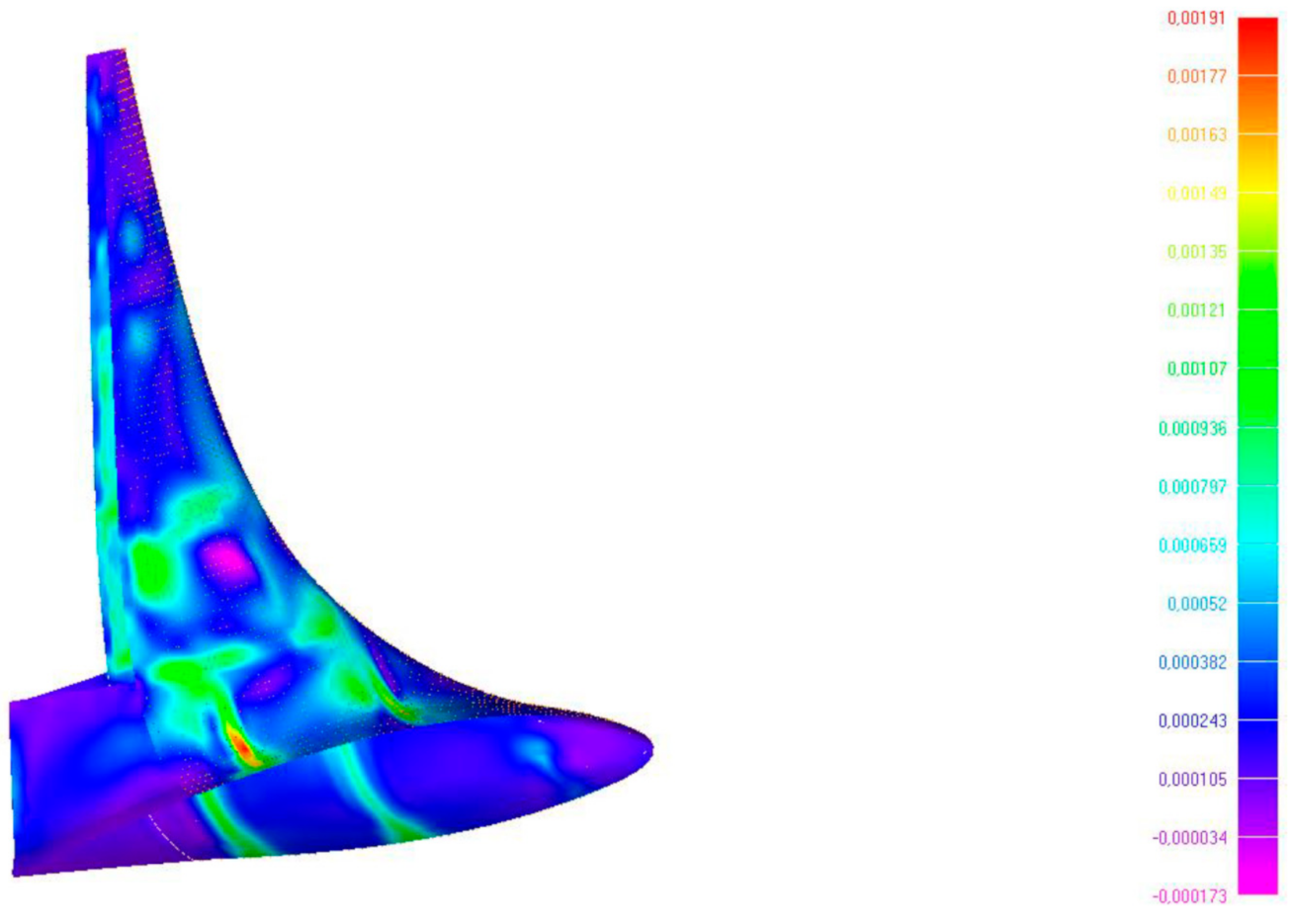
5.3. FE Model
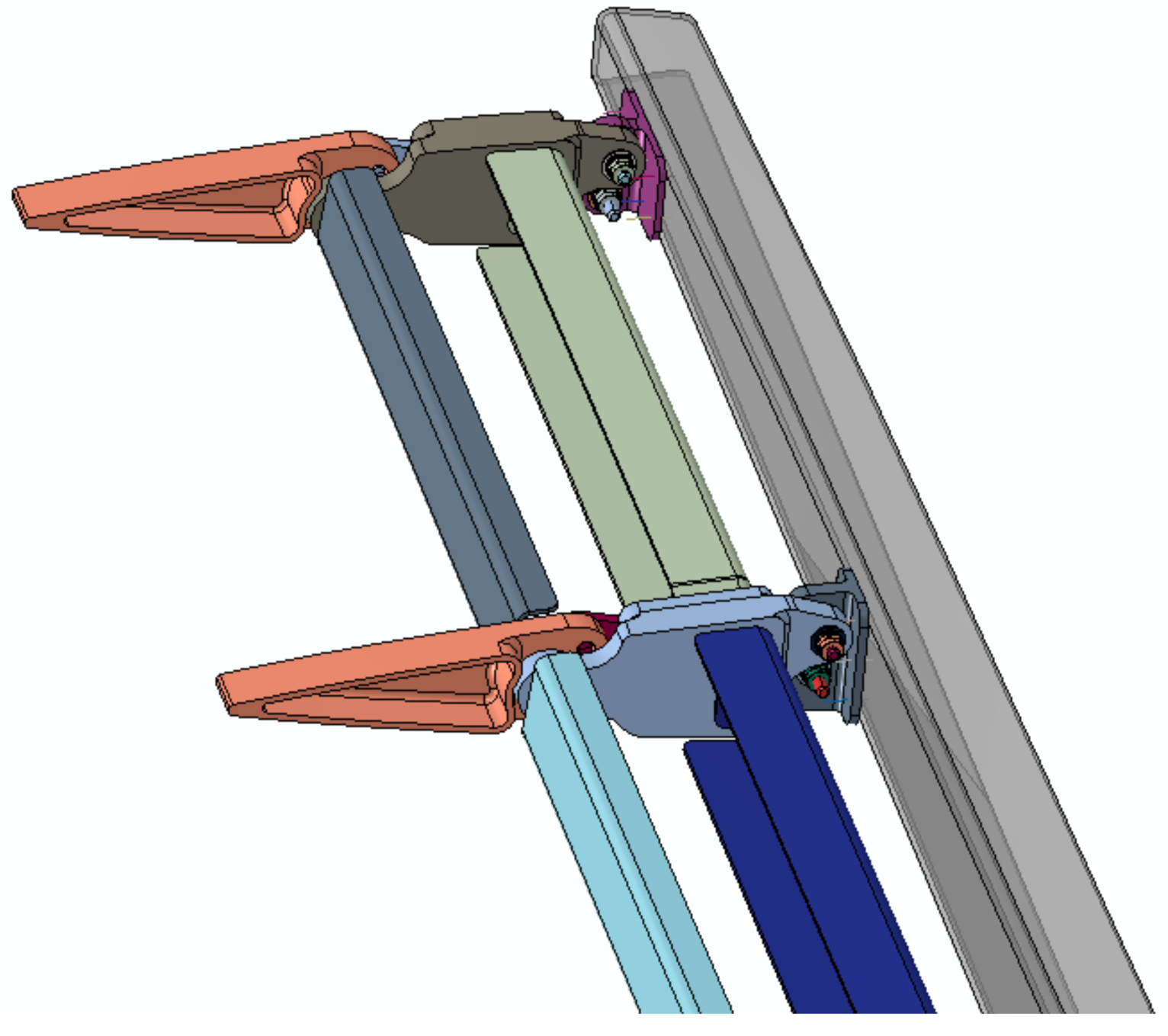
5.4. Actuation Layout
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A/C | Aircraft |
| AG2 | Airgreen 2 project |
| AG2-NLF | Regional aircraft of the AIRGREEN2 project equipped with the NLF wing |
| CFD | Computational Fluid Dynamics |
| CS2 | Clean Sky 2 |
| CL | Lift coefficient |
| CD | Drag coefficient |
| EMA | Electromechanical actuators |
| LCA | Load Control and Alleviation |
| LoD | Lift over Drag ratio |
| MLA | Maneuver Load Alleviation |
| NLF | Natural Laminar Flow |
| TP90 | 90-passenger Regional Turboprop Aircraft |
References
- Holle, A.A. Plane and the Like for Aeroplanes. U.S. Patent No.1225711, 8 May 1917. [Google Scholar]
- Parker, H.F.; National Advisory Committee for Aeronautics. The Parker Variable Camber Wing, NACA Technical Report 77; 1920. Retrieved 7 April 2016. Available online: https://digital.library.unt.edu/ark:/67531/metadc65726/ (accessed on 9 February 2021).
- Culick, F. Wright brothers: First aeronautical engineers and test pilots. In Proceedings of the 45th Annual Symposium The Society of Experimental Test Pilots, Los Angeles, CA, USA, 26–29 September 2001. [Google Scholar]
- Ader, C. Appareille Aile‘ Pour la Navigation Aerienne. France Patent No.205155, 11 August 1890. [Google Scholar]
- Smith, J.W.; Lock, W.P.; Payne, G.A. Variable-Camber Systems Integration and Operational Performance of the AFTI/F-111 Mission Adaptive Wing; NASA Technical Memorandum TM-4370; National Aeronautics and Space Administration: Edwards, CA, USA, April 1992.
- Hilbig, R.; Koerner, H. Aerodynamische Entwicklungsrichtungen fuer Verkehrsflugzeuge, Deutsche Gesellschaft fuer Luft-und Raumfahrt (DGLR). In Proceedings of the DGLR Annual Convention 1984, Hamburg, Germany, 1–3 October 1984. [Google Scholar]
- Kudva, J.N. Overview of the DARPA smart wing project. J. Intell. Mater. Syst. Struct. 2004, 15, 261–267. [Google Scholar]
- NASA; US AFRL. Adaptive Compliant Trailing Edge Flight Experiment; RC Soaring Digest: Olalla, WA, USA, 2014; Volume 31, pp. 85–86. [Google Scholar]
- Kuzmina, S.; Ishmuratov, F.; Zichenkov, M.; Chedrik, V.; Amiryants, G.A.; Kulesh, V.; Malyutin, V.; Chedrik, A.; Timokhin, V.; Shalaev, S.; et al. Wind Tunnel Testing of Adaptive Wing Structures. Morphing Wing Technol. 2018, 1, 713–755. [Google Scholar]
- Wildschek, A.; Storm, S.; Herring, M.; Drezga, D.; Korian, V.; Roock, O. Design, Optimization, Testing, Verification, and Validation of the Wingtip Active Trailing Edge. In Smart Intelligent Structures (SARISTU); Springer: Berlin/Heidelberg, Germany, 2016; pp. 219–255. [Google Scholar]
- Cooper, J.E.; Chekkal, I.; Cheung, R.C.M.; Wales, C.; Allen, N.J.; Lawson, S.; Peace, A.J.; Cook, R.; Standen, P.; Hancock, S.D.; et al. Design of a Morphing Wingtip. AIAA J. Aircr. 2015, 52. [Google Scholar] [CrossRef] [Green Version]
- Liauzun, C.; le Bihan, D.; David, J.M.; Joly, D.; Paluch, B. Study of Morphing Winglet Concepts Aimed at Improving Load Control and the Aeroelastic Behavior of Civil Transport Aircraft. Aerosp. Lab. J. 2018, 14, 1–15. [Google Scholar]
- Ameduri, S.; Concilio, A.; Dimino, I.; Pecora, R.; Ricci, S. AIRGREEN2—Clean Sky 2 programme: Adaptive wing technology maturation, challenges and perspectives. In Proceedings of the ASME conference on smart materials, adaptive structures and intelligent systems, San Antonio, TX, USA, 10–12 September 2018; Paper no. SMASIS2018-8235. ASME: New York, NY, USA, 2018. [Google Scholar]
- Moens, F. Augmented Aircraft Performance with the Use of Morphing Technology for a Turboprop Regional Aircraft Wing. Biomimetics 2019, 4, 64. [Google Scholar] [CrossRef] [Green Version]
- De Gaspari, A.; Moens, F. Aerodynamic Shape Design and Validation of an Advanced High-Lift Device for a Regional Aircraft with Morphing Droop Nose. Int. J. Aerosp. Eng. 2019, 2019, 7982168. [Google Scholar] [CrossRef] [Green Version]
- Dimino, I.; Ameduri, S.; Concilio, A. Preliminary failure analysis and structural design of a morphing winglet for green regional aircraft. In Proceedings of the ASME 2018 Conference on Smart Materials, Adaptive Structures and Intelligent Systems (SMASIS2018), San Antonio, TX, USA, 10–12 September 2018. [Google Scholar]
- Dimino, I.; Gallorini, F.; Palmieri, M.; Pispola, G. Electromechanical Actuation for Morphing Winglets. Actuators 2019, 8, 42. [Google Scholar] [CrossRef] [Green Version]
- Noviello, M.C.; Dimino, I.; Concilio, A.; Amoroso, F.; Pecora, R. Aeroelastic Assessments and Functional Hazard Analysis of a Regional Aircraft Equipped with Morphing Winglets. Aerospace 2019, 6, 104. [Google Scholar] [CrossRef] [Green Version]
- Pecora, R.; Amoroso, F.; Noviello, M.C.; Concilio, A.; Dimino, I. Aeroelastic Stability Analysis of a Large Civil Aircraft Equipped with Morphing Winglets and Adaptive Flap Tabs. In Proceedings of the SPIE. 10595, Active and Passive Smart Structures and Integrated Systems XII, Bellingham, WA, USA, 4–8 March 2018. [Google Scholar]
- Verrastro, M.; Dimino, I. Morphing devices: Safety, reliability, and certification prospects. In Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Elsevier Inc.: Amsterdam, The Netherlands, 2018; pp. 647–682. ISBN 9780081009642. [Google Scholar] [CrossRef]
- Regional Aircraft Innovation Takes a Great Leap Forward. Available online: https://cordis.europa.eu/article/id/422623-regional-aircraft-innovation-takes-a-great-leap-forward (accessed on 9 February 2021).
- Cambier, L.; Heib, S.; Plot, S. The Onera elsA CFD Software: Input from Research and Feedback from Industry. Mech. Ind. 2013, 14, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical Solutions of the Euler Equations by Finite Volume Methods Using Runge-Kutta Time Stepping. In Proceedings of the 14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA, 23–25 June 1981. [Google Scholar]
- Spalart, P.R. Strategies for Turbulence Modelling and Simulation. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar]
- Wölcken, P.; Papadopoulos, M. (Eds.) Smart Intelligent Aircraft Structures (SARISTU): Proceedings of the Final Project Conference; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Concilio, A.; Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies. Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Moens, F.; Perraud, J.; Krumbein, A.; Toulorge, T.; Iannelli, P.; Hanifi, A. Transition Prediction and Impact on 3D High-Lift Wing Configuration. In Proceedings of the 25th AIAA Applied Aerodynamics Conference, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Cavagna, L.; Ricci, S.; Travaglini, L. NeoCASS: An integrated tool for structural sizing, aeroelastic analysis and MDO at conceptual design level. Prog. Aerosp. Sci. 2011, 47, 621–635. [Google Scholar]
- Ghiringhelli, G.L.; Masarati, P.; Mantegazza, P. Multibody implementation of finite volume C beams. AIAA J. 2000, 38, 131–138. [Google Scholar]
- Albano, E.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Allen, J.B. Articulating Winglets. U.S. Patent 5,988,563 A, 23 November 1999. [Google Scholar]
- Irving, J.; Davies, R. Wing Tip Device. U.S. Patent 7,275,722 B2, 2 October 2007. [Google Scholar]
- Wildschek, A.; Prananta, B.; Kanakis, T.; van Tongeren, H.; Huls, R. Concurrent Optimization of a Feed-Forward Gust Loads Controller and Minimization of Wing Box Structural Mass on an Aircraft with Active Winglets. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015; pp. 1–24. [Google Scholar] [CrossRef]
- Gatto, A.; Bourdin, P.; Friswell, M.I. Experimental Investigation into the Control and Load Alleviation Capabilities of Articulated Winglets. Int. J. Aerosp. Eng. 2012, 2012, 789501. [Google Scholar] [CrossRef]
- Concilio ADimino, I.; Pecora, R. SARISTU: Adaptive Trailing Edge Device (ATED) design process review. Chin. J. Aeronaut. 2020. [Google Scholar] [CrossRef]
- Pecora, R.; Concilio, A.; Dimino, I.; Amoroso, F.; Ciminello, M. Structural design of an adaptive wing trailing edge for enhanced cruise performance. In Proceedings of the 24th AIAA/AHS Adaptive Structures Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Pecora, R.; Amoroso, F.; Magnifico, M.; Dimino, I. Concilio, KRISTINA: Kinematic rib-based structural system for innovative adaptive trailing edge. In Proceedings of the SPIE—The International Society for Optical Engineering, Las Vegas, NV, USA, 20–24 March 2016; Volume 9801, p. 980107. [Google Scholar]
- Amendola, G.; Dimino, I.; Concilio, A.; Magnifico, M.; Pecora, R. Numerical design of an adaptive aileron. In Proceedings of the SPIE—The International Society for Optical Engineering, Las Vegas, NV, USA, 20–24 March 2016; Volume 9803, p. 98032. [Google Scholar] [CrossRef]
- Amendola, G.; Dimino, I.; Concilio, A.; Amoroso, F.; Pecora, R. Preliminary design of an adaptive aileron for the next generation regional aircraft. J. Theor. Appl. Mech. 2017, 55, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Amendola, G.; Dimino, I.; Concilio, A.; Pecora, R.; Amoroso, F.; Lecce, L. Technological demonstration of an adaptive aileron system. In Proceedings of the SPIE 10593, Bioinspiration, Biomimetics, and Bioreplication VIII, Denver, CO, USA, 27 March 2018; p. 1059304. [Google Scholar] [CrossRef]
- Iuliano, E.; Andreutti, G.; Quagliarella, D.; Vitagliano, P.L. Evolutionary-Based Aero-Structural Optimization of a Joined Wing UAV Using Advanced Potential Methods. In Proceedings of the ECCOMAS 2008 Conference, Venice, Italy, 30 June–4 July 2008. [Google Scholar]
- Drela, M.; Youngren, H. AVL 3.36 User Primer. 2017. Available online: http://web.mit.edu/drela/Public/web/avl/avl_doc.txt (accessed on 9 February 2021).
- Vitagliano, P.L.; Quagliarella, D. A hybrid genetic algorithm for constrained design of wing and wing-body configurations. In Proceedings of the Conference on Evolutionary Methods for Design, Optimization and Control Applications to Industrial and Societal Problems, Barcelona, Spain, 15–17 September 2003. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons Inc.: New York, NY, USA, 2001. [Google Scholar]
- Fonte, F.; Iannaccone, G.; Cimminiello, N.; Dimino, I.; Ricci, S. Active Load Control of a Regional Aircraft Wing Equipped With Morphing Winglets. In Proceedings of the ASME 2018 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Volume 1: Development and Characterization of Multifunctional Materials; Modeling, Simulation, and Control of Adaptive Systems; Integrated System Design and Implementation, San Antonio, TX, USA, 10–12 September 2018. V001T04A021. [Google Scholar] [CrossRef]
- Rodden, W.P.; Love, J.R. Equations of motion of a quasisteady flight vehicle utilizing restrained static aeroelastic characteristics. J. Aircr. 1985, 22, 802–809. [Google Scholar] [CrossRef]
- Fonte, F.; Toffol, F.; Ricci, S. Design of a wing tip device for active maneuver and gust load alleviation. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA SciTech Forum, (AIAA 2018-1442), Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Ripepi, M.; Mantegazza, P. Improved Matrix Fraction Approximation of Aerodynamic Transfer Matrices. AIAA J. 2013, 51, 1156–1173. [Google Scholar] [CrossRef]
- Molyneux, W.G. The Flutter of Swept and Unswept: Wings with Fixed-Root Conditions; Technical Reports No. 2796; Aeronautical Research Council: London, UK, 1954. [Google Scholar]
- Broadbent, E.G. Flutter and Response Calculations in Practice. In AGARD Manual on Aeroelasticity; AGARD: Neuilly-sur-Seine, France, 1963; Volume 3, Chapter 4. [Google Scholar]
- Arena, M.; Concilio, A.; Pecora, R. Aero-servo-elastic design of a morphing wing trailing edge system for en-hanced cruise performance. Aerosp. Sci. Technol. 2019, 86. [Google Scholar] [CrossRef]

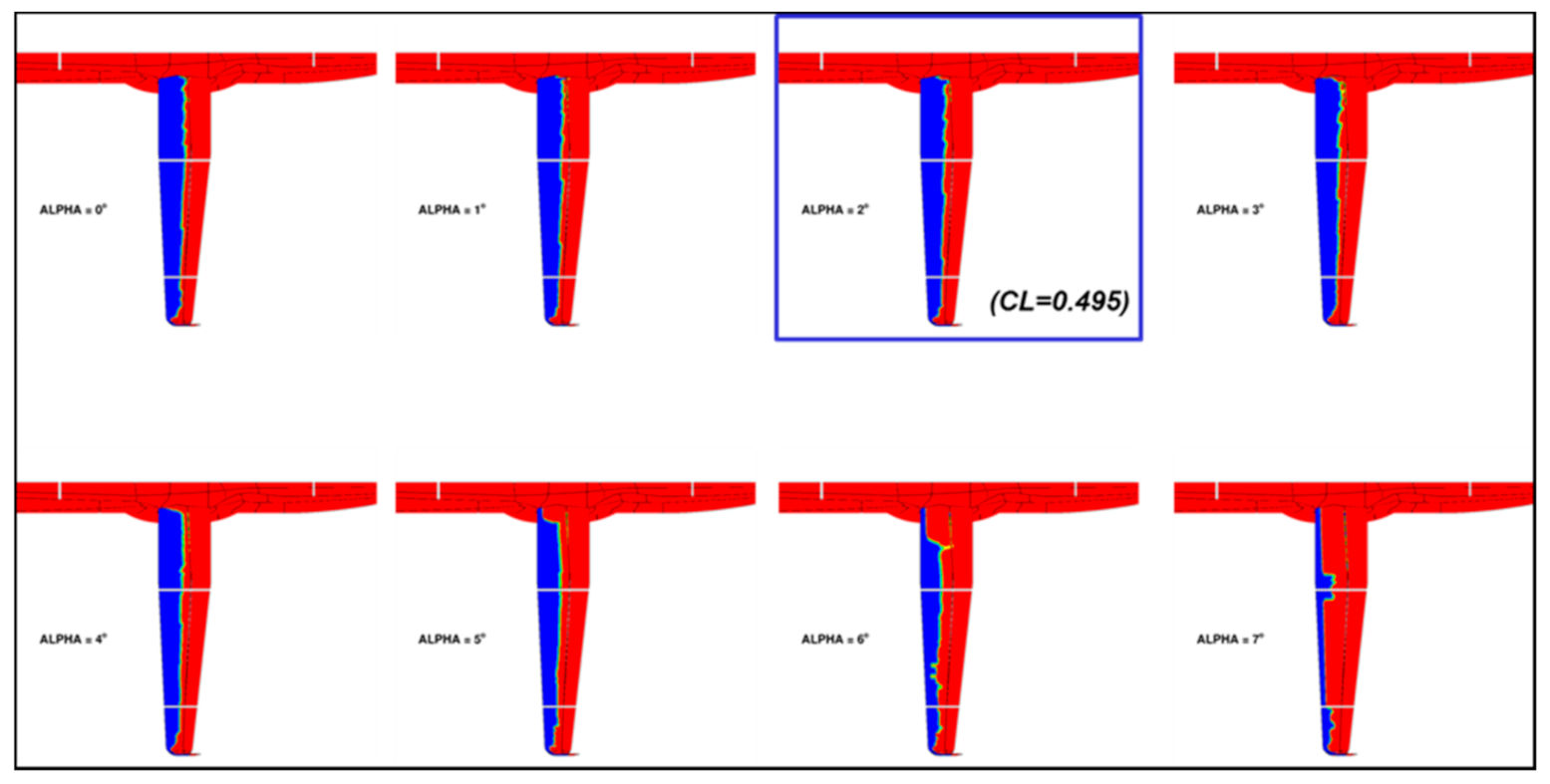
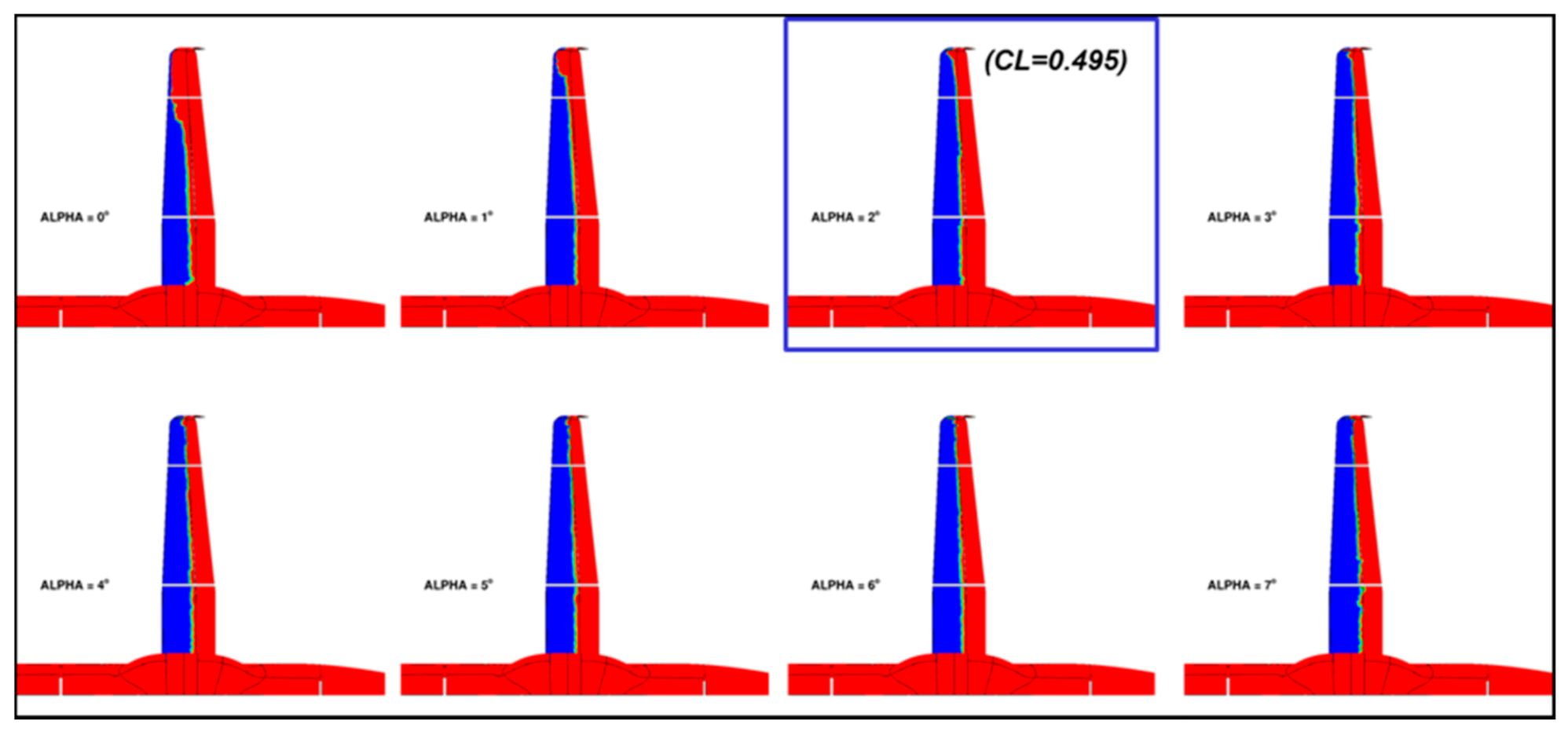
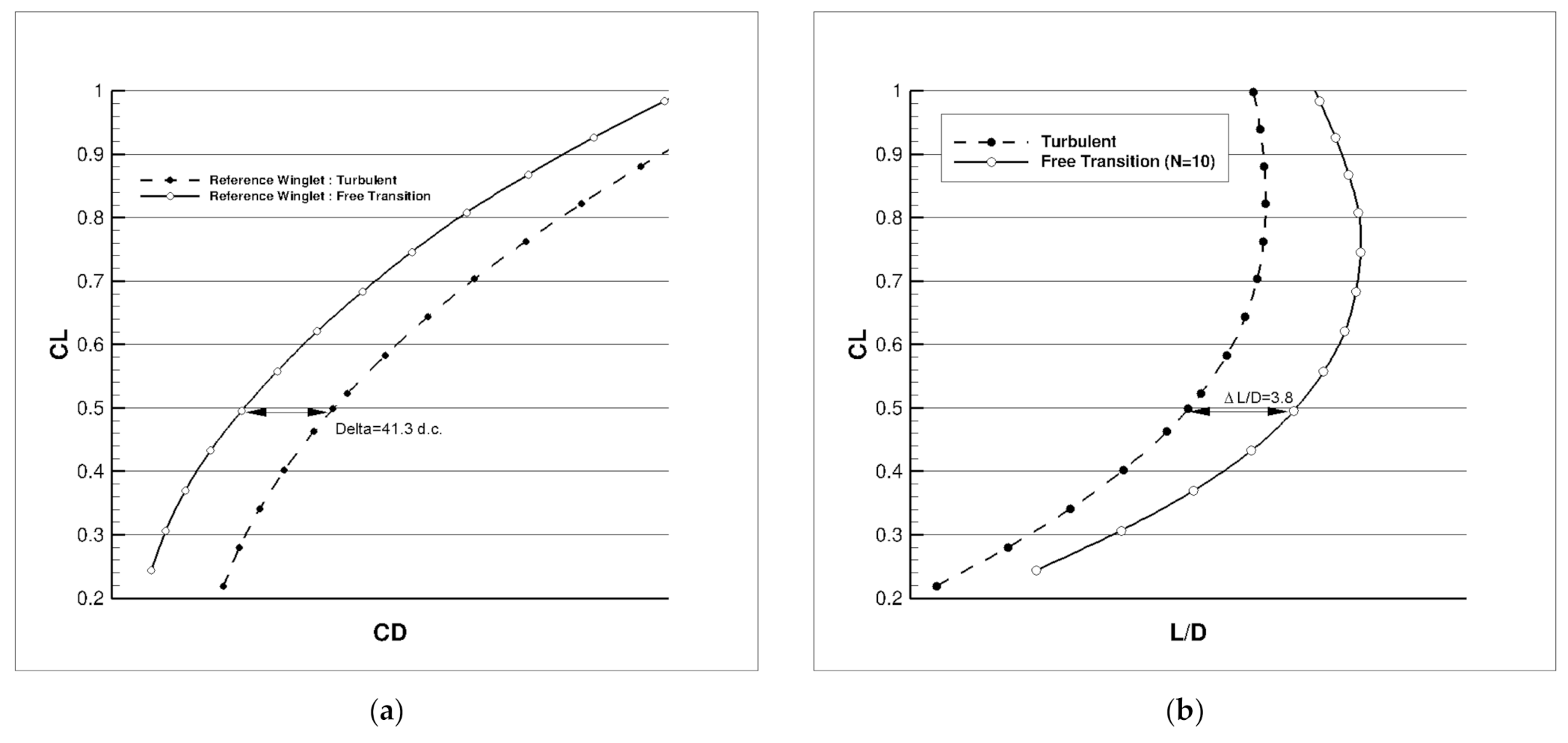

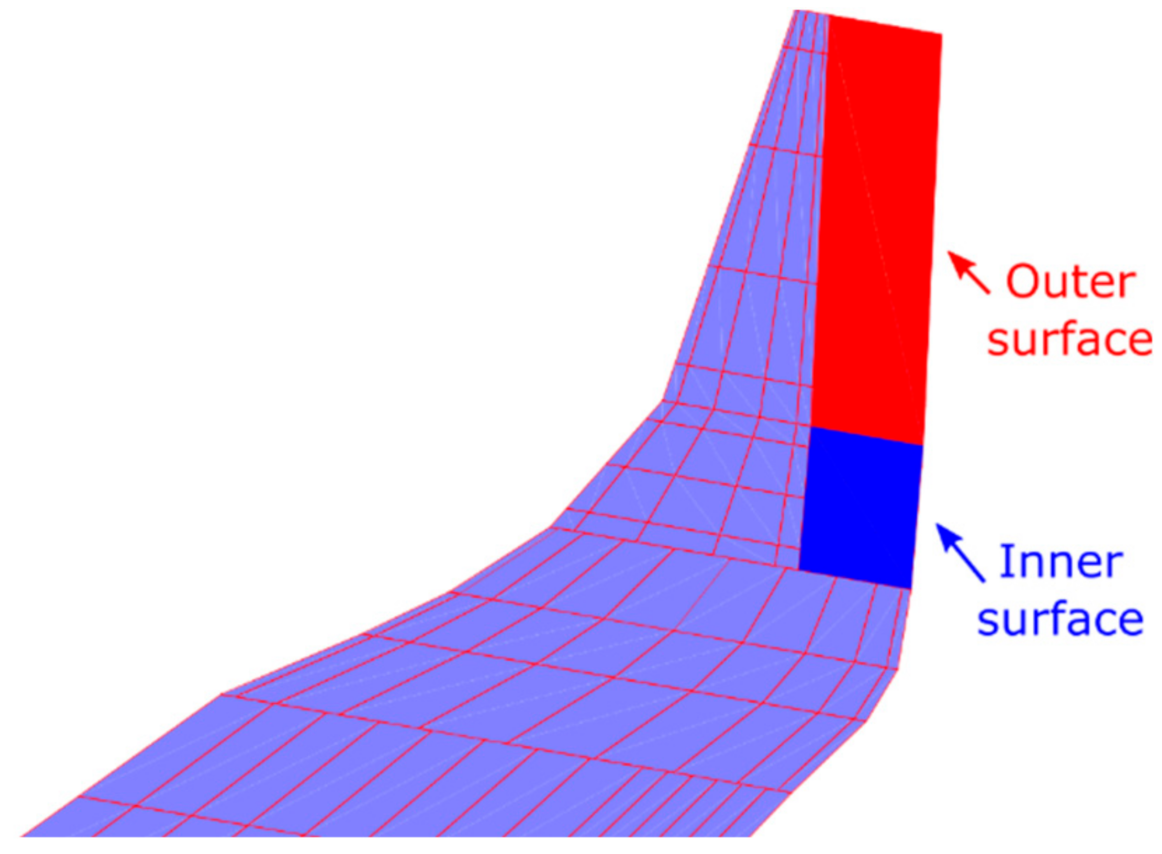
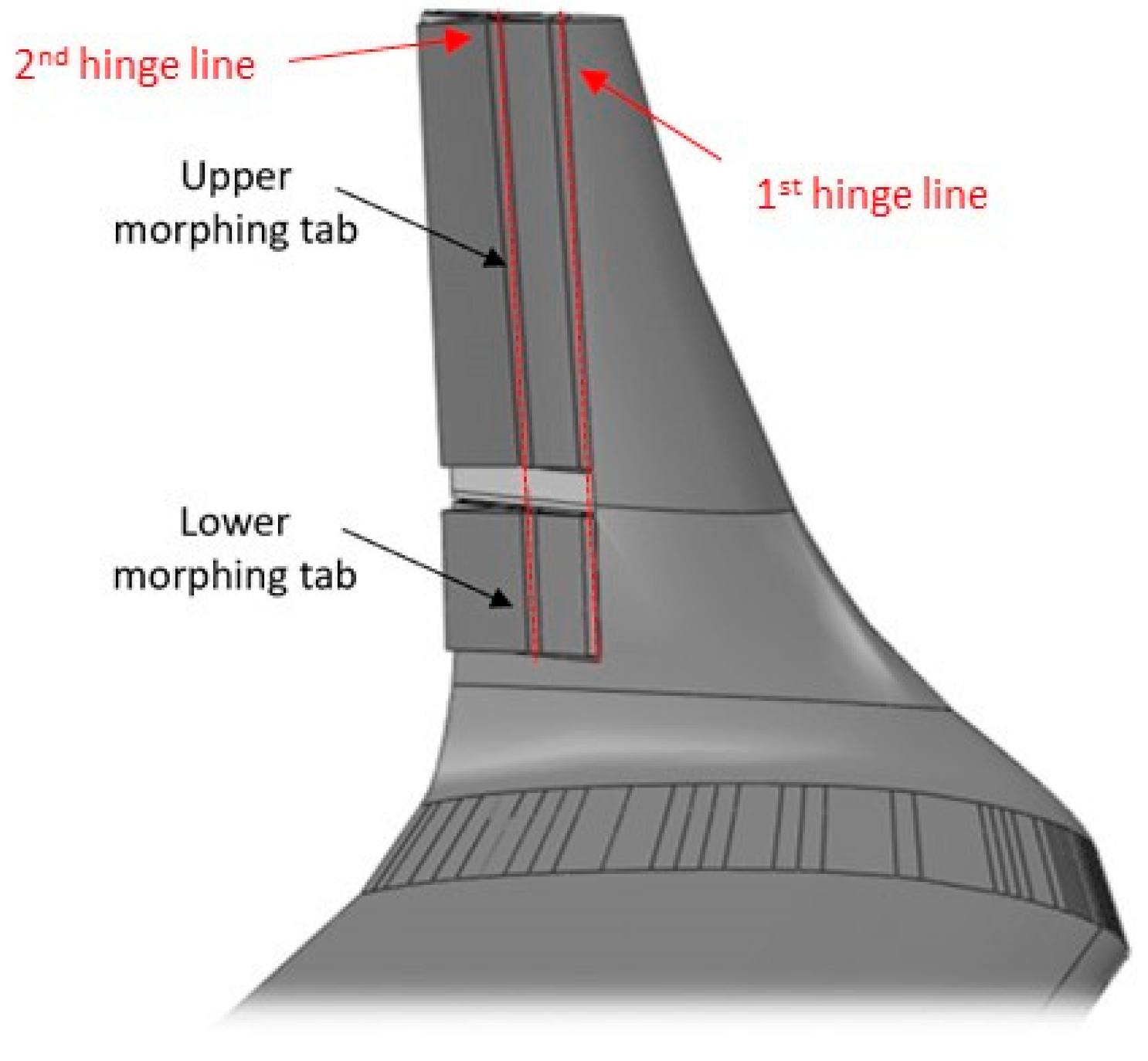
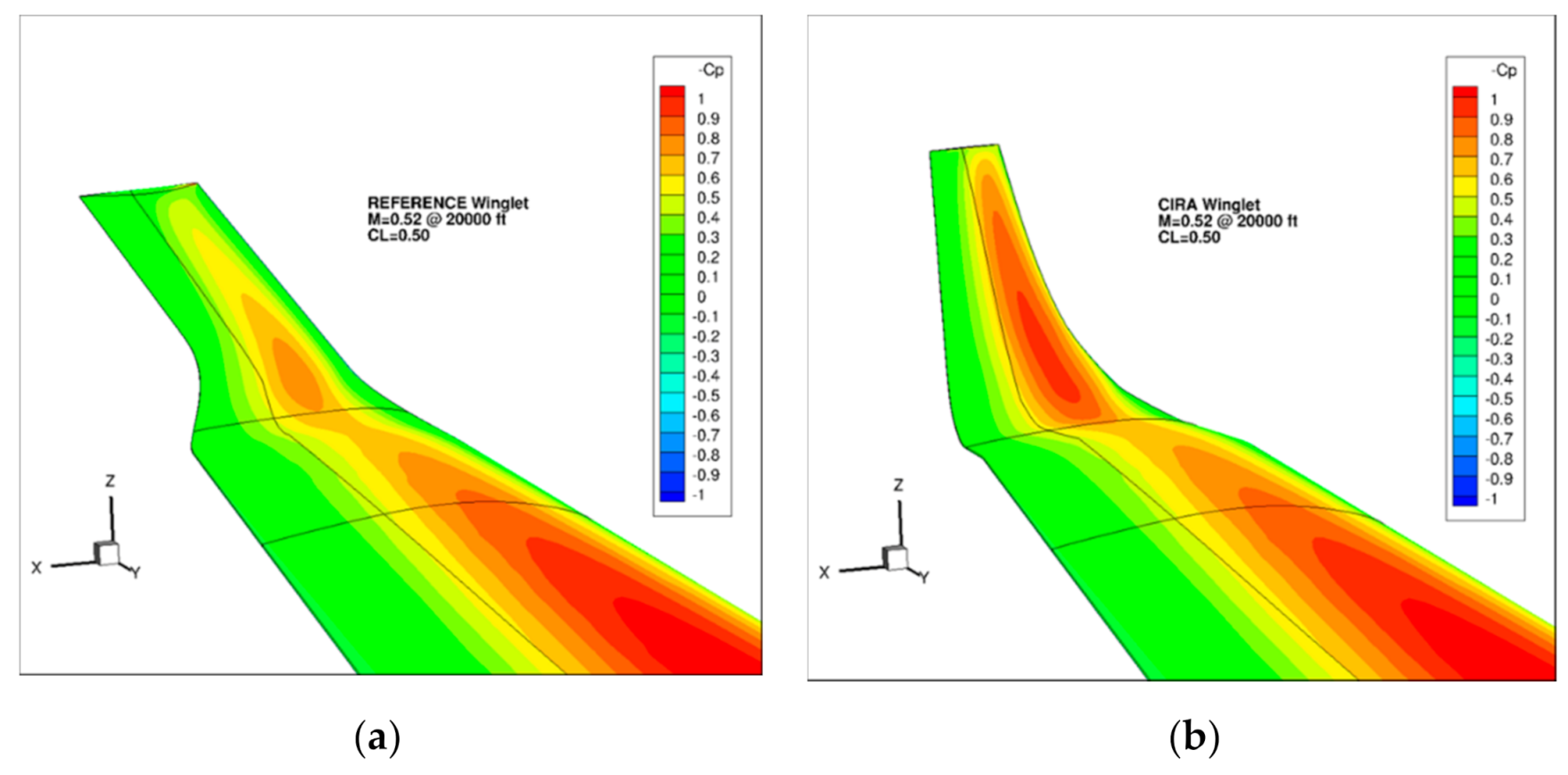
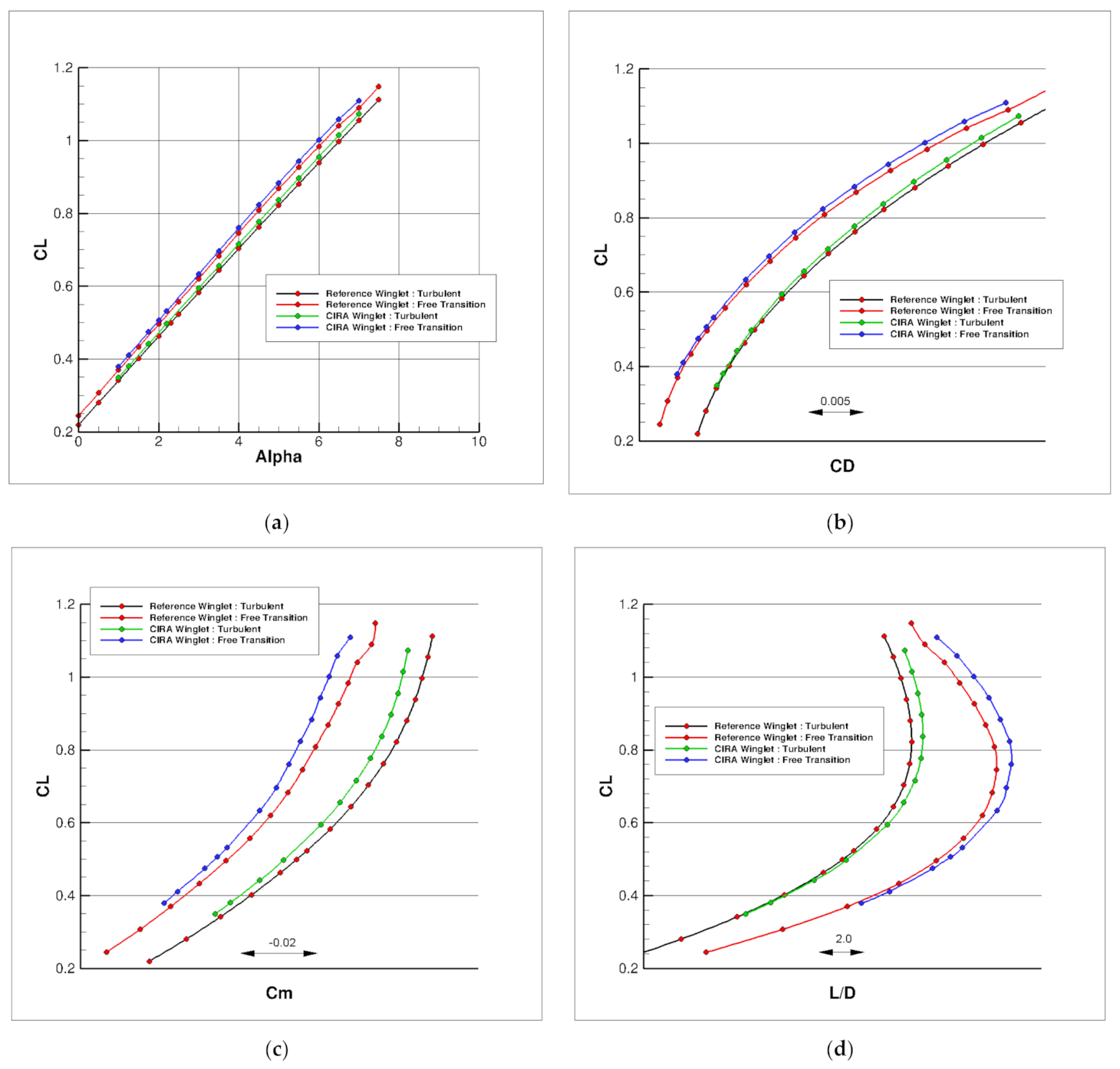
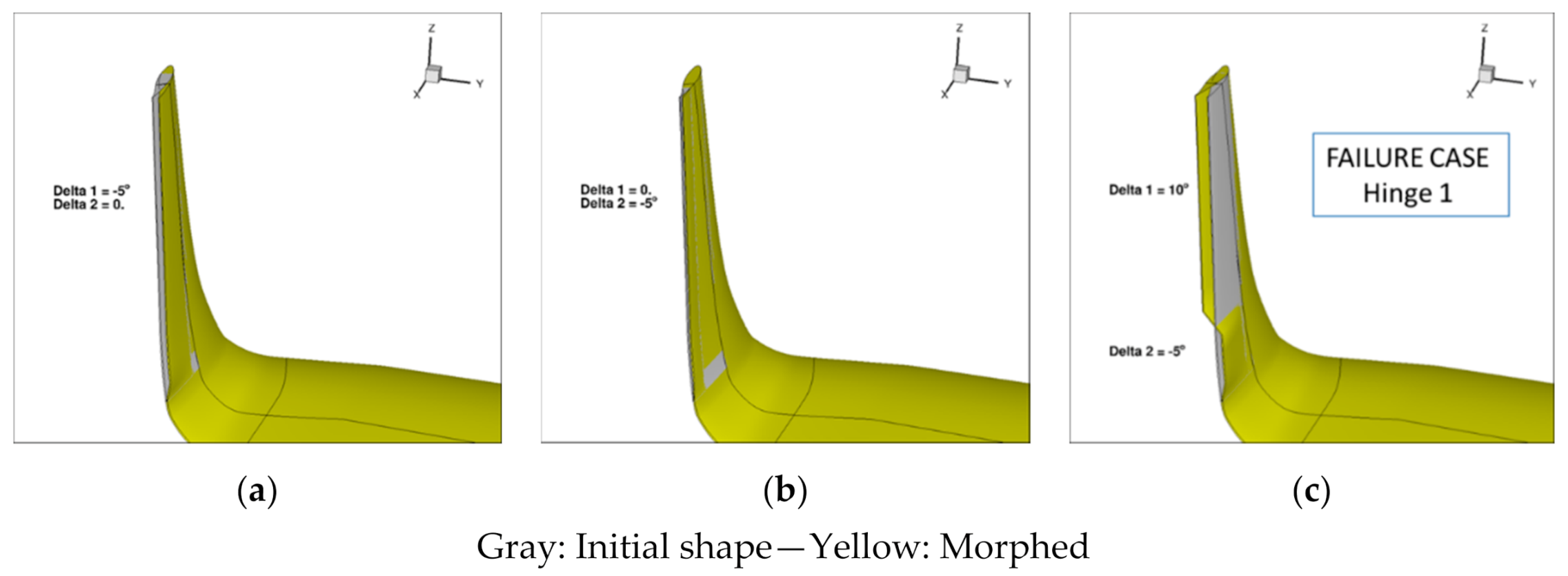
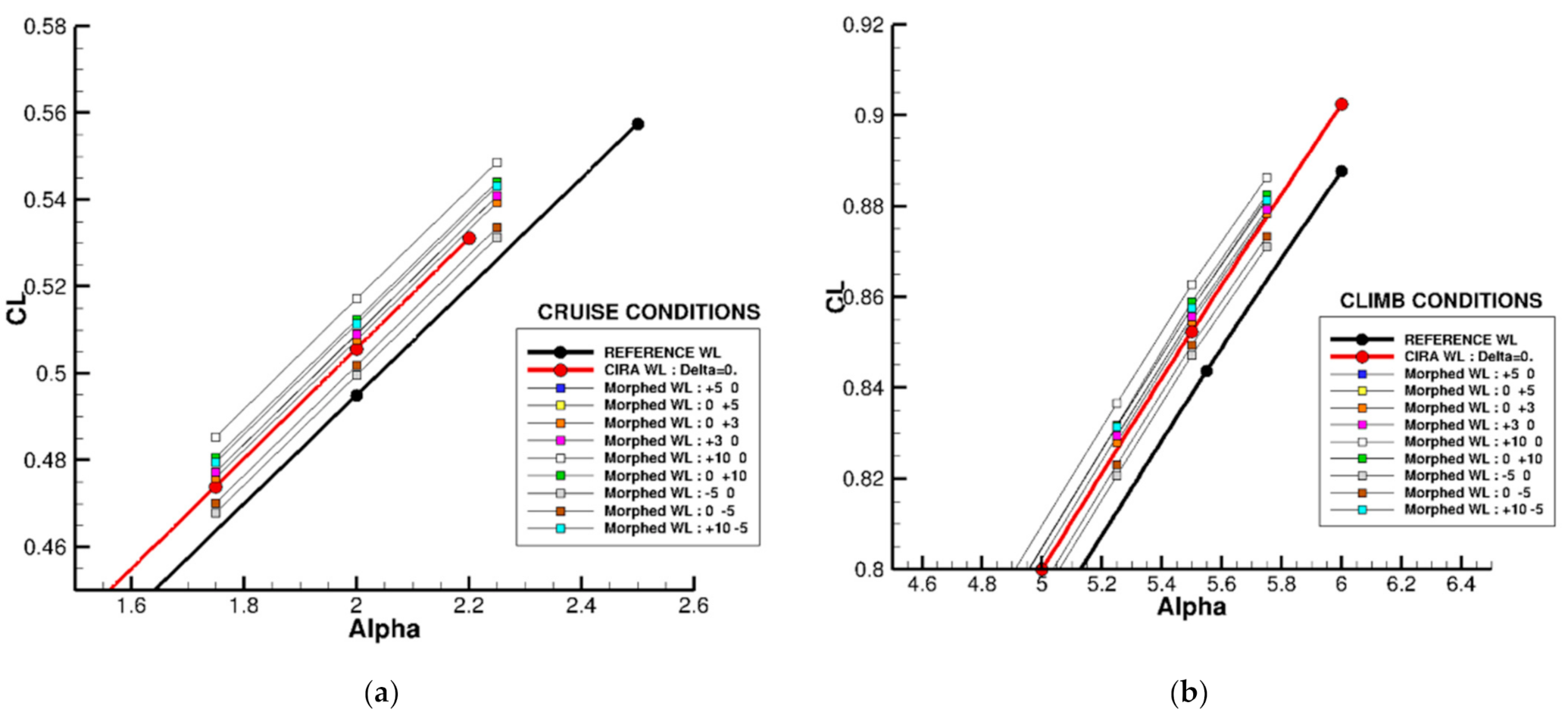
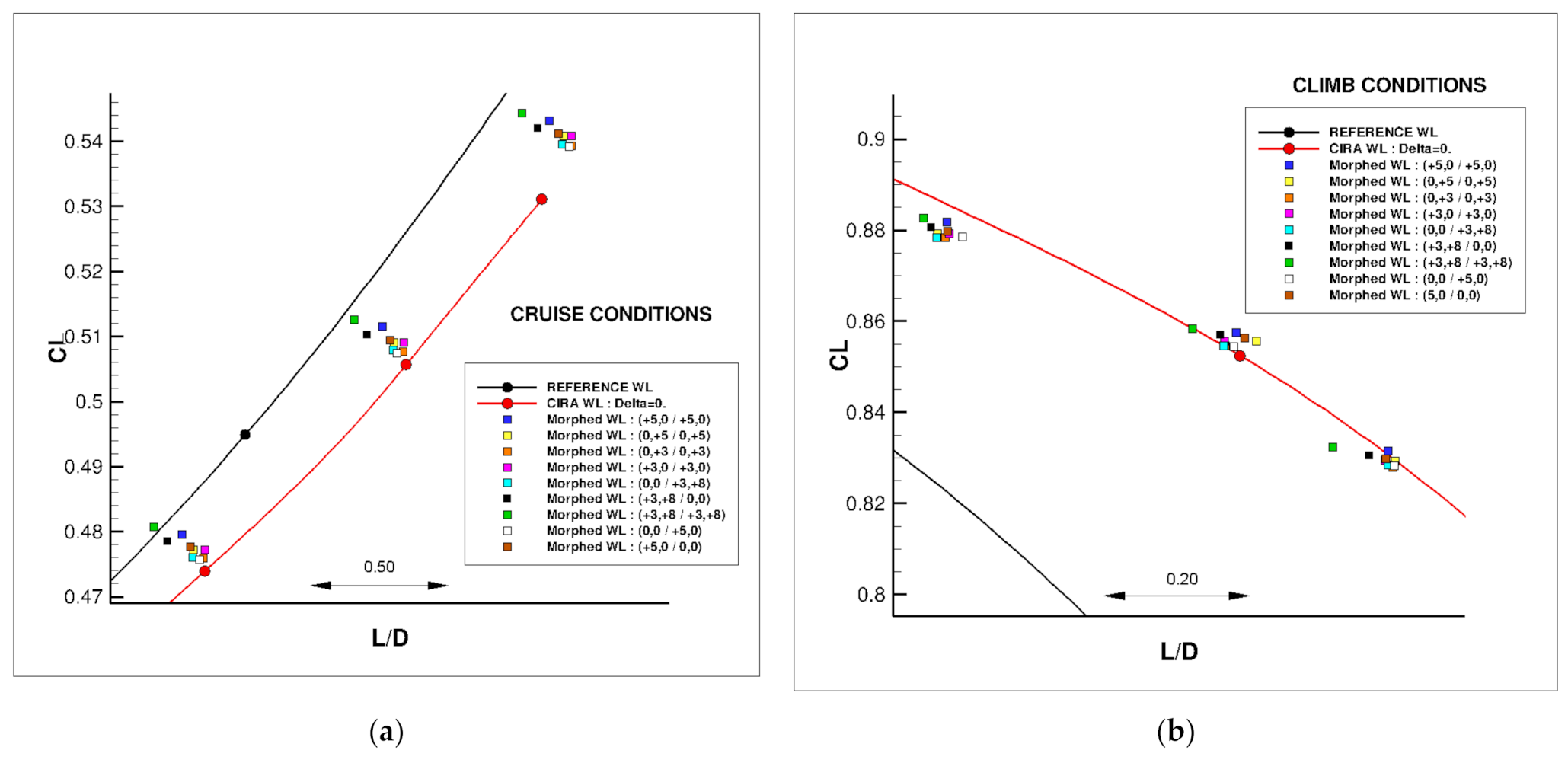
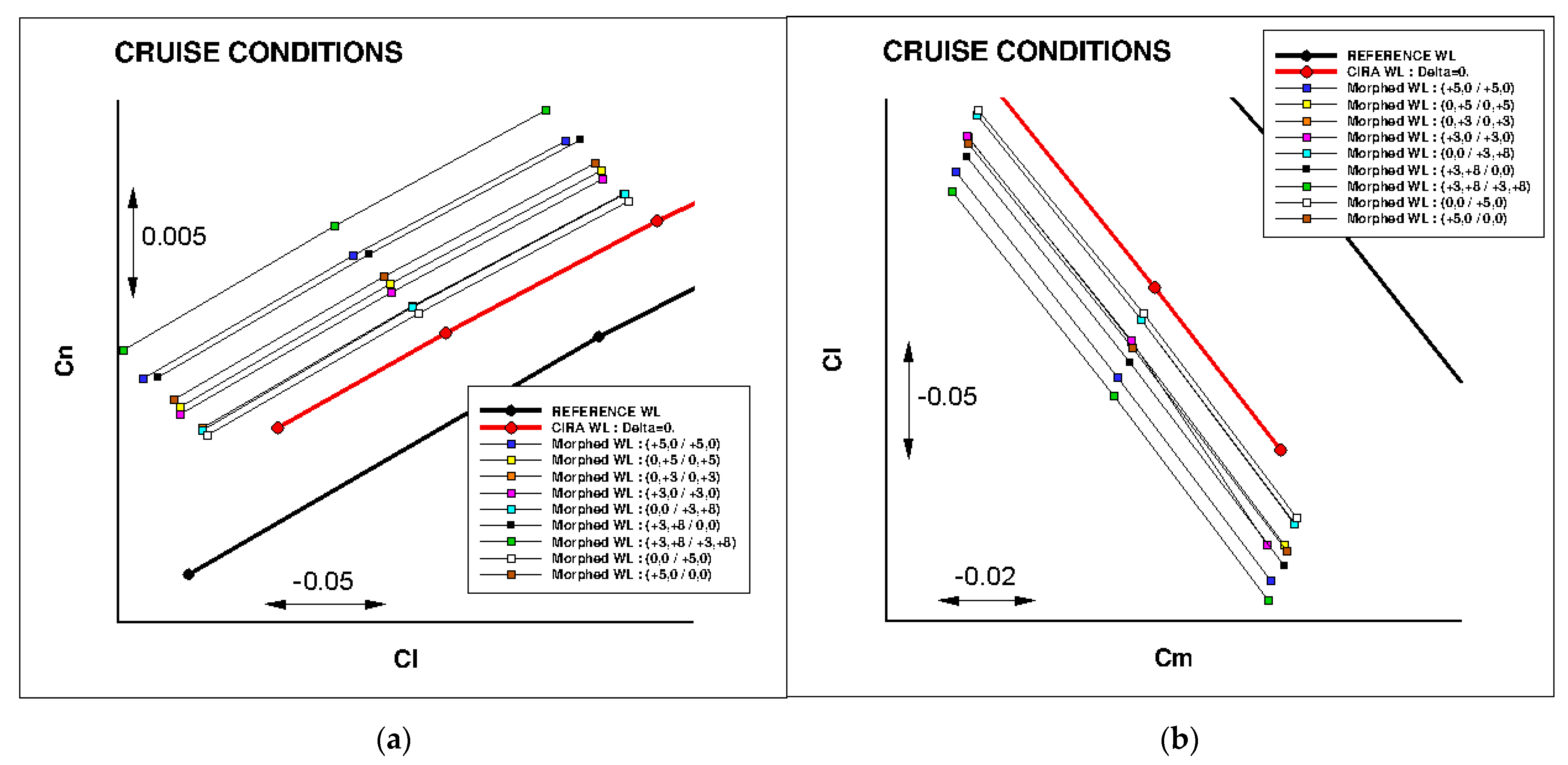
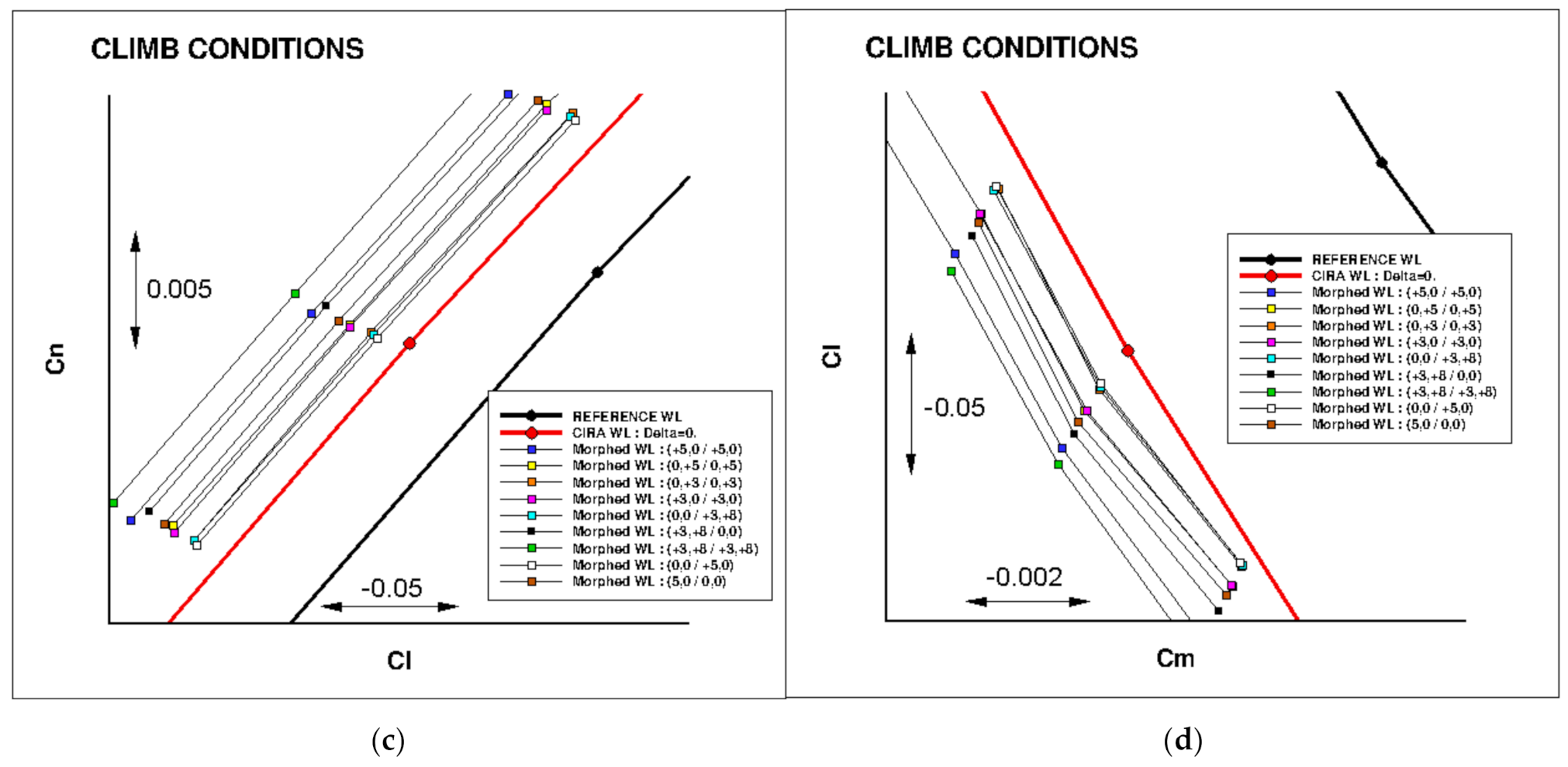


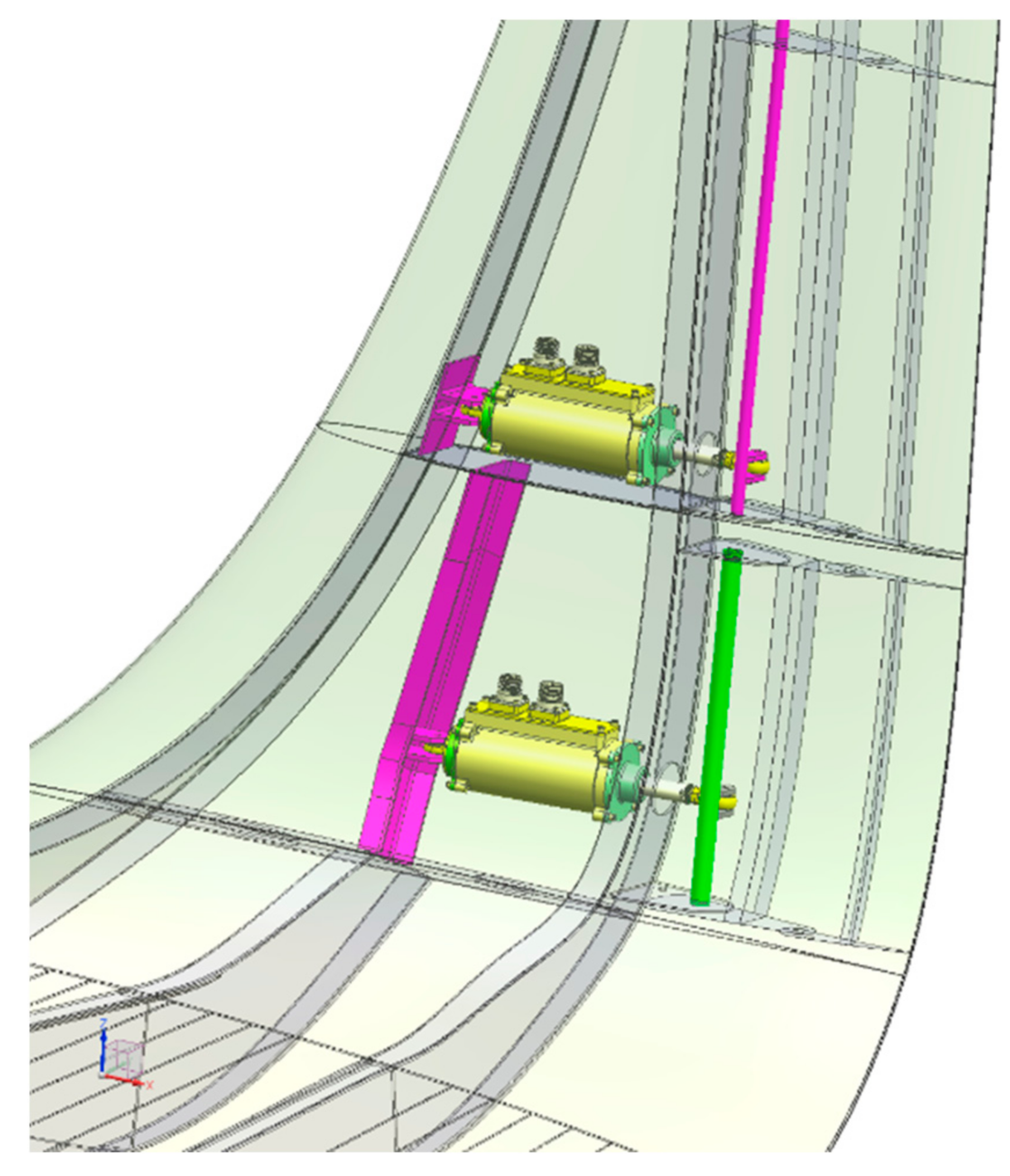
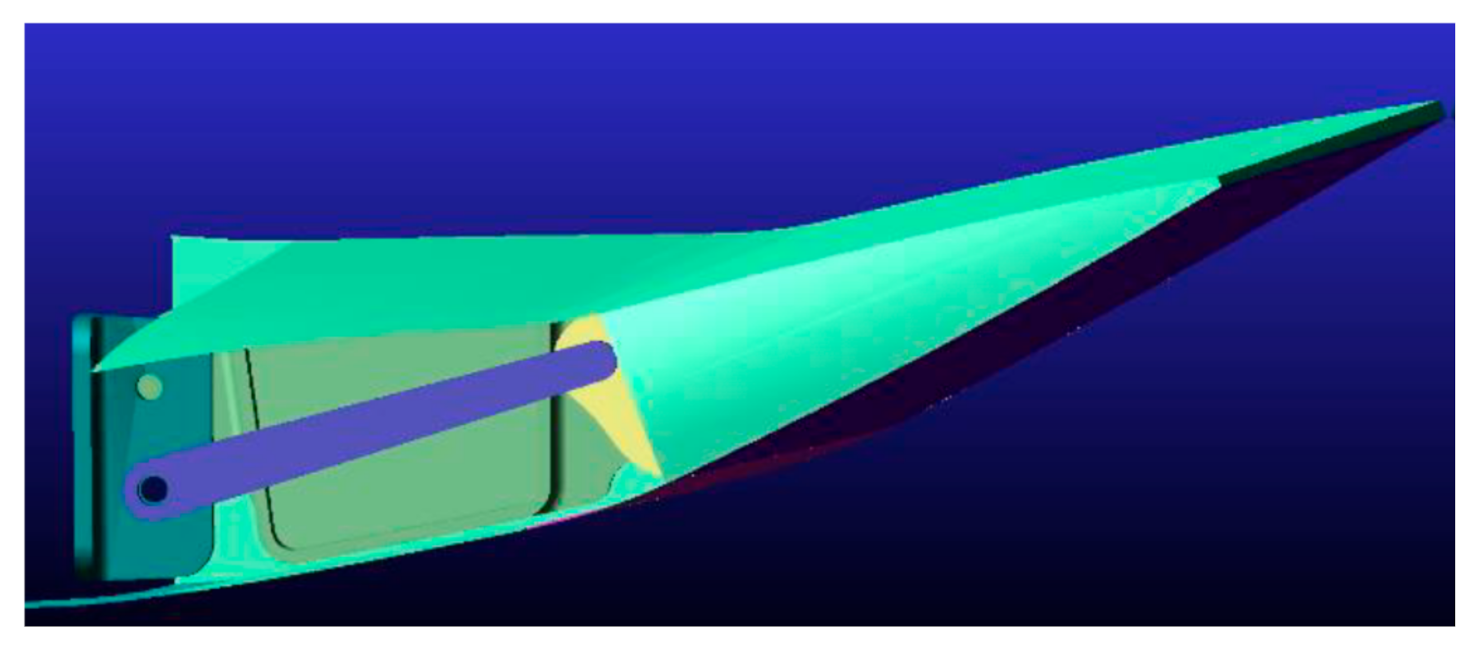
| Cruise: Turbulent CL = 0.50 | Cruise: Free Transition CL = 0.50 | Climb: Free Transition CL = 0.84 |
|---|---|---|
| ΔL/D = +0.89% | ΔL/D = +1.45% | ΔL/D = +2.68% |
| Parameter | Value |
|---|---|
| Maximum operating axial load | 3500 N |
| Maximum static axial load | 5000 N |
| Total operating stroke | 10 mm for the lower surface 20 mm for the upper surface |
| Max speed | 5 mm/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimino, I.; Andreutti, G.; Moens, F.; Fonte, F.; Pecora, R.; Concilio, A. Integrated Design of a Morphing Winglet for Active Load Control and Alleviation of Turboprop Regional Aircraft. Appl. Sci. 2021, 11, 2439. https://doi.org/10.3390/app11052439
Dimino I, Andreutti G, Moens F, Fonte F, Pecora R, Concilio A. Integrated Design of a Morphing Winglet for Active Load Control and Alleviation of Turboprop Regional Aircraft. Applied Sciences. 2021; 11(5):2439. https://doi.org/10.3390/app11052439
Chicago/Turabian StyleDimino, Ignazio, Giovanni Andreutti, Frédéric Moens, Federico Fonte, Rosario Pecora, and Antonio Concilio. 2021. "Integrated Design of a Morphing Winglet for Active Load Control and Alleviation of Turboprop Regional Aircraft" Applied Sciences 11, no. 5: 2439. https://doi.org/10.3390/app11052439
APA StyleDimino, I., Andreutti, G., Moens, F., Fonte, F., Pecora, R., & Concilio, A. (2021). Integrated Design of a Morphing Winglet for Active Load Control and Alleviation of Turboprop Regional Aircraft. Applied Sciences, 11(5), 2439. https://doi.org/10.3390/app11052439









