Numerical Phase-Field Model Validation for Dissolution of Minerals
Abstract
1. Introduction
2. Dissolution Mechanisms
2.1. Types of Dissolution
2.2. Diffusion-Controlled Dissolution Mechanisms
3. Mathematical Methods
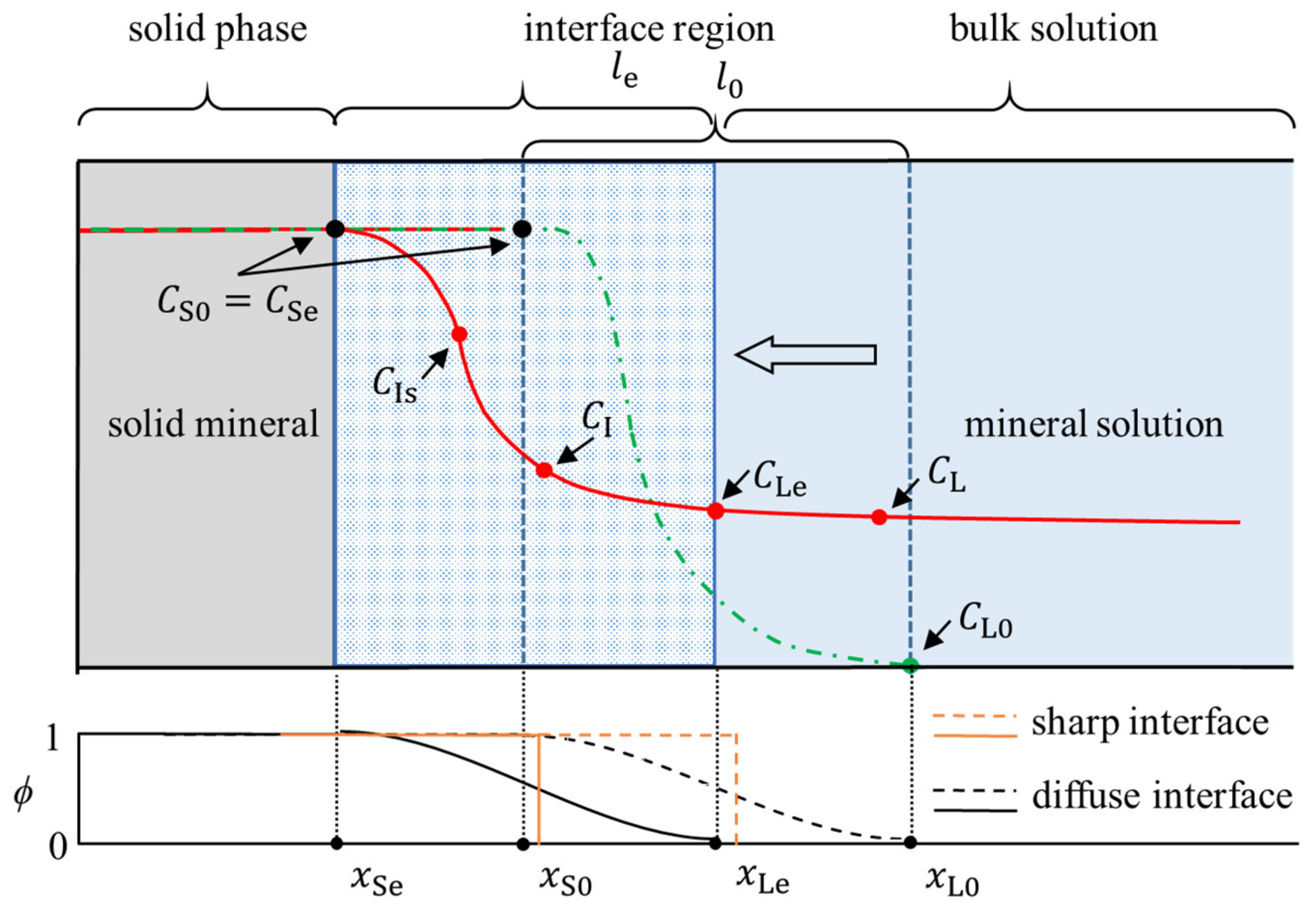
3.1. Analytical Solutions
3.2. The Phase-Field (PF) Method
4. Problem Description and Model Tests
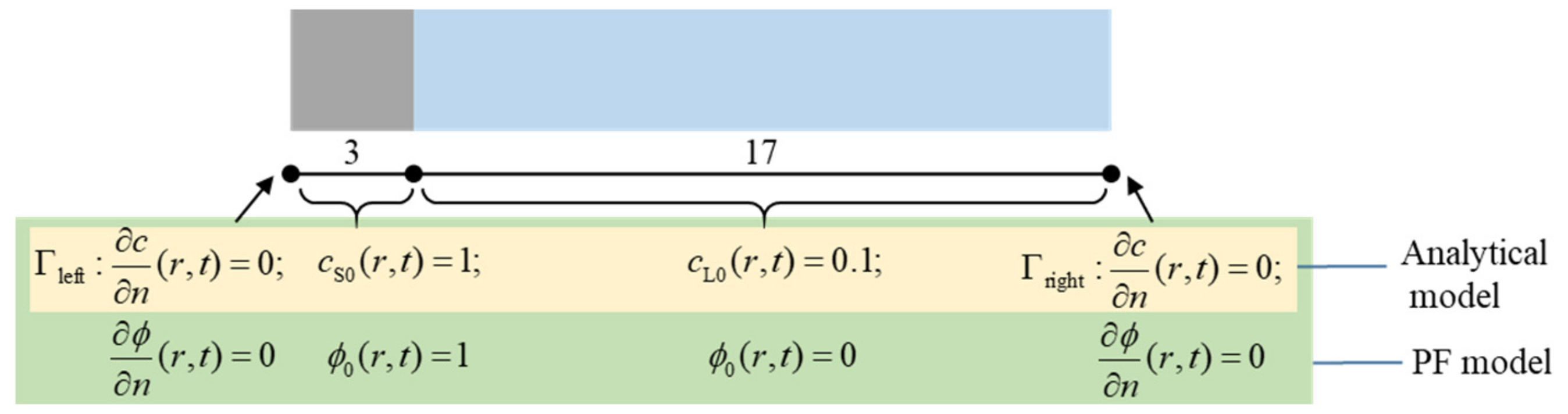
4.1. Benchmark with Analytical Model for One-Dimensional (1D) Congruent Dissolution
4.2. Simulation Case Study Based on Available Measured Experimental Data of Mineral Particle Dissolution
5. PF Modelling Methodology and Numerical Implementation
5.1. Summary of Modelling Assumptions
- The NaCl particle dissolves isotropically;
- The diffusion coefficients of aqueous species in solids and in solution are constants, respectively;
- The diffusion of all aqueous species is expressed in terms of a single ionic concentration;
- The solubility of NaCl in solution is independent of particle size.
5.2. Parameterization
5.3. Parameter Normalization
5.4. Finite Element Implementation
5.5. Central Processing Unit (CPU) Computation
6. Results and Discussion
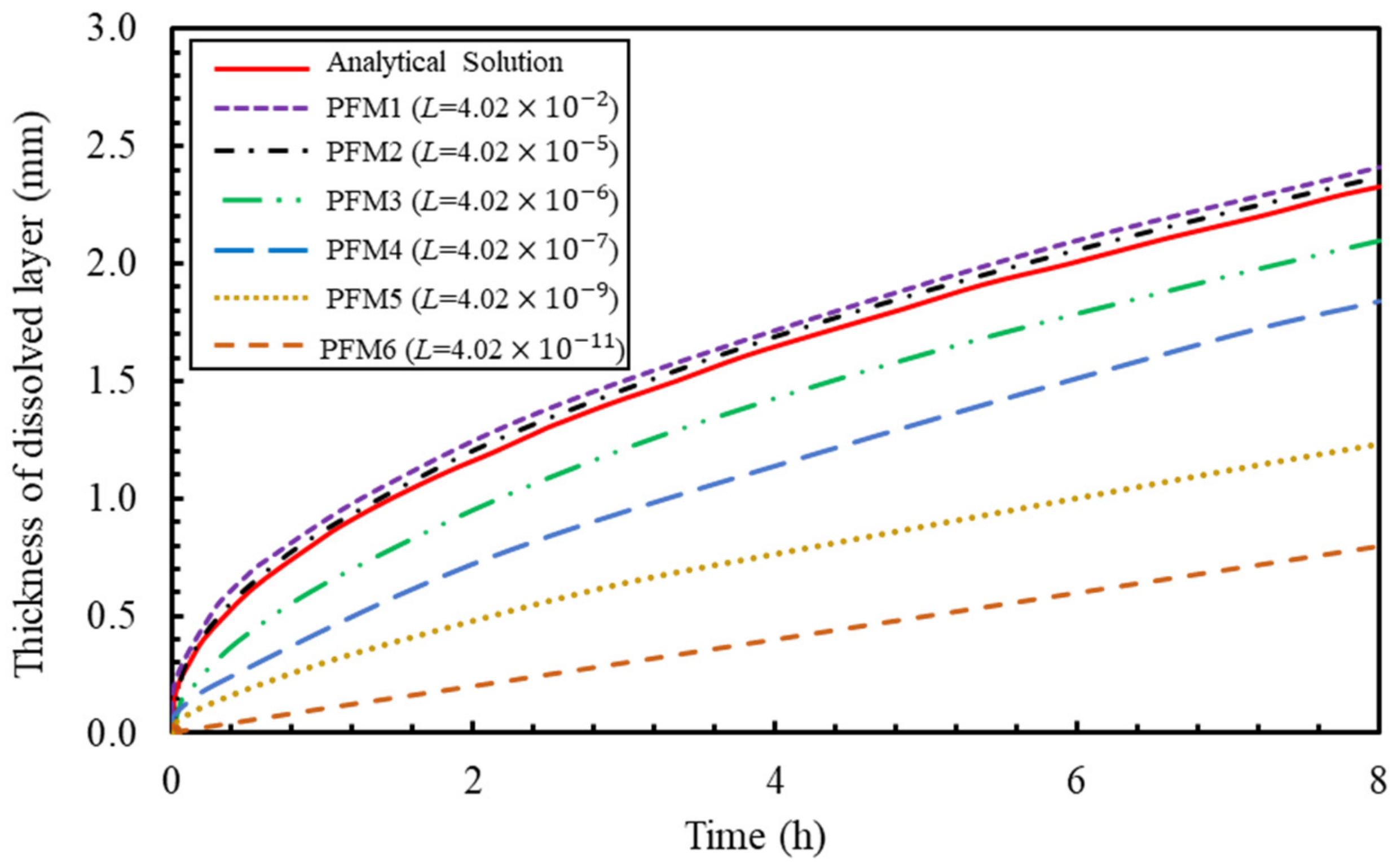
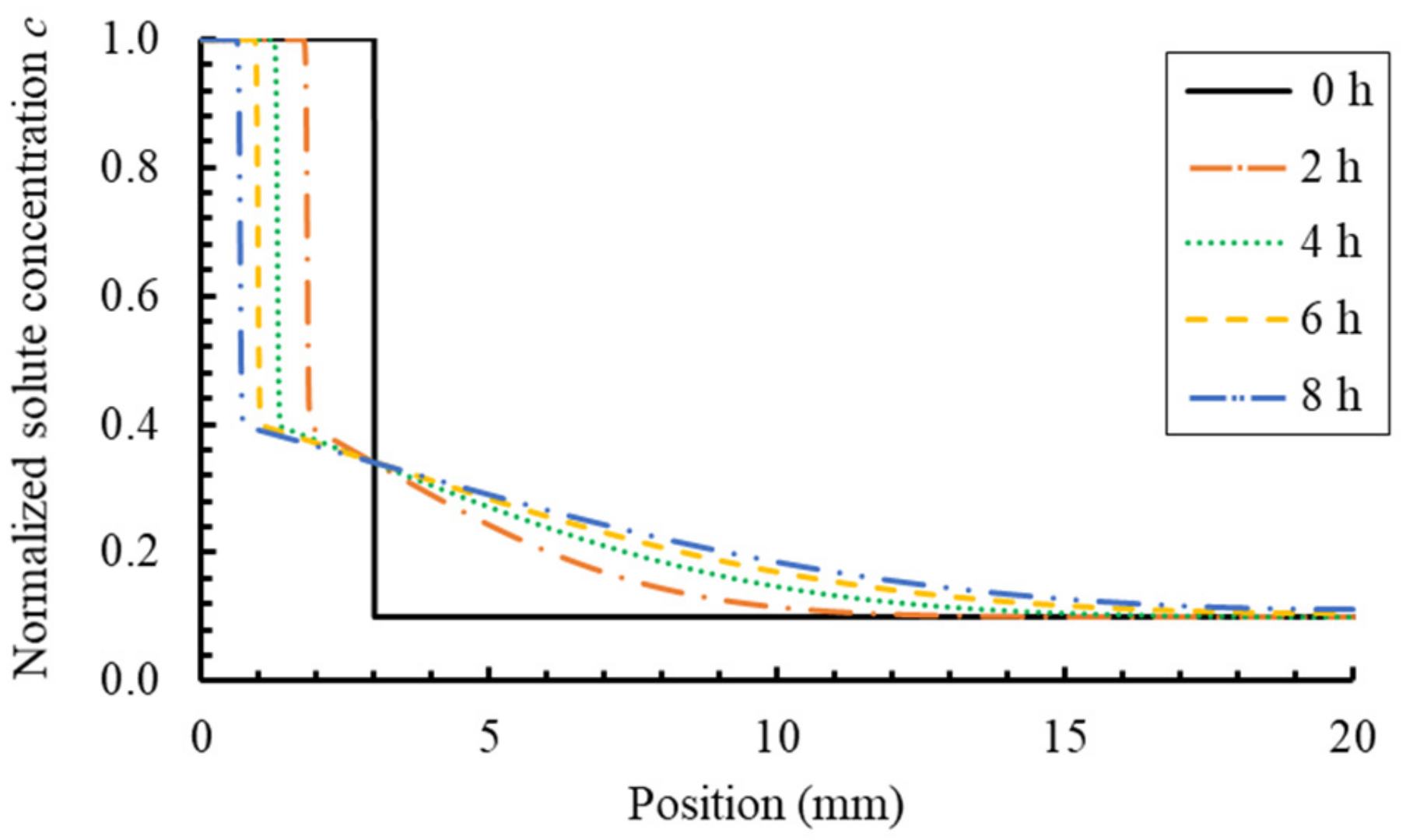
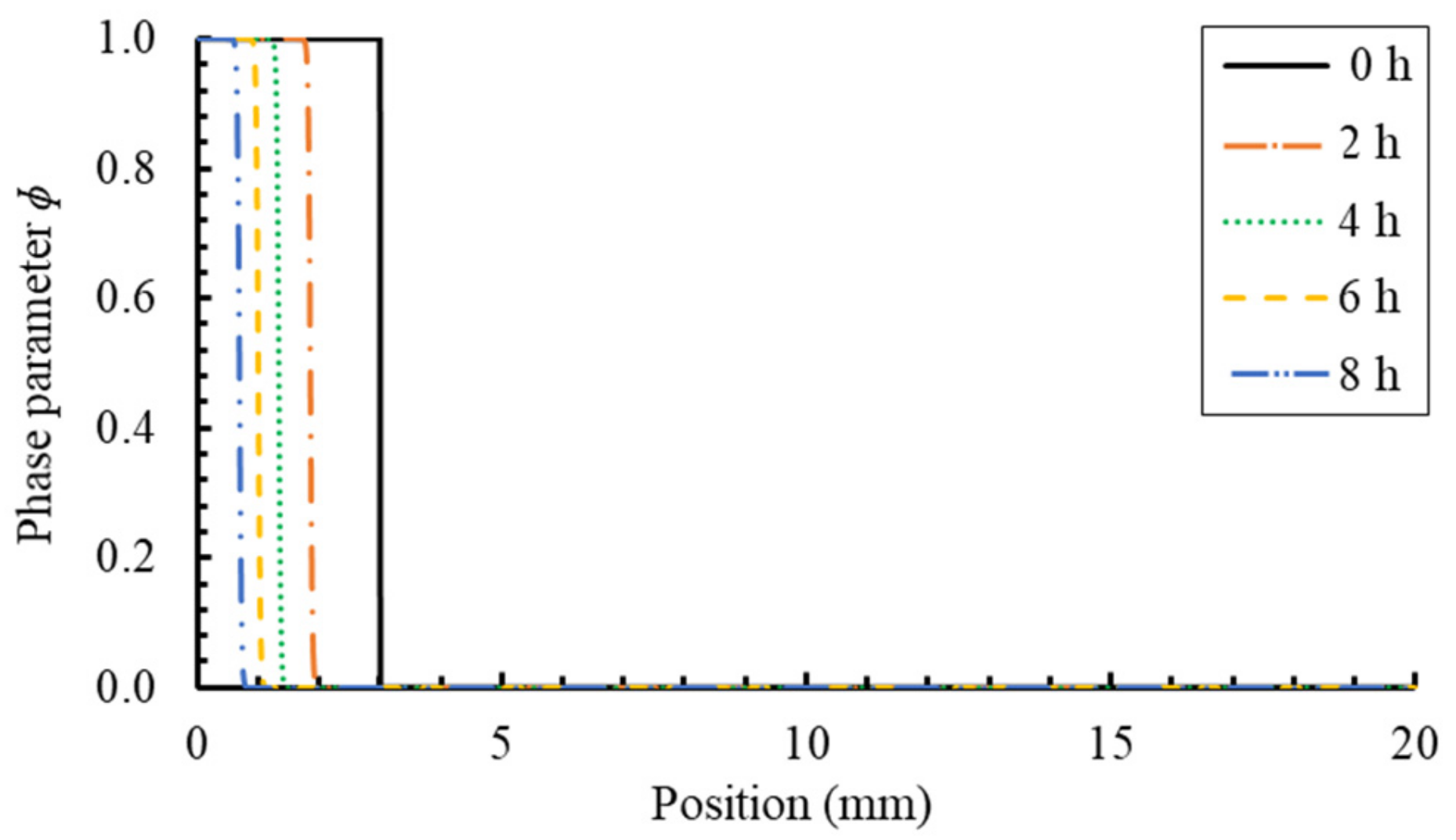
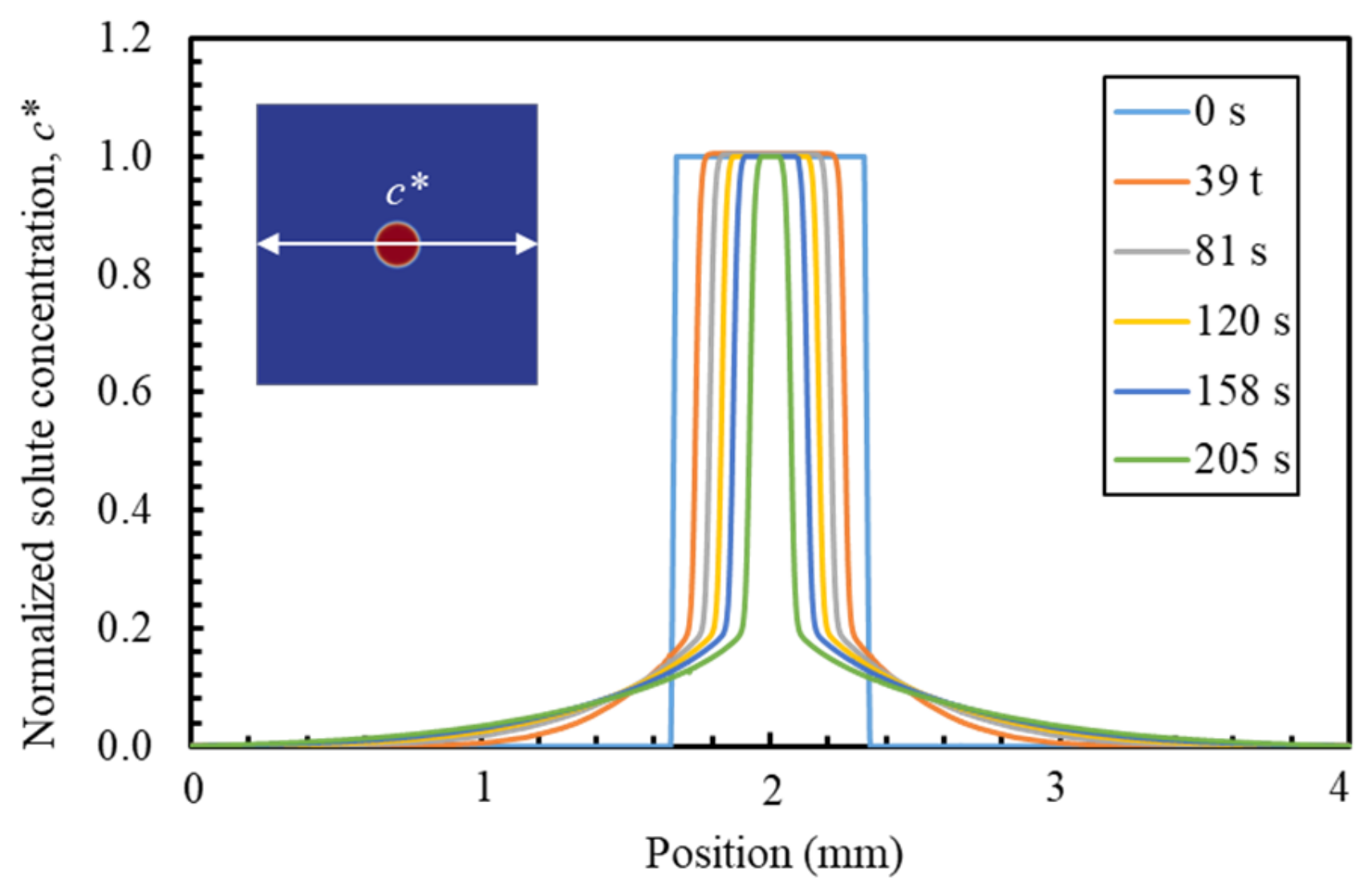
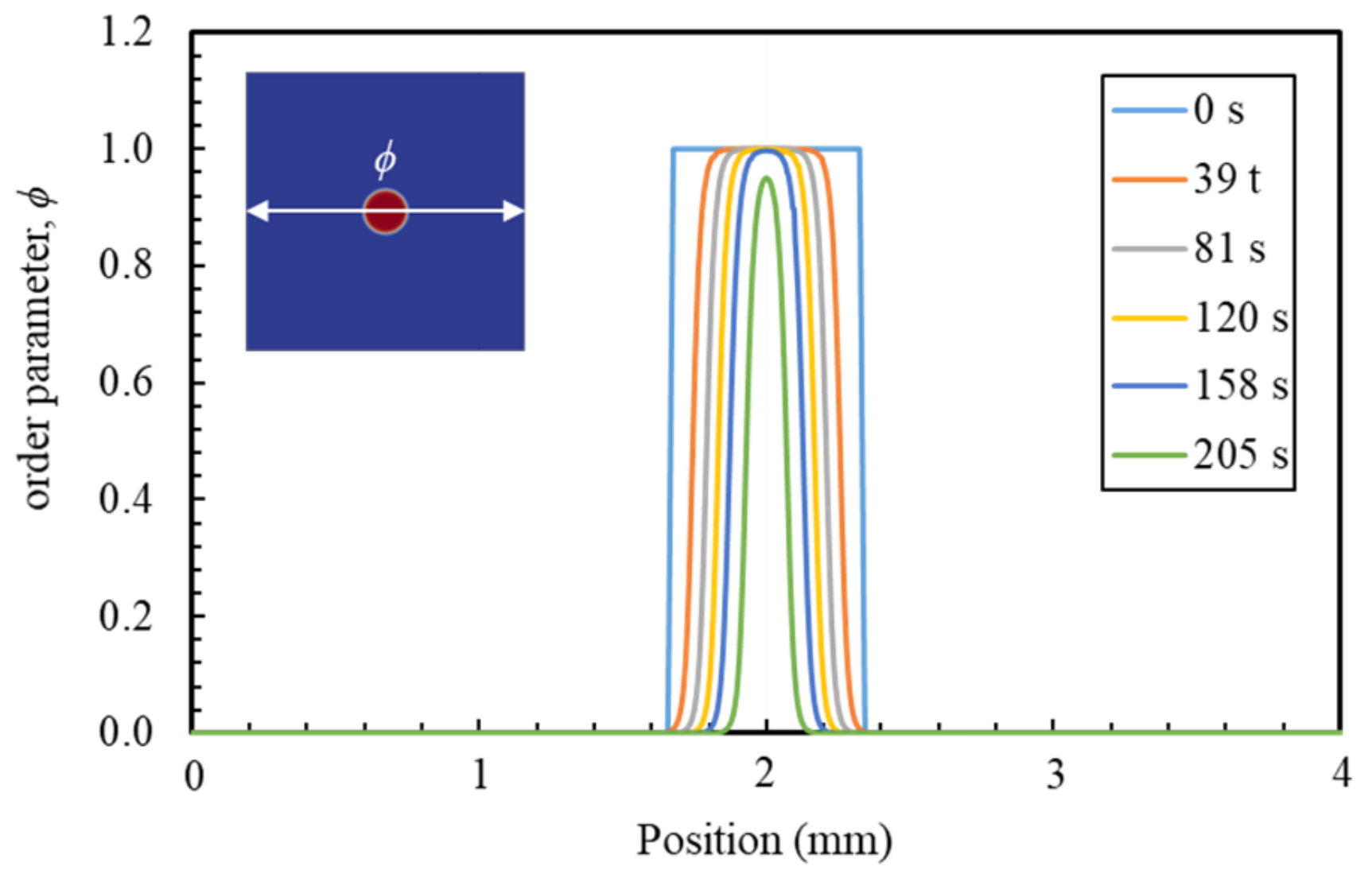
6.1. PF Validation against Analytical Solution for a Dissolution of Planar Mineral
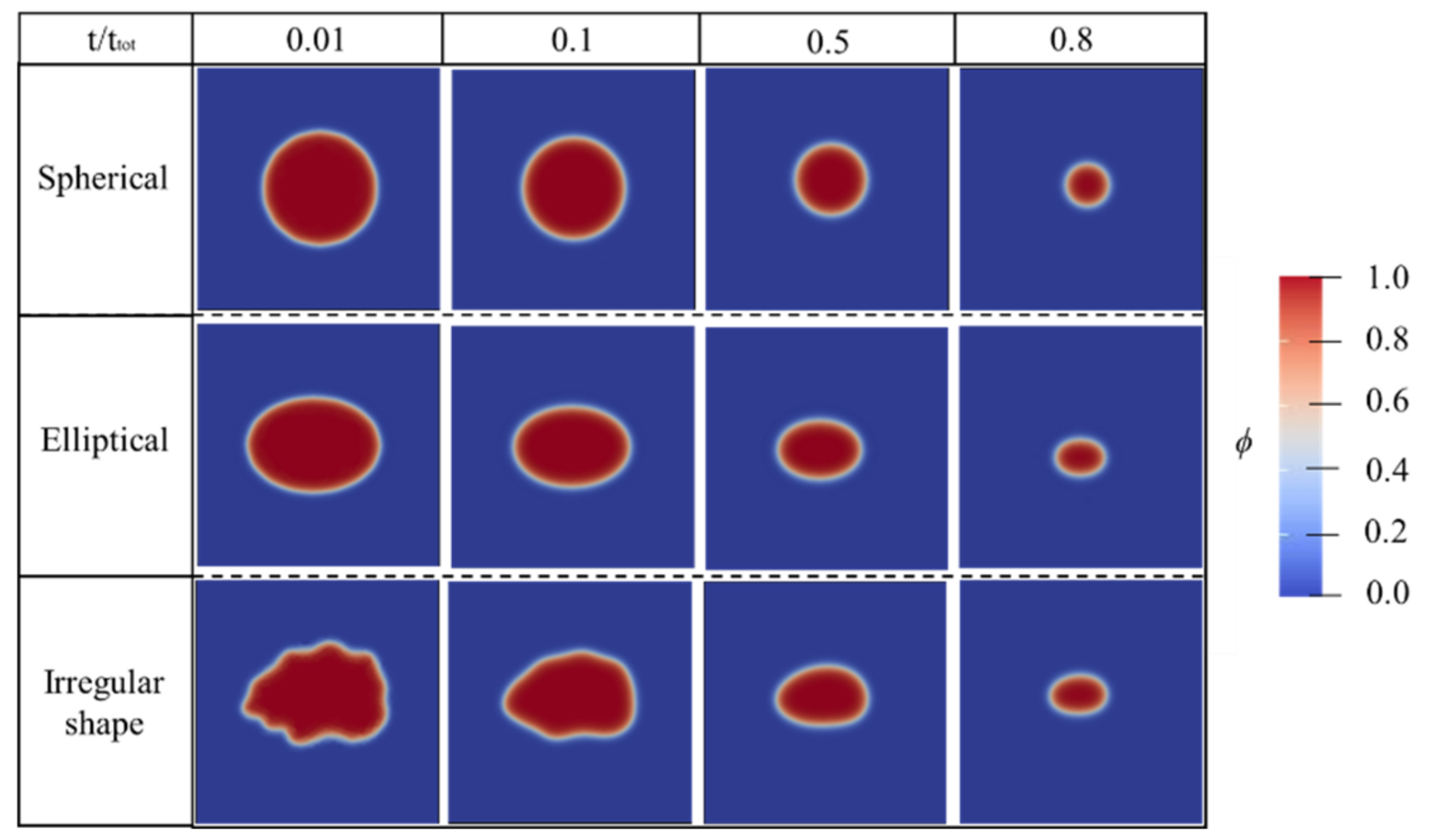
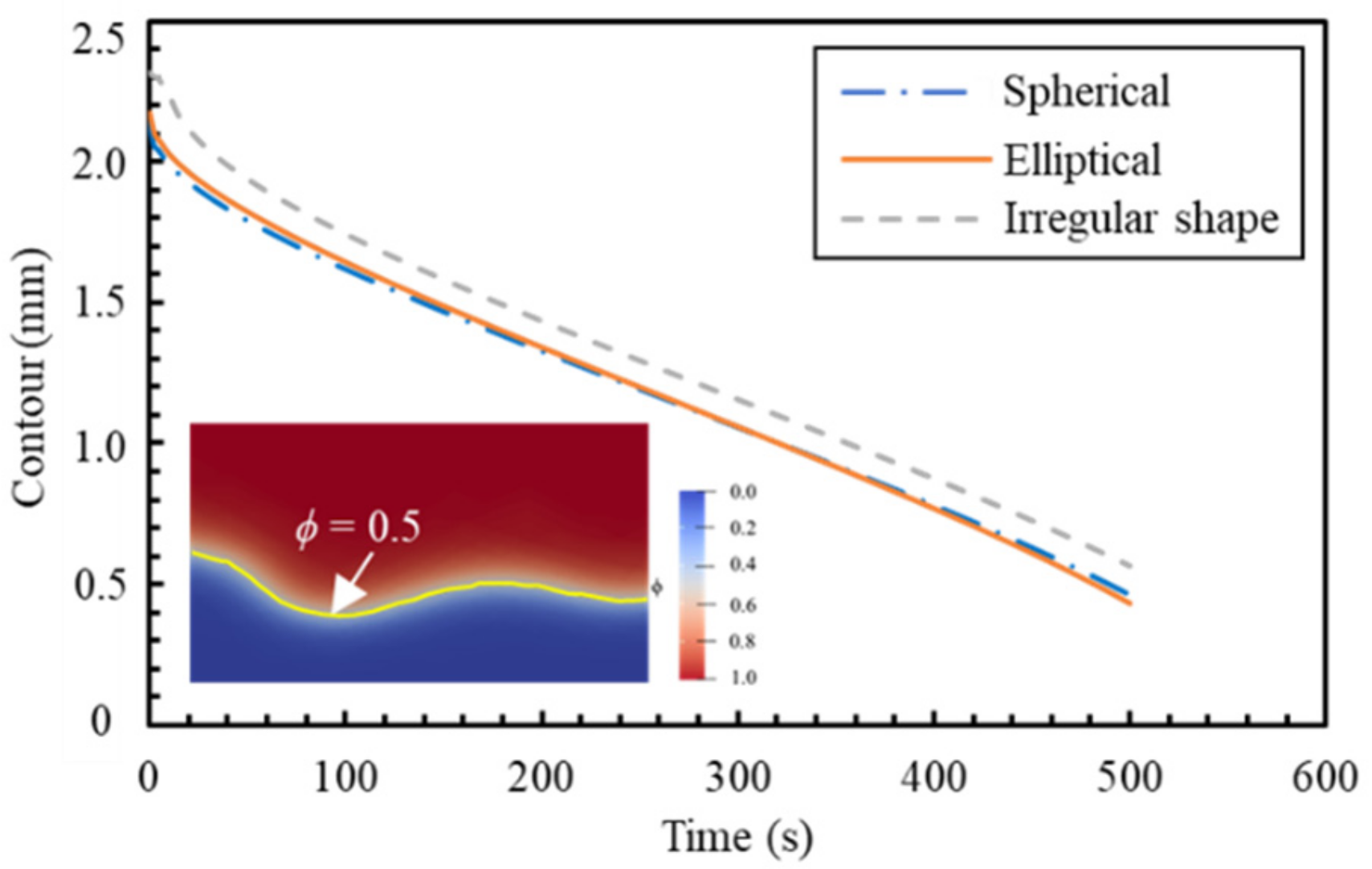
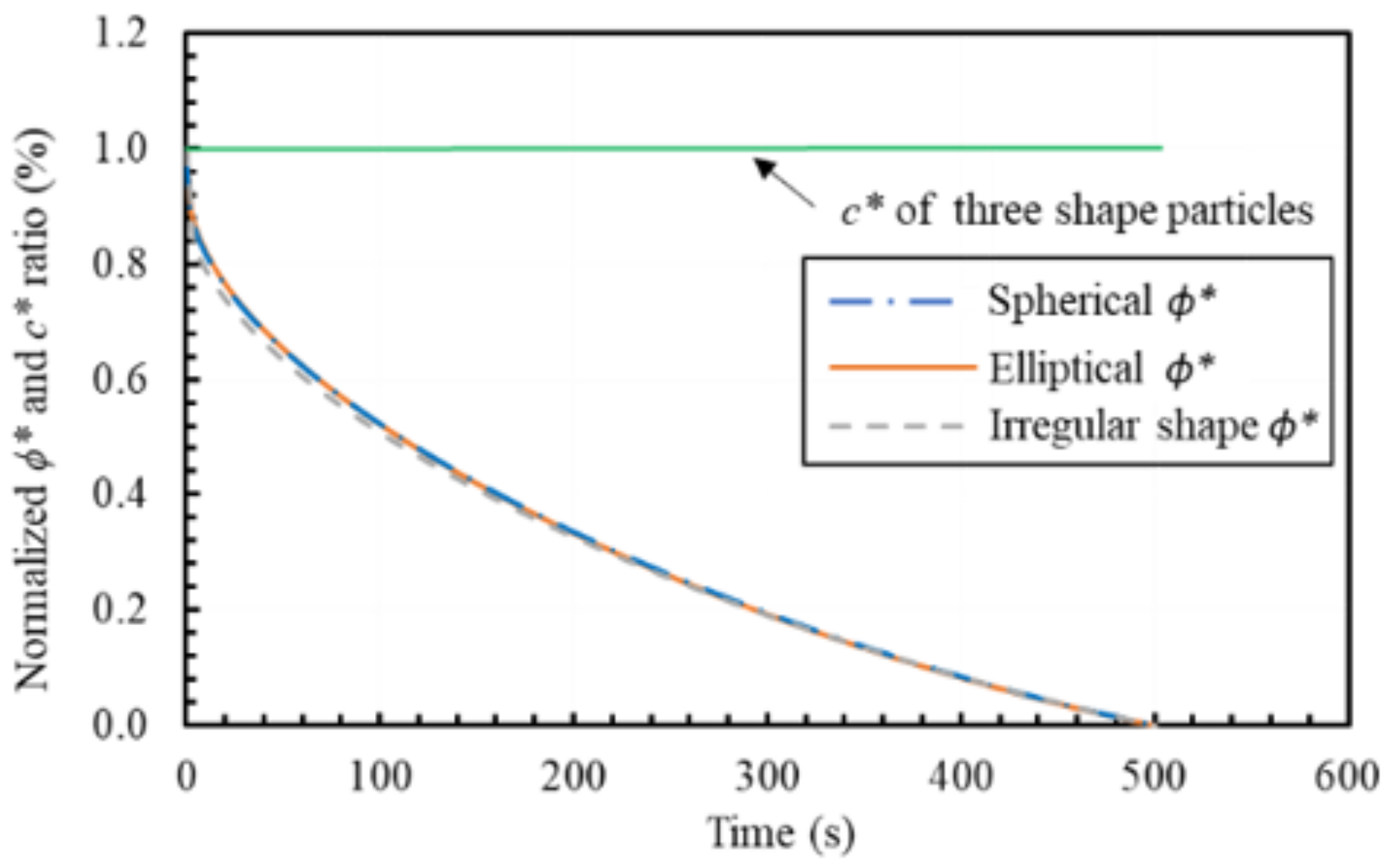
6.2. The Effect of Mineral Shape: Dissolution Simulation by Two-Dimensional (2D) PF Model
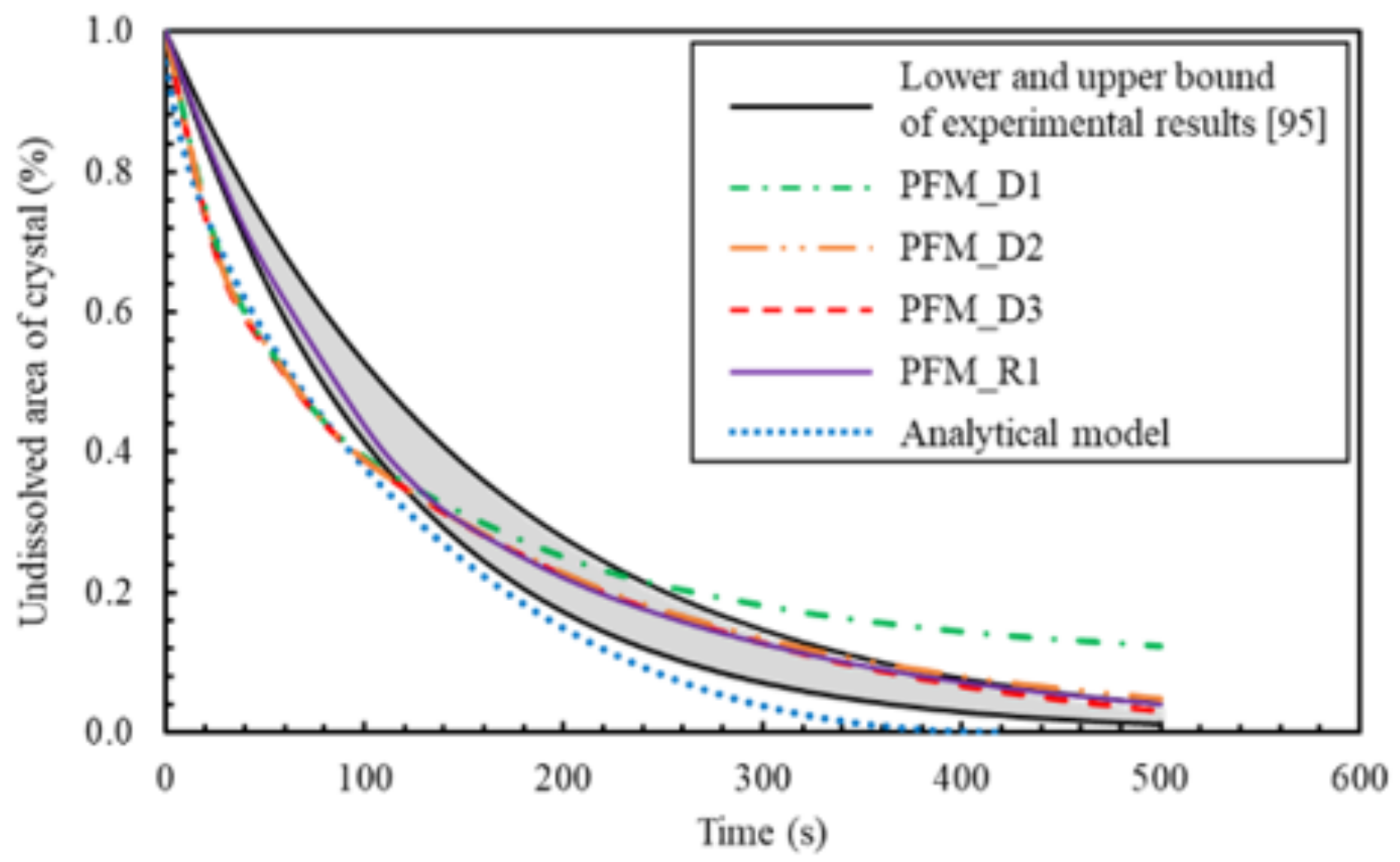
6.3. PF Validation against Experimental Results and Analytical Solution
7. Conclusions
- by comparing with the results of the analytical method, it is verified that the PF model can accurately handle the dynamic evolution of the general diffusion-controlled phase transformation process;
- using NaCl as an example, the PF model can successfully simulate the mesoscopic evolution of inorganic non-metallic materials caused by diffusion-controlled dissolution. Using the derived interfacial mobility, the PF numerical simulation results show accurate and consistent agreement with the analytical method results, as well as with the experimental ones derived with video-microscopy images analyses. It is worth mentioning that all the input parameters of the PF model have real physical meaning and are based on the experiments data;
- an observed discrepancy was related to the dissolution mechanism, which was found to be initially limited by the reaction rate, being slower than the diffusion flux due to the rapid change of solute concentration. This change in dissolution mechanism was successfully captured by adjusting the PF interface mobility ().
- the dissolution characteristics of NaCl particles with different circularity factors were analysed by the 2D PF model. The simplification of spherical shape for NaCl particles was verified to hold.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Height of the Double Well Potential and Gradient Energy Coefficient
Appendix A.2. The Interface Mobility
Appendix A.3. The Curvature of the Free Energy Density Function
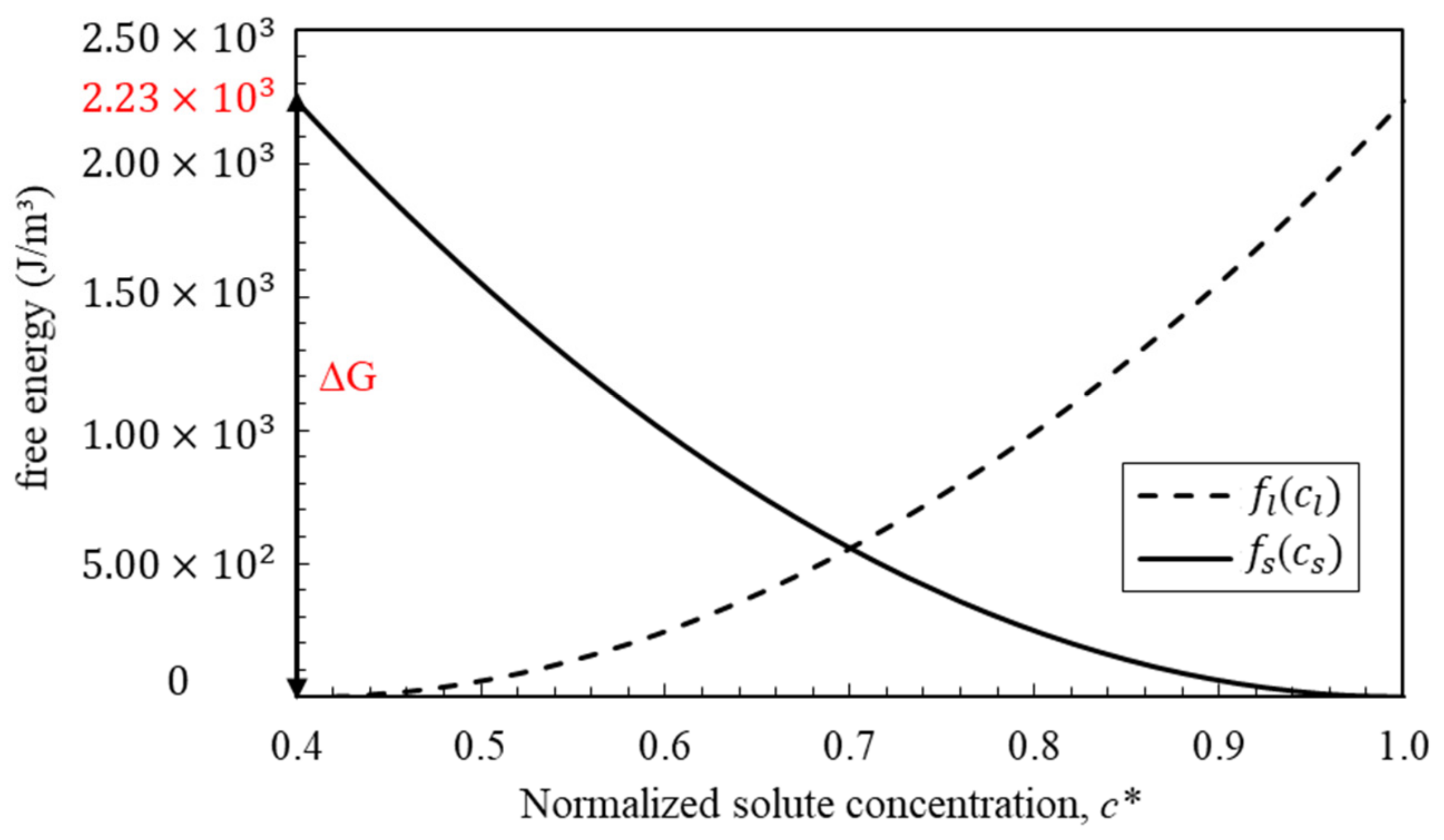
Appendix B. PF Parameters Normalization
References
- Weissbart, E.J.; Rimstidt, J. Wollastonite: Incongruent dissolution and leached layer formation. Geochim. Cosmochim. Acta 2000, 64, 4007–4016. [Google Scholar] [CrossRef]
- Bluteau, M.-C.; Demopoulos, G.P. The incongruent dissolution of scorodite—Solubility, kinetics and mechanism. Hydrometallurgy 2007, 87, 163–177. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Jonkers, H.M.; Van Tittelboom, K.; Snoeck, D.; De Belie, N.; De Muynck, W.; Verstraete, W.; Wang, J.; Mechtcherine, V. Recovery against Environmental Action; Springer: Dordrecht, The Netherlands, 2013; pp. 65–117. [Google Scholar]
- Yang, Y.; Lepech, M.D.; Yang, E.-H.; Li, V.C. Autogenous healing of engineered cementitious composites under wet-dry cycles. Cem. Concr. Res. 2009, 39, 382–390. [Google Scholar] [CrossRef]
- De Belie, N.; Gruyaert, E.; Al-Tabbaa, A.; Antonaci, P.; Baera, C.; Bajare, D.; Darquennes, A.; Davies, R.; Ferrara, L.; Jefferson, T.; et al. A Review of Self-Healing Concrete for Damage Management of Structures. Adv. Mater. Interfaces 2018, 5, 1800074. [Google Scholar] [CrossRef]
- Aaron, H.B.; Fainstein, D.; Kotler, G.R. Diffusion-limited phase transformations: A comparison and critical evaluation of the mathematical approximations. J. Appl. Phys. 1970, 41, 4404–4410. [Google Scholar] [CrossRef]
- Wehrli, B. Monte Carlo simulations of surface morphologies during mineral dissolution. J. Colloid Interface Sci. 1989, 132, 230–242. [Google Scholar] [CrossRef]
- Yang, X.; Liu, X.; Wang, J.; Zhao, Z.; Lei, H. Analytical solution of a mathematical model for rock salt dissolution in still water. Arab. J. Geosci. 2018, 11, 732. [Google Scholar] [CrossRef]
- Shekunov, B.; Montgomery, E.R. Theoretical Analysis of Drug Dissolution: I. Solubility and Intrinsic Dissolution Rate. J. Pharm. Sci. 2016, 105, 2685–2697. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J. Mathematical modeling of drug dissolution. Int. J. Pharm. 2013, 453, 12–24. [Google Scholar] [CrossRef]
- Wang, Y.; Abrahamsson, B.; Lindfors, L.; Brasseur, J.G. Comparison and Analysis of Theoretical Models for Diffusion-Controlled Dissolution. Mol. Pharm. 2012, 9, 1052–1066. [Google Scholar] [CrossRef]
- Guo, X.; Sietsma, J.; Yang, Y.; Sun, Z.; Guo, M. Diffusion-limited dissolution of spherical particles: A critical evaluation and applications of approximate solutions. AIChE J. 2017, 63, 2926–2934. [Google Scholar] [CrossRef]
- Samaha, D.; Shehayeb, R.; Kyriacos, S. Modeling and comparison of dissolution profiles of diltiazem modified-release formulations. Dissolution Technol. 2009, 16, 41–46. [Google Scholar] [CrossRef]
- Wang, J.; Flanagan, D.R. General solution for diffusion-controlled dissolution of spherical particles. 2. Evaluation of experimental data. J. Pharm. Sci. 2002, 91, 534–542. [Google Scholar] [CrossRef]
- Matsubara, H.; Tomonori, Y. Mathematical and numerical modelling of limestone dissolution. Environ. Geotech. 2019, 40, 1–12. [Google Scholar] [CrossRef]
- Nicoleau, L.; Bertolim, M.A. Analytical Model for the Alite (C 3 S) Dissolution Topography. J. Am. Ceram. Soc. 2015, 99, 773–786. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, N.; Wu, K.; Wang, Y. Quantitative phase field modeling of diffusion-controlled precipitate growth and dissolution in Ti–Al–V. Scr. Mater. 2004, 50, 471–476. [Google Scholar] [CrossRef]
- Nambu, S.; Sagala, D.A. Domain formation and elastic long-range interaction in ferroelectric perovskites. Phys. Rev. B 1994, 50, 5838–5847. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.G.; Kim, D.I.; Kim, W.T.; Park, Y.B. Computer simulations of two-dimensional and three-dimensional ideal grain growth. Phys. Rev. E 2006, 74, 061605. [Google Scholar] [CrossRef]
- Wang, Y.U.; Jin, Y.M.; Cuitiño, A.M.; Khachaturyan, A.G. Phase field microelasticity theory and modeling of multiple dislocation dynamics. Appl. Phys. Lett. 2001, 78, 2324–2326. [Google Scholar] [CrossRef]
- Wen, Y.-H.; Chen, L.-Q.; Hawk, J.A. Phase-field modeling of corrosion kinetics under dual-oxidants. Model. Simul. Mater. Sci. Eng. 2012, 20. [Google Scholar] [CrossRef]
- Kobayashi, R.; Warren, J.; Carter, W. Vector-valued phase field model for crystallization and grain boundary formation. Phys. D: Nonlinear Phenom. 1998, 119, 415–423. [Google Scholar] [CrossRef]
- Chen, L.-Q. Phase-Field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-field simulation of solidification. Annu. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics. Phys. Rev. E 1996, 53, R3017–R3020. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-Field model for microstructure evolution at the mesoscopic scale. Annu. Rev. Mater. Res. 2013, 43, 89–107. [Google Scholar] [CrossRef]
- Wang, S.L.; Sekerka, R.F.; Wheeler, A.A.; Murray, B.T.; Coriell, S.R.; Braun, R.; McFadden, G.B. Thermodynamically-consistent phase-field models for solidification. Phys. D Nonlinear Phenom. 1993, 69, 189–200. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Provatas, N.; Elder, K. Phase-Field Methods in Materials Science and Engineering; John Wiley & Sons: Weinheim, Germany, 2011. [Google Scholar]
- Wheeler, A.A.; Boettinger, W.J.; McFadden, G.B. Phase-field model for isothermal phase transitions in binary alloys. Phys. Rev. A 1992, 45, 7424–7440. [Google Scholar] [CrossRef] [PubMed]
- Cha, P.-R.; Yeon, D.-H.; Yoon, J.-K. A phase field model for isothermal solidification of multicomponent alloys. Acta Mater. 2001, 49, 3295–3307. [Google Scholar] [CrossRef]
- Suzuki, T.; Ode, M.; Kim, S.G.; Kim, W.T. Phase-field model of dendritic growth. J. Cryst. Growth 2002, 237–239, 125–131. [Google Scholar] [CrossRef]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative phase-field model of alloy solidification. Phys. Rev. E 2004, 70, 061604. [Google Scholar] [CrossRef]
- Nestler, B.; Garcke, H.; Stinner, B. Multicomponent alloy solidification: Phase-field modeling and simulations. Phys. Rev. E 2005, 71, 041609. [Google Scholar] [CrossRef] [PubMed]
- Badalassi, V.E.; Ceniceros, H.D.; Banerjee, S. Computation of multiphase systems with phase field models. J. Comput. Phys. 2003, 190, 371–397. [Google Scholar] [CrossRef]
- Petersen, T.; Valdenaire, P.-L.; Pellenq, R.; Ulm, F.-J. A reaction model for cement solidification: Evolving the C–S–H packing density at the micrometer-scale. J. Mech. Phys. Solids 2018, 118, 58–73. [Google Scholar] [CrossRef]
- Steinbach, I.; Zhang, L.; Plapp, M. Phase-field model with finite interface dissipation. Acta Mater. 2012, 60, 2689–2701. [Google Scholar] [CrossRef]
- Tonegawa, Y. Phase field model with a variable chemical potential. Proc. R. Soc. Edinburgh: Sect. A Math. 2002, 132, 993–1019. [Google Scholar] [CrossRef]
- Bazant, M.Z. Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Accounts Chem. Res. 2012, 46, 1144–1160. [Google Scholar] [CrossRef]
- Chen, L.Q.; Fan, F.; Hong, L.; Chen, J.; Ji, Y.Z.; Zhang, S.L.; Zhu, T. A phase-field model coupled with large elasto-plastic deformation: Application to lithiated silicon electrodes. J. Electrochem. Soc. 2014, 161, F3164–F3172. [Google Scholar] [CrossRef]
- Lin, C.; Ruan, H. Multi-phase-field modeling of localized corrosion involving galvanic pitting and mechano-electrochemical coupling. Corros. Sci. 2020, 177, 108900. [Google Scholar] [CrossRef]
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Hesch, C.; Weinberg, K. Thermodynamically consistent algorithms for a finite-deformation phase-field approach to fracture. Int. J. Numer. Methods Eng. 2014, 99, 906–924. [Google Scholar] [CrossRef]
- Heider, Y.; Markert, B. A phase-field modeling approach of hydraulic fracture in saturated porous media. Mech. Res. Commun. 2017, 80, 38–46. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Wheeler, A.A.; McFadden, G.B.; Boettinger, W.J. Phase-field model for solidification of a eutectic alloy. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1996, 452, 495–525. [Google Scholar]
- Kim, S.G.; Kim, W.T.; Suzuki, T. Phase-field model for binary alloys. Phys. Rev. E 1999, 60, 7186–7197. [Google Scholar] [CrossRef] [PubMed]
- Steinbach, I.; Pezzolla, F.; Nestler, B.; Seeßelberg, M.; Prieler, R.; Schmitz, G.; Rezende, J. A phase field concept for multiphase systems. Phys. D Nonlinear Phenom. 1996, 94, 135–147. [Google Scholar] [CrossRef]
- Losert, W.; Stillman, D.A.; Cummins, H.Z.; Kopczyński, P.; Rappel, W.-J.; Karma, A. Selection of doublet cellular patterns in directional solidification through spatially periodic perturbations. Phys. Rev. E 1998, 58, 7492–7506. [Google Scholar] [CrossRef]
- Ode, M.; Lee, J.S.; Kim, S.G.; Kim, W.T.; Suzuki, T. Phase-field Model for Solidification of Ternary Alloys. ISIJ Int. 2000, 40, 870–876. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, W.T.; Suzuki, T. Interfacial compositions of solid and liquid in a phase-field model with finite interface thickness for isothermal solidification in binary alloys. Phys. Rev. E 1998, 58, 3316. [Google Scholar] [CrossRef]
- Tiaden, J.; Nestler, B.; Diepers, H.; Steinbach, I. The multiphase-field model with an integrated concept for modelling solute diffusion. Phys. D Nonlinear Phenom. 1998, 115, 73–86. [Google Scholar] [CrossRef]
- Eiken, J.; Böttger, B.; Steinbach, I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application. Phys. Rev. E 2006, 73, 066122. [Google Scholar] [CrossRef]
- Wheeler, A.A.; Boettinger, W.J.; McFadden, G.B. Phase-field model of solute trapping during solidification. Phys. Rev. E 1993, 47, 1893. [Google Scholar] [CrossRef]
- Ode, M.; Suzuki, T.; Kim, S.; Kim, W. Phase–field model for solidification of Fe–C alloys. Sci. Technol. Adv. Mater. 2000, 1, 43–49. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.-J.; Steinbach, I.; Karma, A.; Tong, X. Modeling melt convection in phase-field simulations of solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Cha, P.R.; Yeon, D.H.; Yoon, J.K. Phase-field model for multicomponent alloy solidification. J. Cryst. Growth. 2005, 274, 281–293. [Google Scholar] [CrossRef]
- Qin, R.S.; Bhadeshia, H.K. Phase field method. Mater. Sci. Technol. 2010, 26, 803–811. [Google Scholar] [CrossRef]
- Xu, Z.; Meakin, P. Phase-field modeling of solute precipitation and dissolution. J. Chem. Phys. 2008, 129, 014705. [Google Scholar] [CrossRef] [PubMed]
- Abubakar, A.A.; Akhtar, S.S.; Arif, A.F.M. Phase field modeling of V2O5 hot corrosion kinetics in thermal barrier coatings. Comput. Mater. Sci. 2015, 99, 105–116. [Google Scholar] [CrossRef]
- Grafe, U.; Böttger, B.; Tiaden, J.; Fries, S.G. Coupling of multicomponent thermodynamic databases to a phase field model: Application to solidification and solid state transformations of superalloys. Scr. Mater. 2000, 42, 1179–1186. [Google Scholar] [CrossRef]
- Qin, R.; Wallach, E.; Thomson, R. A phase-field model for the solidification of multicomponent and multiphase alloys. J. Cryst. Growth 2005, 279, 163–169. [Google Scholar] [CrossRef]
- Ansari, T.Q.; Xiao, Z.; Hu, S.; Li, Y.; Luo, J.L.; Shi, S.Q. Phase-field model of pitting corro-sion kinetics in metallic materials. NPJ Comput. Mater. 2018, 4, 1–9. [Google Scholar] [CrossRef]
- Mai, W.; Soghrati, S.; Buchheit, R.G. A phase field model for simulating the pitting corrosion. Corros. Sci. 2016, 110, 157–166. [Google Scholar] [CrossRef]
- Mai, W.; Soghrati, S. A phase field model for simulating the stress corrosion cracking initiated from pits. Corros. Sci. 2017, 125, 87–98. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, Y.; Hu, S.; Li, Y.; Shi, S.-Q. A quantitative phase-field model of gas bubble evolution in UO2. Comput. Mater. Sci. 2020, 184, 109867. [Google Scholar] [CrossRef]
- Mai, W.; Soghrati, S. New phase field model for simulating galvanic and pitting corrosion processes. Electrochim. Acta 2018, 260, 290–304. [Google Scholar] [CrossRef]
- Zhang, R.; Jing, T.; Jie, W.; Liu, B. Phase-field simulation of solidification in multicomponent alloys coupled with ther-modynamic and diffusion mobility databases. Acta Mater. 2006, 54, 2235–2239. [Google Scholar] [CrossRef]
- Kobayashi, H.; Ode, M.; Kim, S.G.; Kim, W.T.; Suzuki, T. Phase-field model for solidification of ternary alloys coupled with thermodynamic database. Scr. Mater. 2003, 48, 689–694. [Google Scholar] [CrossRef]
- Böttger, B.; Eiken, J.; Steinbach, I. Phase field simulation of equiaxed solidification in technical alloys. Acta Mater. 2006, 54, 2697–2704. [Google Scholar] [CrossRef]
- Clark, J.B.; Hastie, J.W.; Kihlborg, L.H.E.; Metselaar, R.; Thackeray, M.M. Definitions of terms relating to phase transitions of the solid state. IUPAC Standards Online 2016, 66, 577–594. [Google Scholar] [CrossRef][Green Version]
- McGillen, M.R.; Fairchild, I.J. An experimental study of incongruent dissolution of CaCO3 under analogue glacial conditions. J. Glaciol. 2005, 51, 383–390. [Google Scholar] [CrossRef][Green Version]
- Simon, B. Dissolution rates of NaCl and KCl in aqueous solution. J. Cryst. Growth 1981, 52, 789–794. [Google Scholar] [CrossRef]
- Antignano, A.; Manning, C.E. Rutile solubility in H2O, H2O—SiO2, and H2O—NaAlSi3O8 fluids at 0.7–2.0 GPa and 700–1000 C: Implications for mobility of nominally insoluble elements. Chem. Geol. 2008, 255, 283–293. [Google Scholar] [CrossRef]
- Xie, Z.; Walther, J.V. Incongruent dissolution and surface area of kaolinite. Geochim. Cosmochim. Acta 1992, 56, 3357–3363. [Google Scholar] [CrossRef]
- Scheiner, S.; Hellmich, C. Stable pitting corrosion of stainless steel as diffusion-controlled dissolution process with a sharp moving electrode boundary. Corros. Sci. 2007, 49, 319–346. [Google Scholar] [CrossRef]
- Yang, C.; Li, S.; Wang, X.; Wang, J.; Huang, H. Phase-field simulation of multi-phase interactions in Fe-C peritectic solidification. Comput. Mater. Sci. 2020, 171, 109220. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, W.T.; Suzuki, T.; Ode, M. Phase-field modeling of eutectic solidification. J. Cryst. Growth 2004, 261, 135–158. [Google Scholar] [CrossRef]
- Wang, Y.; Abrahamsson, B.; Lindfors, L.; Brasseur, J.G. Analysis of diffusion-controlled dissolution from polydisperse collec-tions of drug particles with an assessed mathematical model. J. Pharm. Sci. 2015, 104, 2998–3017. [Google Scholar] [CrossRef] [PubMed]
- Burt, H.M.; Mitchell, A. Crystal defects and dissolution. Int. J. Pharm. 1981, 9, 137–152. [Google Scholar] [CrossRef]
- Wang, J.; Keener, T.C.; Li, G.; Khang, S.-J. The dissolution rate of CA(OH)2 in aqueous solutions. Chem. Eng. Commun. 1998, 169, 167–184. [Google Scholar] [CrossRef]
- Vermilyea, D.A. The Dissolution of MgO and Mg(OH)2 in Aqueous Solutions. J. Electrochem. Soc. 1969, 116, 1179–1183. [Google Scholar] [CrossRef]
- Johannsen, K.; Rademacher, S. Modelling the kinetics of calcium hydroxide dissolution in water. Acta Hydrochim. Hydrobiol. 1999, 27, 72–78. [Google Scholar] [CrossRef]
- Giles, D.; Ritchie, I.; Xu, B.-A. The kinetics of dissolution of slaked lime. Hydrometallurgy 1993, 32, 119–128. [Google Scholar] [CrossRef]
- Lanaro, G.; Patey, G.N. Molecular Dynamics Simulation of NaCl Dissolution. J. Phys. Chem. B 2015, 119, 4275–4283. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Meng, S.; Xu, L.F.; Wang, E.G.; Gao, S. Dissolution dynamics of NaCl nanocrystal in liquid water. Phys. Rev. E 2005, 72, 012602. [Google Scholar] [CrossRef]
- Garcia, J.; Hernandez, J.; Rubio, J. Dissolution of in monocrystalline sodium chloride. Phys. Rev. B 1980, 21, 5012. [Google Scholar]
- Ohtaki, H.; Fukushima, N.; Hayakawa, E.; Okada, I. Dissolution process of sodium chloride crystal in water. Pure Appl. Chem. 1988, 60, 1321–1324. [Google Scholar] [CrossRef]
- Langlet, M.; Nadaud, F.; Benali, M.; Pezron, I.; Saleh, K.; Guigon, P.; Metlas-Komunjer, L. Kinetics of dissolution and recrystallization of sodium chloride at controlled relative humidity. KONA Powder Part. J. 2011, 29, 168–179. [Google Scholar] [CrossRef]
- Utoft, A.; Kinoshita, K.; Bitterfield, D.L.; Needham, D. Manipulating single microdroplets of NaCl solutions: Solvent dissolution, microcrystallization, and crystal morphology. Langmuir 2018, 34, 3626–3641. [Google Scholar] [CrossRef]
- Holmberg, N.; Chen, J.-C.; Foster, A.S.; Laasonen, K. Dissolution of NaCl nanocrystals: An ab initio molecular dynamics study. Phys. Chem. Chem. Phys. 2014, 16, 17437–17446. [Google Scholar] [CrossRef]
- Yang, Y.; Meng, S.; Wang, E.G. A molecular dynamics study of hydration and dissolution of NaCl nanocrystal in liquid water. J. Phys. Condens. Matter 2006, 18, 10165–10177. [Google Scholar] [CrossRef][Green Version]
- Ohtaki, H.; Fukushima, N. Dissolution of an NaCl crystal with the (111) and (-1-1-1) faces. Pure Appl. Chem. 1989, 61, 179–185. [Google Scholar] [CrossRef]
- Quilaqueo, M.; Aguilera, J.M. Dissolution of NaCl crystals in artificial saliva and water by video-microscopy. Food Res. Int. 2015, 69, 373–380. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Vega, C.; Valeriani, C.; Sanz, E. The crystal-fluid interfacial free energy and nucleation rate of NaCl from different simulation methods. J. Chem. Phys. 2015, 142, 194709. [Google Scholar] [CrossRef]
- Plewa, T.; Linde, T.; Weirs, V.G. Adaptive Mesh Refinement-Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Mosharraf, M.; Nyström, C. The effect of particle size and shape on the surface specific dissolution rate of microsized practically in-soluble drugs. Int. J. Pharm. 1995, 122, 35–47. [Google Scholar] [CrossRef]
- Liu, J.; Aruguete, D.M.; Jinschek, J.R.; Rimstidt, J.D.; Hochella, M.F., Jr. The non-oxidative dissolution of galena nanocrystals: Insights into mineral dissolution rates as a function of grain size, shape, and aggregation state. Geochim. Cosmochim. Acta 2008, 72, 5984–5996. [Google Scholar] [CrossRef]
- Higuchi, W.I.; Hiestand, E.N. Dissolution rates of finely divided drug powders I. Effect of a distribution of particle sizes in a diffu-sion-controlled process. J. Pharm. Sci. 1963, 52, 1963. [Google Scholar] [CrossRef]
- Higuchi, W.I.; Rowe, E.L.; Hiestand, E.N. Dissolution rates of finely divided drug powders II: Micronized methylprednisolone. J. Pharm. Sci. 1963, 52, 162–164. [Google Scholar] [CrossRef] [PubMed]
- De Almeida, L.P.; Simões, S.; Brito, P.; Portugal, A.; Figueiredo, M. Modeling dissolution of spar-ingly soluble multisized powders. J. Pharm. Sci. 1997, 86, 726–732. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, A. The interface response-functions in multi-componental alloy solidification. Phys. D Nonlinear Phenom. 1998, 124, 271–284. [Google Scholar] [CrossRef]
- Aziz, M.J.; Boettinger, W.J. On the transition from short-range diffusion-limited to collision-limited growth in alloy solidification. Acta Metall. Mater. 1994, 42, 524–537. [Google Scholar] [CrossRef]

| Parameter | Description | Value | Unit |
|---|---|---|---|
| Gibbs free energy | 2233.23 | ||
| curvature of the free energy density function | 6.20 × 103 | ||
| height of the double well potential | 1.94 × 104 | ||
| interface mobility | 4.02 × 10−5 | ||
| gradient energy coefficient | 1.12 × 10−5 | ||
| initial thickness of the diffuse interface | 1.0 × 10−4 | ||
| interfacial energy | 1.1 × 10−1 | ||
| diffusion coefficient in solution | 1.0 × 10−9 | ||
| diffusion coefficient in solute | 1.0 × 10−15 | ||
| saturation concentration in the solid phase | 1.0 | ||
| saturation concentration in the solution | 4.0 × 10−1 | ||
| gas constant | 8.31 | ||
| ambient temperature | 2.93 × 102 | Kelvin | |
| K | equilibrium constant | 0.4 | [-] |
| calculation time | 2.88 × 104 | s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Ukrainczyk, N.; Caggiano, A.; Koenders, E. Numerical Phase-Field Model Validation for Dissolution of Minerals. Appl. Sci. 2021, 11, 2464. https://doi.org/10.3390/app11062464
Yang S, Ukrainczyk N, Caggiano A, Koenders E. Numerical Phase-Field Model Validation for Dissolution of Minerals. Applied Sciences. 2021; 11(6):2464. https://doi.org/10.3390/app11062464
Chicago/Turabian StyleYang, Sha, Neven Ukrainczyk, Antonio Caggiano, and Eddie Koenders. 2021. "Numerical Phase-Field Model Validation for Dissolution of Minerals" Applied Sciences 11, no. 6: 2464. https://doi.org/10.3390/app11062464
APA StyleYang, S., Ukrainczyk, N., Caggiano, A., & Koenders, E. (2021). Numerical Phase-Field Model Validation for Dissolution of Minerals. Applied Sciences, 11(6), 2464. https://doi.org/10.3390/app11062464








