A Single-Shot 3D Measuring Method Based on Quadrature Phase-Shifting Color Composite Grating Projection
Abstract
:1. Introduction
2. Principle
2.1. The Phase Measuring Principle of the Traditional Color PMP
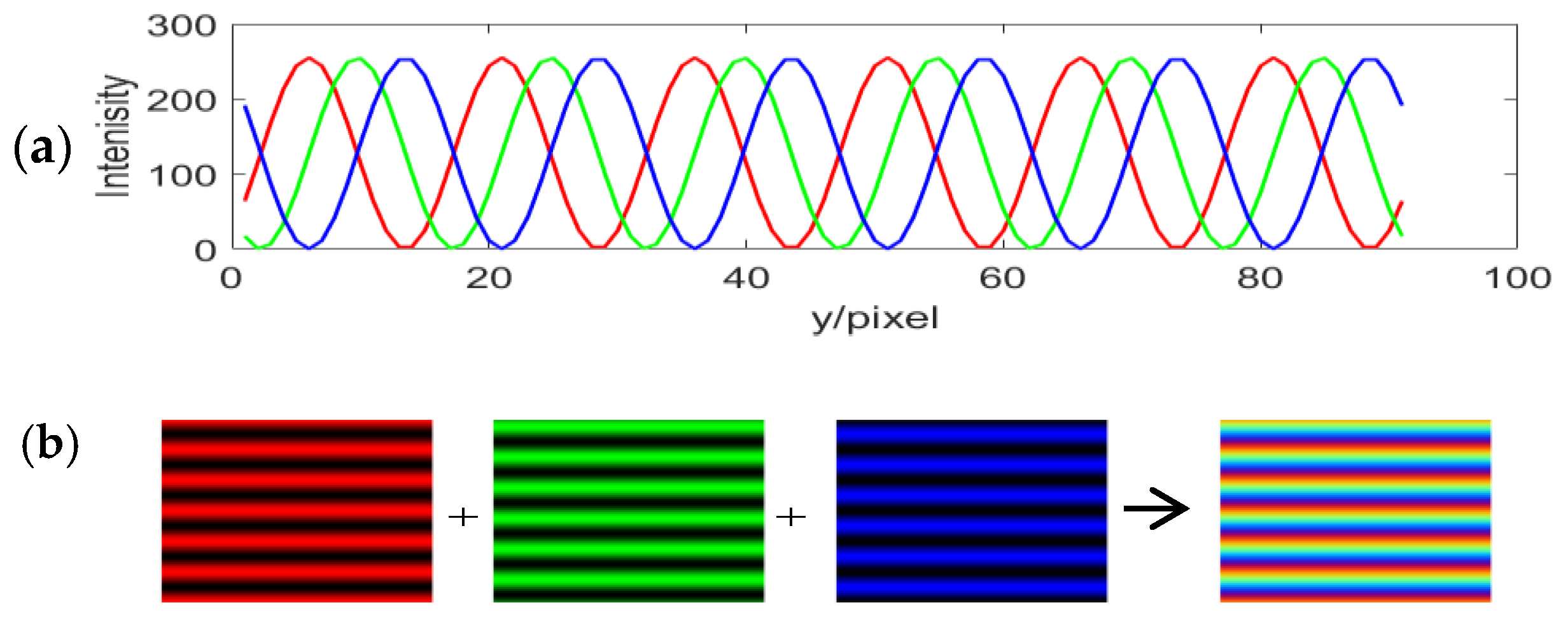
2.2. The Phase Measuring Principle of Single-Shot Quadrature Phase-Shifting Color Composite Grating
2.3. Gray Imbalance Correction Method
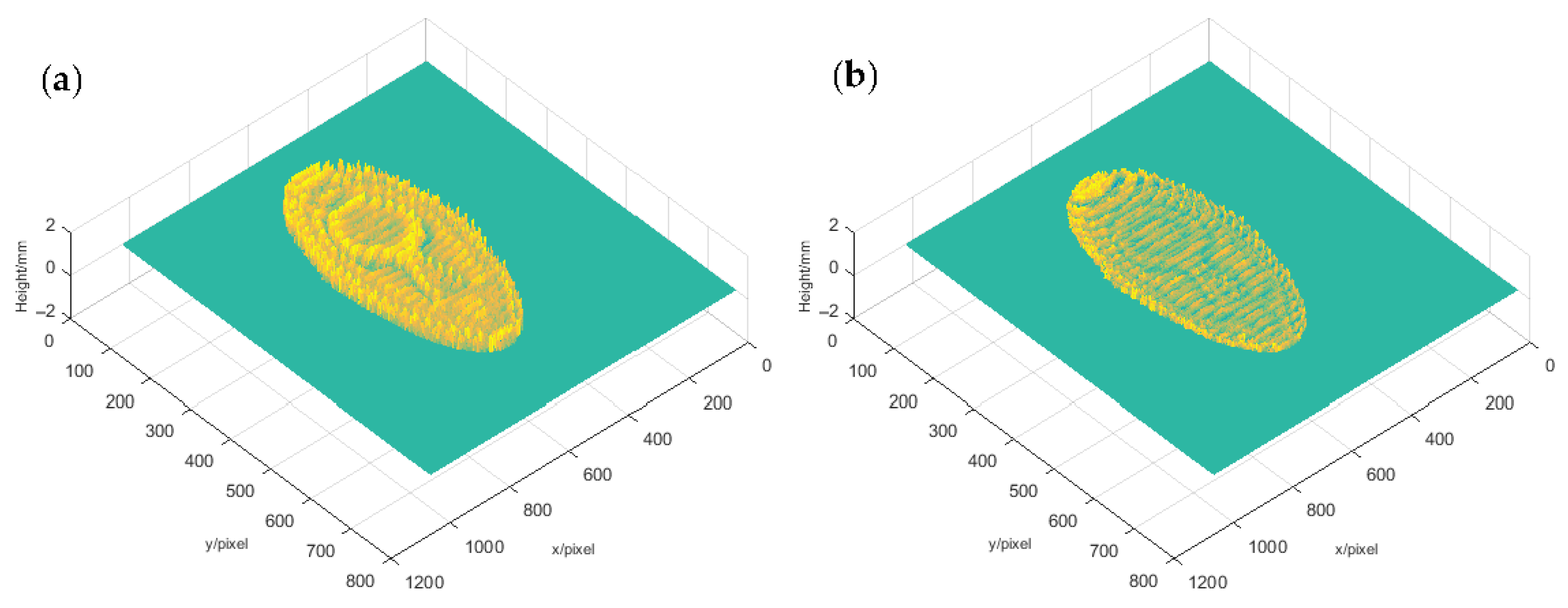
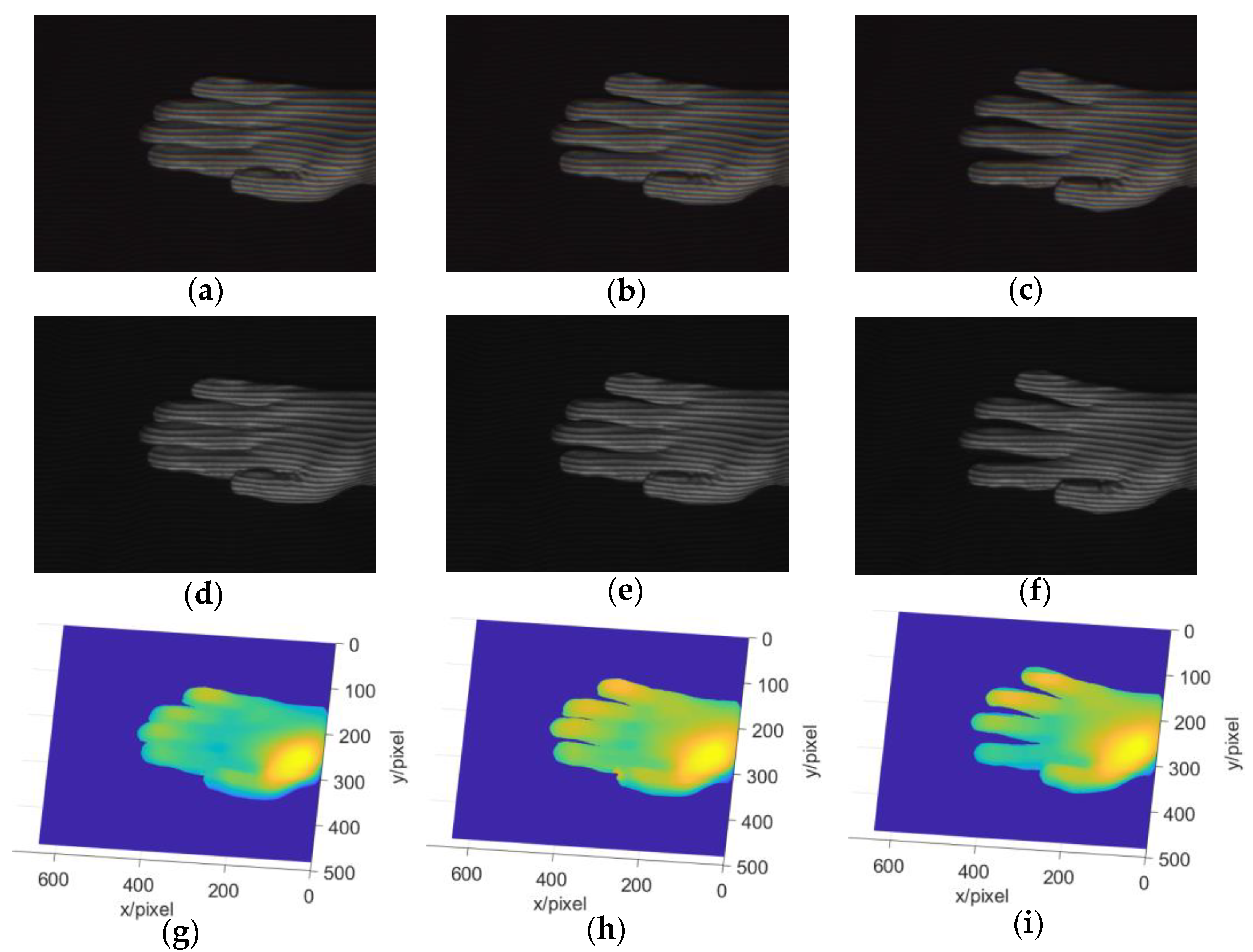
3. Experiments and Analysis
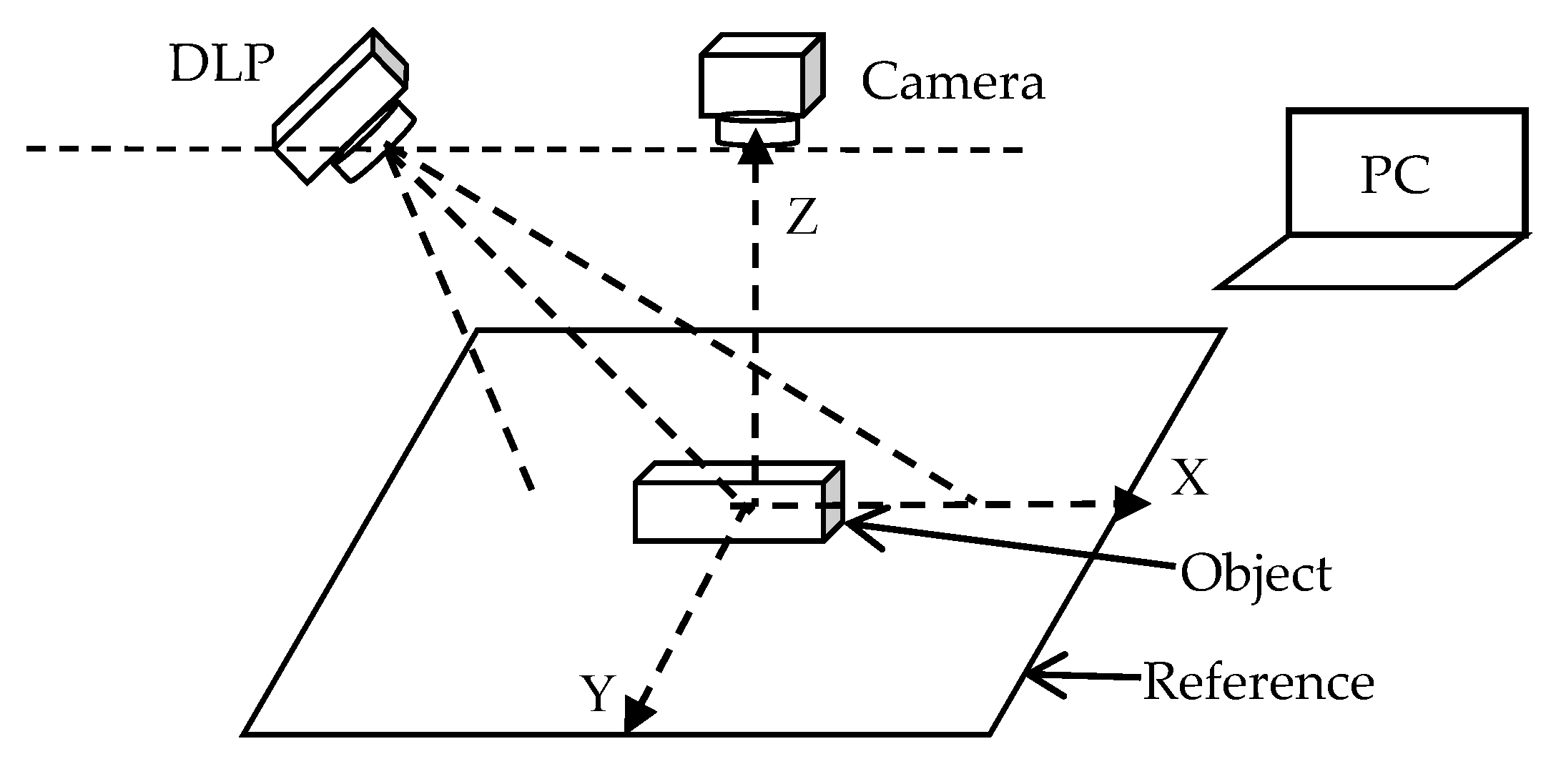
3.1. Experimental System
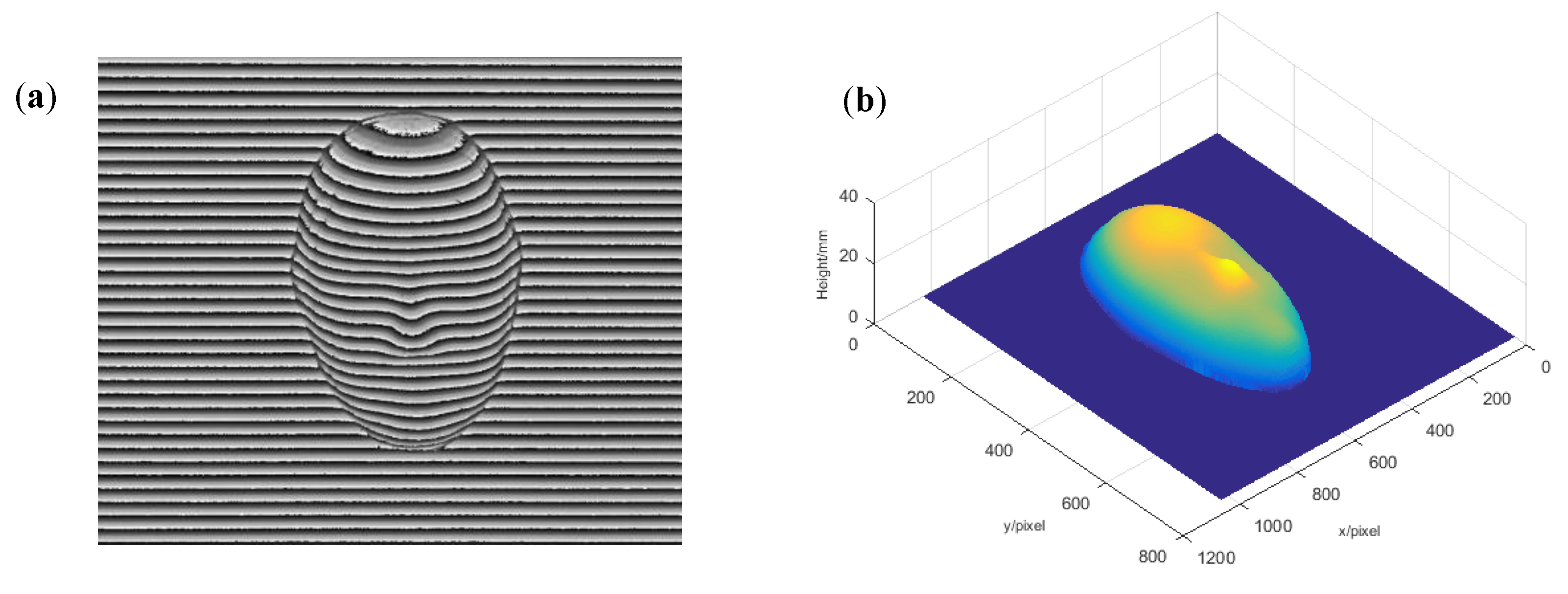
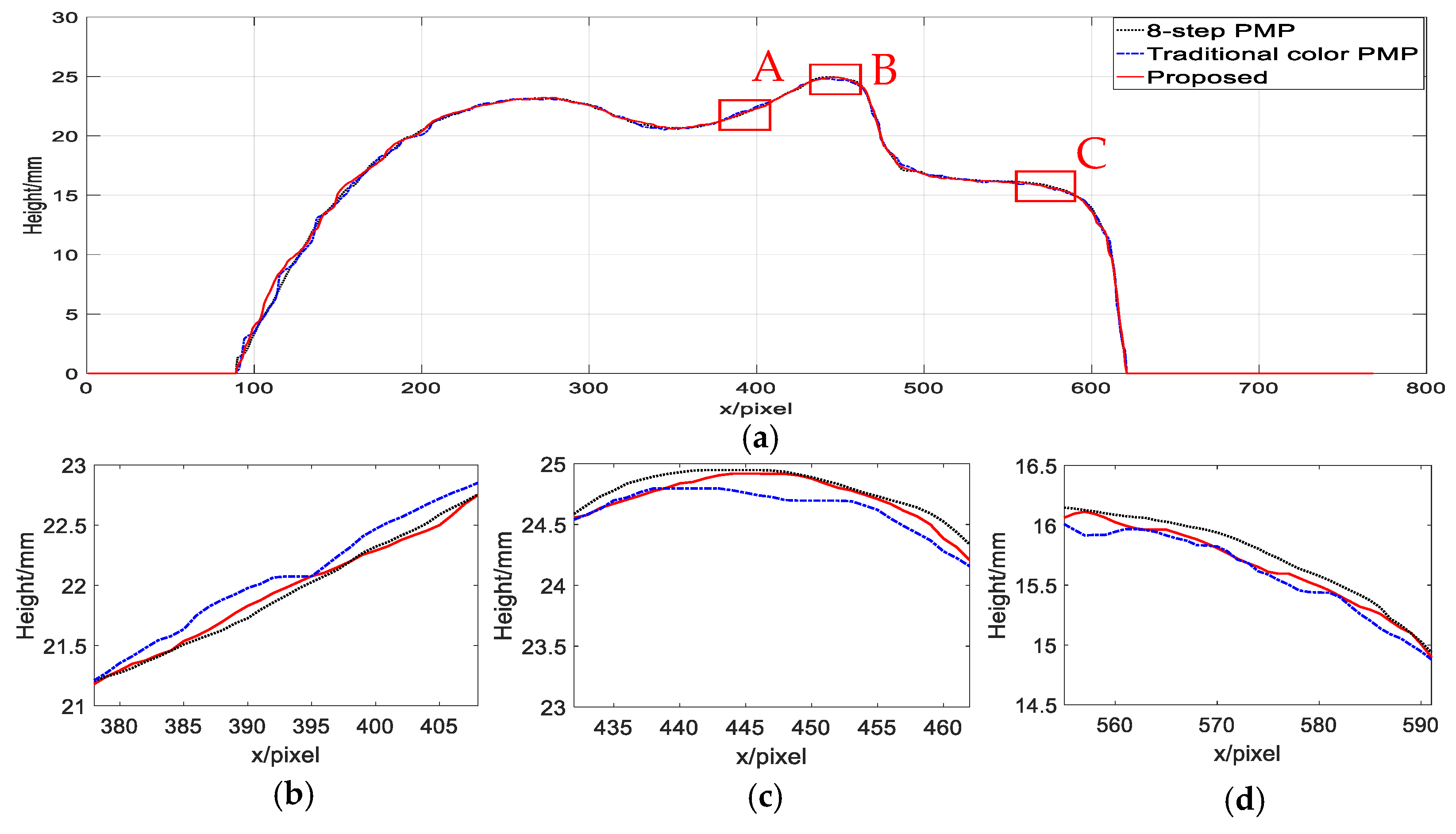
3.2. Experiments and Analysis
3.3. Real-Time Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, X.; Zhang, Q. Dynamic 3-D shape measurement method: A review. Opt. Lasers Eng. 2010, 48, 191–204. [Google Scholar] [CrossRef]
- Zhang, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Zhan, G.; Tang, H.; Zhong, K.; Li, Z.; Shi, Y.; Wang, C. High-speed FPGA-based phase measuring profilometry architecture. Opt. Express 2017, 25, 10553–10564. [Google Scholar] [CrossRef]
- Huang, P.S.; Zhang, C.; Chiang, F.-P. High-speed 3-D shape measurement based on digital fringe projection. Opt. Eng. 2003, 42, 163–168. [Google Scholar] [CrossRef]
- He, Y.; Cao, Y. A composite-structured-light 3D measurement method based on fringe parameter calibration. Opt. Lasers Eng. 2011, 49, 773–779. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Xu, J.; Xi, N.; Zhang, C.; Zhao, J.; Gao, B.; Shi, Q. Rapid 3D surface profile measurement of industrial parts using two-level structured light patterns. Opt. Lasers Eng. 2011, 49, 907–914. [Google Scholar] [CrossRef]
- Khan, D.; Shirazi, M.A.; Kim, M.Y. Single shot laser speckle based 3D acquisition system for medical applications. Opt. Lasers Eng. 2018, 105, 43–53. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Jeught, S.V.; Dirckx, J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Zhang, Z. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques. Opt. Lasers Eng. 2012, 50, 1097–1106. [Google Scholar] [CrossRef]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-C.; Cao, Y.-P.; Huang, Z.-F.; Lu, M.-T.; Chen, D.-L. Improved composite Fourier transform profilometry. Opt. Laser Technol. 2012, 44, 2037–2042. [Google Scholar] [CrossRef]
- He, Y.; Cao, Y. Three-dimensional measurement method with orthogonal composite grating aided by fringe contrast and background calibration. Opt. Eng. 2010, 49, 717–720. [Google Scholar] [CrossRef]
- Chengmeng, L.; Yiping, C.; Cheng, C.; Yingying, W.; Guangkai, F.; Yapin, W. Computer-generated moiré profilometry. Opt. Express 2017, 25, 26815. [Google Scholar]
- Li, C.; Cao, Y.; Wang, L.; Wan, Y.; Wang, Y. Real-time computer-generated moiré profilometry with adaptive filtering algorithm. Opt. Eng. 2020, 59, 034102. [Google Scholar] [CrossRef]
- Wan, Y.; Cao, Y.; Chen, C.; Fu, G.; Wang, Y.; Li, C. Single-shot real-time three dimensional measurement based on hue-height mapping. Opt. Commun. 2018, 416, 10–18. [Google Scholar] [CrossRef]
- Huang, P.; Hu, Q.; Jin, F.; Chiang, F. Color-encoded digital fringe projection technique for high-speed three-dimensional surface contouring. Opt. Eng. 1999, 38, 1065–1071. [Google Scholar] [CrossRef]
- Hu, Y.; Xi, J.; Chicharo, J.; Yang, Z. Blind color isolation for color-channel-based fringe pattern profilometry using digital projection. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2007, 24, 2372–2382. [Google Scholar] [CrossRef]
- Zhang, Z.; Towers, C.; Towers, D. Compensating lateral chromatic aberration of a colour fringe projection system for shape metrology. Opt. Lasers Eng. 2010, 48, 159–165. [Google Scholar] [CrossRef]
- Jiang, C.; Jia, S.; Dong, J.; Bao, Q.; Yang, J.; Lian, Q.; Li, D. Multi-frequency color-marked fringe projection profilometry for fast 3D shape measurement of complex objects. Opt. Express 2015, 23, 24152–24162. [Google Scholar] [CrossRef]
- Zhu, L.; Cao, Y.; He, D.; Chen, C. Grayscale imbalance correction in real-time phase measuring profilometry. Opt. Commun. 2016, 376, 72–80. [Google Scholar] [CrossRef]
- Ma, M.; Cao, Y.; He, D.; Chen, C.; Wan, Y. Grayscale imbalance correcting method based on fringe normalization in RGB tricolor real-time three-dimensional measurement. Opt. Eng. 2016, 55, 034102. [Google Scholar] [CrossRef]
- Cao, Y.; Su, X. RGB Tricolor Based Fast Phase Measuring Profilometry. In Proceedings of the SPIE/COS Photonics Asia, Photonics Asia Symposium 2002, Shanghai, China, 14–18 October 2002. [Google Scholar] [CrossRef]
- Pan, J.; Huang, P.S.; Chiang, F.-P. Color-encoded digital fringe projection technique for high-speed 3D shape measurement: Color coupling and imbalance compensation. In Proceedings of the SPIE Optics East, February 2004, Conference on Two- and Three-Dimensional Vision Systems for Inspection, Control and Metrology, Providence, RI, USA, 29–30 October 2003; Volume 5265, pp. 205–212. [Google Scholar] [CrossRef]
- Huang, P.S.; Pan, J.; Chiang, F.-P. Color phase-shifting technique for three-dimensional shape measurement. Opt. Eng. 2006, 45, 013602. [Google Scholar] [CrossRef]
- Fu, G.; Cao, Y.; Wang, Y.; Wan, Y.; Wang, L.; Li, C. Real-time three-dimensional shape measurement based on color binary fringe projection. Opt. Eng. 2019, 58, 044102. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Reliability-guided phase unwrapping algorithm: A review. Opt. Lasers Eng. 2004, 42, 245–261. [Google Scholar] [CrossRef]
- Song, W.; Su, X.; Cao, Y.; Xiang, L. Phase-height mapping and coordinate calibration simultaneously in phase-measuring profilometry. Opt. Eng. 2004, 43, 708–712. [Google Scholar] [CrossRef]
- Ma, Q.; Cao, Y.; Chen, C.; Wan, Y.; Fu, G.; Wang, Y. Intrinsic feature revelation of phase-to-height mapping in phase measuring profilometry. Opt. Laser Technol. 2018, 108, 46–52. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Cao, Y.; Yang, C.; Zhang, Y.; Gao, J. A Single-Shot 3D Measuring Method Based on Quadrature Phase-Shifting Color Composite Grating Projection. Appl. Sci. 2021, 11, 2522. https://doi.org/10.3390/app11062522
Huang X, Cao Y, Yang C, Zhang Y, Gao J. A Single-Shot 3D Measuring Method Based on Quadrature Phase-Shifting Color Composite Grating Projection. Applied Sciences. 2021; 11(6):2522. https://doi.org/10.3390/app11062522
Chicago/Turabian StyleHuang, Xiuzhang, Yiping Cao, Chaozhi Yang, Yujiao Zhang, and Jie Gao. 2021. "A Single-Shot 3D Measuring Method Based on Quadrature Phase-Shifting Color Composite Grating Projection" Applied Sciences 11, no. 6: 2522. https://doi.org/10.3390/app11062522





