Experimental Study on the Behavior of Existing Reinforced Concrete Multi-Column Piers under Earthquake Loading
Abstract
1. Introduction
2. Test Model of Multi-Column Bridge Piers
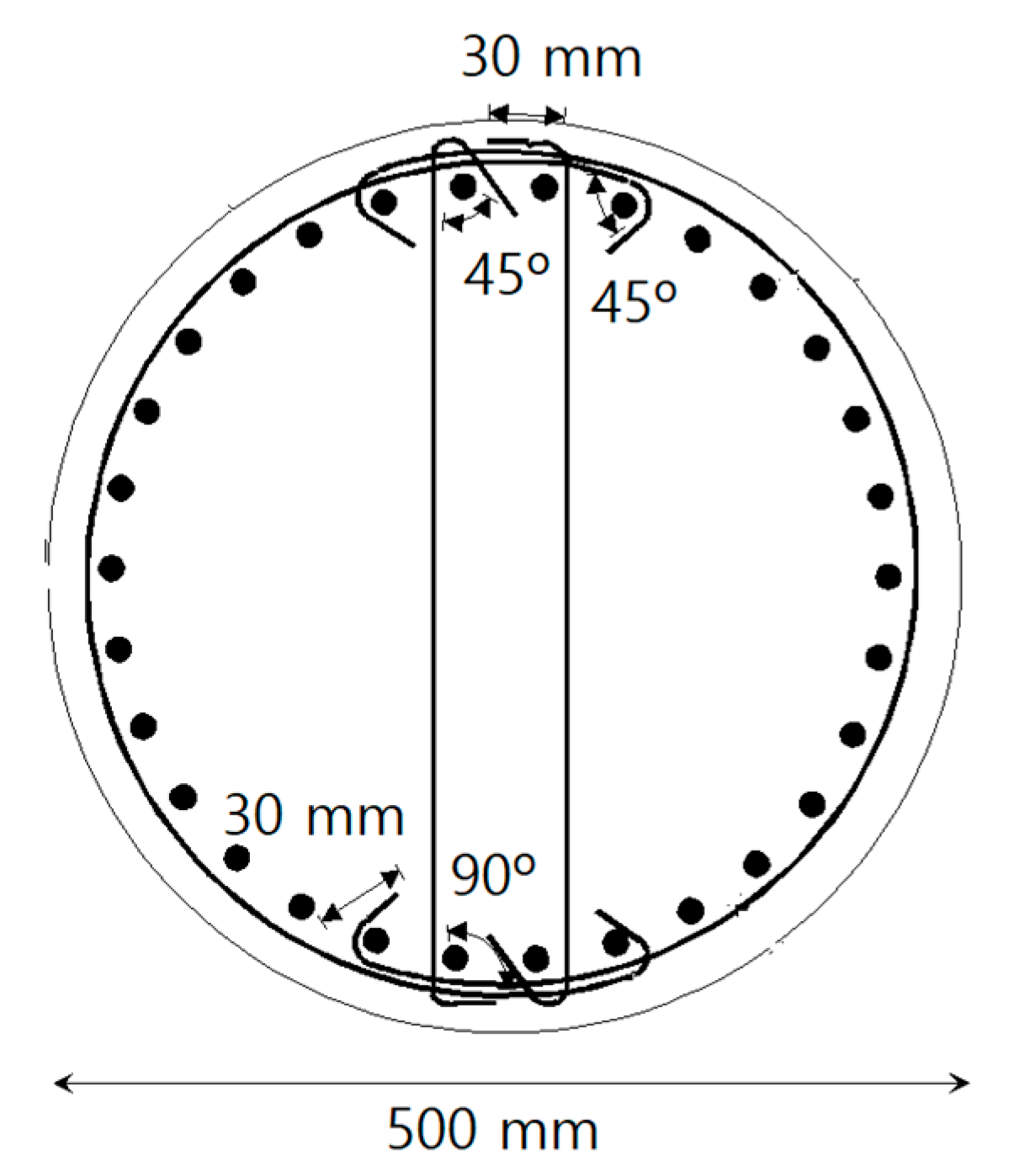
2.1. Test Specimens
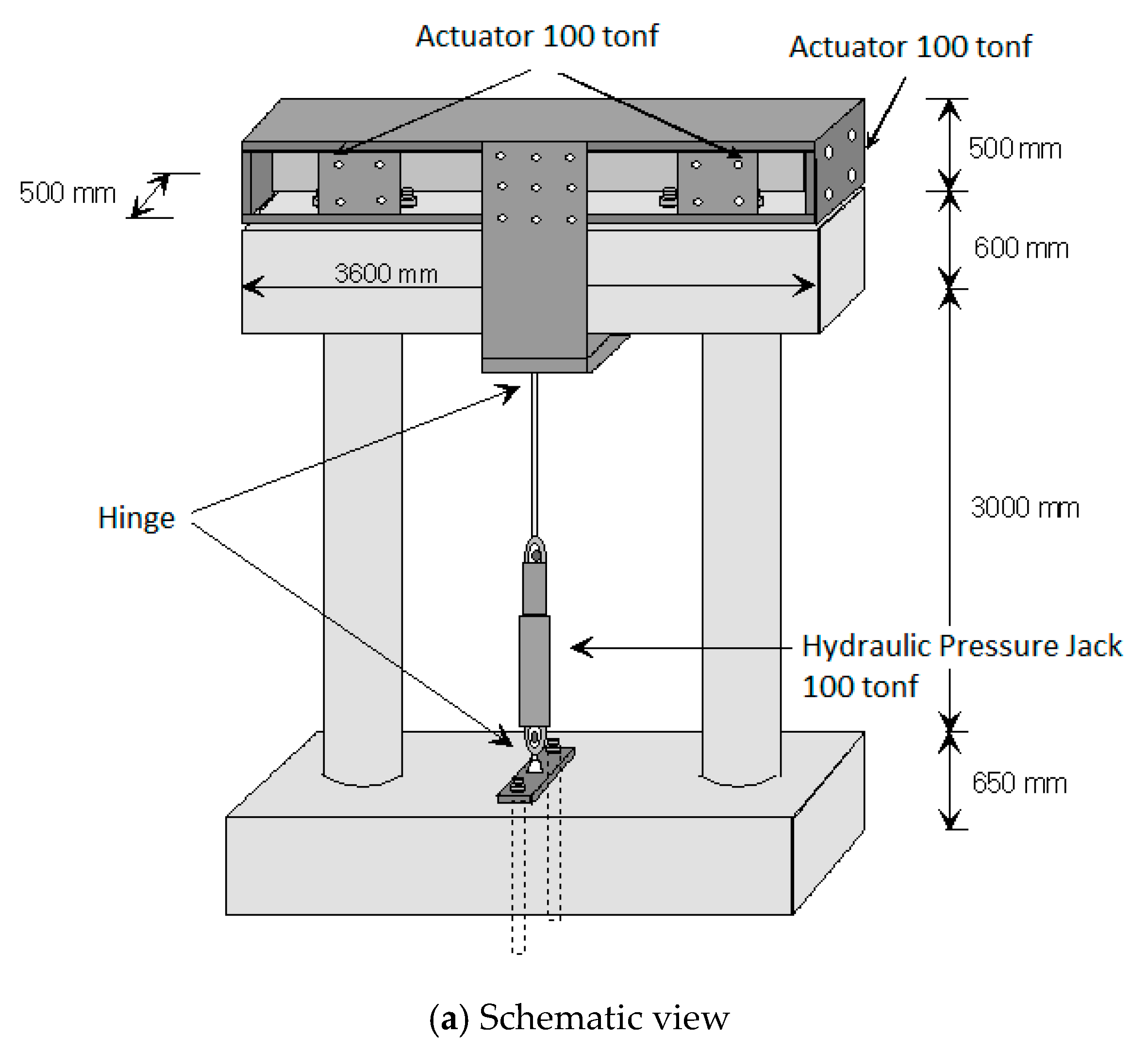
2.2. Test Setup
2.3. Loading Protocol
3. Seismic Behavior of Specimens
3.1. Longitudinal Loading Test
3.1.1. Failure Mode of Longitudinal Loading Specimen
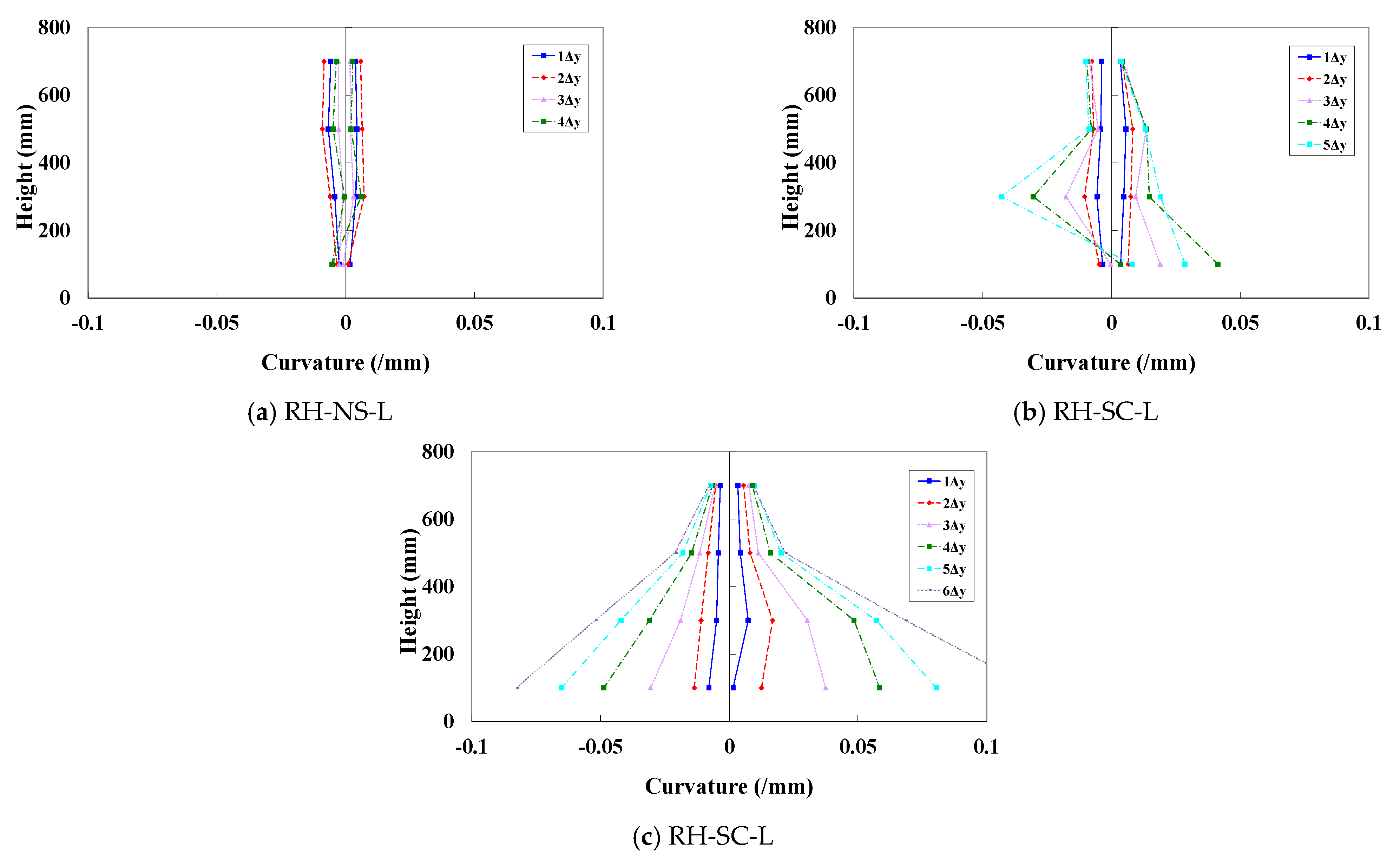
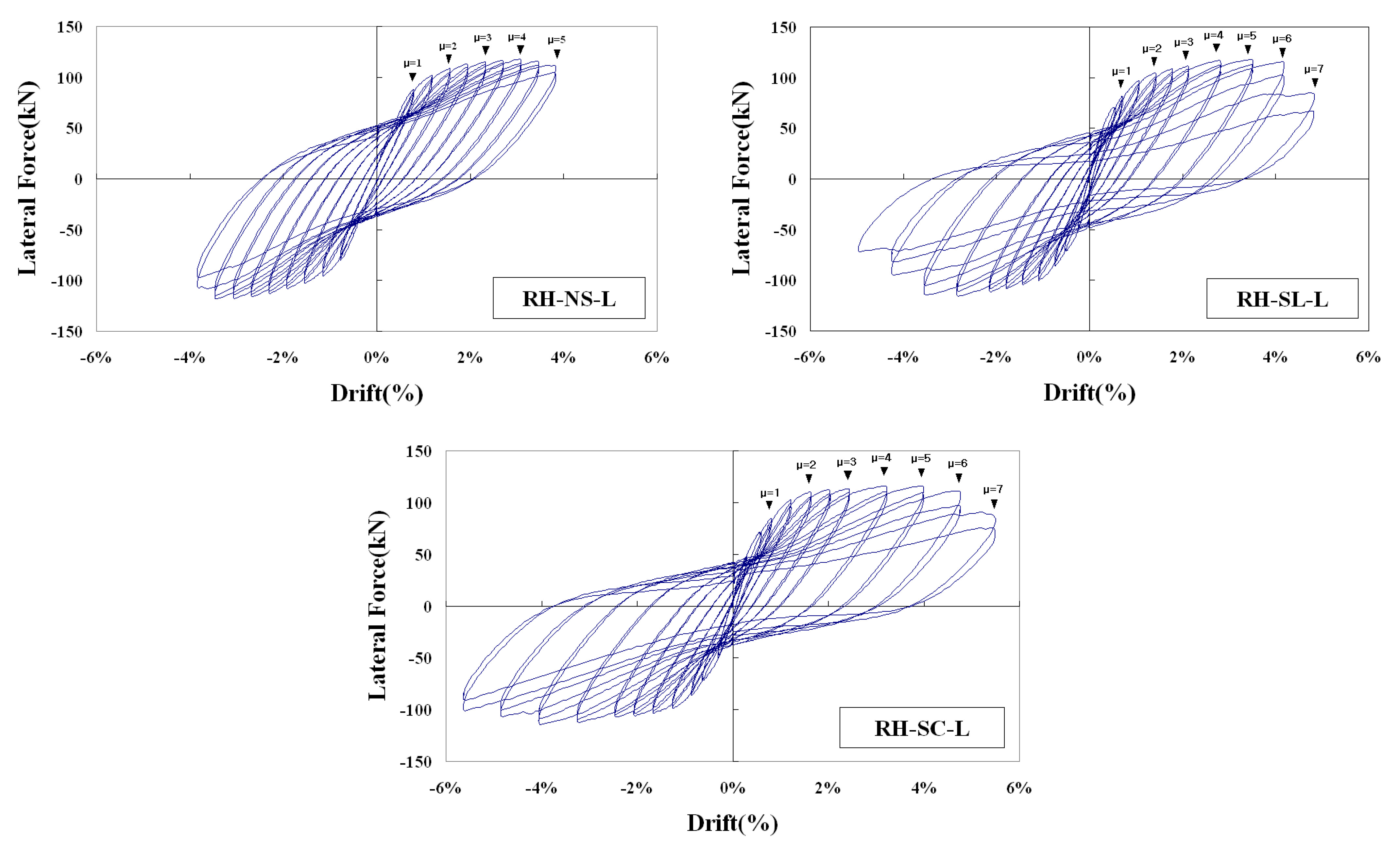
3.1.2. Hysteresis Curve of Longitudinal Loading Specimen
3.2. Transverse Loading Test
3.2.1. Failure Mode of Transverse Loading Specimen
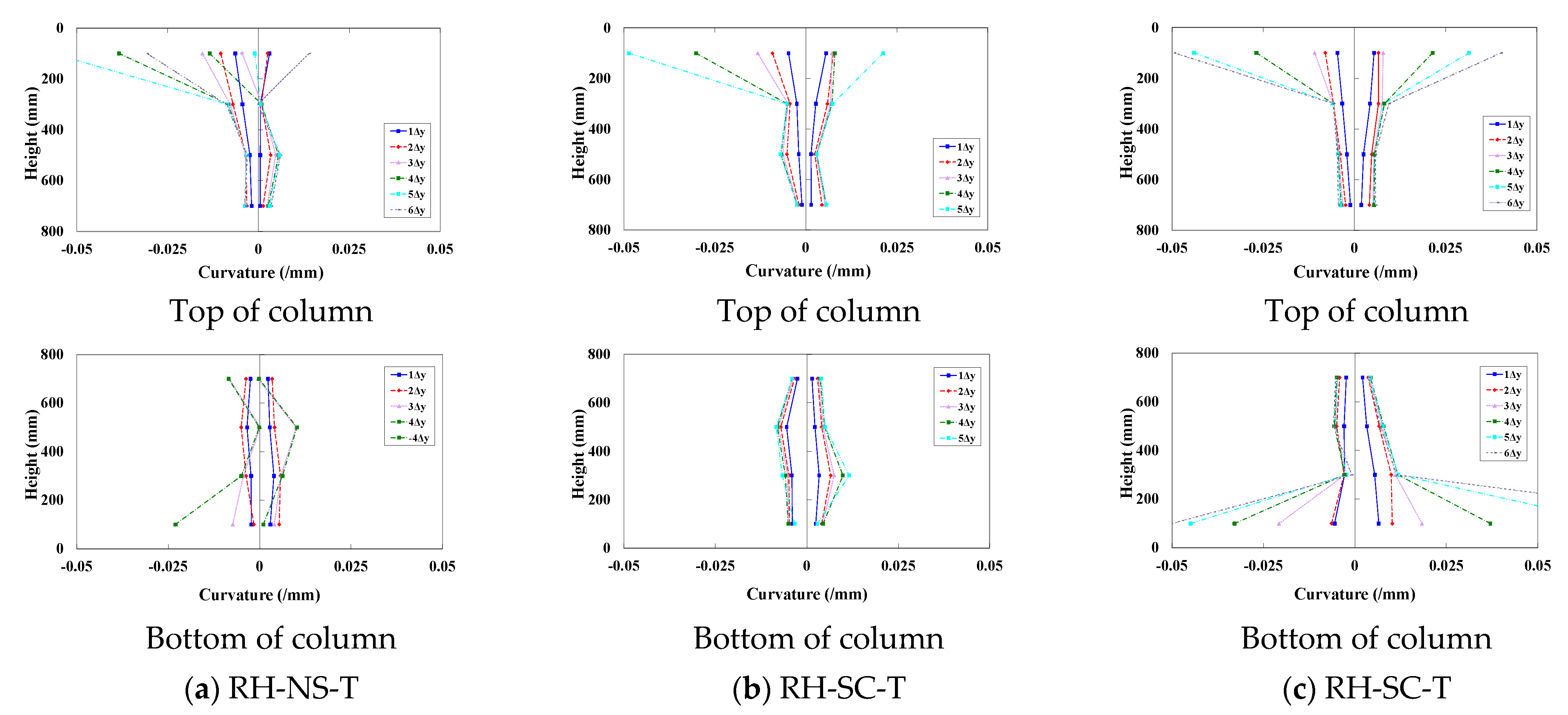
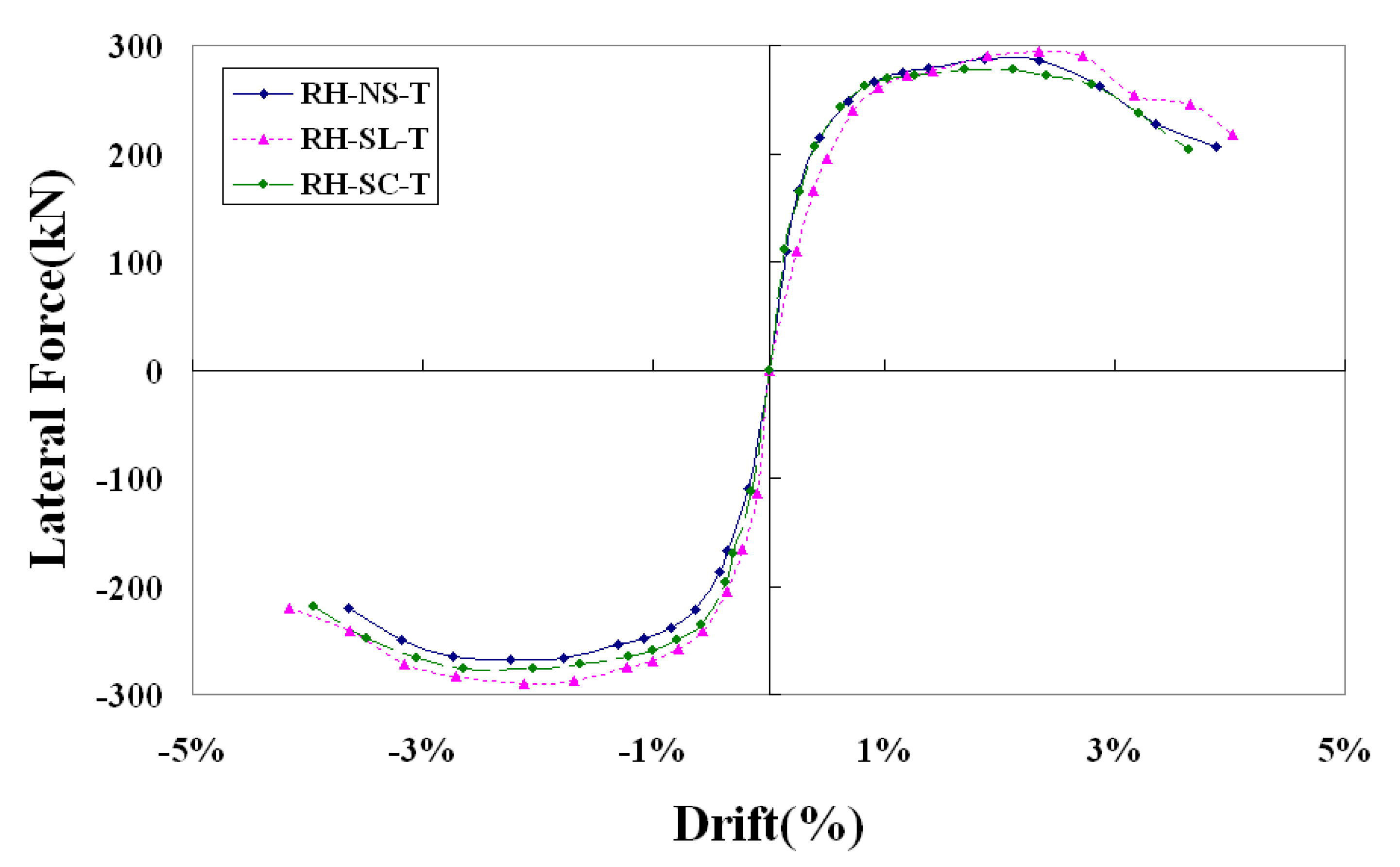
3.2.2. Hysteresis Curve of Transverse Loading Specimen
4. Result of Seismic Capacity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheok, G.S.; Stone, W.C. Behavior of 1/6-scale model bridge columns subjected to inelastic cyclic loading. ACI Struct. J. 1990, 87, 630–638. [Google Scholar]
- Brito, M.B.; Ishibashi, H.; Akiyama, M. Shaking table tests of a reinforced concrete bridge pier with a low-cost sliding pendulum system. Earthq. Eng. Struct. Dyn. 2019, 48, 366–386. [Google Scholar] [CrossRef]
- Kim, T.; Lee, K.; Yoon, C.; Shin, H.M. Inelastic behavior and ductility capacity of reinforced concrete bridge piers under earthquake. I: Theory and formulation. ASCE J. Struct. Eng. 2003, 129, 1199–1207. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress–strain model for confined concrete. ASCE J. Struct. Eng. 1998, 114, 1804–1826. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Park, R. Strength and ductility of concrete bridge columns under seismic loading. ACI Struct. J. 1987, 84, 61–76. [Google Scholar]
- Chai, Y.H.; Priestley, M.J.N.; Seible, F. Seismic retrofit of circular bridge columns for enhanced flexural performance. ACI Struct. J. 1991, 88, 572–584. [Google Scholar]
- Hoshikuma, J.; Kawashima, K.; Nagaya, K.; Taylor, A.W. Stress-strain model for confined reinforced concrete in bridge piers. J. Struct. Eng. 1997, 123, 624–633. [Google Scholar] [CrossRef]
- Sheikh, S.A.; Uzumeri, S.M. Strength and ductility of tied concrete columns. ASCE J. Struct. Div. 1980, 106, 1079–1102. [Google Scholar] [CrossRef]
- Saadatmanesh, H.; Ehsani, M.R.; Li, M.W. Strength and ductility of concrete columns externally reinforced with fiber composite straps. ACI Struct. J. 1994, 91, 434–447. [Google Scholar]
- Moehle, J.P.; Cavanagh, T. Confinement effectiveness of crossties in RC. ASCE J. Struct. Eng. 1985, 111, 2105–2120. [Google Scholar] [CrossRef]
- Lukkunaprasit, P.; Sittipunt, C. Ductility enhancement of moderately confined concrete tied columns with hook-clips. ACI Struct. J. 2003, 100, 422–429. [Google Scholar]
- Lee, T.; Chen, C.; Tsou, P.; Lin, K.; Lee, W.; Pan, A.D.E. Experimental evaluation of crossties in large reinforced concrete columns under pure compression. Adv. Struct. Eng. 2012, 15, 1717–1727. [Google Scholar] [CrossRef]
- Sheikh, S.A.; Toklucu, M.T. Reinforced concrete columns confined by circular spirals and hoops. ACI Struct. J. 1993, 90, 542–553. [Google Scholar]
- Tanaka, T.H.; Park, R. Behavior of axially loaded concrete columns confined by elliptical hoops. ACI Struct. J. 1999, 96, 967–971. [Google Scholar]
- Jaradat, O.A.; McLean, D.I.; Marsh, M.L. Performance of existing bridge columns under cyclic loading-Part1: Experimental results and observed behavior. ACI Struct. J. 1998, 95, 695–704. [Google Scholar]
- Ichinose, T. Splitting Bond Failure of Columns under Seismic Action. ACI Struct. J. 1995, 92, 535–542. [Google Scholar]
- Sultana, N.; Ray, T. Implications of bond-slip in inelastic dynamic responses of degrading structural systems. Int. J. Civ. Eng. 2020, 18, 1039–1052. [Google Scholar] [CrossRef]
- Mousa, M.I. Flexural behaviour and ductility of high strength concrete (HSC) beams with tension lap splice. Alex. Eng. J. 2015, 54, 551–563. [Google Scholar] [CrossRef]
- Rakhshanimehr, M.; Reza Esfahani, M.; Reza Kianoush, M.; Ali Mohammadzadeh, B.; Roohollah Mousavi, S. Flexural ductility of reinforced concrete beams with lap-spliced bars. Can. J. Civ. Eng. 2014, 41, 594–604. [Google Scholar] [CrossRef]
- Azizinamini, A.; Pavel, R.; Hatfield, E.; Ghosh, S. Behavior of lap-spliced reinforcing bars embedded in high strength concrete. ACI Struct. J. 1999, 96, 826–835. [Google Scholar]
- Hamad, B.S.; Najjar, S.S. Evaluation of the role of transverse reinforcement in confining tension lap splices in high strength concrete. Mater. Struct. 2002, 35, 219–228. [Google Scholar] [CrossRef]
- Bournas, D.A.; Triantafillou, T.C. Bond strength of lap-spliced bars in concrete confined with composite jackets. Asce J. Compos. Constr. 2011, 15, 156–167. [Google Scholar] [CrossRef]
- Hadhood, A.; Agamy, M.H.; Abdelsalam, M.M.; Mohamed, H.M.; El-Sayed, T.A. Shear strengthening of hybrid externally-bonded mechanically-fastened concrete beams using short CFRP strips: Experiments and theoretical evaluation. Eng. Struct. 2019, 201, 109795. [Google Scholar] [CrossRef]
- Sexsmith, R.; Anderson, D.; English, D. Cyclic behavior of concrete bridge bents. ACI Struct. J. 1997, 94, 103–113. [Google Scholar]
- Mander, J.B.; Kim, J.H.; Ligozio, C.A. Seismic Performance of a Model Reinforced Concrete Bridge Pier before and after Retrofit; Technical Report NCEER-96-0009; NCEER: New York, NY, USA, 1996. [Google Scholar]
- Wua, R.; Pantelides, C.P. Seismic evaluation of repaired multi-column bridge bent using static and dynamic analysis. Constr. Build. Mater. 2019, 208, 792–807. [Google Scholar] [CrossRef]
- Kar, D.; Roy, R. Seismic behavior of RC bridge piers under bidirectional excitations: Implications of site effects. J. Earthq. Eng. 2018, 22, 3030–3331. [Google Scholar] [CrossRef]
- AASHTO. Standard Specifications for Highway Bridges, 17th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010. [Google Scholar]
- Prestley, M.J.N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Lee, J.H.; Seok, S.G.; Yun, S.G.; Kang, S.K. Seismic performance of circular columns considering transverse steel details. In Proceedings of the EESK Conference, Seoul, Korea, 4 March 2000; Volume 4, pp. 259–266. [Google Scholar]
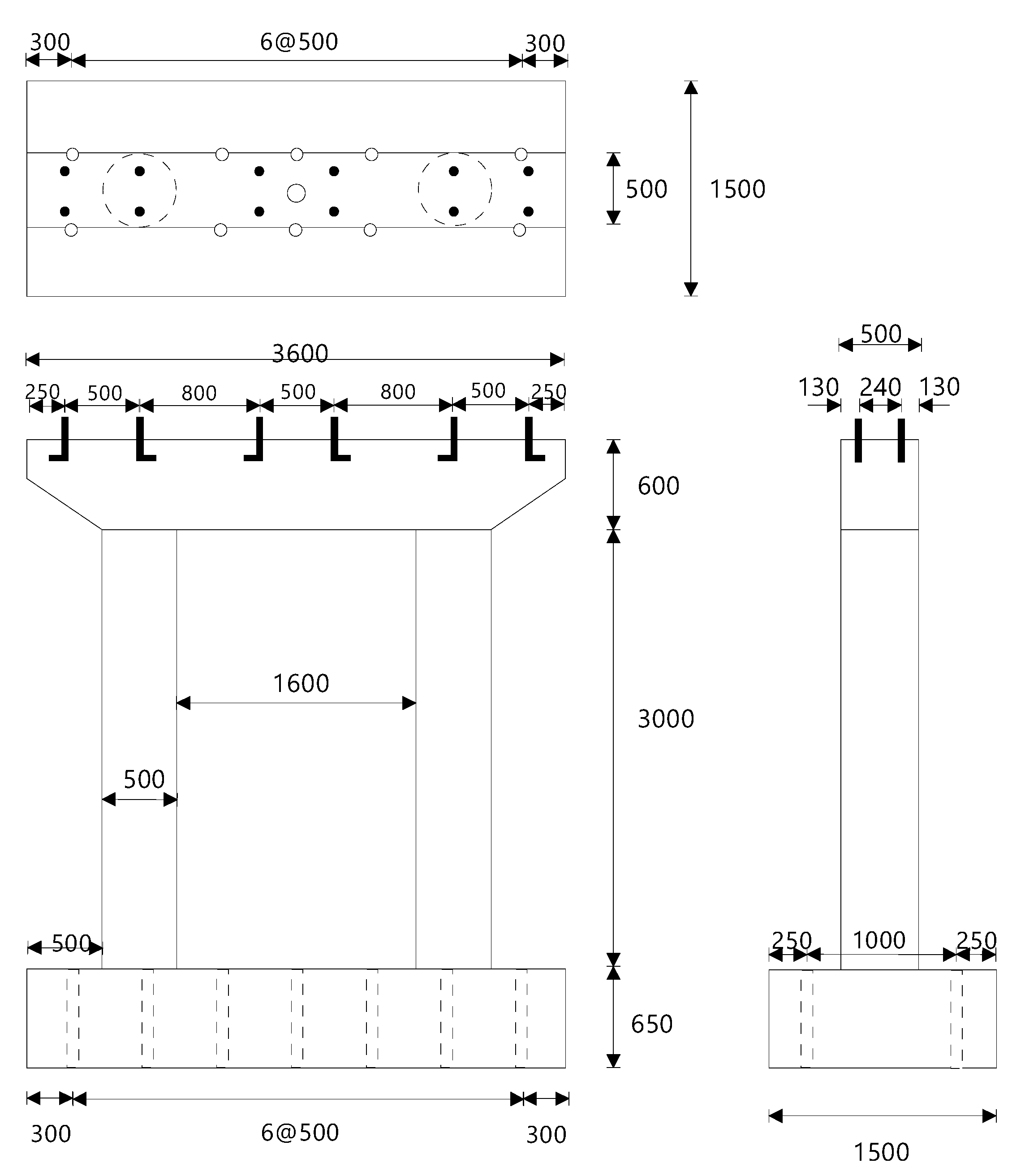










| Property | Prototype | Model | |
|---|---|---|---|
| Material strength (MPa) | Concrete strength (MPa) | 24 | 24 |
| Reinforcement steel bar strength (MPa) | 300 | 300 | |
| Column | Diameter (m) | 2.0 | 0.5 |
| Height (m) | 12.0 | 3.0 | |
| Longitudinal reinforcement | Diameter (mm) | 29 | 10 |
| Reinforcement ratio (%) | 1.174 | 1.174 | |
| Diameter of lateral reinforcement (mm) | 16 | 4 | |
| Axial force | 0.052 | 0.052 | |
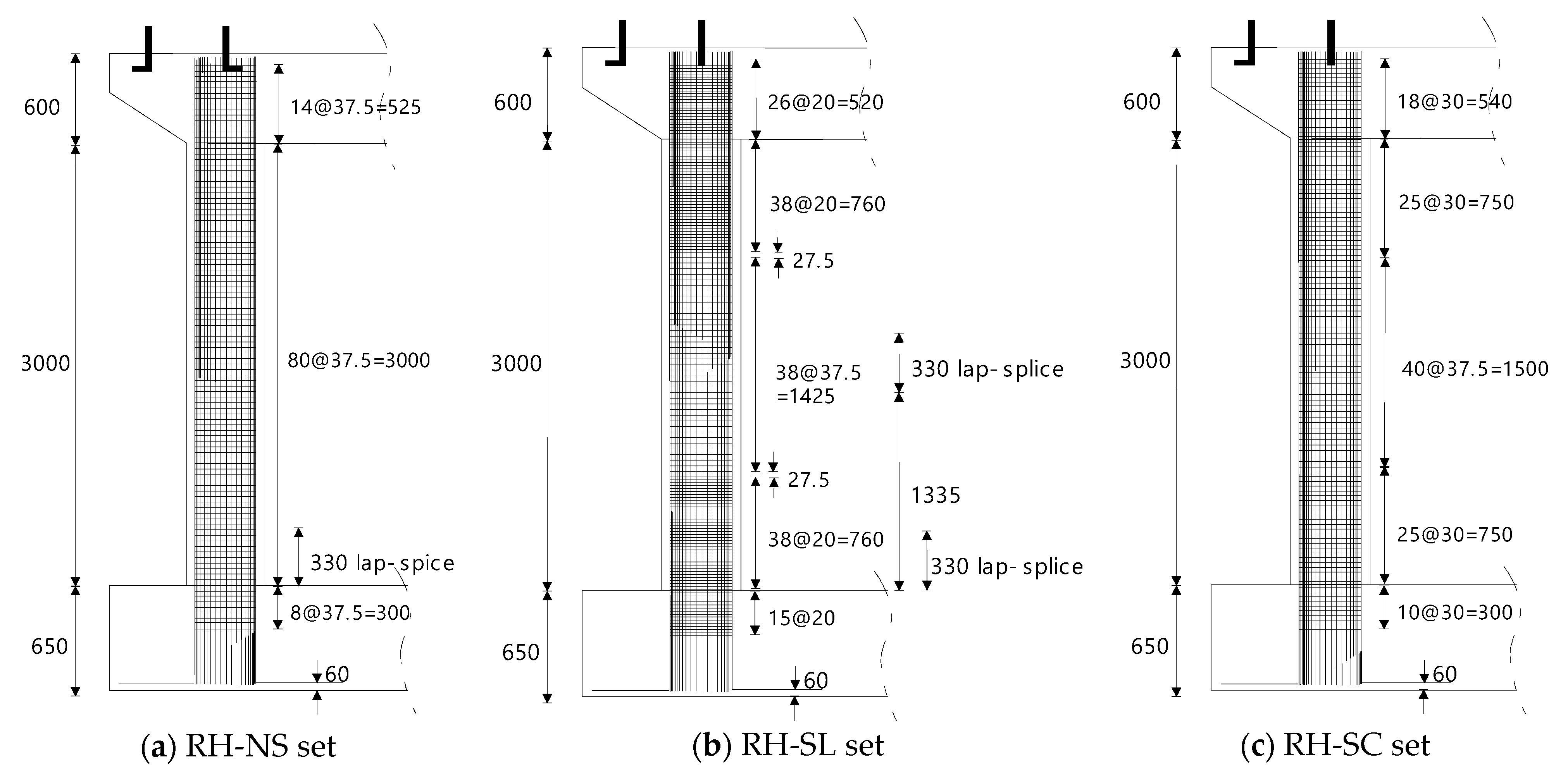
| Specimen | Loading Direction | Lap-Splice of Longitudinal Reinforcement | Lateral Reinforcement Detail | Spacing of Lateral Reinforcement | Volumetric Reinforcement Ratio |
|---|---|---|---|---|---|
| RH-NS-L | Longitudinal | 100% in the lower region | No consideration of seismic performance | 37.5 mm | 0.268% |
| RH-NS-T | Transverse | ||||
| RH-SL-L | Longitudinal | 50% in the lower region | 50% of what is required by AASHTO specifications | 20 mm | 0.503% |
| RH-SL-T | Transverse | ||||
| RH-SC-L | Longitudinal | No lap-splice | Preventing local buckling of the longitudinal bar | 30 mm | 0.335% |
| RH-SC-T | Transverse |
| RH-NS-L | RH-SL-L | RH-SC-L | RH-NS-T | RH-SL-T | RH-SC-T | |
|---|---|---|---|---|---|---|
| Yield displacement (mm) | 43.67 | 19.21 | ||||
| Maximum lateral force, (kN) | 117.72 | 118.13 | 116.06 | 287.93 | 294.06 | 277.06 |
| Displacement at (mm) | 118.34 | 132.94 | 153.30 | 56.25 | 70.27 | 63.58 |
| Displacement at failure (mm) | 171.47 | 193.46 | 93.68 | 101.69 | 96.73 | |
| Drift ratio at failure | 4.45% | 5.02% | 3.12% | 3.39% | 3.22% | |
| Displacement ductility at failure | 3.92 | 4.43 | 4.87 | 5.29 | 5.03 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.H.; Kim, I.-H.; Lee, J.H. Experimental Study on the Behavior of Existing Reinforced Concrete Multi-Column Piers under Earthquake Loading. Appl. Sci. 2021, 11, 2652. https://doi.org/10.3390/app11062652
Kim JH, Kim I-H, Lee JH. Experimental Study on the Behavior of Existing Reinforced Concrete Multi-Column Piers under Earthquake Loading. Applied Sciences. 2021; 11(6):2652. https://doi.org/10.3390/app11062652
Chicago/Turabian StyleKim, Jung Han, Ick-Hyun Kim, and Jin Ho Lee. 2021. "Experimental Study on the Behavior of Existing Reinforced Concrete Multi-Column Piers under Earthquake Loading" Applied Sciences 11, no. 6: 2652. https://doi.org/10.3390/app11062652
APA StyleKim, J. H., Kim, I.-H., & Lee, J. H. (2021). Experimental Study on the Behavior of Existing Reinforced Concrete Multi-Column Piers under Earthquake Loading. Applied Sciences, 11(6), 2652. https://doi.org/10.3390/app11062652







