Application of Statistical Distribution Models to Predict Health Index for Condition-Based Management of Transformers
Abstract
:1. Introduction
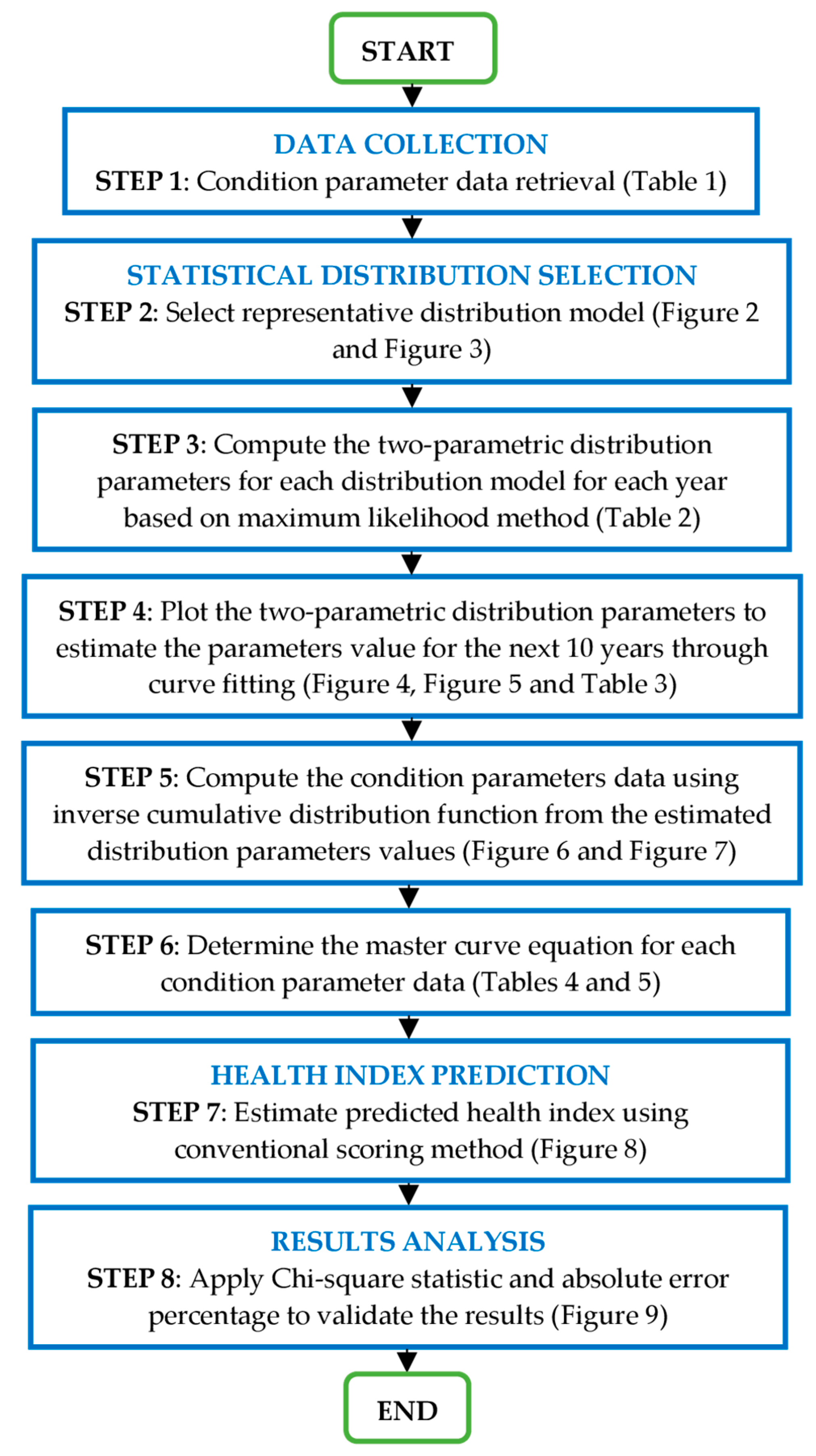
2. Transformer Health Index Estimation Model
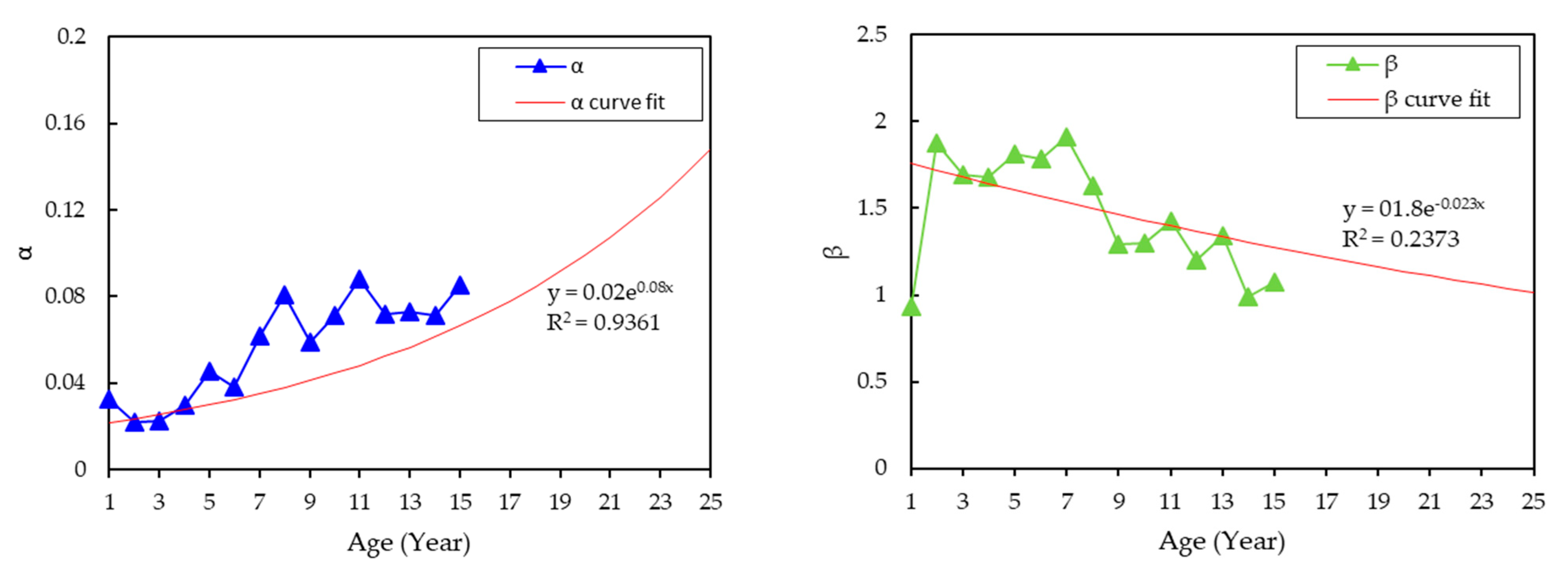
2.1. Estimations Distribution Parameters Estimation
2.2. Condition Data Estimation
2.3. Health Index Model Based on Scoring Algorithm
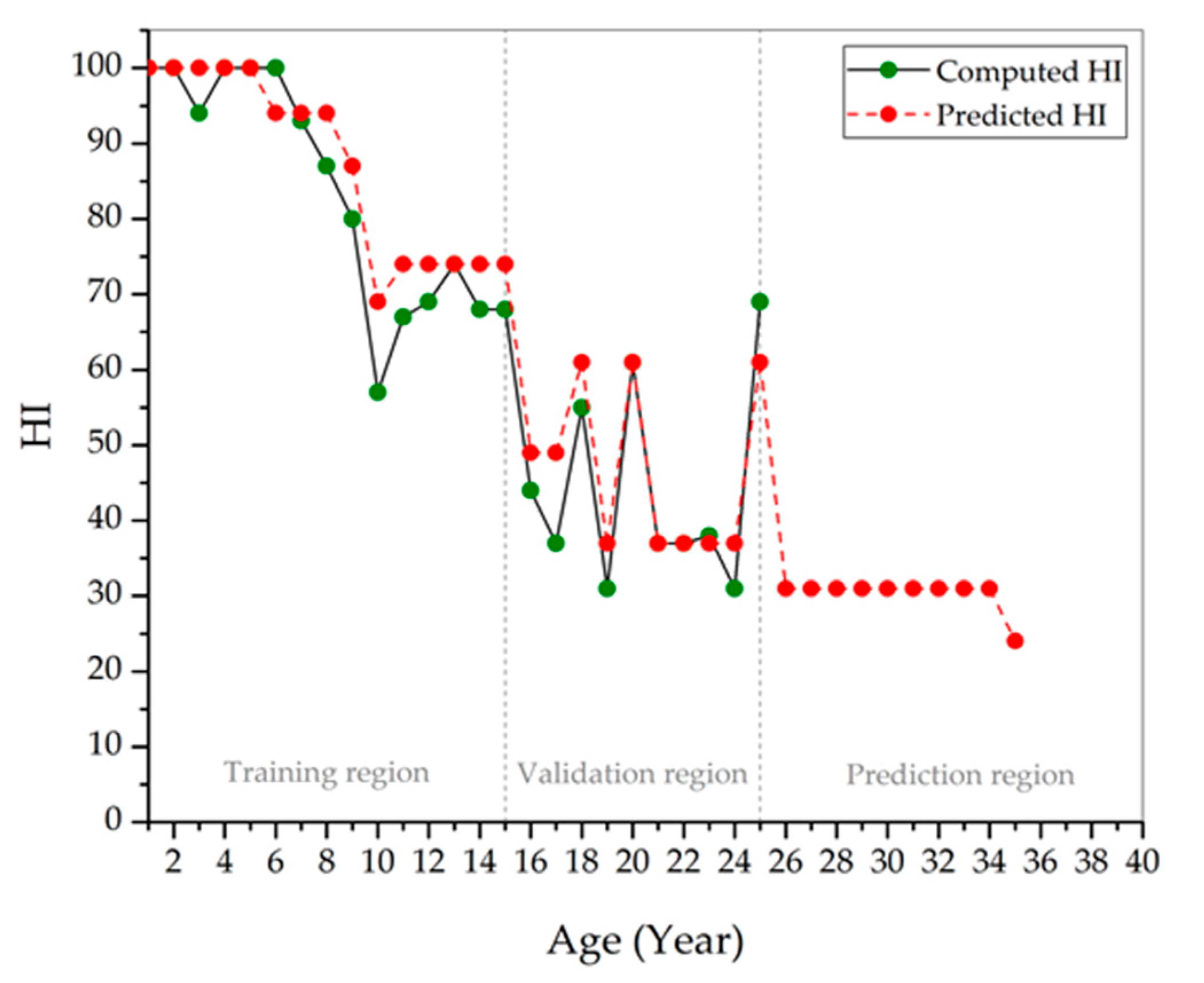
3. Case Study
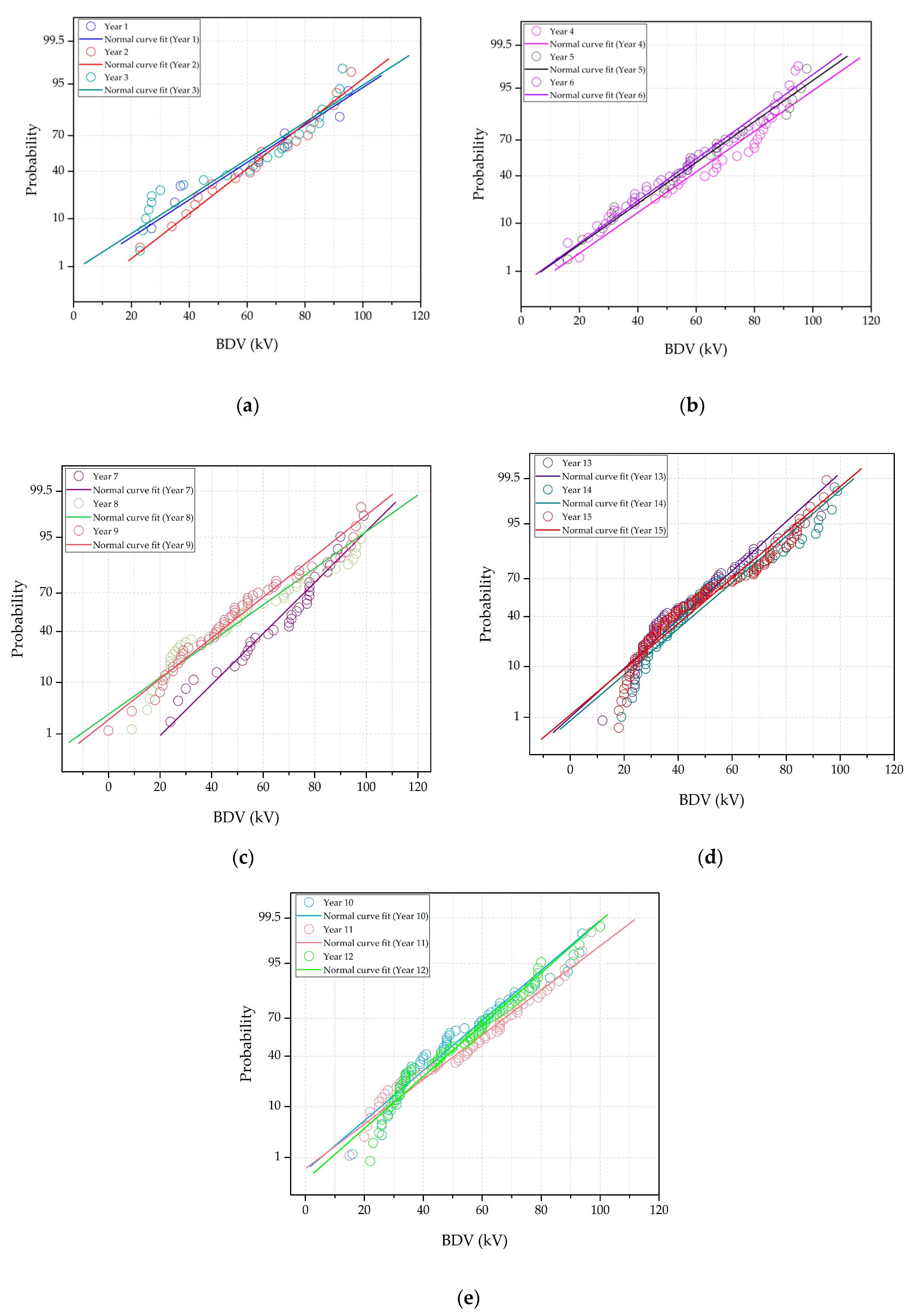
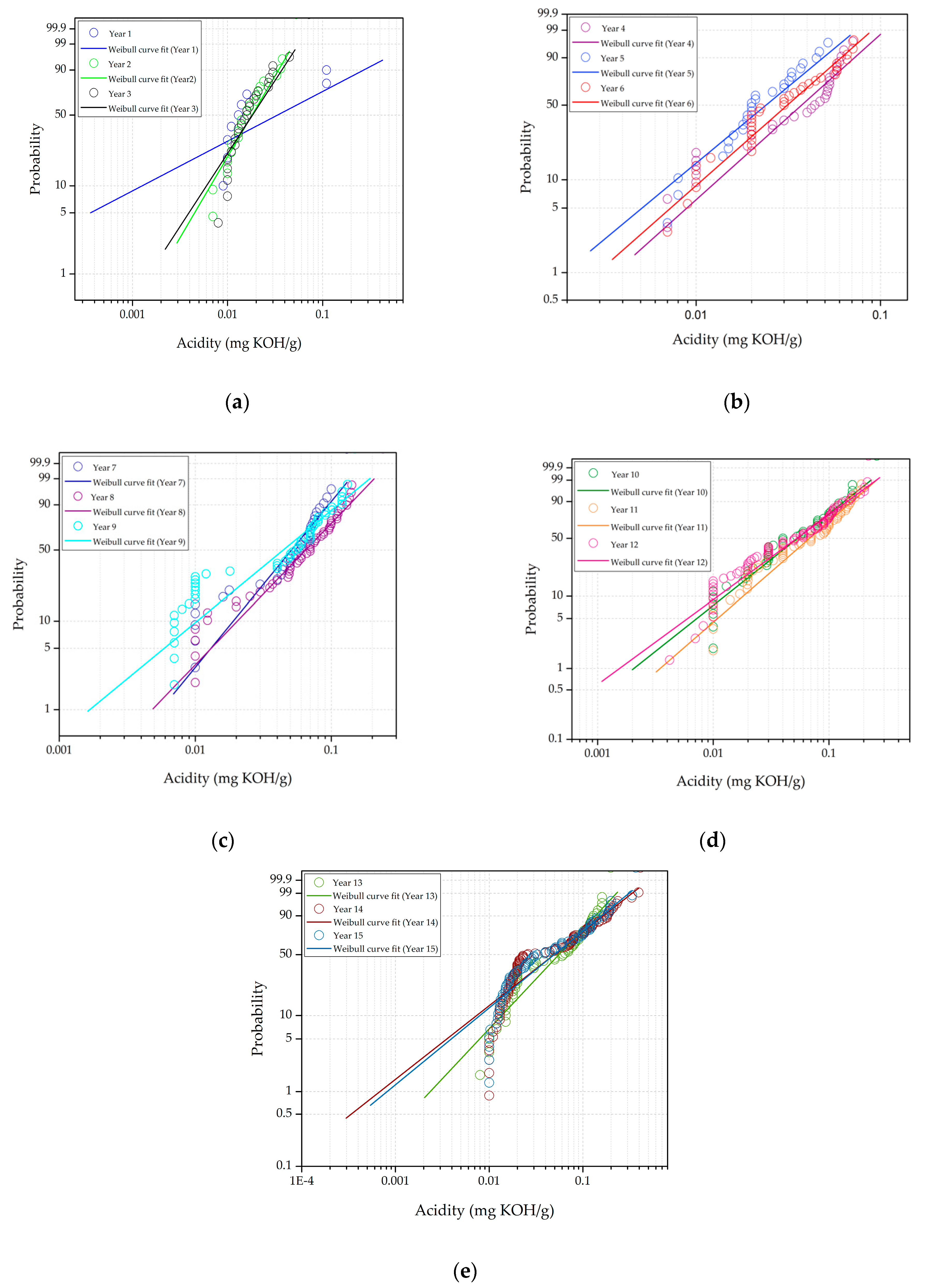
3.1. Implementation of Statistical Distribution Models to Transformer CBM Data
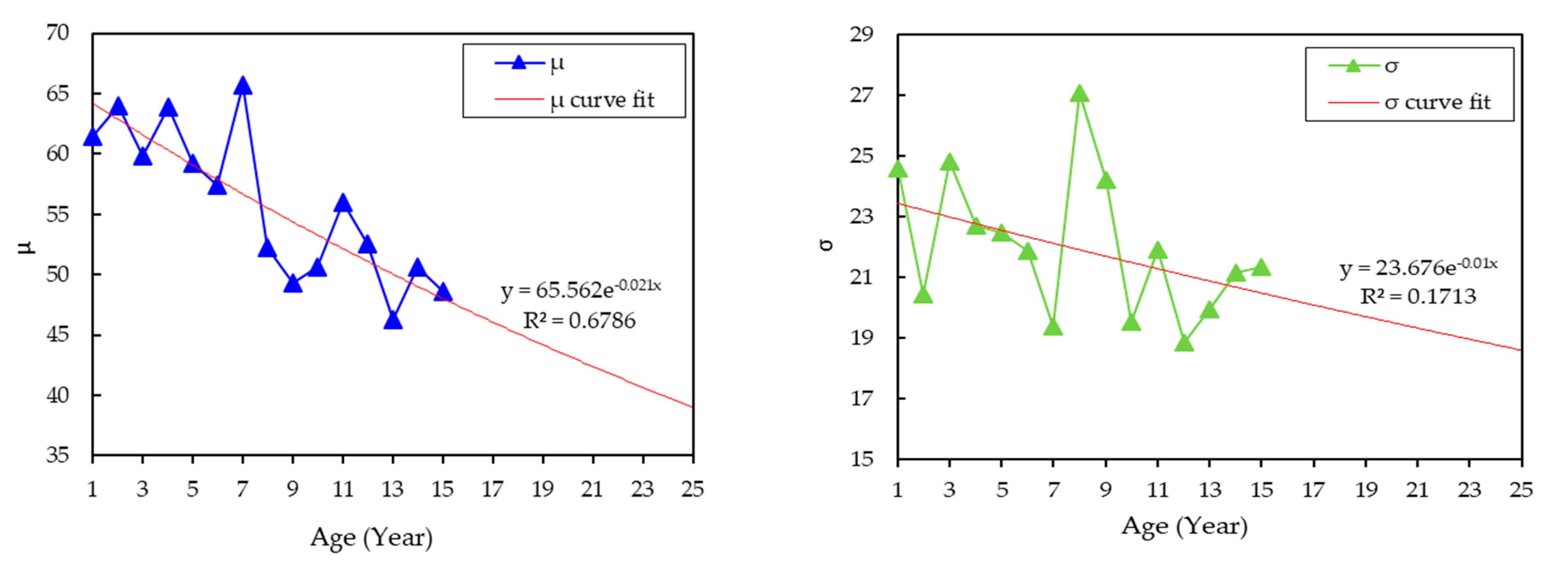
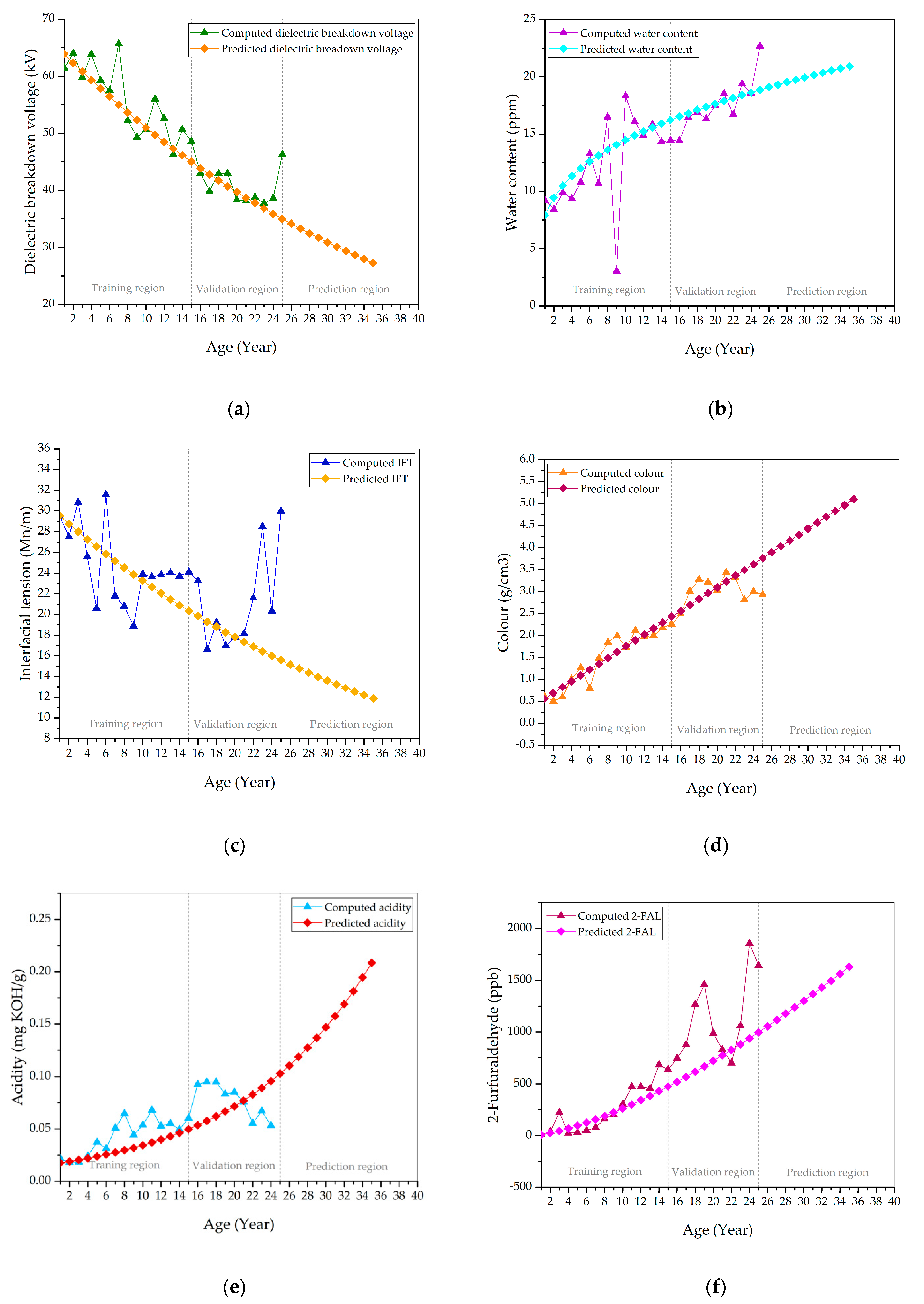
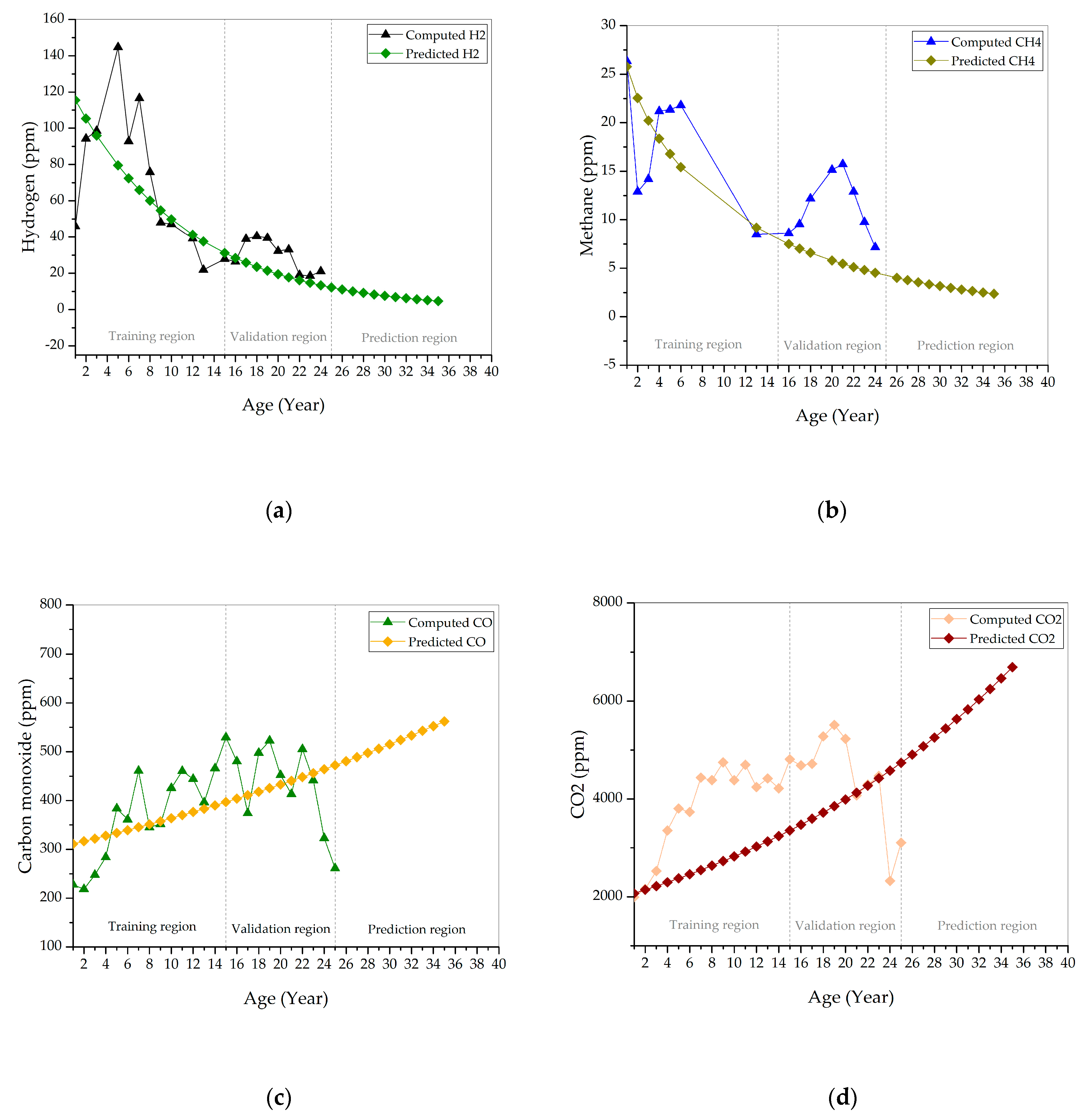
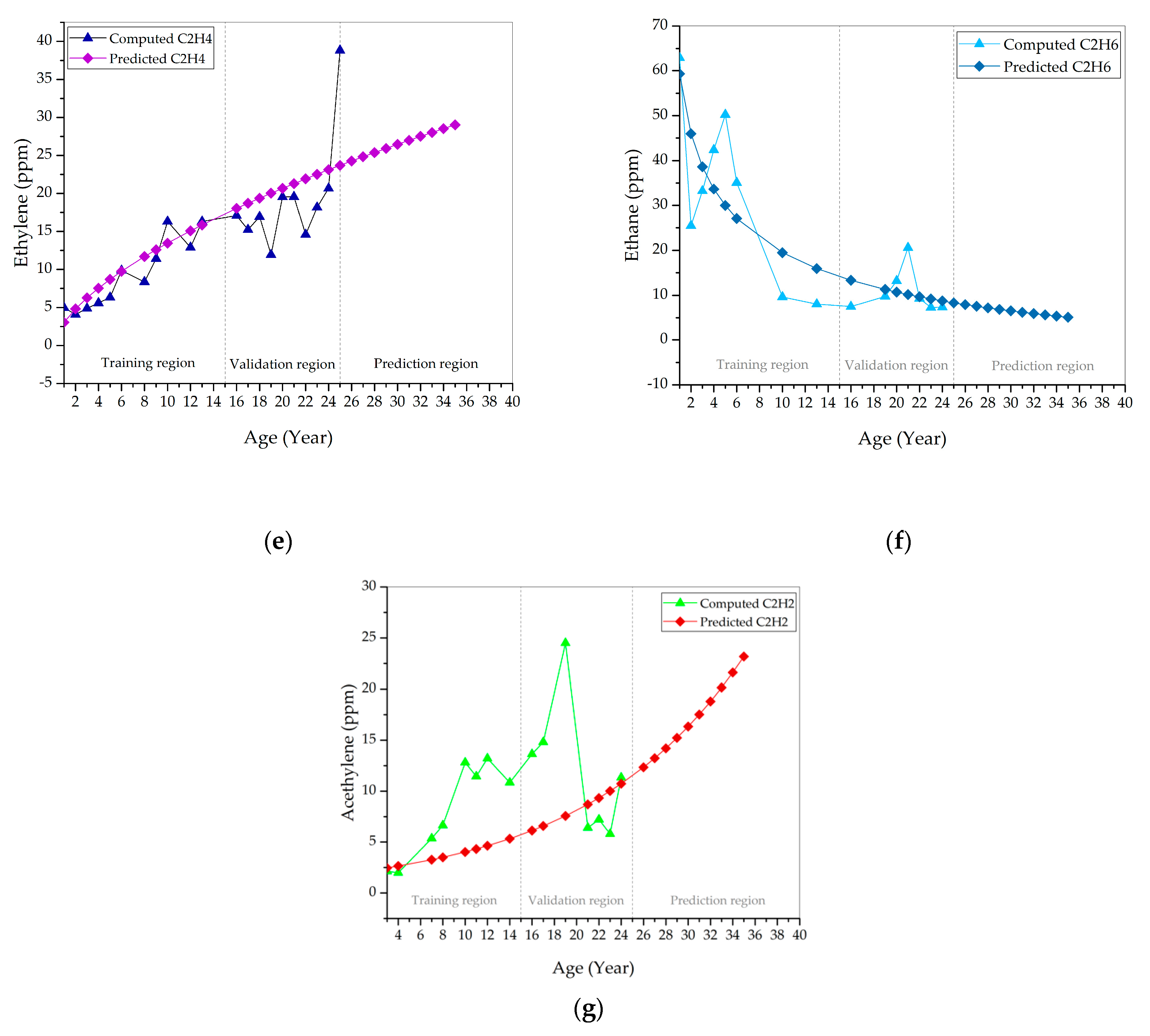
3.2. Distribution Parameters and Condition Data Estimations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AI | Artificial intelligence |
| CBM | Condition-based management |
| CDF | Cumulative distribution function |
| CH4 | Methane |
| C2H2 | Acetylene |
| C2H4 | Ethylene |
| C2H6 | Ethane |
| CO | Carbon monoxide |
| CO2 | Carbon dioxide |
| CDF | Cumulative distribution function |
| 2-FAL | 2-Furfuraldehyde |
| g/cm3 | gram per cubic centimeter |
| H2 | Hydrogen |
| HI | Health index |
| ICDF | Inverse cumulative distribution function |
| KOH/g | mass of potassium hydroxide per grams |
| kV | kilo-volt |
| OLS | Ordinary least square |
| MLE | Maximum likelihood estimate |
| mg | milligrams |
| mN/m | millinewton per metre |
| MOM | Method of moments |
| Probability distribution function | |
| ppm | parts-per-million |
| ppb | parts-per-billion |
| WLS | Weighted least square method |
References
- Jahromi, A.N.; Piercy, R.; Service, J.R.R.; Fan, W. An Approach to Power Transformer Asset Management Using Health Index. IEEE Electr. Insul. Mag. 2009, 25, 20–34. [Google Scholar] [CrossRef]
- Scatiggio, F.; Pompili, M.; Calacara, L. Transformers Fleet Management Through the use of an Advanced Health Index. In Proceedings of the 2018 IEEE Electrical Insulation Conference (EIC), San Antonio, TX, USA, 17–20 June 2018; pp. 395–397. [Google Scholar] [CrossRef]
- Haema, J.; Phadungthin, R. Condition Assessment of the Health Index for Power Transformer. In Proceedings of the 2012 Power Engineering and Automation Conference, Wuhan, China, 18–20 September 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Picher, P.; Boudreau, J.F.; Manga, A.; Rajotte, C.; Tardif, C.; Bizier, G.; Di Gaetano, N.; Garon, D.; Giard, B.; Hamel, J.F.; et al. Use of Health Index and Reliability Data for Transformer Condition Assessment and Fleet Ranking. In Proceedings of the Hydro-Québec, A2-101 CIGRE 2014, Paris, France, 24–29 August 2014. [Google Scholar]
- Vermeer, M.; Wetzer, J.; van der Wielen, P.; de Haan, E.; de Meulemeester, E. Asset-Management Decision-Support Modeling, Using a Health and Risk Model. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Zaidey, Y.; Ghazali, Y.; Rosli, H.A. TNB Experience in Condition Assessment and Life Management. In Proceedings of the 20th International Conference and Exhibition on Electricity Distribution, Prague, Czech Republic, 8–11 June 2009; pp. 8–11. [Google Scholar]
- Zec, F.; Kartalović, N.; Stojić, T. Prediction of High-Voltage Asynchronous Machines Stators Insulation Status Applying Law on Increasing Probability. Int. J. Electr. Power Energy Syst. 2019, 116, 105524. [Google Scholar] [CrossRef]
- Feng, X.; Zhou, Y.; Hua, T.; Zou, Y.; Xiao, J. Contact Temperature Prediction of High Voltage Switchgear Based on Multiple Linear Regression Model. In Proceedings of the 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 277–280. [Google Scholar] [CrossRef]
- Manninen, H.; Kilter, J.; Landsberg, M. Health Index Prediction of Overhead Transmission Lines: A Machine Learning Approach. IEEE Trans. Power Deliv. 2021, 8977, 1–9. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Yang, A.; Rong, M.; Yang, K. Failure Prognosis of High Voltage Circuit Breakers with Temporal Latent Dirichlet Allocation. Energies 2017, 10, 1913. [Google Scholar] [CrossRef] [Green Version]
- Shaban, K.B.; El-Hag, A.H.; Benhmed, K. Prediction of Transformer Furan Levels. IEEE Trans. Power Deliv. 2016, 31, 1778–1779. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, R.; Chen, M.; Wang, W.; Zhang, C. Dynamic Fault Prediction of Power Transformers Based on Hidden Markov Model of Dissolved Gases Analysis. IEEE Trans. Power Deliv. 2019, 34, 1393–1400. [Google Scholar] [CrossRef]
- Qi, B.; Wang, Y.; Zhang, P.; Li, C.; Wang, H. A Novel Deep Recurrent Belief Network Model for Trend Prediction of Transformer DGA Data. IEEE Access 2019, 7, 80069–80078. [Google Scholar] [CrossRef]
- El-Aal, R.A.A.; Helal, K.; Hassan, A.M.M.; Dessouky, S.S. Prediction of Transformers Conditions and Lifetime Using Furan Compounds Analysis. IEEE Access 2019, 7, 102264–102273. [Google Scholar] [CrossRef]
- Yahaya, M.; Azis, N.; Mohd Selva, A.; Ab Kadir MZ, A.; Jasni, J.; Kadim, E.J.; Hairi, M.H.; Ghazali, Y.Z.Y. A Maintenance Cost Study of Transformers Based on Markov Model Utilizing Frequency of Transition Approach. Energies 2018, 11, 2006. [Google Scholar] [CrossRef] [Green Version]
- Selva, A.M.; Azis, N.; Yahaya, M.S.; Ab Kadir MZ, A.; Jasni, J.; Yang Ghazali, Y.Z.; Talib, M.A. Application of Markov Model to Estimate Individual Condition Parameters for Transformers. Energies 2018, 11, 2114. [Google Scholar] [CrossRef] [Green Version]
- Selva, A.M.; Yahaya, M.S.; Azis, N.; Kadir, M.Z.A.A.; Jasni, J.; Ghazali, Y.Z.Y. Estimation of Transformers Health Index Based on Condition Parameter Factor and Hidden Markov Model. In Proceedings of the 2018 IEEE 7th International Conference on Power and Energy (PECon), Kuala Lumpur, Malaysia, 3–4 December 2018; pp. 288–292. [Google Scholar] [CrossRef]
- Ranga, C.; Chandel, A.K. Expert System for Health Index Assessment of Power Transformers. Int. J. Electr. Eng. Inform. 2017, 9, 850–865. [Google Scholar] [CrossRef]
- Islam, M.M.; Lee, G.; Hettiwatte, S.N.; Williams, K. Calculating a Health Index for Power Transformers Using a Subsystem-Based GRNN Approach. IEEE Trans. Power Deliv. 2018, 33, 1903–1912. [Google Scholar] [CrossRef]
- EKadim, J.; Azis, N.; Jasni, J.; Ahmad, S.A.; Talib, M.A. Transformers Health Index Assessment Based on Neural-Fuzzy Network. Energies 2018, 11, 710. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, M.S.; Swami, P.S.; Thosar, A.G. Prognostication of Health Index for Oil-Immersed Transformers Using Random Forest. Int. J. Sci. Technol. Res. 2019, 8, 1322–1329. [Google Scholar]
- Ashkezari, A.D.; Ma, H.; Saha, T.K.; Ekanayake, C. Application of Fuzzy Support Vector Machine for Determining the Health Index of the Insulation System of In-service Power Transformers. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 965–973. [Google Scholar] [CrossRef] [Green Version]
- Tee, S.; Liu, Q.; Wang, Z. Insulation Condition Ranking of Transformers through Principal Component Analysis and Analytic Hierarchy Process. IET Gener. Transm. Distrib. 2017, 11, 110–117. [Google Scholar] [CrossRef]
- Elfarra, M.A.; Kaya, M. Comparison of Optimum Spline-Based Probability Density Functions to Parametric Distributions for the Wind Speed Data in terms of Annual Energy Production. Energies 2018, 11, 3190. [Google Scholar] [CrossRef] [Green Version]
- Koizumi, D. On the Maximum Likelihood Estimation of Weibull Distribution with Lifetime Data of Hard Disk Drives. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA’17); CSREA Press: Las Vegas, NV, USA, 2017; pp. 314–320. [Google Scholar]
- Bala, R.J.; Govinda, R.M.; Murthy, C.S.N. Reliability Analysis and Failure Rate Evaluation of Load Haul Dump Machines Using Weibull Distribution Analysis. Math. Model. Eng. Probl. 2018, 5, 116–122. [Google Scholar] [CrossRef]
- Verma, A.; Narula, A.; Katyal, A.; Yadav, S.K.; Anand, P.; Jahan, A.; Pruthi, S.K.; Sarin, N.; Gupta, R.; Singh, S. Failure Rate Prediction of Equipment: Can Weibull Distribution Be Applied to Automated Hematology Analyzers? Clin. Chem. Lab. Med. 2018, 56, 2067–2071. [Google Scholar] [CrossRef]
- Xia, X.; Chang, Z.; Zhang, L.; Yang, X. Estimation on Reliability Models of Bearing Failure Data. Math. Probl. Eng. 2018, 2018, 6189527. [Google Scholar] [CrossRef] [Green Version]
- Badune, J.; Vitolina, S.; Maskalonok, V. Methods for Predicting Remaining Service Life of Power Transformers and Their Components. Power Electr. Eng. 2013, 31, 123–126. [Google Scholar]
- Zhou, D. Transformer Lifetime Modelling Based on Condition Monitoring Data. Int. J. Adv. Eng. Technol. 2013, 6, 613–619. [Google Scholar]
- Barabadi, A.; Ghodrati, B.; Barabady, J.; Markeset, T. Reliability and Spare Parts Estimation Taking into Consideration The Operational Environment—A Case Study. In Proceedings of the 2012 IEEE International Conference on Industrial Engineering and Engineering Management, Hong Kong, China, 10–13 December 2012; pp. 1924–1929. [Google Scholar] [CrossRef]
- Kontrec, N.; Panić, S. Spare Parts Forecasting Based on Reliability. Syst. Reliab. 2017. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, P.; Bhattacharjee, R. A Study on Weibull Distribution for Estimating the Parameters. Wind Eng. 2009, 33, 469–476. [Google Scholar] [CrossRef]
- Zhou, D. Comparison of Two Popular Methods for Transformer Weibull Lifetime Modelling. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 1170–1177. [Google Scholar]
- Bowling, S.R.; Khasawneh, M.T.; Kaewkuekool, S.; Cho, B.R. A Logistic Approximation to the Cumulative Normal Distribution. J. Indutrial Eng. Manag. 2013, 2, 114–127. [Google Scholar] [CrossRef] [Green Version]
- Yerukala, R.; Boiroju, N.K. Approximations to Standard Normal Distribution Function. Int. J. Sci. Eng. Res. 2015, 6, 2015. [Google Scholar]
- Pobočíková, I.; Sedliačková, Z. Comparison of Four Methods for Estimating the Weibull Distribution Parameters. Appl. Math. Sci. 2014, 8, 4137–4149. [Google Scholar] [CrossRef]
- Van Gelder, P.H.A.J.M. Statistical Methods for the Risk-Based Design of Civil Structures; Technische Universiteit Delft: Delft, The Netherlands, 2000; Volume 100. [Google Scholar]
- Ruhi, S.; Sarker, S.; Karim, M.R. Mixture Models for Analyzing Product Reliability Data: A Case Study. Springerplus 2015, 4, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chu, Y.K.; Ke, J.C. Computation Approaches for Parameter Estimation of Weibull Distribution. Math. Comput. Appl. 2011, 16, 702–711. [Google Scholar] [CrossRef] [Green Version]
- Pishro-Nik, H. Introduction to Probability, Statistics, and Random Processes; Kappa Research, LLC: Blue Bell, PA, USA, 2014. [Google Scholar]
- Yang, P.; Pan, S.; Jiang, J.; Rao, W.; Qiao, J. DGA and Weibull Distribution Model-based Transformer Fault Early Warning. IOP Conf. Ser. Mater. Sci. Eng. 2019, 569, 032072. [Google Scholar] [CrossRef]
- Yahaya, M.S.; Azis, N.; Kadir, M.Z.A.A.; Jasni, J.; Hairi, M.H.; Talib, M.A. Estimation of Transformers Health Index Based on the Markov Chain. Energies 2017, 10, 1824. [Google Scholar] [CrossRef] [Green Version]
- CIGRE-WG 12-05: An International Survey on Failures in Large power Transformers in Service. Electra 1983, 88, 21–48.

| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Dataset | 9 | 22 | 26 | 30 | 32 | 37 | 33 | 49 | 52 | 52 | 56 | 77 | 76 | 61 |
| Year | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | Total | ||
| Dataset | 113 | 116 | 86 | 103 | 87 | 65 | 55 | 37 | 31 | 10 | 7 | 1322 | ||
| Transformer Age | Dielectric Breakdown Voltage | Acidity | ||
|---|---|---|---|---|
| 1 | 61.444 | 24.587 | 0.0323 | 0.9318 |
| 2 | 64.000 | 20.459 | 0.0220 | 1.8741 |
| 3 | 59.808 | 24.832 | 0.0227 | 1.6902 |
| 4 | 63.862 | 22.696 | 0.0298 | 1.6803 |
| 5 | 59.250 | 22.489 | 0.0457 | 1.8153 |
| 6 | 57.460 | 21.898 | 0.0384 | 1.7849 |
| 7 | 65.727 | 19.391 | 0.0617 | 1.9102 |
| 8 | 52.265 | 27.099 | 0.0810 | 1.6304 |
| 9 | 49.308 | 24.218 | 0.0588 | 1.2918 |
| 10 | 50.654 | 19.531 | 0.0712 | 1.2977 |
| 11 | 56.000 | 21.916 | 0.0880 | 1.4233 |
| 12 | 52.605 | 18.849 | 0.0716 | 1.1990 |
| 13 | 46.324 | 19.959 | 0.0727 | 1.3391 |
| 14 | 50.656 | 21.168 | 0.0714 | 0.9885 |
| 15 | 48.566 | 21.355 | 0.0850 | 1.0715 |
| Transformer Age | Dielectric Breakdown Voltage | Acidity | ||
|---|---|---|---|---|
| 16 | 43.877 | 20.170 | 0.0719 | 1.2458 |
| 17 | 42.790 | 19.970 | 0.0779 | 1.2175 |
| 18 | 41.729 | 19.771 | 0.0844 | 1.1898 |
| 19 | 40.695 | 19.574 | 0.0914 | 1.1627 |
| 20 | 39.686 | 19.379 | 0.0991 | 1.1363 |
| 21 | 38.702 | 19.187 | 0.1073 | 1.1105 |
| 22 | 37.743 | 18.996 | 0.1163 | 1.0852 |
| 23 | 36.807 | 18.807 | 0.1259 | 1.0605 |
| 24 | 35.895 | 18.619 | 0.1364 | 1.0364 |
| 25 | 35.005 | 18.434 | 0.1478 | 1.0129 |
| Parameter | Fitted Distribution | Master Curve Equation | |
|---|---|---|---|
| Dielectric breakdown voltage | Normal | y = exp(4.204 − 0.026x + 0.0001x2) | 0.8379 |
| Water content | Weibull | y = exp(2.181 + 0.423x − 0.0004x2) | 0.6167 |
| Interfacial tension | Weibull | y = exp(3.468 − 0.056x + 0.002x2) | 0.3602 |
| Color | Normal | y = 0.321(1 + x)0.727 | 0.9044 |
| Acidity | Weibull | y = 0.015(1 + x)0.531 | 0.6224 |
| 2-FAL | Normal | y = 9.088x1.459 | 0.4674 |
| Parameter | Fitted Distribution | Master Curve Equation | |
|---|---|---|---|
| H2 | Weibull | y = exp(4.491 + 0.021x − 0.005x2) | 0.5986 |
| CH4 | Weibull | y = exp(3.121 − 0.056 + 0.001x2) | 0.4785 |
| CO | Normal | y = −305.6exp0.017x | 0.2375 |
| CO2 | Normal | y = 2000exp0.035x | 0.5168 |
| C2H4 | Weibull | y = 2.183x0.732 | 0.6714 |
| C2H6 | Weibull | y = exp(4.090 − 0.135 + 0.002x2) | 0.7155 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Selva, A.; Azis, N.; Shariffudin, N.S.; Ab Kadir, M.Z.A.; Jasni, J.; Yahaya, M.S.; Talib, M.A. Application of Statistical Distribution Models to Predict Health Index for Condition-Based Management of Transformers. Appl. Sci. 2021, 11, 2728. https://doi.org/10.3390/app11062728
Mohd Selva A, Azis N, Shariffudin NS, Ab Kadir MZA, Jasni J, Yahaya MS, Talib MA. Application of Statistical Distribution Models to Predict Health Index for Condition-Based Management of Transformers. Applied Sciences. 2021; 11(6):2728. https://doi.org/10.3390/app11062728
Chicago/Turabian StyleMohd Selva, Amran, Norhafiz Azis, Nor Shafiqin Shariffudin, Mohd Zainal Abidin Ab Kadir, Jasronita Jasni, Muhammad Sharil Yahaya, and Mohd Aizam Talib. 2021. "Application of Statistical Distribution Models to Predict Health Index for Condition-Based Management of Transformers" Applied Sciences 11, no. 6: 2728. https://doi.org/10.3390/app11062728
APA StyleMohd Selva, A., Azis, N., Shariffudin, N. S., Ab Kadir, M. Z. A., Jasni, J., Yahaya, M. S., & Talib, M. A. (2021). Application of Statistical Distribution Models to Predict Health Index for Condition-Based Management of Transformers. Applied Sciences, 11(6), 2728. https://doi.org/10.3390/app11062728






