Multi-Criteria Optimization in Operations Scheduling Applying Selected Priority Rules

Abstract

The utilization of a specific priority rule in scheduling operations in flexible job shop systems strongly influences production goals. In a context of production control in real practice, production performance indicators are evaluated always en bloc. This paper addresses the multi-criteria evaluating five selected conflicting production objectives via scalar simulation-based optimization related to applied priority rule. It is connected to the discrete-event simulation model of a flexible job shop system with partially interchangeable workplaces, and it investigates the impact of three selected priority rules—FIFO (First In First Out), EDD (Earliest Due Date), and STR (Slack Time Remaining). In the definition of the multi-criteria objective function, two scalarization methods—Weighted Sum Method and Weighted Product Method—are employed in the optimization model. According to the observations, EDD and STR priority rules outperformed the FIFO rule regardless of the type of applied multi-criteria method for the investigated flexible job shop system. The results of the optimization experiments also indicate that the evaluation via applying multi-criteria optimization is relevant for identifying effective solutions in the design space when the specific priority rule is applied in the scheduling operations.

1. Introduction

In a competitive environment of manufacturing, production control, including the scheduling operations via modules associated with a variety of management tools, must reflect both customer’s demands, and, on the other hand, the production capability, sustainability, and profit. The effective scheduling in a sense of achievement of a high production performance leads to generating benefits in the form of shortening processing time and reduction of costs. To ensure the changing requirements effectively and to generate suitable production schedules, implementation of heuristics, simulation, analytical models [1,2], artificial intelligence techniques [3], or dispatching rules, especially in case of dynamic scheduling [4,5], can be employed in this type of decision-making.

In the production sector, scheduling can be in a wider perspective defined as “a process of arranging, controlling, and optimizing work or workloads” [1]. With regard to finding the optimal schedule for a specific structure and production system conditions, the scheduling is considered as a complex combinatorial optimization problem [4], mostly proved of NP-hard type [1]. Exact optimization methods are mainly used only for the systems which have a specific topology where very strong simplifying assumptions must be used [6], so they are not too applicable in a real-world scenario for more complex systems. In that case, approximate optimization methods and metaheuristics [7] based on stochastic local search approach, machine learning techniques, especially artificial neural networks (ANN), fuzzy logic methods, and expert systems, are at the center of research interest to find optimal or near-optimal solutions [8,9] instead of exact mathematical optimization models.

In contrast to other methods, dispatching rules (we also use the term priority rules throughout the following text) represent the valuable practical and dominant approach of the shop floor control in the complex industry environment [10,11], such as, e.g., in semiconductor manufacturing for solving complex scheduling problems in real-time [12]. Priority rules are popular because they are characterized by the simplicity of implementation, satisfactory performance, and a substantially reduced computational requirement [2,11,13]. Nevertheless, the choice of appropriate dispatching rules is not a trivial task and depends on the relevant key performance indicators [11].

When considering the application of specific priority rule in production control, a question appears on how the selection of priority rule influences the production performance objectives. Years of research on the field of priority rules have shown that in general, no rule outperforms the others, whereas there are different system configurations, operating conditions, and production performance indicators [14,15]. This is understandable, considering that the rules are developed for a specific category of system configurations involving a specific set of performance objectives, therefore they generally do not work well in an environment where they were not intended [15].

The impacts generated by the selected priority rule are mostly difficult to explain by analytical methods [1], thus the simulation is used very often to evaluate the schedule efficiency in the complex scheduling problem [10,16]. As an illustration, in the simulation study, Vinod and Sridharan [13] evaluated the performance measures based on flow time and tardiness of jobs for the different combinations of due-date assignment methods and seven scheduling decision rules applied in a dynamic job shop system. Xanthopoulos et al. [5] compared seventeen dispatching rules in the study focused on stochastic dynamic scheduling problems with sequence-dependent setups. Performance measures were mean work-in-progress (WIP), mean cycle time, mean tardiness, and a fraction of tardy jobs.

In opposition to the simulation, the optimization approach offers to find the optimal or near-optimal scheduling concerning one or more desired objectives. Specifically, simulation-based optimization uses metaheuristics to determine nearly optimal parameter configurations for simulations, and it can solve even complex stochastic combinatorial optimization problems. Simulation-based optimization with genetic algorithm applyication has been successfully applied in the work of Vieira et al. [17]. Freitag and Hildebrandt [18] applied simulation-based optimization employing multi-objective genetic programming to solve the complex problem of automated design of scheduling rules for short-term scheduling in a semiconductor manufacturing environment. The authors investigated seven standard rules: FIFO (First In First Out), ERD (Earliest Release Date), EDD (Earliest Due Date), ODD (Operation Due Date), MOD (Modified Operation Due Date), SPT (Shortest Processing Time), and CR (Critical Ratio). Additionally, the ODD+ rule was used. Kuck et al. [11] proposed an adaptive simulation-based optimization approach to select suitable dispatching rules including FIFO, EDD, FASFS (First Arrival in the System First Served), CR, ODD, SPT, and MOD rules for each machine in the production system with different strategies to react to system changes. Solutions obtained via genetic algorithm were evaluated by applying a discrete-event simulation model.

In the related literature, research performed to investigate the impact of priority rules on production results in job shop systems has focused mostly on one or two optimization objectives, such as tardiness, makespan (completion time), mean flowtime, or proportion of tardy jobs, with one priority rule applied to all the machines on the shop floor. Zahmani et al. [16] presented a simulation model for makespan minimization using different priority rules for each machine on the shop floor. Obtained experimental results served for learning base construction, which was utilized for developing an inference model for the selection of the most suitable priority rule. In the work of Demir and Erden [19], Genetic Algorithm (GA) and Ant Colony Optimization (ACO) were used together to obtain the best combination of dispatching rule, due date assignment rule, and route of all jobs to minimize earliness, tardiness, and due dates of each job.

We can find a lot of literature that mainly tackles single and bi-criteria job shop scheduling problems [20], and more objectives are taken into account rather exceptionally. The reason is that when reflecting many aspects of production evaluation concurrently, multi-criteria optimization is needs to be considered to obtain satisfying results for production parameters setting. An identification of optimal solution is not trivial in this case because there is no single solution, but a set of possible optimal solutions, all equivalent in a mathematical sense. The individual solutions in this set form the so-called Pareto front (or Pareto frontier) in the objective space [21]. Methods for finding optimal solutions to the multi-criteria problem are still in progress nowadays, concerning an improvement in finding very accurate and highly diverse solutions for an approximation of true Pareto front to offer design-makers a diverse range of design options [22].

In this study, based on preliminary experiments with single-objective optimization performed for a flexible job shop production system with partially interchangeable workstations, we focused on solving the multi-objective problem to evaluate and compare production results with respect to the priority rule applied for operations scheduling. The simulation-based optimization of five contradictory production objectives: Average flowtime, average machine utilization, average work in progress, average number of products, and an average costs per part unit is connected to the discrete-event simulation model of one-piece flow type when applying three specific well-known and often studied priority rules [5]. The rules are FIFO, which considers the order of incoming parts, EDD, which selects an operation of a part with the closest due date, and STR (Slack Time Remaining), where an operation of a part with the lowest time reserve is favored. We choose the FIFO priority rule as the most common one and simplest to implement. The reason for selection of another standard and very known EDD and STR scheduling principles was that they outperform other rules in a shortening flow time. It is important for the production of the type of make-to-order typical for flexible job shops and a lean production concept. Additionally, EDD and STR were involved in this investigation because they are widely used in the literature as benchmarks for metrics related to due date [5,23]. Two types of scalarization methods (Weighted Sum Method and Weighted Product Method) in a priori arrangement are applied for the definition of multi-objective function in the optimization model of the production system.

Compared with other related works, the main contribution of this study is considering more interesting conflicting performance production indicators of various types to offer the complex view to production results via multi-criteria evaluating many objectives simultaneously when employing a selected priority rule in scheduling operations. In addition, based on results of scalar multi-criteria simulation optimization, the global effective solutions can be recommended as support for decision-making in production control. Additionally, when solving a multi-criteria optimization problem (MOP), we have experimented with a modified approach in the transformation of individual objective functions in a scalar multi-criteria objective function comparing to works in the related literature. In this context, the most relevant publication to this work is the paper by Marler and Arora [24] dealing with practical aspects of multi-criteria methods usage and transformations for scalar multi-criteria objective function that inspired us to employ them in this work.

The main structure of the paper is as follows. Firstly, we briefly describe the problem of scheduling operations when priority rules are applied in the scheduling process. In the next part, a concept of Pareto-optimality in multi-criteria optimization and applied methods are mentioned. The part concerning the methodology of experiments introduces the simulation and optimization model and the design of optimization experiments. Finally, in the last section, we present and compare the obtained results focusing on the practical aspect of production control.

2. Scheduling Operations Based on Priority/Dispatching Rules

In job shop production systems, a shop floor control level makes decisions about all production and material handling resources including order release strategies, batch sizes, dispatching rules, and schemes related to preventive maintenance [4]. It ensures the generating production schedule that specifies the decision, at what time, and on what machine must start and end each job needed for manufacturing to optimize desired production objective/s.

Scheduling can be defined as the planning process that “deals with the allocation of resources to tasks over given periods” intending to optimize one or more performance measures [1]. Scheduling accomplishes two succeeding phases—loading and sequencing. The loading phase ensures an allocating of released jobs among workplaces. Sequencing specifies an order for jobs in the queue for the individual machine respecting the assigning in the loading phase. Grundstein et al. [25] differentiate sequencing into dispatching, which means an assignment of an order to a station, and queue processing, i.e., the sequence in which orders in a queue in front of a station are processed.

2.1. Scheduling in the Flexible Job Shop Systems

Flexible job shop (FJS) scheduling addresses problems of specific types of job shop production systems and faced to more complexity and flexibility comparing to job shop system scheduling. Generally, in job shop systems of each machine can perform only one operation for each job which is processed on machines with a given operation time. Flexible manufacturing job shop systems represent a specific more complex type of the job shop systems [20]. In FJS, the operation can be performed on any machine selected from a set of available identical machines with the flexible operation time depending on the processed product and the selected machine. To define deterministic FJS more precisely, we demand a set of N jobs to be processed on a set of M work centers. Within each job j, there is a set of operations that need to be processed in a specific order. Each operation can be processed by any identical machine of a given set. The processing time of the operation is explicitly known, and it may vary, depending on the machine on which it is running. The machine can only perform one operation at a time. The assignment of operation to the machine is given to the occupancy of the machine and the relevance of the machine to carry out the operation [7,26], so only some number of routings are possible for individual product.

Solving the flexible job shop scheduling problem means finding a schedule to ensure the utilization of sources optimally following production demands. Optimization techniques for generating a schedule performed in several main modes of scheduling—a forward scheduling mode, a backward scheduling mode, and a multi-pass mode [1]. The approach of the forward scheduling means that product processing starts in the first possible time, and jobs are assigned to machines towards the future [27]. Namely, this approach is built-in in algorithms of computer simulation methods that are employed to schedule production tasks. In this context, heuristic procedures, nature-inspired methods, neural networks, and utilizing priority dispatching rules are the most applied methods to solve the optimization problem in scheduling [1]. The most common metaheuristic procedures, such as Simulating Annealing [6], Tabu search [12], Random Search, or many types of nature-inspired optimization methods, such as evolutionary [7,28,29] and genetic algorithms [18], ant colony optimization [30], or particle swarm optimization [16,19,31], can provide acceptable solutions near the optimum. Although metaheuristics are advantageous in the sense of the solution quality and robustness, they do not guarantee solution optimality [1,27], they depend on the choice of method’s parameters [11], and they are often too complex to implement computationally in a real-time system [2]. To enhance the efficiency of metaheuristic, a hybrid approach based on combining different methods has been often proposed by several authors in their works [9,19,32,33].

Objectives related to the scheduling problems can be categorized into three groups—objectives based on the completion time, due date, and on inventory and utilization costs [34]. According to an extensive survey [34], flowtime and makespan were the most frequent and significant objectives considered in practice because of the minimization of makespan increases the production system efficiency and minimization of flowtime ensures a stable resources utilization and minimization of work-in-progress. The optimization of these two objectives simultaneously reduces the production costs [34].

To include more production aspects, scheduling based on multi-criteria optimization in job shop systems has been at the center of interest for a long time [9,14]. According to related literature, the frequently studied performance objectives in this area were, e.g., mean flow time, the maximum makespan (completion time), the mean weighted completion time, the mean weighted tardiness, the maximum tardiness, the mean weighted earliness, the maximum earliness, maximum lateness, the ratio of tardy jobs, or mean WIP (Work In Progress) [20]. In real practice, the consideration of several performance goals is challenging from the control aspect because it demands either an a priori decision about the hierarchy of objectives or a responsive adjustment to varying conditions on the shop floor [23].

2.2. Priority/Dispatching Rules

In a flexible job shop scheduling area, dispatching rules are often applied as part of the operational control of a manufacturing system. Whenever a machine becomes status idle and some jobs are waiting and ready to process, the dispatching rule gives the priority to each job and determines the job with the highest priority to be started [18]. Results of optimization experiments in studies carried out in job shop systems have demonstrated that the schedule generation based on priority dispatching rules is a practicable method of finding good solutions, although without the optimality guarantee [27].

Pinedo [1] gives an overview of the most common and better-known elementary dispatching rules, together with the type of needed data and an environment where rules are suitable to apply. The main classification of the rules concerning their time dependence to static and dynamic and according to the system information to local and global is stated, too. Additionally, Baker and Trietsch [27] provide a comprehensive overview of dispatching rules and a comparison of their performance according to different performance measures. Similarly, for an excellent review of priority rules with an emphasis on the classification and identification of dominant rules we refer to [23]. Three selected rules FIFO, EDD, and STR which have been found very often in use [23], and they are relevant to this work are described below.

FIFO or FCFS (First Come First Served) rule is a simple planning method that is frequently favored because is easy to implement, and no specific information and calculation are needed. It is a random priority rule [35], the first job arriving at a work center is manufactured first and the order of the jobs determined by the pass through the first machine maintains throughout the system. After completion of the job at one machine, it leaves the queue at the next machine. Typically, all queues in the system are supposed to operate on the base rule, therefore, common is an issue with an occurrence of blocking, mainly in some types of assembly lines due to limited buffers. Although the FIFO rule is considered to not be very profitable for effective scheduling, it can reach slightly better results than other rules under some circumstances. In the investigation, Savasci and Herrmann [36] focused on automotive logistics in a real production environment of job shop production with replacing stations. They compared fifteen priority rules for delivery reliability and tardiness. They showed that seven of the rules provided no better solutions than the FIFO rule already used, whereas others improve the performance.

The EDD rule also belongs to the group of static rules which generate a schedule taking due date information into account. It can be applied in case, individual jobs have different due dates, and it belongs to one of the most used rules in practice [23,35]. It selects the operation associated with the job that has the earliest due date and uses the target due date as a priority key. The operation with the earliest target completion time receives the highest priority and is processed first. A list containing all available jobs ordered to non-decreasing due dates determines the sequence assigned to the machines for all available jobs [37]. Therefore, to use this rule, the information about the due dates of the jobs must be known in an ordinal sense, but we do not have to know job processing times. This rule and other similar based on due dates information are important in the customer-oriented complex job shop manufacturing environment. If production works based on “make-to-order”, the due dates are agreed upon and must be kept. In this case, the due date adherence is the most significant production objective [25]. The EDD rule provides outstanding performance when there are sufficient production capacity, light load, and smaller shop configurations [23]. This coordinate mechanism is mainly useful when the goal is to reduce job lateness, minimize flow time and it also guarantees minimization of maximum and variance tardiness [23].

STR, MST (Minimum Slack Time) in [27], or MS (Minimum Slack) in [1] is a static rule concerning a specific operation, but a dynamic one with respect to a specific job [27], since the same job has assigned the different relative priorities to its individual operations. It chooses the waiting operation related to the job with minimum slack time. Slack time s_j of given job j with due date d_j and processing time p_j at time t is calculated by the expression (1):

$$s_j\left(t\right)=d_j-p_j-t$$

(1)

that represents the difference between the due date and the earliest possible finish time of the job [27]. The EDD rule or the STR rule ensures the optimal production performance when all due dates are sufficiently loose and spread out [1,23].

3. Multi-Criteria Optimization in Scheduling

Multiple conflicting objectives are a natural feature of most production scheduling environments. Therefore, at first, let us briefly introduce the multi-criteria optimization problem (MOP) and a concept of identification of MOP solutions based on the notion of Pareto-optimality and Pareto dominance.

3.1. Multi-Criteria Optimization Problem

In general, we consider a MOP (2) with n decision variables and k objectives (k > 1). Solving MOP is a procedure of simultaneous optimization of a set of k individual objective functions Fi (x) subjected to constraints given by the system of inequalities and equalities. It can be represented in the form (2):

$$\begin{array}{ll}\mathrm{Minimize}& \\ \mathit{x}\in D& \mathit{F}\left(\mathit{x}\right)={\left[F_1\left(\mathit{x}\right),F_2\left(\mathit{x}\right),\dots ,F_k\left(\mathit{x}\right)\right]}^T;k>1\\ \mathrm{subject}\mathrm{to}& g_s\left(\mathit{x}\right)\le 0,s=1,2,\dots ,m;m\ge 0,\\ & h_l\left(\mathit{x}\right)=0,l=1,2,\dots ,r;r\ge 0.\end{array}$$

(2)

Vector x is the decision vector in the feasible region D in n-dimensional design (decision) space, constrained by inequalities x_L ≤ x ≤ x_U. In case of a combinatorial problem, the D region is discrete. Vector $\mathit{F}\left(\mathit{x}\right) \in E_k$ consists of k objective functions F_i(x): $E_n\to E_1$ in the feasible objective (criterion) space Z, $Z\subset E_k$. As a result of solving MOP, if the objectives F_i(x) are conflicting, one cannot be able to find one single solution as the best one, rather a set of trade-offs, all with a compromising nature. Due to the absence of an absolute ordering in the vector space, the way how to identify MOP solution is via the preference relationship of partial preorder based on Pareto relation. It is built on the following associated definitions:

Pareto dominance: A decision vector x $\left(\mathit{x}\in D\right)$ (Pareto) dominates a decision vector y (denoted $\mathit{x}\prec \mathit{y}$) if and only if $F_i\left(\mathit{x}\right)\le F_i\left(\mathit{y}\right) \forall i \in \left\{1,2,\dots ,k\right\} \wedge F_i\left(\mathit{x}\right)<F_i\left(\mathit{y}\right)$ for at least one $i\in \left\{1,2,\dots ,k\right\}, k\ge 2$.

Pareto optimality: A solution $\mathit{x}\in D$ is Pareto optimal if does not exists any other ${\mathit{x}}^{\prime }\in D$ that dominates x [34].

The set of Pareto optimal solutions is called the Pareto optimal set. Its image in the objective space is referred to as the Pareto optimal front [38]. Pareto optima correspond to “best trade-off’ solutions between different conflicting criteria” [39]. From a geometric perspective, the Pareto front represents a hypersurface in k-dimensional space of objective functions, where all non-dominated solutions are located.

The optimal solution of MOP can be also characterized by terms of efficient solution and non-dominated solution according to space where the MOP solutions are located. Typically, efficiency refers to a vector of design variables in the design space, whereas dominance refers to a vector of functions in objective space [24]. These basic terms are explained by the following definitions, adopted from Marler and Arora [24]:

A feasible solution x* situated in design (decision) space D is efficient if and only if there does not exist any other $\mathit{x}\in D$ such that $\mathit{F}\left(\mathit{x}\right)\le \mathit{F}\left({\mathit{x}}^{*}\right)$ with at least one $F_i\left(\mathit{x}\right)<F_i\left({\mathit{x}}^{*}\right)$. With relation to the objective space, a corresponding vector $\mathit{F}\left({\mathit{x}}^{*}\right)$ in the objective space is non-dominated if and only if there does not exist another vector $\mathit{F}\left(\mathit{x}\right)\in Z$ such that $\mathit{F}\left(\mathit{x}\right)\le \mathit{F}\left({\mathit{x}}^{*}\right)$ with at least one $F_i\left(\mathit{x}\right)<F_i\left({\mathit{x}}^{*}\right)$. That means all non-dominated solutions dominate the others, but do not dominate themselves.

Both introduced definitions represent a similar idea and “a recipe” for how to identify Pareto-optimal solutions via a vector´s coordinates comparison. We will use the term Pareto-optimal solution in the sense of non-dominated solution yielded by solving MOP throughout the following text. For an excellent survey of multicriteria scheduling, we refer to the book by T’Kindt and Billaut [39]. Additionally, Hoogeveen [40] provided a comprehensive introduction and survey of research results in multicriteria scheduling.

In the context of scheduling problems with multiple objectives, the concept of Pareto-optimality acts as commonly accepted. Pinedo [1] states that “a schedule is Pareto-optimal if it is impossible to improve on one of the objectives without making at least one other objective worse”. The idea of Pareto-optimality in MOP solving implies the existence of the set of trade-off solutions instead of one single solution, therefore an expert in a position of decision maker (DM) is needed to support the identification of the most preferred solution of all available. If a priori method of MOP solving is used, DM expresses the preferences at the start of a solving process. In the case of the a posteriori method, the selection of MOP solution is generated after finding a set of optimal solutions. An interactive method is employing DM preferences directly into the running process of solving.

Within the classification of the a priori methods, several approaches are developed to deal with multi-objective scheduling problems in a priori arrangement. To mention some of them, in a hierarchical approach, the objectives are ranked in priority order and optimized in this order. In goal programming, all the objectives are considered as constraints expressing satisficing levels, and the aim is to obtain a solution that offers a value as close as possible to the desired goal for each objective. One objective can also be selected as the main one and then an optimized subject to other objectives [14]. The utility approach is based on an aggregation of multiple optimization objectives into one single utility or weighting function. The utility function very frequently employs a weighted linear combination of the objectives, and it represents the composite objective function in the most popular Weighted Sum Method (WSM). Marler and Arora [24] present other methods from the utility approach category, such as the more general weighted global criterion method, or weighted min-max method, weighted product method, and exponential weighted criterion method.

3.2. Applied Multi-Criteria Optimization Methods

In this study, the utility approach was employed to compare production system performance under different priority rules via WSM and Weighted Product Method (WPM).

WSM belongs to the most common scalarization procedure in the literature. It is a special type of global criterion method, expressed by the weighted sum of k individual objectives F_i (3):

$$U={\displaystyle \sum _{i=1}^k{w}_i}.F_i;w_i>0;{\displaystyle \sum _{i=1}^k{w}_i}=1$$

(3)

where weights w_i as method parameters are used to model preferences. Assuming the vector w is fixed, then minimizing U function (3) is a necessary and sufficient condition for Pareto optimality under convex constraint conditions (Geoffrion’s theorem [39]). This method suffers from a well-known disadvantage related to the geometric point of view. Since the scalar MOO function is generated as a linear combination of individual objective functions, the ability to yield the Pareto optimal solutions is restricted to the convex part of Pareto front only. Despite it, this method is rather popular in the application in a job shop scheduling area. To mention works that solved multicriteria problems applying WSM or via sum approach, e.g., Loukil et al. [14] published an extensive study of model types of production systems with seven objective functions studied alone or in different mutual combinations, and compared to the results in the literature. To perform multicriteria optimization, they used the multi-objective simulated annealing procedure for solving a given combinatorial optimization problem. Adibi et al. [9] studied dynamic job shop scheduling problems considering makespan and tardiness simultaneously when employing a variable neighborhood search method and ANN for finding optimal rescheduling. The work of Huang and Yu [41] addressed a multi-objective job-shop scheduling problem with equal-size lot splitting. It was solved via hybrid ant colony optimization-based algorithms. In the paper, the authors minimized scalar objective function generated in the form of the weighted sum of makespan, tardiness, and lot-splitting cost with an accent to issue related to lot-splitting of jobs and tradeoff between lot-splitting costs and makespan. To compare the effect of the first employed multi-objective method, the Weighted Product Method (WPM) was selected. The utility function U based on the multiplication of k objectives F_i was expressed in the form (4).

$$U={\displaystyle \prod _{i=1}^k{F}_i{}^{w_i}};w_i>0;{\displaystyle \sum _{i=1}^k{w}_i}=1$$

(4)

Weights w_i represent the relative importance of the individual objectives [24]. WPM is known mostly as a component of decision making methods in the Multiple Criteria Decision Making (MCDM) domain [42,43,44]. It supposed that the potential nonlinearities in the utility function and resulting computational issues can be the reason for lack of extensive application of this method [24]. According to Mateo [45], a major weakness of the method is that it overestimates the extremes leading to undesirable results, as it significantly favors/disfavors the final evaluation of any alternative that is far from the average in relation to one criterion.

4. Experimental Study

The effect of linking priority rules and multi-criteria optimization methods on optimization of production goals in the studied production system was explored via simulation-based optimization experiments performed in two phases. At first, single objective experiments were needed to find reference points for the transformation of production objectives. Secondly, multi-objective optimization according to general formulation (2) was conducted to determined MOP solutions for both WSM and WPM methods applied in definitions of multi-criteria objective functions in an optimization model (Equations (3) and (4)) when three different priority rules were consequently applied.

4.1. Simulation Model

The discrete-event simulation model in this study represents a hypothetical partially flexible job-shop production system adopted from [46]. It can be categorized as such a class of production systems that produce smaller numbers of different types of products according to several routings in a one-piece flow way, especially following the lean production concept. Regarding to its flexibility, some operations are only achievable on part of the available machines.

The model system has been built to maintain the main characteristics of FJS, which are mentioned in the Section 2.1. It meets the typical demands regarding the jobs and machines assumed in the deterministic flexible job shop scheduling problem [5,20,27]:

• All machines and all jobs are available at time t = 0.
• The number of jobs and machines are assumed to be finite;
• a job cannot be processed by two machines at the same time;
• each machine is always accessible for production, i.e., no machine breakdowns or order cancelations are supposed;
• the machine can execute only one operation at a time on any job;
• an operation of a job cannot be performed until its preceding operations are completed;
• once started operation must not be interrupted;
• operation is processed by any machine from a given set;
• the model does not include any assembly operations.

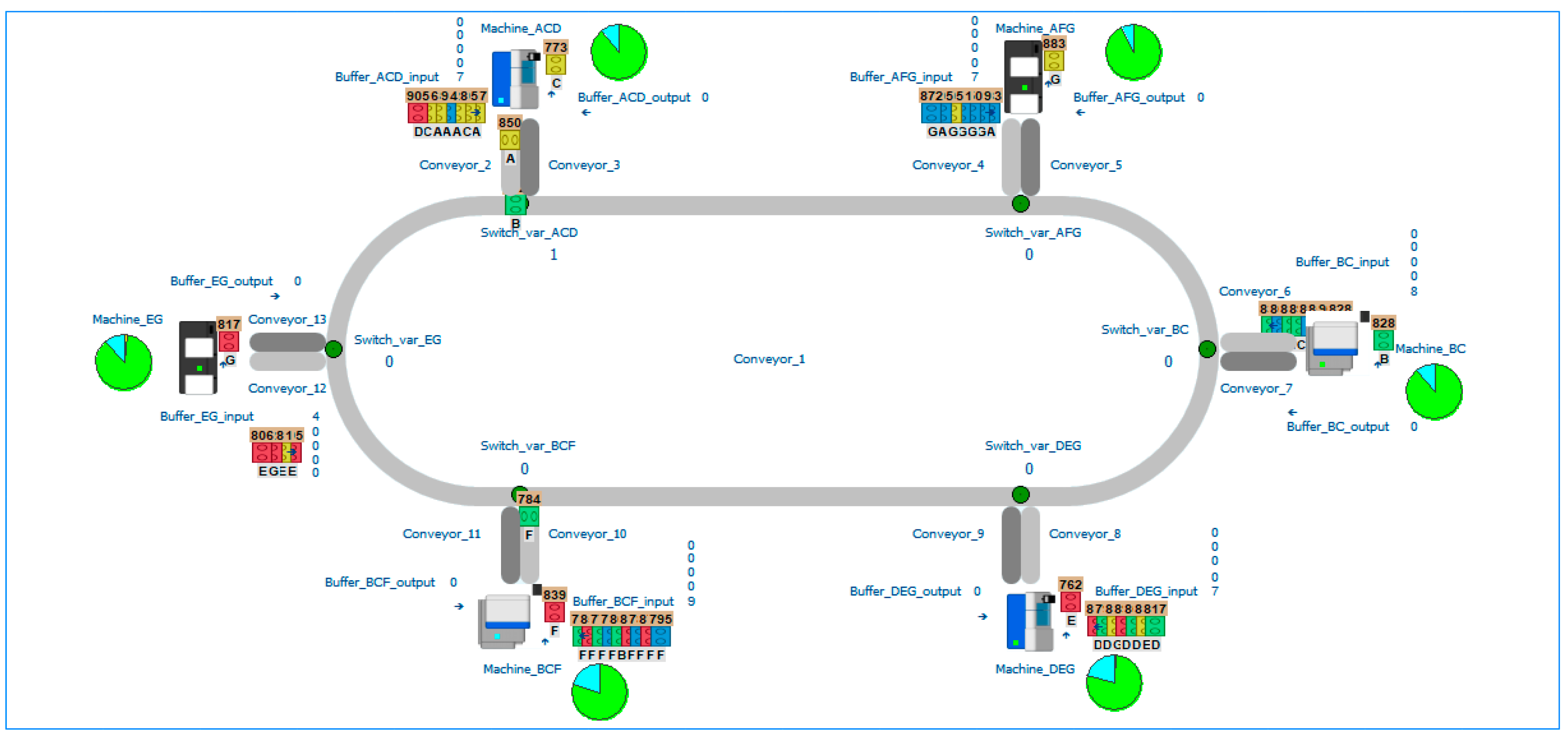
The studied model system consisted of six partially interchangeable machines with their input and output buffer [46]. A total of seven types of operations (A, B, C, D, E, F, G) were performed in the production system. The system manufactured four types of products, each with the specified determination of the sequence of four operations (that cannot be interchanged) defined in

Table 1. Definition of order operations for coming parts.

Product Type	Operations Order
1	A, G, B, F
2	C, B, D, F
3	D, F, G, E
4	G, E, A, C

.

Transportation of parts between buffers was ensured by conveyors with sensors that allow identifying every coming part. If the appropriate attribute of a part was detected, then the part was accepted for the next processing. The interchangeability of workplaces according to the operations possible to perform at individual machines in the system is shown in

Table 2. The interchangeability of workplaces.

Workplace Number	Possible Operation Performance
1	A, C, D
2	A, F, G
3	B, C
4	D, E, G
5	B, F, C
6	E, G

.

In this study, we implemented consequently selected priority rules FIFO, EDD, and STR to define the order in which the individual operations will be done. This order was determined by the calculated priority with respect to the rule performing. When implementing priority rule EDD into the simulation model, the priority key for the operation associated with a given job was updated with respect to the earliest due date information. In the case of the STR priority rule, Equation (1) was used for the calculation of the priority. Based on the determined priority rule, the machine always selected the operation that had the highest priority of all. If multiple operations had the same priority, these operations were grouped randomly. If the next operation can be done on different machines, the machine with minimal setup costs was selected to process it.

The simulation model was designed and built in such a way that it involved the possibility of choice of priority rule at the start of simulation. After selecting the priority rule by the user, the studied system was fully deterministic. Neither breakdowns due to order cancellations nor machine failures were allowed. All internal parameters, such like operation and setup times, and all costs items were keeping as constants during experiments, too. Most of operation times slightly differed due to the type of processing operation and type of product. Every machine was set up when the type of operation was changed. To simplify the investigated problem, the question of the impact of the different range of operating times was not included in the design of simulation experiments. The detailed information about operation times and costs for individual operation is given in

Table 3. Values of internal system parameters.

Product Type	Routing	Operation Time	Costs for Operation
1	A	4	5
	G	6	7
	B	5	6
	F	3	4
2	C	5	6
	B	4	5
	D	3	4
	F	4	5
3	D	3	4
	F	3	4
	G	5	6
	E	3	4
4	G	5	6
	E	3	4
	A	4	5
	C	4	5

.

The model of the production system was created in simulation software Witness Horizon ver. 22, developed by Lanner. Simulation environment of Witness Horizon is designed for modelling, simulation, predictive analytics, and optimization of production and logistic processes, or services with the aim to verify consequences of different scenarios in the virtual world via simulation, or to find an effective set of system parameters. We used it for simulation and optimization experiments in the presented study. The discrete-event simulation model is depicted in Figure 1.

4.2. Preliminary Simulation Experiments

Conditions of optimization experiments were proposed on the base of preliminary simulation experiments performed on the presented simulation model for three priority rules consequently in Witness simulator. The experiments served for understanding the simulation model’s behavior under different loadings and its limits associated with production results.

Different loadings were modelled by changing the time between arrivals (inter-arrival time) for the entry of each of four parts in the range 1 min to 20 min. Each of the parts entered in one piece lot size to the system.

Simulation runs lasted 1440 min, which represented standard period of 1 day covering three shifts. The warm-up period of 90 min was found out as the period which is needed to produce one product of each four types using simulation.

As system response, we observed values of five production indicators: Average flowtime (min.), average machine utilization (%), average work in progress (pcs), average number of products (pcs), and the average costs per part unit (€) as outputs from simulation runs. These experiments showed production limits according to the design variables and rules setting.

4.3. Optimization Model

When considering the avoidance of the extreme situations in production, which mean too few processed products and, on the other hand, the system overload, the space of design variables for optimization was determined as a four-dimensional domain defined by time between arrivals for the entry of each of four products in a reasonable range of 8 min to 16 min, based on the simulation results for this system. In this case, the modelled system showed acceptable values of production goals for all three priority rules.

Based on observed production results, the suitable values of constraints of production goals for optimization model were also suggested. As for the machine utilization constraints, from the practical point of view referring to [35], the decision was influenced by the fact that the machine utilization more than 80% generally corresponds to moderate and heavy shop load level in job shops. The constraints concerning production objectives applied in all optimization experiments are specified in

Table 4. Constraints for optimization experiments.

Production Goal	Constraint
Average flow time (min)	<180
Average machine utilization (%)	>80
Average number of products (pcs)	>400

.

The optimization objectives represented five selected aforementioned key performance indicators: Average flowtime, average machine utilization, average work in progress, average number of products, and the average costs per part unit. For MOP solving, they were combined into two types of scalar multi-criteria objective functions. This scalarization procedure generating multi-criteria objective function based on WSM and WPM methods (Equations (3) and (4)) is described in detail in the following paragraphs.

4.3.1. Transformation (Normalization) of Production Objectives

When applying a weighted sum approach or other types of scalarization, it is reasonable to normalize individual objectives Fi entering the scalar multi-objective function to avoid the scaling effects and thus ensure their comparable impact in the objective function expression. We utilized the transformation which represented a robust min-max type of normalization. It can also be referred to as the upper-lower-bound transformation in the literature [47]. This transformation and many other potential ones are provided in a survey by Marler and Arora [24] in a comprehensive overview. The applied robust transformation was in this study implemented in a form (5) involving two so-called reference points as maximal and minimal values of the individual objective functions $F_i$.

$$F_i^{transform}=\frac{F_i-F_i^W}{F_i^U-F_i^W}$$

(5)

Here, the transformation (5) includes a component of an ideal point [38] vector $F_i^U$ (maybe replaced the point, referred also as a utopia point [23]) and a component of the worst point vector $F_i^W$. They represent the unreachable solution for individual production objectives as the best (ideal), and as the worst one. The ideal point vector ${\mathit{F}}^{\mathit{U}}$ is determined as the optimum of the single-criterion function according to the optimization goal regardless of other objectives. Vector ${\mathit{F}}^{\mathit{W}}$ is composed of the worst values of production goals, obtained from single-optimization experiments. Value F_i in the expression (5) represents the individual objective value, resulted from the simulation run. The transformation scheme ensures the same range and magnitude for all objectives within the range between 0 and 1. Comparing to works [24,47] where the distance between solution F_i and utopia point is minimized, we modified the transformation scheme to (5) and maximized the distance between solution F_i and the worst point.

4.3.2. Single-Objective Optimizations

The presented approach demanded to find the minimum and maximum value for each of five selected production goals with respect to constraints presented in Table 4. We used a set of single-objective optimizations for this purpose instead of an estimation [24,38]. The objective functions for obtaining ideal and worst points were optimized according to the type of production objective. The objective functions and target of optimization for each of them are shown in

Table 5. The target of the single-objective optimization.

Objective Function	Optimization Target When Finding Ideal Point	Optimization Target When Finding Worst Point
Flow time	minimize	maximize
Costs per part unit	minimize	maximize
Work in progress	minimize	maximize
Machine utilization	maximize	minimize
Number of products	maximize	minimize

.

Simulation environment Witness Horizon includes the optimization module Experimenter with its Advanced Mode for the performance of simulation-based optimization. Implemented optimization algorithms comprise Random solutions, Hill Climb, Min/Mid/Max, and All Combinations algorithms, and metaheuristic, such as Adaptive Thermostatistical Simulated Annealing (SA). The optimum of the individual objective functions representing production goals was obtained via simulation-based optimization in two steps. Firstly, employing a metaheuristic algorithm briefly explored the design space with respect to the local optima at the beginning of optimization process. None of the values reached by SA represented global optimum, only local ones, therefore we did not present them. Secondly, we used the Brute Force algorithm All Combinations, which runs all constrained combinations of design parameters. The optimization process via the All Combinations algorithm was time consuming, but with the guarantee that the optimal solution will be found. For all experiments, the length of the one simulation run was set up to 1440 min and the warm-up period was 90 min. We used one replication for one simulation run due to the deterministic nature of the model. The resulted values of the ideal and worst points are listed in

Table 6. Results of single-objective optimization of production objectives. FIFO: First In First Out; EDD: Earliest Due Date; STR: Slack Time Remaining.

Priority Rule	Single-Objective Function	Coordinates of the Ideal Point in the Objective Space	Coordinates of the Worst Point in the Objective Space
FIFO	Flow time	47.534	179.884
	Costs per part unit	31.645	37.507
	Work in progress	3.189	21.229
	Machine utilization	87.245	84.902
	Number of products	467	421
EDD	Flow time	45.128	179.527
	Costs per part unit	31.410	37.297
	Work in progress	2.637	22.109
	Machine utilization	89.283	82.096
	Number of products	482	429
STR	Flow time	44.892	179.934
	Costs per part unit	31.250	37.455
	Work in progress	2.747	22.034
	Machine utilization	89.449	83.508
	Number of products	479	433

.

4.3.3. The Formation of Scalar Multi-Criteria Objective Functions and Conditions of Optimization

After the determination of all reference ideal and worst points necessary for the transformation of production goals, further experiments based on respecting all five production goals simultaneously are carried out under the same conditions. The scalar multi-criteria objective functions for each of the three priority rules were built on WSM and WPM methods.

Multi-objective U_WSM function (6) was formed on the base of the Weighted Sum Method (defined by Equation (3)) as the linear combination of the normalized individual objectives $F_i^{transform}$ expressed by (5) using the weight vector w.

$$U_{WSM}={\displaystyle \sum }_{i=1}^k{w}_i{F}_i^{transform},w_i>0\forall i,{\displaystyle \sum }_{i=1}^k{w}_i=1$$

(6)

All components w_i were equal to the value 0.2 to not give priority to any of five production goals. Due to the normalization of objectives given by (5), the structure of the proposed scalar objective function U_WSM demands the maximization of (6) to lead to the single preferred Pareto optimal solution finding.

When adopting the Weighted Product Method (defined by Equation (4)) with the same settings of weights, U_WPM function is defined by Equation (7), and, on the contrary, the minimization of (7) yields the Pareto optimal solution.

$$U_{WPM}={\displaystyle \prod }_{i=1}^k{\left(F_i^{transform}\right)}^{w_i},w_i>0\forall i,{\displaystyle \sum }_{i=1}^k{w}_i=1$$

(7)

The objectives that need to be maximized were transformed using a reciprocal of (5).

Box 1 and Box 2 contain an example of code which shows the transformation in WSM and WPM-based multi-criteria objective functions for EDD priority rule, written in the versatile WITNESS Action Language. (WITNESS also supports external code libraries written in common languages such as C++, C#, and VB.net).

Box 1. A code in a body of Weighted Sum Method (WSM)-based objective function using EDD priority rule in simulator.

IF Number_of_products >= 400 AND Flow_Time <= 180 AND Machine_utilization >= 80

RETURN 0.2 * ((Number_of_products − 429)/(482 − 429)) + 0.2 * ((Work_in_progress − 22.109)/(2.637 − 22.109)) + 0.2 * ((Flow_Time − 179.527)/(45.128 − 179.527)) + 0.2 * ((Machine_utilization − 82.096)/(89.283 − 82.096)) + 0.2 * ((Costs_per_part_unit − 37.297)/(31.410 − 37.297))

ELSE

RETURN 0.2 * ((Number_of_products − 429)/(482 − 429)) + 0.2 * ((Work_in_progress − 22.109)/(2.637 − 22.109)) + 0.2 * ((Flow_Time − 179.527)/(45.128 − 179.527)) + 0.2 * ((Machine_utilization − 82.096)/(89.283 − 82.096)) + 0.2 * ((Costs_per_part_unit − 37.297)/(31.410 − 37.297)) – 10

ENDIF

Box 2. A code in a body of Weighted Product Method (WPM)-based objective function using EDD priority rule in simulator.

IF Number_of_products >= 400 AND Flow_Time <= 180 AND Machine_utilization >= 80

RETURN ((482 − 429)/(Number_of_products − 429)) ** 0.2 * ((Work_in_progress − 22.109)/(2.637 − 22.109)) ** 0.2 * ((Flow_Time − 179.527)/(45.128 − 179.527)) ** 0.2 * ((89.283 − 82.096)/(Machine_utilization − 82.096)) ** 0.2 * ((Costs_per_part_unit − 37.297)/(31.41 − 37.297)) ** 0.2

ELSE

RETURN ((482 − 429)/(Number_of_products − 429)) ** 0.2 * ((Work_in_progress − 22.109)/(2.637 − 22.109)) ** 0.2 * ((Flow_Time − 179.527)/(45.128 − 179.527)) ** 0.2 * ((89.283 − 82.096)/(Machine_utilization − 82.096)) ** 0.2 * ((Costs_per_part_unit − 37.297)/(31.41 − 37.297)) ** 0.2 + 10

ENDIF

For other rules, the form of body function was created analogically, with corresponding ideal and worst points shown in Table 6. In all cases, the same weights of 0.2 were used as parameters expressed a priori articulated decision-maker´s preferences. Independently on the type of objective function, the key optimization idea was to ensure the maximization of a distance between the solution and the worst point. As can be seen in Box 1 and Box 2, all objective functions were constrained by the values presented in Table 4. For these optimization experiments, simulation-based optimization with All Combinations algorithm was applied with one replication for one simulation run lasting 1440 min, with the warm-up period 90 min to find global optimum.

5. Experimental Results

The performed optimization experiments were of two categories. Firstly, the single-objective optimizations exploring 4096 scenarios for each of the three priority rules were conducted to find the reference points involved in the robust transformation of production objectives (with the aims given in Table 5). All results were obtained under the same conditions, which are described in previous section with respect to design space, objective functions, constraints, and conditions of simulation runs.

The column graph in Figure 2 shows a comparison of ideal point values when applying different priority rules.

Analogically, Figure 3 depicts a comparison of obtained values of the worst point. All data were presented in Table 6 above.

Secondly, the experiments focused on multi-criteria optimization carried out to acquire the optimal daily production results according to given a priori preferences. When applying the WPM method, the minimization of objective function regarding the best and worst values of production performance, introduced in Box 2 and subjected to constraints, was performed. On the contrary, the objective function built via WSM scalarization method presented in Box 1 was maximized. In contrast to the approach in the works of Marler and Arora [24] or Xiang et al. [47], where the distance of the solution to the ideal point was minimized, we modified the structure of scalar objective function so that the maximization of the distance between solution and the worst point was needed.

The individual values of five production objectives for obtained optimal solutions in objective space applying WSM and WPM methods linked to three selected scheduling principles are shown in

Table 7. Results of multi-criteria optimization based on scalarization for three priority rules.

Scalarization Method	Priority Rule	Optimum of the Objective Function	Number of Products (pcs)	Flow Time (min.)	Work in Progress (pcs)	Machine Utilization (%)	Costs Per Part Unit (€)
WSM	FIFO	0.826	460	69.173	5.544	86.569	31.940
	EDD	0.879	472	60.377	4.453	87.923	31.577
	STR	0.883	475	60.649	5.000	88.039	31.719
WPM	FIFO	1.042	447	47.946	3.826	82.756	31.766
	EDD	1.050	452	45.360	3.004	83.590	32.043
	STR	1.014	455	46.399	2.778	84.315	31.971

.

The graphical comparison of production goals obtained employing WSM and WPM methods for three different priority rules is presented in Figure 4a–e.

On the basis of obtained production goals as nondominated solutions in objective space presented in Table 7, the four design variables—the times between arrivals for entry of each of four parts P1, P2, P3, and P4 (the inter-arrival times (IATP1—IATP4)) were identified as effective solutions in the design space. They are presented for both methods and three priority rules in

Table 8. Design input values of the inter-arrival times for parts P1—P4 in the design space corresponding to optimal production outputs (shown in Table 7) in objective space.

Scalarization Method	Priority Rule	IATP1 (min.)	IATP2 (min.)	IATP3 (min.)	IATP4 (min.)
WSM	FIFO	12	15	15	9
	EDD	12	15	14	9
	STR	14	13	13	9
WPM	FIFO	15	15	15	9
	EDD	14	14	14	10
	STR	15	12	15	10

.

In this work, we address not only solving multi-objective optimization problem in scheduling itself, but also the way, how to evaluate the impact of the applied priority rule to the production results via obtaining the trade-off solution, and comparing it to the best values of many production goals determined by limits of the studied system. To compare the obtained trade-off solutions, simple ordering based on obtained optimization results presented in Table 7 from the best one (1.) to the worst (5.) according to the optimization target for each of the production objectives was assigned. In addition, an average of the order values was calculated to evaluation the less is better, as it is presented in

Table 9. The individual ordering production goals values according to the results of multi-criteria optimization.

Scalarization Method	Priority Rule	Number of Products	Flow Time	Work in Progress	Machine Utilization	Costs Per Part Unit	Average of the Order Values
WSM	FIFO	3.	6.	6.	3.	4.	4.4
	EDD	2.	4.	4.	2.	1.	2.6
	STR	1.	5.	5.	1.	2.	2.8
WPM	FIFO	6.	3.	3.	6.	3.	4.2
	EDD	5.	1.	2.	5.	6.	3.8
	STR	4.	2.	1.	4.	5.	3.2

.

On the base of average values relating to the ordering given in Table 9, we assigned the final ranking to each of the applied methods in the conjunction with the evaluated priority rule to determine the best performance result. A ranking “1” was given to the rule with the method that provided the best performance, i.e., to the summarized evaluation with the smallest average value. A ranking “2” to the next one, etc. The result of the final evaluation is introduced in Figure 5.

Finally, we compared the obtained compromise solution for the best evaluated scheduling to the coordinates of an unfeasible ideal point when the EDD priority rule was employed in production control. The differences due to the compromise character of the solution are presented in Figure 6.

6. Discussion

The obtained experimental outcomes reflect the dynamical structure of the system determined by applied priority rule. As the precise analytical expression of the transformation of input parameters (time between arrivals for the entry of the parts) to the outputs (production goals) is not known, all objective function values were determined by simulation in a simulation-based optimization process.

The results of experiments related to single-objective optimization of production objectives, which are presented in Table 6 and compared in Figure 2 and Figure 3, show that priority rules EDD and STR provided the comparable ideal and worst values for almost all production objectives in the studied model system. That means the daily production limits of the investigated production system according to both rules were similar, therefore the reference points would have to influence the MOP solution only insignificantly. The ideal and the worst values were applied in the robust transformation involved in both employed multi-criteria optimization methods in the next step.

The following optimization experiments were conducted with the focus on comparing results of multi-criteria optimization with the relation to the evaluation of reached production goals, respecting the implemented specific priority rule. The results presented in Table 9 demonstrate that there does not exist a single dispatching rule that achieves the highest ranking in the connection to applied multicriteria methods according to all observed performance objectives. As can be seen in Figure 5, according to the type of scalar objective function used in the multi-criteria optimization, the best ranking overall was obtained for the WSM when the EDD priority rule was applying. Very similar although slightly worse results were achieved by the WSM using the STR rule. Both scalarization methods in the presence of the FIFO priority rule achieved the worst results with a relatively large loss. The result has confirmed what, e.g., Kemppainen [23] states, that the FIFO rule is not recommended for manufacturing operations since it is usually overcome by any other priority rule.

The presented findings point to that employing the EDD and STR rule brought similar production performance results in the context of the complex view to obtained compromise solutions in the studied production system. The relatively long inter-arrival times for EDD rule presented as effective solutions in design space in Table 8 are in consonance with the fact that due date based dispatching rules are expected to work well at low utilization levels [35], and outperformed other rules under light load and smaller job shop configurations [23].

Based on the findings of this investigation, a practical suggestion for production how to set up the input arrival time of each of four entering parts into the system under the specific rule can be proposed. It is determined by design variables presented in Table 8. When utilizing the EDD rule and WSM method, the effective solution is following the values of the design vector (12; 15; 14; 9), determined in minutes. Comparing to the unreachable best results determined by ideal point, the loss of production performance is 2.07% for an average number of manufactured products, 25.26% for an average flow time, 1.52% for average machine utilization, 40.78% for average work in progress, and 0.52% for average cost per part unit, respectively.

As for the recommendation of input arrival times when utilizing the STR rule with WSM, it is the design vector (14; 13; 13; 9), determined in minutes. The loss when comparing the compromise solution to the best values in case of setting relating to the WSM+STR rule, is 0.84% for an average number of manufactured products, 25.98% for an average flow time, 1.58% for average machine utilization, 45.06% for average work in progress, and 1.48% for average cost per part unit.

For the setup of design variables going up from the WPM + STR rule, the suggested design vector is (15; 12; 15; 10), determined in minutes. The corresponding loss is 5.01% for an average number of manufactured products, 3.25% for average flow time, 5.74% for average machine utilization, 1.12% for average work in progress, and 2.26% for average cost per part unit, respectively, all in the relation to the values of ideal point.

Despite the weights in scalar objective function were the same, we can notice that in contrast to WSM methods that prioritized some of the production objectives, the compromise solution yielded by WPM is in a relative evaluation more balanced. In this context, the results confirmed that the scalarization methods applying in a priori arrangement bring the problem with the precise reflection of the weights to desired Pareto optimal solutions [24]. The coordinates of the weight vector serve as the model parameters in a multi-objective function and influence the location of Pareto front points.

When exploring the compromise solutions found in the objective space from the perspective of the production goals control, we can see a noticeable impact of the applied scalarization method on the evaluation of production results. The comparison of the reached results in Figure 4a–e shows that all production goals that we wish to maximize, such as the number of products and machine utilization, were substantially higher in the case of the WSM method employed, regardless of the applied priority rule. On the contrary, the WPM method provided better results for production goal values that need to be minimized. As we can see in Figure 4, the production objectives, such as the average flow time and the average work in progress, achieved smaller values in comparison to results yielded by the WSM method. Finally, in the case of the average costs per part unit, we can notice very similar and comparable results for all applied methods.

Working with many contradictory objectives assumes that they are not completely independent, and a correlation can appear between some of them. As can be noticed in the results introduced in Figure 4, there exist two pairs of objectives which are correlated. We can observe the positive correlation between the number of products and machine utilization (Figure 4a,b), as well as between flow time and work-in-progress (Figure 4c,d). We supposed that correlations, applied transformation of production objectives, and different expressions defining the structure of objective function themselves could explain the obtained results significantly. To evaluate the direct influence of correlations on optimization results will need further experiments with a reduced set of objectives.

The rankings of priority rules strongly depend on selected performance measures involved in evaluation and the structure of the production system model itself. The interesting different approach, how to optimize multiple objectives in flexible job shop system, is introduced in a comparative study in the work of Sels et al. [48]. They conducted single-objective optimizations for five individual objectives in the presence of 30 priority rules consequently to evaluate the individual performance objective with respect to the scheduling principle. The observed objectives were makespan, mean flow time, proportion of tardy jobs, mean tardiness, and maximum tardiness. As for ranking of rules, each priority rule’s performance was measured as the percentage deviation from the best performing priority rule. Based on the best results via ranking, they constructed the hybrid scheduling rule to ensure optimization of all five objectives simultaneously. EDD and Slack (called STR in our study) rules were the part of the hybrid priority rules in the top 5 of the priority rules that performed best on the five objective functions. Their experiments showed that an integrated optimization approach outperforms the hierarchical approach when solving the flexible job shop scheduling problem [48].

7. Conclusions

In this study, we presented the results of the wider investigation of common priority rules FIFO, EDD, and STR applied in the partially flexible job shop system in terms of several conflicting production performance indicators evaluated simultaneously. We employed scalar multi-criteria simulation-based optimization in a priori arrangement to identify the impact of applied priority rule to production results. From this perspective, the evaluation of the influence of the applied priority rule and system loading to daily production for five selected production objectives at the same time based on MOP solving offers the possibility to find effective settings of external input parameters with respect to the scheduling principle, and it can support decision-making in production control.

Combination of metaheuristic algorithm Simulated Annealing and full combinatorial analysis in the final phase of the optimization process yielded a global solution of defined MOPs for each of the selected priority rules. The experimental results demonstrated that the found compromise solutions strongly depended on a selected scalar multi-criteria method and applied priority rule. Although the weights in the scalar objective function were the same, based on the performed experiments, we can conclude that results for production goals which need to be minimized were better when the WPM method was applied, in contrast to WSM, which developed the values of other production objectives, regardless of the employed priority rule. EDD and STR priority rules were shown as more suitable than the FIFO rule, both with comparable production performance.

Despite these facts, from the complex point of view, all effective solutions in the design space resulted from scalar multi-criteria simulation-based optimization obtained independently from the applied rule and applied optimization method, and were situated in the area connected to the lower production system load. For the modelled production system, the recommended settings for inter-arrival time of entering part for four types of manufactured products were presented to obtain acceptable values of production goals.

Future research will be focused on other multi-criteria method applications, and the question of the effect of other priority rules is still open. The evaluation of stochastic system performance will be in the center of interest, too.