Assimilation of Dynamic Combined Finite Discrete Element Methods Using the Ensemble Kalman Filter

Abstract

Simulation of fracture initiation, propagation, and arrest is a problem of interest for many applications in the scientific community. There are a number of numerical methods used for this purpose, and among the most widely accepted is the combined finite-discrete element method (FDEM). To model fracture with FDEM, material behavior is described by specifying a combination of elastic properties, strengths (in the normal and tangential directions), and energy dissipated in failure modes I and II, which are modeled by incorporating a parameterized softening curve defining a post-peak stress-displacement relationship unique to each material. In this work, we implement a data assimilation method to estimate key model parameter values with the objective of improving the calibration processes for FDEM fracture simulations. Specifically, we implement the ensemble Kalman filter assimilation method to the Hybrid Optimization Software Suite (HOSS), a FDEM-based code which was developed for the simulation of fracture and fragmentation behavior. We present a set of assimilation experiments to match the numerical results obtained for a Split Hopkinson Pressure Bar (SHPB) model with experimental observations for granite. We achieved this by calibrating a subset of model parameters. The results show a steady convergence of the assimilated parameter values towards observed time/stress curves from the SHPB observations. In particular, both tensile and shear strengths seem to be converging faster than the other parameters considered.

1. Introduction

The accurate simulation of fracture initiation, propagation, and arrest in materials is an important problem for a number of applications, ranging from the study of micro-scale behavior of materials to the analysis of large-scale fracture initiation and propagation. Many numerical solutions have been proposed to simulate fractures; one of the most widely accepted is the Combined Finite-Discrete Element Method (FDEM) [1,2]. FDEM, which merges solutions developed under both finite elements and discrete element methods, is mainly aimed at modelling failing, fracturing, and/or fragmenting solids. This is achieved by the usage of Finite Element formulations to resolve stresses in the material combined with Discrete Element formulations to resolve fracture and contact problems [2]. A review of the current fracture models based on FDEM is presented by [3]. Furthermore, FDEM has been widely used in real-world problems, such as dam and rock slope stability [4,5], hydraulic fracture and fracture propagation on shale [6,7,8], fracture coalescence [9,10], rock mass strength [11], dynamic fault rupture [12,13,14], and granular gouge response [15,16].

As with many models, several material-specific parameters (i.e., material properties) are needed for a FDEM simulation, such as density, Young’s modulus, Poisson’s ratio, and strength parameters for failure modes I (normal) and II (tangential). Additionally, the specific fracture energies for these two modes are also needed. Closely related to the specific fracture energies is the use (within FDEM) of a displacement-softening curve to represent the strength of degradation as micro-fractures form in the material. In previous work, the sensitivity of the FDEM model to perturbations in these parameters was analyzed [17,18], where the authors found a relatively small number of parameters influencing the behaviour of the stress versus time curve obtained from FDEM.

To accurately simulate fracture behavior, the characterization of displacement-softening parameters need to be correctly specified. However, experimental information that could be used to determine these parameters is very often not easy to find, and modelers are forced to establish them in an ad hoc manner or based on their own experience. Data assimilation is a method that fuses observational data into models to improve the nowcast and/or forecast of the model [19,20]. There are several types of data assimilation methods, from statistical based on Bayesian theory, to optimization-based methods. Data assimilation methods are used in several geophysical sciences, including climate, atmospheric weather prediction, space weather, and ocean sciences, to name a few. Additionally, assimilation methods are increasingly being implemented in geomaterials and fracture propagation to improve the simulation of geophysical models (weather, climate, subsurface flow, etc.) [19,20,21].

The calibration of model parameters is of relevance for a number of applications. For example, it is relevant to the simulation of complex masonry construction problems [22,23] where non-linear analysis of the response of the structures are needed. In these cases, the problem itself is complex enough, and the uncertainty on the parameter determination can be quite high. This is also the case for the simulation of underground processes, such as hydraulic fracturing and earthquake ruptures, where knowledge about material properties is limited to areas where core sampling can be extracted and analyzed. This provides a starting point for analysts to populate their models, but in many cases this is not sufficient, and further calibration is needed. Sensitivity analysis [17] and assimilation methods [18] provide a robust and systematic way of analyzing the system under consideration as a whole, while identifying the key parameters and establishing a confidence interval for them.

The Split Hopkinson Pressure Bar (SHPB) is a standard laboratory experiment where the tensile strength of geologic materials, measured at high rates of strain, is obtained. It is worth noting that the simulation of the SHPB experiment is very demanding for the numerical method being used, mainly in the post-peak portion of the stress-time curve. The correct representation of damage after the material has reached its peak poses many numerical challenges, for example with the proper accounting of the energy being dissipated. In this work, it will be demonstrated that via this assimilation process, the Combined Finite Discrete Element Method is able to simulate the post-peak behavior of granite at high strain rates. Furthermore, the calibrated properties obtained from this assimilation exercise can be used to populate more complicated models, such as when trying to simulate underground mining explosions, or dynamic earthquake rupture problems. This paper presents the procedure to obtain such calibrated strength parameter sets, but the application to other types of problems is outside its scope.

This work presents the implementation of the ensemble Kalman filter to estimate key model parameters of a dynamic Combined Finite Discrete Element model, which simulates the evolution of fractures and cracks in different geomaterials. Specifically, the ensemble Kalman filter (EnKF) is applied to the Hybrid Optimization Software Suite (HOSS) to better simulate a set of laboratory experiments. The main objective is to estimate a set of key strength parameters for the model which have the most influence on the material response to the imparted load. For this, the FDEM numerical results are contrasted against observations obtained for a SHPB experiment on granite samples.

The paper is organized as follows: Section 2 provides a brief introduction of the HOSS model and the parameters to be estimated; Section 3 presents the SHPB experiment description, as well as the HOSS model setup to simulate an SHPB experiment; Section 4 provides a brief overview of the ensemble Kalman filter and the assimilation algorithm, and the results of the assimilation are presented in Section 5; and Section 6 provides the conclusions and discussion of the results.

2. Description of the Model

In this work, the 2D version of the Hybrid Optimization Software Suite (HOSS) [24,25,26,27], which is an in-house implementation of the Combined Finite-Discrete Element method (FDEM) [2,28,29], is used. For an in-depth description of FDEM, the following references are recommended: [2,3,5,17,30]. In a previous work [17], the authors performed a detailed sensitivity analysis using the Fourier Amplitude Sensitivity Test (FAST [31,32]), where seven HOSS parameters were explored. These parameters include tensile and shear strengths, ${\sigma }_n^{max}$ and ${\sigma }_t^{max}$, the maximum relative displacements in the normal and tangential directions, ${\delta }_n^{max}$ and ${\delta }_t^{max}$, and the shape of the displacement-softening curve (see [17]). The sensitivity analysis study showed that only two parameters had an impact on the stress versus time curve (for a point located at the center of the sample) obtained from HOSS for this type of problem. These parameters are the shear strength ${\sigma }_t^{max}$ and the maximum relative displacements in the tangential direction ${\delta }_t^{max}$. The sensitivity results are consistent with a previous work performed on the HOSS model by Osthus et al. [18], where only the ${\sigma }_t^{max}$ is found to be of significant influence on the model. A combination of these parameters defines the specific fracture energy dissipated in mode II, $E_t$, which is given by

$$E_t={\sigma }_t^{\max }{\delta }_t^{\max }{A}_0,$$

(1)

where $A_0$ is given by $A_0={\int }_0^{1}z\left(x\right)dx$ (see [17]). The question remains: How do we select all these coefficients or material parameters, when there is not enough experimentally-based information, in a way that the model response is both physically sound and in agreement with available experimental data? As a way of circumventing the information limitation mentioned previously, in this work, an assimilation estimation of these parameters is proposed. In order to perform a comprehensive assimilation estimation of the HOSS model to the input parameters, both the shear strength ${\sigma }_t^{max}$ and the maximum relative displacement in tangential direction ${\delta }_t^{max}$ are estimated through data assimilation. It is worth noticing that both parameters ${\sigma }_t^{max}$ and ${\delta }_t^{max}$ are independent from each other. The way in which the ${\delta }_t^{max}$ is perturbed in this work is by changing the energy in tangential direction and therefore obtaining the maximum displacement using Equation (1). A more detailed description of the HOSS model and its parameters is presented in Appendix A and in [17].

3. SHPB Experiment and HOSS Model Setup

The SHPB experiment is used to indirectly determine the tensile strength of materials at high rates of strain. In this type of experimental setup, a cylindrical sample is positioned between two slender metal bars (see Figure 1). The load is generated by the impact of a projectile on the free end of the incident bar. This impact creates a stress wave that travels along the incident bar, and after a certain amount of time it reaches the sample, imposing a compressive load on it. A portion of the wave is transmitted to the sample, while the rest is reflected back into the incident bar [33,34]. Similar wave reflection behavior is observed between the sample and the transmission bar. In order to measure the amplitudes of the wave trains, strain gauges are placed in both bars. This allows for the determination of the initial load in the form of a velocity versus time series, and also of the contact force between the bars and the sample, $f\left(t\right)$, which in turn allows for the calculation of the stress at the middle of the sample as follows [30]:

$${\sigma }_n=\frac{2f\left(t\right)}{\pi dh},$$

(2)

where h and d are the sample’s thickness and the diameter, respectively.

Observational data from the SHPB experiment described above is obtained for granite. The elastic properties and the density of the material are listed in

Table 1. Elastic properties and density for granite.

Parameter	Description	Units	Value
E	Young’s Modulus	GPa	35.0
$\nu$	Poisson’s ratio	-	0.16
$\rho$	Density	kg/m${}^3$	2550.0

. More details about the setups and the experiment in general are provided in [30,35]. For the simulation of the SHPB experiment with HOSS, the bars are discretized using around 5000 constant-strain triangular finite elements. For the granite sample in the middle of the experiment (circle in Figure 1), a mesh is generated using 17,500 finite elements with an average size of 0.5 mm. The action of the impactor was simulated by enforcing a velocity boundary condition on the x direction, $v\left(t\right)$, on the nodes that are located on the incident bar’s free end (left bar on Figure 1), as shown in Figure 2.

4. Data Assimilation

The simulation of complex physical phenomena is commonplace in many areas of science. As our knowledge of the physical phenomena increases, more complete models can be developed. Nevertheless, model errors and bias, resulting from uncertain parameters, incorrect initial and/or boundary conditions, and unaccounted physical processes have a significant influence on the accuracy of model forecasts. In this regard, the use of data assimilation methods, which combine data collected from the model, observations, and corresponding error statistics, is a viable method for estimating improved model forecasts [19,20]. This is accomplished by modifying the model parameters, as well as the model variables, in order to better agree with observational data using the Bayesian probability theory. In this way, data assimilation provides an improved model forecast, along with its probability distribution function to evaluate how trustworthy the resulting forecast is. Depending on the model, its dimension, and its complexity, there are different data assimilation methods that can be applied. The methods range from deterministic to Monte-Carlo-based methods which take advantage of the model dynamics. There are several assimilation methods, and the most widely used are the variational methods (3D-Var and 4D-Var) [36], Kalman filtering [37], as well as the Monte Carlo techniques [38,39,40,41].

In this work, the ensemble Kalman filter has been selected to assimilate data into the HOSS model. The main motivation for selecting an EnKF method to calibrate the model parameters in HOSS was because the EnKF is one of the most computationally inexpensive and easy to implement [42]. There are other methods that can potentially be used for the model calibration, such as control theory. Unfortunately, due to the complexity of the model and its simulation requirements, these methods might be hard to implement. The EnKF has been shown to be computationally feasible and efficient for parameter estimation problems, since it is a compromise between Monte Carlo methods and Bayesian theory for Gaussian distributions [42]. This compromise enables the EnKF to use statistical information efficiently and provide an estimate of the probability distribution function of the model parameter. Practically, the computational efficiency of the EnKF translates to the number of model simulations needed to achieve convergence. A typical number of model simulation that the EnKF needs is around 30, whereas other methods might need significantly more simulations, without even providing a probability distribution of the model parameters. This advantage makes the EnKF an attractive alternative to estimate the parameters for a complex model like HOSS. A description of the EnKF method is presented in the following subsection.

Ensemble Kalman Filter

The ensemble Kalman Filter (EnKF) [41,43] is an approximation to the Kalman filter [37] designed for non-linear models. The EnKF is widely implemented in several fields of science for its effectiveness in producing good results and the overall ease of implementation. The model mean and error covariance matrix is approximated through an ensemble of simulation results, which are used in the EnKF formulation. The observations are used to update the ensemble, through the Kalman filter formulas, and then evolved through the model between assimilation cycles. Details on the EnKF method and algorithm can be found in [43,44].

The EnKF algorithm analysis equations are performed in the following way: For a vector of m observations ${\mathbf{y}}^o$ and an ensemble of N model simulations valid at time $t_k$, the EnKF analysis equations are given by:

$$\begin{array}{ccc}\hfill {\mathbf{x}}_i^a& =& {\mathbf{x}}_i^f+\mathbf{K}\left({\mathbf{y}}_i^o-\mathbf{H}{\mathbf{x}}_i^f\right),i=1,\dots ,N,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \mathbf{K}& =& {\mathbf{P}}^f{\mathbf{H}}^T{\left(\mathbf{H}{\mathbf{P}}^f{\mathbf{H}}^T+\mathbf{R}\right)}^{-1},\hfill \end{array}$$

(4)

where $\mathbf{K}\in {\mathbb{R}}^{n\times m}$ is the Kalman gain matrix; ${\mathbf{x}}_i^a\in {\mathbb{R}}^n$ is the analysis; ${\mathbf{P}}^f\in {\mathbb{R}}^{n\times n}$ is the model covariance matrix; $\mathbf{R}\in {\mathbb{R}}^{m\times m}$ is the covariance matrix of the observations; $\mathbf{H}\in {\mathbb{R}}^{m\times n}$ is the observation operator used to map the model state to the observations; and ${\mathbf{y}}_i^o\in {\mathbb{R}}^m$ is the observation vector with Gaussian white noise.

The EnKF approximates the model covariance matrix using the ensemble simulation. There are a number of problems with this approximation, namely the introduction of artificial cross-correlations between model state variables, which can introduce errors when performing assimilation with the Kalman filter equations [45]. To solve this particular problem, the correlation matrix of the model (${\mathbf{P}}^f$) is modified by removing the cross-correlation between parameters and variables that we know are not correlated. That is, the off-diagonal terms in ${\mathbf{P}}^f$ that correspond to correlation between parameters and variables that we know are not correlated is set to zero. This is called localization of the covariance matrix.

It is also well-known that using the EnKF to estimate model parameters can lead to ensemble collapse, that is, when the parameter estimate in all ensemble members is essentially the same. In order to avoid ensemble collapse in the model parameters, an inflation technique is implemented. The inflation, as the name suggests, increases the difference between the ensemble parameter average and each individual ensemble parameter value. That is, the parameters are inflated as

$${\widehat{p}}_i=\overline{p}+\lambda \left(p_i-\overline{p}\right),$$

(5)

where $p_i$ is the HOSS parameter value from ensemble i, $\overline{p}$ is the average, ${\widehat{p}}_i$ is the inflated parameter for ensemble i, and the inflation factor is denoted by $\lambda$. For our problem, $\lambda$ is set to approximately $45\%$ of the standard deviation for the initial parameter spread.

For the HOSS model, the parameters considered cannot be changed mid-simulation. That is, the HOSS parameters are set at the start of the simulation, and once the simulation is underway, they cannot be modified. Due to this, the EnKF is implemented as a smoother [46], which considers the results of HOSS over time as a single state vector to be assimilated using the observations over time. Additionally, the EnKF is implemented in an iterative way to better approximate the HOSS parameter values. The full mathematical framework for the iterative EnKF can be found in [47,48,49]. EnKF algorithm implementation is done in the following steps:

• Initialization: An ensemble of parameter values ${\mathbf{p}}_i$, $i=1,\dots ,N$ is provided by the latin hypercube sampling strategy, where ${\mathbf{p}}_i=\left({\sigma }_{t,i}^{\max },E_{t,i}\right)$;
• Simulation: For each ensemble member ${\mathbf{p}}_i$ simulate HOSS for the SHPB experiment, where the output is a stress versus time curve (${\mathbf{x}}_i$ for $i=1,\dots ,N$);
• Assimilation: Using the HOSS output from the ensemble ${\mathbf{x}}_i$ for $i=1,\dots ,N$ and observations $y^o$ from the SHPB experiment, assimilate using the Kalman analysis Equations (3) and (4), where this will provide updated parameter values ${\mathbf{p}}_i^a=\left({\sigma }_{t,i}^{\max ,a},E_{t,i}^a\right)$ for all ensemble members;
• Cycle: Feedback the updated parameter values ${\mathbf{p}}_i^a$ to HOSS and repeat Steps 2 and 3 until we see convergence of the error between the HOSS output and SHPB experiment ($∥\overline{\mathbf{x}}-{\mathbf{y}}^o∥<tol$, where $\overline{\mathbf{x}}$ is the ensemble average);
• Forecast: Once convergence is achieved, perform a “forecast” of the HOSS model (best simulation with estimated parameter values).

The workflow is illustrated in Figure 3, where there are the five basic steps as in the description above.

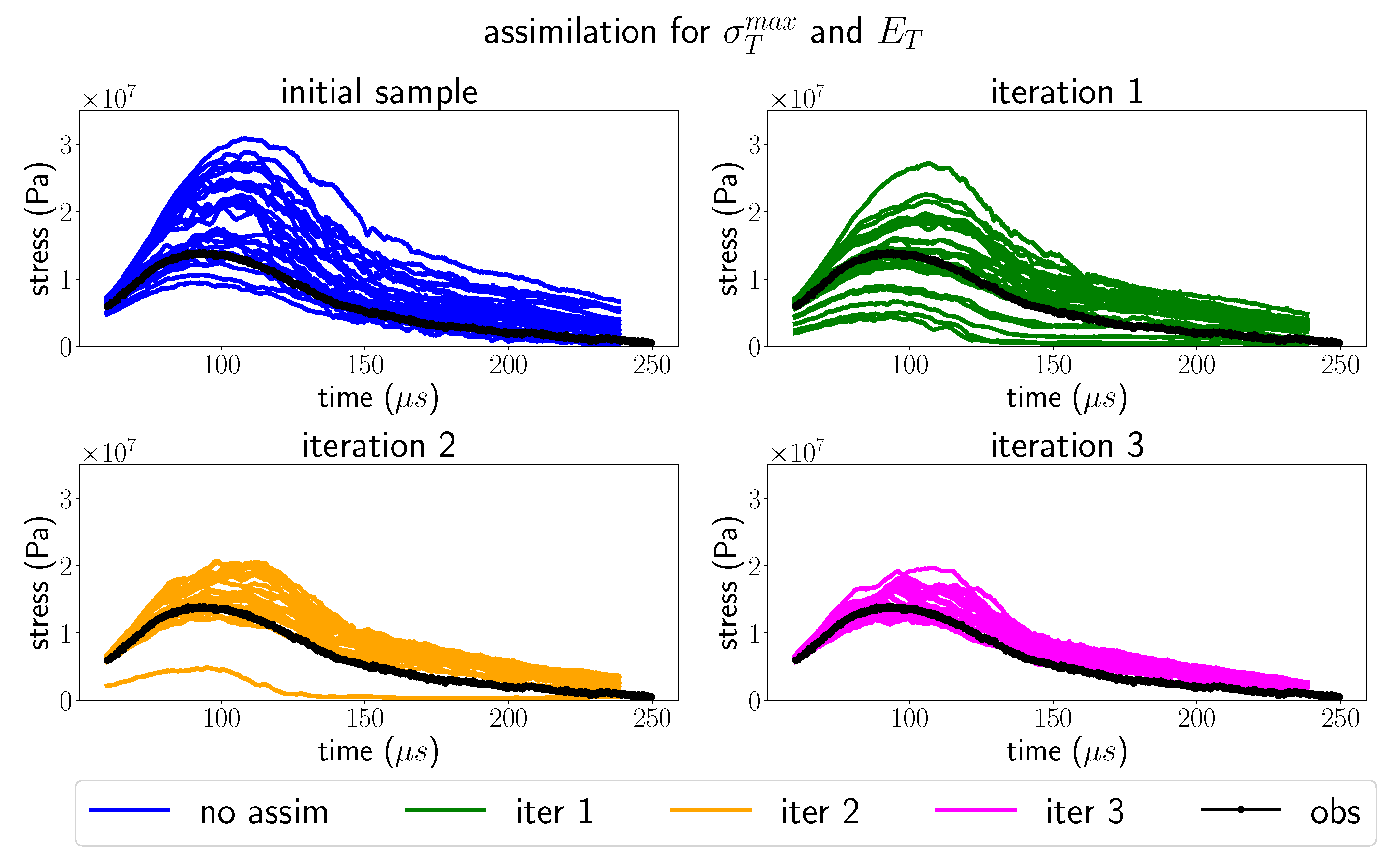
5. Assimilation Results

5.1. Data Assimilation Simulation Setup

For the EnKF experiments, the ensemble is generated by perturbing/assimilating each of the HOSS parameters of interest at the beginning of the simulation. The parameters of interest are the shear strength ${\sigma }_t^{max}$ and the maximum relative displacement in tangential direction ${\delta }_t^{max}$. Due to the set-up of HOSS, we cannot directly modify the maximum relative displacement, and instead, for the assimilation experiments, we use the relationship given by Equation (1) and modify the specific energy in the tangential direction $E_t$. That is, the two parameters that are perturbed are ${\sigma }_t^{max}$ and $E_t$. The parameters are described in

Table 2. Table with the parameter use for data assimilation, with  their corresponding interval values, as well as a “reference value” for the validation of the assimilation algorithm. The  parameters are sampled using the LHS strategy, where each parameter is assumed to have a uniform distribution. The intervals for each parameter are derived in an ad hoc manner from previous HOSS simulations for granite materials.

Parameter	Description	Units	Interval	Reference val. (Validation)
${\sigma }_t^{\max }$	shear strength	${10}^9$ Pa	$\left[4.0\times {10}^{-3},6.0\times {10}^{-2}\right]$	4.5 $\times {10}^{-2}$
$E_t$	specific energy in tangential direction	${10}^6$ J/m 2	$\left[2.0\times {10}^{-4},24.0\times {10}^{-4}\right]$	5.0 $\times {10}^{-4}$

, where the interval indicates the range of values for each parameter, and are sampled using the Latin Hypercube Sampling method (LHS) [50] to generate the initial HOSS ensemble simulations. The initial distribution for each of the parameters is a uniform distribution with lower and upper limits provided in Table 2. The HOSS simulation uses the parameter values for ${\sigma }_t^{max}$ and $E_t$, given in Table 2, to define the properties of the HOSS model. An ensemble of 25 HOSS simulations is used for all EnKF assimilation experiments presented. Each HOSS simulation requires 31 CPU cores for approximately 40–50 min of CPU time; hence, each HOSS simulation requires 1240–1550 min in CPU time (number of cores × CPU time requested for all cores). In total, the ensemble then requires between 31,000 and 38,750 min in CPU time (number of cores × CPU time per core × number of HOSS simulations). The HOSS simulation was performed on a Intel Xeon Broadwell CPU on the Grizzly high-performance computing platform available at the Los Alamos National Laboratory.

5.2. Data Assimilation Validation Experiments

The data assimilation algorithm, described in Figure 3, is validated using model-generated synthetic observations. This is performed with a HOSS setup to simulate the SHPB experiment described in Section 3. The synthetic observations experiment, referred to as a twin experiment, consists of selecting a set of “reference” parameter values for ${\sigma }_t^{max}$ and $E_t$, from which a HOSS model simulation for the SHPB is generated and used to get synthetic observations. In this case, the observations are the stress versus time curve generated from this reference HOSS simulation. Afterwards, an EnKF assimilation experiment is performed using these SHPB synthetic observations. To validate the EnKF assimilation method if the estimated parameters provided by the EnKF are close to the “reference” parameters chosen to generate the synthetic data, then the assimilation method is validated, since it provided the correct parameter values for this synthetic observation experiment.

The parameter values given by the EnKF validation experiment show steady convergence from the very first iteration, and provides a very good approximation at three iterations (see Figure 4). This steady convergence proves that the EnKF can accurately estimate the correct parameter values for ${\sigma }_t^{max}$ and $E_t$ for the current setup. In order to ensure that the EnKF is actually converging to the correct solution, we compared the synthetic observed SHPB with the EnKF HOSS ensemble. As expected, the HOSS ensemble time-stress curves converge to the synthetic SHPB time-stress curve, as shown in Figure 5.

To verify that the data assimilation performed consistently over different parameter values, an additional two experiments with different reference parameter values were performed. The assimilation results on those two additional experiments are consistent with the results presented in this section—that is, both parameters ${\sigma }_t^{max}$ and $E_t$ converged to the reference parameter values in no more than three EnKF iterations.

5.3. Results with SHPB Observations

The EnKF assimilation estimates the most likely mean and covariance of a normal distribution for each parameter that produces the HOSS SHPB simulation that best matches the data. The assimilation experiment setup is the same as in Section 5.1, where we are estimating ${\sigma }_t^{max}$ and $E_t$.

From our twin experiments shown in Section 5.2, three EnKF assimilation iterations are needed to estimate a fairly accurate parameter value for ${\sigma }_t^{max}$ and $E_t$. The observations are composed of a series of stress versus time points obtained from a SHPB laboratory experiment. The results show a good convergence for ${\sigma }_t^{max}$, where the assimilation provides a parameter value of around 0.15 (see Figure 6). For ${\sigma }_t^{max}$, the assimilation is able to hone in to the most likely value. This might not be the case for $E_t$, where the assimilation provides a monotonically decreasing parameter value. Given that no strong suggestion of convergence is seen in this parameter value, it is difficult to conclude that the final value provided in the third iteration of the assimilation is the most likely parameter value for this SHPB observations.

To provide a clearer assessment of the convergence of the assimilation, the time–stress curve for all ensemble members, from the initial estimation to the second iteration, is plotted against the observed SHPB stress versus time curve. Figure 7 shows the time–stress curve for the initial ensemble with uniform distribution (blue lines), the curves for the first EnKF assimilation iteration (green curves), and the second assimilation iteration (red lines). As can be seen, the curves are converging towards the observed SHPB curves, but with the risk of ensemble collapse, it is more prudent to avoid over-iterating the EnKF.

6. Conclusions

Accurate simulation of fracture propagation for a number of materials is an important problem in the engineering community in general. There are a number of state-of-the-art numerical models in the community for fracture simulations, and among them is the HOSS model. In the HOSS model, as well as in other models, a number of important processes are determined by the value of key model parameters, such as material softening or degradation behavior, and energy dissipation and strength in both normal and tangential directions. Oftentimes, the appropriate value of these parameters becomes elusive for a number of materials, which poses a difficulty for the accurate simulation of fracture behavior in these materials. In this work, we present a systematic and reliable framework to estimate two key model parameters for HOSS using data assimilation for a Split Hopkinson Pressure Bar experiment for granite material. This was achieved via the implementation of an ensemble Kalman filter assimilation method. The main advantage of the EnKF is its ease of implementation and reliability to provide an estimate of the parameter values for the SHPB observational data.

Given that the parameters are set only at the beginning of the HOSS simulation, and have an impact throughout the simulation, the assimilation approach is based on the comparison of the stress versus time curve from HOSS against the one obtained from SHPB experiments. In essence, the EnKF assimilation utilizes this stress versus time curve as a state vector, computes the correlation between the stress versus time curve and the parameters, and exploits that correlation to adjust the values of the parameters so as to agree with the SHPB stress versus time curve. The EnKF assimilation, as explained, was applied three times (called, in this work, EnKF iterations) to obtain the parameter values. A previous sensitivity analysis test [17] indicated that the two main parameters that play a significant role in determining the stress versus time curve in the HOSS experiment are the strength and energy parameters in the tangential direction (${\sigma }_t$ and $E_t$). Therefore, only these two parameters are estimated using the EnKF assimilation method. To determine the accuracy and reliability of the assimilation method, we performed a twin experiment test. In this twin experiment, we generated synthetic data by sampling from a stress versus time curve from a HOSS simulation, where we fix the parameter values to a chosen reference value. Afterwards, we assimilate the synthetic observations to determine whether the assimilation method can recover the reference values used to generate the observations. Our twin experiment indicates that the assimilation can, in fact, recover the reference values (see Section 5.2).

The stress versus time curve from a SHPB experiment is used to estimate the model parameters ${\sigma }_t$ and $E_t$ using EnKF data assimilation. We observed that after three EnKF iterations, there is convergence in ${\sigma }_t$, but there is no such convergence on $E_t$ (see Figure 6). The lack of convergence in $E_t$ might be attributed to the need of more EnKF iterations, or, alternatively, that the EnKF might not be able to correctly estimate this parameter. Nevertheless, the resulting model parameter estimates provide a HOSS simulation which show good convergence to the SHPB observational data (see Figure 7). Since the parameters are estimated through the assimilation, the HOSS convergence in the stress versus time curve indicates that the EnKF is adjusting the parameter’s values towards the best HOSS simulation for the observations considered.

Future work is still to be done for the parameter estimation of HOSS, specifically the exploration of other model parameters, as well as different observation types for calibration. One of the advantages of the EnKF data assimilation method is that it can handle a moderate increase in the number of model parameters to estimate without changing the algorithm outlined in the paper and with no considerable increase in computational cost [42]. In this paper, we only considered stress versus time curves, which might provide enough information to estimate certain HOSS parameters, but other parameters, such as the softening curve parameters [17] were not analyzed. Additionally, multiple sets of SHPB time–stress curves can be considered to further constrain the possible parameter values, and provide a template for the parameter values that are possible for SHPB experiments for certain materials.