Quantum Modular Adder over GF(2ⁿ − 1) without Saving the Final Carry

Abstract

Addition is the most basic operation of computing based on a bit system. There are various addition algorithms considering multiple number systems and hardware, and studies for a more efficient addition are still ongoing. Quantum computing based on qubits as the information unit asks for the design of a new addition because it is, physically, wholly different from the existing frequency-based computing in which the minimum information unit is a bit. In this paper, we propose an efficient quantum circuit of modular addition, which reduces the number of gates and the depth. The proposed modular addition is for the Galois Field $GF(2^n-1)$, which is important as a finite field basis in various domains, such as cryptography. Its design principle was from the ripple carry addition (RCA) algorithm, which is the most widely used in existing computers. However, unlike conventional RCA, the storage of the final carry is not needed due to modifying existing diminished-1 modulo $2^n-1$ adders. Our proposed adder can produce modulo sum within the range $\left\{0,2^n-2\right\}$ by fewer qubits and less depth. For comparison, we analyzed the proposed quantum addition circuit over $GF(2^n-1)$ and the previous quantum modular addition circuit for the performance of the number of qubits, the number of gates, and the depth, and simulated it with IBM’s simulator ProjectQ.

1. Introduction

Recently, quantum computers have been actively researched and developed by Google, IBM, Microsoft, and Rigetti, and each has reported that they have reached quantum supremacy (quantum superiority) that exceeds the performance of existing supercomputers [1,2,3,4,5]. IBM announced its plan to commercialize it as a cloud service, and Amazon and Intel have opened a quantum cloud service for research and development [6,7]. Such a quantum computer is a device operated by the principle of quantum mechanics and quantum phenomena using quantum photons [1,8,9]. It processes information in it, which is 0, 1, or a superposition of the two states in a quantum register as a qubit. This superposition is associated with the "uncertainty" of the quantum state. The unit for quantum information processing is a qubit, where 0 and 1 can exist simultaneously. However, existing computers are devices that operate by electronic phenomena using semiconductor devices such as transistors, and process information in a deterministic system that produces one output for one input based on 0 or 1 bit as the minimum unit for information processing. Since quantum computing processes information on a device that is entirely different from today’s computer, logic gates, basic operations, data structures, and algorithms for quantum information processing must be newly designed and implemented according to the characteristics of quantum computers.

Because the most basic logic gates are open as needed, researchers have designed quantum circuits for various operations, data structures, and algorithms using logic gates. In a quantum computer, the algorithm is represented by a quantum circuit using a qubit and a gate, and the number of qubits, the number of gates, and the depth are significant elements for evaluating the performance of the quantum circuit, and the smaller the number, the better.

As the newly designed addition circuit is the most fundamental operation, developing an efficient addition circuit leads to the practical design of other essential operations such as multiplication, division, and modular addition, which are primitives for solving various problems [10,11,12]. Thus far, various quantum modular adders for specific fields have been proposed based on existing classical addition algorithms [13], utilizing quantum adders, such as Quantum Ripple Carry Adder (QRCA), Quantum Carry Save Adder (QCSA), and Quantum Carry Lookahead Adder (QCLA), classified by how to handle the carry propagation [14]. A more special addition circuit, such as Lu’s quantum adder for superposition states, as one of the quantum principles has also been proposed [12]. However, a primary quantum algorithm, such as Shor’s algorithm, still uses general quantum adders based on the current adders [15,16,17,18]. The representative quantum adder is the adder modulo N proposed by Vedral et al., among the QRCAs based on the Ripple Carry Adder (RCA), which is the most widely applied in classical computing [10].

The RCA is the simplest adder with the lowest power, area, and design time suitable for various ultra-low-power IoT (Internet of Things) applications such as implantable biomedical devices, RADAR system, linear convolution, Harr transformation, and fast Fourier transformation [19,20,21,22]. Moreover, it is usually used to design a hybrid adder with other faster adders such as the Carry Lookahead Adder (CLA) and Kogge Stone Adder (KSA). A single adder cannot optimally operate to improve the speed, area, leakage current, overall power dissipation, and the design time because there is a trade-off among various adders [23,24]. Although the CLA or the KSA are used for higher speeds, the power consumption, the energy dissipation, and the area consumption for the RCA are far lower than those at the same speed [20]. Nevertheless, the RCA is slower than the CLA or the KSA because of solving the carry propagation problem. Using the RCA, Vedral’s quantum adder also has the carry propagation problem, which has to use additional qubits for carrying or saving all carries—the same problem as the RCA [12].

These existing adders support modular addition over the Galois Field $GF\left(2^n\right)$. However, since the Galois Field $GF(2^n-1)$ contains special numbers that play an important role in a public cryptographic system, there is a need to develop an efficient modular addition over $GF(2^n-1)$. In particular, the $GF\left(521\right)$ is one of the recommended numbers for elliptic curve cryptography (ECC), the $GF\left(31\right)$ is for multivariate quadratic-based post-quantum cryptography (MQ-PQC), such as Rainbow and MQDSS, and large prime numbers are for RSA [25,26]. Since the speed of the adder affects the performance and analysis of these public key cryptographic algorithms with specific secure parameters, it is essential to design an optimized modular adder for particular numbers, such as the $GF\left(31\right)$ for improving the performance of and analyzing MQ-PQC.

In this paper, we propose a new quantum modular adder over $GF(2^n-1)$ without saving the final carry. The main contributions of this paper are as follows:

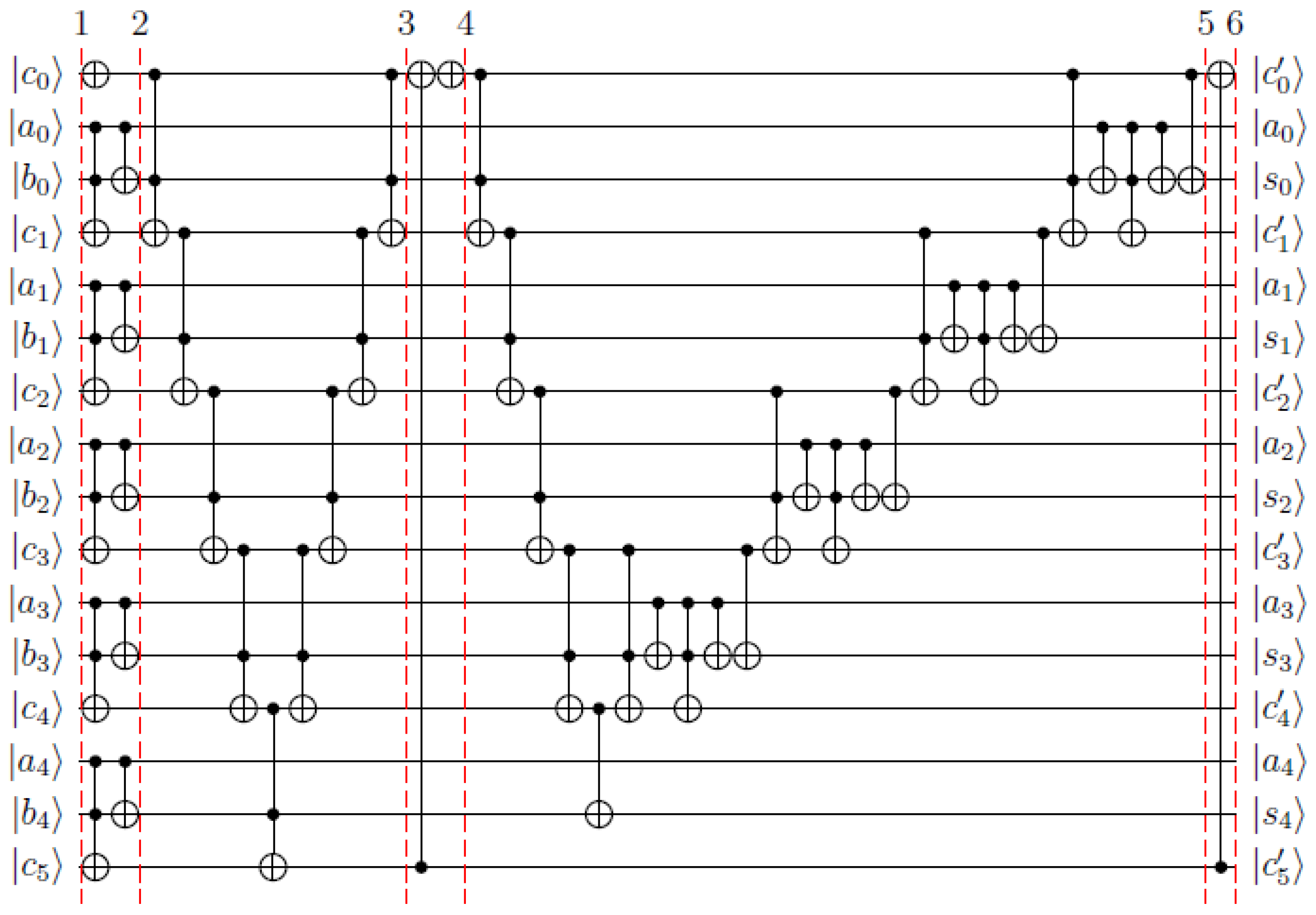
• We propose a lightweight quantum modular adder over $GF(2^n-1)$ using one full adder based on RCA and one carry-truncated adder. In contrast, the general modular adder usually uses multiple dividers or multipliers. The final carry in the carry-truncated adder affects the decision to add one or not for completing the modular operation and is not included in the results.
• We designed the algorithm of the proposed quantum modular adder as a quantum circuit, called a referenced quantum circuit. Then, we optimized the circuit as a more efficient circuit, called an optimized quantum circuit, by an equivalence rule of quantum circuits.
• We simulated the referenced quantum circuit and the optimized quantum circuit to add two numbers over $GF(2^n-1)$ via IBM’s ProjectQ when $n=5$ with 16 qubits, and compared them to other RCA-based quantum modular adders.

The organization of this paper is as follows. Section 2 introduces the representative quantum modular adder based on the RCA; Section 3 describes the quantum circuit of the proposed quantum modular adder over $GF(2^n-1)$ in quantum computing; Section 4 presents the analyzed results in terms of the number of qubits, the number of gates, and the depth, and compares the differences from the existing quantum modular adder. Finally, Section 5 presents our conclusions.

2. Related Works

2.1. Quantum Modular Adder Circuit

Vedral et al. proposed several elementary quantum circuits for two n-qubit binary numbers a and b, such as the quantum full adder $|a,b>\to |a,a+b>$ and the quantum modulo N adder. The quantum modulo N adder called Adder-Mod, as shown in Figure 1, computes $|a,b>\to |a,a+bmodN>$, where $0\le a$, $b<N$. The third resister for $|b>$ as the input is one qubit larger than the second register for $|a>$ as the input to prevent overflow. The last qubit in the third register is for the last carry of $|a+b>$, and the third register finally provides the results from calculating $|a+b$ mod $N>$, denoted $|S>$.

Vedral’s Adder-Mod gate consists of five full adder $FA$ gates, including two inverse full adder $F{A}^{†}$, as shown in Figure 2. $FA$ is the addition of a given number to b, and $F{A}^{†}$ is the inverse of $FA$ to subtract a given number from b. The parameters in Figure 2 are N for modulo, a and b for two numbers to add, c for carries, and t for checking whether $a+b$ is smaller than N or not. Vedral’s approach for calculating the modulo operation is taking the output of $a+b$ and subtracting N. The subtraction of N depends on whether the value $a+b$ is bigger than N or not. Looking at the Adder-Mod in Figure 2 step by step, the first $FA$ in steps 1 and 2 performs a simple addition on the state $|a,b>$, returning $|a,a+b>$; the second $FA$ in steps 3 and 4 adds $-N$, obtaining the state $|N,a+b-N>$ as the inverse $FA$ after swapping a and N in steps 2 and 3. After the second $FA$, denoted $F{A}^{†}$, the most significant qubit of $|b>$ takes a value for whether an overflow occurred or not. $|t>$ saves this information in steps 4 to 7 through the NOT gate and the CNOT (CONTROL-NOT) gate, as shown in Figure 6. If there is no overflow ($a+b-N$ is smaller than N), the value of the $(n+1)$-th qubit $|b_n>$ is 0, 1, 1, and 0 in steps 4, 5, 6, and 7, respectively. At this stage, the value of $|t>$ conditionally becomes 1 in steps 5 to 6 and resets the first resister $|a>$ with N to zero in steps 7 and 8. On the contrary ($a+b-N$ is larger than N), $|b_n>$ is 1, 0, 0, and 1 in steps 4, 5, 6, and 7, respectively. $|t>$ is 0 in steps 5 and 6 and the qubits $|a>$ keep N as their value. After the third $FA(+N)$ in steps 8 and 9, the value of $|a>$ swaps back from N to a in steps 10 and 11, subtracting a in the total state $|a,((a+b)modN)-a>$ in steps 11 and 12, and adding a in the final state $|a,(a+b)modN>$ in steps 13 and 14. This operation is for leaving $|a>$ and $|b>$ in state $|a,(a+b)modN>$. Moreover, $|c>$ and $|t>$ are reset to their original value in state $|0>$ through a second CONTROL-NOT gate in steps 12 and 13. Finally, the last $FA$ returns original $N,a,c,t$, and the result of sum $|S>$, which is $(a+b)modN$.

They also defined the quantum circuit of $FA$$|a,b>\to |a,a+b>$ based on RCA, as shown in Figure 3, and used it for modular addition such as Figure 2. The $FA$ shown in Figure 4 composites n carry gates called $CR$, $n-1$ inverse carry gates called $C{R}^{†}$, and n sum gates called $SM$, where the $CR$ and $SM$ gates are shown in Figure 5. Unlike a half adder, $FA$ computes the most significant bit of the result $a+b$. This computation requires computing all carries $c_i$, through the relation $c_i\leftarrow a_i$ and $b_i$ and $c_{i-1}$, where $a_i$, $b_i$, and $c_i$ represent the i-th qubits in states $|a>,|b>$, and $|c>$ in Figure 2. For this computation, the $FA$ uses n-qubits $|c>$, n-qubits $|a>$, and $(n+1)$-qubits $|b>$.

The elementary gates, such as the CNOT gate and the CCNOT (Controlled Controlled NOT) gate, are shown in Figure 6 [27]. The CNOT is the same as the XOR operation in classical computing and comprises one control qubit $x_1$ and one target qubit $x_2$. It changes the target qubit, where the state of the control qubit is $|1>$. If $|x_1>$ is $|1>$, the CNOT changes $|x_2>$ in the state $|0>$ into $|1>$, where $|x_2>$ is $|0>$. The CCNOT gate has two control qubits, namely, $x_1$ and $x_2$, and one target qubit, i.e., $x_3$, and is called the Toffoli gate, which is an important gate to evaluate the cost of a circuit. The CCNOT gate turns the state of the target qubit, where the state of both control qubits is $|1>$. If both $|x_1>$ and $|x_2>$ are $|1>$, it changes the value of $|x_3>$ in state $|0>$ into $|1>$, where $|x_3>$ is $|0>$.

2.2. Residue Number System

The Residue Number System (RNS) has been widely applied to efficient carry-free arithmetic operations in classical computers without the carry propagation problem [28,29,30]. RNS-based arithmetic modulo $2^n-1$ computation is one of the most common RNS operations that is used in pseudorandom number generation and various cryptographic algorithms [31,32]. The basic idea for modulo $2^n-1$ operation is to use the constant value $-(2^n-1)$ to be added by the sum of two numbers A and B, where the two inputs A and B are to be in the range $\left\{0,2^n-2\right\}$.

Given the two n-bit inputs $A=a_{n-1},\dots ,a_0$ and $B=b_{n-1},\dots ,b_0$, where $0\le A,B<2^n-1$, the modulo $2^n-1$ of $A+B$ can be represented as follows:

$$(A+B)mod(2^n-1)=\left\{\begin{array}{cc}A+B-(2^n-1),\hfill & if(A+B)>2^n\hfill \\ A+B,\hfill & otherwise.\hfill \end{array}\right.$$

(1)

The sum of A and B over binary system-based computation can be an $n+1$-bit output $C=c_n,c_{n-1},\dots ,c_0$ because of the carry. The most significant bit, $c_n$, saves the final carry of $a_{n-1}$ and $b_{n-1}$, where $(A+B)>2^n$, such as the first case in Equation (1). $A+B-2^n$ is equivalent to removing the most significant bit, $c_n$, from the bit sequence $C=c_n,c_{n-1},\dots ,c_0$, where $A+B-(2^n-1)=(A+B-2^n)+1$.

3. Quantum Modular Adder over $\mathit{GF}({\mathbf{2}}^{\mathit{n}}-\mathbf{1})$

We introduce our proposed quantum modular adder over Galois Field $GF(2^n-1)$. Quantum algorithms are usually presented as quantum circuits for better understanding. We also modeled the circuit $MA$ (modular adder) with $3n+1$ index register qubits in the proposed algorithm, as shown in Figure 7. The Modular Adder (MA) realizes $|c,a,b>\to |c^{\prime },a,(a+b)mod(2n-1)>$, where n-bit numbers $a,boverGF(2^n-1)$.

This MA achieves its function based on the classical RCA as a full adder for two numbers and a value of the final carry. If the value is 1, 1 is added into the interim calculation result of $(a+b)$, and the final carry is truncated. In comparison, the general modular full adder usually adds $2^n$, as shown in Figure 2. Specifically, c for carry is $|c_0>,|c_1>,...,|c_n>=|0>,|0>,\dots ,|0>$ with $n+1$ resister qubits. The two numbers $a=|a_0>,|a_1>,...,|a_{(n-1)}>$ and $b=|b_0>,|b_1>,...,|b_{(n-1)}>$ use n resister qubits each. After quantum computation of MA, the result $(a+b)mod{2}^n-1$ as $S=s_0,s_1,\dots ,s_{(n-1)}$ is the measured value for the register qubit $b=b_0,\dots ,b_{(n-1)}$.

The final carry, $|c_n^{\prime }>$, in Figure 10 is $s_n$ in Figure 8 as a flag to distinguish the case of specifications, but is truncated. The basic idea of our design with consideration of $s_n$ is based on the following specifications:

• If $s_n$ is 0 and the sum of $s_{(n-1)},...,s_0$ is not n, S represents $S=a+b$.
• If $s_n$ is 0 and the sum of $s_{(n-1)},...,s_0$ is n, S represents 0.
• If $s_n$ is 1, $a+b$ consists of $(n+1)$-bit and S is represented by Equation (2).

$$S:=(a+b)mod(2^n-1):=(a+b)-(2^n-1):=(a+b+1)-2^n$$

(2)

where a, b, and s consist of n bits $a_{n-1},\dots ,a_0,b_{n-1},\dots ,b0$, and $n+1$ bits $s_n,s_{n-1},...,s_0$, sequentially, and S is $(a+b)$ mod $2^n-1$.

In the first specification, the final carry $c_n$, called $s_n$, is zero because the sum of the two numbers does not exceed $2^n-1$. The idea to define the first specification is based on the fact that the number of bits that are 1 is always less than n. In the second specification, $s_n$ is also zero because the sum of them equals $2^n-1$. Because the remainder divided by $2^n-1$ is zero, there is no need for any operation except to set zero into the register b as the result $s_0,...,s_n-1$. The idea to define the second specification is based on the fact that every bit of $2^n-1$ is 1. In the third specification, the sum of the two numbers exceeds $2^n-1$, and $s_n$ is 1 because of the final carry. If the $s_n$ in register $c_n$ is 1, the result $s_0,...,s_n-1$ is calculated by Equation (2). Subtraction of $2^n$ in Equation (2) is just a bit truncation of $s_n$ without any operation, as shown in Figure 8 when $s_n=1$. Because there is the difference of 1 as a binary $0...01$ between $2^n$ and ${\sum }_{i=0}^{n-1}{2}^i$, 1 is added to S instead of truncating $s_n$. Such a subtraction strategy by truncation is one of the common methods to speed up the modular calculation [29]. Such $s_n$ is the flagship value to distinguish the above three cases before truncation. Compared to the RCA, our design does not store the final carry $s_n$. This means it is more efficient when adding two numbers over $GF(2^n-1)$.

Figure 9 shows the sub-modules FA (full adder), SZ (set zero), and AT (adder truncated) designed with an intuitive arrangement of the specification. The first module, FA, is the full adder based on the ripple carry adder for the first specification, in which the final carry $|c_n>$ as $s_n$ is 0, and the result is $a+b$. The second module, SZ, sets the register qubits $|b_i>(i=0,\dots ,n-1)$ to zero when $|c_n>$ is also 0 but all $|b_i>$ is 1 according to the second specification. The third module, AT, cuts out $|c_n>$ and adds 1 to $|b_0>$ when $|c_n>$ is 1 following the third specification. As a result, the output of the two numbers a and b over $GF(2^n-1)$ through the three-level modules is s over $GF(2^n-1)$ with $|s_i>$ measuring register $|b_i>$. Figure 10 shows the specific quantum circuit of the proposed quantum modular adder when n is 5.

Figure 11 shows the optimized circuit for Figure 9, which is an intuitive configuration of the proposed quantum circuit. Quantum circuits can be converted very effectively by an equivalence rule [33]. If a circuit, C, turned into an equivalent circuit, C’, by the rules, size(C’) is the same as O(size(C)). The converted circuit, C’, consists of the number of qubits and the result is the same as C, while having fewer gates and a different depth. Reconstruction of this quantum circuit by the equivalence rules increases the efficiency of the quantum circuit by reducing the number of gates and the depth.

The optimized quantum modular adder over $GF(2^n-1)$ in Figure 11 consists of the two submodules AT and FA with additional two NOT gates and two CNOT gates. The transposition of the two submodules and the four additional gates has the effect of replacing the second module SZ in Figure 9. Figure 12 shows a more detailed quantum circuit of the optimized quantum modular adder over $GF(2^n-1)$ at the unit gate level. Figure 13 shows a simple example of the quantum circuit when $n=5$ at the elementary gate level.

This optimized quantum modular adder will be very useful for quantum operations that require a full adder over $GF(2^n-1)$. For example, Cho et al. proposed an efficient classical quantum and quantum–quantum modular multiplication circuit over $GF\left(2^n\right)$ and $GF(2^n-1)$ [34]. Their multiplication circuit can be applied to any full adder, and they used QCLA focused on speed in their simulation. As described in the third paragraph of the introduction, our quantum modular adder was designed based on RCA for simplicity and cost. Applying our quantum modular adder to Cho’s quantum modular multiplication enables more efficient multiplication operations over $GF(2^n-1)$ than other RCA-based quantum additions.

4. Implementation and Results of the Simulation

To assess our quantum modular adder accuracy over $GF(2^n-1)$, we simulated a quantum circuit using IBM ProjectQ [35]. ProjectQ provides a full-stack software framework for writing and running the proposed quantum algorithms in Python as a high-level domain-specific language. It also provides the various back-ends, which run circuits on a simulator and quantum hardware, such as the default simulation back-end and the IBM Quantum Experience back-end. There are seven back-ends on quantum hardware, such as ibmqx2, ibmq_16_melbourne, ibmq_armonk, imbq_athens, ibmq_santiago, ibmq_lima, and ibmq_quito. The ibmq_16_melbourne has 15 qubits, the ibmq_armonk has one qubit, and others have five qubits, while the default simulation back-end can simulate numerous qubits. We used the default simulation back-end because we needed 16 qubits when $n=5$, as shown in

Table 1. Comparison of the quantum modular adders based on the ripple carry adder when n = 5.

Modular Adder	Qubits	CCNOT	Reduction rate of CCNOT	Depth	Reduction Rate of Depth
V-AM	22	90	-	148	-
C-AM	17	45	−50.0%	88	−40.5%
OurR	16	33	−63.3%	46	−68.9%
OurO	16	26	−71.1%	39	−73.6%

. Through this simulation, it was possible to confirm the accuracy when $n=5$ by measuring the register $|b_i>$ as a result $|s_i>(i=0,\dots ,n-1)$. For getting the circuits as one of the results based on this ProjectQ, the CircuitDrawer back-end instead of the default simulation back-end helped save and return the circuit by LaTeX code, as shown in Figure 10 and Figure 13.

We also evaluated the cost of the proposed quantum circuits. The cost for a quantum circuit mainly includes the number of qubits, the number of CCNOT gates, and the depth, which is the number of gates that can be run in parallel [36]. In all these measures, a lower value implies better performance and less cost.

Table 2. Comparison of the quantum modular adders based on the ripple carry adder.

Modular Adder	Qubits	CCNOT Gates	Depth	Circuit for $\mathbf{GF}(2^{\mathit{n}}-1)$	Simulation
V-AM	$4n+2$	$20n-10$	$30n-2$	Y	N
C-AM	$3n+2$	$10n-5$	$10n+38$	N	N
OurR	$3n+1$	$8n-7$	$10n-4$	Y	Y
OurO	$3n+1$	$6n-4$	$8n-1$	Y	Y

shows these for Cuccaro et al.’s adder-based modular adder called C-AM [37], Vedral et al.’s Adder-Mod, called V-AM [11], our referenced modular adder OurR in Figure 9, and our optimized modular adder OurO in Figure 11, respectively. Since there is no adder of Cuccaro et al. for modular $2^n-1$, we evaluated the C-AM by applying Cuccaro et al.’s adder to the sub-module $FA$ of Vedral et al.’s Adder-Mod, as shown in Figure 2. Our optimized modular adder OurO has the lowest complexity for the number of qubits, gates, and depth. The number of qubits for OurR and OurO is about n less than that of the C-AM or the V-AM. By comparison to the V-AM, the number of gates and the depth for OurR and OurO indeed appear much less. OurO has about $3.34$ and $1.67$ times lower gate than them, as well as has about $3.75$ and $1.25$ times lower depth than them. Figure 14 visually shows the number of qubits, gates, and depth for different $GF(2^n-1)$, where $n=1,\dots ,9$. If $n=5$, we can conclude the following, as listed in Table 1:

• The number of qubits for OurO was six qubits less than V-AM.
• The number of gates for OurO was 26 gates, showing a 71.1% decrease from V-AM.
• The depth for OurO was 39, showing a 73.6% decrease from V-AM.
• The cost dropped tremendously thanks to reducing the number of qubits, the number of gates, and the depth by the proposed quantum circuit.

5. Conclusions

We designed an efficient quantum modular adder algorithm for $GF(2^n-1)$ by utilizing the difference by one bit and one between $2n$ and ${\sum }_{i=0}^{n-1}{2}^i$. Because of these correlations, the modular operation for $2n-1$ was performed by truncating the n-th bit as a final carry and adding 1 to the remaining value. As a result, the proposed circuit of the quantum modular addition over $GF(2^n-1)$ reduced the number of gates and the depth compared to the existing circuits of quantum modular addition over $GF(2^n-1)$. In particular, in the case of $GF(2^5-1)$, which is one of the fields in multivariate quadratic-based post-quantum cryptography, the cost of the proposed circuit reduced the number of gates by 71.1% and the depth by 73.6%. These results show that the proposed circuit can be extended to multiplication, exponentiation, cumulative sum, and cumulative multiplication over $GF(2^n-1)$ and improve the efficiency of quantum information processing for data on $GF(2^n-1)$.