Control of a Robotic Swarm Formation to Track a Dynamic Target with Communication Constraints: Analysis and Simulation
Abstract
:1. Introduction
2. Problem Formulation
2.1. The General MOSL Problem
2.2. The Toy Problem Used in This Paper
- (1)
- a spatial term which decreases with the distance between target position and any position in the workspace; this is the inverse square law induced by mechanisms of conservation of power through propagation, modified with a constant additive term in the denominator to prevent the value from becoming unreasonably large when ;
- (2)
- a temporal term, representing a decay, inspired by the response to a first-order filter model parameterized by the time constant ;
- (3)
- an additive white Gaussian noise in the whole environment, with max, representing measurement noise.
3. Models
3.1. The PSO Algorithm
- (1)
- The previous speed vector of tracker , weighted by a constant coefficient . For the convergence of the algorithm, we need to have [44]. is homogeneous to a (pseudo) mass and is sometimes called “inertia” in the community.
- (2)
- The difference between the current position of tracker i and its best historical position noted ( “b” for “”). The best historical position is the position , with between time 0 and t where measure was the greatest. This component is weighted by a constant coefficient .
- (3)
- The difference between the position (“g” for “”) of the current swarm’s best tracker and the current position of tracker i. The position of the best tracker of swarm is the tracker j measuring the greatest among the N trackers of the swarm. This component is weighted by a constant coefficient .
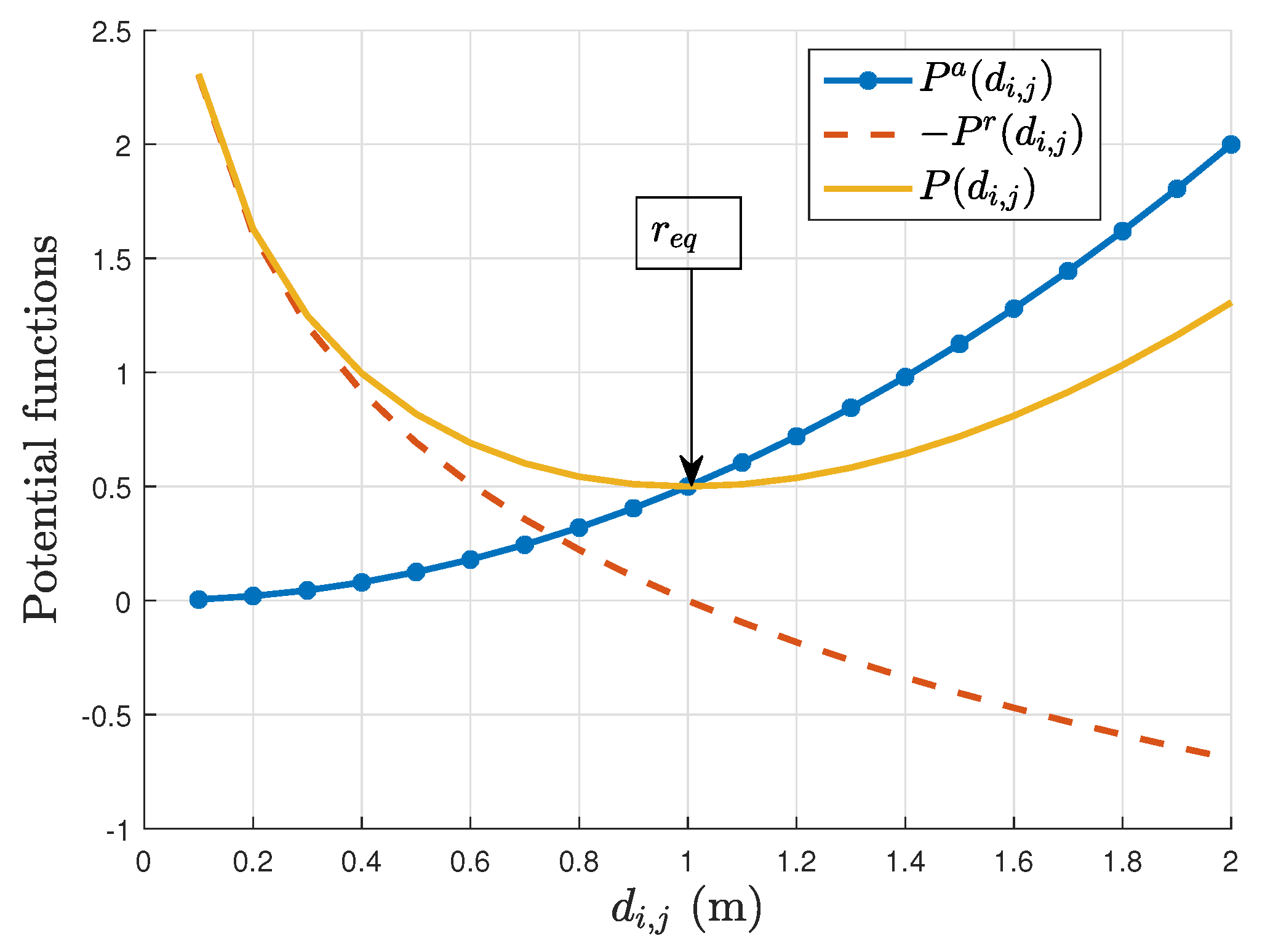
3.2. APF Theory and Flocking Principles
- is a non-negative function of the distance between agents i and j,
- is monotonically increasing in and its gradient is the highest when ,
- is monotonically increasing in and its gradient is the highest when ,
- is convex and even,
- attains its unique minimum when i and j are located at a desired distance .
3.3. PSO Formulated Using the APF Theory
3.4. The LCPSO Algorithm
3.4.1. Adding an Anti-Collision Behavior to PSO: CPSO
3.4.2. LCPSO, a CPSO Variant to Deal with Some Real-World Constraints
4. Analysis of the Properties of LCPSO
4.1. Metrics and Hypothesis
- Communication range is unlimited. As a result, the local-best attractor is the best tracker position of the swarm .
- We focus our efforts on the APF analysis, and to ease the analysis we set to 0. So the speed vector is updated only with the gradient descent of the potential field equation.
- The target’s behavior is not known from the swarm’s point of view and can be dynamic. Tracker i measures and adjusts its local-best position as a function of maximum measurement of the neighborhood. Since the communication range is small, we make the hypothesis that information exchange is instantaneous between the trackers and is limited to their position in absolute coordinates and their measurements, without noise.
4.2. Behavior of LCPSO
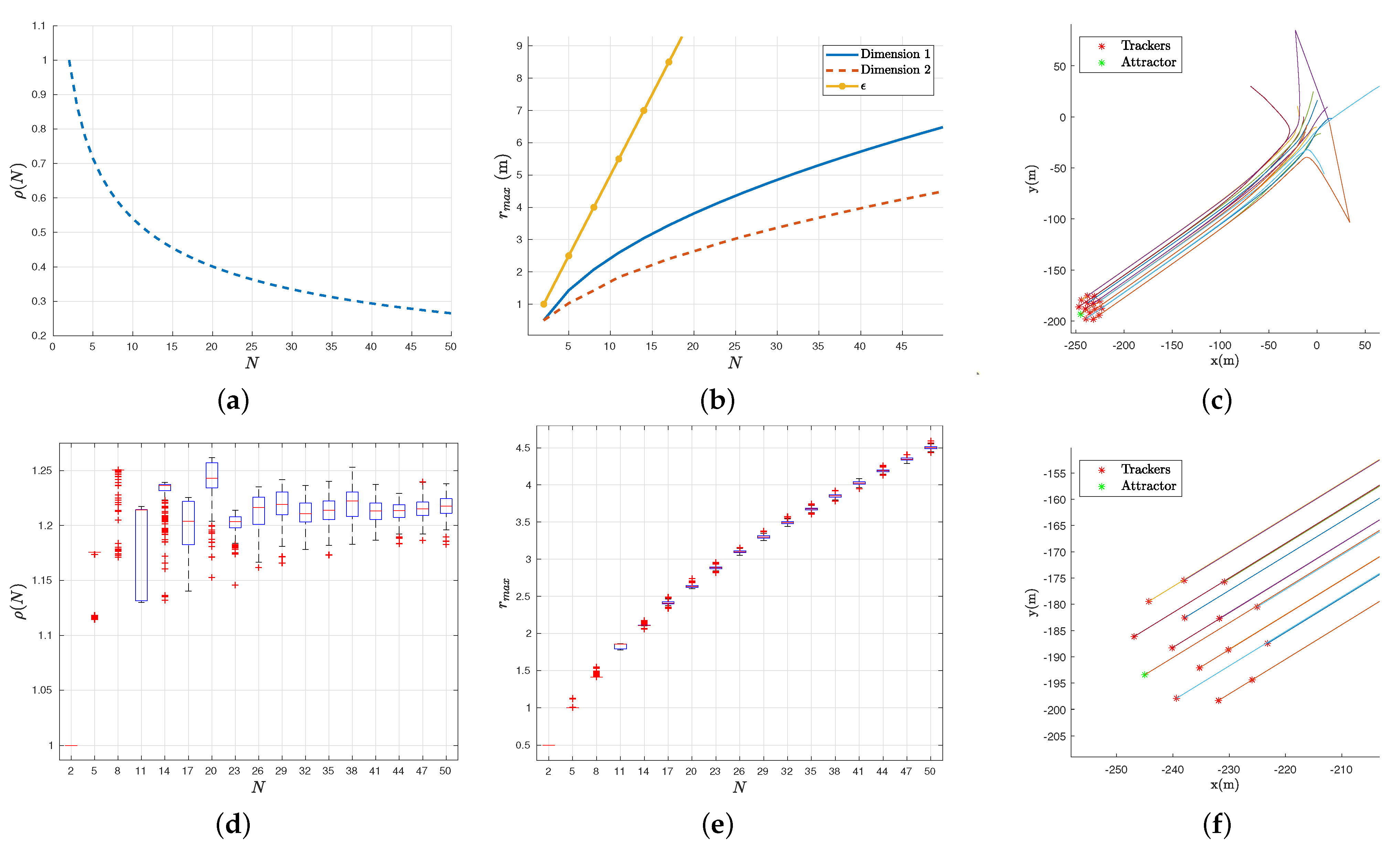
4.3. Analysis with Agents
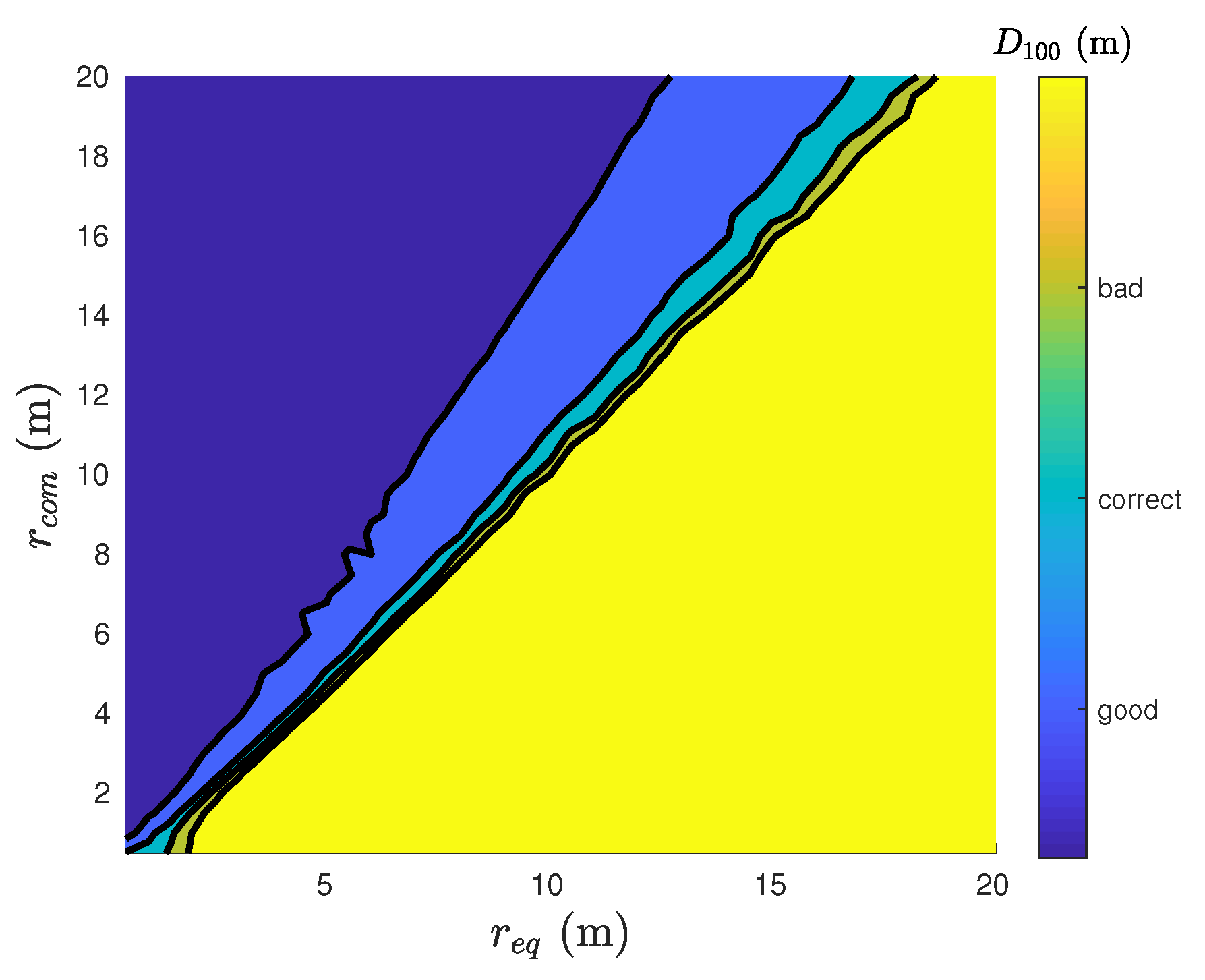
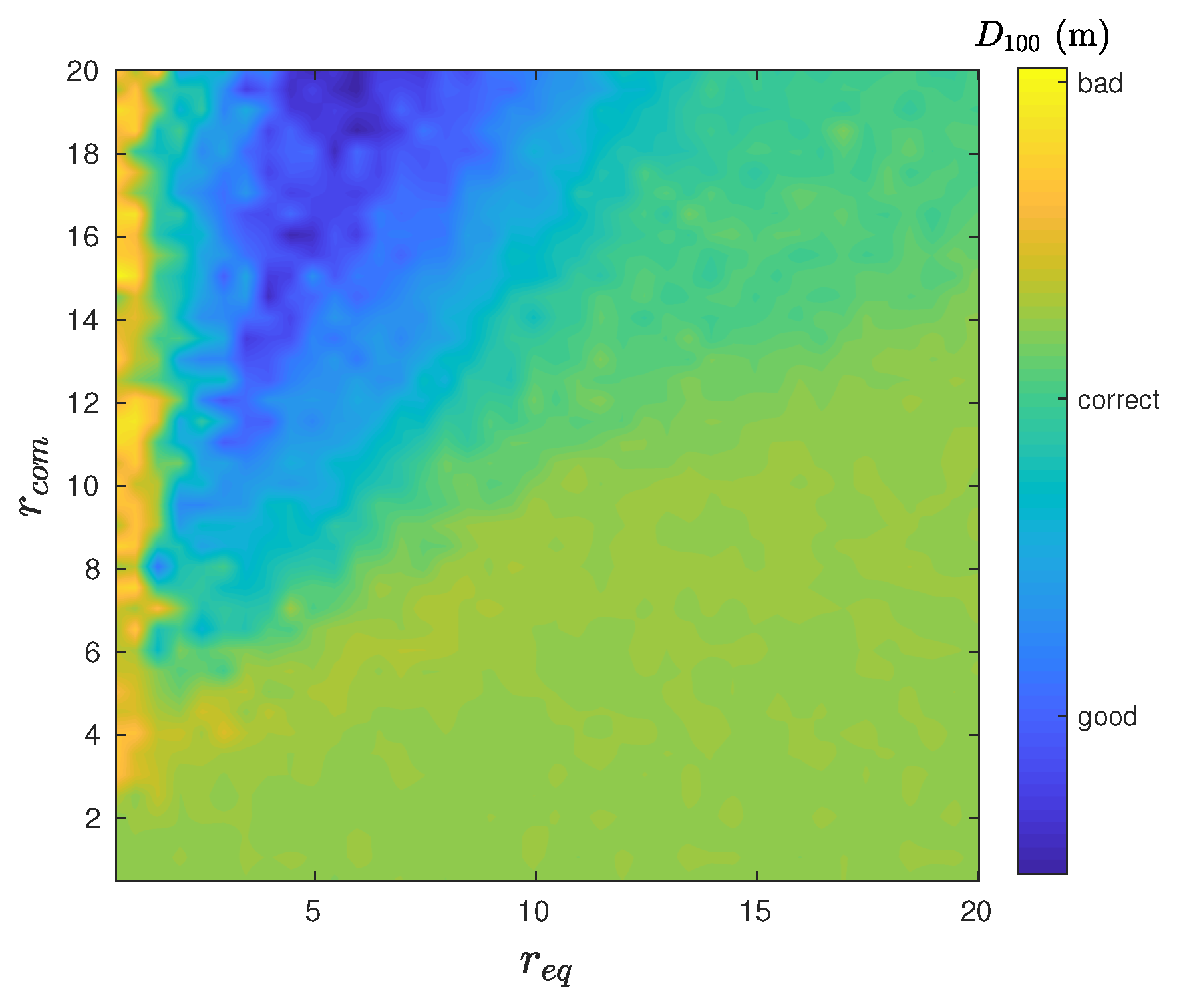
4.4. Swarm Stability
4.5. Symmetry and Robustness of the Swarm Formation
4.6. Removing the Simplifying Hypotheses
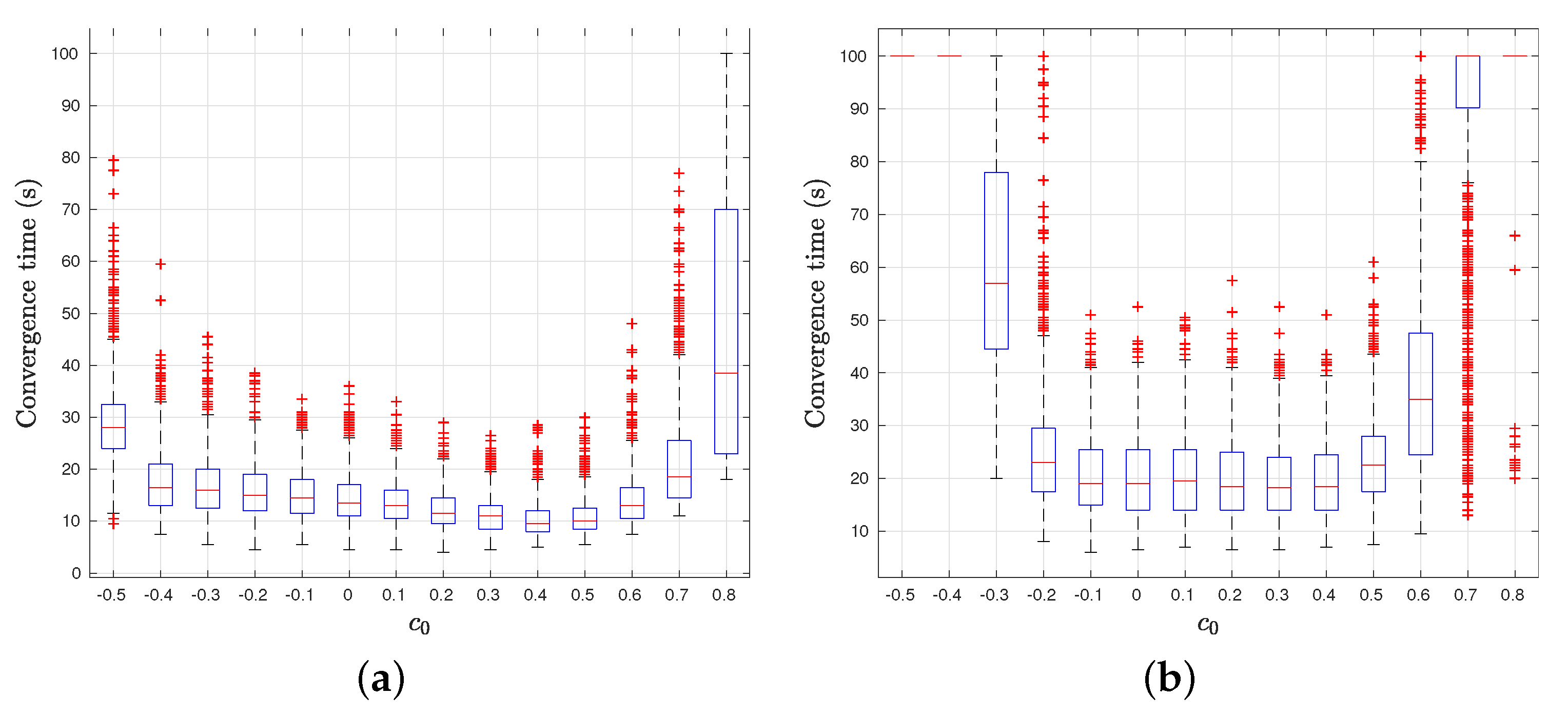
4.6.1. Non-Zero Mass
4.6.2. Communication Constraints
- Isolation of individuals: if, at any given time, one or more agents make bad choices, they may be unable to communicate with anyone, and consequently they will be unable to move following Equation (18).
- Emergence of subgroups: two opposite attractors in the group can lead to the fission of the group where all the agents are connected in two or more subgroups, so there is no more direct or indirect link between any agent i and j.
5. Results
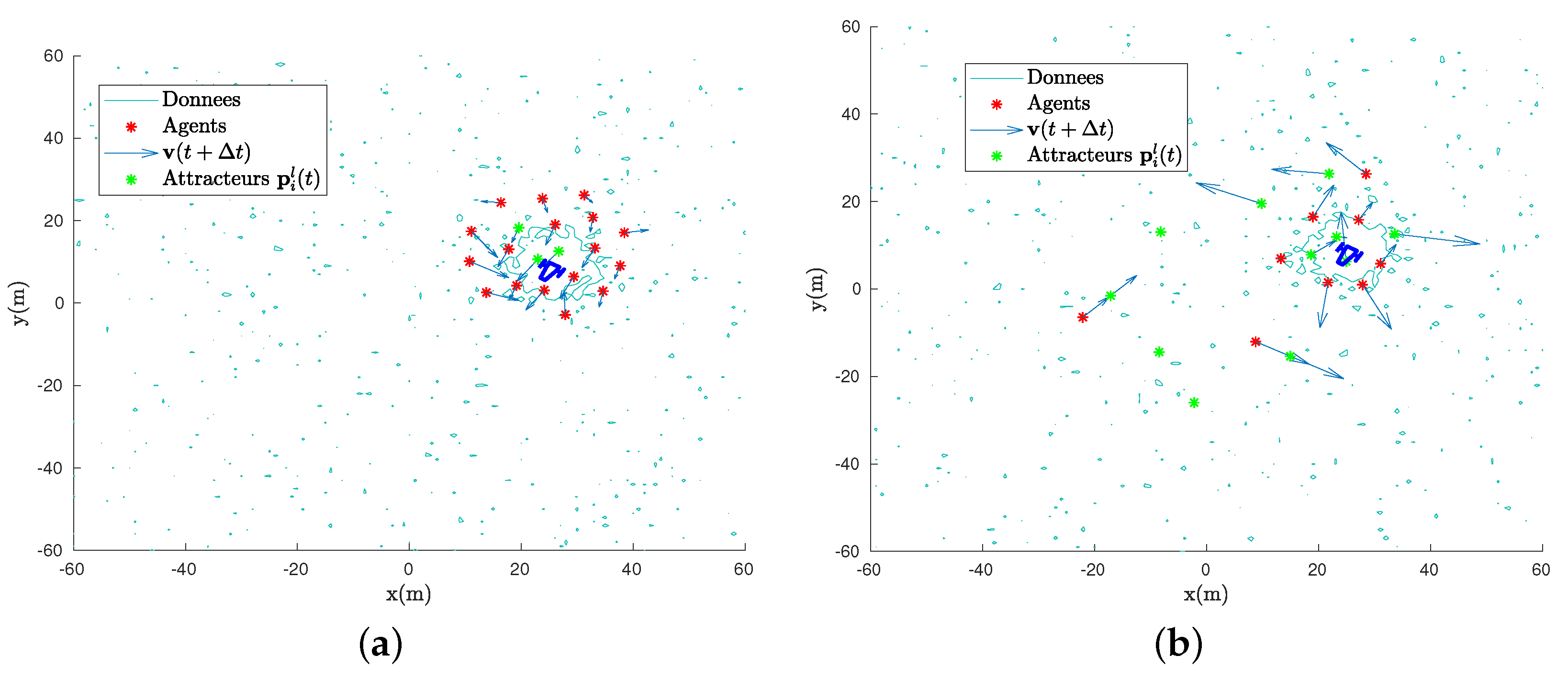
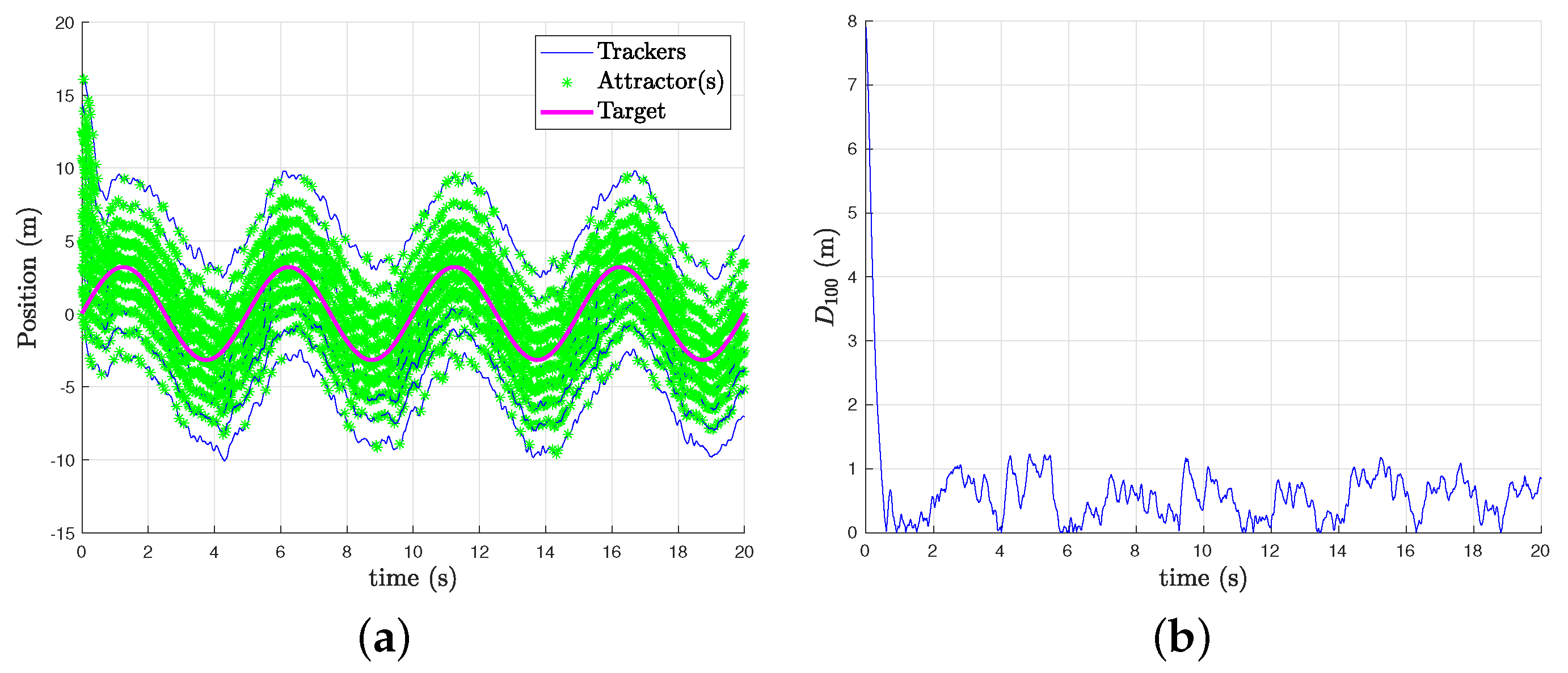
5.1. Dimension 1
5.2. Dimension 2
- The source follows an elliptical trajectory, centered on , with radius m and m and initial position at point . This choice is arbitrary, but the important thing is to see how the swarm reacts with violent heading changes, periodically coming back in the area that the agents are monitoring. The speed of the source oscillates between 2 and 4 m.s.
- The source has a constant trajectory, that is, a constant heading. It always starts from the point , with a speed of 3 m.s and a heading of 0.8 rad. The heading is chosen to cross the area monitored by our agents.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Sample Availability
Abbreviations
| ACO | Ant Colony optimisation |
| APF | Artificial Potential Field |
| CPSO | Charged Particle Swarm Optimization |
| LCPSO | Local Charged Particle Swarm Optimization |
| MOSL | Moving odor Source Localisation |
| OSL | Odor Source Localization |
| PSO | Particle Swarm Optimization |
| SAR | Search and Rescue |
| SLAM | Simultaneous Localization And Mapping |
| SNR | Signal-to-noise ratio |
| UAV | Unmanned Aerial Vehicles |
Appendix A. Proofs
References
- Gueron, S.; Levin, S.A.; Rubenstein, D. The Dynamics of Herds: From Individuals to Aggregations. J. Theoret. Biol. 1996, 182, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Camazine, S.; Franks, N.R.; Sneyd, J.; Bonabeau, E.; Deneubourg, J.L.; Theraula, G. Self-Organization in Biological Systems; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Ballerini, M.; Cabibbo, N.; Candelier, R.; Cavagna, A.; Cisbani, E.; Giardina, I.; Lecomte, V.; Orlandi, A.; Parisi, G.; Procaccini, A.; et al. Interaction Ruling Animal Collective Behaviour Depends on Topological rather than Metric Distance: Evidence from a Field Study. Proc. Natl. Acad. Sci. USA 2008, 105, 1232–1237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pitcher, T.J.; Wyche, C.J. Predator-avoidance behaviours of sand-eel schools: Why schools seldom split. In Predators and Prey in Fishes, Proceedings of the 3rd Biennial Conference on the Ethology and Behavioral Ecology of Fishes, Normal, IL, USA, 19–22 May 1981; Noakes, D.L.G., Lindquist, D.G., Helfman, G.S., Ward, J.A., Noakes, D.L.G., Lindquist, D.G., Helfman, G.S., Ward, J.A., Eds.; Springer: Dordrecht, The Netherlands, 1983; pp. 193–204. [Google Scholar]
- Lopez, U.; Gautrais, J.; Couzin, I.D.; Theraulaz, G. From behavioural analyses to models of collective motion in fish schools. Interface Focus 2012, 2, 693–707. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Bechinger, C.; Di Leonardo, R.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Choi, Y.P.; Perez, S.P. A Review on Attractive–Repulsive Hydrodynamics for Consensus in Collective Behavior. In Active Particles, Volume 1: Advances in Theory, Models, and Applications; Bellomo, N., Degond, P., Tadmor, E., Choi, Y.P., Eds.; Springer: Cham, Switzerland, 2017; pp. 259–298. [Google Scholar]
- Vásárhelyi, G.; Virágh, C.; Somorjai, G.; Nepusz, T.; Eiben, A.E.; Vicsek, T. Optimized flocking of autonomous drones in confined environments. Sci. Robot. 2018, 3, eaat3536. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, C.W. Flocks, Herds and Schools: A Distributed Behavioral Model. SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Tanner, H.G.; Jadbabaie, A.; Pappas, G.J. Stable flocking of mobile agents, Part I: Fixed topology. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No. 03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 2, pp. 2010–2015. [Google Scholar]
- Tanner, H.G.; Jadbabaie, A.; Pappas, G.J. Stable flocking of mobile agents, Part II: Dynamic topology. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No. 03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 2, pp. 2016–2021. [Google Scholar]
- Pugh, J.; Martinoli, A. Inspiring and Modeling Multi-Robot Search with Particle Swarm Optimization. In Proceedings of the 2007 IEEE Swarm Intelligence Symposium, Honolulu, HI, USA, 1–5 April 2007; pp. 332–339. [Google Scholar]
- Xue, S.; Zhang, J.; Zeng, J. Parallel asynchronous control strategy for target search with swarm robots. Int. J. Bio-Inspired Comput. 2009, 1, 151–163. [Google Scholar] [CrossRef]
- Liu, Z.; Xue, S.; Zeng, J.; Zhao, J.; Zhang, G. An evaluation of PSO-type swarm robotic search: Modeling method and controlling properties. In Proceedings of the 2010 International Conference on Networking, Sensing and Control (ICNSC), Chicago, IL, USA, 10–12 April 2010; pp. 360–365. [Google Scholar]
- La, H.M.; Sheng, W. Adaptive flocking control for dynamic target tracking in mobile sensor networks. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 4843–4848. [Google Scholar] [CrossRef]
- Kwa, H.L.; Leong Kit, J.; Bouffanais, R. Optimal Swarm Strategy for Dynamic Target Search and Tracking. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems, Auckland, New Zealand, 9–13 May 2020. [Google Scholar]
- Kumar, A.S.; Manikutty, G.; Bhavani, R.R.; Couceiro, M.S. Search and rescue operations using robotic darwinian particle swarm optimization. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 1839–1843. [Google Scholar]
- Marques, L.; Nunes, U.; de Almeida, A.T. Particle swarm-based olfactory guided search. Auton. Robot. 2006, 20, 277–287. [Google Scholar] [CrossRef] [Green Version]
- Jatmiko, W.; Sekiyama, K.; Fukuda, T. A PSO-based mobile robot for odor source localization in dynamic advection-diffusion with obstacles environment: Theory, simulation and measurement. IEEE Comput. Intell. Mag. 2007, 2, 37–51. [Google Scholar] [CrossRef]
- Jatmiko, W.; Pambuko, W.; Mursanto, P.; Muis, A.; Kusumoputro, B.; Sekiyama, K.; Fukuda, T. Localizing multiple odor sources in dynamic environment using ranged subgroup PSO with flow of wind based on open dynamic engine library. In Proceedings of the 2009 International Symposium on Micro-NanoMechatronics and Human Science, Nagoya, Japan, 8–11 November 2009; pp. 602–607. [Google Scholar]
- Sinha, A.; Kumar, R.; Kaur, R.; Mishra, R.K. Consensus-Based Odor Source Localization by Multiagent Systems under Resource Constraints. IEEE Trans. Cybern. 2019, 50, 3254–3263. [Google Scholar] [CrossRef] [PubMed]
- Fu, Z.; Chen, Y.; Ding, Y.; He, D. Pollution Source Localization Based on Multi-UAV Cooperative Communication. IEEE Access 2019, 7, 29304–29312. [Google Scholar] [CrossRef]
- Lu, Q.; Han, Q.L. A Probability Particle Swarm Optimizer with Information-Sharing Mechanism for Odor Source Localization. IFAC Proc. Vol. 2011, 44, 9440–9445. [Google Scholar] [CrossRef]
- Lu, Q.; Han, Q.; Xie, X.; Liu, S. A Finite-Time Motion Control Strategy for Odor Source Localization. IEEE Trans. Ind. Electron. 2014, 61, 5419–5430. [Google Scholar]
- Lu, Q.; Han, Q.; Liu, S. A Cooperative Control Framework for a Collective Decision on Movement Behaviors of Particles. IEEE Trans. Evol. Comput. 2016, 20, 859–873. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Yang, J.; Wang, X.; Bauer, P. Extended PSO Based Collaborative Searching for Robotic Swarms With Practical Constraints. IEEE Access 2019, 7, 76328–76341. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization—An Overview. Swarm Intell. 2007, 1. [Google Scholar] [CrossRef]
- Zarzhitsky, D.; Spears, D.; Thayer, D. Experimental studies of swarm robotic chemical plume tracing using computations fluid dynamics simulations. Int. J. Intell. Comput. Cybern. 2010, 3. [Google Scholar] [CrossRef] [Green Version]
- Farrell, J.; Murlis, J.; Long, X.; Li, W.; Cardé, R. Filament-Based Atmospheric Dispersion Model to Achieve Short Time-Scale Structure of Odor Plumes. Environ. Fluid Mech. 2002, 2, 143–169. [Google Scholar] [CrossRef]
- Hettiarachchi, S.; Spears, W.M. Distributed adaptive swarm for obstacle avoidance. Int. J. Intell. Comput. Cybern. 2009, 2, 644–671. [Google Scholar] [CrossRef]
- Liu, A.H.; Bunn, J.J.; Chandy, K.M. Sensor networks for the detection and tracking of radiation and other threats in cities. In Proceedings of the 10th ACM/IEEE International Conference on Information Processing in Sensor Networks, Chicago, IL, USA, 12–14 April 2011; pp. 1–12. [Google Scholar]
- Liu, Z.; Smith, P.; Park, T.; Trindade, A.A.; Hui, Q. Automated Contaminant Source Localization in Spatio-Temporal Fields: A Response Surface and Experimental Design Approach. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 569–583. [Google Scholar] [CrossRef]
- Briñon Arranz, L. Cooperative Control Design for a Fleet of AUVs under Communication Constraints. Ph.D. Thesis, Université de Grenoble, Saint-Martin-d’Hères, France, 2011. [Google Scholar]
- Tian, Y.; Li, W.; Zhang, F. Moth-inspired plume tracing via autonomous underwater vehicle with only a pair of separated chemical sensors. In Proceedings of the OCEANS 2015—MTS/IEEE, Washington, DC, USA, 19–22 October 2015; pp. 1–8. [Google Scholar]
- Lochmatter, T. Bio-Inspired and Probabilistic Algorithms for Distributed Odor Source Localization Using Mobile Robots. Ph.D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 2010; p. 135. [Google Scholar]
- Mogilner, A.; Edelstein-Keshet, L.; Bent, L.; Spiros, A. Mutual interactions, potentials, and individual distance in a social aggregation. J. Math. Biol. 2003, 47, 353–389. [Google Scholar] [CrossRef] [PubMed]
- Gazi, V.; Passino, K.M. Swarm Stability and Optimization, 1st ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Coquet, C.; Aubry, C.; Arnold, A.; Bouvet, P. A Local Charged Particle Swarm Optimization to track an underwater mobile source. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Stojanovic, M.; Beaujean, P.P.J. Acoustic Communication. In Springer Handbook of Ocean Engineering; Dhanak, M.R., Xiros, N.I., Eds.; Springer: Cham, Switzerland, 2016; pp. 359–386. [Google Scholar]
- Hosseinzadeh, M. Chapter 22—UAV geofencing: Navigation of UVAs in constrained environments. In Unmanned Aerial Systems; Koubaa, A., Azar, A.T., Eds.; Advances in Nonlinear Dynamics and Chaos (ANDC); Academic Press: Cambridge, MA, USA, 2021; pp. 567–594. [Google Scholar] [CrossRef]
- Chen, X.; Huang, J. Odor source localization algorithms on mobile robots: A review and future outlook. Robot. Auton. Syst. 2019, 112, 123–136. [Google Scholar] [CrossRef]
- Cleghorn, C.W.; Engelbrecht, A.P. Particle swarm stability: A theoretical extension using the non-stagnate distribution assumption. Swarm Intell. 2018, 12, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Van Den Bergh, F. An Analysis of Particle Swarm Optimizers. Ph.D. Thesis, University of Pretoria South Africa, Pretoria, South Africa, 2002. [Google Scholar]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef] [Green Version]
- Borzì, A.; Wongkaew, S. Modeling and control through leadership of a refined flocking system. Math. Model. Methods Appl. Sci. 2015, 25, 255–282. [Google Scholar] [CrossRef]
- Jaulin, L. Mobile Robotics; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Soares, G.L.; Arnold-Bos, A.; Jaulin, L.; Maia, C.A.; Vasconcelos, J.A. An Interval-Based Target Tracking Approach for Range-Only Multistatic Radar. IEEE Trans. Magn. 2008, 44, 1350–1353. [Google Scholar] [CrossRef]
Samples of the compounds are available from the authors. |


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coquet, C.; Arnold, A.; Bouvet, P.-J. Control of a Robotic Swarm Formation to Track a Dynamic Target with Communication Constraints: Analysis and Simulation. Appl. Sci. 2021, 11, 3179. https://doi.org/10.3390/app11073179
Coquet C, Arnold A, Bouvet P-J. Control of a Robotic Swarm Formation to Track a Dynamic Target with Communication Constraints: Analysis and Simulation. Applied Sciences. 2021; 11(7):3179. https://doi.org/10.3390/app11073179
Chicago/Turabian StyleCoquet, Charles, Andreas Arnold, and Pierre-Jean Bouvet. 2021. "Control of a Robotic Swarm Formation to Track a Dynamic Target with Communication Constraints: Analysis and Simulation" Applied Sciences 11, no. 7: 3179. https://doi.org/10.3390/app11073179
APA StyleCoquet, C., Arnold, A., & Bouvet, P.-J. (2021). Control of a Robotic Swarm Formation to Track a Dynamic Target with Communication Constraints: Analysis and Simulation. Applied Sciences, 11(7), 3179. https://doi.org/10.3390/app11073179






