Robust Quadrotor Control through Reinforcement Learning with Disturbance Compensation
Abstract
1. Introduction
2. Preliminary Information
2.1. Quadrotor Dynamic Model
2.2. Reinforcement Learning
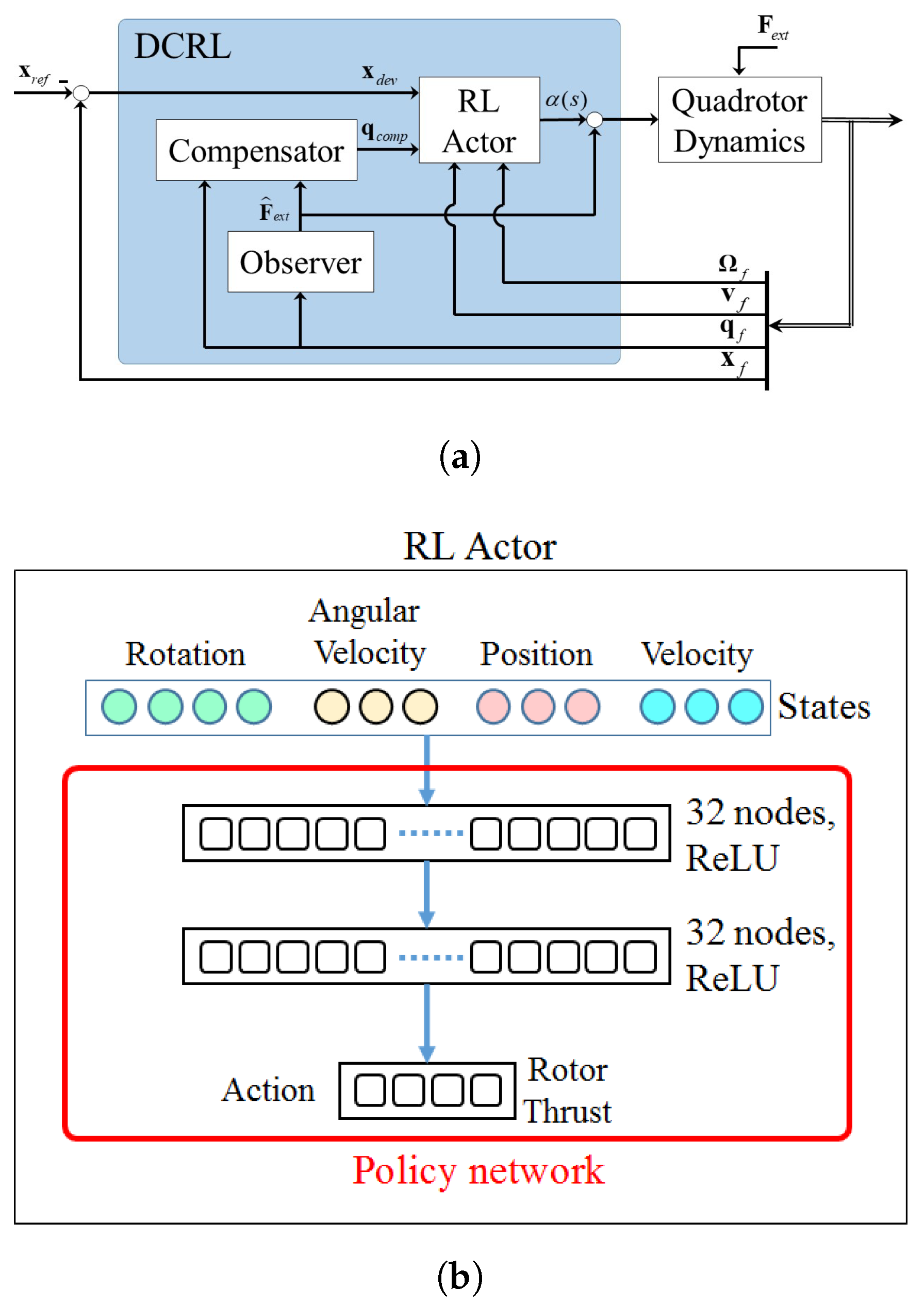
3. Disturbance Observation and Control Strategy
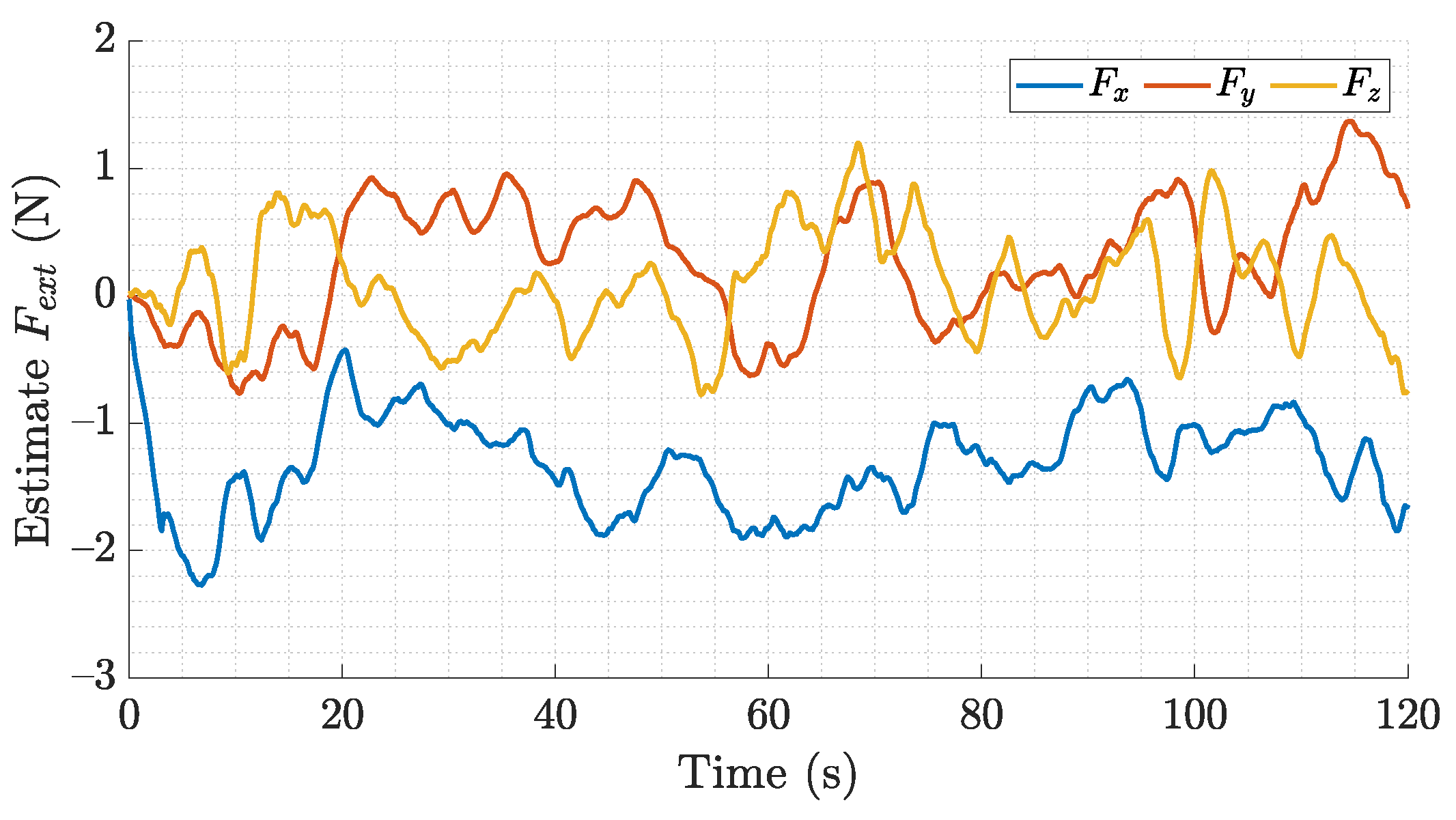
3.1. Disturbance Observer
3.2. Disturbance Compensator
4. Experiments
4.1. RL Controller Training
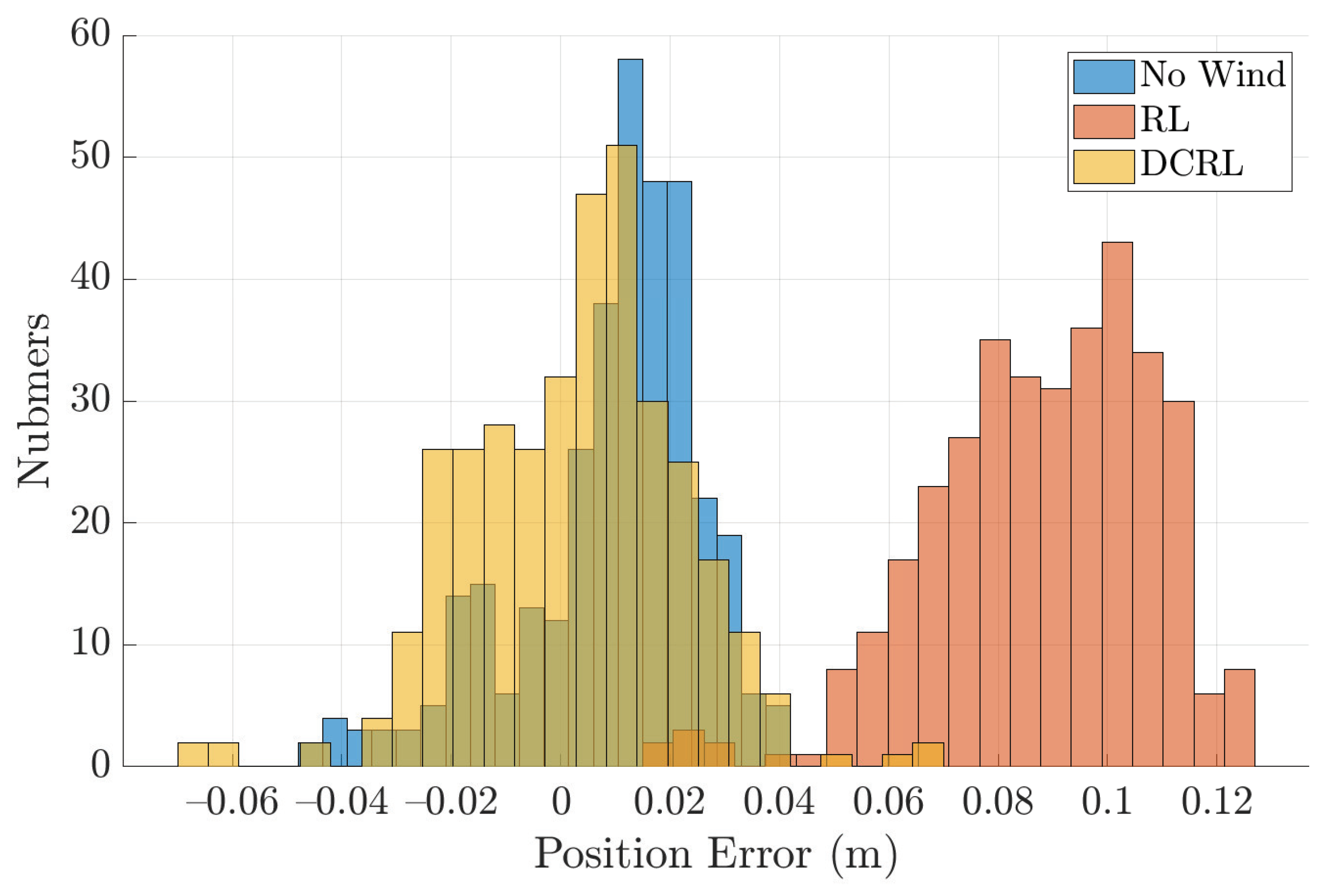
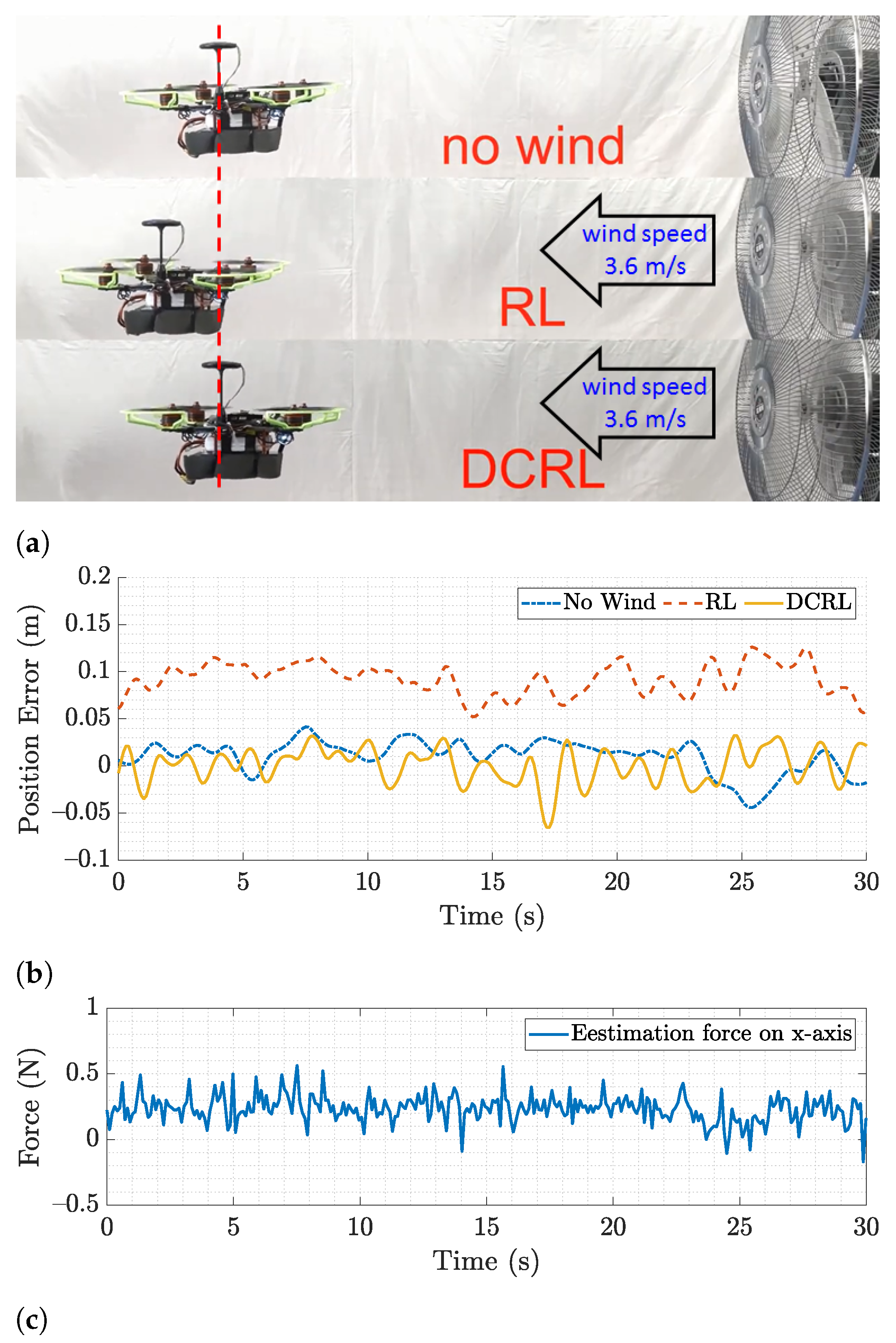
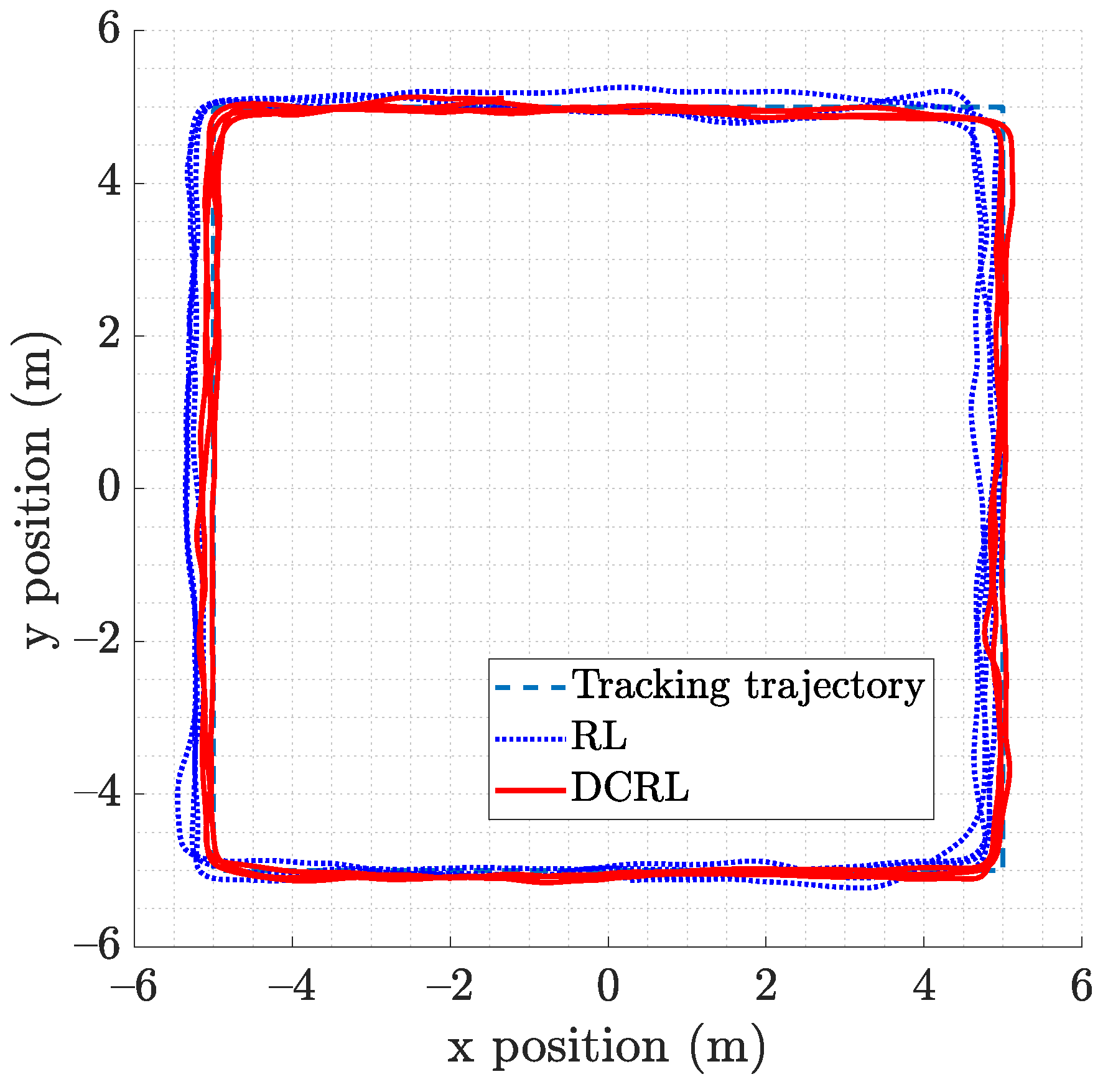
4.2. Results of the Indoor Experiment
4.3. Results of the Outdoor Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bouabdallah, S.; Noth, A.; Siegwart, R. PID vs. LQ control techniques applied to an indoor micro quadrotor. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2451–2456. [Google Scholar]
- Lee, D.; Kim, H.J.; Sastry, S.S. Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter. Int. J. Control. Autom. Syst. 2009, 7, 419–428. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances. Control Eng. Pract. 2011, 19, 1195–1207. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude and position experimental studies. IET Control Theory Appl. 2012, 6, 1812–1827. [Google Scholar] [CrossRef]
- Lee, T. Robust Adaptive Attitude Tracking on ${SO}(3)$ With an Application to a Quadrotor UAV. IEEE Trans. Control Syst. Technol. 2013, 21, 1924–1930. [Google Scholar]
- Wang, H.; Ye, X.; Tian, Y.; Zheng, G.; Christov, N. Model-free–based terminal SMC of quadrotor attitude and position. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2519–2528. [Google Scholar] [CrossRef]
- Xu, B. Composite Learning Finite-Time Control With Application to Quadrotors. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1806–1815. [Google Scholar] [CrossRef]
- Xu, R.; Özgüner, Ü. Sliding Mode Control of a Quadrotor Helicopter. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4957–4962. [Google Scholar]
- Dydek, Z.T.; Annaswamy, A.M.; Lavretsky, E. Adaptive Control of Quadrotor UAVs: A Design Trade Study with Flight Evaluations. IEEE Trans. Control Syst. Technol. 2013, 21, 1400–1406. [Google Scholar] [CrossRef]
- Zou, Y.; Meng, Z. Immersion and Invariance-Based Adaptive Controller for Quadrotor Systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2288–2297. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, W.; Zuo, Z.; Zhong, Y. Robust control for quadrotors with multiple time-varying uncertainties and delays. IEEE Trans. Ind. Electron. 2016, 64, 1303–1312. [Google Scholar] [CrossRef]
- Chovancova, A.; Fico, T.; Hubinský, P.; Duchon, F. Comparison of various quaternion-based control methods applied to quadrotor with disturbance observer and position estimator. Robot. Auton. Syst. 2016, 79, 87–98. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Xu, L.X.; Ma, H.J.; Guo, D.; Xie, A.H.; Song, D.L. Backstepping sliding-mode and cascade active disturbance rejection control for a quadrotor UAV. IEEE/ASME Trans. Mechatronics 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, L.; Xia, Y.; Yuan, Y. Active Disturbance Rejection Attitude Control for a Dual Closed-Loop Quadrotor Under Gust Wind. IEEE Trans. Control Syst. Technol. 2018, 26, 1400–1405. [Google Scholar] [CrossRef]
- Besnard, L.; Shtessel, Y.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Chen, F.; Lei, W.; Zhang, K.; Tao, G.; Jiang, B. A novel nonlinear resilient control for a quadrotor UAV via backstepping control and nonlinear disturbance observer. Nonlinear Dyn. 2016, 85, 1281–1295. [Google Scholar] [CrossRef]
- McKinnon, C.D.; Schoellig, A.P. Unscented external force and torque estimation for quadrotors. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5651–5657. [Google Scholar]
- Smolyanskiy, N.; Kamenev, A.; Smith, J.; Birchfield, S. Toward low-flying autonomous MAV trail navigation using deep neural networks for environmental awareness. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 4241–4247. [Google Scholar]
- Greatwood, C.; Richards, A. Reinforcement learning and model predictive control for robust embedded quadrotor guidance and control. Auton. Robot. 2019, 1–13. [Google Scholar] [CrossRef]
- Hwangbo, J.; Sa, I.; Siegwart, R.; Hutter, M. Control of a quadrotor with reinforcement learning. IEEE Robot. Autom. Lett. 2017, 2, 2096–2103. [Google Scholar] [CrossRef]
- Pi, C.H.; Hu, K.C.; Cheng, S.; Wu, I.C. Low-level autonomous control and tracking of quadrotor using reinforcement learning. Control Eng. Pract. 2020, 95, 104222. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; He, H.; Sun, C. Deterministic Policy Gradient With Integral Compensator for Robust Quadrotor Control. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3713–3725. [Google Scholar] [CrossRef]
- Tomić, T.; Ott, C.; Haddadin, S. External wrench estimation, collision detection, and reflex reaction for flying robots. IEEE Trans. Robot. 2017, 33, 1467–1482. [Google Scholar] [CrossRef]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 2000; pp. 1057–1063. [Google Scholar]
- Degris, T.; White, M.; Sutton, R.S. Off-Policy Actor-Critic. arXiv 2012, arXiv:1205.4839. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction. IEEE Trans. Neural Netw. 1988, 16, 285–286. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]



| Weight (g) | (kgm) |
|---|---|
| 665 |
| RMSE (m) | RMSE (m) | RMSE (m) | ||
|---|---|---|---|---|
| Indoor | RL | 0.08 | 0.04 | 0.02 |
| DCRL | 0.02 | 0.06 | 0.02 | |
| Outdoor | RL | 0.80 | 0.46 | 0.17 |
| DCRL | 0.45 | 0.41 | 0.07 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pi, C.-H.; Ye, W.-Y.; Cheng, S. Robust Quadrotor Control through Reinforcement Learning with Disturbance Compensation. Appl. Sci. 2021, 11, 3257. https://doi.org/10.3390/app11073257
Pi C-H, Ye W-Y, Cheng S. Robust Quadrotor Control through Reinforcement Learning with Disturbance Compensation. Applied Sciences. 2021; 11(7):3257. https://doi.org/10.3390/app11073257
Chicago/Turabian StylePi, Chen-Huan, Wei-Yuan Ye, and Stone Cheng. 2021. "Robust Quadrotor Control through Reinforcement Learning with Disturbance Compensation" Applied Sciences 11, no. 7: 3257. https://doi.org/10.3390/app11073257
APA StylePi, C.-H., Ye, W.-Y., & Cheng, S. (2021). Robust Quadrotor Control through Reinforcement Learning with Disturbance Compensation. Applied Sciences, 11(7), 3257. https://doi.org/10.3390/app11073257






