A Geometrical Structure-Based New Approach for City Logistics System Planning with Cargo Bikes and Its Application for the Shopping Malls of Budapest
Abstract
:Featured Application
Abstract
1. Introduction
- Materials and Methods: use of cargo bikes in city logistics systems—presentation of existing cargo bike projects, previous research experiences, data analysis for Budapest regarding the possible city logistics use of cargo bikes, the simulation model of the examined city logistics system, and results of the simulation.
- Results: the theoretical geometrical model and its application for Budapest—presentation of the related urban structures, the theoretical, the symmetrical, and the real geometrical model with graph theory-based notation and its application for Budapest.
- Discussion and future research—discussion of the results and presentation of the next steps of the research, highlighting the analysis of the reference geometrical structure and the development of a multicriterial ranking model for decision support.
- Conclusions—summary of the paper and its conclusions.
2. Materials and Methods: Use of Cargo Bikes in City Logistics Systems
2.1. Existing City Logistics Systems with Cargo Bikes
2.2. Summary of Research on Cargo Bikes
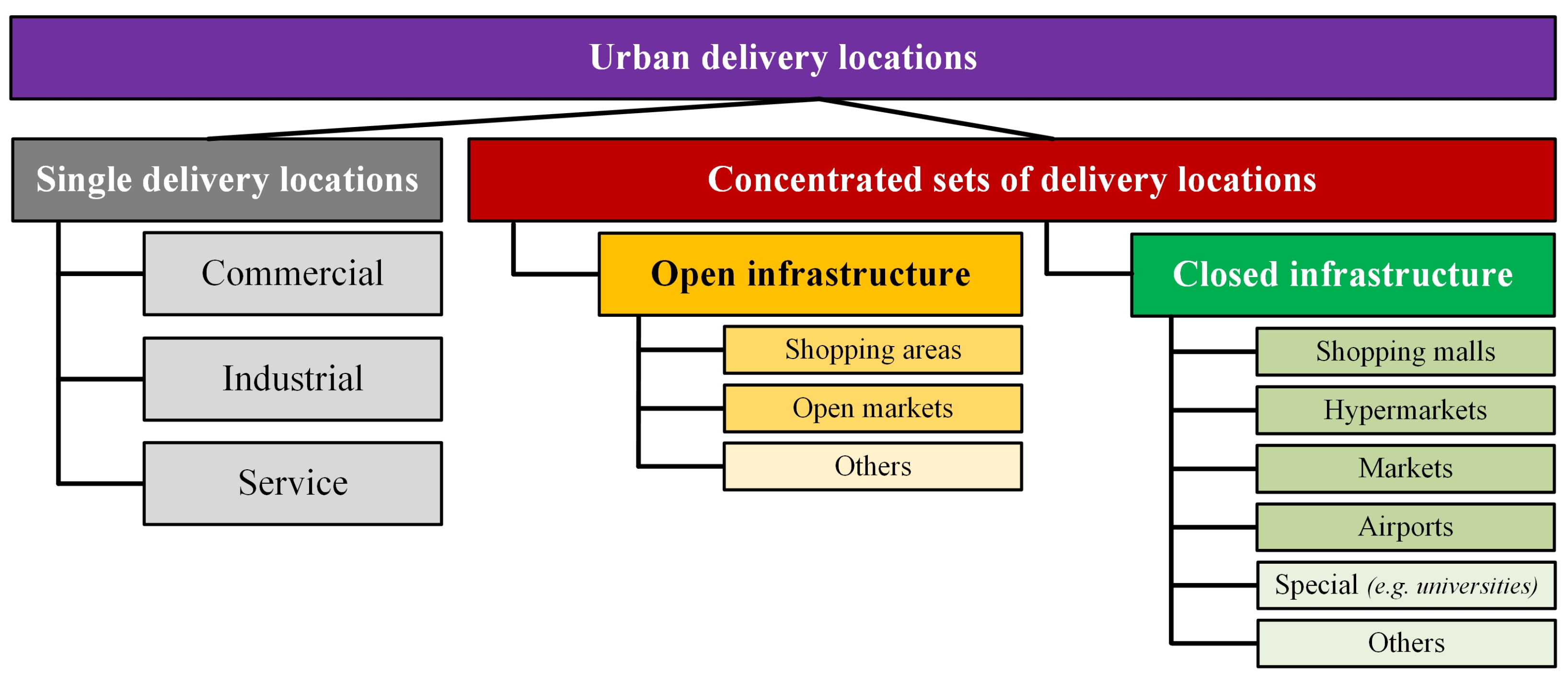
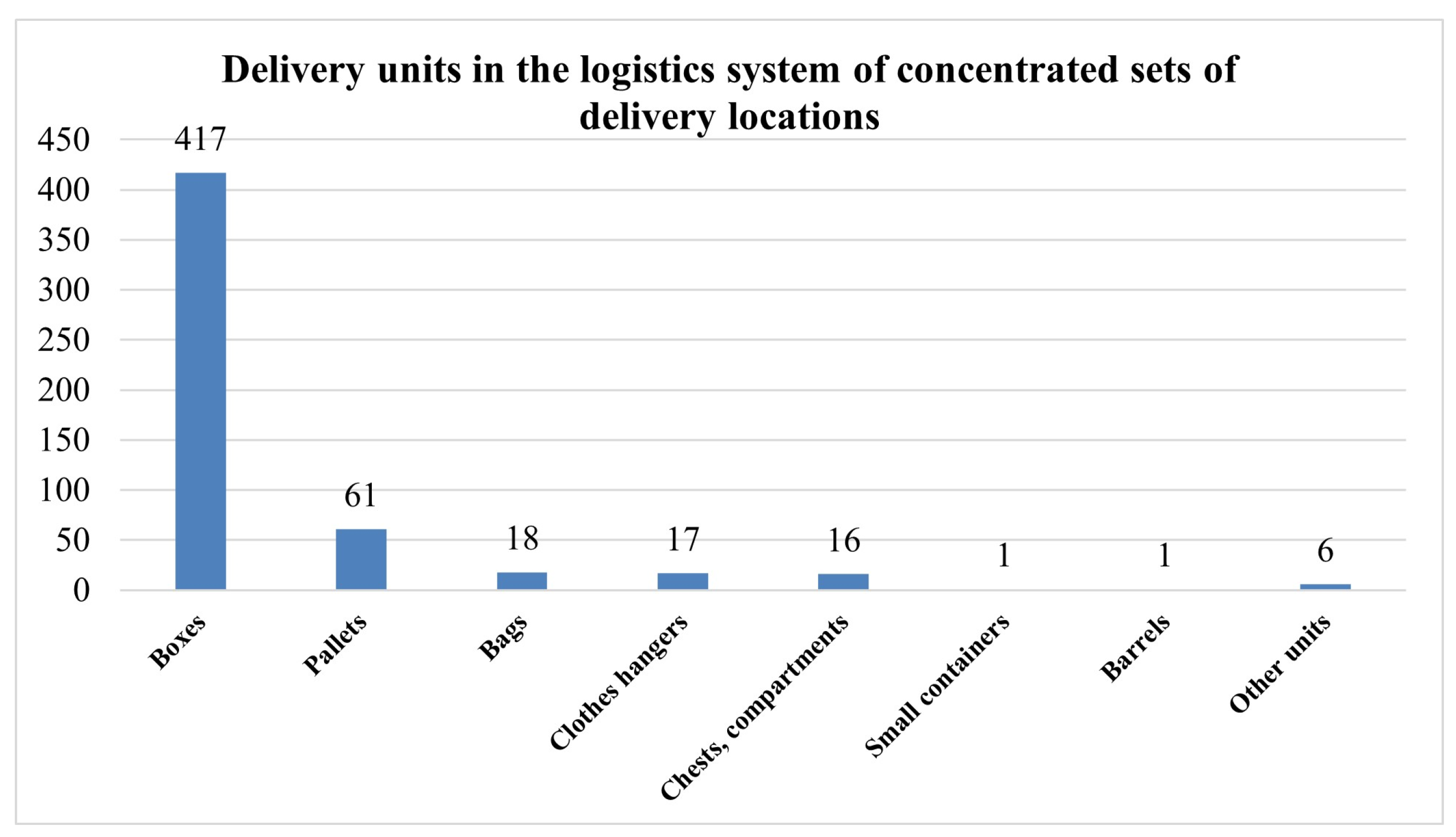
2.3. Possible Use of Cargo Bikes in the City Logistics System of Concentrated Sets of Delivery Locations in Budapest
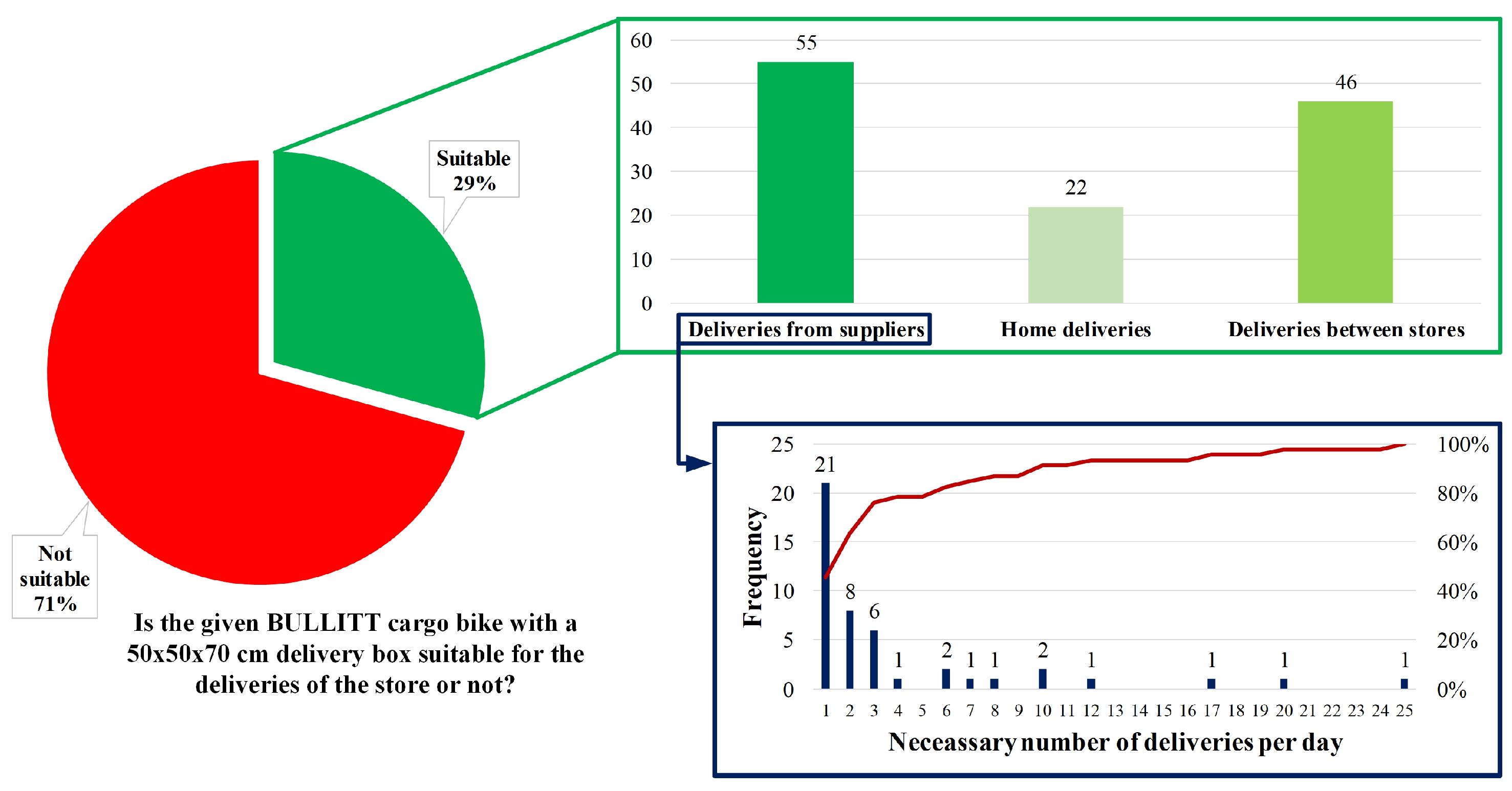
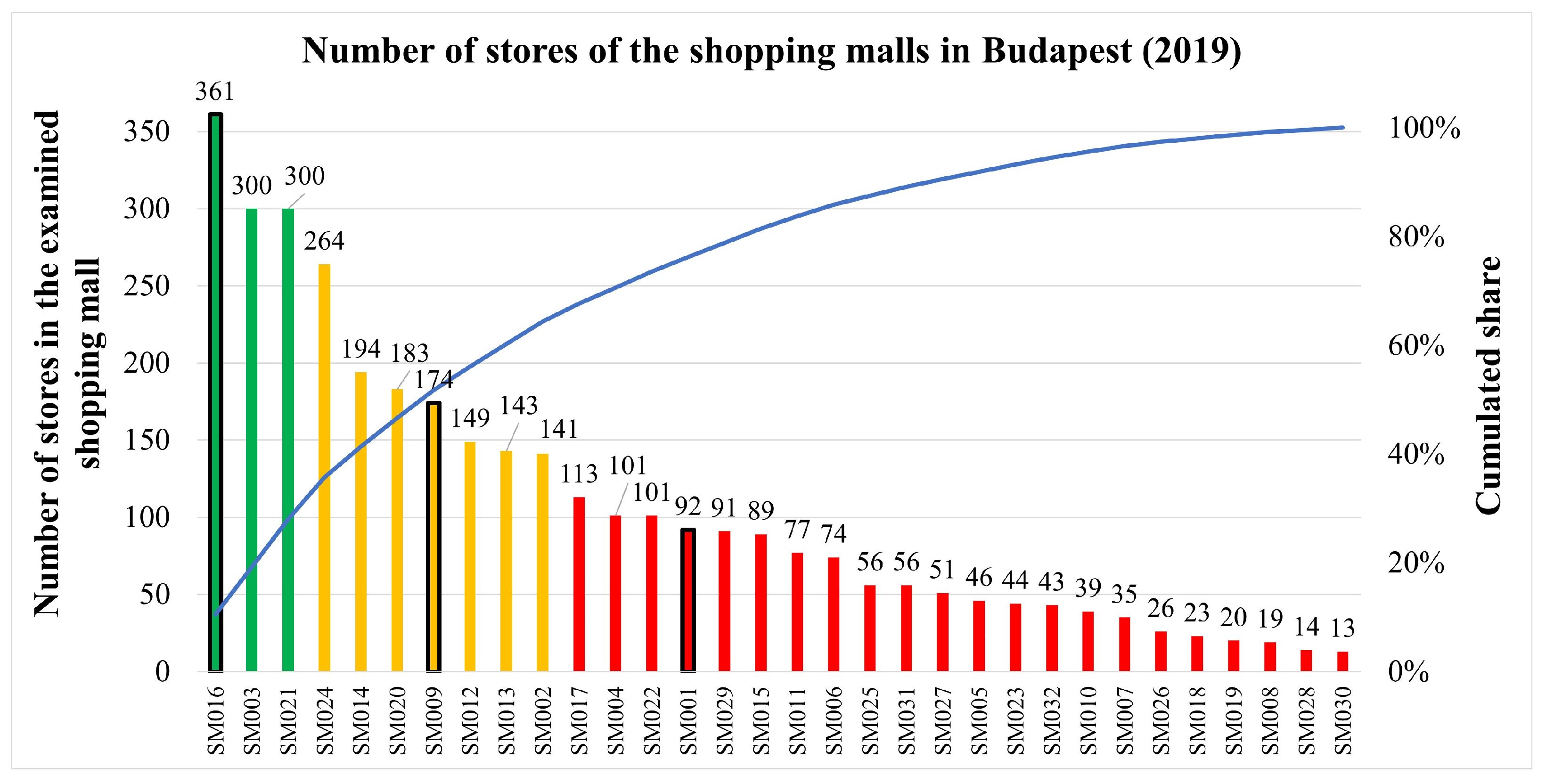
2.4. Application of Cargo Bikes in the City Logistics System of Shopping Malls in a Geometrical Model-Based Approach
- Category A: shopping malls with a big number of stores, mostly smaller stores with smaller demands. Their demands are expected to be served easily by cargo bikes.
- Category B: shopping malls with a middle number of stores, mostly stores with a bigger floor area and bigger demands. Their demands are expected more challenging to be handled by cargo bikes, but still, a significant share of the stores can be served by them.
- Category C: shopping malls with a low number of stores, most stores with a bigger floor area and bigger demands. Their demands are expected to be more challenging to be handled by cargo bikes, but there is still a share of the stores which could be served by them.
3. Results: The Theoretical Geometrical Model and Its Application for Budapest
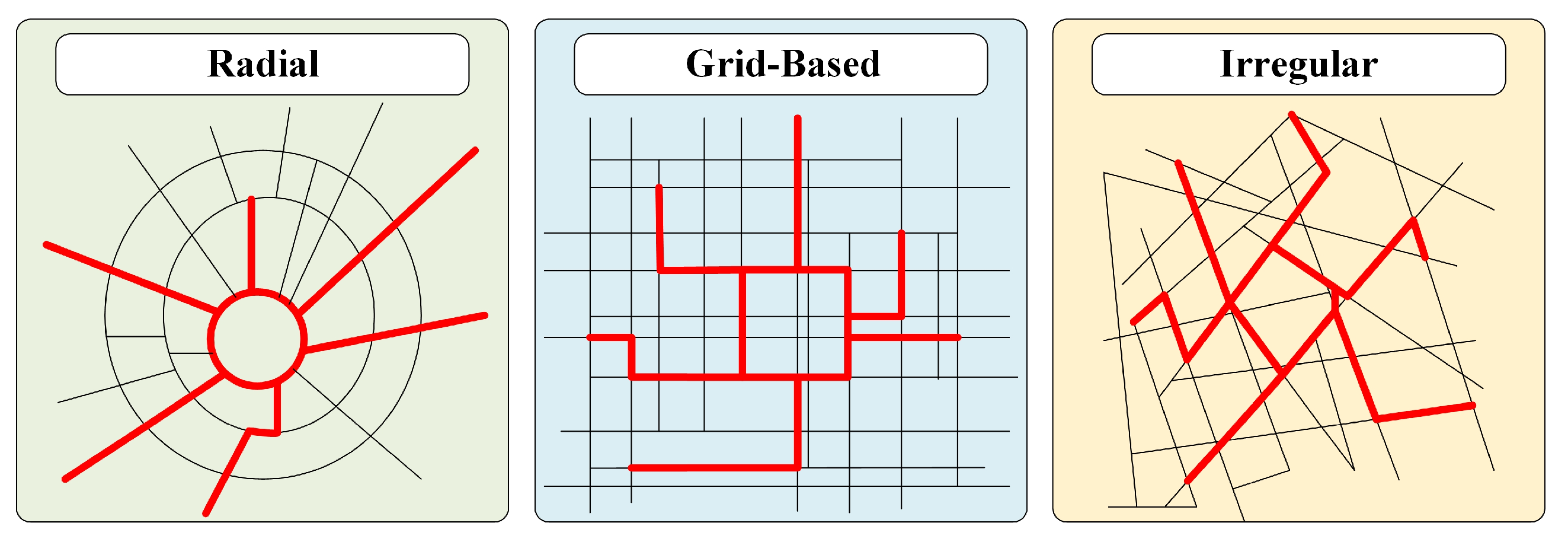
3.1. Urban Structures
- irregular structure,
- grid-based structure, and
- radial structure.
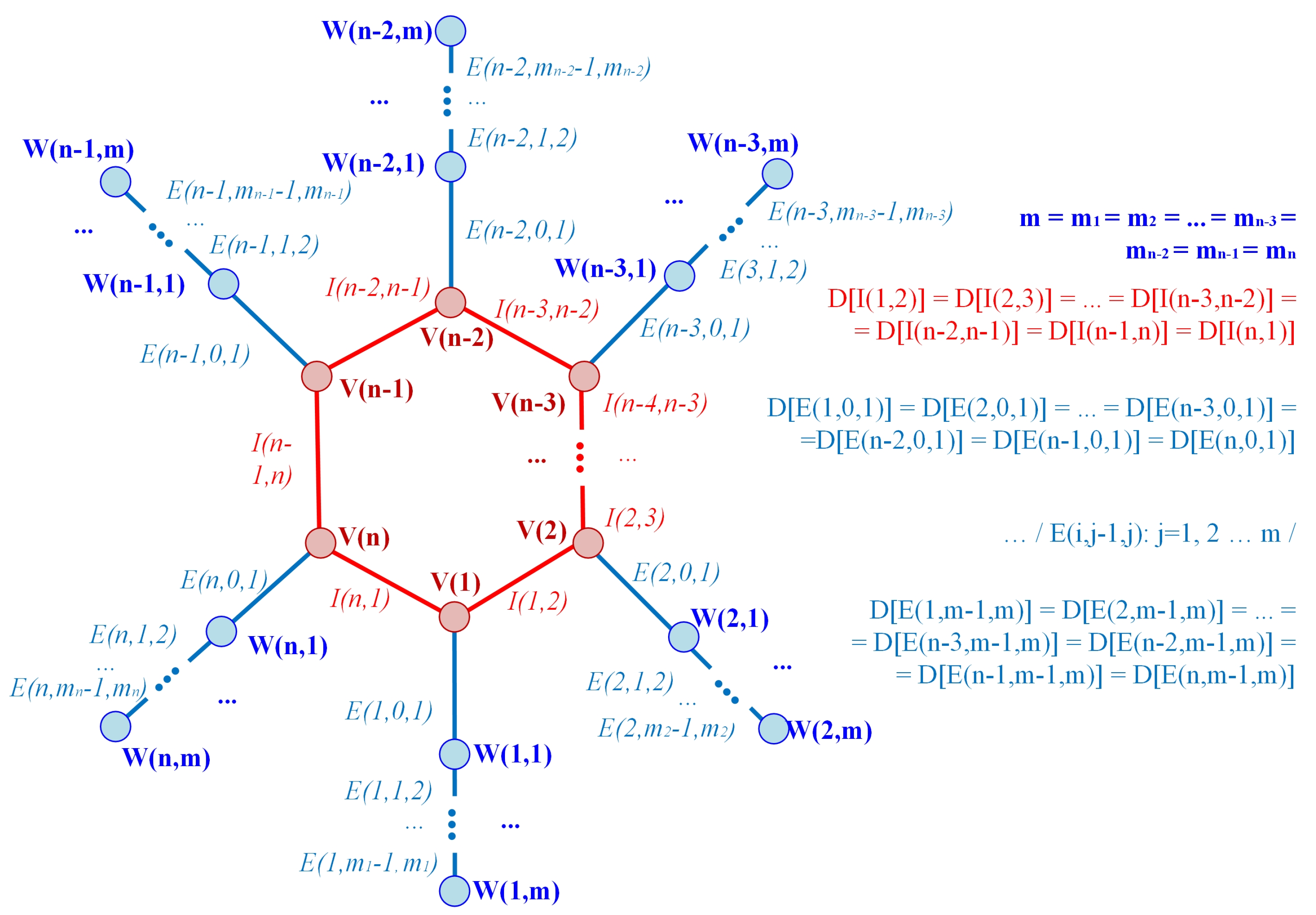
3.2. The Theoretical Geometrical Model
- n: number of vertices (CSDLs) on the central ring (given as polygons)
- mi: number of vertices (CSDLs) on ray “i”
- V(i): CSDL No. “i” on the central ring; its sum demand is QV(i)
- W(i,j): CSDL No. “j” on ray “i”; its sum demand is QW(i,j) (based on this logic, the CSDL on the central ring can be marked as W(i,0)
- I(i,i + 1): the edge (road section) between V(i) and V(i + 1) on the central ring; its length is D[I(i,i + 1)], i = 1… n; I(n,n + 1) = I(n,1)
- E(i,j − 1,j): the edge (road section) between W(i,j − 1) and W(i,j) on ray “i”; its length is D[E(i,j − 1,j)], j = 1… mi
- R: the ray of the best fitting circle of the polygon of the central ring
3.3. The Symmetrical Geometrical Model
- the number of the CSDLs on the rays is the same on every ray (m)
- the length of the I(i − 1,i) edges is the same for every “i” value (I = 1… n), so the central ring will be a regular polygon
- the length of the E(i,j − 1,j) edge is the same on every ray, for every “i” and “j” value (i = 1… n; j = 1… m)
- the demands are the same for every CSDL, as in Formula (7):
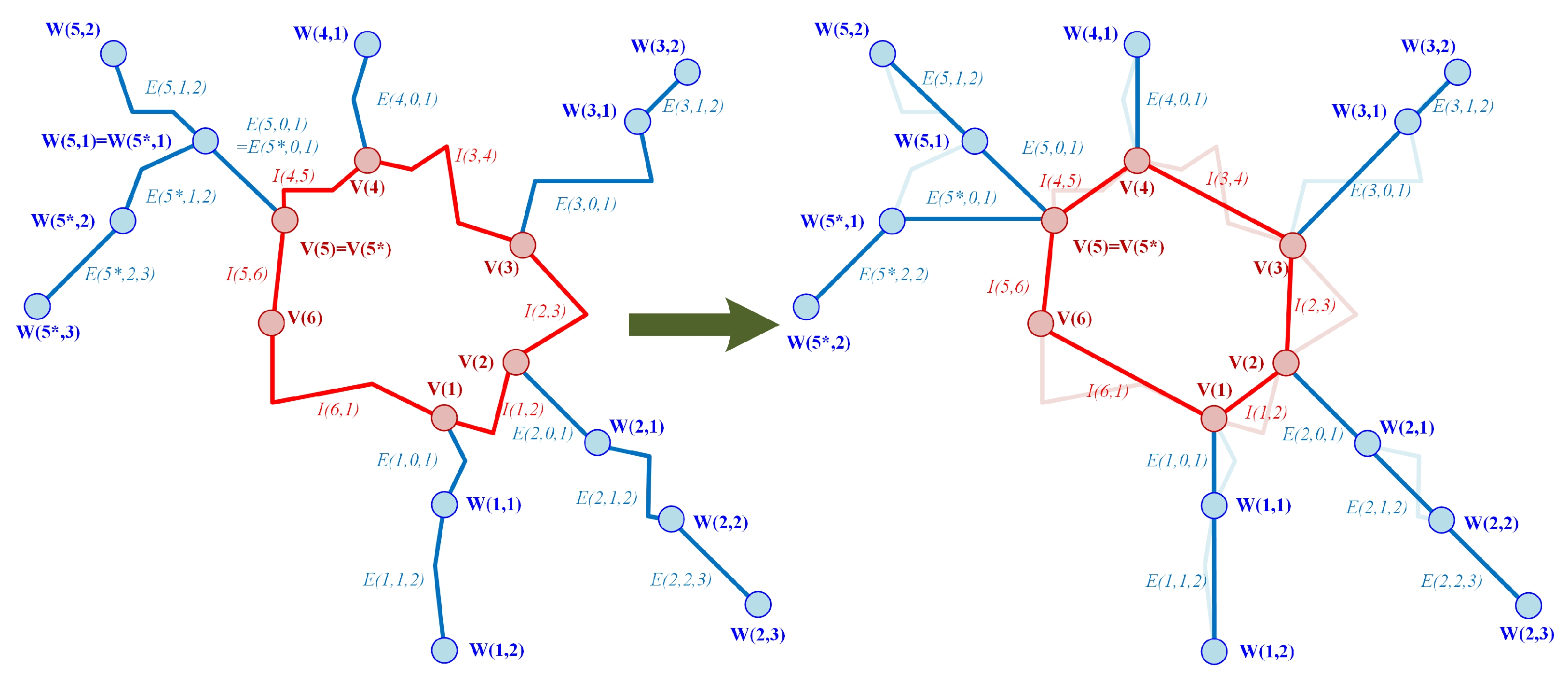
3.4. Geometrical Model of the Real Network
- the number of CSDLs on one ray is not equal in every case: in the example m1 = 2, m2 = 3, m3 = 2, m4 = 1, m5 = 2, m5* = 2, m6 = 0
- the length of the I(i − 1,i) edges is not the same in every case
- the length of the E(i,j − 1,j) edges is not the same in every case; there can be differences between the rays and on the rays as well
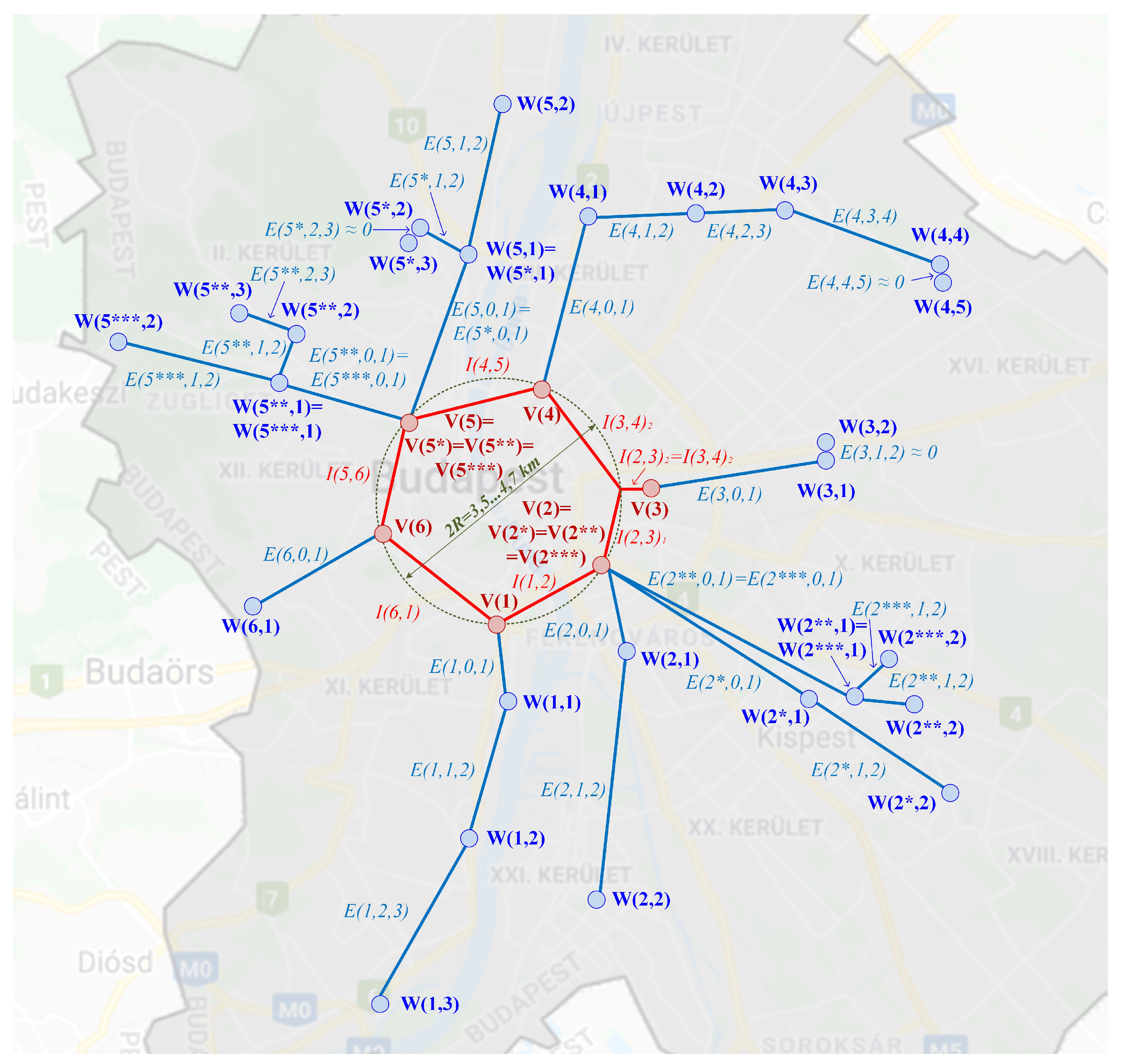
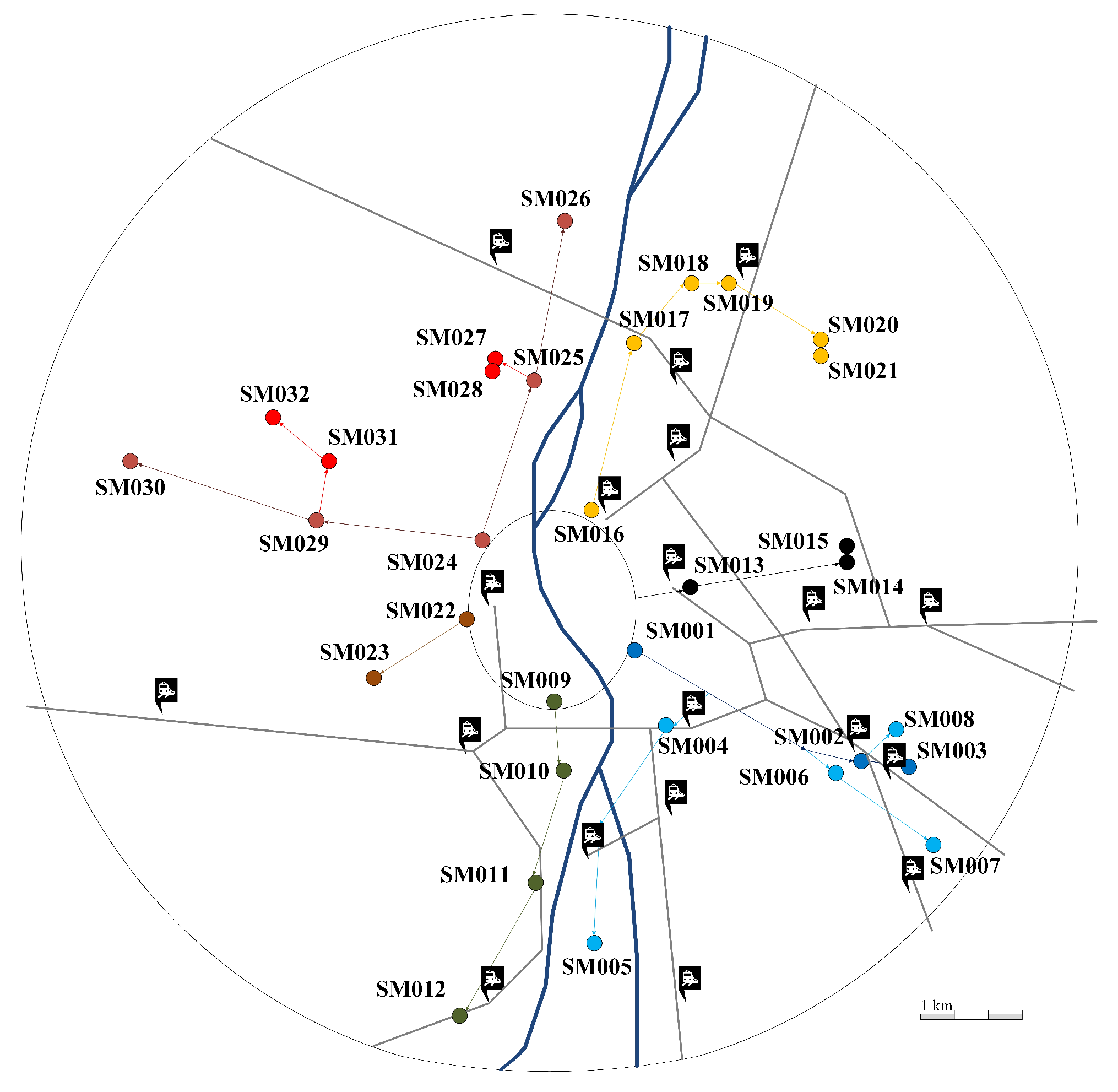
3.5. Application of the Geometrical Model: Results for Budapest
4. Discussion and Future Research
- two- or three-wheeled cargo bikes without electric power assistance;
- two-, three-, or four-wheeled cargo bikes (with or without trailer) with electric power assistance;
- non-pedal small electric delivery vehicles (e.g., cargo mopeds; they must be considered as their capabilities and advantages are very similar to cargo bikes)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Specific Values for the Three Examined Categories
| Estimated Specific Parameters of the Categories | A | B | C | |
|---|---|---|---|---|
| Number of deliveries/store | Daily | 0.52 | 0.79 | 0.81 |
| Weekly | 3.67 | 5.52 | 5.68 | |
| Monthly | 15.23 | 23.14 | 23.95 | |
| Yearly | 192.76 | 288.85 | 296.53 | |
| The daily amount of goods/store | Daily minimum [kg] | 28.57 | 163.83 | 102.29 |
| Daily maximum [kg] | 129.35 | 843.17 | 404.95 | |
| Daily minimum [m3] | 1.20 | 3.59 | 2.00 | |
| Daily maximum [m3] | 3.66 | 10.43 | 6.29 | |
| The monthly amount of goods/store | Monthly minimum [kg] | 814.71 | 4851.19 | 3027.25 |
| Monthly maximum [kg] | 3689.10 | 24,932.04 | 11,958.33 | |
| Monthly minimum [m3] | 34.47 | 105.24 | 58.48 | |
| Monthly maximum [m3] | 105.58 | 306.29 | 183.65 | |
| Necessary number of cargo bike deliveries/store | eBULLITT/day | 0.11 | 0.11 | 0.04 |
| eBULLITT/month | 3.22 | 3.02 | 1.03 | |
| Trike/day | 0.23 | 0.20 | 0.14 | |
| Trike/month | 6.43 | 5.72 | 3.90 | |
| Armadillo/day | 0.19 | 0.17 | 0.11 | |
| Armadillo/month | 5.42 | 4.96 | 3.04 | |
| Armadillo with trailer/day | 0.23 | 0.21 | 0.10 | |
| Armadillo with trailer/month | 6.51 | 6.06 | 2.73 | |
| Expected share of stores, they can be served by cargo bikes/store | eBULLITT | 25.8% | 20.3% | 7.5% |
| Trike | 63.4% | 55.4% | 32.5% | |
| Armadillo | 52.7% | 45.9% | 25.0% | |
| Armadillo with trailer | 71.0% | 63.5% | 32.5% | |
| Amount of goods to be delivered by cargo bikes/store | eBULLITT daily [kg] | 1.09 | 0.26 | 0.05 |
| eBULLITT monthly [kg] | 30.73 | 7.32 | 1.53 | |
| Trike daily [kg] | 11.23 | 5.83 | 4.44 | |
| Trike monthly [kg] | 321.10 | 167.30 | 124.88 | |
| Armadillo daily [kg] | 6.32 | 4.73 | 3.74 | |
| Armadillo monthly [kg] | 178.16 | 135.79 | 105.38 | |
| Armadillo with trailer daily [kg] | 13.70 | 8.86 | 4.44 | |
| Armadillo with trailer monthly [kg] | 391.69 | 253.41 | 124.88 | |
Appendix B. Number of Stores, Deliveries and Amounts of Goods
| ID | Category | Number of Stores | Number of Deliveries | |||
|---|---|---|---|---|---|---|
| Daily | Weekly | Monthly | Yearly | |||
| SM001 | C | 92 | 68 | 470 | 1984 | 24,553 |
| SM002 | B | 141 | 100 | 701 | 2936 | 36,656 |
| SM003 | A | 300 | 142 | 992 | 4111 | 52,047 |
| SM004 | C | 101 | 74 | 516 | 2178 | 26,955 |
| SM005 | C | 46 | 34 | 235 | 992 | 12,277 |
| SM006 | C | 74 | 54 | 378 | 1596 | 19,749 |
| SM007 | C | 35 | 26 | 179 | 755 | 9341 |
| SM008 | C | 19 | 14 | 98 | 410 | 5071 |
| SM009 | B | 174 | 124 | 865 | 3624 | 45,235 |
| SM010 | C | 39 | 29 | 200 | 841 | 10,409 |
| SM011 | C | 77 | 57 | 394 | 1660 | 20,550 |
| SM012 | B | 149 | 106 | 741 | 3103 | 38,735 |
| SM013 | B | 143 | 102 | 711 | 2978 | 37,176 |
| SM014 | B | 194 | 138 | 964 | 4040 | 50,434 |
| SM015 | C | 89 | 65 | 455 | 1919 | 23,752 |
| SM016 | A | 361 | 171 | 1194 | 4947 | 62,629 |
| SM017 | C | 113 | 83 | 578 | 2436 | 30,157 |
| SM018 | C | 23 | 17 | 118 | 496 | 6139 |
| SM019 | C | 20 | 15 | 103 | 432 | 5338 |
| SM020 | B | 183 | 130 | 910 | 3811 | 47,574 |
| SM021 | A | 300 | 142 | 992 | 4111 | 52,047 |
| SM022 | C | 101 | 74 | 516 | 2178 | 26,955 |
| SM023 | C | 44 | 33 | 225 | 949 | 11,743 |
| SM024 | B | 264 | 188 | 1312 | 5498 | 68,632 |
| SM025 | C | 56 | 41 | 287 | 1208 | 14,945 |
| SM026 | C | 26 | 19 | 133 | 561 | 6939 |
| SM027 | C | 51 | 38 | 261 | 1100 | 13,611 |
| SM028 | C | 14 | 11 | 72 | 302 | 3737 |
| SM029 | C | 91 | 67 | 465 | 1962 | 24,286 |
| SM030 | C | 13 | 10 | 67 | 281 | 3470 |
| SM031 | C | 56 | 41 | 287 | 1208 | 14,945 |
| SM032 | C | 43 | 32 | 220 | 927 | 11,476 |
| ID | The Daily Amount of Goods | The Monthly Amount of Goods | ||||||
|---|---|---|---|---|---|---|---|---|
| Daily Min. [kg] | Daily Max. [kg] | Daily Min. [m3] | Daily Max. [m3] | Monthly Min. [kg] | Monthly Max. [kg] | Monthly Min. [m3] | Monthly Max. [m3] | |
| SM001 | 8470 | 33,530 | 166 | 521 | 250,656 | 990,150 | 4843 | 15,207 |
| SM002 | 20,791 | 106,999 | 456 | 1324 | 615,617 | 3,163,876 | 13,356 | 38,869 |
| SM003 | 7715 | 34,926 | 324 | 990 | 219,971 | 996,057 | 9307 | 28,507 |
| SM004 | 9298 | 36,810 | 182 | 572 | 275,177 | 1,087,012 | 5317 | 16,694 |
| SM005 | 4235 | 16,765 | 83 | 261 | 125,328 | 495,075 | 2422 | 7604 |
| SM006 | 6813 | 26,970 | 134 | 419 | 201,615 | 796,425 | 3895 | 12,231 |
| SM007 | 3222 | 12,756 | 63 | 199 | 95,359 | 376,688 | 1843 | 5785 |
| SM008 | 1750 | 6925 | 35 | 108 | 51,766 | 204,488 | 1001 | 3141 |
| SM009 | 25,656 | 132,042 | 563 | 1633 | 759,697 | 3,904,358 | 16,482 | 47,965 |
| SM010 | 3591 | 14,214 | 71 | 221 | 106,257 | 419,738 | 2053 | 6447 |
| SM011 | 7089 | 28,063 | 139 | 436 | 209,789 | 828,712 | 4053 | 12,727 |
| SM012 | 21,970 | 113,070 | 482 | 1399 | 650,545 | 3,343,387 | 14,114 | 41,074 |
| SM013 | 21,086 | 108,517 | 463 | 1343 | 624,349 | 3,208,754 | 13,545 | 39,420 |
| SM014 | 28,605 | 147,219 | 627 | 1821 | 847,019 | 4,353,134 | 18,376 | 53,479 |
| SM015 | 8194 | 32,437 | 161 | 504 | 242,483 | 957,862 | 4685 | 14,711 |
| SM016 | 9283 | 42,027 | 389 | 1191 | 264,698 | 1,198,588 | 11,199 | 34,303 |
| SM017 | 10,403 | 41,184 | 204 | 640 | 307,871 | 1,216,162 | 5948 | 18,678 |
| SM018 | 2118 | 8383 | 42 | 131 | 62,664 | 247,538 | 1211 | 3802 |
| SM019 | 1842 | 7290 | 36 | 114 | 54,491 | 215,250 | 1053 | 3306 |
| SM020 | 26,984 | 138,871 | 592 | 1718 | 798,992 | 4,106,307 | 17,334 | 50,446 |
| SM021 | 7715 | 34,926 | 324 | 990 | 219,971 | 996,057 | 9307 | 28,507 |
| SM022 | 9298 | 36,810 | 182 | 572 | 275,177 | 1,087,012 | 5317 | 16,694 |
| SM023 | 4051 | 16,036 | 80 | 250 | 119,879 | 473,550 | 2316 | 7273 |
| SM024 | 38,927 | 200,339 | 853 | 2478 | 1,152,644 | 5,923,853 | 25,007 | 72,775 |
| SM025 | 5156 | 20,410 | 101 | 318 | 152,574 | 602,700 | 2948 | 9256 |
| SM026 | 2394 | 9476 | 47 | 148 | 70,838 | 279,825 | 1369 | 4298 |
| SM027 | 4695 | 18,588 | 92 | 289 | 138,951 | 548,888 | 2685 | 8430 |
| SM028 | 1289 | 5103 | 26 | 80 | 38,144 | 150,675 | 737 | 2314 |
| SM029 | 8378 | 33,166 | 164 | 516 | 247,932 | 979,387 | 4790 | 15,041 |
| SM030 | 1197 | 4738 | 24 | 74 | 35,419 | 139,913 | 685 | 2149 |
| SM031 | 5156 | 20,410 | 101 | 318 | 152,574 | 602,700 | 2948 | 9256 |
| SM032 | 3959 | 15,672 | 78 | 244 | 117,155 | 462,788 | 2264 | 7108 |
| Sum | Average (for One Shopping Mall) | Average (for One Store) | ||
|---|---|---|---|---|
| Number of stores | 3432 | 107.3 | 1 | |
| Cargo bike deliveries | eBULLITT/day | 258.3 | 8.1 | 0.1 |
| eBULLITT/month | 7310.5 | 228.5 | 2.1 | |
| Trike/day | 570.2 | 17.8 | 0.2 | |
| Trike/month | 16,269.7 | 508.4 | 4.7 | |
| Armadillo/day | 477.3 | 14.9 | 0.1 | |
| Armadillo/month | 13,605.4 | 425.2 | 4.0 | |
| Armadillo with trailer/day | 540.3 | 16.9 | 0.2 | |
| Armadillo with trailer/month | 15,451.9 | 482.9 | 4.5 | |
| The average number of stores to be served by cargo bikes | eBULLITT | 548 | 17.1 | 16.0% |
| Trike | 1545 | 48.3 | 45.0% | |
| Armadillo | 1263 | 39.5 | 36.8% | |
| Armadillo with trailer | 1699 | 53.1 | 49.5% | |
| Amount of goods to be delivered by cargo bikes | eBULLITT daily [kg] | 1290.1 | 40.3 | 0.4 |
| eBULLITT daily [m3] | 63.3 | 2.0 | 0.0 | |
| eBULLITT monthly [kg] | 36,477.1 | 1139.9 | 10.6 | |
| eBULLITT monthly [m3] | 1790.9 | 56.0 | 0.5 | |
| Trike daily [kg] | 21,146.0 | 660.8 | 6.2 | |
| Trike daily [m3] | 743.6 | 23.2 | 0.2 | |
| Trike monthly [kg] | 603,087.1 | 18,846.5 | 175.7 | |
| Trike monthly [m3] | 21,214.5 | 663.0 | 6.2 | |
| Armadillo daily [kg] | 14,900.1 | 465.6 | 4.3 | |
| Armadillo daily [m3] | 427.4 | 13.4 | 0.1 | |
| Armadillo monthly [kg] | 422,597.9 | 13,206.2 | 123.1 | |
| Armadillo monthly [m3] | 12,185.2 | 380.8 | 3.6 | |
| Armadillo with trailer daily [kg] | 26,689.0 | 834.0 | 7.8 | |
| Armadillo with trailer daily [m3] | 998.5 | 31.2 | 0.3 | |
| Armadillo with trailer monthly [kg] | 760,858.2 | 23,776.8 | 221.7 | |
| Armadillo with trailer monthly [m3] | 28,549.1 | 892.2 | 8.3 | |
References
- BME-ALRT. Website of the City Logistics Research Group of the Department of Material Handling and Logistics Systems at the Budapest University of Technology and Economics. 2021. Available online: https://www.logisztika.bme.hu/citylog/ (accessed on 3 March 2021).
- Sárdi, D.L.; Bóna, K. AHP-based multicriterial ranking model for the city logistics analysis of urban areas. In Proceedings of the 10th International Conference on Logistics, Informatics and Service Sciences (LISS2020), Beijing, China, 27–28 July 2020; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Sárdi, D.L.; Bóna, K. Examination of logistics systems of concentrated sets of urban delivery points by simulation. In Proceedings of the 21st International Conference on Harbor, Maritime and Multimodal Logistic Modeling & Simulation (HMS 2019); Cal-Tek Srl, Lisbon, Portugal, 18–20 September 2019; Available online: http://www.msc-les.org/proceedings/hms/2019/HMS2019.pdf (accessed on 3 March 2021).
- Mészáros, B.; Sárdi, D.L.; Bóna, K. Monitoring, measurement and statistical analysis-based methodology for improving city logistics of shopping malls in Budapest. World Rev. Intermodal Transp. Res. 2017, 6, 352. [Google Scholar] [CrossRef]
- Bóna, K.; Róka, Á.; Sardi, D.L. Mathematical Modelling of the Cost Structure of the Logistics System of Shopping Malls in Budapest. Period. Polytech. Transp. Eng. 2018, 46, 142–150. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.Z.; Moodie, D.R. Locating urban logistics terminals and shopping centres in a Chinese city. Int. J. Logist. Res. Appl. 2011, 14, 165–177. [Google Scholar] [CrossRef]
- Chiara, G.D.; Cheah, L. Data stories from urban loading bays. Eur. Transp. Res. Rev. 2017, 9, 50. [Google Scholar] [CrossRef] [Green Version]
- Van Duin, J.; Van Dam, T.; Wiegmans, B.; Tavasszy, L. Understanding Financial Viability of Urban Consolidation Centres: Regent Street (London), Bristol/Bath & Nijmegen. Transp. Res. Procedia 2016, 16, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Sardi, D.L.; Bona, K. Macroscopic simulation model of a multi-stage, dynamic cargo bike-based logistics system in the supply of shopping malls in Budapest. In Proceedings of the 2018 Smart City Symposium Prague (SCSP), Prague, Czech Republic, 24–25 May 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- European Comission. White Paper 2011. 2011. Available online: https://ec.europa.eu/transport/themes/strategies/2011_white_paper_en (accessed on 3 March 2021).
- Dong, X.; Wang, B.; Yip, H.L.; Chan, Q.N. CO2 Emission of Electric and Gasoline Vehicles under Various Road Conditions for China, Japan, Europe and World Average—Prediction through Year 2040. Appl. Sci. 2019, 9, 2295. [Google Scholar] [CrossRef] [Green Version]
- Lebeau, P.; Macharis, C.; Van Mierlo, J. Exploring the choice of battery electric vehicles in city logistics: A conjoint-based choice analysis. Transp. Res. Part E Logist. Transp. Rev. 2016, 91, 245–258. [Google Scholar] [CrossRef]
- Csonka, B.; Havas, M.; Csiszár, C.; Földes, D. Operational Methods for Charging of Electric Vehicles. Period. Polytech. Transp. Eng. 2020, 48, 369–376. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Banaszak, Z. Unmanned Aerial Vehicle Routing Problems: A Literature Review. Appl. Sci. 2020, 10, 4504. [Google Scholar] [CrossRef]
- Kim, J.; Moon, H.; Jung, H. DroneBased Parcel Delivery Using the Rooftops of City Buildings: Model and Solution. Appl. Sci. 2020, 10, 4362. [Google Scholar] [CrossRef]
- Kilián, Z. Környezetbarát Trendek a City Logisztikában. In Proceedings of the Nagyvállalatok Logisztikai Vezetőinek 9. Országos és 4. Nemzetközi Konferenciája, Eger, Hungary, 14 May 2015; Available online: https://docplayer.hu/2478203-Kornyezetbarat-trendek-a-city-logisztikaban.html (accessed on 3 March 2021).
- Blaauw, E. DHL Lanceert Nieuwe Vervoerscombinatie Voor Stadsdistributie. 2017. Available online: https://www.dhlparcel.nl/nl/zakelijk/kennisplatform/nieuws/city-hub (accessed on 3 March 2021).
- Chioda, E. Dall’Ungheria in Italia Inventa un Business con le Bici. 2015. Available online: https://www.millionaire.it/dallungheria-in-italia-inventa-un-business-con-le-bici/# (accessed on 3 March 2021).
- Parr, T. RIPPL #31: UPS—Reducing Vehicle Movements with City Centre Container Hubs. 2017. Available online: https://www.rippl.bike/en/rippl-31-ups-reducing-vehicle-movements-with-city-centre-container-hubs/ (accessed on 3 March 2021).
- Verlinde, S.; Macharis, C.; Milan, L.; Kin, B. Does a Mobile Depot Make Urban Deliveries Faster, More Sustainable and More Economically Viable: Results of a Pilot Test in Brussels. Transp. Res. Procedia 2014, 4, 361–373. [Google Scholar] [CrossRef] [Green Version]
- Berlin.de. Modellprojekt in Berlin Startet: Lieferverkehr mit Lastenrädern Nachhaltig Gestalten. 2018. Available online: https://www.berlin.de/sen/uvk/presse/pressemitteilungen/2018/pressemitteilung.706285.php (accessed on 3 March 2021).
- Bertram, I. Hermes Trials Parcel Delivery by Cargo Bikes in Berlin. 2018. Available online: https://newsroom.hermesworld.com/international/city-logistics-hermes-trials-parcel-delivery-by-cargo-bikes-in-berlin-837/ (accessed on 3 March 2021).
- Vert Chez Cous. Our Vehicles. 2021. Available online: https://www.vertchezvous.com/en/nos-vehicules/ (accessed on 3 March 2021).
- Janjevic, M.; Ndiaye, A.B. Inland Waterways Transport for City Logistics: A Review of Experiences and the Role of Local Public Authorities. WIT Trans. Built Environ. 2014, 138, 279–290. [Google Scholar] [CrossRef] [Green Version]
- LogistikTram. Idee. 2021. Available online: http://www.logistiktram.de/index.html (accessed on 3 March 2021).
- Giglio, C.; Musmanno, R.; Palmieri, R. Cycle Logistics Projects in Europe: Intertwining Bike-Related Success Factors and Region-Specific Public Policies with Economic Results. Appl. Sci. 2021, 11, 1578. [Google Scholar] [CrossRef]
- Budapestcity.org. Kerékpár-közlekedés Budapesten—Kétkeréken a Városban. 2020. Available online: http://budapestcity.org/11-egyeb/kozlekedes/kerekpar/index-hu.htm (accessed on 15 July 2020).
- Hajtás Pajtás. GLS—Hajtás Pajtás Összefogás a Kipufogógázmentes Csomagszállításért. 2015. Available online: https://hajtaspajtas.hu/blog/gls-hajtas-pajtas-oesszefogas-a-kipufogogazmentes-csomagszallitasert (accessed on 15 July 2020).
- Schliwa, G.; Armitage, R.; Aziz, S.; Evans, J.; Rhoades, J. Sustainable City Logistics—Making Cargo Cycles Viable for Urban Freight Transport. Res. Transp. Bus. Manag. 2015, 15, 50–57. [Google Scholar] [CrossRef] [Green Version]
- Cortés-Murcia, D.L.; Prodhon, C.; Afsar, H.M. The electric vehicle routing problem with time windows, partial recharges and satellite customers. Transp. Res. Part E Logist. Transp. Rev. 2019, 130, 184–206. [Google Scholar] [CrossRef]
- Gruber, J.; Kihm, A.; Lenz, B. A new vehicle for urban freight? An ex-ante evaluation of electric cargo bikes in courier services. Res. Transp. Bus. Manag. 2014, 11, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Lenz, B.; Riehle, E. Bikes for Urban Freight? Transp. Res. Rec. J. Transp. Res. Board 2013, 2379, 39–45. [Google Scholar] [CrossRef]
- Melo, S.; Baptista, P. Evaluating the impacts of using cargo cycles on urban logistics: Integrating traffic, environmental and operational boundaries. Eur. Transp. Res. Rev. 2017, 9, 30. [Google Scholar] [CrossRef] [Green Version]
- Sheth, M.; Butrina, P.; Goodchild, A.; McCormack, E. Measuring delivery route cost trade-offs between electric-assist cargo bicycles and delivery trucks in dense urban areas. Eur. Transp. Res. Rev. 2019, 11, 11. [Google Scholar] [CrossRef] [Green Version]
- Niels, T.; Hof, M.T.; Bogenberger, K. Design and Operation of an Urban Electric Courier Cargo Bike System. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 2531–2537. [Google Scholar]
- Conway, A. Urban micro-consolidation and last mile goods delivery by freight-tricycle in Manhattan: Opportunities and challenges. In Proceedings of the Transportation Research Board 91st Annual Meeting, Washington DC, USA, 22–26 January 2012; Available online: https://trid.trb.org/view/1129890 (accessed on 3 March 2021).
- Telhada, J.; Duffrayer Ormond Junior, P.A. Using urban consolidation centre with cycloscargos support to increase the performance and sustainability of urban logistics: A literature review and a case study in the city of São Paulo. In Proceedings of the 3rd International Conference on Energy and Environment: Bringing together Engineering and Economics, Porto, Portugal, 29–30 June 2017. [Google Scholar]
- Browne, M.; Allen, J.; Leonardi, J. Evaluating the use of an urban consolidation centre and electric vehicles in central London. IATSS Res. 2011, 35, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Chae, J.; Kim, J. A Courier Service with Electric Bicycles in an Urban Area: The Case in Seoul. Sustainability 2019, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Anderluh, A.; Hemmelmayr, V.C.; Nolz, P.C. Synchronizing vans and cargo bikes in a city distribution network. Central Eur. J. Oper. Res. 2017, 25, 345–376. [Google Scholar] [CrossRef] [Green Version]
- Fikar, C.; Gronalt, M. Agent-based simulation of restaurant deliveries facilitating cargo-bikes and urban consolidation. In Proceedings of the International Conference on Harbor Maritime and Multimodal Logistics, Budapest, Hungary, 17–19 September 2018. [Google Scholar]
- Fikar, C.; Hirsch, P.; Gronalt, M. A decision support system to investigate dynamic last-mile distribution facilitating cargo-bikes. Int. J. Logist. Res. Appl. 2018, 21, 300–317. [Google Scholar] [CrossRef]
- Hofmann, W.; Assmann, T.; Neghabadi, P.D.; Cung, V.D.; Tolujevs, J. A simulation tool to assess the integration of cargo bikes into an urban distribution system. In Proceedings of the 5th International Workshop on Simulation for Energy, Sustainable Development & Environment, Barcelona, Spain, 18–20 September 2017; Available online: https://hal.archives-ouvertes.fr/hal-01875988/document (accessed on 3 March 2021).
- Miller, J. Vehicle-to-vehicle-to-infrastructure (V2V2I) intelligent transportation system architecture. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2008; pp. 715–720. [Google Scholar]
- Khan, Z.; Koubaa, A.; Farman, H. Smart Route: Internet-of-Vehicles (IoV)-Based Congestion Detection and Avoidance (IoV-Based CDA) Using Rerouting Planning. Appl. Sci. 2020, 10, 4541. [Google Scholar] [CrossRef]
- Krikke, H.; van Harten, A.; Schuur, P. Business case Océ: Reverse logistic network re-design for copiers. OR Spectr. 1999, 21, 381–409. [Google Scholar] [CrossRef]
- Čejka, J.; Kampf, R. The Winter Maintenance Optimization by Graph Theory. Period. Polytech. Transp. Eng. 2018, 47, 106–110. [Google Scholar] [CrossRef] [Green Version]
- Flores, B.E.; Whybark, D.C. Multiple Criteria ABC Analysis. Int. J. Oper. Prod. Manag. 1986, 6, 38–46. [Google Scholar] [CrossRef]
- Eurostat. Electricity Prices (Including Taxes) for Household Consumers, Second Half 2019. 2020. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics#Electricity_prices_for_non-household_consumers (accessed on 3 March 2021).
- Pirisi, G.; Trócsányi, A. Általános Társadalom- és Gazdaságföldrajz 3. Fejezet Településföldrajz—A Települések Szerkezete. Pécsi Tudományegyetem. 2018. Available online: http://tamop412a.ttk.pte.hu/files/foldrajz2/index.html (accessed on 3 March 2021).
- Ballare, S.; Lin, J. Investigating the use of microhubs and crowdshipping for last mile delivery. Transp. Res. Procedia 2020, 46, 277–284. [Google Scholar] [CrossRef]


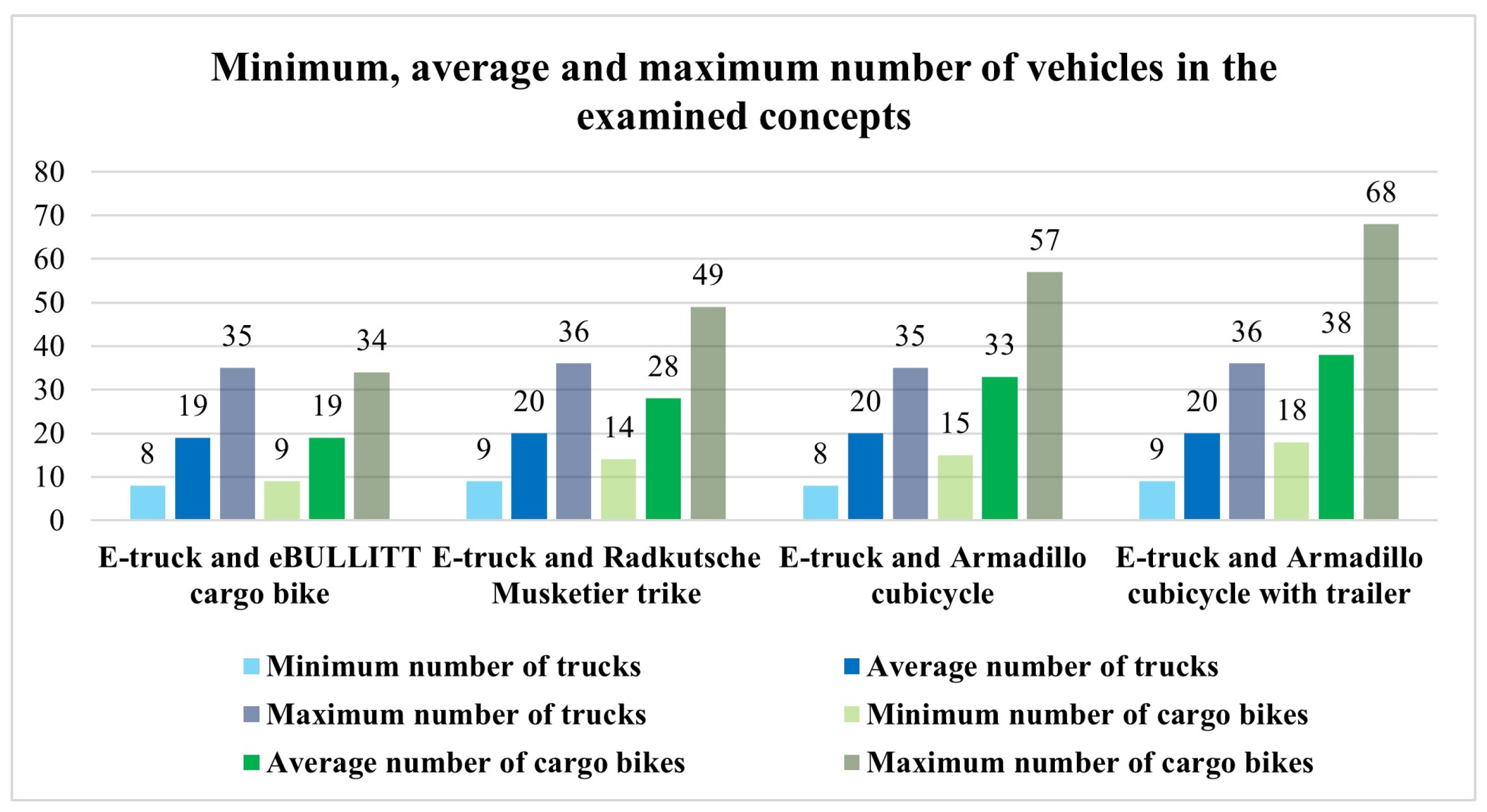
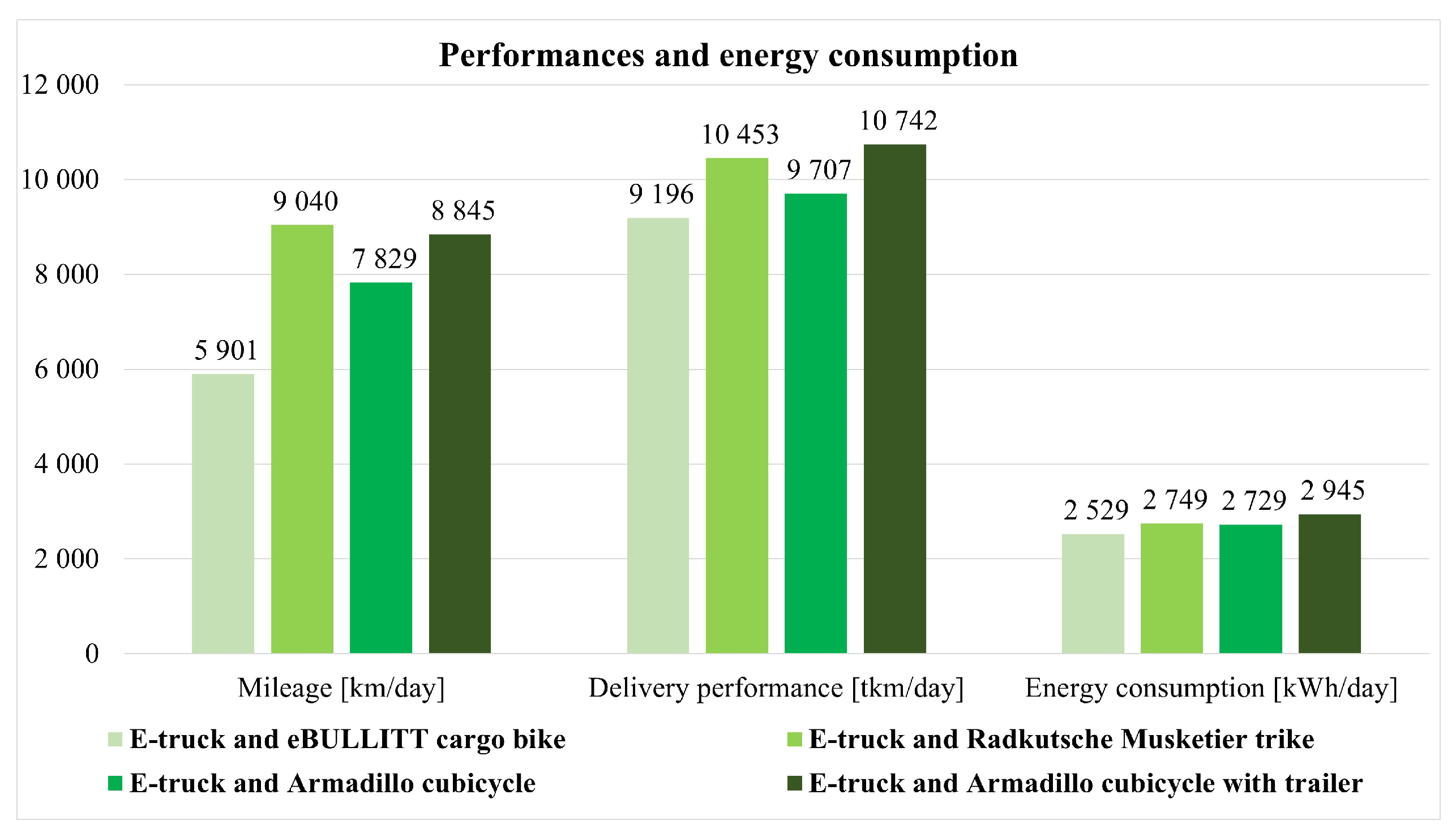
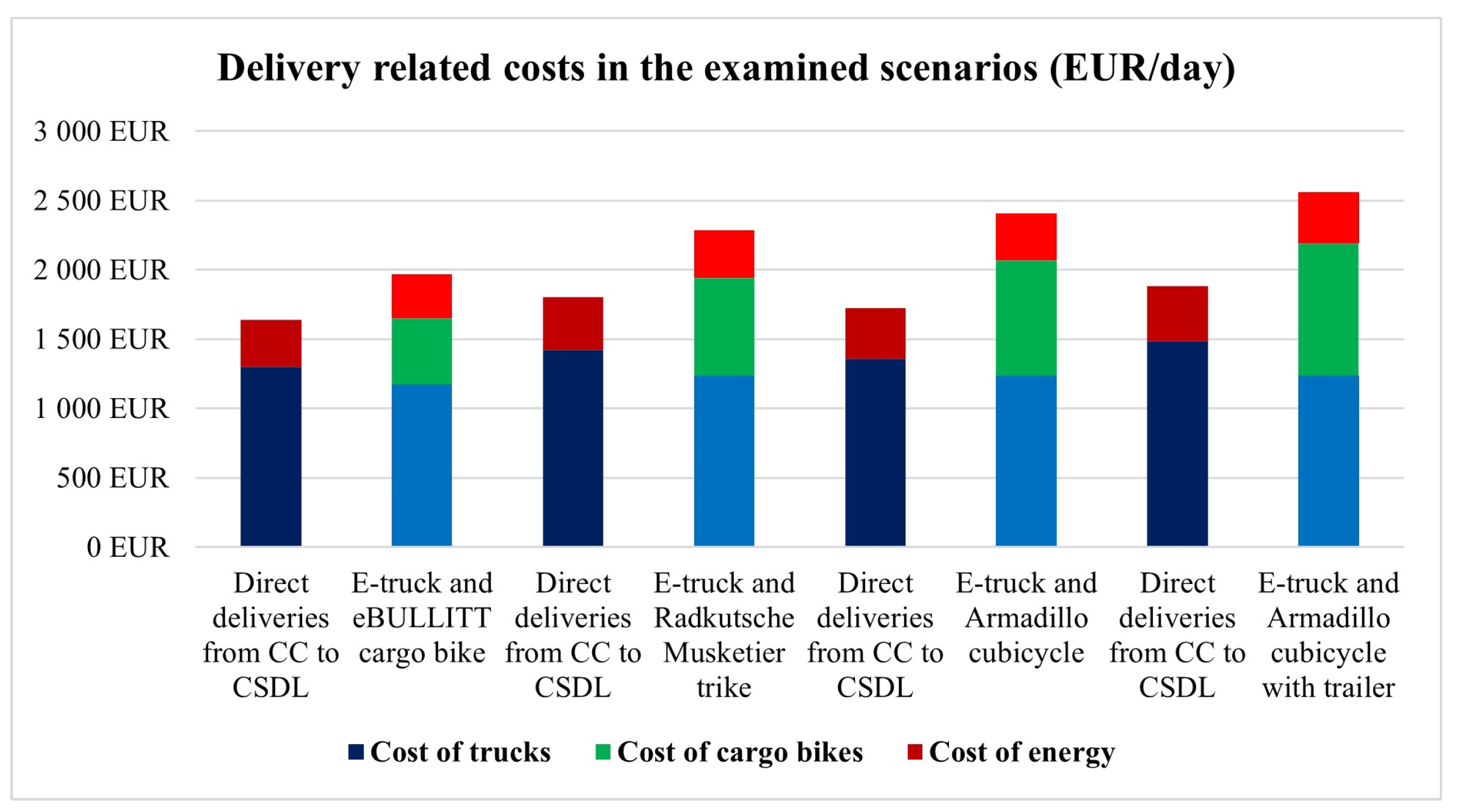




| Cargo Bike Type | STePS eBULLITT | Radkutsche Musketier Trike | Armadillo Cubicycle | Armadillo Cubicycle with Trailer |
|---|---|---|---|---|
| Wheels | 2 | 3 | 4 | 6 |
| Load capacity [kg] | 100 | 242 | 125 | 250 |
| Load capacity [m3] | 0.245 | 1.339 | 0.960 | 1.920 |
| Number of delivery units | 1 | 1 | 1 | 2 |
| Length of the delivery unit—L [m] | 0.70 | 1.27 | 1.20 | 1.20 |
| Width of the delivery unit—B [m] | 0.50 | 0.83 | 0.80 | 0.80 |
| Hight of the delivery unit—H [m] | 0.70 | 1.27 | 1.00 | 1.00 |
| Battery [kWh] | 0.504 | 0.540 | 1.200 | 1.200 |
| Electric power assistance [W] | 250 | 250 | 250 | 250 |
| Average distance with one charge [km] | 90 | 200 | 50 | 50 |
| Charging time [h] | 4 | 4 | 4 | 4 |
| Ray | Length of Ray i (di) [km] | Average Length of Rays (D) [km] | Number of Concentrated Sets of Delivery Locations (CSDLs) on Ray i (mi) | Average Number of CSDLs per Ray | Number of CSDLs on the Central Ring (n) | Average Demand of a CSDL on the Central Ring | Average Demand of a CSDL on Ray i | Average Demand of a CSDL in the System |
|---|---|---|---|---|---|---|---|---|
| 1 | 8.84 | 7.46 | 3 | 2.42 | 6 | 1636.7 | 926.4 | 841.3 |
| 2 | 9.47 | 2 | 495.6 | |||||
| 2 * | 11.44 | 2 | 367.5 | |||||
| 2 ** | 8.84 | 2 | 1248.9 | |||||
| 2 *** | 7.54 | 2 | 1008.9 | |||||
| 3 | 3.80 | 2 | 1600.1 | |||||
| 4 | 11.10 | 5 | 822.5 | |||||
| 5 | 8.58 | 2 | 276.5 | |||||
| 5 * | 5.76 | 3 | 272.0 | |||||
| 5 ** | 4.62 | 3 | 330.4 | |||||
| 5 *** | 5.73 | 2 | 350.7 | |||||
| 6 | 3.85 | 1 | 296.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sárdi, D.L.; Bóna, K. A Geometrical Structure-Based New Approach for City Logistics System Planning with Cargo Bikes and Its Application for the Shopping Malls of Budapest. Appl. Sci. 2021, 11, 3300. https://doi.org/10.3390/app11083300
Sárdi DL, Bóna K. A Geometrical Structure-Based New Approach for City Logistics System Planning with Cargo Bikes and Its Application for the Shopping Malls of Budapest. Applied Sciences. 2021; 11(8):3300. https://doi.org/10.3390/app11083300
Chicago/Turabian StyleSárdi, Dávid Lajos, and Krisztián Bóna. 2021. "A Geometrical Structure-Based New Approach for City Logistics System Planning with Cargo Bikes and Its Application for the Shopping Malls of Budapest" Applied Sciences 11, no. 8: 3300. https://doi.org/10.3390/app11083300
APA StyleSárdi, D. L., & Bóna, K. (2021). A Geometrical Structure-Based New Approach for City Logistics System Planning with Cargo Bikes and Its Application for the Shopping Malls of Budapest. Applied Sciences, 11(8), 3300. https://doi.org/10.3390/app11083300







