Estimation of Mode I Fracture of U-Notched Polycarbonate Specimens Using the Equivalent Material Concept and Strain Energy Density
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimens
2.2. Tests
2.3. Theoretical Methods
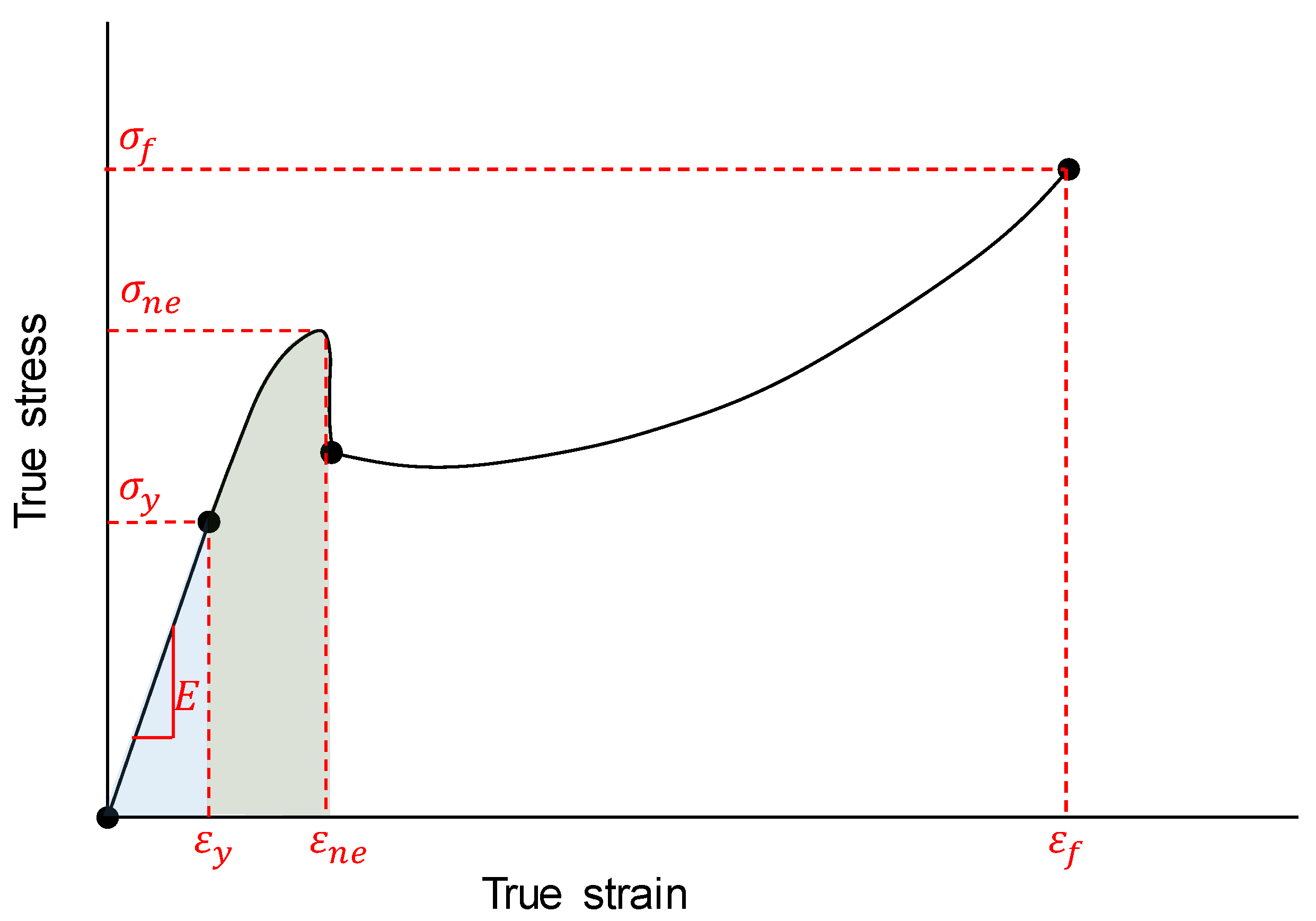
2.3.1. Equivalent Material Concept (EMC)
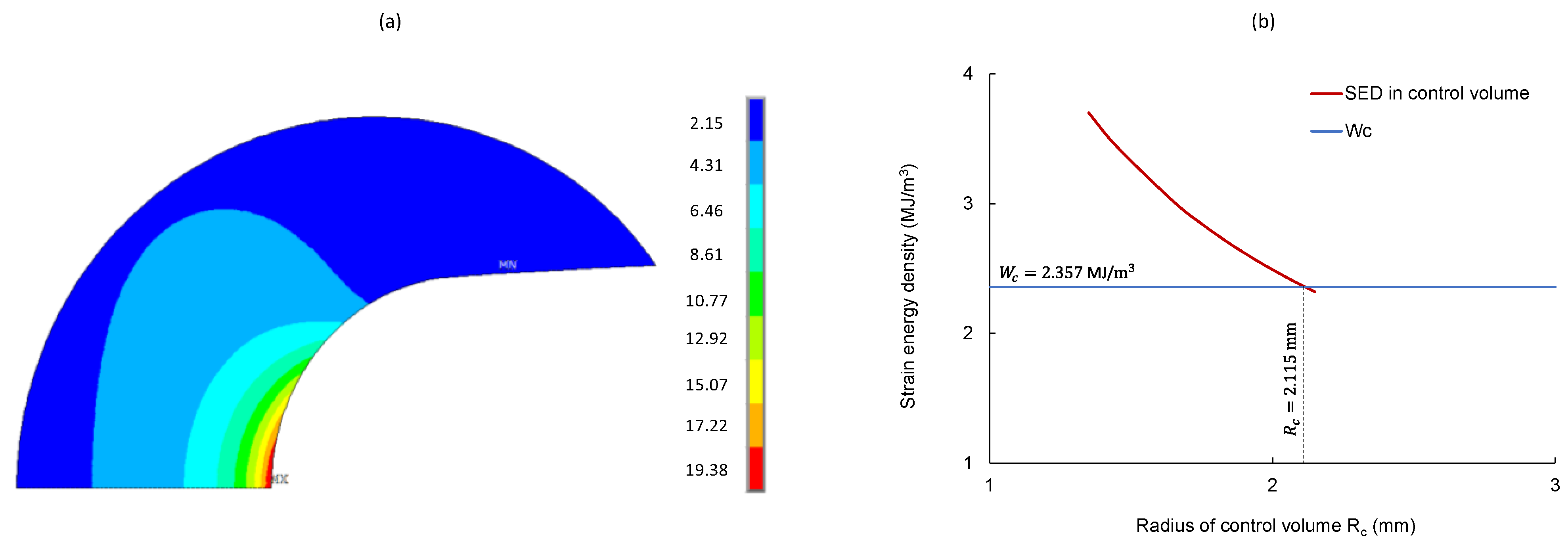
2.3.2. Strain Energy Density Criterion (SED)
2.4. Modeling Polycarbonate
2.5. Finite Element Analysis
3. Results
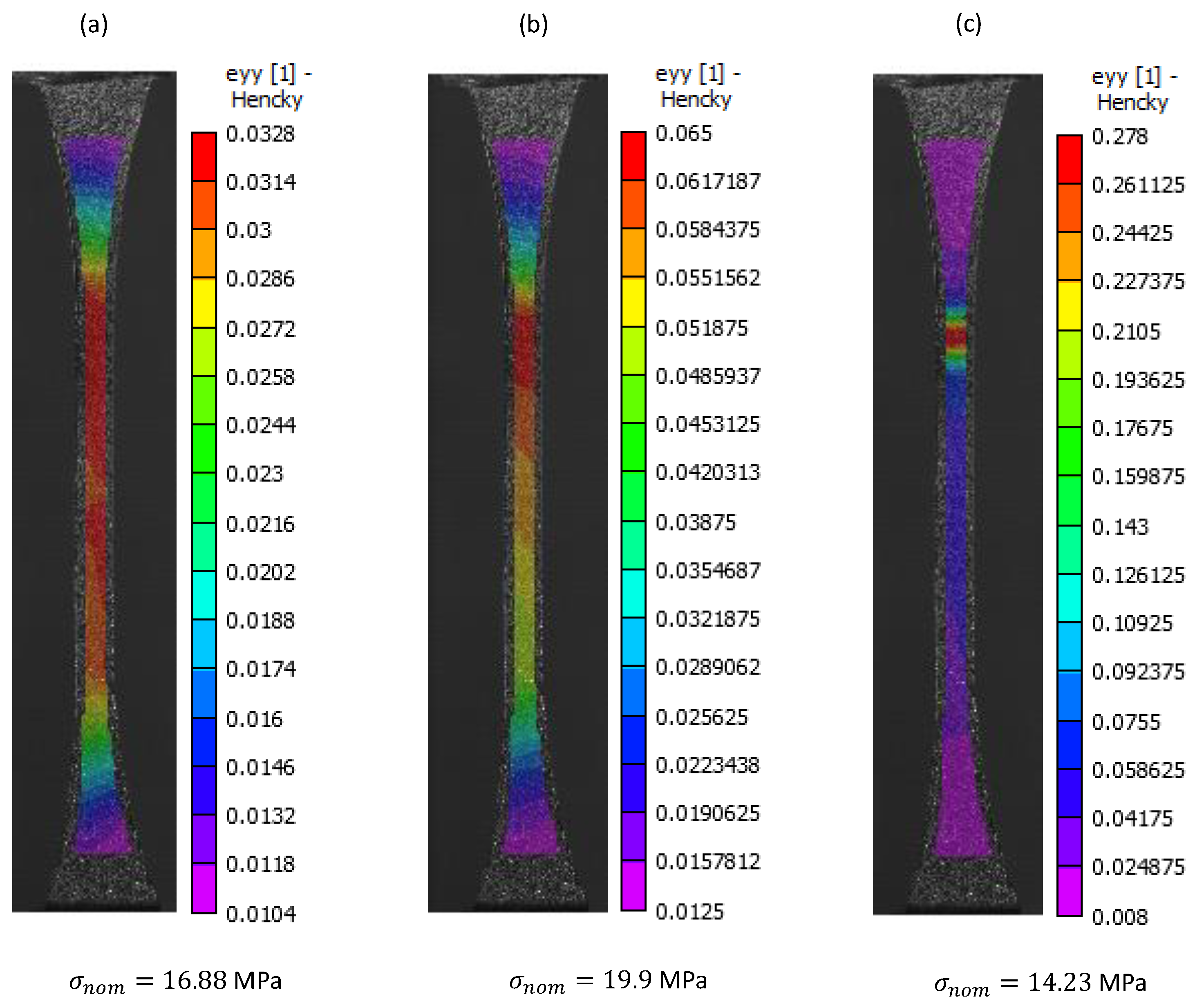
3.1. Monotonic Tensile Specimens
3.2. U-Notched Specimens
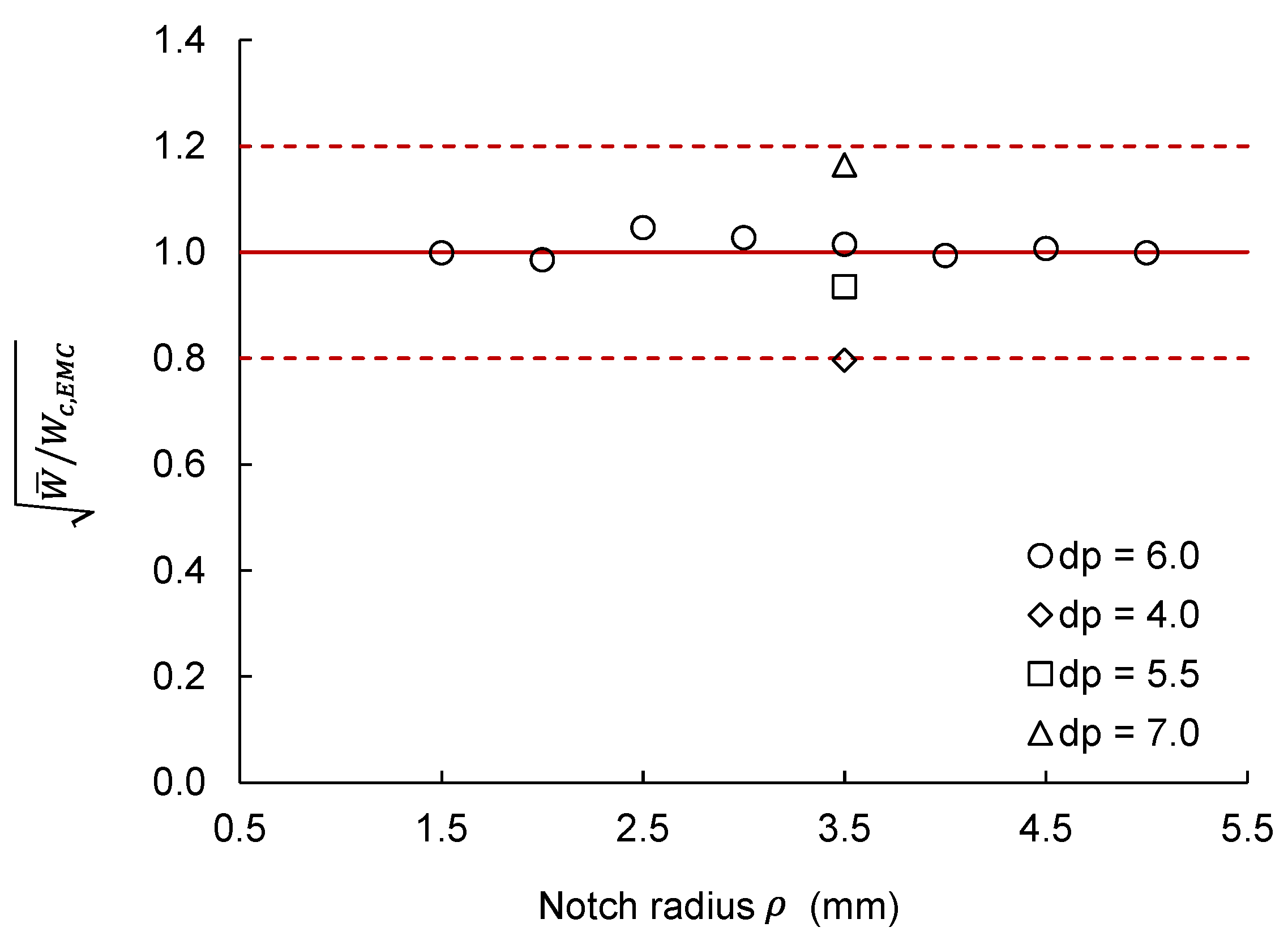
3.3. Predictions of Fracture Load Using EMC-SED
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- James, M.N.; Lu, Y.; Christopher, C.J.; Patterson, E.A. Crack Path Support for Deformation Mechanisms in Fatigue of Polycarbonate. Eng. Fract. Mech. 2013, 108, 89–97. [Google Scholar] [CrossRef]
- James, M.N.; Christopher, C.J.; Lu, Y.; Patterson, E.A. Fatigue Crack Growth and Craze-Induced Crack Tip Shielding in Polycarbonate. Polymer 2012, 53, 1558–1570. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Zhang, W.; Zhang, P. Optimization of Injection Molding Process Parameters to Improve the Mechanical Performance of Polymer Product against Impact. Int. J. Adv. Manuf. Technol. 2015, 76, 2199–2208. [Google Scholar] [CrossRef]
- Merah, N.; Albinmousa, J. Experimental and Numerical Determination of Mixed Mode Crack Extension Angle. J. Test. Eval. 2009, 37, 101668. [Google Scholar] [CrossRef]
- Albinmousa, J.; Merah, N.; Khan, S.M.A. A Model for Calculating Geometry Factors for a Mixed-Mode I–II Single Edge Notched Tension Specimen. Eng. Fract. Mech. 2011, 78, 3300–3307. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, T.; Wang, J.; Zhang, W. Experimentation and Modeling of the Tension Behavior of Polycarbonate at High Strain Rates. Polymers 2016, 8, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ASM International. Mechanical Testing and Evaluation. In ASM Handbook, 11th ed.; Kuhn, H., Ed.; ASM International: Materials Park, OH, USA, 2000; ISBN 978-0-87170-389-7. [Google Scholar]
- Sarva, S.; Boyce, M. Mechanics of Polycarbonate during High-Rate Tension. JOMMS 2007, 2, 1853–1880. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, B.M.; Tippur, H.V. Dynamic Mixed-Mode Fracture Behaviors of PMMA and Polycarbonate. Eng. Fract. Mech. 2017, 176, 186–212. [Google Scholar] [CrossRef]
- Fu, S.; Wang, Y.; Wang, Y. Tension Testing of Polycarbonate at High Strain Rates. Polym. Test. 2009, 28, 724–729. [Google Scholar] [CrossRef]
- Cao, K.; Ma, X.; Zhang, B.; Wang, Y.; Wang, Y. Tensile Behavior of Polycarbonate over a Wide Range of Strain Rates. Mater. Sci. Eng. A 2010, 527, 4056–4061. [Google Scholar] [CrossRef]
- Dwivedi, A.; Bradley, J.; Casem, D. Mechanical Response of Polycarbonate with Strength Model Fits; Dynamic Science Inc.: Aberdeen, MD, USA, 2012. [Google Scholar]
- Safari, K.H.; Zamani, J.; Ferreira, F.J.; Guedes, R.M. Constitutive Modeling of Polycarbonate during High Strain Rate Deformation. Polym. Eng. Sci. 2013, 53, 752–761. [Google Scholar] [CrossRef]
- Foster, M.; Love, B.; Kaste, R.; Moy, P. The Rate Dependent Tensile Response of Polycarbonate and Poly-Methylmethacrylate. J. Dyn. Behav. Mater. 2015, 1, 162–175. [Google Scholar] [CrossRef] [Green Version]
- Al-Juaid, A.A.; Othman, R. Modeling of the Strain Rate Dependency of Polycarbonate’s Yield Stress: Evaluation of Four Constitutive Equations. J. Eng. 2016, 2016, 6315421. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhou, H.; Huang, Z.; Zhang, Y.; Zhao, X. Constitutive Modeling of Polycarbonate over a Wide Range of Strain Rates and Temperatures. Mech. Time-Depend. Mater. 2017, 21, 97–117. [Google Scholar] [CrossRef]
- Rey Calderón, A.A.; Díaz Díaz, A. New Aspects in the Mechanical Behavior of a Polycarbonate Found by an Experimental Study. Adv. Mater. Sci. Eng. 2018, 2018, 1540919. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Xu, Y. Mechanical Properties of Polycarbonate: Experiment and Modeling for Aeronautical and Aerospace Applications; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 0-12-820454-0. [Google Scholar]
- Gearing, B.P.; Anand, L. Notch-Sensitive Fracture of Polycarbonate. Int. J. Solids Struct. 2004, 41, 827–845. [Google Scholar] [CrossRef]
- Takaffoli, M.; Hangalur, G.; Bakker, R.; Chandrashekar, N. Thermo-Visco-Hyperelastic Behavior of Polycarbonate in Forming of a Complex Geometry. J. Manuf. Process. 2020, 57, 105–113. [Google Scholar] [CrossRef]
- Malwad, D.; Tungikar, V. Development and Performance Testing of Reflector Materials for Concentrated Solar Power: A Review. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Alder, F.A.; Charrault, E.; Zuber, K.; Fabretto, M.; Patil, A.; Murphy, P.; Llusca, M. Fabrication of Robust Solar Mirrors on Polymeric Substrates by Physical Vapor Deposition Technique. Sol. Energy Mater. Sol. Cells 2020, 209, 110476. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A Finite-Volume-Energy Based Approach to Predict the Static and Fatigue Behavior of Components with Sharp V-Shaped Notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Susmel, L.; Taylor, D. On the Use of the Theory of Critical Distances to Predict Static Failures in Ductile Metallic Materials Containing Different Geometrical Features. Eng. Fract. Mech. 2008, 75, 4410–4421. [Google Scholar] [CrossRef]
- Chebat, F.; Peron, M.; Viespoli, L.M.; Welo, T.; Berto, F. Fatigue Strength Assessment of Steel Rollers: On the Reliability of the Strain Energy Density Approach on Real Components. Appl. Sci. 2018, 8, 1015. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.-P.; Liu, Y.; Liu, Q.; Yu, Z.-Y. Strain Energy Gradient-Based LCF Life Prediction of Turbine Discs Using Critical Distance Concept. Int. J. Fatigue 2018, 113, 33–42. [Google Scholar] [CrossRef]
- Cicero, S.; Fuentes, J.D.; Torabi, A.R. Using the Equivalent Material Concept and the Average Strain Energy Density to Analyse the Fracture Behaviour of Structural Materials. Appl. Sci. 2020, 10, 1601. [Google Scholar] [CrossRef] [Green Version]
- Albinmousa, J.; Peron, M.; Jose, J.; Abdelaal, A.F.; Berto, F. Fatigue of V-Notched ZK60 Magnesium Samples: X-Ray Damage Evolution Characterization and Failure Prediction. Int. J. Fatigue 2020, 139, 105734. [Google Scholar] [CrossRef]
- Albinmousa, J. Fatigue Failure Prediction of U-Notched ZK60 Magnesium Samples Using the Strain Energy Density Approach. Metals 2021, 11, 113. [Google Scholar] [CrossRef]
- Torabi, A.R. Estimation of Tensile Load-Bearing Capacity of Ductile Metallic Materials Weakened by a V-Notch: The Equivalent Material Concept. Mater. Sci. Eng. A 2012, 536, 249–255. [Google Scholar] [CrossRef]
- Torabi, A.R. Ultimate Bending Strength Evaluation of U-Notched Ductile Steel Samples under Large-Scale Yielding Conditions. Int. J. Fract. 2013, 180, 261–268. [Google Scholar] [CrossRef]
- Torabi, A.R.; Habibi, R.; Mohammad Hosseini, B. On the Ability of the Equivalent Material Concept in Predicting Ductile Failure of U-Notches under Moderate- and Large-Scale Yielding Conditions. Phys. Mesomech. 2015, 18, 337–347. [Google Scholar] [CrossRef]
- Gómez, F.J.; Elices, M.; Valiente, A. Cracking in PMMA Containing U-Shaped Notches. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 795–803. [Google Scholar] [CrossRef]
- Torabi, A.R.; Rahimi, A.S.; Ayatollahi, M.R. Tensile Fracture Analysis of a Ductile Polymeric Material Weakened by U-Notches. Polym. Test. 2017, 64, 117–126. [Google Scholar] [CrossRef]
- Bahadur, S. Strain Hardening Equation and the Prediction of Tensile Strength of Rolled Polymers. Polym. Eng. Sci. 1973, 13, 266–272. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G.C. On the Crack Extension in Plates Under Plane Loading and Transverse Shear. J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Rahimi, A.S.; Ayatollahi, M.R.; Torabi, A.R. Fracture Study in Notched Ductile Polymeric Plates Subjected to Mixed Mode I/II Loading: Application of Equivalent Material Concept. Eur. J. Mech. A/Solids 2018, 70, 37–43. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Zolfagharian, A. Fracture and Load-Carrying Capacity of 3D-Printed Cracked Components. Extrem. Mech. Lett. 2020, 37, 100692. [Google Scholar] [CrossRef]
- D20 Committee. Test Method for Tensile Properties of Plastics; ASTM International: West Conshohocken, PE, USA, 2014. [Google Scholar]
- Yosibash, Z.; Bussiba, A.; Gilad, I. Failure Criteria for Brittle Elastic Materials. Int. J. Fract. 2004, 125, 307–333. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. Recent Developments in Brittle and Quasi-Brittle Failure Assessment of Engineering Materials by Means of Local Approaches. Mater. Sci. Eng. R Rep. 2014, 75, 1–48. [Google Scholar] [CrossRef]
- Torabi, A.R.; Berto, F.; Campagnolo, A.; Akbardoost, J. Averaged Strain Energy Density Criterion to Predict Ductile Failure of U-Notched Al 6061-T6 Plates under Mixed Mode Loading. Theor. Appl. Fract. Mech. 2017, 91, 86–93. [Google Scholar] [CrossRef]
- Lazzarin, P.; Berto, F.; Zappalorto, M. Rapid Calculations of Notch Stress Intensity Factors Based on Averaged Strain Energy Density from Coarse Meshes: Theoretical Bases and Applications. Int. J. Fatigue 2010, 32, 1559–1567. [Google Scholar] [CrossRef]





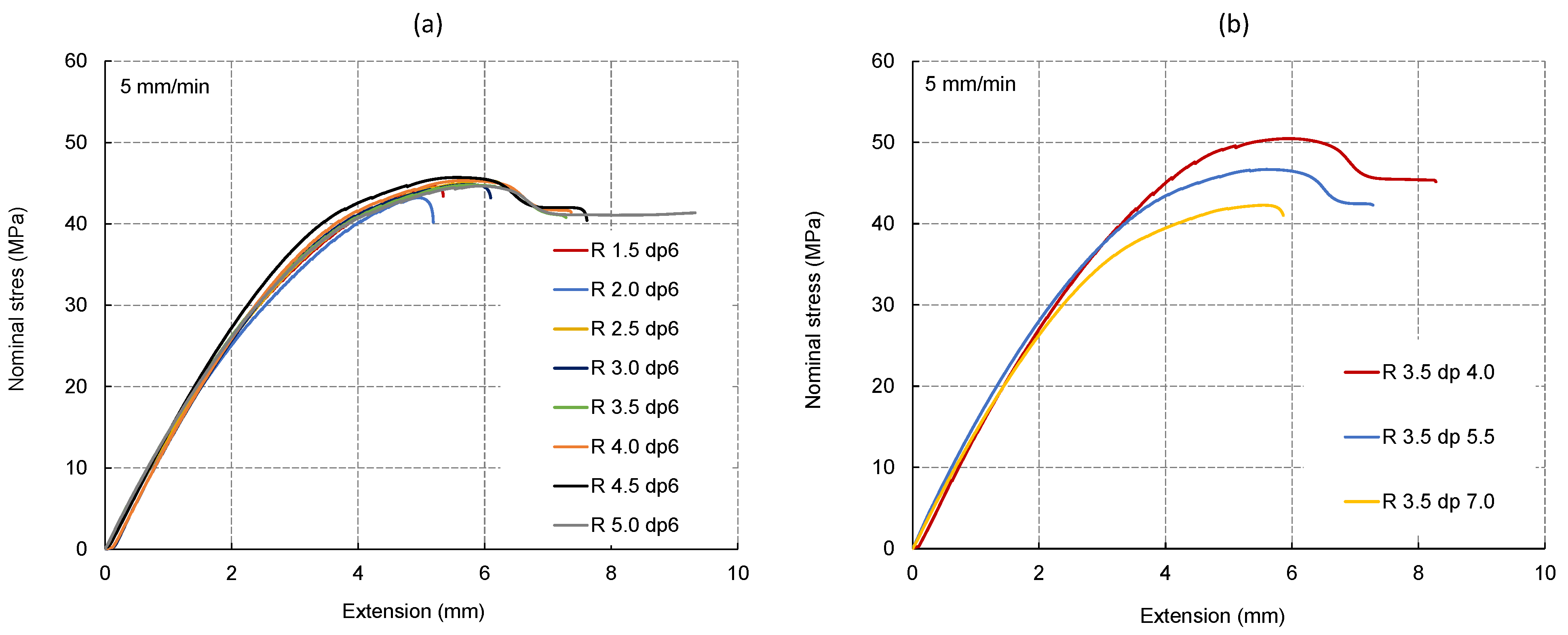




| (mm) | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 4.0 | 5.5 | 7.0 |
| (mm) | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 3.5 | 3.5 | 3.5 |
| | | | | | |
|---|---|---|---|---|---|
| Average | 2267.6 | 36.1 | 0.0177 | 66.0 | 0.055 |
| St. Dev | 47.01 | 1.96 | 0.0013 | 0.59 | 0.0029 |
| St. Dev (N) | ||||||
|---|---|---|---|---|---|---|
| 1.5 | 6.0 | 6870.6 | 6954.4 | 6832.4 | 6885.8 | 50.94 |
| 2.0 | 6.0 | 6914.0 | 6741.0 | 6456.5 | 6703.8 | 188.63 |
| 2.5 | 6.0 | 6966.0 | 7063.0 | 7026.0 | 7018.3 | 39.97 |
| 3.0 | 6.0 | 6996.3 | 6988.1 | 6410.8 | 6798.4 | 274.12 |
| 3.5 | 6.0 | 6614.9 | 6415.0 | 6882.0 | 6637.3 | 191.33 |
| 4.0 | 6.0 | 6510.0 | 6495.0 | 6341.5 | 6448.8 | 76.14 |
| 4.5 | 6.0 | 6583.0 | 6600.0 | 6316.0 | 6499.7 | 130.06 |
| 5.0 | 6.0 | 6566.0 | 6444.0 | 6271.0 | 6427.0 | 121.03 |
| 3.5 | 4.0 | 7045.0 | 7115.0 | 7003.0 | 7054.3 | 46.20 |
| 3.5 | 5.5 | 6554.0 | 6616.0 | 6577.0 | 6582.3 | 25.59 |
| 3.5 | 7.0 | 6582.0 | 6669.0 | 6522.0 | 6591.0 | 60.35 |
| 2.0 | 6.0 | 6804.1 | 6703.8 | 1.50 |
| 2.5 | 6.0 | 6708.3 | 7018.3 | −4.42 |
| 3.0 | 6.0 | 6616.1 | 6798.4 | −2.68 |
| 3.5 | 6.0 | 6540.6 | 6637.3 | −1.46 |
| 4.0 | 6.0 | 6488.3 | 6448.8 | 0.61 |
| 4.5 | 6.0 | 6455.7 | 6499.7 | −0.68 |
| 5.0 | 6.0 | 6435.6 | 6427.0 | 0.13 |
| 3.5 | 4.0 | 8856.9 | 7054.3 | 25.55 |
| 3.5 | 5.5 | 7039.0 | 6582.3 | 6.94 |
| 3.5 | 7.0 | 5661.0 | 6591.0 | −14.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albinmousa, J.; AlSadah, J.; Hawwa, M.A.; Al-Qahtani, H.M. Estimation of Mode I Fracture of U-Notched Polycarbonate Specimens Using the Equivalent Material Concept and Strain Energy Density. Appl. Sci. 2021, 11, 3370. https://doi.org/10.3390/app11083370
Albinmousa J, AlSadah J, Hawwa MA, Al-Qahtani HM. Estimation of Mode I Fracture of U-Notched Polycarbonate Specimens Using the Equivalent Material Concept and Strain Energy Density. Applied Sciences. 2021; 11(8):3370. https://doi.org/10.3390/app11083370
Chicago/Turabian StyleAlbinmousa, Jafar, Jihad AlSadah, Muhammad A. Hawwa, and Hussain M. Al-Qahtani. 2021. "Estimation of Mode I Fracture of U-Notched Polycarbonate Specimens Using the Equivalent Material Concept and Strain Energy Density" Applied Sciences 11, no. 8: 3370. https://doi.org/10.3390/app11083370






