Equivalent Electrical Circuit Modeling of CNT-Based Transparent Electrodes
Abstract
:1. Introduction
2. Modeling of a Carbon Nanotube
2.1. Atomistic Modeling
2.2. Continuum Modeling
2.3. Equivalent Transmission Line (TL) Modeling
3. Electrical Modeling of CNT Networks
3.1. Percolation Theory for the Modeling of CNT/Polymer Composites Conductivity
3.2. 2D Models for CNT Networks Simulations
3.3. Layered 2D Models for CNT Network Simulations
3.4. 3D Models for CNT Networks Simulations
3.4.1. Resistive 3D Networks
3.4.2. Resistive-Capacitive 3D Networks
4. Discussion
- Is the thickness of the CNT-based conductive layer small enough to assume that the CNT network is planar and the percolative paths are all lying on the conduction plane?
- Is the quantity of interest frequency-dependent?
- Is the CNT network dispersed inside a material that contributes to determining the quantity of interest in a non-negligible way?
- Are the CNTs mostly metallic, semiconducting, or mixed?
- Are there experimental data available?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Yu, L.; Shearer, C.; Shapter, J. Recent Development of Carbon Nanotube Transparent Conductive Films. Chem. Rev. 2016, 116, 13413–13453. [Google Scholar] [CrossRef]
- Zhou, Y.; Azumi, R. Carbon nanotube based transparent conductive films: progress, challenges, and perspectives. Sci. Technol. Adv. Mater. 2016, 17, 493–516. [Google Scholar] [CrossRef] [Green Version]
- Salvatierra, R.V.; Cava, C.E.; Roman, L.S.; Zarbin, A.J.G. ITO-Free and Flexible Organic Photovoltaic Device Based on High Transparent and Conductive Polyaniline/Carbon Nanotube Thin Films. Adv. Funct. Mater. 2013, 23, 1490–1499. [Google Scholar] [CrossRef]
- Saw, L.N.; Mariatti, M.; Azura, A.R.; Azizan, A.; Kim, J.K. Transparent, electrically conductive, and flexible films made from multiwalled carbon nanotube/epoxy composites. Compos. Part B Eng. 2012, 43, 2973–2979. [Google Scholar] [CrossRef]
- Wang, R.; Yu, H.; Dirican, M.; Chen, L.; Fang, D.; Tian, Y.; Yan, C.; Xie, J.; Jia, D.; Liu, H.; et al. Highly Transparent, Thermally Stable, and Mechanically Robust Hybrid Cellulose-Nanofiber/Polymer Substrates for the Electrodes of Flexible Solar Cells. ACS Appl. Energy Mater. 2020, 3, 785–793. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Hecht, D.S.; Gruner, G. Percolation in transparent and conducting carbon nanotube networks. Nano Lett. 2004, 4, 2513–2517. [Google Scholar] [CrossRef]
- Kong, B.S.; Jung, D.H.; Oh, S.K.; Han, C.S.; Jung, H.T. Single-walled carbon nanotube gold nanohybrids: Application in highly effective transparent and conductive films. J. Phys. Chem. C 2007, 111, 8377–8382. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, C. The race to replace tin-doped indium oxide: Which material will win? ACS Nano 2010, 4, 11–14. [Google Scholar] [CrossRef]
- Marin, E.G.; Perucchini, M.; Marian, D.; Iannaccone, G.; Fiori, G. Modeling of Electron Devices Based on 2-D Materials. IEEE Trans. Electron Devices 2018, 65, 4167–4179. [Google Scholar] [CrossRef]
- Znidarsic, A.; Kaskela, A.; Laiho, P.; Gaberscek, M.; Ohno, Y.; Nasibulin, A.G.; Kauppinen, E.I.; Hassanien, A. Spatially resolved transport properties of pristine and doped single-walled carbon nanotube networks. J. Phys. Chem. C 2013, 117, 13324–13330. [Google Scholar] [CrossRef]
- Schießl, S.P.; De Vries, X.; Rother, M.; Massé, A.; Brohmann, M.; Bobbert, P.A.; Zaumseil, J. Modeling carrier density dependent charge transport in semiconducting carbon nanotube networks. Phys. Rev. Mater. 2017, 1, 46003. [Google Scholar] [CrossRef]
- Statz, M.; Schneider, S.; Berger, F.J.; Lai, L.; Wood, W.A.; Abdi-Jalebi, M.; Leingang, S.; Himmel, H.J.; Zaumseil, J.; Sirringhaus, H. Charge and thermoelectric transport in polymer-sorted semiconducting single-walled carbon nanotube networks. ACS Nano 2020, 14, 15552–15565. [Google Scholar] [CrossRef]
- Rafiee, R.; Moghadam, R.M. On the modeling of carbon nanotubes: A critical review. Compos. Part B Eng. 2014, 56, 435–449. [Google Scholar] [CrossRef]
- Pal, G.; Kumar, S. Modeling of carbon nanotubes and carbon nanotube-polymer composites. Prog. Aerosp. Sci. 2016, 80, 33–58. [Google Scholar] [CrossRef]
- Maiti, A. Multiscale modeling with carbon nanotubes. Microelectron. J. 2008, 39, 208–221. [Google Scholar] [CrossRef] [Green Version]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput. Mater. Sci. 2012, 51, 303–313. [Google Scholar] [CrossRef]
- Burke, P.J. An RF circuit model for carbon nanotubes. IEEE Trans. Nanotechnol. 2003, 2, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Portal, D.; Artacho, E.; Soler, J.M.; Rubio, A.; Ordejon, P. Ab-initio structural, elastic, and vibrational properties of carbon nanotubes. Phys. Rev. B-Condens. Matter Mater. Phys. 1998, 59, 12678–12688. [Google Scholar] [CrossRef] [Green Version]
- Prylutskyy, Y.I.; Durov, S.S.; Ogloblya, O.V.; Buzaneva, E.V.; Scharff, P. Molecular dynamics simulation of mechanical, vibrational and electronic properties of carbon nanotubes. Comput. Mater. Sci. 2000, 17, 352–355. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, Y.; Geubelle, P.H.; Hwang, K. On the continuum modeling of carbon nanotubes. Acta Mech. Sin. Xuebao 2002, 18, 528–536. [Google Scholar] [CrossRef]
- Odegard, G.M.; Gates, T.S.; Nicholson, L.M.; Wise, K.E. Equivalent-continuum modeling of nano-structured materials. Compos. Sci. Technol. 2002, 62, 1869–1880. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Banerjee, K. Performance analysis of carbon nanotube interconnects for VLSI applications. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, Digest of Technical Papers, (ICCAD 2005), San Jose, CA, USA, 6–10 November 2005; pp. 383–390. [Google Scholar]
- Lamberti, P.; Tucci, V.; Sarto, M.S.; Tamburrano, A. Impact of physical parameters on time-delay performances of CNT-based interconnects. In Proceedings of the 2009 9th IEEE Conference on Nanotechnology (IEEE NANO 2009), Genoa, Italy, 26–30 July 2009; pp. 54–57. [Google Scholar]
- Sarto, M.S.; Tamburrano, A.; D’Amore, M. New electron-waveguide-based modeling for carbon nanotube interconnects. IEEE Trans. Nanotechnol. 2009, 8, 214–225. [Google Scholar] [CrossRef]
- Sarto, M.S.; Tamburrano, A. Single-conductor transmission-line model of multiwall carbon nanotubes. IEEE Trans. Nanotechnol. 2010, 9, 82–92. [Google Scholar] [CrossRef]
- Green, A.A.; Hersam, M.C. Colored semitransparent conductive coatings consisting of monodisperse metallic single-walled carbon nanotubes. Nano Lett. 2008, 8, 1417–1422. [Google Scholar] [CrossRef] [PubMed]
- Topinka, M.A.; Rowell, M.W.; Goldhaber-Gordon, D.; McGehee, M.D.; Hecht, D.S.; Gruner, G. Charge transport in interpenetrating networks of semiconducting and metallic carbon nanotubes. Nano Lett. 2009, 9, 1866–1871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuhrer, M.S.; Nygård, J.; Shih, L.; Forero, M.; Yoon, Y.G.; Mazzoni, M.S.C.; Choi, H.J.; Ihm, J.; Louie, S.G.; Zettl, A.; et al. Crossed nanotube junctions. Science (80-. ) 2000, 288, 494–497. [Google Scholar] [CrossRef] [Green Version]
- Stadermann, M.; Papadakis, S.J.; Falvo, M.R.; Novak, J.; Snow, E.; Fu, Q.; Liu, J.; Fridman, Y.; Boland, J.J.; Superfine, R.; et al. Nanoscale study of conduction through carbon nanotube networks. Phys. Rev. B-Condens. Matter Mater. Phys. 2004, 69, 201402. [Google Scholar] [CrossRef] [Green Version]
- Nirmalraj, P.N.; Lyons, P.E.; De, S.; Coleman, J.N.; Boland, J.J. Electrical Connectivity in Single-Walled Carbon Nanotube Networks. Nano Lett. 2009, 9, 3890–3895. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Essam, J.W. Percolation theory. Reports Prog. Phys. 1980, 43, 833–912. [Google Scholar] [CrossRef]
- Marsden, A.J.; Papageorgiou, D.G.; Vallés, C.; Liscio, A.; Palermo, V.; Bissett, M.A.; Young, R.J.; Kinloch, I.A. Electrical percolation in graphene-polymer composites. 2D Mater. 2018, 5. [Google Scholar] [CrossRef] [Green Version]
- McLachlan, D.S.; Chiteme, C.; Park, C.; Wise, K.E.; Lowther, S.E.; Lillehei, P.T.; Siochi, E.J.; Harrison, J.S. AC and DC percolative conductivity of single wall carbon nanotube polymer composites. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 3273–3287. [Google Scholar] [CrossRef]
- Bottacchi, F.; Bottacchi, S.; Späth, F.; Namal, I.; Hertel, T.; Anthopoulos, T.D. Nanoscale Charge Percolation Analysis in Polymer-Sorted (7,5) Single-Walled Carbon Nanotube Networks. Small 2016, 12, 4211–4221. [Google Scholar] [CrossRef]
- Wen, L.; Zhang, M. A theoretical and numerical study on percolation mechanism of carbon nanotube network. In Proceedings of the 16th International Conference on Nanotechnology-IEEE NANO 2016, Sendai, Japan, 22–25 August 2016; pp. 959–962. [Google Scholar]
- Jung, S.; Choi, H.W.; Mocanu, F.C.; Shin, D.W.; Chowdhury, M.F.; Han, S.D.; Suh, Y.H.; Cho, Y.; Lee, H.; Fan, X.; et al. Modeling Electrical Percolation to optimize the Electromechanical Properties of CNT/Polymer Composites in Highly Stretchable Fiber Strain Sensors. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, J.; Zhang, X. Modulating the percolation network of polymer nanocomposites for flexible sensors. J. Appl. Phys. 2020, 128, 220901. [Google Scholar] [CrossRef]
- Hu, N.; Masuda, Z.; Yan, C.; Yamamoto, G.; Fukunaga, H.; Hashida, T. The electrical properties of polymer nanocomposites with carbon nanotube fillers. Nanotechnology 2008, 19, 215701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eken, A.E.; Tozzi, E.J.; Klingenberg, D.J.; Bauhofer, W. A simulation study on the combined effects of nanotube shape and shear flow on the electrical percolation thresholds of carbon nanotube/polymer composites. J. Appl. Phys. 2011, 109, 084342. [Google Scholar] [CrossRef]
- Balberg, I. The physical fundamentals of the electrical conductivity in nanotube-based composites. J. Appl. Phys. 2020, 128, 204304. [Google Scholar] [CrossRef]
- Tarasevich, Y.Y.; Vodolazskaya, I.V.; Eserkepov, A.V.; Goltseva, V.A.; Selin, P.G.; Lebovka, N.I. Simulation of the electrical conductivity of two-dimensional films with aligned rod-like conductive fillers: Effect of the filler length dispersity. J. Appl. Phys. 2018, 124, 145106. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Nam, J. Systematic analysis for electrical conductivity of network of conducting rods by Kirchhoff’s laws and block matrices. J. Appl. Phys. 2018, 124, 215104. [Google Scholar] [CrossRef]
- Frank, D.J.; Lobb, C.J. Highly efficient algorithm for percolative transport studies in two dimensions. Phys. Rev. B 1988, 37, 302–307. [Google Scholar] [CrossRef] [PubMed]
- Tripathy, S.; Bose, B.; Chakrabarti, P.P.; Bhattacharyya, T.K. Resistive Analysis of Scattering-Dependent Electrical Transport in Single-Wall Carbon-Nanotube Networks. IEEE Trans. Electron Devices 2020, 67, 5676–5684. [Google Scholar] [CrossRef]
- Behnam, A.; Ural, A. Computational study of geometry-dependent resistivity scaling in single-walled carbon nanotube films. Phys. Rev. B-Condens. Matter Mater. Phys. 2007, 75, 125432. [Google Scholar] [CrossRef] [Green Version]
- Hicks, J.; Behnam, A.; Ural, A. Resistivity in percolation networks of one-dimensional elements with a length distribution. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2009, 79, 012102. [Google Scholar] [CrossRef] [Green Version]
- Lamberti, P.; Mousavi, S.A.; Spinelli, G.; Tucci, V.; Wagner, V. Fabrication and charge transport modeling of thin-film transistor based on carbon nanotubes network. IEEE Trans. Nanotechnol. 2014, 13, 795–804. [Google Scholar] [CrossRef]
- Colasanti, S.; Bhatt, V.D.; Abdelhalim, A.; Lugli, P. 3-D Percolative Model-Based Multiscale Simulation of Randomly Aligned Networks of Carbon Nanotubes. IEEE Trans. Electron Devices 2016, 63, 1346–1351. [Google Scholar] [CrossRef]
- De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. Numerical investigation on the influence factors of the electrical properties of carbon nanotubes-filled composites. J. Appl. Phys. 2013, 113, 244301. [Google Scholar] [CrossRef]
- De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. A morphological and structural approach to evaluate the electromagnetic performances of composites based on random networks of carbon nanotubes. J. Appl. Phys. 2014, 115, 154311. [Google Scholar] [CrossRef]
- Spinelli, G.; Giustiniani, A.; Lamberti, P.; Tucci, V.; Zamboni, W. Numerical study of electrical behaviour in carbon nanotube composites. Int. J. Appl. Electromagn. Mech. 2012, 39, 21–27. [Google Scholar] [CrossRef]
- De Vivo, B.; Lamberti, P.; Tucci, V.; Kuzhir, P.P.; Maksimenko, S.A.; Bellucci, S. Equivalent electric circuits for the simulation of carbon Nanotube-epoxy composites. IEEE Trans. Nanotechnol. 2013, 12, 696–703. [Google Scholar] [CrossRef]
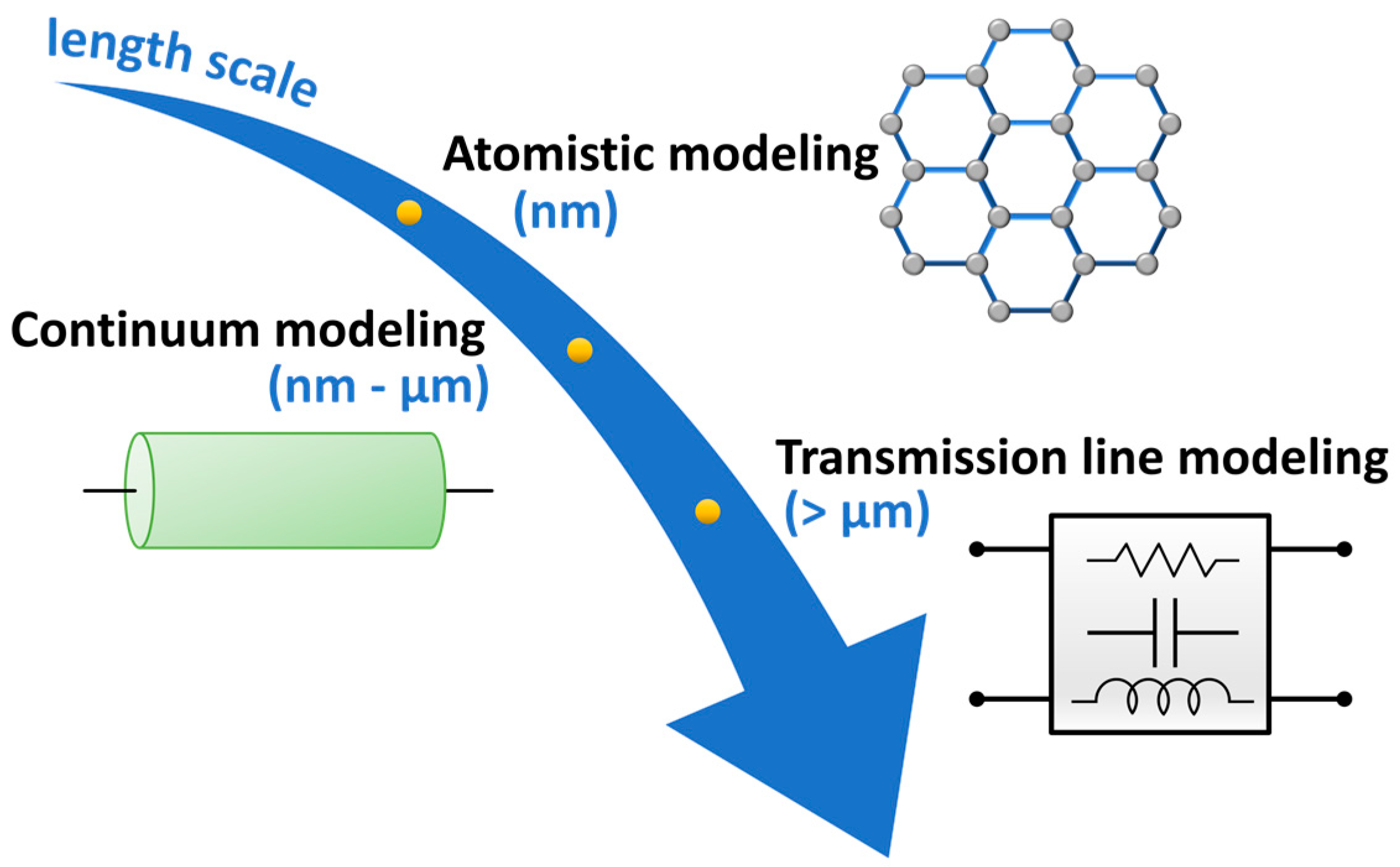



| Model | Description | Application | Length Scale | Strengths | Limitations |
|---|---|---|---|---|---|
| Atomistic modeling | Computation of the position of atoms in the nanostructure for the solution of the Schrödinger equation | Extraction of the quantum-level properties of the CNT | nm | Very high accuracy | Very high computational burden requires limiting the analysis to a few hundreds of atoms. |
| Continuum modeling | Simulation of an equivalent continuum structure with distributed effective material properties | Effective behavior of the CNT | nm-μm | Allows multiphysical simulation of the CNT behavior | Neglects the discrete nature of the atomic structure. |
| Transmission line modeling | Analysis of the electric signal propagation, based on equivalent circuit parameters describing the CNT resistive, capacitive, and inductive properties | Computation of the electrical response of the CNT | >μm | Fast simulation of the electrical properties | Application is limited to the electrical analysis. |
| Ref. | CNT Configuration | Hosting Material | CNTMetallic Resistance | Tunneling Resistance | Dynamic Elements | Solution Method | Outcome | Notes | |
|---|---|---|---|---|---|---|---|---|---|
| Burke, 2003 [17] | Single CNT | n.a. | No | No | Kinetic inductance, quantum and electrostatic capacitance | 2-port network analysis | CNT frequency-dependent electrical impedance computation (theoretical) | Transmission line model, frequency-dependent | |
| Behnam et al.,2007 [46] | Layered 2D network | n.a. | Yes | Effective resistance (indirectcomputation) | No | Kirchhoff’s equations in terms of node voltages | Computation of the CNT layer resistivity, compared to measurement of layers with different length and width | Accounts for the thickness increasing the n. of conductive planes | |
| De Vivo et al., 2013 [50,51] | 3D CNT-filled composite | R-C parallel | Yes | Yes | Capacitance between CNTs | Parallel of RC branches of existing conductive paths | Investigation of electromagnetic performance of nanocomposites. Percolation threshold compared with literature values | Impenetrable CNTs, comprisingmatrix | |
| Lamberti et al., 2014 [48] | 3D network of SWCNTs | n.a. | Yes | Yes | No | Parallel of resistive branches. | Assessment of CNT-based transistors performance, validated by measurement of TFT on-resistance | Metallic and semiconducting CNTs | |
| Colasanti et al., 2016 [49] | 3D network | n.a. | Indirectly computed by Ohm’s law, comprises DOS | Experim. values taken from the literature | No | SPICE circuitsimulator | CNT network behavior under different working conditions. Comparison with the resistance measurement of a 3 × 3 mm2 spray-coated layer | RRN of cylindrical tubes, bending at the intersections | |
| Schießl et al., 2017 [11] | 2D network of semiconducting SWCNT | n.a. | No | Yes. Bond conductivity accounting for the DOS | No | Kirchhoff’s equations | Assessment of carrier mobility in semiconducting CNT networks by varying the carriers density, compared with experiments | RRN of impenetrating 1D sticks | |
| Sarto et al., 2009 [24,25] | SWCNT, SWCNT bundle, MWCNT | n.a. | Intrinsic resistance and diffusion resistance | Magnetic and kinetic inductance, quantum and electrostatic capacitance | 2-port network analysis | Computation of MWCNT and SWCNT bundles input impedance, study of CNT interconnects performance | Electron-waveguide-based TL modeling | ||
| Tarasevic et al., 2018 [42] | 2D network ofconductive rods | Fixed value of conductivityσp = 2 × 106 a.u. for rods and σm = 2 a.u. for insulating matrix | No | Franke-Lobb algorithm for RRNs | Computation of the electrical conductivity of 2D CNT films (theoretical) | Zero-width intersecting rods with tunable anisotropy | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Mura, M.; Lamberti, P.; Tucci, V. Equivalent Electrical Circuit Modeling of CNT-Based Transparent Electrodes. Appl. Sci. 2021, 11, 3408. https://doi.org/10.3390/app11083408
La Mura M, Lamberti P, Tucci V. Equivalent Electrical Circuit Modeling of CNT-Based Transparent Electrodes. Applied Sciences. 2021; 11(8):3408. https://doi.org/10.3390/app11083408
Chicago/Turabian StyleLa Mura, Monica, Patrizia Lamberti, and Vincenzo Tucci. 2021. "Equivalent Electrical Circuit Modeling of CNT-Based Transparent Electrodes" Applied Sciences 11, no. 8: 3408. https://doi.org/10.3390/app11083408
APA StyleLa Mura, M., Lamberti, P., & Tucci, V. (2021). Equivalent Electrical Circuit Modeling of CNT-Based Transparent Electrodes. Applied Sciences, 11(8), 3408. https://doi.org/10.3390/app11083408










