An All-Mach Number HLLC-Based Scheme for Multi-Phase Flow with Surface Tension
Abstract
:1. Introduction
2. Mathematical Formulation
2.1. Governing Equations
2.2. Equation of State (EOS)
2.3. Mixture Rules
2.4. Thermal EOS
3. Numerical Methodology
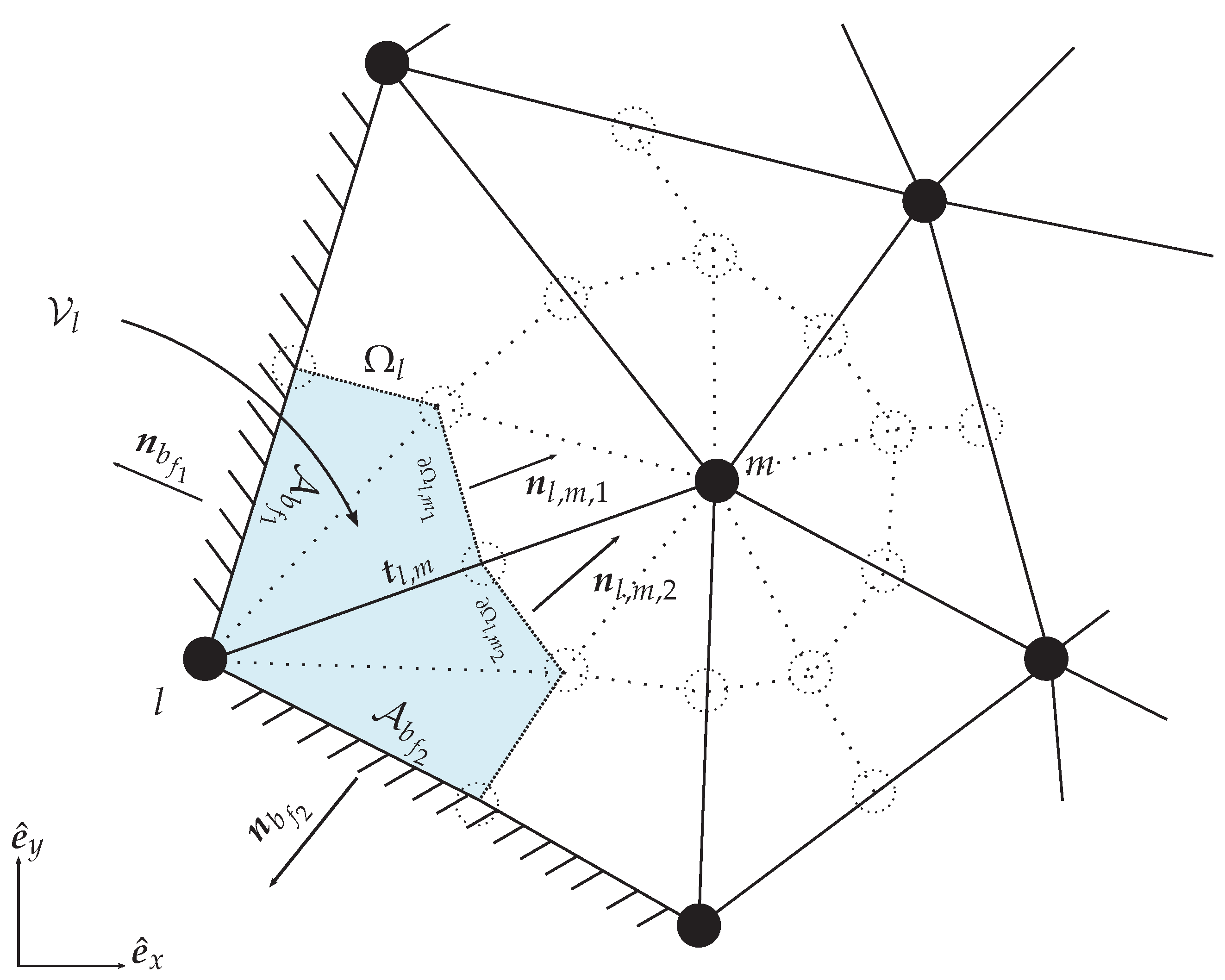
3.1. Finite Volume Dual-Cell Mesh
3.2. Second-Order Spatial Reconstruction
3.3. Temporal Integration and Stability
3.4. HLLC Solver
Consistency Conditions
3.5. Inviscid HLLC-CICSAM Edge Flux
3.5.1. Numerical Energy Consistency Criteria
3.5.2. Intermediate Star-State
3.5.3. Face-Flux
3.5.4. Surface Tension Term
3.6. Curvature Reconstruction
3.7. VoF Equation
3.8. Summary of Algorithm
| Algorithm 1: HLLC-CICSAM |
 |
4. Numerical Test Cases
4.1. 1-D Problems
Gas–Liquid Riemann Problem
4.2. 2-D Problems
4.2.1. Advecting Bubble in an Oblique Velocity Field
4.2.2. Underwater Explosion
4.2.3. Shock-Bubble Interaction
4.2.4. Spurious Currents in a Static Bubble
4.2.5. Oscillating Bubble
4.2.6. Rayleigh–Plesset Collapse Problem
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Thermal EOS
Appendix B. Eigenvalues and Vectors
Appendix C. Derivation of Star-State
References
- Garrick, D.P.; Owkes, M.; Regele, J.D. A finite-volume HLLC-based scheme for compressible interfacial flows with surface tension. J. Comput. Phys. 2017, 339, 46–67. [Google Scholar] [CrossRef] [Green Version]
- Sussman, M. A second order coupled level set and volume-of-fluid method for computing growth and collapse of vapor bubbles. J. Comput. Phys. 2003, 187, 110–136. [Google Scholar] [CrossRef]
- Cummins, S.; Francois, M.; Kothe, D. Estim. Curvature Vol. Fractions. Comput. Struct. 2005, 83, 425–434. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A Continuum Method for Modeling Surface-Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, F.; Yang, X.; Li, Y. Measurement of Gas-Oil Two-Phase Flow Patterns by Using CNN Algorithm Based on Dual ECT Sensors with Venturi Tube. Sensors 2020, 20, 1200. [Google Scholar] [CrossRef] [Green Version]
- Roshani, M.; Phan, G.; Roshani, G.H.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil-water three phase flows. Measurement 2021, 168. [Google Scholar] [CrossRef]
- Fang, L.; Zeng, Q.; Wang, F.; Faraj, Y.; Zhao, Y.; Lang, Y.; Wei, Z. Identification of two-phase flow regime using ultrasonic phased array. Flow Meas. Instrum. 2020, 72. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.T.T.; Ali, P.J.M.; Roshani, G.H.; Hanus, R.; Duong, T.; Corniani, E.; Nazemi, E.; Kalmoun, E.M. Evaluation of flow pattern recognition and void fraction measurement in two phase flow independent of oil pipeline’s scale layer thickness. Alex. Eng. J. 2021, 60, 1955–1966. [Google Scholar] [CrossRef]
- Signor, L.; Dragon, A.; Roy, G.; De Resseguier, T.; Llorca, F. Dynamic fragmentation of melted metals upon intense shock wave loading. Some modelling issues applied to a tin target. Arch. Mech. 2008, 60, 323–343. [Google Scholar]
- Milne, A.; Longbottom, A.; Frost, D.L.; Loiseau, J.; Goroshin, S.; Petel, O. Explosive fragmentation of liquids in spherical geometry. Shock Waves 2017, 27, 383–393. [Google Scholar] [CrossRef] [Green Version]
- Milne, A.M.; Parrish, C.; Worland, I. Dynamic fragmentation of blast mitigants. Shock Waves 2010, 20, 41–51. [Google Scholar] [CrossRef]
- Fuster, D.; Popinet, S. An all-Mach method for the simulation of bubble dynamics problems in the presence of surface tension. J. Comput. Phys. 2018, 374, 752–768. [Google Scholar] [CrossRef] [Green Version]
- Durand, O.; Jaouen, S.; Soulard, L.; Heuze, O.; Colombet, L. Comparative simulations of microjetting using atomistic and continuous approaches in the presence of viscosity and surface tension. J. Appl. Phys. 2017, 122. [Google Scholar] [CrossRef]
- Baer, M.R.; Nunziato, J.W. A two-phase mixture theory for the Deflagaration—to—Detonation Transition (DDT) in reactive Granular Materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Saurel, R.; Abgrall, R. A Multiphase Godunov Method for Compressible Multifluid and Multiphase Flows. J. Comput. Phys. 1999, 150, 425–467. [Google Scholar] [CrossRef]
- Tian, B.; Toro, E.F.; Castro, C.E. A path-conservative method for a five-equation model of two-phase flow with an HLLC-type Riemann solver. Comput. Fluids 2011, 46, 122–132. [Google Scholar] [CrossRef]
- Pelanti, M.; Shyue, K.M. A mixture-energy-consistent numerical approximation of a two-phase flow model for fluids with interfaces and cavitation. Am. Inst. Math. Sci. 2014, 839–846. [Google Scholar]
- Furfaro, D.; Saurel, R. A simple HLLC-type Riemann solver for compressible non-equilibrium two-phase flows. Comput. Fluids 2015, 111, 159–178. [Google Scholar] [CrossRef]
- Kapila, A.; Menikoff, R.; Bdzil, J.; Son, S.; Stewart, D. Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations. Phys. Fluids 2001, 13, 3002–3024. [Google Scholar] [CrossRef]
- Daude, F.; Galon, P.; Gao, Z.; Blaud, E. Numerical experiments using a HLLC-type scheme with ALE formulation for compressible two-phase flows five-equation models with phase transition. Comput. Fluids 2014, 94, 112–138. [Google Scholar] [CrossRef]
- He, Z.; Tian, B.; Zhang, Y.; Gao, F. Characteristic-based and interface-sharpening algorithm for high-order simulations of immiscible compressible multi-material flows. J. Comput. Phys. 2017, 333, 247–268. [Google Scholar] [CrossRef]
- Jibben, Z.; Velechovsky, J.; Masser, T.; Francois, M.M. Modeling surface tension in compressible flow on an adaptively refined mesh. Comput. Math. Appl. 2019, 78, 504–516. [Google Scholar] [CrossRef]
- Ilangakoon, N.A.; Malan, A.G.; Jones, B.W.S. A higher-order accurate surface tension modelling volume-of-fluid scheme for 2D curvilinear meshes. J. Comput. Phys. 2020, 420. [Google Scholar] [CrossRef]
- Heyns, J.A.; Malan, A.G.; Harms, T.M.; Oxtoby, O.F. A weakly compressible free-surface flow solver for liquid-gas systems using the volume-of-fluid approach. J. Comput. Phys. 2013, 240, 145–157. [Google Scholar] [CrossRef]
- Oxtoby, O.F.; Malan, A.G.; Heyns, J.A. A computationally efficient 3D finite-volume scheme for violent liquid-gas sloshing. Int. J. Numer. Methods Fluids 2015, 79, 306–321. [Google Scholar] [CrossRef]
- Malan, L.C.; Malan, A.G.; Zaleski, S.; Rousseau, P.G. A geometric VOF method for interface resolved phase change and conservative thermal energy advection. J. Comput. Phys. 2021, 426. [Google Scholar] [CrossRef]
- Shyue, K. A wave-propagation based volume tracking method for compressible multicomponent flow in two space dimensions. J. Comput. Phys. 2006, 215, 219–244. [Google Scholar] [CrossRef]
- Corot, T.; Hoch, P.; Labourasse, E. Surface tension for compressible fluids in ALE framework. J. Comput. Phys. 2020, 407. [Google Scholar] [CrossRef]
- Perigaud, G.; Saurel, R. A compressible flow model with capillary effects. J. Comput. Phys. 2005, 209, 139–178. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Xiao, F. Unified formulation for compressible and incompressible flows by using multi-integrated moments I: One-dimensional inviscid compressible flow. J. Comput. Phys. 2004, 195, 629–654. [Google Scholar] [CrossRef]
- Chiapolino, A.; Saurel, R.; Nkonga, B. Sharpening diffuse interfaces with compressible fluids on unstructured meshes. J. Comput. Phys. 2017, 340, 389–417. [Google Scholar] [CrossRef] [Green Version]
- Ubbink, O.; Issa, R. A method for capturing sharp fluid interfaces on arbitrary meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, B.S.; Jain, S.S.; Dodd, M.S. Interface-capturing methods for two-phase flows: An overview and recent developments. In Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2017; pp. 117–135. [Google Scholar] [CrossRef]
- Weymouth, G.D.; Yue, D.K.P. Conservative Volume-of-Fluid method for free-surface simulations on Cartesian-grids. J. Comput. Phys. 2010, 229, 2853–2865. [Google Scholar] [CrossRef]
- Zhang, D.; Jiang, C.; Liang, D.; Chen, Z.; Yang, Y.; Shi, Y. A refined volume-of-fluid algorithm for capturing sharp fluid interfaces on arbitrary meshes. J. Comput. Phys. 2014, 274, 709–736. [Google Scholar] [CrossRef] [Green Version]
- Ivey, C.B.; Moin, P. Conservative and bounded volume-of-fluid advection on unstructured grids. J. Comput. Phys. 2017, 350, 387–419. [Google Scholar] [CrossRef]
- Malan, A.G.; Oxtoby, O.F. An accelerated, fully-coupled, parallel 3D hybrid finite-volume fluid-structure interaction scheme. Comput. Methods Appl. Mech. Eng. 2013, 253, 426–438. [Google Scholar] [CrossRef]
- Malan, L.C.; Ling, Y.; Scardovelli, R.; Llor, A.; Zaleski, S. Detailed numerical simulations of pore competition in idealized micro-spall using the VOF method. Comput. Fluids 2019, 189, 60–72. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Pattinson, J.; Malan, A.G.; Meyer, J.P. A cut-cell non-conforming Cartesian mesh method for compressible and incompressible flow. Int. J. Numer. Methods Eng. 2008, 72, 1332–1354. [Google Scholar] [CrossRef]
- Oxtoby, O.F.; Malan, A.G. A matrix-free, implicit, incompressible fractional-step algorithm for fluid-structure interaction applications. J. Comput. Phys. 2012, 231, 5389–5405. [Google Scholar] [CrossRef]
- Johnsen, E.; Colonius, T. Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 2006, 219, 715–732. [Google Scholar] [CrossRef]
- Shyue, K.M. An Efficient Shock-Capturing Algorithm for Compressible Multicomponent Problems. J. Comput. Phys. 1998, 142, 208–242. [Google Scholar] [CrossRef] [Green Version]
- Le Metayer, O.; Saurel, R. The Noble-Abel Stiffened-Gas equation of state. Phys. Fluids 2016, 28. [Google Scholar] [CrossRef] [Green Version]
- Van Albada, G.D.; van Leer, B.; Roberts, W.W. A Comparative Study of Computational Methods in Cosmic Gas Dynamics. In Upwind and High-Resolution Schemes; Springer: Berlin/Heidelberg, Germany, 1997; pp. 95–103. [Google Scholar] [CrossRef] [Green Version]
- Batten, P.; Clarke, N.; Lambert, C.; Causon, D.M. On the choice of wavespeeds for the HLLC riemann solver. SIAM J. Sci. Comput. 1997, 18, 1553–1570. [Google Scholar] [CrossRef]
- Einfeldt, B.; Munz, C.; Roe, P.; Sjogreen, B. On Godunov-Type Methods near Low-Densities. J. Comput. Phys. 1991, 92, 273–295. [Google Scholar] [CrossRef]
- Popinet, S. An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 2009, 228, 5838–5866. [Google Scholar] [CrossRef] [Green Version]
- Popinet, S. Numerical Models of Surface Tension. Annu. Rev. Fluid Mech. 2018, 50, 49–75. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.W.S.; Malan, A.G.; Ilangakoon, N.A. The initialisation of volume fractions for unstructured grids using implicit surface definitions. Comput. Fluids 2019, 179, 194–205. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. A front-tracking algorithm for accurate representation of surface tension. Int. J. Numer. Methods Fluids 1999, 30, 775–793. [Google Scholar] [CrossRef]
- Afkhami, S.; Bussmann, M. Height functions for applying contact angles to 2D VOF simulations. Int. J. Numer. Methods Fluids 2008, 57, 453–472. [Google Scholar] [CrossRef]
- Torres, D.J.; Brackbill, J.U. The Point-Set Method: Front-Tracking without Connectivity. J. Comput. Phys. 2000, 165, 620–644. [Google Scholar] [CrossRef] [Green Version]
- Fuster, D.; Agbaglah, G.; Josserand, C.; Popinet, S.; Zaleski, S. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dyn. Res. 2009, 41. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. Bubble collapse near a solid boundary: A numerical study of the influence of viscosity. J. Fluid Mech. 2002, 464, 137–163. [Google Scholar] [CrossRef] [Green Version]
- Plesset, M.; Prosperetti, A. Bubble Dynamics and Cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Jain, S.S.; Mani, A.; Moin, P. A conservative diffuse-interface method for compressible two-phase flows. J. Comput. Phys. 2020, 418. [Google Scholar] [CrossRef]
- Minnaert, M. XVI. On musical air-bubbles and the sounds of running water. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1933, 16, 235–248. [Google Scholar] [CrossRef]


















| Capturing Scheme | |||
|---|---|---|---|
| HLLC | Height | 2.83 × 10 | 4.15 × 10 |
| HLLC-CICSAM | Height | 6.54 × 10 | 3.20 × 10 |
| HLLC | Convolution | 5.98 × 10 | 8.74 × 10 |
| HLLC-CICSAM | Convolution | 2.40 × 10 | 1.27 × 10 |
| 20 | 4.90 | 2.19 | 0.001522 |
| 40 | 2.43 | 0.91 | 0.001405 |
| 80 | 1.23 | 0.49 | 0.001375 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oomar, M.Y.; Malan, A.G.; Horwitz, R.A.D.; Jones, B.W.S.; Langdon, G.S. An All-Mach Number HLLC-Based Scheme for Multi-Phase Flow with Surface Tension. Appl. Sci. 2021, 11, 3413. https://doi.org/10.3390/app11083413
Oomar MY, Malan AG, Horwitz RAD, Jones BWS, Langdon GS. An All-Mach Number HLLC-Based Scheme for Multi-Phase Flow with Surface Tension. Applied Sciences. 2021; 11(8):3413. https://doi.org/10.3390/app11083413
Chicago/Turabian StyleOomar, Muhammad Y., Arnaud G. Malan, Roy A. D. Horwitz, Bevan W. S. Jones, and Genevieve S. Langdon. 2021. "An All-Mach Number HLLC-Based Scheme for Multi-Phase Flow with Surface Tension" Applied Sciences 11, no. 8: 3413. https://doi.org/10.3390/app11083413
APA StyleOomar, M. Y., Malan, A. G., Horwitz, R. A. D., Jones, B. W. S., & Langdon, G. S. (2021). An All-Mach Number HLLC-Based Scheme for Multi-Phase Flow with Surface Tension. Applied Sciences, 11(8), 3413. https://doi.org/10.3390/app11083413







