Abstract
Recently, several new metaheuristic schemes have been introduced in the literature. Although all these approaches consider very different phenomena as metaphors, the search patterns used to explore the search space are very similar. On the other hand, second-order systems are models that present different temporal behaviors depending on the value of their parameters. Such temporal behaviors can be conceived as search patterns with multiple behaviors and simple configurations. In this paper, a set of new search patterns are introduced to explore the search space efficiently. They emulate the response of a second-order system. The proposed set of search patterns have been integrated as a complete search strategy, called Second-Order Algorithm (SOA), to obtain the global solution of complex optimization problems. To analyze the performance of the proposed scheme, it has been compared in a set of representative optimization problems, including multimodal, unimodal, and hybrid benchmark formulations. Numerical results demonstrate that the proposed SOA method exhibits remarkable performance in terms of accuracy and high convergence rates.
1. Introduction
Metaheuristic algorithms refer to generic optimization schemes that emulate the operation of different natural or social processes. In metaheuristic approaches, the optimization strategy is performed by a set of search agents. Each agent maintains a possible solution to the optimization problem, and is initially produced by considering a random feasible solution. An objective function determines the quality of the solution of each agent. By using the values of the objective function, at each iteration, the position of the search agents is modified, employing a set of search patterns that regulate their movements within the search space. Such search patterns are abstract models inspired by natural or social processes [1]. These steps are repeated until a stop criterion is reached. Metaheuristic schemes have confirmed their supremacy in diverse real-world applications in circumstances where classical methods cannot be adopted.
Essentially, a clear classification of metaheuristic methods does not exist. Despite this, several categories have been proposed that considered different criteria, such as a source of inspiration, type of operators or cooperation among the agents. In relation to inspiration, nature-inspired metaheuristic algorithms are classified into three categories: Evolution-based, swarm-based, and physics-based. Evolution-based approaches correspond to the most consolidate search strategies that use evolution elements as operators to produce search patterns. Consequently, operations, such as reproduction, mutation, recombination, and selection are used to generate search patterns during their operations. The most representative examples of evolution-based techniques, include Evolutionary Strategies (ES) [2,3,4], Genetic Algorithms (GA) [5], Differential Evolution (DE) [6] and Self-Adaptative Differential Evolution (JADE) [7]. Swarm-inspired techniques use behavioral schemes extracted from the collaborative interaction of different animals or species of insects to produce a search strategy. Recently, a high number of swarm-based approaches have been published in the literature. Among the most popular swarm-inspired approaches, include the Crow Search Algorithm (CSA) [8], Artificial Bee Colony (ABC) [9], Particle Swarm Optimization (PSO) algorithm [10,11,12], Firefly Algorithm (FA) [13,14], Cuckoo Search (CS) [15], Bat Algorithm (BA) [16], Gray Wolf Optimizer (GWO) [17], Moth-flame optimization algorithm (MFO) [18] to name a few. Metaheuristic algorithms that consider the physics-based scheme use simplified physical models to produce search patterns for their agents. Some examples of the most representative physics-based techniques involve the States of Matter Search (SMS) [19,20], the Simulated Annealing (SA) algorithm [21,22,23], the Gravitational Search Algorithm (GSA) [24], the Water Cycle Algorithm (WCA) [25], the Big Bang-Big Crunch (BB-BC) [26] and Electromagnetism-like Mechanism (EM) [27]. Figure 1 visually exhibits the taxonomy of the metaheuristic classification. Although all these approaches consider very different phenomena as metaphors, the search patterns used to explore the search space are exclusively based on spiral elements or attraction models [10,11,12,13,14,15,16,17,28]. Under such conditions, the design of many metaheuristic methods refers to configuring a recycled search pattern that has been demonstrated to be successful in previous approaches for generating new optimization schemes through a marginal modification.
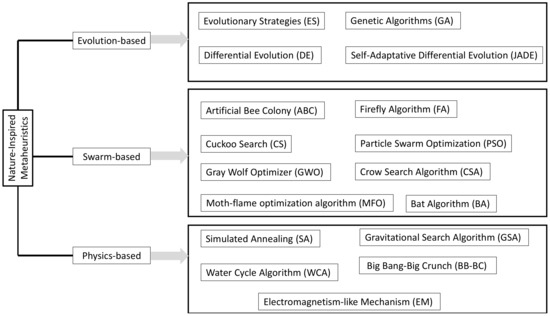
Figure 1.
Visual taxonomy of the nature-inspired metaheuristic schemes.
On the other hand, the order of a differential equation refers to the highest degree of derivative considered in the model. Therefore, a model whose input-output formulation is a second-order differential equation is known as a second-order system [29]. One of the main elements that make a second-order model important is its ability to present very different behaviors, depending on the configuration of its parameters. Through its different behaviors, such as oscillatory, underdamped, or overdamped, a second-order system can exhibit distinct temporal responses [30]. Such behaviors can be observed as search trajectories under the perspective of metaheuristic schemes. Therefore, with second-order systems, it is possible to produce oscillatory movements within a certain region or build complex search patterns around different points or sections of the search space.
In this paper, a set of new search patterns are introduced to explore the search space efficiently. They emulate the response of a second-order system. The proposed set of search patterns have been integrated as a complete search strategy, called Second-Order Algorithm (SOA), to obtain the global solution of complex optimization problems. To analyze the performance of the proposed scheme, it has been compared in a set of representative optimization problems, including multimodal, unimodal, and hybrid benchmark formulations. The competitive results demonstrate the promising results of the proposed search patterns.
The main contributions of this research can be stated as follows:
- A new physics-based optimization algorithm, namely SOA, is introduced. It uses search patterns obtained from the response of second-order systems.
- New search patterns are proposed as an alternative to those known in the literature.
- The statistical significance, convergence speed and exploitation-exploration ratio of SOA are evaluated against other popular metaheuristic algorithms.
- SOA outperforms other competitor algorithms on two sets of optimization problems.
The remainder of this paper is structured as follows: A brief introduction of the second-order systems is given in Section 2; in Section 3, the most important search patterns in metaheuristic methods are discussed; in Section 4, the proposed search patterns are defined; in Section 5, the measurement of exploration-exploitation is described; in Section 6, the proposed scheme is introduced; Section 7 presents the numerical results; in Section 8, the main characteristics of the proposed approach are discussed; in Section 9, finally, the conclusions are drawn.
2. Second-Order Systems
A model whose input -output formulation is a second-order closed-loop transfer function is known as a second-order system. One of the main elements that make a second-order model important is its ability to present very different behaviors depending on the configuration of its parameters. A generic second-order model can be formulated under the following expression [29],
where ζ and ωn represent the damping ratio and ωn the natural frequency, respectively, while s symbolizes the Laplace domain.
The dynamic behavior of a system is evaluated in terms of the temporal response obtained through a unitary step signal as input . The dynamic behavior is defined as the way in which the system reacts, trying to reach the value of one as time evolves. The dynamic behavior of the second-order system is described in terms of and [30]. Assuming such parameters, the second-order system presents three different behaviors: Underdamped (, critically damped (, and overdamped (.
2.1. Underdamped Behavior (
In this behavior, the poles (roots of the denominator) of Equation (1) are complex conjugated and located in the left-half of the plane. Under such conditions, the system underdamped response in the Laplace domain can be characterized as follows:
Applying partial fraction operations and the inverse Laplace transform, it is obtained the temporal response that describe the underdamped behavior as it is indicated in Equation (3):
If , a special case is presented in which the temporal system response is oscillatory. The output of these behaviors is visualized in Figure 2 for the cases of , , and . Under the underdamped behavior, the system response starts with high acceleration. Therefore, the response produces an overshoot that surpasses the value of one. The size of the overshoot inversely depends on the value of .
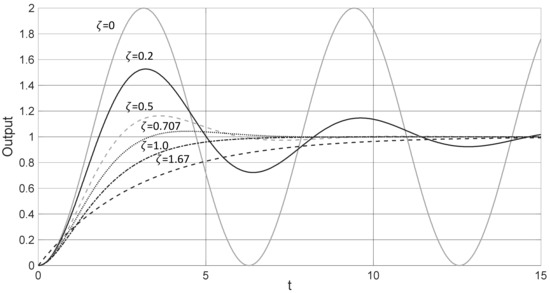
Figure 2.
Temporal responses of second-order system considering its different behaviors: Underdamped , critically damped , and overdamped .
2.2. Critically Damped Behavior (
Under this behavior, the two poles of the transfer function of Equation (1) present a real number and maintain the same value. Therefore, the response of the critically damped behavior in the Laplace domain can be described as follows:
Considering the inverse Laplace transform of Equation (4), the temporal response of the critically damped behavior is determined under the following model:
Under the critically damped behavior, the system response presents a temporal pattern similar to a first-order system. It reaches the objective value of one without experimenting with an overshoot. The output of the critically damped behavior is visualized in Figure 2.
2.3. Overdamped Behavior (
In the overdamped case, the two poles of a transfer function of Equation (1) have real numbers but with different values. Its response in the Laplace domain is modeled under the following formulation:
After applying the inverse Laplace transform, it is obtained the temporal response of the overdamped behavior defined as follows:
Under the Overdamped behavior, the system slowly reacts until reaching the value of one. The deceleration of the response depends on the value of . The greater the value of , the slower the response will be. The output of this behavior is visualized in Figure 2 for the case of .
3. Search Patterns in Metaheuristics
The generation of efficient search patterns for the correct exploration of a fitness landscape could be complicated, particularly in the presence of ruggedness and multiple local optima. Recently, several new metaheuristic schemes have been introduced in the literature. Although all these approaches consider very different phenomena as metaphors, the search patterns, used to explore the search space, are very similar. A search pattern is a set of movements produced by a rule or model in order to examine promising solutions from the search space.
Exploration and exploitation correspond to the most important characteristics of a search pattern. Exploration refers to the ability of a search pattern to examine a set of solutions spread in distinct areas of the search space. On the other hand, exploitation represents the capacity of a search pattern to improve the accuracy of the existent solutions through a local examination. The combination of both mechanisms in a search pattern is crucial for attaining success when solving a particular optimization problem.
To solve the optimization formulation, from a metaheuristic point of view, a population of of candidate solutions (individuals) evolve from an initial point ( = 1) to a number of generations (). In the population, each individual corresponds to a -dimensional element which symbolizes the decision variables involved by the optimization problem. At each generation, search patterns are applied over the individuals of the population to produce the new population . The quality of each individual is evaluated in terms of its solution regarding the objective function whose result represents the fitness value of . As the metaheuristic method evolves, the best current individual is maintained since represents the best available solution seen so-far.
In general, a search pattern is applied to each individual using the best element as a reference. Then, following a particular model, a set of movements are produced to modify the position of until the location of has been reached. The idea behind this mechanism is to examine solutions in the trajectory from to with the objective to find a better solution than the current . Search patterns differ in the model employed to produce the trajectories from to .
Two of the most popular search models are attraction and spiral trajectories. The attraction model generates attraction movements from to . The attraction model is used extensively by several metaheuristic methods such as PSO [10,11,12], FA [13,14], CS [15], BA [16], GSA [24], EM [27] and DE [6]. On the other hand, the spiral model produces a spiral trajectory that encircles the best element . The spiral model is employed by the recently published WOA and GWO schemes. Trajectories produced by the attraction, and spiral models are visualized in Figure 3a,b, respectively.
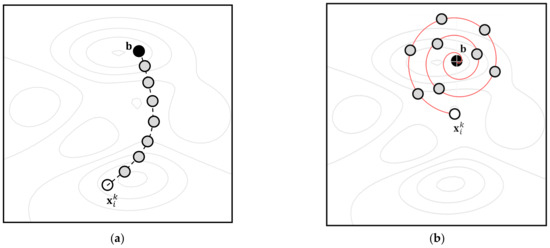
Figure 3.
Trajectories produced by, (a) attraction, and (b) spiral models.
4. Proposed Search Patterns
In this paper, a set of new search patterns are introduced to explore the search space efficiently. They emulate the response of a second-order system. The proposed set of search patterns have been integrated as a complete search strategy to obtain the global solution of complex optimization problems. Since the proposed scheme is based on the response of the second-order systems, it can be considered as a physics-based algorithm. In our approach, the temporal response of second-order system is used to generate the trajectory from the position of to the location of . With the use of such models, it is possible to produce more complex trajectories that allow a better examination of the search space. Under such conditions, we consider the three different responses of a second-order system to produce three distinct search patterns. They are the underdamped, critically damped and overdamped modeled by the expressions Equations (8)–(10), respectively:
where () corresponds to the search agent while () symbolizes the decision variable or dimension. Since the behavior of each search pattern depends on the value of , it is easy to combine elements to produce interesting trajectories. Figure 4 presents some examples of trajectories produced by using different values for . In the Figure, it is assumed a two-dimensional case () where the initial position of the search agent is and the final location or the best location . Figure 4a presents the case of and . Figure 4b presents the case of and . Figure 4c presents the case of and . Finally, Figure 4d presents the case of and . From the figures, it is clear that the second-order responses allow producing several complex trajectories, which include most of the other search patterns known in the literature. In all cases (a)–(d), the value of has been set to 1.
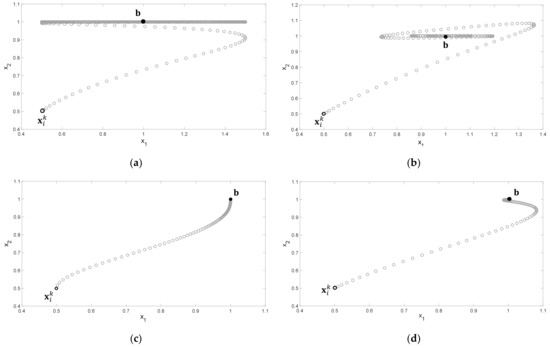
Figure 4.
Some examples of trajectories produced by using different values for ζ. (a) and , (b) and , (c) and and (d) and .
5. Balance of Exploration and Exploitation
Metaheuristic methods employ a set of search agents to examine the search space with the objective to identify a satisfactory solution for an optimization formulation. In metaheuristic schemes, search agents that present the best fitness values tend to regulate the search process, producing an attraction towards them. Under such conditions, as the optimization process evolves, the distance among individuals diminishes while the effect of exploitation is highlighted. On the other hand, when the distance among individuals increases, the characteristics of the exploration process are more evident.
To compute the relative distance among individuals (increase and decrease), a diversity indicator known as the dimension-wise diversity index [31] is used. Under this approach, the diversity is formulated as follows,
where symbolizes the median of dimension of all search agents. represents the variable decision of the individual . is the number of individuals in the population while corresponds to the number of dimensions of the optimization formulation. The diversity (of the -th dimension) evaluates the relative distance between the variable of each individual and its median value. The complete diversity (of the entire population) corresponds to the averaged diversity in each dimension. Both elements and are calculated in every iteration.
Having evaluated the diversity values, the level of exploration and exploitation can be computed as the percentage of the time that a search strategy invests exploring or exploiting in terms of its diversity values. These percentages are calculated in each iteration by means of the following models,
where symbolizes the maximum diversity value obtained during the optimization process. The percentage of exploration corresponds to the size of exploration as the rate between and . On the other hand, the percentage of exploitation symbolizes the level of exploitation. is computed as the complemental percentage to since the difference between and is generated because of the concentration of individuals.
6. Proposed Metaheuristic Algorithm
The set of search patterns based on the second-order systems have been integrated as a complete search strategy to obtain the global solution of complex optimization problems. In this section, the complete metaheuristic method, called Second-Order Algorithm (SOA), is completely described.
The scheme considers four different stages: (A) Initialization, (B) trajectory generation, (C) reset of bad elements, and (D) avoid premature convergence mechanism. The steps (B)–(D) are sequentially executed until a stop criterion has been reached. Figure 5 shows the flowchart of the complete metaheuristic method.
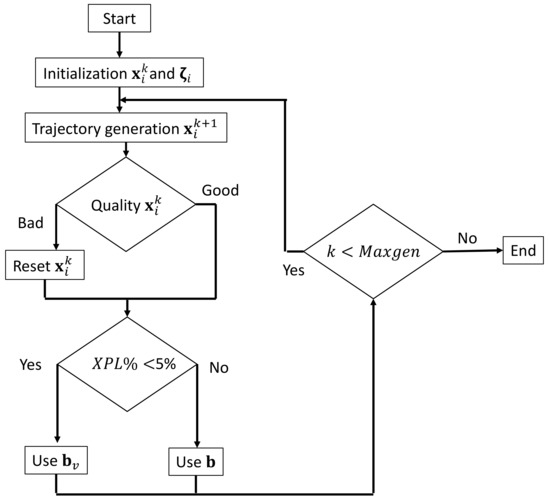
Figure 5.
Flowchart of the proposed metaheuristic method based on the response of second-order systems.
6.1. Initialization
In the first iteration , a population of agents is randomly produced considering to the following equation,
where and are the limits of the decision variable and is a uniformly distributed random number between [0,1].
To each individual from the population, it is assigned a vector whose elements determine the trajectory behavior of each -th dimension. Initially, each element is set to a random value between [0,2]. Under this interval, all the second-order behavior are possible: Underdamped (, critically damped (, and overdamped (.
6.2. Trajectory Generation
Once the population has been initialized, it is obtained the best element of the population . Then, the new position of each agent is computed as a trajectory generated by a second-order system. Once all new positions in the population are determined, it is also defined the best element .
6.3. Reset of Bad Elements
To each agent is allowed to move in its own trajectory for ten iterations. After ten iterations, if the search agent maintains the worst performance in terms of the fitness function, it is reinitialized in both position and in its vector . Under such conditions, the search agent will be in another position and with the ability to perform another kind of trajectory behavior.
6.4. Avoid Premature Convergence Mechanism
If the percentage of exploration is less than 5%, the best value is replaced by the best virtual value . The element is computed as the averaged value of the best five individuals of the population. The idea behind this mechanism is to identify a new position to generate different trajectories that avoid that the search process gets trapped in a local optimum.
7. Experimental Results
To evaluate the results of the proposed SOA algorithm, a set of experiments has been conducted. Such results have been compared to those produced by the Artificial Bee Colony (ABC) [9], the Covariance matrix adaptation evolution strategy (CMAES) [4], the Crow Search Algorithm (CSA) [8], the Differential Evolution (DE) [6], the Moth-flame optimization algorithm (MFO) [18] and the Particle Swarm Optimization (PSO) [10], which are considered the most popular metaheuristic schemes in many optimization studies [32].
For the comparison, all methods have been set according to their reported guidelines. Such configurations are described as follows:
- ABC: Onlooker Bees = 50, acceleration coefficient = 1 [9].
- DE: crossover probability = 0.2, Betha = 1 [6].
- CMAES: Lambda = 50, father number = 25, sigma = 60, csigma = 0.32586, dsigma = 1.32586 [4].
- CSA: Flock = 50, awareness probability = 0.1, flight length = 2 [8].
- MFO: search agents = 50, “a” linearly decreases from 2 to 0 [18].
- SOA: the experimental results give the best algorithm performance with the next parameter set par1 = 0.7, par2 = 0.3 and par3 = 0.05.
In our analysis, the population size N has been set to 50 search agents. The maximum iteration number for all functions has been set to 1000. This stop criterion has been decided to keep compatibility with similar works published in the literature [33,34]. To evaluate the results, three different indicators are considered: The Average Best-so-far (AB) solution, the Median Best-so-far (MB) solution and the Standard Deviation (SD) of the best-so-far solutions. In the analysis, each optimization problem is solved using every algorithm 30 times. From this operation, 30 results are produced. From all these values, the mean value of all best-found solutions represents the Average Best-so-far (AB) solution. Likewise, the median of all 30 results is computed to generate MB and the standard deviation of the 30 data is estimated to obtain SD of the best-so-far solutions. Indicators AB and MB correspond to the accuracy of the solutions, while SD their dispersion, and thus, the robustness of the algorithm.
The experimental section is divided into five sub-sections. In the first Section 7.1, the performance of SOA is evaluated with regard to multimodal functions. In the second Section 7.2, the results of the OTSA method in comparison with other similar approaches are analyzed in terms of unimodal functions. In the third Section 7.3, a comparative study among the algorithms examining hybrid functions is accomplished. In the fourth Section 7.4, the ability of all algorithms to converge is analyzed. Finally, in the fifth Section 7.5, the performance of the SOA method to solve the CEC 2017 set of functions is also analyzed.
7.1. Multimodal Functions
In this sub-section, the SOA approach is evaluated considering 12 unimodal functions ( reported in Table A1 from Appendix A. Multimodal functions present optimization surfaces that involve multiple local optima. For this reason, these function presents more complications in their solution. In this analysis, the performance of the SOA method is examined in comparison with ABC, CMAES, CSA, DE, MFO and PSO in terms of the multimodal functions. Multimodal objective functions correspond to functions from to in Table A1 from the Appendix, where the set of local minima augments as the dimension of the function also increases. Therefore, the study exhibits the capacity of each metaheuristic scheme to identify the global optimum when the function contains several local optima. In the experiments, it is assumed objective functions operating in 30 dimensions ( = 30). The averaged best (AB) results considering 30 independent executions are exhibit in Table 1. It also reports the median values (MD) and the standard deviations (SD).

Table 1.
Minimization results of multimodal benchmark functions.
According to Table 1, the proposed SOA scheme obtain a better performance than ABC, CMAES, CSA, DE, MFO and PSO in functions , , , , , , , and . Nevertheless, the results of SOA exhibit similar as the obtained by DE, CMAES and MFO in functions , and .
To statistically validate the conclusions from Table 1, a non-parametric study is considered. In this test, the Wilcoxon rank-sum analysis [35] is adopted with the objective to validate the performance results. This statistical test evaluates if exists a significant difference when two methods are compared. For this reason, the analysis is performed considering a pairwise comparison such as SOA versus ABC, SOA versus CMAES, SOA versus CSA, SOA versus DE, SOA versus MFO and SOA versus PSO. In the Wilcoxon analysis, a null hypothesis (H0) was adopted that showed that there is no significant difference in the results. On the other hand, it is assumed as an alternative hypothesis (H1) that the result has a similar structure. For the Wilcoxon analysis, it is assumed a significance value of 0.05 considering 30 independent execution for each test function. Table 2 shows the p-values assuming the results of Table 2 (where n = 30) produced by the Wilcoxon study. For faster visualization, in the Table, we use the following symbols ▲ ▼, and ►. The symbol ▲ refers that the SOA algorithm produces significantly better solutions than its competitor. ▼ symbolizes that SOA obtains worse results than its counterpart. Finally, the symbol ► denotes that both compared methods produce similar solutions. A close inspection of Table 2 demonstrates that for functions , , , , , , , and the proposed SOA scheme obtain better solutions than the other methods. On the other hand, for functions , and , it is clear that the groups SOA versus ABC, SOA versus CMAES, SOA versus DE and SOA versus MFO and EA-HC versus SCA present similar solutions.

Table 2.
Wilcoxon analysis for multimodal benchmark functions.
7.2. Unimodal Functions
In this subsection, the performance of SOA is compared with ABC, DE, DE, CMAES CSA and MFO, considering four unimodal functions with only one optimum. Such functions are represented by functions from to in Table A1. In the test, all functions are considered in 30 dimensions (). The experimental results, obtained from 30 independent executions, are presented in Table 3. They report the results in terms of AB, MB and SD obtained in the executions. According to Table 3, the SOA approach provides better performance than ABC, DE, DE, CMAES CSA and MFO for all functions. In general, this study demonstrates big differences in performance among the metaheuristic scheme, which is directly related to a better trade-off between exploration and exploitation produced by the trajectories of the SOA scheme. Considering the information from Table 3, Table 4 reports the results of the Wilcoxon analysis. An inspection of the -values from Table 4, it is clear that the proposed SOA method presents a superior performance than each metaheuristic algorithm considered in the experimental study.

Table 3.
Minimization results of unimodal benchmark functions.

Table 4.
Wilcoxon analysis for unimodal benchmark functions.
7.3. Hybrid Functions
In this study, hybrid functions are used to evaluate the optimization solutions of the SOA scheme. Hybrid functions refer to multimodal optimization problems produced by the combination of several multimodal functions. These functions correspond to the formulations from to which are shown in Table A1 in Appendix A. In the experiments, the performance of our proposed SOA approach has been compared with other metaheuristic schemes.
The simulation results are reported in Table 5. It exhibits the performance of each algorithm in terms of AB, MB and SD. From Table 5, it can be observed that the SOA method presents a superior performance than the other techniques in all functions. Table 6 reports the results of the Wilcoxon analysis assuming the index of the Average Best-so-far (AB) values of Table 5. Since all elements present the symbol ▲, they validate that the proposed SOA method produces better results than the other methods. The remarkable performance of the proposed SOA scheme for hybrid functions is attributed to a better balance between exploration and exploitation of its operators provoked by the properties of the second system trajectories. This denotes that the SOA approach generates an appropriate number of promising search agents that allow an adequate exploration of the search space. On the other hand, a balanced number of candidate solutions is also produced that make it possible to improve the quality of the already-detected solutions, in terms of the objective function.

Table 5.
Minimization results of hybrid benchmark functions.

Table 6.
Wilcoxon analysis for hybrid benchmark functions.
7.4. Convergence Analysis
The evaluation of accuracy in the final solution cannot completely assess the abilities of an optimization algorithm. On the other hand, the convergence of a metaheuristic scheme represents an important property to assess its performance. This analysis determined the velocity, which determined metaheuristic scheme reaches the optimum solution. In this subsection, a convergence study has been carried out. In the comparisons, for the sake of space, the performance of the best four metaheuristic schemes is considered adopting a representative set of six functions (two multimodal, two unimodal and two hybrids), operated in 30 dimensions. To generate the convergence graphs, the raw simulation data produced in the different experiments was processed. Since each simulation is executed 30 times for each metaheuristic method, the convergence data of the execution corresponds to the median result. Figure 6, Figure 7 and Figure 8 show the convergence graphs for the four best-performing metaheuristic methods. A close inspection of Figure 6 demonstrates that the proposed SOA scheme presents a better convergence than the other algorithms for all functions.
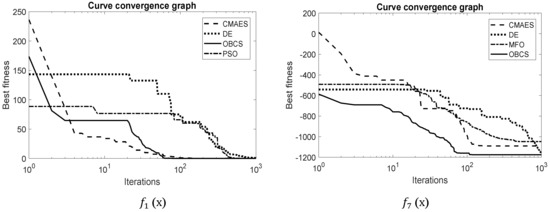
Figure 6.
Convergence graphs in two representative multimodal-functions.
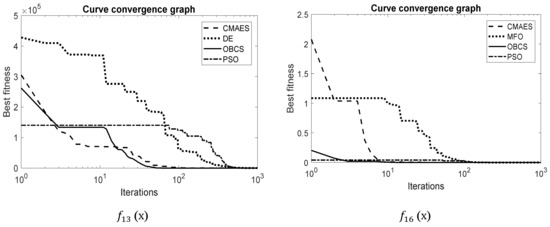
Figure 7.
Convergence graphs in two representative unimodal functions.
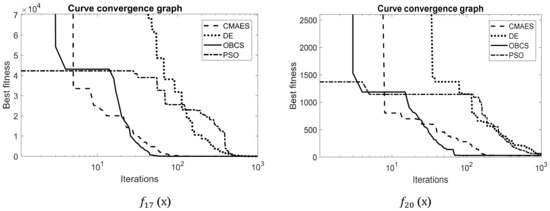
Figure 8.
Convergence graphs in two representative hybrid functions.
7.5. Performance Evaluation with CEC 2017
In this sub-section, the performance of the SOA method to solve the CEC 2017 set of functions is also analyzed. The set of functions from the CEC2017 [36] represents one the most elaborated platform for benchmarking and comparing search strategies for numerical optimization. The CEC2017 benchmarks correspond to a test environment of 30 different functions with distinct features. They will be identified from to . Most of these functions are similar to those exhibited in Appendix A, but with different translations and/or rotations effects. The average obtained results, corresponding to 30 independent executions, are re-registered in Table 7. The results are reported in terms of the performance indexes: Average Best fitness (AB), Median Best fitness (MB), and the standard deviation of the best finesses (SD).

Table 7.
Optimization results from benchmark functions of CEC2017.
According to Table 7, SOA provides better results than ABC, CMAES, CSA, DE, MFO and PSO for almost all functions. A close inspection of this table reveals that the SOA scheme attained the best performance level, obtaining the best results in 22 functions from the CEC2017 function set. Likewise, the CMAES presents second place, in terms of most of the performance indexes, while DE and CSA techniques reach the third category with performance slightly minor. On the other hand, the MFO and PSO methods produce the worst results. In particular, the results show considerable precision differences, which are directly related to the different search patterns presented by each metaheuristic algorithm. This demonstrates that the search patterns, produced by second-order systems, are able to provide excellent search patterns. The results show good performance of the proposed SOA method in terms of accuracy and high convergence rates.
8. Analysis and Discussion
The extensive experiments, performed in previous sections, demonstrate the remarkable characteristics of the proposed SOA algorithm. The experiments included not only standard benchmark functions but also the complex set of optimization functions from CEC2017. In both sets of functions, they have been solved in 30 dimensions. Therefore, a total of 50 optimization problems were employed to comparatively evaluate the performance of SOA with other popular metaheuristic approaches, such as ABC, CMAES, CSA, DE, MFO and PSO. From the experiments, important information has been obtained by observing the end-results, in terms of the mean and standard deviations found over a certain number of runs or convergence graphs, but also in-depth search behavioral evidence in the form of exploration and exploitation measurements were also used.
The generation of efficient search patterns for the correct exploration of a fitness landscape could be complicated, particularly in the presence of ruggedness and multiple local optima. A search pattern is a set of movements produced by a rule or model that is used to examine promising solutions from the search space. Exploration and exploitation correspond to the most important characteristics of a search strategy. The combination of both mechanisms in a search pattern is crucial for attaining success when solving a particular optimization problem.
In our approach, the temporal response of second-order system is used to generate the trajectory from the position of to the location of . Three different search patterns have been considered based on the second-order system responses. The proposed search patterns can explore areas of considerable size by using a high rate of velocity and the same time, refining the solution of the best individual by the exploitation of its location. This behavior represents the most important property of the proposed search patterns. According to the results provided by the experiments, the search patterns produce more complex trajectories that allow a better examination of the search space.
Similar to other metaheuristic methods, SOA tries to improve its solutions based on its interaction with the objective function or on a ‘trial and error’ scheme through defined stochastic processes. Different from other popular metaheuristic methods such as DE, ABC, GA or CMAES, our proposed approach uses search patterns represented by trajectories to explore and exploit the search space. Since SOA employs search patterns, it presents more similarities with algorithms such as CSA, MFO and GWO. However, the search patterns used in their search strategy are very different. While CSA, MFO and GWO consider only spiral patterns, our proposed method uses complex trajectories produced by the response of second-order systems.
9. Conclusions
A search pattern is a set of movements produced by a rule or model, in order to examine promising solutions from the search space. In this paper, a set of new search patterns are introduced to explore the search space efficiently. They emulate the response of a second-order system. Under such conditions, it is considered three different responses of a second-order system to produce three distinct search patterns, such as underdamped, critically damped and overdamped. These proposed set of search patterns have been integrated as a complete search strategy, called Second-Order Algorithm (SOA), to obtain the global solution of complex optimization problems.
The form of the search patterns allows for balancing the exploration and exploitation abilities by efficiently traversing the search-space and avoiding suboptimal regions. The efficiency of the proposed SOA has been evaluated through 20 standard benchmark functions and 30 functions of CEC2017 test-suite. The results over multimodal functions show remarkable exploration capabilities, while the result over unimodal test functions denotes adequate exploitation of the search space. On hybrid functions, the results demonstrate the effectivity of the search patterns on more difficult formulations. The search efficacy of the proposed approach is also analyzed in terms of the Wilcoxon test results and convergence curves. In order to compare the performance of the SOA scheme, many other popular optimization techniques such as the Artificial Bee Colony (ABC), the Covariance matrix adaptation evolution strategy (CMAES), the Crow Search Algorithm (CSA), the Differential Evolution (DE), the Moth-flame optimization algorithm (MFO) and the Particle Swarm Optimization (PSO), have also been tested on the same experimental environment. Future research directions include topics such as multi-objective capabilities, incorporating chaotic maps and include acceleration process to solve other real-scale optimization problems.
Author Contributions
Conceptualization, E.C. and M.J.; Data curation, M.P.; Formal analysis, H.E.; Funding acquisition, M.J.; Investigation, H.B. and H.F.E.; Methodology, H.B., A.L.-C. and H.F.E.; Resources, H.E. and M.J.; Supervision, A.L.-C.; Visualization, M.P.; Writing—original draft, E.C. and H.F.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
List of Benchmark Functions.
Table A1.
List of Benchmark Functions.
| Name | Function | S | Dim | Minimum | |
|---|---|---|---|---|---|
| Levy | 30 | ||||
| Mishra 1 | 30 | ||||
| Mishra 2 | 30 | ||||
| Mishra 11 | 30 | ||||
| Penalty 1 | 30 | ||||
| Perm1 | 30 | ||||
| Plateau | 30 | ||||
| Step | 30 | ||||
| Styblinski tang | 30 | ||||
| Trid | 30 | ||||
| Vincent | 30 | ||||
| Zakharov | 30 | ||||
| Rothyp | 30 | ||||
| Schwefel 2 | 30 | ||||
| Sum2 | 30 | ||||
| Sum of different powers | 30 | ||||
| Rastringin + Schwefel22 + Sphere | 30 | ||||
| Griewank + Rastringin + Rosenbrock | 30 | ||||
| Ackley + Penalty2 + Rosenbrock + Schwefel2 | 30 | ||||
| Ackley + Griewnk + Rastringin + Rosenbrock + Schwefel22 | 30 |
References
- Cuevas, E.; Gálvez, J.; Avila, K.; Toski, M.; Rafe, V. A new metaheuristic approach based on agent systems principles. J. Comput. Sci. 2020, 47, 101244. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Schwefel, H.-P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Bäck, T.; Hoffmeister, F.; Schwefel, H.-P. A survey of evolution strategies. In Proceedings of the Fourth International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991; p. 8. [Google Scholar]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2016, arXiv:1604.00772102, 75–102. [Google Scholar]
- Tang, K.S.; Man, K.F.; Kwong, S.; He, Q. Genetic algorithms and their applications. IEEE Signal Process. Mag. 1996, 13, 22–37. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Self-adaptive differential evolution with fast and reliable convergence performance. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, CEC 2007, Singapore, 25–28 September 2007. [Google Scholar]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICCN’95 International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO): A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In Proceedings of the 5th International Conference on Stochastic Algorithms: Foundations and Applications, Sapporo, Japan, 26–28 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithm, Lévy Flights and Global Optimization. In Research and Development in Intelligent Systems XXVI; Springer: London, UK, 2010; pp. 209–218. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.-S. A new metaheuristic Bat-inspired Algorithm. Stud. Comput. Intell. 2010, 284, 65–74. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Cuevas, E.; Echavarría, A.; Ramírez-Ortegón, M.A. An optimization algorithm inspired by the States of Matter that improves the balance between exploration and exploitation. Appl. Intell. 2013, 40, 256–272. [Google Scholar] [CrossRef]
- Valdivia-Gonzalez, A.; Zaldívar, D.; Fausto, F.; Camarena, O.; Cuevas, E.; Perez-Cisneros, M. A States of Matter Search-Based Approach for Solving the Problem of Intelligent Power Allocation in Plug-in Hybrid Electric Vehicles. Energies 2017, 10, 92. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Rutenbar, R.A. Simulated Annealing Algorithms: An Overview. IEEE Circuits Devices Mag. 1989, 5, 19–26. [Google Scholar] [CrossRef]
- Siddique, N.; Adeli, H. Simulated Annealing, Its Variants and Engineering Applications. Int. J. Artif. Intell. Tools 2016, 25, 1630001. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big Bang–Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Birbil, Ş.I.; Fang, S.C. An electromagnetism-like mechanism for global optimization. J. Glob. Optim. 2003, 25, 263–282. [Google Scholar] [CrossRef]
- Sörensen, K.; Glover, F. Metaheuristics. In Encyclopedia of Operations Research and Management Science; Gass, S.I., Fu, M., Eds.; Springer: New York, NY, USA, 2013; pp. 960–970. [Google Scholar]
- Zill, D.G. A First Course in Differential Equations with Modeling Applications; Cengage Learning: Boston, MA, USA, 2012; ISBN 978-1-285-40110-2. [Google Scholar]
- Haidekker, M.A. Linear Feedback Controls; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Morales-Castañeda, B.; Zaldívar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A better balance in metaheuristic algorithms: Does it exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Boussaïda, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Han, M.; Liu, C.; Xing, J. An evolutionary membrane algorithm for global numerical optimization problems. Inf. Sci. 2014, 276, 219–241. [Google Scholar] [CrossRef]
- Meng, Z.; Pan, J.-S. Monkey King Evolution: A new memetic evolutionary algorithm and its application in vehicle fuel consumption optimization. Knowl. Based Syst. 2016, 97, 144–157. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 80–83. [Google Scholar] [CrossRef]
- Wu, G.H.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization. Available online: https://www.researchgate.net/profile/Guohua-Wu-5/publication/317228117_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2017_Competition_and_Special_Session_on_Constrained_Single_Objective_Real-Parameter_Optimization/links/5982cdbaa6fdcc8b56f59104/Problem-Definitions-and-Evaluation-Criteria-for-the-CEC-2017-Competition-and-Special-Session-on-Constrained-Single-Objective-Real-Parameter-Optimization.pdf (accessed on 16 September 2019).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).