Application of Semi-Empirical Models Based on Satellite Images for Estimating Solar Irradiance in Korea
Abstract
:1. Introduction
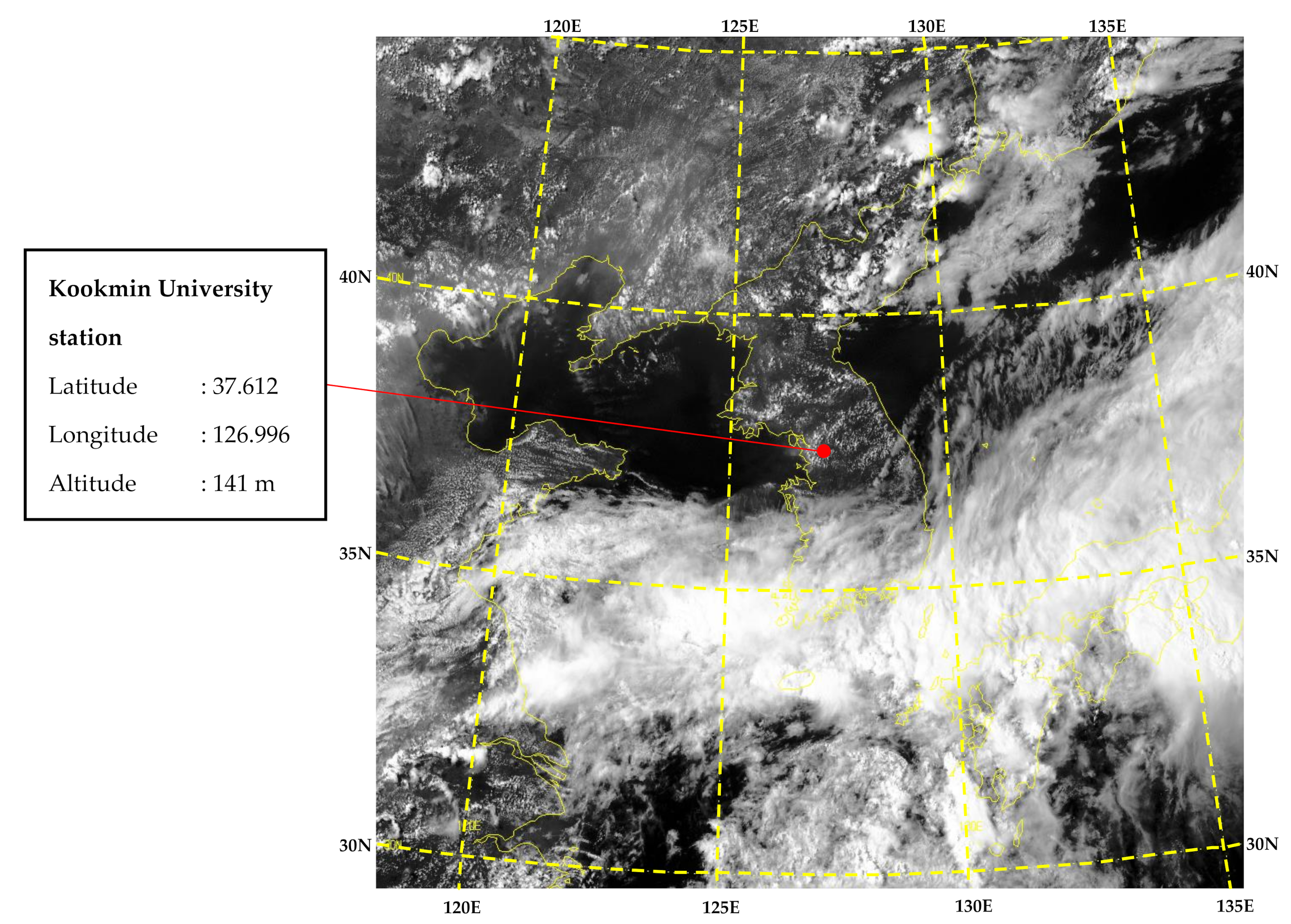
2. Satellite Images, Ground Measurement, and AERONET Dataset
- ,
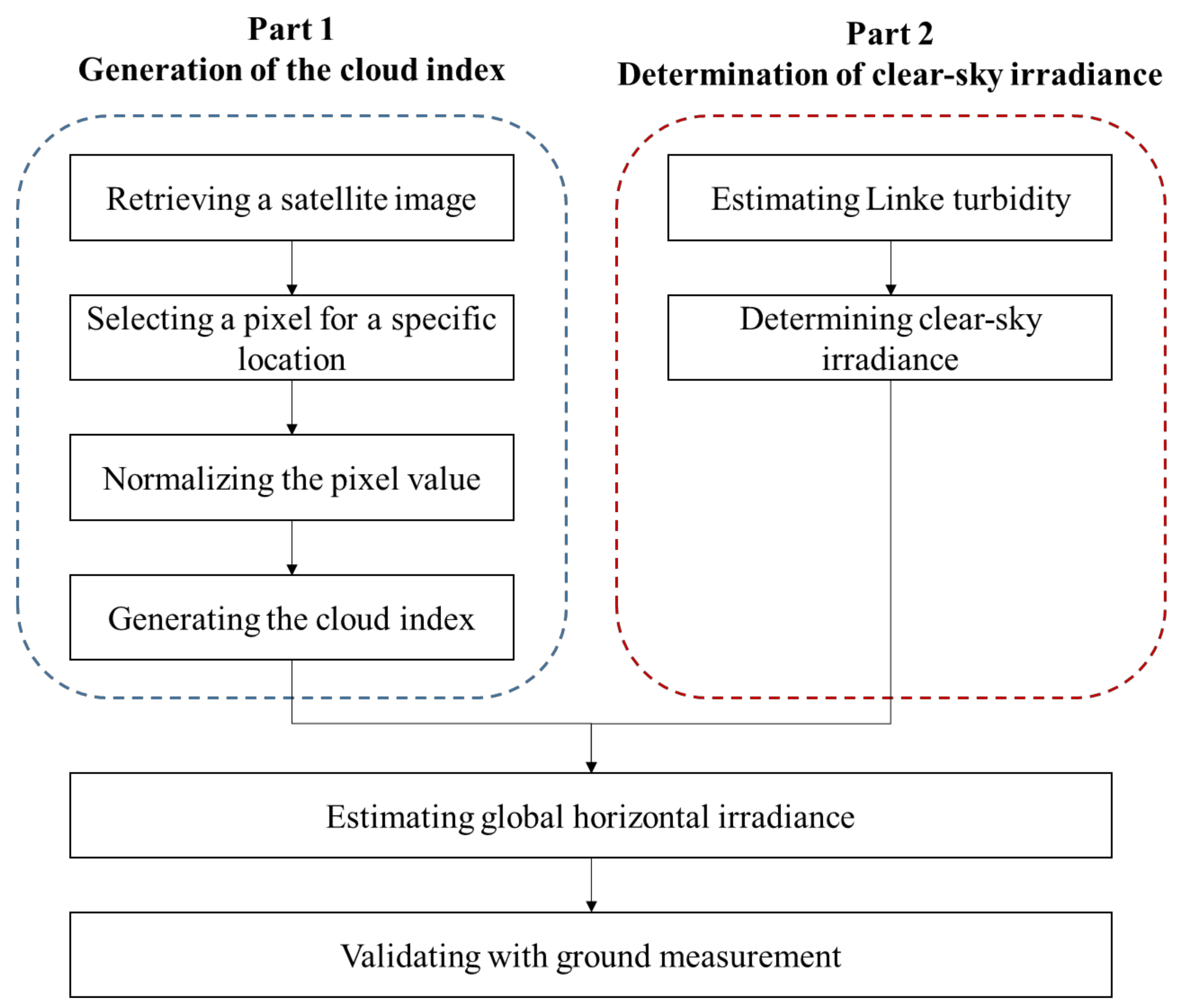
3. Global Horizontal Irradiance Models
3.1. Cloud Index Formula
| Model | Equation | |
|---|---|---|
| Beyer | (3) | |
| (4) | ||
| Rigollier | (5) | |
| (6) | ||
| Hammer | (7) | |
| (8) | ||
| (9) | ||
| Perez | (10) | |
| Hybrid | (11) | |
| (12) |
3.2. Clear-Sky Irradiance Formula
| Model | Equation | |
|---|---|---|
| Beyer | (14) | |
| Rigollier | (15) | |
| (16) | ||
| (17) | ||
| (18) | ||
| (19) | ||
| (20) | ||
| (21) | ||
| (22) | ||
| Hammer | (23) | |
| (24) | ||
| (25) | ||
| Perez | (26) | |
| (27) | ||
| (28) | ||
| (29) | ||
| (30) | ||
| Hybrid | (31) |
3.3. GHI Conversion Formula
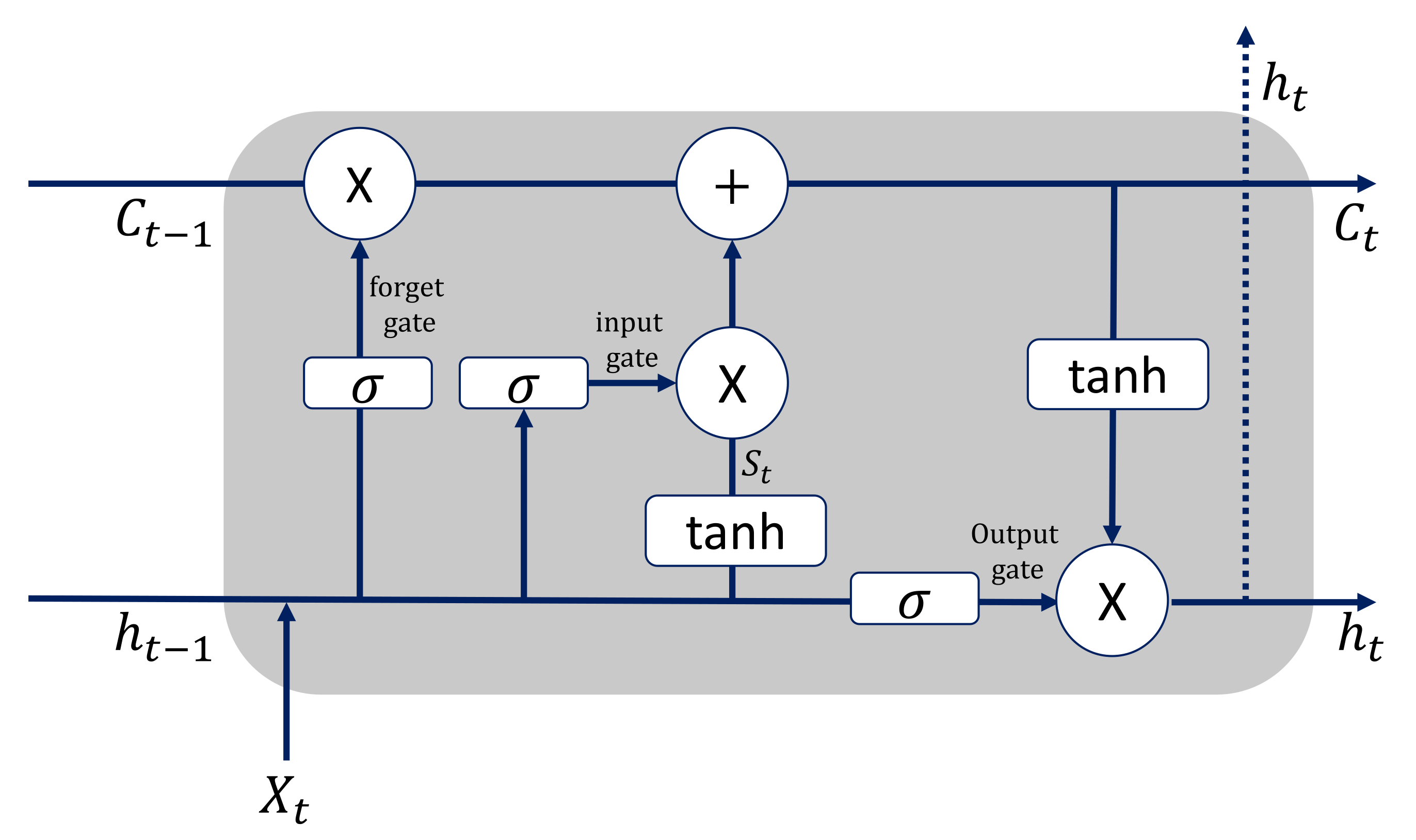
3.4. Long Short-Term Memory Model
- is the input vector to the memory cell at time .
- is the sigmoid function.
- is the bias vector.
- , and are weight matrices.
- , , and are the values of the input, forget, and output gates at time , respectively.
- , , and are the values of candidate state of the memory cell, the state of the memory cell at time , and the value of the memory cell at time , respectively.
3.5. Error Metrics for Model Validation
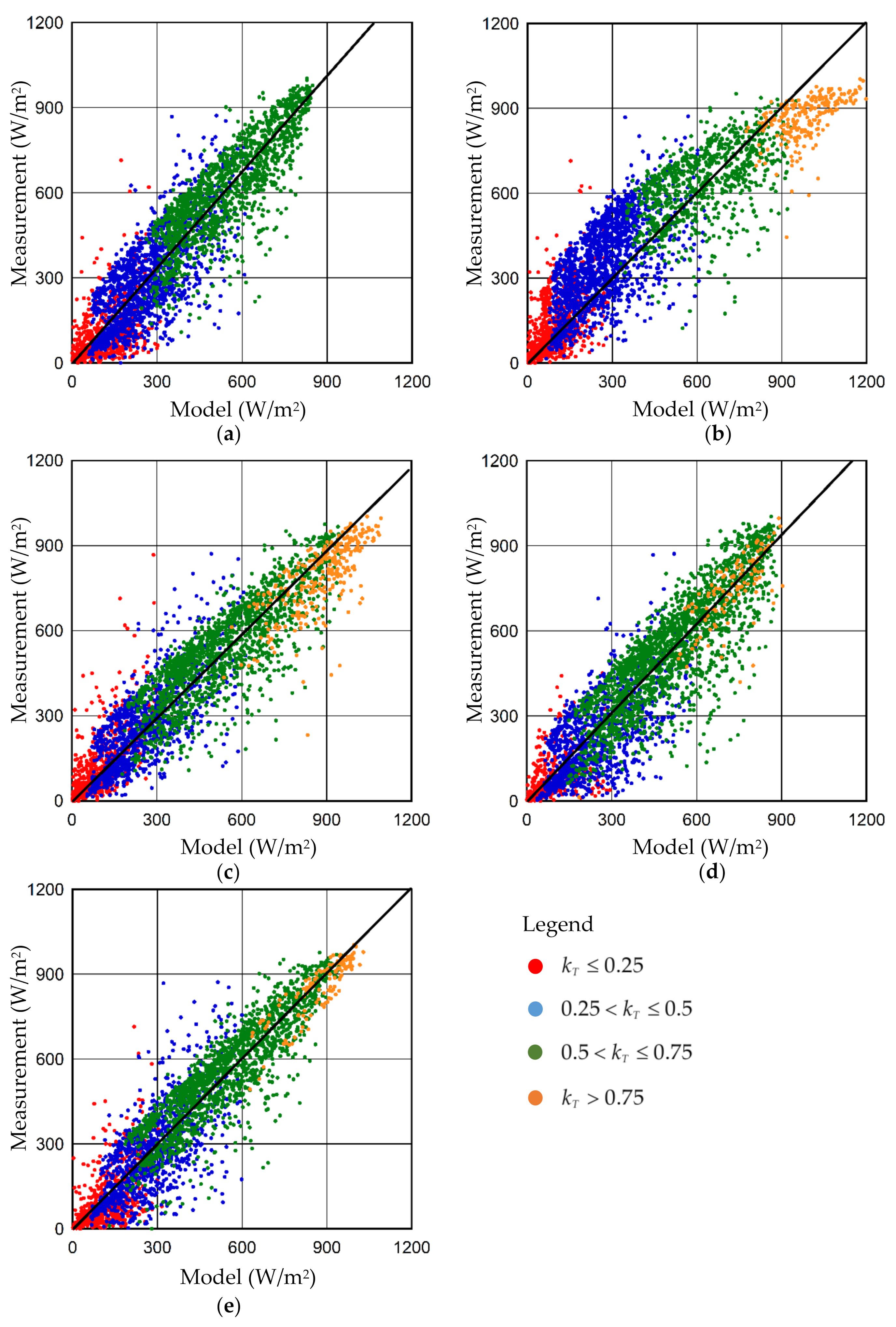
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Air mass | |
| Cloud index | |
| Raw satellite pixel value | |
| Total atmospheric air mass correction, backscattering effect correction, and satellite sensor system correction | |
| Normalized actual satellite pixel value | |
| Normalized minimum satellite pixel value | |
| Normalized maximum satellite pixel value | |
| Extraterrestrial irradiance on a horizontal plane (W/m2) | |
| Solar constant of 1367 W/m2 | |
| Total irradiance in the visible sensor of the satellite system (W/m2) | |
| clear-sky index | |
| clearness index | |
| Atmospheric path transmittance from the sun to the earth’s surface | |
| Linke turbidity | |
| Atmospheric path transmittance from the earth’s surface to the visible sensor of satellite | |
| Diffuse irradiance transmission function | |
| Precipitable water vapor | |
| Site elevation (m) | |
| Greek Symbols | |
| Solar zenith angle (deg) | |
| Solar elevation angle (deg) | |
| Backscatter angle (deg) | |
| Satellite zenith angle (deg) | |
| Normalized variation of the sun-to-earth distance from its mean value | |
| Rayleigh optical thickness | |
| Angstrom turbidity | |
| Subscripts | |
| Clear sky | |
| Heliosat-1 Beyer model | |
| Heliosat-2 Rigollier model | |
| Heliosat-2 Hammer model | |
| Perez model | |
| Hybrid model | |
| Abbreviations | |
| COMS | Communication, ocean, and meteorological satellite system |
| DNI | Direct normal irradiance (W/m2) |
| DHI | Diffuse horizontal irradiance (W/m2) |
| GHI | Global horizontal irradiance (W/m2) |
| KMA | Korean Meteorological Administration |
| MBE | Mean bias error (W/m2) |
| RMSE | Root-mean-square error (W/m2) |
| rRMSE | Relative root-mean-square error (%) |
| rMBE | Relative mean bias error (%) |
| PV | Photovoltaic |
References
- Ineichen, P.; Perez, R. Derivation of Cloud Index from Geostationary Satellites and Application to the Production of Solar Irradiance and Daylight Illuminance Data. Theor. Appl. Climatol. 1999, 64, 119–130. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A New Operational Model for Satellite-Derived Irradiances: Description and Validation. Sol. Energy 2002, 73, 307–317. [Google Scholar] [CrossRef]
- Rigollier, C.; Lefèvre, M.; Wald, L. The Method Heliosat-2 for Deriving Shortwave Solar Radiation from Satellite Images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef]
- Yang, L.; Gao, X.; Hua, J.; Wu, P.; Li, Z.; Jia, D. Very Short-Term Surface Solar Irradiance Forecasting. Sensors 2020, 20, 2606. [Google Scholar] [CrossRef]
- Zelenka, A.; Perez, R.; Seals, R.; Renné, D. Effective Accuracy of Satellite-Derived Hourly Irradiances. Theor. Appl. Climatol. 1999, 62, 199–207. [Google Scholar] [CrossRef]
- Mouhamet, D.; Tommy, A.; Primerose, A.; Laurent, L. Improving the Heliosat-2 Method for Surface Solar Irradiation Estimation under Cloudy Sky Areas. Sol. Energy 2018, 169, 565–576. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory National Solar Radiation Database 1991–2005 Update: User’s Manual. Task No. PVA7.6102; National Renewable Energy Lab.: Golden, CO, USA, 2007; Available online: https://www.nrel.gov/docs/fy07osti/41364.pdf (accessed on 12 April 2021). [CrossRef]
- Hammer, A.; Heinemann, D.; Hoyer, C.; Kuhlemann, R.; Lorenz, E.; Müller, R.; Beyer, H.G. Solar Energy Assessment Using Remote Sensing Technologies. Remote Sens. Environ. 2003, 86, 423–432. [Google Scholar] [CrossRef]
- Cano, D.; Monget, J.M.; Albuisson, M.; Guillard, H.; Regas, N.; Wald, L. A Method for the Determination of the Global Solar Radiation from Meteorological Satellite Data. Sol. Energy 1986, 37, 31–39. [Google Scholar] [CrossRef]
- Beyer, H.G.; Costanzo, C.; Heinemann, D. Modifications of the Heliosat Procedure for Irradiance Estimates from Satellite Images. Sol. Energy 1996, 56, 207–212. [Google Scholar] [CrossRef]
- Moradi, I.; Mueller, R.; Alijani, B.; Kamali, G.A. Evaluation of the Heliosat-II Method Using Daily Irradiation Data for Four Stations in Iran. Sol. Energy 2009, 83, 150–156. [Google Scholar] [CrossRef]
- Eissa, Y.; Chiesa, M.; Ghedira, H. Assessment and Recalibration of the Heliosat-2 Method in Global Horizontal Irradiance Modeling over the Desert Environment of the UAE. Sol. Energy 2012, 86, 1816–1825. [Google Scholar] [CrossRef]
- Janjai, S.; Sricharoen, K.; Pattarapanitchai, S. Semi-Empirical Models for the Estimation of Clear Sky Solar Global and Direct Normal Irradiances in the Tropics. Appl. Energy 2011, 88, 4749–4755. [Google Scholar] [CrossRef]
- Sengupta, M.; Heidinger, A.; Miller, S. Validating an Operational Physical Method to Compute Surface Radiation from Geostationary Satellites. Reliab. Photovolt. Cells Modul. Compon. Syst. III 2010, 7773, 77730T. [Google Scholar] [CrossRef]
- Seok, C.W.; Ram, S.A.; Yong, K. Solar Irradiance Estimation in Korea by Using Modified Heliosat-II Method and COMS-MI Imagery. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2015, 33, 463–472. [Google Scholar] [CrossRef]
- Jia, D.; Hua, J.; Wang, L.; Guo, Y.; Guo, H.; Wu, P.; Liu, M.; Yang, L. Estimations of Global Horizontal Irradiance and Direct Normal Irradiance by Using Fengyun-4a Satellite Data in Northern China. Remote Sens. 2021, 13, 790. [Google Scholar] [CrossRef]
- Yeom, J.M.; Han, K.S.; Kim, J.J. Evaluation on Penetration Rate of Cloud for Incoming Solar Radiation Using Geostationary Satellite Data. Asia Pac. J. Atmos. Sci. 2012, 48, 115–123. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A New Model Estimating Downwelling Solar Radiation at Ground Level in Clear-Sky Conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Zo, I.S.; Jee, J.B.; Lee, K.T.; Kim, B.Y. Analysis of Solar Radiation on the Surface Estimated from GWNU Solar Radiation Model with Temporal Resolution of Satellite Cloud Fraction. Asia Pac. J. Atmos. Sci. 2016, 52, 405–412. [Google Scholar] [CrossRef]
- Qu, Z.; Oumbe, A.; Blanc, P.; Espinar, B.; Gesell, G.; Gschwind, B.; Klüser, L.; Lefèvre, M.; Saboret, L.; Schroedter-Homscheidt, M.; et al. Fast Radiative Transfer Parameterisation for Assessing the Surface Solar Irradiance: The Heliosat-4 Method. Meteorol. Z. 2017, 26, 33–57. [Google Scholar] [CrossRef]
- Xie, Y.; Sengupta, M.; Dudhia, J. A Fast All-Sky Radiation Model for Solar Applications (FARMS): Algorithm and Performance Evaluation. Sol. Energy 2016, 135, 435–445. [Google Scholar] [CrossRef]
- Yeom, J.M.; Seo, Y.K.; Kim, D.S.; Han, K.S. Solar Radiation Received by Slopes Using COMS Imagery, a Physically Based Radiation Model, and GLOBE. J. Sens. 2016, 2016, 4834579. [Google Scholar] [CrossRef]
- Kim, C.K.; Kim, H.-G.; Kang, Y.-H.; Yun, C.-Y.; Lee, S.-N. Evaluation of Global Horizontal Irradiance Derived from CLAVR-x Model and COMS Imagery Over the Korean Peninsula. New Renew. Energy 2016, 12, 13. [Google Scholar] [CrossRef]
- Carver, S.; Mikkelsen, N.; Woodward, J. Updated World Map of the Köppen-Geiger Climate Classification. Permafr. Periglac. Process. 2002, 13, 243–249. [Google Scholar] [CrossRef]
- Ascencio-Vásquez, J.; Brecl, K.; Topič, M. Methodology of Köppen-Geiger-Photovoltaic Climate Classification and Implications to Worldwide Mapping of PV System Performance. Sol. Energy 2019, 191, 672–685. [Google Scholar] [CrossRef]
- Kawamura, H.; Tanahashi, S.; Takahashi, T. Estimation of Insolation over the Pacific Ocean off the Sanriku Coast. J. Oceanogr. 1998, 54, 457–464. [Google Scholar] [CrossRef]
- EKO Instrument Co., Ltd. MS-57 Instruction Manual Pyrheliometer Ver. 3; Version 3; EKO Instrument Co., Ltd.: Tokyo, Japan, 2019. [Google Scholar]
- EKO Instrument Co., Ltd. MS-802 Instruction Manual Pyranometer Ver. 3; Version 3; EKO Instrument Co., Ltd.: Tokyo, Japan, 2019. [Google Scholar]
- Gueymard, C.A.; Ruiz-Arias, J.A. Extensive Worldwide Validation and Climate Sensitivity Analysis of Direct Irradiance Predictions from 1-Min Global Irradiance. Sol. Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Emery, W.; Camps, A. Introduction to Satellite Remote Sensing: Atmosphere, Ocean, Land, and Cryosphere Applications; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Kumar, K.R.; Sivakumar, V.; Reddy, R.R.; Gopal, K.R.; Adesina, A.J. Inferring Wavelength Dependence of AOD and Ångström Exponent over a Sub-Tropical Station in South Africa Using AERONET Data: Influence of Meteorology, Long-Range Transport and Curvature Effect. Sci. Total Environ. 2013, 461–462, 397–408. [Google Scholar] [CrossRef]
- Rigollier, C.; Bauer, O.; Wald, L. On the Clear Sky Model of the ESRA—European Solar Radiation Atlas—With Respect to the Heliosat Method. Sol. Energy 2000, 68, 33–48. [Google Scholar] [CrossRef]
- Kasten, F. Parametriesirung Der Globalstahlung Durch Bedeckungsgrad Und Trubungsfaktor. Ann. Meteorol. Neue Folge 1984, 20, 49–50. [Google Scholar]
- Diabaté, L.; Demarcq, H.; Michaud-Regas, N.; Wald, L. Estimating Incident Solar Radiation at The Surface from Images of The Earth Transmitted by Geostationary Satellites: The Heliosat Project. Int. J. Sol. Energy 1987, 5, 261–278. [Google Scholar] [CrossRef]
- Song, A.; Choi, K.; Jung, M.; Kim, Y. Estimation of the Linke Turbidity Factor and the Solar Irradiance under a Clear Sky Over the Korean Peninsula Using COMS MI. New Renew. Energy 2016, 12, 21. [Google Scholar] [CrossRef]
- Ineichen, P.; Perez, R. A New Airmass Independent Formulation for the Linke Turbidity Coefficient. Sol. Energy 2002, 73, 151–157. [Google Scholar] [CrossRef]
- Marif, Y.; Bechki, D.; Zerrouki, M.; Belhadj, M.M.; Bouguettaia, H.; Benmoussa, H. Estimation of Atmospheric Turbidity over Adrar City in Algeria. J. King Saud Univ. Sci. 2019, 31, 143–149. [Google Scholar] [CrossRef]
- Bourges, G. Courbes de Fréquence Cumulées de l’irradiation Solaire Globale Horaire Reçue Par Une Surface Plane; Tome II; European Commission: Brussels, Luxembourg, 1979. [Google Scholar]
- Page, J. Algorithms for The Satellight Programme; Projektinterner Berict; 1996. [Google Scholar]
- Jacovides, C.P. Model Comparison For The Calculation of Linke’s Turbidity Factor. Int. J. Climatol. 1997, 17, 551–563. [Google Scholar] [CrossRef]
- Remund, J.; Wald, L.; Lefevre, M.; Ranchin, T.; Page, J.; Remund, J.; Wald, L.; Lefevre, M.; Ranchin, T.; Page, J.; et al. Worldwide Linke Turbidity Information. In Proceedings of the ISES Solar World Congress, Göteborg, Sweden, 14–19 June 2003. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.-J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Aslam, M.; Lee, J.M.; Kim, H.S.; Lee, S.J.; Hong, S. Deep Learning Models for Long-Term Solar Radiation Forecasting Considering Microgrid Installation: A Comparative Study. Energies 2019, 13, 147. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.Y. Day-Ahead Solar Irradiance Forecasting for Microgrids Using a Long Short-Term Memory Recurrent Neural Network: A Deep Learning Approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef]
- Jeon, B.K.; Kim, E.J. Next-Day Prediction of Hourly Solar Irradiance Using Local Weather Forecasts and LSTM Trained with Non-Local Data. Energies 2020, 13, 5258. [Google Scholar] [CrossRef]
- Choi, W.; Song, A.; Kim, Y. Estimation of Solar Radiation by Using Modified Heliosat-II Method and COMS-MI Imagery. Remote Sens. Clouds Atmos. XX 2015, 9640, 964015. [Google Scholar] [CrossRef]


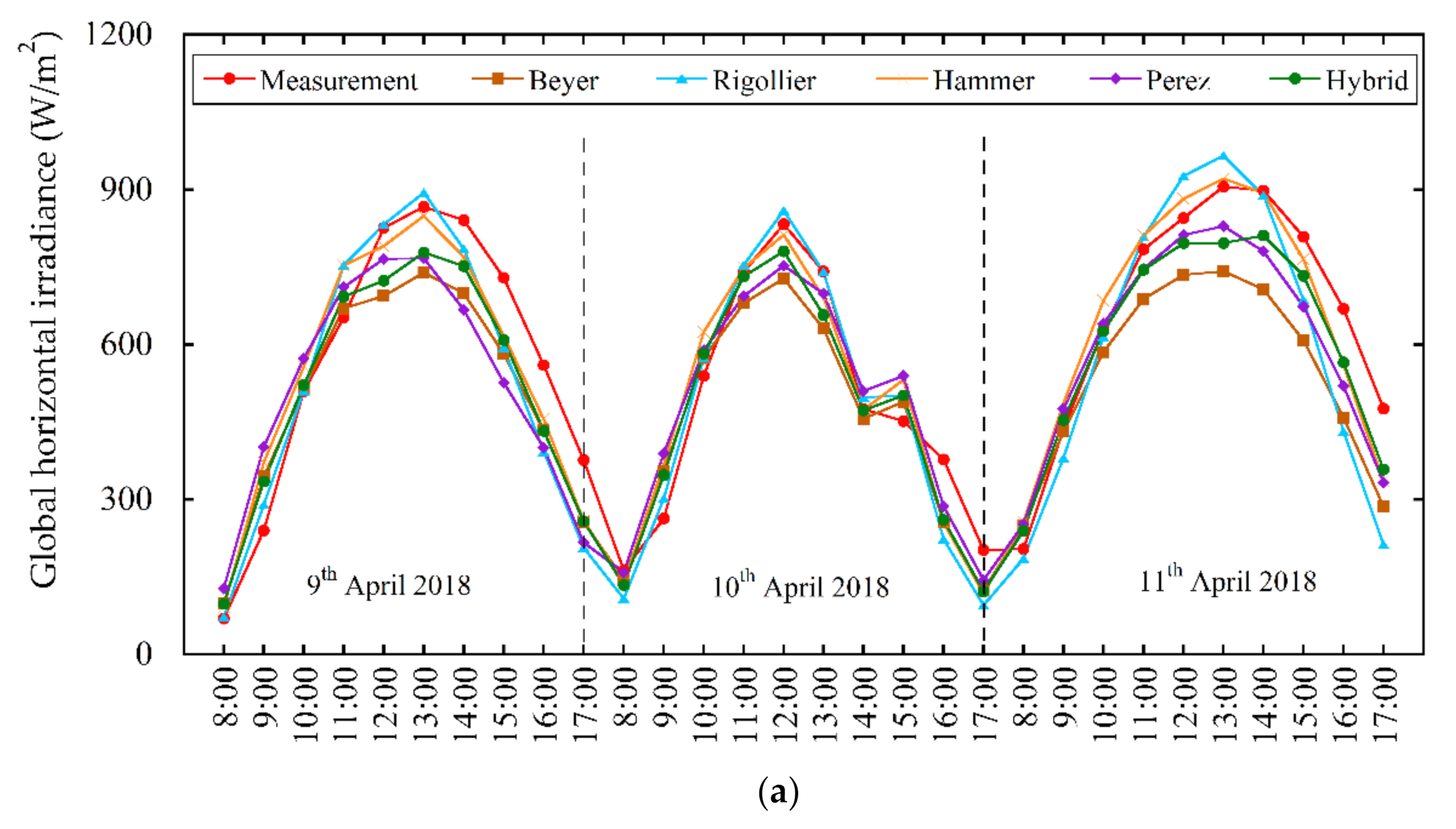
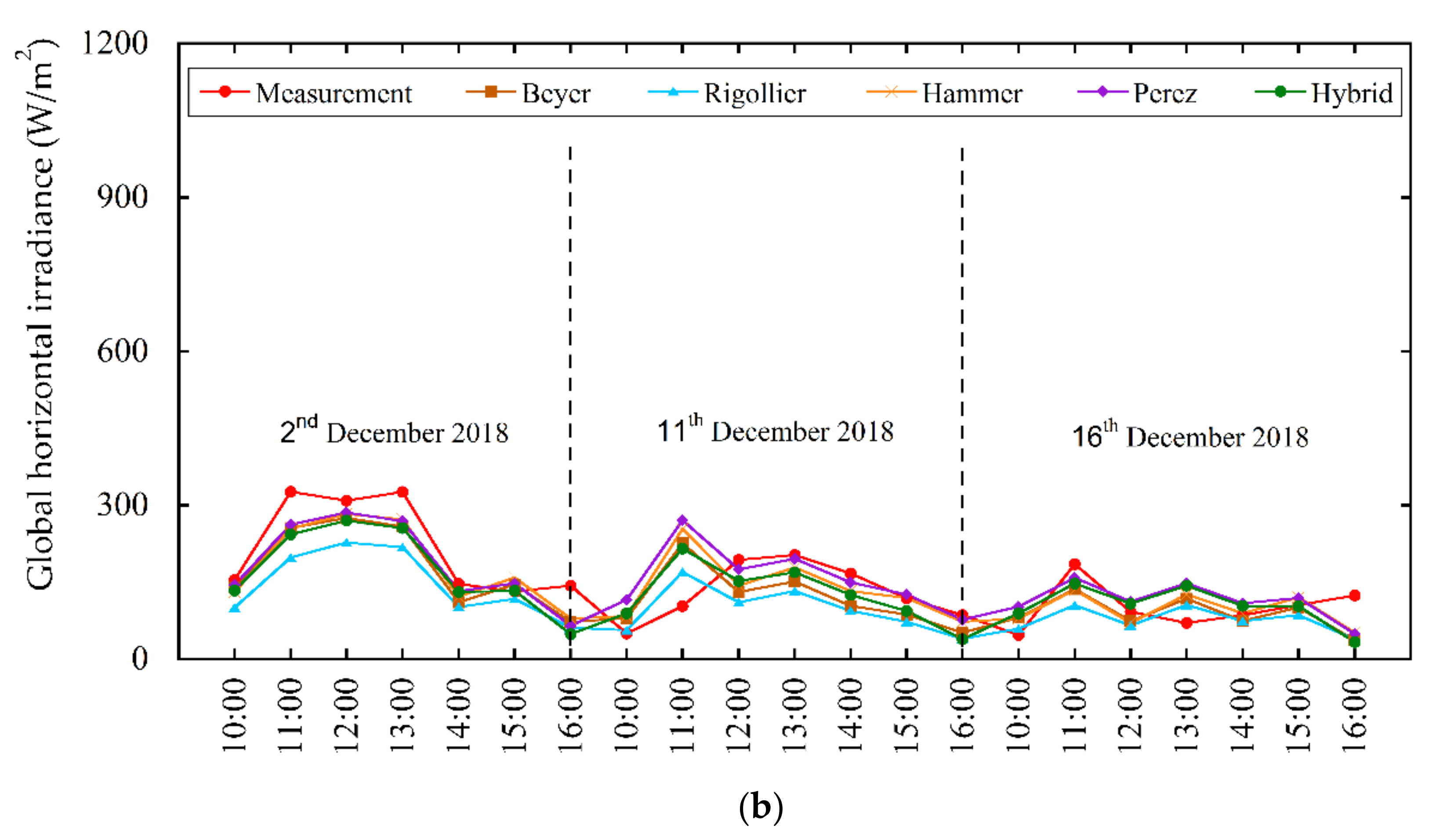
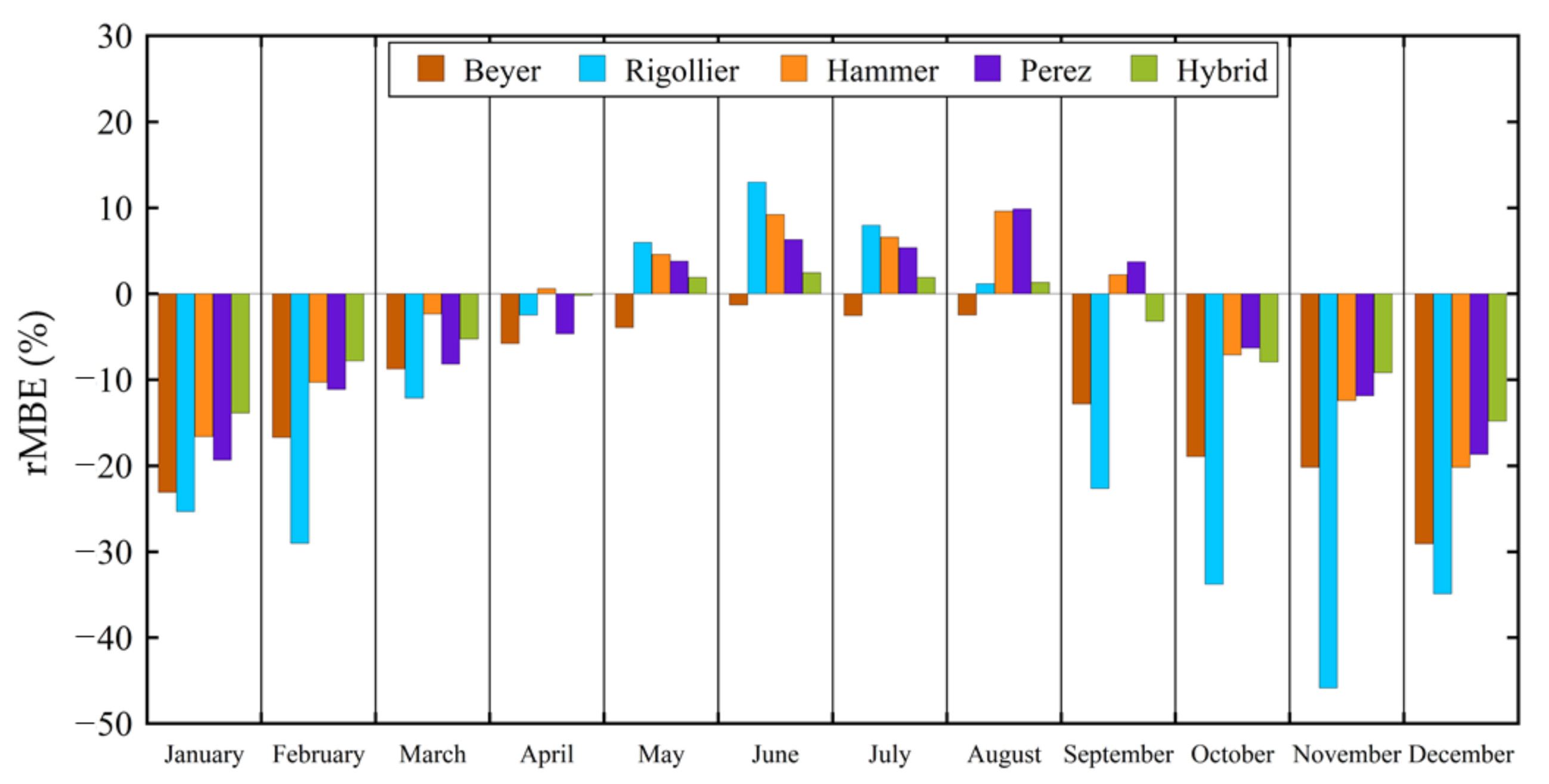
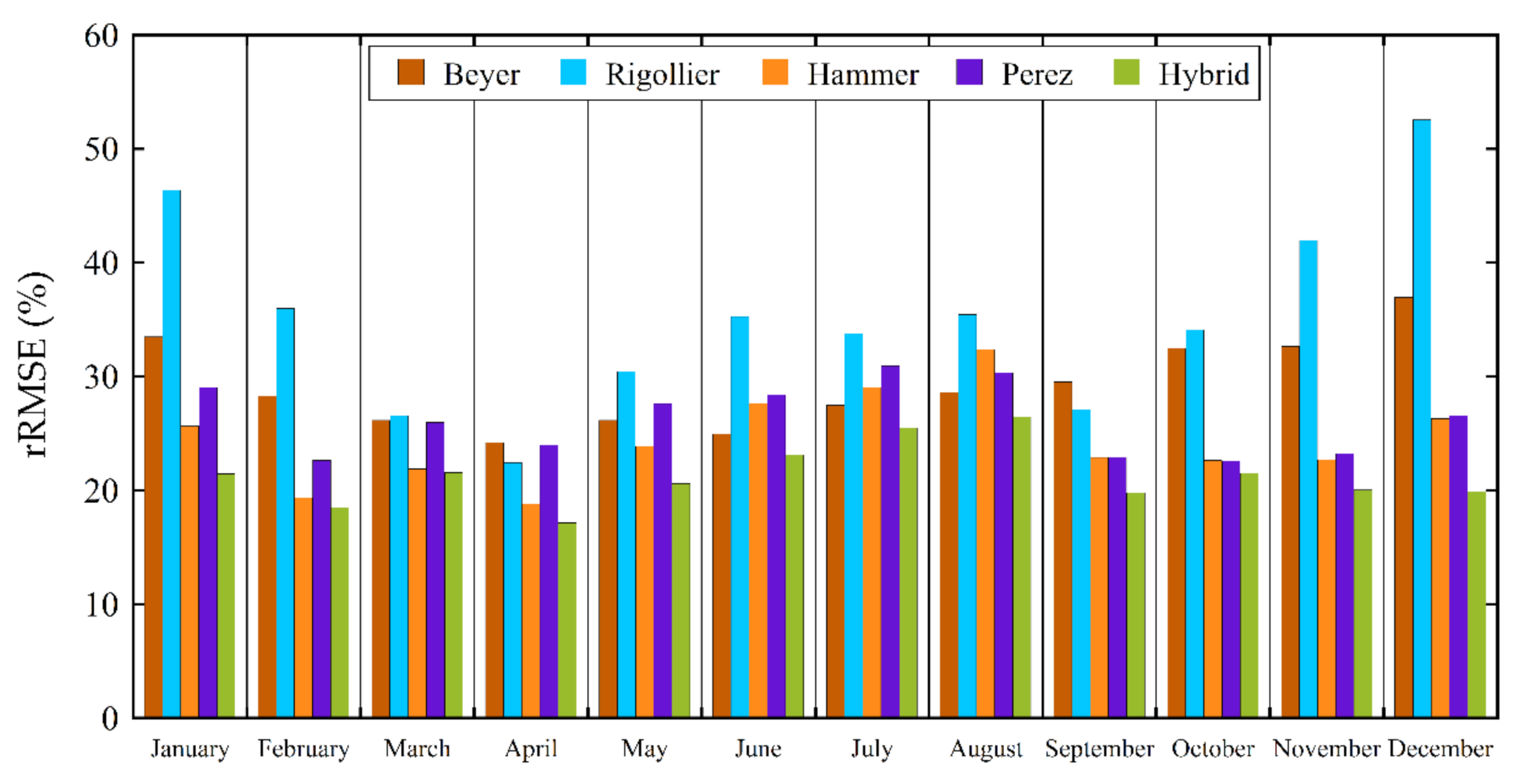
| Reference | Year | Area | Köppen Climate Classification (Subtype) | Model | RMSE (W/m2) | rRMSE (%) | Satellite System |
|---|---|---|---|---|---|---|---|
| Beyer et al. [10] | 1996 | Germany | Continental (Dfb, Dfc) Temperate (Cfa, Cfb) | Semi-empirical | − | 16 | Meteosat-1 |
| Perez et al. [2] | 2002 | United States | Dry (All subtypes) Temperate (All subtypes) Continental (All subtypes) | Semi-empirical | 118 | − | GOES |
| Hammer et al. [8] | 2003 | Europe | Dry (BSk, BWh) Temperate (Cfa, Cfb, Cfc, Csa, Csb) Continental (Dfa, Dfb) | Semi-empirical | − | 35 (1 h ahead) 40 (2 h ahead) | Meteosat-2 |
| Rigollier et al. [3] | 2004 | Europe | Dry (BSk, BWh) Temperate (Cfa, Cfb, Cfc, Csa, Csb) Continental (Dfa, Dfb) | Semi-empirical | − − − | 45 (Jan 95) 27 (Apr 95) 18 (Jul 94) | Meteosat-1 |
| Moradi et al. [11] | 2009 | Iran | Temperate (Csa) | Semi-empirical | − | 11.7 | Meteosat-5 |
| Eissa et al. [12] | 2012 | United Arab Emirates | Dry (Bwh) | Semi-empirical | 123 | 18.3 | Meteosat-2 |
| Choi et al. [15] | 2015 | Korea | Continental (Dwa) | Semi-empirical | − | 30.8 | COMS |
| Diallo et al. [6] | 2018 | French Guiana | Tropical (Af) | Semi-empirical | 133 | 30 | GOES |
| Yang et al. [4] | 2020 | Chengde | Continental (Dwa) | Semi-empirical | 181 (1 h ahead) 200 (2 h ahead) 215 (3 h ahead) | − | Fengyun-4A |
| Jia et al. [16] | 2021 | Northern China | Continental (Dwa) | Semi-empirical | 109 | − | Fengyun-4A |
| Yeom et al. [17] | 2012 | Korea | Continental (Dwa) | Physical | 71 (clear-sky) 90 (cloudy) | − | MTSAT-1R |
| Lefe’vre et al. [18] | 2013 | World | All classifications | Physical | 35 | 7 | Terra EOS |
| Zo et al. [19] | 2014 | Korea | Continental (Dwa) | Physical | 85 | − | COMS |
| Qu et al. [20] | 2016 | Europe and Africa | All classifications | Physical | 90 | 18 | Meteosat-2 |
| Xie et al. [21] | 2016 | United States | Dry (All subtypes) Temperate (All subtypes) Continental (All subtypes) | Physical | 130 | − | − |
| Yeom et al. [22] | 2016 | Korea | Continental (Dwa) | Physical | 72 (clear-sky) 106 (cloudy) | − | COMS |
| Kim et al. [23] | 2016 | Korea | Continental (Dwa) | Physical | 65 (clear-sky) 149 (cloudy) | 13 57 | COMS |
| Model | Equation | |
|---|---|---|
| Beyer | (33) | |
| (34) | ||
| Rigollier | (35) | |
| (36) | ||
| Hammer | (37) | |
| (38) | ||
| Perez | (39) | |
| (40) | ||
| Hybrid | (41) | |
| (42) |
| Model | Input | Total | |||||
|---|---|---|---|---|---|---|---|
| ) | |||||||
| Beyer | ● | ● | ● | 3 | |||
| Rigollier | ● | ● | ● | ● | 4 | ||
| Hammer | ● | ● | ● | ● | 4 | ||
| Perez | ● | ● | ● | 3 | |||
| Hybrid | ● | ● | ● | ● | 4 | ||
| Model | Clearness Level | R2 | RMSE (W/m2) | rRMSE (%) | MBE (W/m2) | rMBE (%) |
|---|---|---|---|---|---|---|
| Beyer | 0.60 | 87.23 | 90.29 | 10.25 | 10.61 | |
| 0.88 | 116.16 | 39.85 | −26.86 | −9.21 | ||
| 0.97 | 121.59 | 19.65 | −67.87 | −10.97 | ||
| − | − | − | − | − | ||
| All | 0.94 | 113.74 | 29.18 | −36.84 | −9.45 | |
| Rigollier | 0.68 | 90.02 | 79.40 | −30.26 | −26.69 | |
| 0.88 | 145.46 | 41.45 | −83.68 | −23.85 | ||
| 0.95 | 133.29 | 20.98 | −12.83 | −2.02 | ||
| 0.99 | 145.97 | 16.85 | 121.16 | 13.98 | ||
| All | 0.91 | 137.38 | 35.09 | −30.12 | −7.69 | |
| Hammer | 0.73 | 84.34 | 78.64 | −21.65 | −20.18 | |
| 0.87 | 105.56 | 40.14 | −11.01 | −4.18 | ||
| 0.96 | 106.23 | 19.89 | 0.39 | 0.07 | ||
| 0.98 | 126.50 | 15.88 | 90.87 | 11.41 | ||
| All | 0.94 | 103.92 | 26.54 | 0.09 | 0.02 | |
| Perez | 0.52 | 84.73 | 89.46 | −1.10 | −1.16 | |
| 0.82 | 122.56 | 40.55 | −16.96 | −5.61 | ||
| 0.96 | 111.29 | 20.46 | −17.50 | −3.21 | ||
| 0.98 | 103.03 | 16.35 | 57.88 | 9.19 | ||
| All | 0.93 | 112.57 | 28.64 | 14.53 | 3.70 | |
| Hybrid | 0.64 | 82.83 | 85.03 | 2.32 | 2.38 | |
| 0.85 | 113.39 | 40.90 | −7.36 | −2.65 | ||
| 0.97 | 89.60 | 15.67 | −19.17 | −3.35 | ||
| 0.99 | 48.24 | 5.47 | 10.06 | 1.14 | ||
| All | 0.95 | 97.08 | 24.12 | −7.24 | −1.80 |
| Model | RMSE (W/m2) | rRMSE (%) | MBE (W/m2) | rMBE (%) |
|---|---|---|---|---|
| Beyer | 118.95 | 28.10 | −88.05 | −20.80 |
| Rigollier | 143.45 | 41.09 | −107.27 | −30.72 |
| Hammer | 88.36 | 25.31 | −35.44 | −10.15 |
| Perez | 89.67 | 25.75 | −28.71 | −8.24 |
| Hybrid | 86.14 | 23.92 | −19.70 | −5.47 |
| LSTM | 76.45 | 21.92 | −24.28 | −6.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garniwa, P.M.P.; Ramadhan, R.A.A.; Lee, H.-J. Application of Semi-Empirical Models Based on Satellite Images for Estimating Solar Irradiance in Korea. Appl. Sci. 2021, 11, 3445. https://doi.org/10.3390/app11083445
Garniwa PMP, Ramadhan RAA, Lee H-J. Application of Semi-Empirical Models Based on Satellite Images for Estimating Solar Irradiance in Korea. Applied Sciences. 2021; 11(8):3445. https://doi.org/10.3390/app11083445
Chicago/Turabian StyleGarniwa, Pranda M. P., Raden A. A. Ramadhan, and Hyun-Jin Lee. 2021. "Application of Semi-Empirical Models Based on Satellite Images for Estimating Solar Irradiance in Korea" Applied Sciences 11, no. 8: 3445. https://doi.org/10.3390/app11083445
APA StyleGarniwa, P. M. P., Ramadhan, R. A. A., & Lee, H. -J. (2021). Application of Semi-Empirical Models Based on Satellite Images for Estimating Solar Irradiance in Korea. Applied Sciences, 11(8), 3445. https://doi.org/10.3390/app11083445






