Boron-Decorated Pillared Graphene as the Basic Element for Supercapacitors: An Ab Initio Study

Abstract

In this work, using the first-principle density functional theory (DFT) method, we study the properties of a new material based on pillared graphene and the icosahedral clusters of boron B₁₂ as a supercapacitor electrode material. The new composite material demonstrates a high specific quantum capacitance, specific charge density, and a negative value of heat of formation, which indicates its efficiency. It is shown that the density of electronic states increases during the addition of clusters, which predictably leads to an increase in the electrode conductivity. We predict that the use of a composite based on pillared graphene and boron will increase the efficiency of existing supercapacitors.

1. Introduction

Currently, the rapid development of electronics requires energy-intensive, safe, and efficient energy storage sources for portable and stationary applications. Lithium-ion batteries (LIBs) are usually used if high energy density and long-term operations are required. Supercapacitors (SCs) are applied when high power density with a short exposure time should be obtained [1]. The operation principles of these two sources are different: LIBs work on electrochemical Faraday processes, while SCs use an electrostatic charge storage process. Faraday processes are slower than electrostatic processes. This limits the maximum power density of batteries and their discharge/charge currents. SCs have a huge power density due to electrostatic interactions, but the energy density is much lower. Modern lithium batteries have a limited life span of tens of thousands of cycles and require sophisticated tracking systems to safely charge and discharge them [2,3]. In turn, the lifetime of SCs exceeds one million cycles, the charging method is quite simple and safe, and full discharge does not lead to degradation of the electrodes [4,5,6]. Thus, in terms of lifetime and ease of use, SCs have obvious advantages over batteries, but low-energy density is still the main limiting factor to their widespread application. The energy of a SC is contained in its capacitance of the double electric layer, which is formed at the media boundary and depends on the effective area of the electrodes [7]. In addition to the double-layer capacitance, there is also a quantum capacitance that directly affects the total electrode capacitance:

$$\frac{1}{C_{Total}}=\frac{1}{C_D}+ \frac{1}{C_Q}$$

(1)

Quantum capacitance, first investigated in [8], is directly related to the density of states (DOS), so for materials with a low DOS near the Fermi level, the quantum capacitance will also be a low value. For metal electrodes (for example, electrodes of a classical dielectric capacitor) in which the DOS is high, the quantum capacitance will also be high.

Here, the quantum capacitance $C_Q$ and the double-layer capacitance $C_D$ contribute to the total capacitance $C_{Total}$, according to the law of addition of capacitors connected in series. From the expression above, it can be concluded that for increasing the efficiency of SCs, it is necessary to simultaneously increase both $C_Q$ and $C_D$.

SCs are divided into two types of devices: EDLC and hybrid. In EDLC, both electrodes have the same structure and electrostatic mechanism of charge accumulation. In hybrid ones, electrostatic charge accumulation occurs on one of the electrodes, and the Faraday process occurs on the other [9]. Hereinafter, according to the SC, we denote the EDLC.

To increase $C_D$, the electrode material must have a sufficiently large effective area. Carbon materials, for example, widely used activated carbon, are suitable for this role [10,11,12]. Due to the developed surface, the electrolyte penetrates into the pores of the activated carbon and thereby creates a double-layer capacitance. The disadvantages of the activated carbon electrode are its low mechanical strength and electrical conductivity due to the amorphous structure and the gaps between the layers [13]. In addition, researchers [14,15] revealed a pattern of reduction in the total capacitance of carbon materials due to the low value of $C_Q$. It is possible to increase the $C_Q$ value of carbon materials by adsorption of various compounds on their surfaces, as shown in theoretical [16,17,18,19] and experimental works [20,21]. Boron compounds are actively used for modification of such carbon structures as single-walled carbon nanotubes (SWCNTs) and graphene. The total capacitance of the synthesized SC in this case ranges from 32.2 F to 1544 F/g [22,23,24,25]. The carbon material by itself must have good electrical conductivity for efficient transfer of stored charge, high porosity for penetration of the electrolyte into the material cavities, and strong mechanical properties, since the flow of large discharge currents can lead to its overheating and destruction. These criteria are well met by a composite based on SWCNTs and graphene-pillared graphene (PGR). The use of this material in SC is currently being actively researched and discussed. Electrodes with a specific capacity of 145 to 200 F/g, excellent cyclicity, and high power density have already been synthesized [25,26,27,28,29], but a numerical experiment can indicate the most effective direction for researchers.

In our study, using the ab initio density functional theory (DFT) method performed in SIESTA software, we predicted methods to increase the efficiency of the SC electrode material on the base of pillared graphene and icosahedral boron clusters.

2. Materials and Methods

The SIESTA 4.1 software package [30,31] is widely used for geometry relaxation, for the search of the potential energy minima, and for the calculation of the carbon nanostructures electronic properties [32,33,34]. We used the density functional theory (DFT) basis set with generalized gradient approximation (GGA) and Perdew-Burke-Ernzerhof (PBE) parameterization, since these calculation parameters have been well-proven both in terms of computational accuracy and calculation duration. The force acting on each atom after relaxation was set to 0.03 eV/Å, and the energy limit was chosen to be 350 Ry. The Brillouin zone was sampled by a 4 × 4 × 1 Monkhorst-Pack grid. The relaxation process was performed by the Broyden algorithm [35] and the Pulay corrections.

The expression for the $C_Q\left(V\right)$ calculation is given below [36]:

$$C_Q\left(V\right)= \frac{1}{mV}\underset{0}{\overset{V}{{\displaystyle \int }}}eD\left(E_F-eV\right)dV.$$

(2)

As can be seen from Equation (2), the quantum capacitance C_Q directly depends on the density of electronic states D, at an applied bias, the Fermi level E_F, and the bias V, calculated as a change in the Fermi level with a change in the object’s charge and object mass m.

The considered model of pillared graphene consisted of SWCNT with a chirality index of (9,9) of 1.2 nm in diameter and two graphene sheets. The choice of SWCNT with such diameter was caused by its stability in pillared graphene framework [37].

3. Results and Discussion

Figure 1a shows a supercell of PRG containing 400 carbon atoms. The translation vectors of the supercell after geometric relaxation are 24.61 Å in the X direction and 21.44 Å in the Y direction. During the PGR supercell building, a SWCNT (9,9) with open edges was attached by chemical bonds to a graphene sheet in the area of the hole that was preliminary cut in the graphene surface. The resulting structure matched the experimental data of pillared graphene [38]. The heat of formation of the supercell is 1.2–142 kcal/mol·atom and does not depend on the CNT length. In the graphene-CNT contact area, six pairs of penta- and heptagons as well as three octagons were formed.

The supercell in Figure 1b has five B₁₂ clusters. B₁₂ clusters are icosahedral clusters with 12 boron atoms. As can be seen from the figure, the B₁₂ clusters formed bonds with the carbon near the defects in the area of the junction between the graphene sheets and SWCNTs. The length of the bonds varied in the range of 1.669 to 1.682 Å. The mass fraction of the boron ranged from 2.64% for one cluster and up to 11.92% for five clusters. The Mulliken charge distribution pattern between the PGR and B₁₂ framework (Figure 1b) shows that the carbon framework received additional electrons from the B₁₂ clusters. For the case of five clusters, the additional charge on the PGR is −0.287 electrons.

To calculate C_Q and predict changes in the material’s conductivity, it was necessary to calculate the DOS curves for all considered cases of B₁₂ concentration. Figure 2 shows the DOS curves for the pure PGR and for PGR decorated with one to five boron clusters. It can be seen that the growth in the B₁₂ amount increases the DOS amplitude over the entire energy range by increasing the number of electronic states.

Earlier [39], we showed that B₁₂ clusters in the modified CNT increase the DOS peak amplitude and the CNT conductivity. Here, we observed a similar effect, so we assumed that the resistance of the boron-decorated PGR-based electrode would also decrease.

To predict the effectiveness of the model as an electron SC material, we built C_Q curves in the voltage range from −3 to 3 V (Figure 3). In comparison with the pure PGR (black curve), the modified model had the characteristic peaks in the positive branch of the plot reaching ~1.266 kF/g for five B₁₂ clusters. In accordance with Formula (2), an increase in DOS in the energy range from −3 to 3 eV (Figure 2) also leads to an increase in C_Q. Despite the increase in the electrode mass due to the addition of clusters, the C_Q continued to grow as the clusters introduced new electronic states. The details of all C_Q values are shown in

Table 1. Heat of formation, specific charge density, and specific capacitance for the pure PGR and for the PGR decorated with 1 to 5 boron clusters.

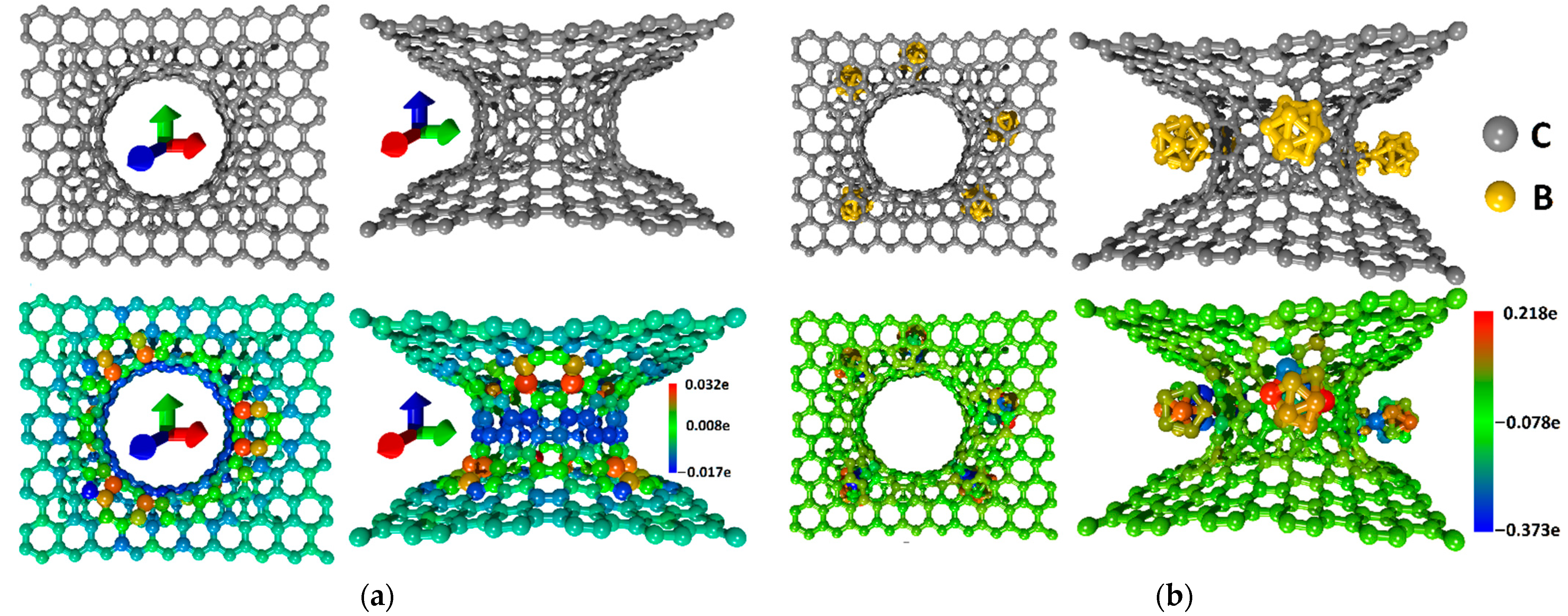
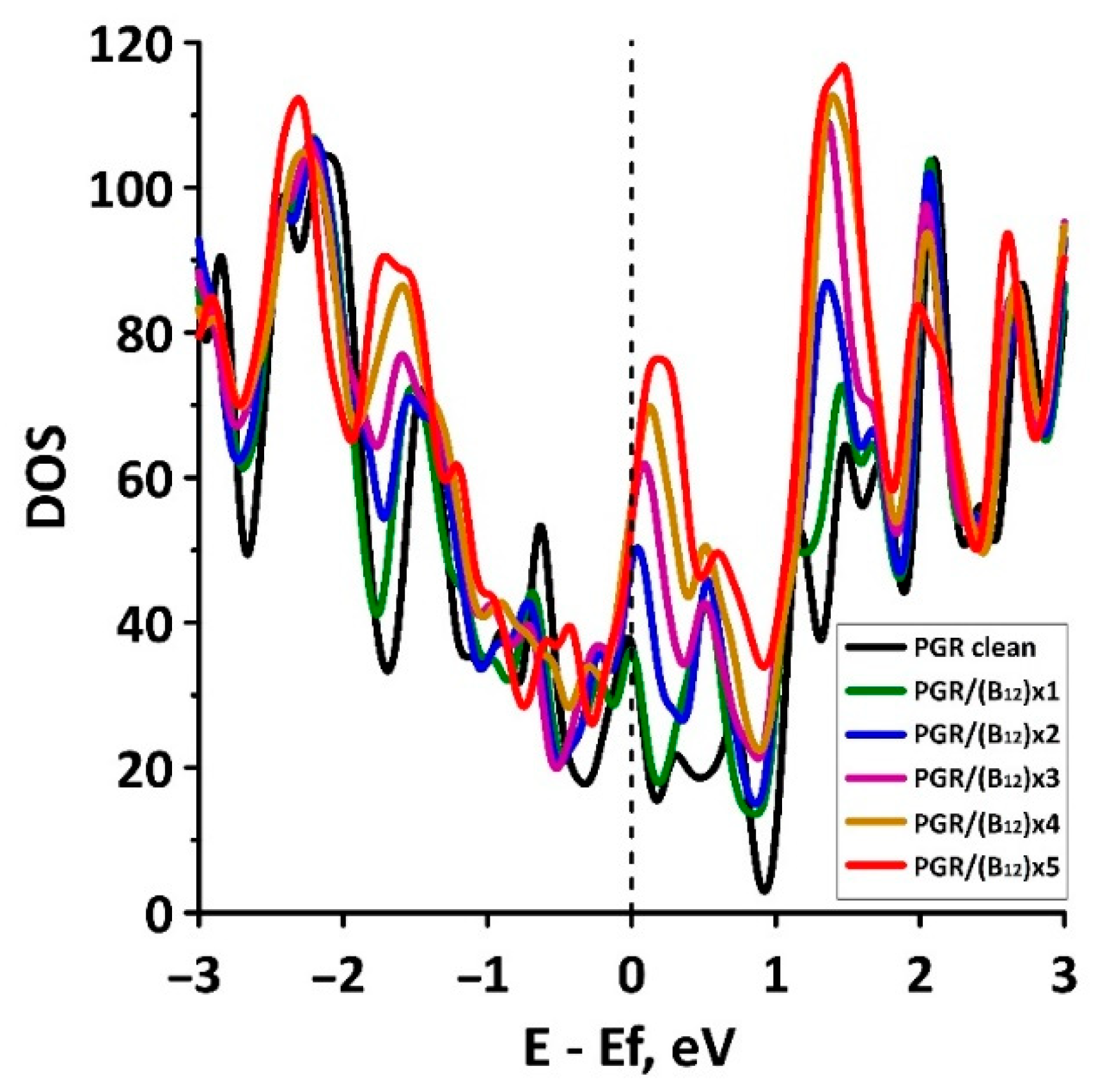
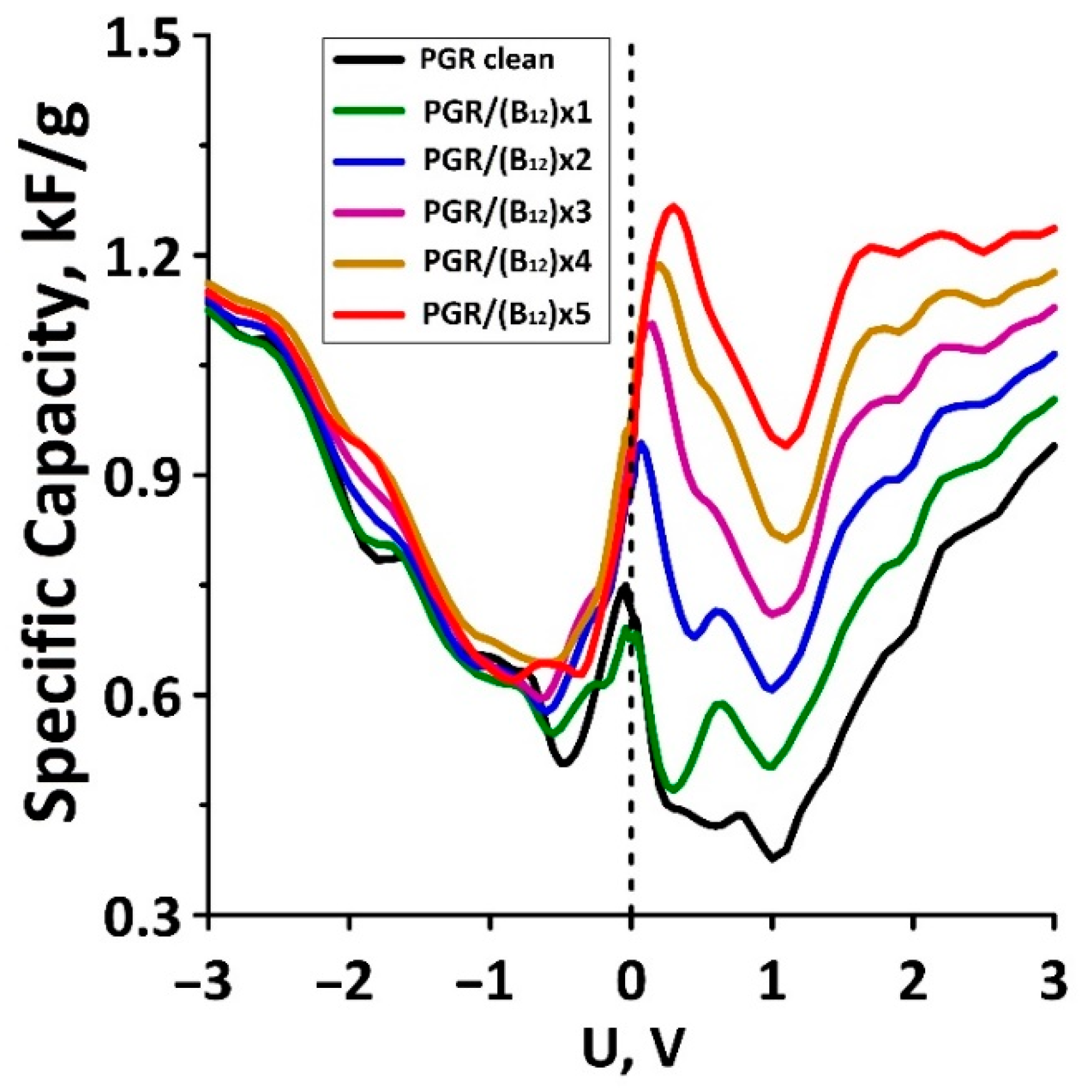
No.	ΔH, eV	QSCD, kC/g	CQ, kF/g
Pure PGR	-	−2.384/1.748	0.749
PGR/(B12) × 1	−0.00607	−2.359/2.036	0.691
PGR/(B12) × 2	−0.00965	−2.466/2.418	0.943
PGR/(B12) × 3	−0.01271	−2.532/2.757	1.105
PGR/(B12) × 4	−0.01743	−2.608/3.030	1.187
PGR/(B12) × 5	−0.02272	−2.534/3.317	1.266

.

In this study, we did not conduct a numerical estimate of the capacitance $C_D$. However, according to previous articles [26,27,28,29], it can be seen that the value of the total capacitance of SCs built on the basis of pillared graphene gives values in the range from 144.5 to 352 F/g, where the value $C_D$ must be greater than these capacitance values. Thus, an increase in $C_Q$ will lead to an increase in the total capacity of the SC.

Finally, to determine whether the electronic material for symmetric SC devices was ELCC or hybrid SC, specific charge density curves were calculated (Figure 4). Q_SCD were calculated by the method described in [40]:

$$Q_{SCD}=\underset{0}{\overset{V}{{\displaystyle \int }}}{C}_Q\left(V\right)dV$$

(3)

The look of the curves in Figure 4 indicates the symmetrical behavior of the material with an increase in number of B₁₂ clusters up to two. However, with further clusters up to five, the picture slightly changed, and the asymmetry of the negative and positive branches appeared. In the negative branch, the curves were almost constant, and this was directly related to the values of C_Q in the voltage range from −3 to 0 V. Here, the change in C_Q was not so pronounced. Specific charge density indicates how much charge, in terms of mass, the electrode material can store. The increase in charge capacity is explained as a direct result of the additional availability of states near the Fermi level in DOS. From the nature of the Q_SCD distribution, it follows that by changing the boron concentration, this electrode material can be used both in hybrid SCs and in symmetric SCs.

Heat of formation per atom (ΔH) for each added boron cluster, C_Q at the 0.1 V and Q_SCD for voltages −3 and 3 V, are shown in Table 1.

4. Conclusions

In the present paper, the objects of research were the models of PGR decorated with boron clusters. Based on the ab initio method in the SIESTA code, the specific quantum capacitance, electronic properties, and energy stability of PGR modified by clusters of boron-containing compounds were calculated. The calculation of the specific charge density demonstrated symmetry with respect to the positive and negative bias at a concentration of 5.13 wt% (two B₁₂ clusters). With the increase in boron concentration, branch asymmetry was observed, which expanded the application of the electrode material for both symmetric and hybrid SC devices. Thus, the modification of PGR by B₁₂ boron clusters can significantly improve the characteristics of the electrode material and expand its application in the electrode material SC.