Travel-Time Inversion Method of Converted Shear Waves Using RayInvr Algorithm
Abstract
:1. Introduction
2. Data and Methodology
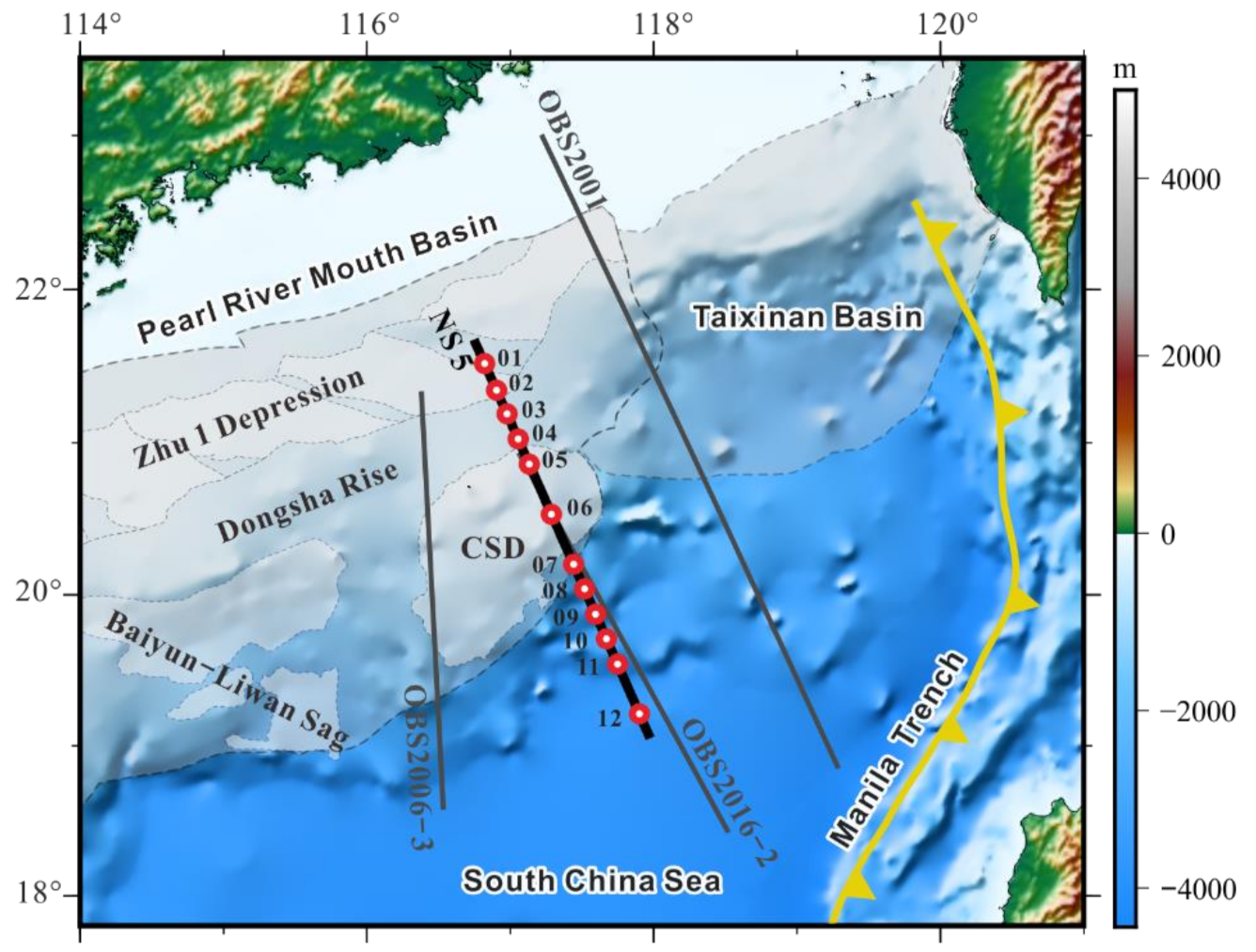
2.1. Data Acquisition and Processing
2.2. Method
3. Types and Applications of Converted S-Waves Phases
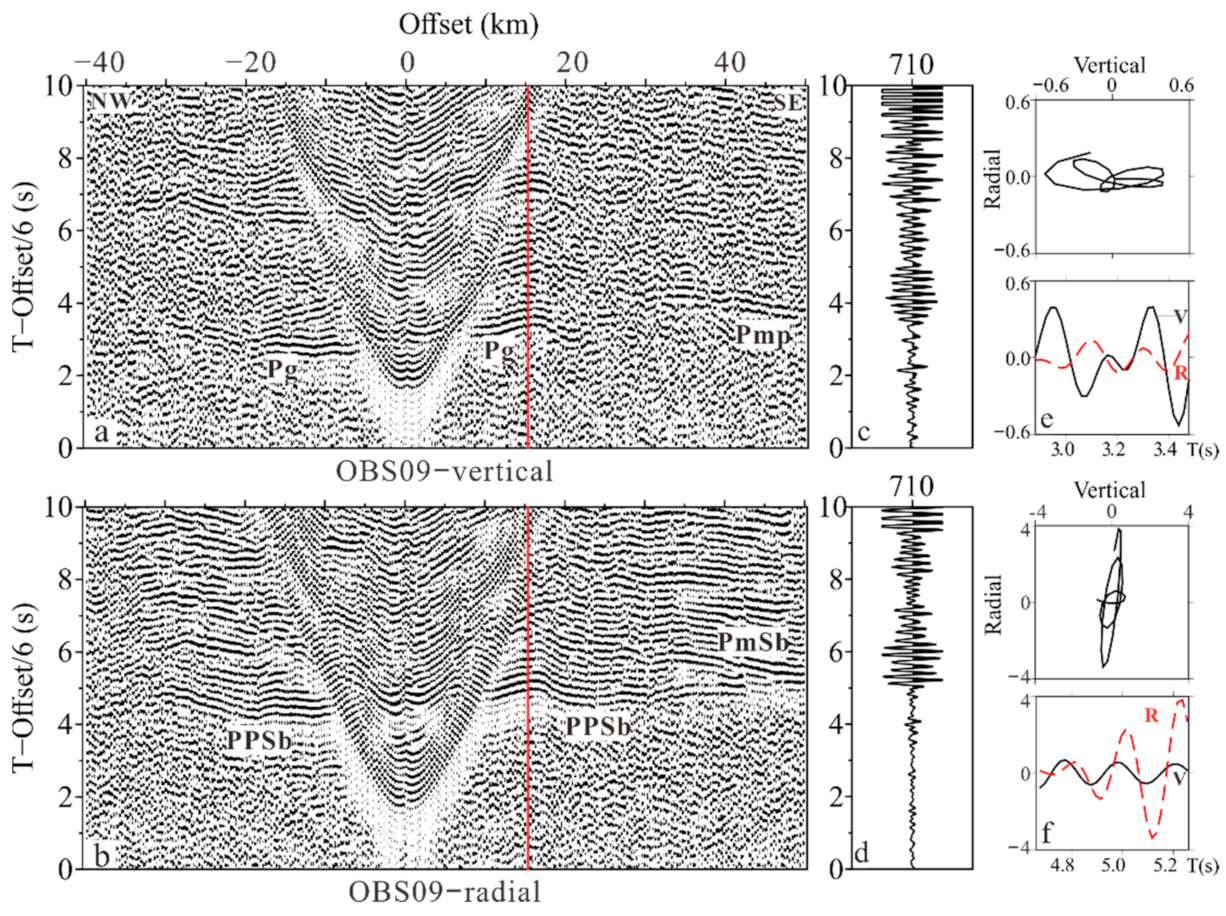
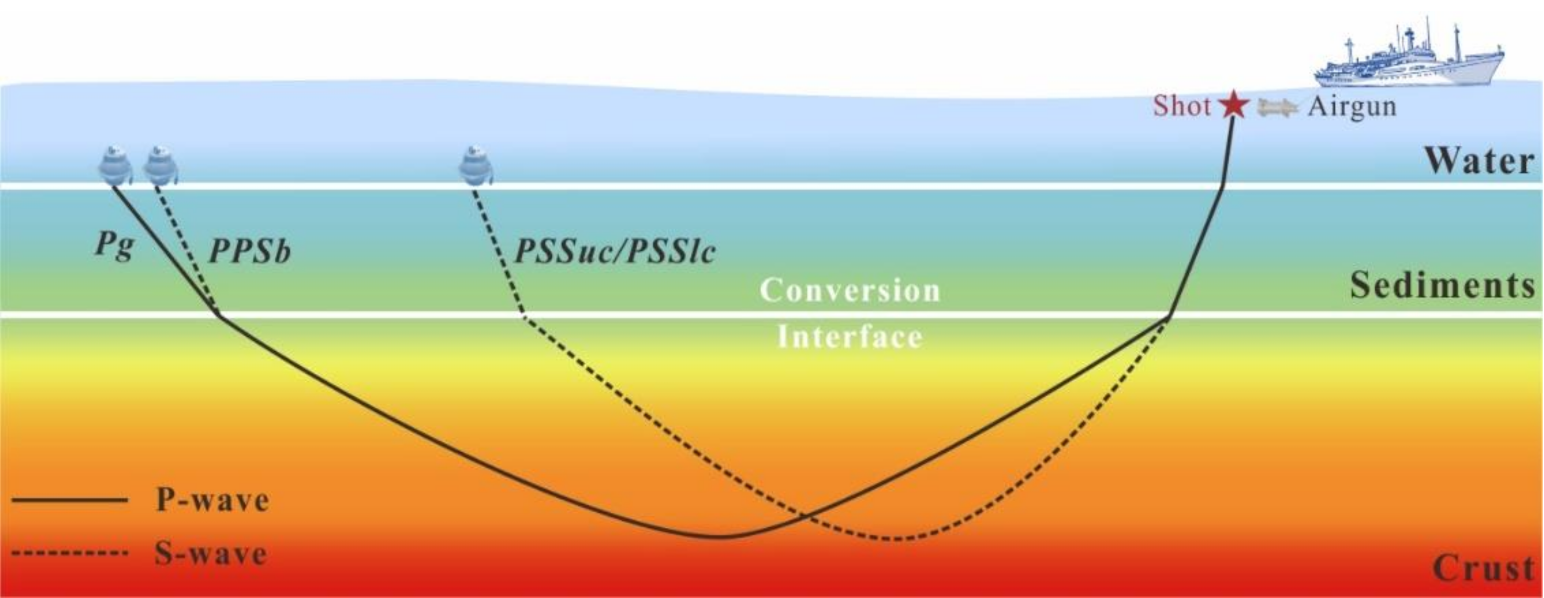
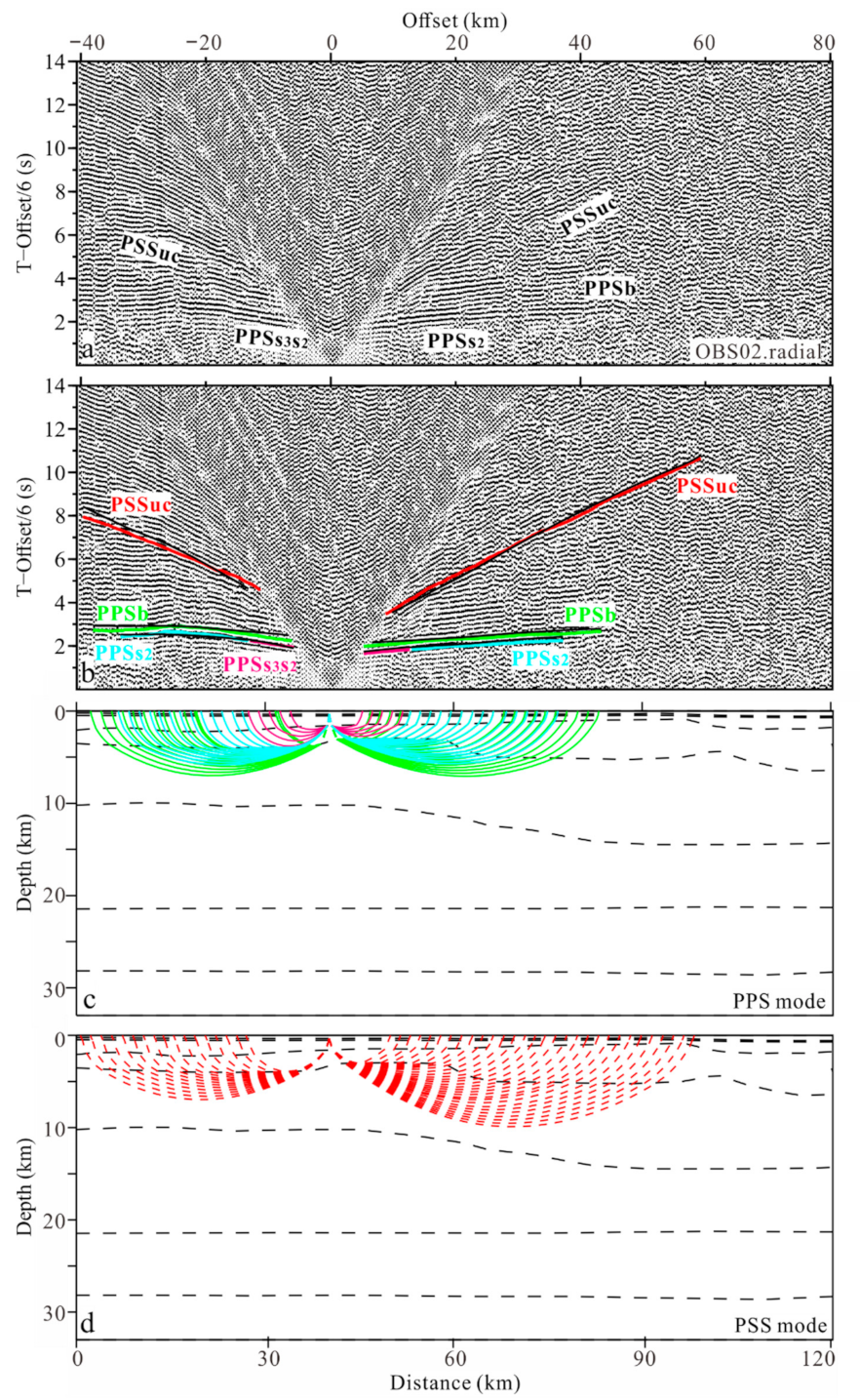
3.1. PPS Phases and Its Role in Constraining Sediments Vp/Vs Ratios
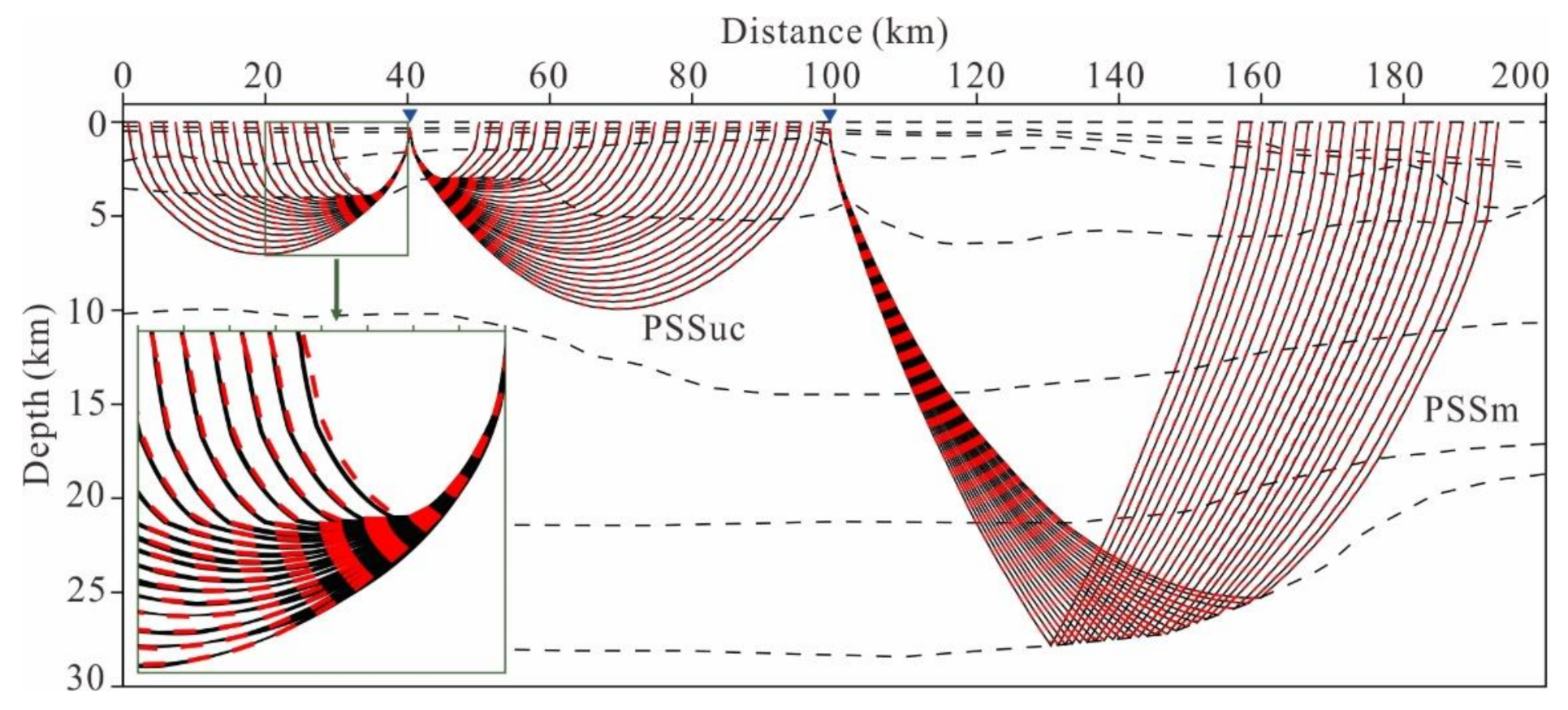
3.2. PSS Phases and Their Travel-Times Correction
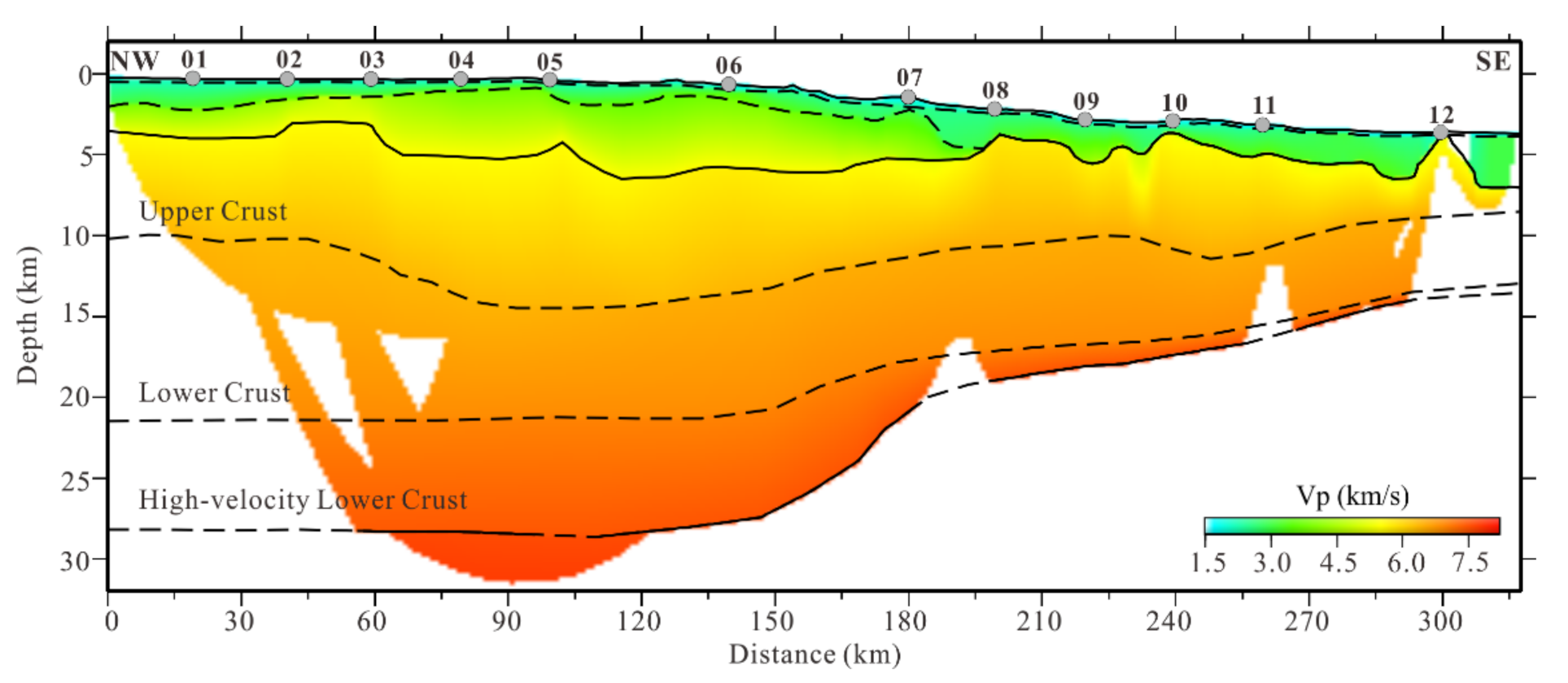
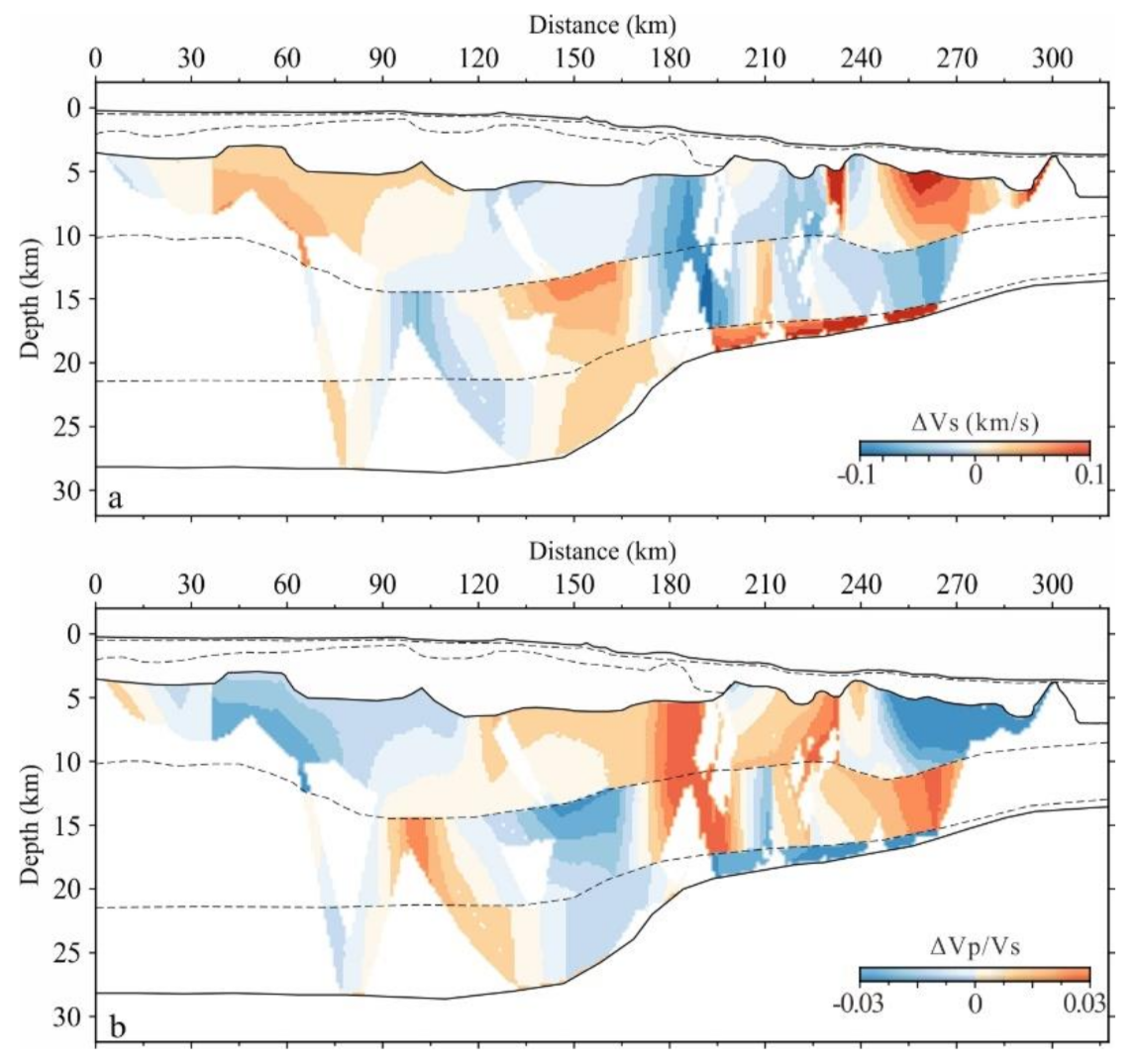
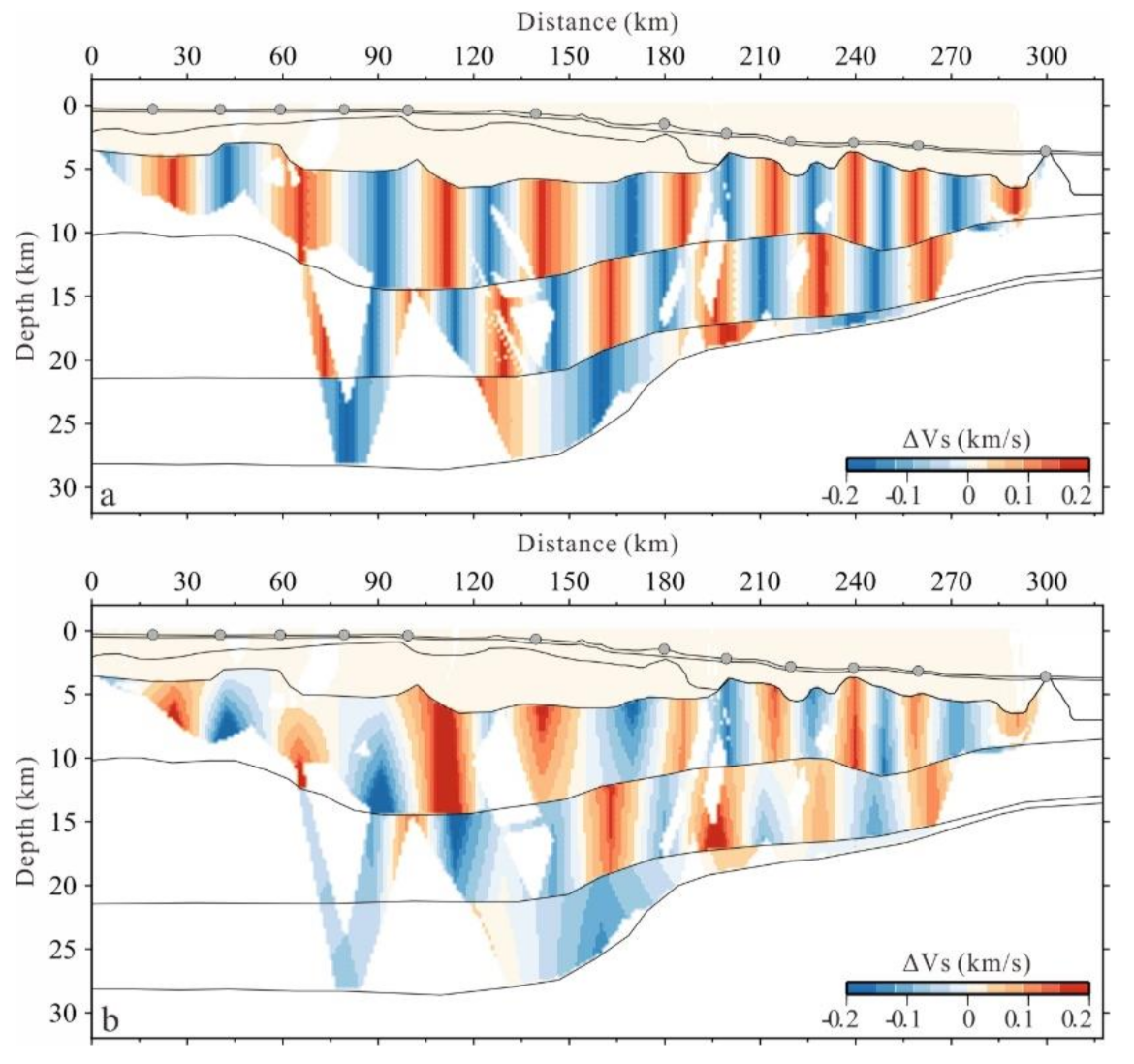
4. Crustal S-Wave Velocity Inversion
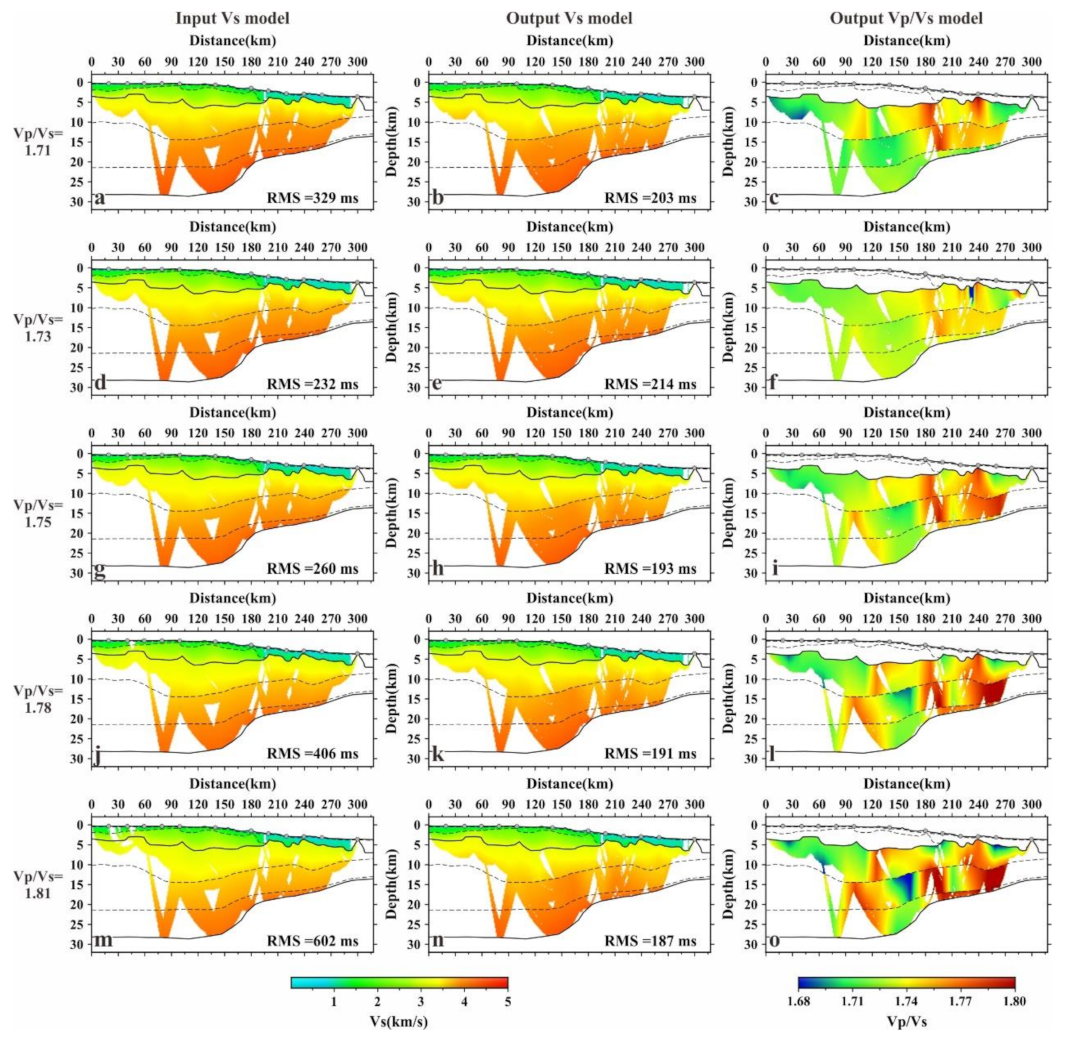
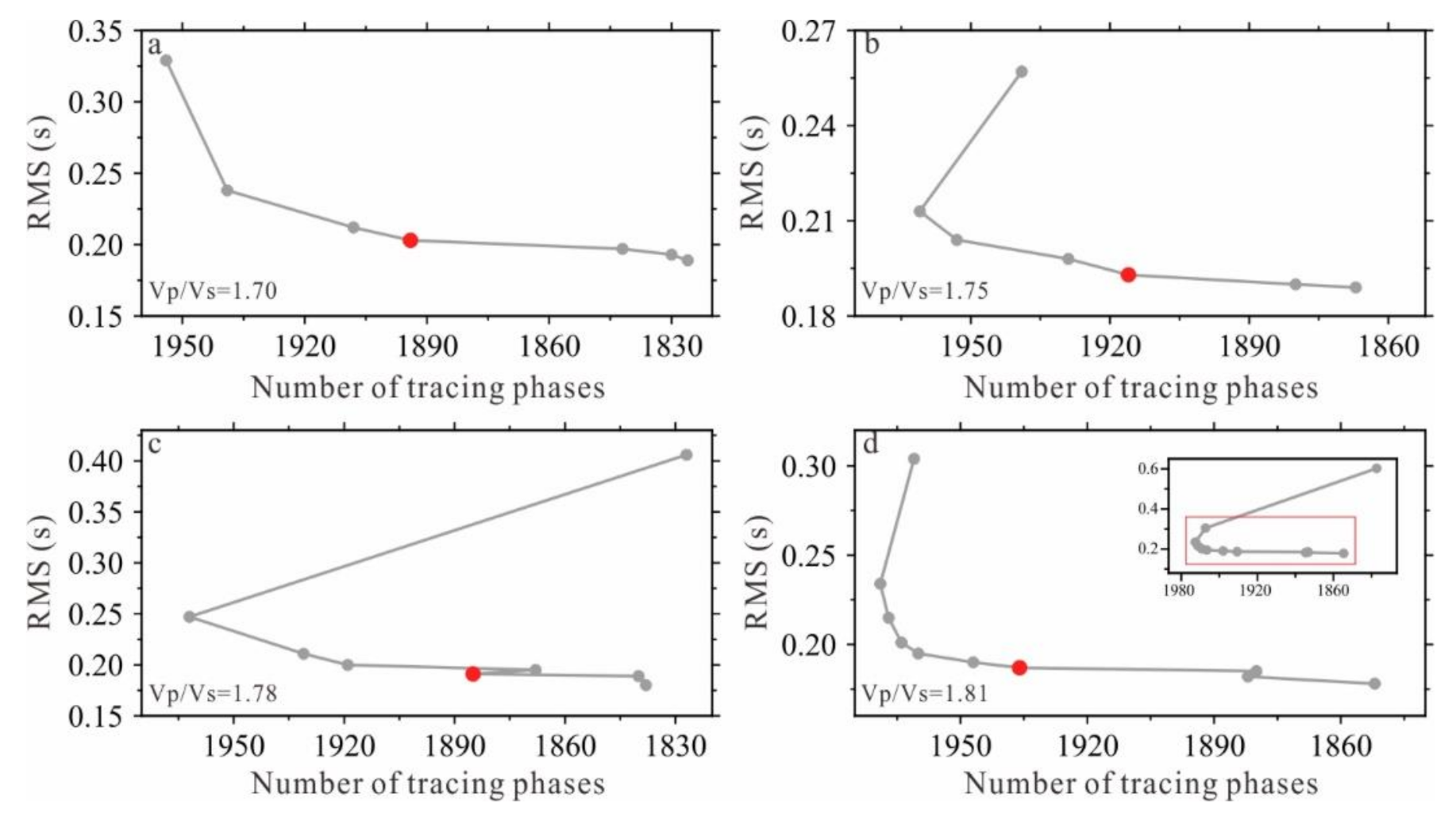
4.1. Initial Models and the Iteration Termination Conditions
4.2. Inversion Results and Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Xia, S.; Zhao, M.; Qiu, X.; Xu, H.; Shi, X. Crustal structure in an onshore–offshore transitional zone near Hong Kong, northern South China Sea. J. Asian Earth Sci. 2010, 37, 460–472. [Google Scholar] [CrossRef]
- Qiu, X.-L.; Zhao, M.-H.; Ao, W.; Lü, C.-C.; Hao, T.-Y.; You, Q.-Y.; Ruan, A.-G.; Li, J.-B. OBS Survey and Crustal Structure of the SW Sub-Basin and Nansha Block, South China Sea. Chin. J. Geophys. 2011, 54, 1009–1021. [Google Scholar] [CrossRef]
- Xia, S.; Qiu, X.; Zhao, M.H.; Ye, C.; Chen, Y.; Xu, H.; Wang, P. Data processing of onshore offshore seismic experiment in Hongkong and Zhujiang River Delta region. J. Trop. Oceanogr. 2007, 26, 35–38. [Google Scholar]
- Zhao, M.; Qiu, X.; Xia, S.; Xu, H.; Wang, P.; Wang, T.K.; Lee, C.-S.; Xia, K. Seismic structure in the northeastern South China Sea: S-wave velocity and Vp/Vs ratios derived from three-component OBS data. Tectonophysics 2010, 480, 183–197. [Google Scholar] [CrossRef]
- Xia, S.; Cao, J.; Wan, K.; Fan, C.; Sun, J. Role of the Wide-angle OBS Seismic Exploration in the Research of Marine Sedimentary Basin. Adv. Earth Sci. 2006, 31, 1111–1124. [Google Scholar] [CrossRef]
- Domenico, S.N. Rock lithology and porosity determination from shear and compressional wave velocity. Geophysics 1984, 49, 1188–1195. [Google Scholar] [CrossRef]
- Christensen, N.I.; Mooney, W.D. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. Space Phys. 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Chian, D.; Louden, K.E. The continent-ocean crustal transition across the southwest Greenland margin. J. Geophys. Res. Space Phys. 1994, 99, 9117–9135. [Google Scholar] [CrossRef]
- Mjelde, R.; Raum, T.; Digranes, P.; Shimamura, H.; Shiobara, H.; Kodaira, S. Vp/Vs ratio along the Vøring Margin, NE Atlantic, derived from OBS data: Implications on lithology and stress field. Tectonophysics 2003, 369, 175–197. [Google Scholar] [CrossRef]
- Mjelde, R. Continent-ocean transition on the Vøring Plateau, NE Atlantic, derived from densely sampled ocean bottom seismometer data. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Wei, X.; Ruan, A.; Zhao, M.; Qiu, X.; Wu, Z.; Niu, X. Shear wave velocity structure of Reed Bank, southern continental margin of the South China Sea. Tectonophysics 2015, 644–645, 151–160. [Google Scholar] [CrossRef]
- Singhroha, S.; Chand, S.; Bünz, S. Constraints on Gas Hydrate Distribution and Morphology in Vestnesa Ridge, Western Svalbard Margin, Using Multicomponent Ocean-Bottom Seismic Data. J. Geophys. Res. Solid Earth 2019, 124, 4343–4364. [Google Scholar] [CrossRef]
- Wei, X.D.; Zhao, M.H.; Ruan, A.G.; Qiu, X.L.; Hao, T.Y.; Wu, Z.L.; Xiong, H. Crustal structure of shear waves and its tectonic sig-nificance in the mid-northern continental margin of the South China Sea. Chin. J. Geophys. 2011, 54, 3150–3160. [Google Scholar] [CrossRef]
- Hou, W.; Li, C.-F.; Wan, X.; Zhao, M.; Qiu, X. Crustal S-wave velocity structure across the northeastern South China Sea continental margin: Implications for lithology and mantle exhumation. Earth Planet. Phys. 2019, 3, 314–329. [Google Scholar] [CrossRef]
- Mjelde, R. Shear waves from three-component ocean bottom seismographs off Lofoten, Norway, indicative of anisotropy in the lower crust. Geophys. J. Int. 1992, 110, 283–296. [Google Scholar] [CrossRef]
- Kodaira, S.; Bellenberg, M.; Iwasaki, T.; Kanazawa, T.; Hirschleber, H.B.; Shimamura, H. VpIVsratio structure of the Lofoten continental margin, northern Norway, and its geological implications. Geophys. J. Int. 1996, 124, 724–740. [Google Scholar] [CrossRef]
- Zelt, C.A.; Smith, R.B. Seismic traveltime inversion for 2-D crustal velocity structure. Geophys. J. Int. 1992, 108, 16–34. [Google Scholar] [CrossRef]
- Mjelde, R.; Eckhoff, I.; Solbakken, S.; Kodaira, S.; Shimamura, H.; Gunnarsson, K.; Nakanishi, A.; Shiobara, H. Gravity and S-wave modelling across the Jan Mayen Ridge, North Atlantic; implications for crustal lithology. Mar. Geophys. Res. 2007, 28, 27–41. [Google Scholar] [CrossRef]
- Fan, C.; Xia, S.; Cao, J.; Zhao, F.; Sun, J.; Wan, K.; Xu, H. Lateral crustal variation and post-rift magmatism in the northeastern South China Sea determined by wide-angle seismic data. Mar. Geol. 2019, 410, 70–87. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, M.; Qiu, X.; Wang, Q. Recent progress of converted shear-wave phase identification in Nansha Block using ocean bottom seismometers data. J. Trop. Oceanogr. 2016, 35, 61–71. [Google Scholar] [CrossRef]
- Sheriff, R.E.; Geldart, L.P. Exploration Seismology, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Tan, P.; Breivik, A.J.; Trønnes, R.G.; Mjelde, R.; Azuma, R.; Eide, S. Crustal structure and origin of the Eggvin Bank west of Jan Mayen, NE Atlantic. J. Geophys. Res. Solid Earth 2017, 122, 43–62. [Google Scholar] [CrossRef]
- Digranes, P.; Mjelde, R.; Kodaira, S.; Shimamura, H.; Kanazawa, T.; Shiobara, H.; Berg, E. A regional shear-wave velocity model in the central Vøring Basin, N. Norway, using three-component Ocean Bottom Seismographs. Tectonophysics 1998, 293, 157–174. [Google Scholar] [CrossRef]
- Eccles, J.D.; White, R.S.; Christie, P.A.F. Identification and inversion of converted shear waves: Case studies from the European North Atlantic continental margins. Geophys. J. Int. 2009, 179, 381–400. [Google Scholar] [CrossRef]
- Eccles, J.D.; White, R.S.; Christie, P.A. The composition and structure of volcanic rifted continental margins in the North Atlantic: Further insight from shear waves. Tectonophysics 2011, 508, 22–33. [Google Scholar] [CrossRef]
- Liu, H.; Wang, F.; Liu, Z. 2-DTraveltime Inversion RAYINVR Algorithm Test. J. Geod. Geodyn. 2017, 37, 977–982. [Google Scholar] [CrossRef]
- Holbrook, S.; Mooney, W.; Christensen, N. The seismic velocity structure of the deep continental crust. Dev. Geotecton. 1992, 23, 1–43. [Google Scholar]
- Wan, K.; Sun, J.; Xu, H.; Xie, X.; Xia, S.; Zhang, X.; Cao, J.; Zhao, F.; Fan, C. Seismotectonics of the Taiwan Shoal region in the northeastern South China Sea: Insights from the crustal structure. J. Ocean Univ. China 2018, 17, 156–168. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F. New, improved version of generic mapping tools released. Eos Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]



| Stations | Phases | Uncertainties (ms) | RMSb (ms) | RMSa (ms) | Conversion Interface |
|---|---|---|---|---|---|
| OBS01 | PSSuc | 80 | 82 | 86 | 1 S1 |
| OBS02 | PSSuc | 180 | 182 | 183 | 1 S1 |
| OBS03 | PSSuc | 160 | 189 | 189 | 1 S1 |
| PSSmb | 200 | 181 | 179 | Basement | |
| OBS05 | PSSm | 180 | 150 | 141 | 1 S1 |
| OBS07 | PSSuc | 140 | 102 | 105 | 1 S1 |
| PPSlc | 140 | 111 | 111 | 1 S1 | |
| PSSm | 180 | 221 | 221 | 1 S1 | |
| OBS08 | PSSuc | 160 | 239 | 241 | 1 S1 |
| PSSm | 200 | 141 | 144 | 1 S1 | |
| OBS09 | PSSmb | 200 | 185 | 167 | Basement |
| OBS10 | PSSuc | 160 | 234 | 240 | 1 S1 |
| PSSmb | 160 | 197 | 198 | Basement | |
| OBS11 | PSSuc | 160 | 256 | 262 | 1 S1 |
| OBS12 | PSSuc | 200 | 193 | 199 | 1 S1 |
| PSSlc | 200 | 205 | 214 | 1 S1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, G.; Wan, K.; Xia, S.; Xu, H.; Fan, C.; Cao, J. Travel-Time Inversion Method of Converted Shear Waves Using RayInvr Algorithm. Appl. Sci. 2021, 11, 3571. https://doi.org/10.3390/app11083571
Wen G, Wan K, Xia S, Xu H, Fan C, Cao J. Travel-Time Inversion Method of Converted Shear Waves Using RayInvr Algorithm. Applied Sciences. 2021; 11(8):3571. https://doi.org/10.3390/app11083571
Chicago/Turabian StyleWen, Genggeng, Kuiyuan Wan, Shaohong Xia, Huilong Xu, Chaoyan Fan, and Jinghe Cao. 2021. "Travel-Time Inversion Method of Converted Shear Waves Using RayInvr Algorithm" Applied Sciences 11, no. 8: 3571. https://doi.org/10.3390/app11083571
APA StyleWen, G., Wan, K., Xia, S., Xu, H., Fan, C., & Cao, J. (2021). Travel-Time Inversion Method of Converted Shear Waves Using RayInvr Algorithm. Applied Sciences, 11(8), 3571. https://doi.org/10.3390/app11083571





