Two-Dimensional Digital Beam Steering Based on Liquid Crystal Phase Gratings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Beam Steerers for Space Applications
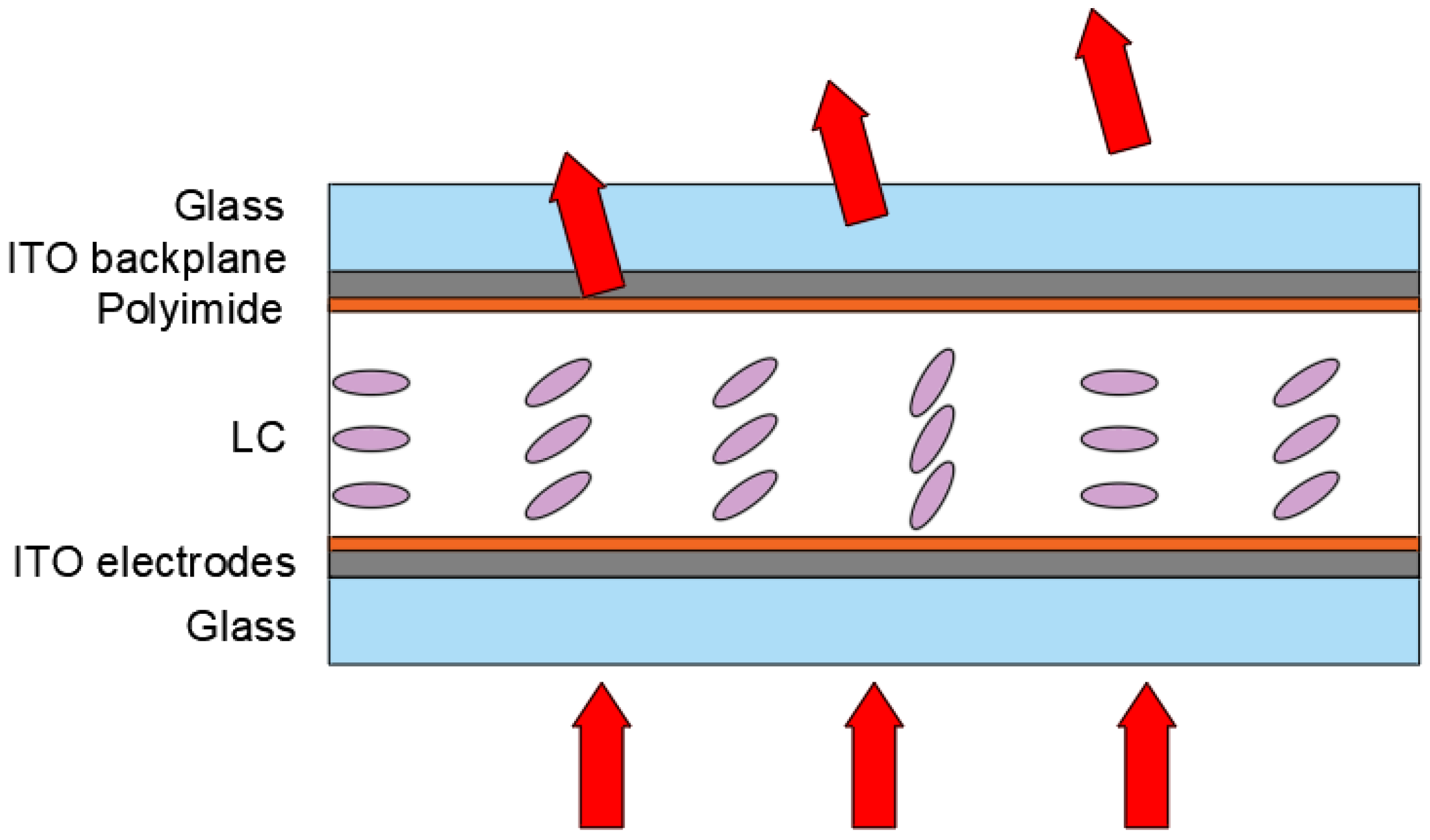
2.2. Device Characteristics
2.3. Manufacturing of LC Cells
2.4. The 2D Device
2.5. Electronic Driver
2.6. Calibration
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hossack, W.J.; Theofanidou, E.; Crain, J.; Heggarty, K.; Birch, M. High-Speed Holographic Optical Tweezers Using a Ferroelectric Liquid Crystal Microdisplay. Opt. Express 2003, 11, 2053. [Google Scholar] [CrossRef]
- Otón, E.; Pérez-Fernández, J.; López-Molina, D.; Quintana, X.; Otón, J.M.; Geday, M.A. Reliability of Liquid Crystals in Space Photonics. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Li, C.; Cao, X.; Wu, K.; Li, X.; Chen, J. Lens-Based Integrated 2D Beam-Steering Device with Defocusing Approach and Broadband Pulse Operation for Lidar Application. Opt. Express 2019, 27, 32970. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Ai, Y.; Shan, X.; Liu, M. Simulation of Two-Dimensional Target Motion Based on a Liquid Crystal Beam Steering Method. Opt. Eng. 2015, 54, 056102. [Google Scholar] [CrossRef]
- Hellman, B.; Luo, C.; Chen, G.; Rodriguez, J.; Perkins, C.; Park, J.-H.; Takashima, Y. Single-Chip Holographic Beam Steering for Lidar by a Digital Micromirror Device with Angular and Spatial Hybrid Multiplexing. Opt. Express 2020, 28, 21993. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S.-T. Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhou, G.; Zhang, X.; Kwon, K.; Blanche, P.-A.; Triesault, N.; Yu, K.; Wu, M.C. 2D Broadband Beamsteering with Large-Scale MEMS Optical Phased Array. Optica 2019, 6, 557. [Google Scholar] [CrossRef] [Green Version]
- Seo, Y.-H.; Hwang, K.; Kim, H.; Jeong, K.-H. Scanning MEMS Mirror for High Definition and High Frame Rate Lissajous Patterns. Micromachines 2019, 10, 67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, B.-W.; Megens, M.; Chan, T.; Sun, T.; Yang, W.; Chang-Hasnain, C.J.; Horsley, D.A.; Wu, M.C. Optical Phased Array Using High Contrast Gratings for Two Dimensional Beamforming and Beamsteering. Opt. Express 2013, 21, 12238. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Su, X.; Xu, P.; Gu, Z. Beam Steering and Deflecting Device Using Step-Based Micro-Blazed Grating. Opt. Commun. 2008, 281, 3969–3976. [Google Scholar] [CrossRef]
- Römer, G.R.B.E.; Bechtold, P. Electro-Optic and Acousto-Optic Laser Beam Scanners. Phys. Procedia 2014, 56, 29–39. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Cua, M.; Zhou, E.H.; Horie, Y.; Faraon, A.; Yang, C. Wide-Angular-Range and High-Resolution Beam Steering by a Metasurface-Coupled Phased Array. Opt. Lett. 2018, 43, 5255. [Google Scholar] [CrossRef] [PubMed]
- Niu, Q.; Wang, C. High Precision Beam Steering Using a Liquid Crystal Spatial Light Modulator. Opt. Quant. Electron. 2019, 51, 180. [Google Scholar] [CrossRef]
- Kim, Y.; Won, K.; Kim, Y.; An, J.; Song, H.; Kim, S.; Choi, C.-S.; Lee, H.-S. Electrically Tunable Transmission-Type Beam Deflector Using Liquid Crystal with High Angular Resolution. Appl. Opt. 2018, 57, 5090. [Google Scholar] [CrossRef] [PubMed]
- Zohrabi, M.; Cormack, R.H.; Gopinath, J.T. Wide-Angle Nonmechanical Beam Steering Using Liquid Lenses. Opt. Express 2016, 24, 23798. [Google Scholar] [CrossRef] [Green Version]
- McManamon, P.F.; Bos, P.J.; Escuti, M.J.; Heikenfeld, J.; Serati, S.; Xie, H.; Watson, E.A. A Review of Phased Array Steering for Narrow-Band Electrooptical Systems. Proc. IEEE 2009, 97, 1078–1096. [Google Scholar] [CrossRef]
- Yousefzadeh, C.; Van Rynbach, A.; Bos, P.J. Design of a Large Aperture, Tunable, Pancharatnam Phase Beam Steering Device. Opt. Express 2020, 28, 991. [Google Scholar] [CrossRef]
- Yang, H.; Chu, D.P. Digital Phase-Only Liquid Crystal on Silicon Device with Enhanced Optical Efficiency. OSA Contin. 2019, 2, 2445. [Google Scholar] [CrossRef]
- Zhang, Z.; You, Z.; Chu, D. Fundamentals of Phase-Only Liquid Crystal on Silicon (LCOS) Devices. Light Sci. Appl. 2014, 3, e213. [Google Scholar] [CrossRef]
- Yin, K.; Lee, Y.-H.; He, Z.; Wu, S.-T. Stretchable, Flexible, Rollable, and Adherable Polarization Volume Grating Film. Opt. Express 2019, 27, 5814. [Google Scholar] [CrossRef]
- Kim, J.; Oh, C.; Escuti, M.J.; Hosting, L.; Serati, S. Wide-Angle Nonmechanical Beam Steering Using Thin Liquid Crystal Polarization Gratings; Gonglewski, J.D., Carreras, R.A., Rhoadarmer, T.A., Eds.; SPIE: San Diego, CA, USA, 2008; p. 709302. [Google Scholar]
- Yin, K.; Zhan, T.; Xiong, J.; He, Z.; Wu, S.-T. Polarization Volume Gratings for Near-Eye Displays and Novel Photonic Devices. Crystals 2020, 10, 561. [Google Scholar] [CrossRef]
- Otón, J.M.; Otón, E.; Quintana, X.; Geday, M.A. Liquid-Crystal Phase-Only Devices. J. Mol. Liq. 2018, 267, 469–483. [Google Scholar] [CrossRef]
- Yin, K.; Xiong, J.; He, Z.; Wu, S.-T. Patterning Liquid-Crystal Alignment for Ultrathin Flat Optics. ACS Omega 2020, 5, 31485–31489. [Google Scholar] [CrossRef] [PubMed]
- Zola, R.S.; Bisoyi, H.K.; Wang, H.; Urbas, A.M.; Bunning, T.J.; Li, Q. Dynamic Control of Light Direction Enabled by Stimuli-Responsive Liquid Crystal Gratings. Adv. Mater. 2019, 31, 1806172. [Google Scholar] [CrossRef]
- Shang, X.; Cuypers, D.; Baghdasaryan, T.; Vervaeke, M.; Thienpont, H.; Beeckman, J.; Neyts, K.; Li, Q.; Wu, C.; Li, H.; et al. Active Optical Beam Shaping Based on Liquid Crystals and Polymer Micro-Structures. Crystals 2020, 10, 977. [Google Scholar] [CrossRef]
- Oton, E.; Morawiak, P.; Mazur, R.; Quintana, X.; Geday, M.A.; Oton, J.M.; Piecek, W. Diffractive and Refractive Liquid Crystal Devices Based on Multilayer Matrices. J. Lightwave Technol. 2019, 37, 2086–2093. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.; Yang, S.; Hwang, J.; Lee, J.-H.; Choi, J. Electro-Optical Properties of a Nematic Liquid Crystal Aligned with a Mixture of Nanofibres and Polyimide. J. Phys. D Appl. Phys. 2014, 47, 345303. [Google Scholar] [CrossRef]
- Bennis, N.; Geday, M.; Quintana, X.; Cerrolaza, B.; Medialdea, D.; Spadło, A.; Dąbrowski, R.; Otón, J. Nearly-Analogue Blazed Phase Grating Using High Birefringence Liquid Crystal. Opto Electron. Rev. 2009, 17. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, J.; Wu, L.Y. Influence of Phase Delay Profile on Diffraction Efficiency of Liquid Crystal Optical Phased Array. Opt. Laser Technol. 2009, 41, 509–516. [Google Scholar] [CrossRef]
- Moser, S.; Ritsch-Marte, M.; Thalhammer, G. Model-Based Compensation of Pixel Crosstalk in Liquid Crystal Spatial Light Modulators. Opt. Express 2019, 27, 25046. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Won, K.; An, J.; Hong, J.-Y.; Kim, Y.; Choi, C.-S.; Song, H.; Song, B.; Suk Kim, H.; Bae, K.-D.; et al. Large-Area Liquid Crystal Beam Deflector with Wide Steering Angle. Appl. Opt. 2020, 59, 7462. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, L.; Li, M.; Wu, S.; Shang, J.; Qiu, Q. Theoretical and Experimental Demonstration on Grating Lobes of Liquid Crystal Optical Phased Array. Int. J. Opt. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Caño-García, M.; Quintana, X.; Otón, J.M.; Geday, M.A. Dynamic Multilevel Spiral Phase Plate Generator. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, 4th ed.; W.H. Freeman: New York, NY, USA, 2017; pp. 130–160. [Google Scholar]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García de Blas, M.; Geday, M.A.; Otón, J.M.; Quintana Arregui, X. Two-Dimensional Digital Beam Steering Based on Liquid Crystal Phase Gratings. Appl. Sci. 2021, 11, 3632. https://doi.org/10.3390/app11083632
García de Blas M, Geday MA, Otón JM, Quintana Arregui X. Two-Dimensional Digital Beam Steering Based on Liquid Crystal Phase Gratings. Applied Sciences. 2021; 11(8):3632. https://doi.org/10.3390/app11083632
Chicago/Turabian StyleGarcía de Blas, Mario, Morten Andreas Geday, Jose Manuel Otón, and Xabier Quintana Arregui. 2021. "Two-Dimensional Digital Beam Steering Based on Liquid Crystal Phase Gratings" Applied Sciences 11, no. 8: 3632. https://doi.org/10.3390/app11083632
APA StyleGarcía de Blas, M., Geday, M. A., Otón, J. M., & Quintana Arregui, X. (2021). Two-Dimensional Digital Beam Steering Based on Liquid Crystal Phase Gratings. Applied Sciences, 11(8), 3632. https://doi.org/10.3390/app11083632





