Validation of Fresnel–Kirchhoff Integral Method for the Study of Volume Dielectric Bodies
Abstract
:1. Introduction
2. Theoretical Models
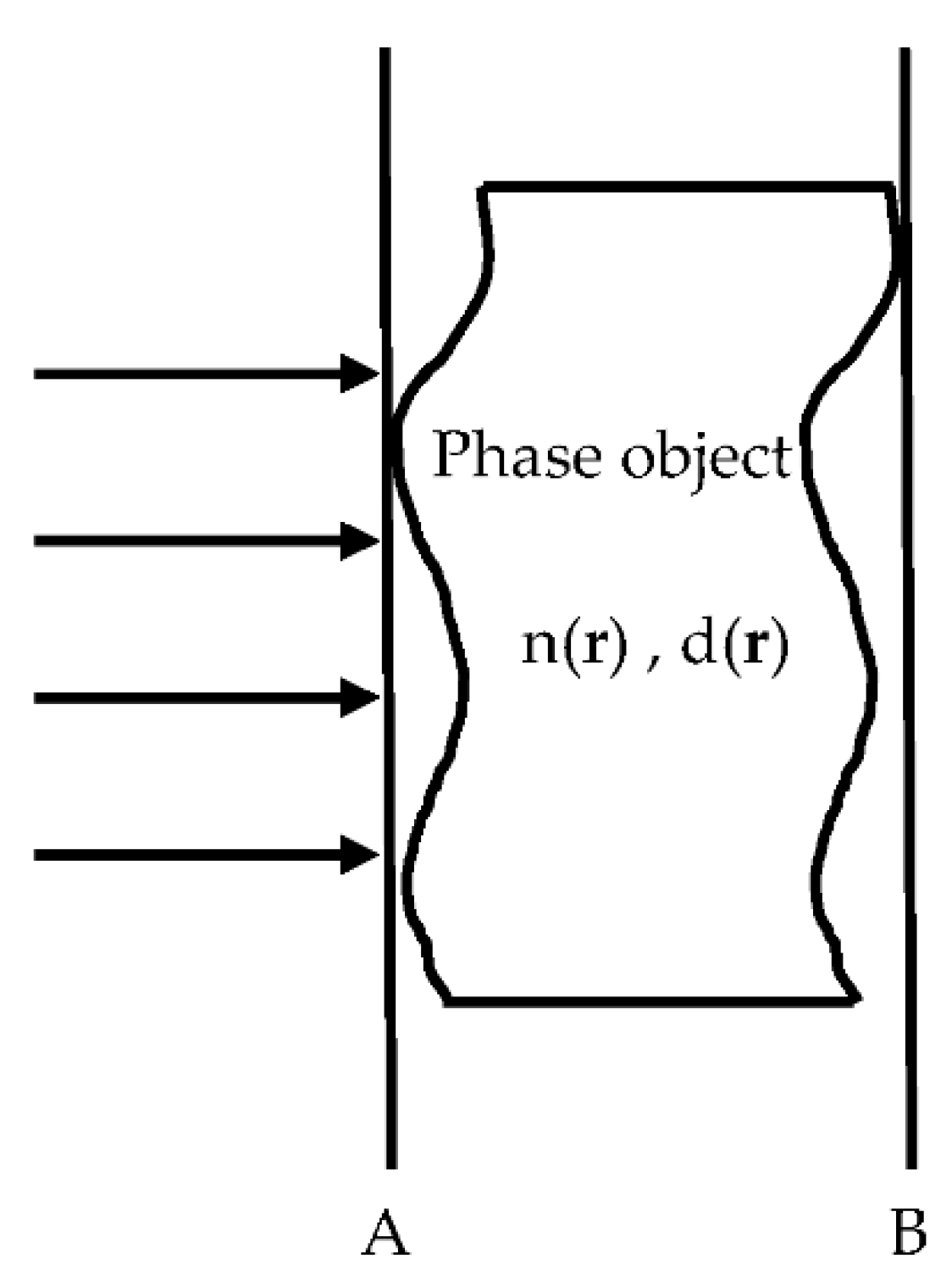
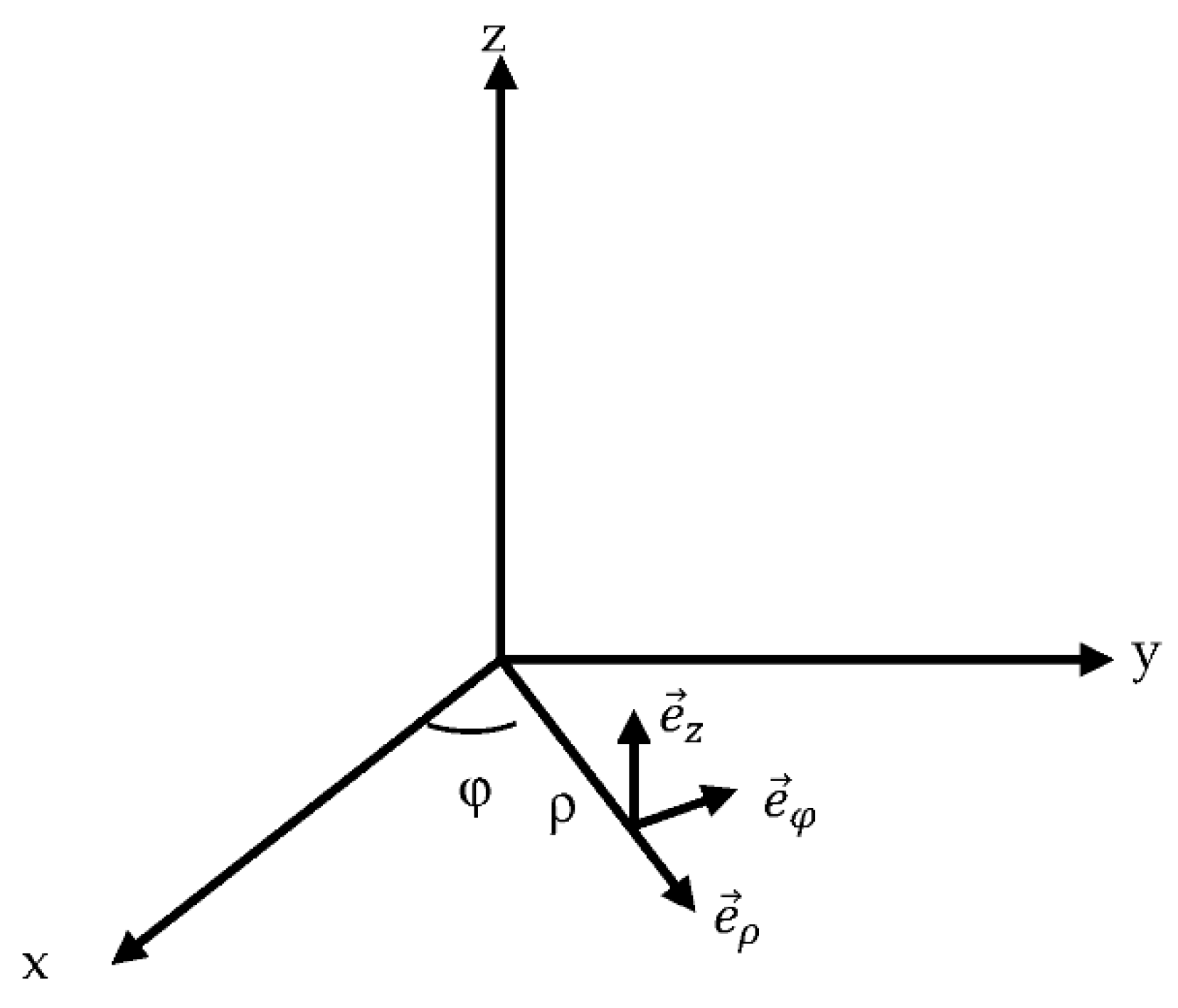
2.1. Fresnel Integral Method
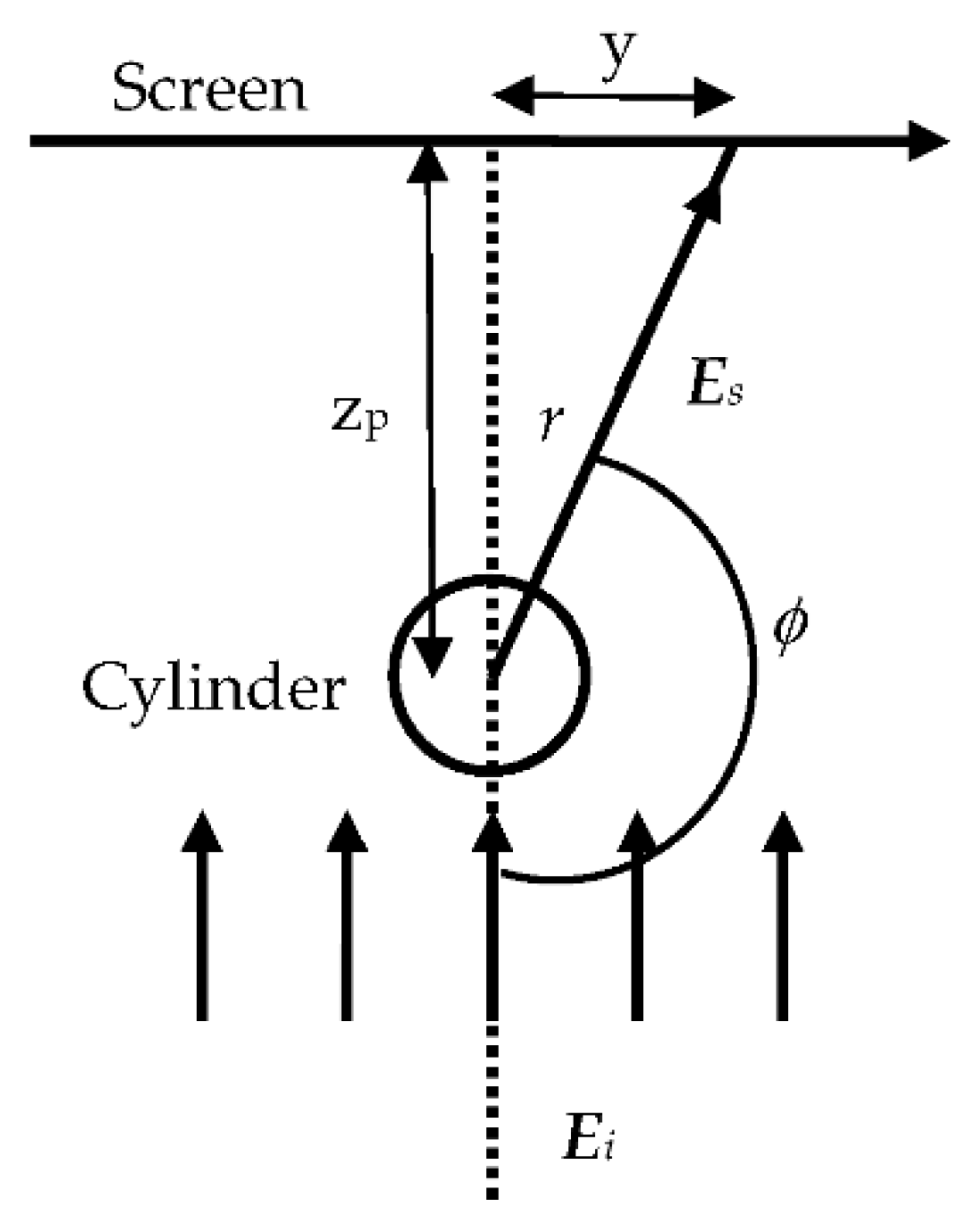
2.2. Rigorous Solution
3. Results and Discussion
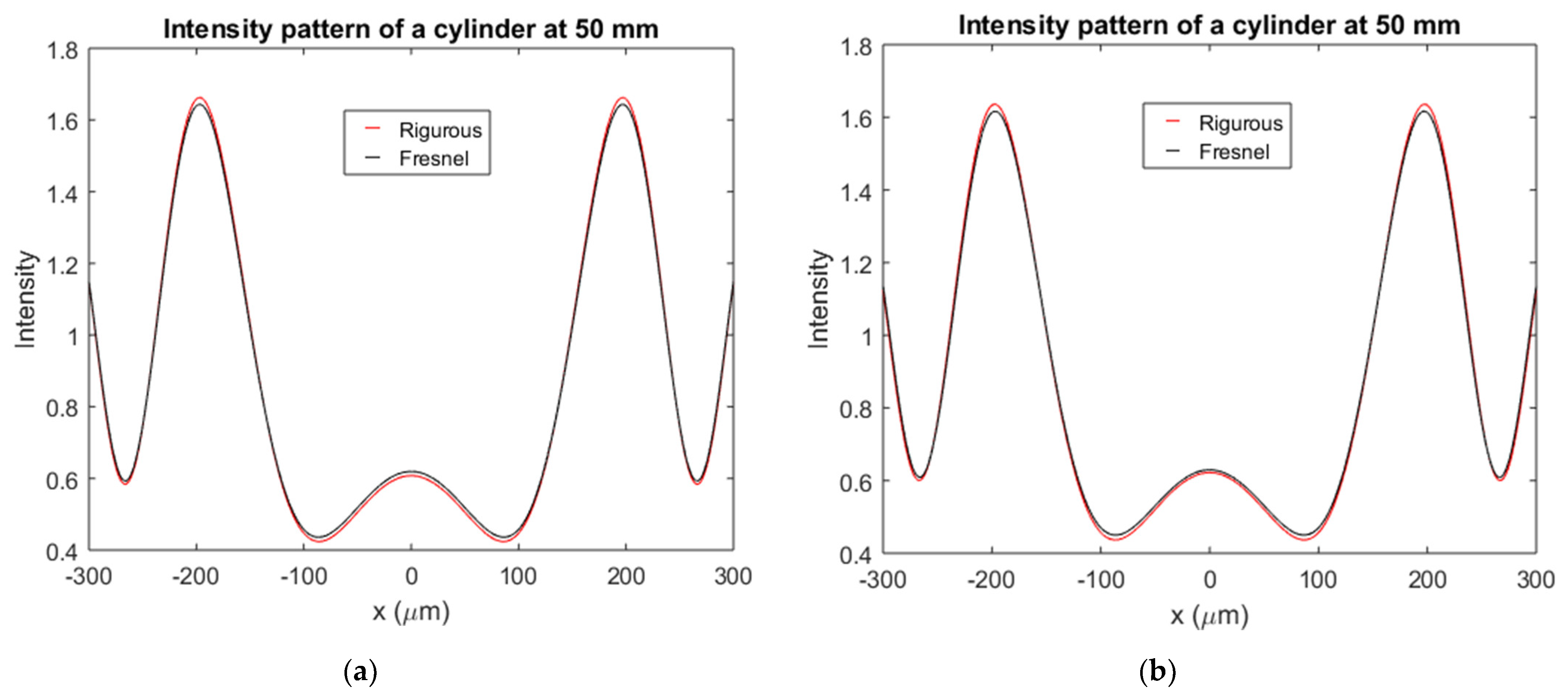
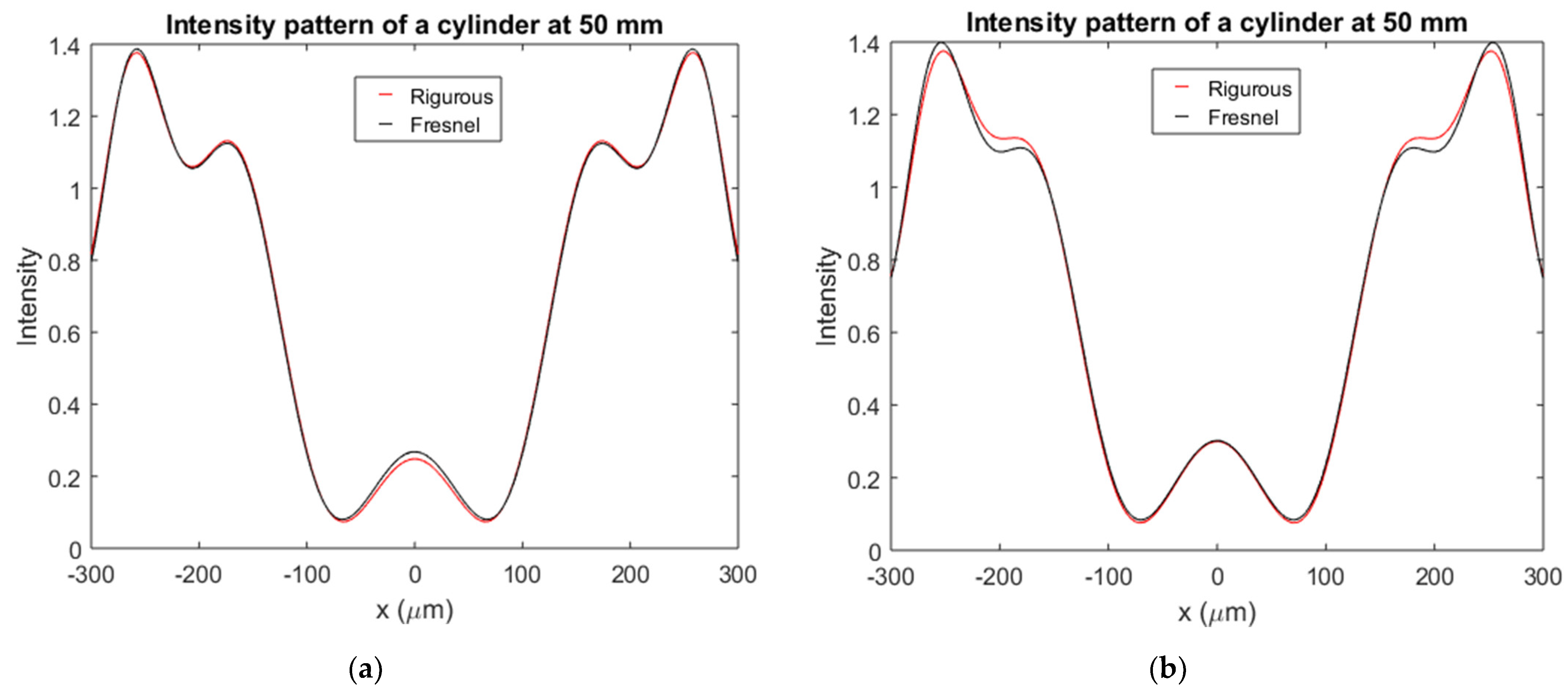
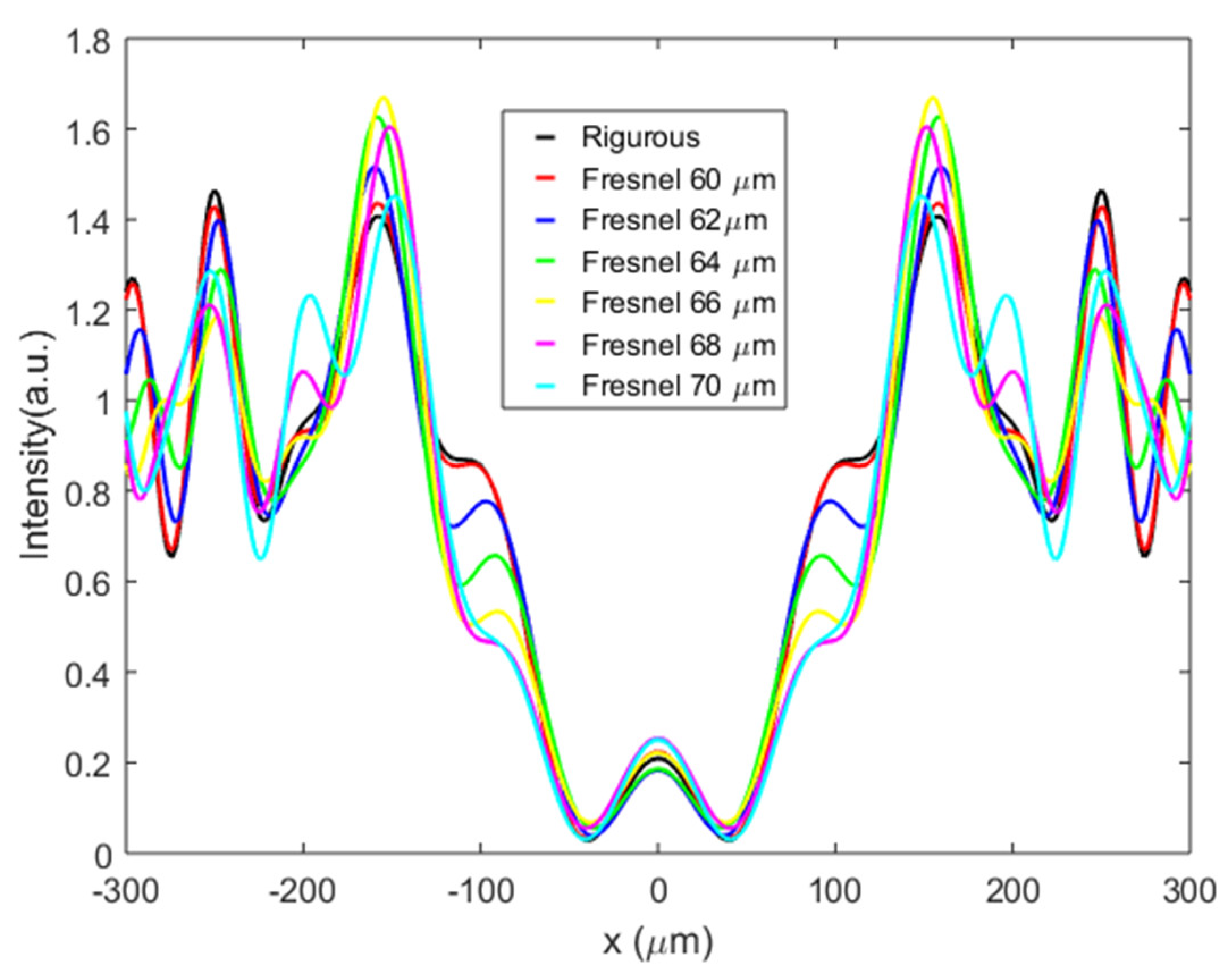
3.1. Validation of the Fresnel Method by Comparison with the Rigorous Solution
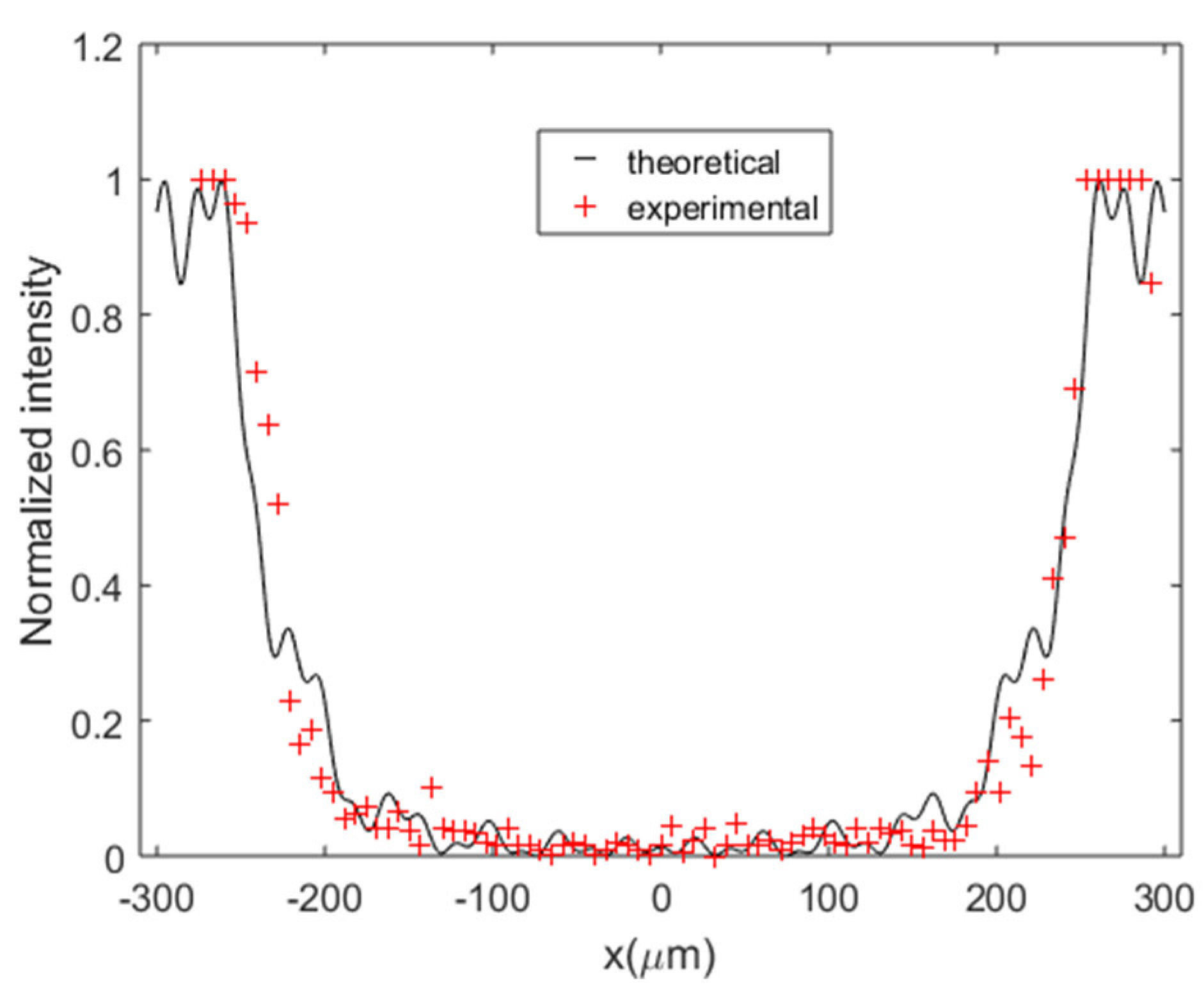
3.2. Experimental Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Deng, L.; Cai, C.S. Applications of fiber optic sensors in civil engineering. Struct. Eng. Mech. 2007, 25, 577–596. [Google Scholar] [CrossRef] [Green Version]
- Banks, J.; Giovannetti, L.M.; Soubeyran, X.; Wright, A.M.; Turnock, S.R.; Boyd, S.W. Assessment of Digital Image Correlation as a method of obtaining deformations of a structure under fluid load. J. Fluids Eng. 2015, 58, 173–187. [Google Scholar] [CrossRef] [Green Version]
- Ifju, P.G.; Han, B. Recent Applications of Moiré Interferometry. Exp. Mech. 2010, 50, 1129–1147. [Google Scholar] [CrossRef]
- Moore, A.; Tyrer, J. Phase-stepped ESPI and moiré interferometry for measuring stress-intensity factor and integral. Exp. Mech. 1995, 35, 306–314. [Google Scholar] [CrossRef]
- Rossmanith, H. Analysis of crack-tip moiré fringe patterns. Int. J. Fract. 1983, 21, 83–106. [Google Scholar] [CrossRef]
- Ramesh, K. Digital Photoelasticity: Advanced Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Patil, P.; Vyasarayani, C.P.; Ramji, M. Linear least squares approach for evaluating crack tip fracture parameters using isochromatic and isoclinic data from digital photoelasticity. Opt. Lasers Eng. 2017, 93, 182–194. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Beygi, M.G.; Karimzadeh, R.; Dashtdar, M. Nonlinear refractive index measurement by Fresnel diffraction from phase object. Opt. Laser Technol. 2015, 66, 151–155. [Google Scholar] [CrossRef]
- Sabatyan, A.; Tavassoly, M.T. Application of Fresnel diffraction to nondestructive measurement of the refractive index of optical fibers. Opt. Eng. 2007, 46, 128001-1–128001-7. [Google Scholar]
- Taleb, S.I.; Neipp, C.; Francés, J. Comment on Application of Fresnel diffraction to nondestructive measurement of the refractive index of optical fibers. Opt. Eng. 2020, 59, 060401. [Google Scholar] [CrossRef]
- Taleb, I.; Neipp, C.; Martínez, F.J.; Alvarez, M.L.; Calzado, E.M.; Márquez, A.; Francés, J.; Gallego, S.; Beléndez, A. Fresnel-Kirchhoff Integral Method Comparison with Scattering Theory for the Study of Volume Dielectric Bodies, Proceedings of the Optics, Photonics and Lasers: Proceedings of the 3rd International Conference on Optics, Photonics and Lasers (OPAL’ 2020), Tenerife (Canary Islands), Spain, 21–22 October 2020; Yurish, S.Y., Ed.; IFSA Publishing: Barcelona, Spain, 2020. [Google Scholar]
- Kahnert, F.M. Numerical methods in electromagnetic scattering theory. J. Quant. Spectrosc. Radiat. Transf. 2003, 79, 775–824. [Google Scholar] [CrossRef]
- Williams, L.A.; Nehmetallah, G.; Aylo, R.; Banerjee, P.P. Application of up-sampling and resolution scaling to Fresnel reconstruction of digital holograms. Appl. Opt. 2015, 54, 1443–1452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van de Hulst, H.C. Light Scattering by Small Particles; John Wiley and Sons: New York, NY, USA, 1957. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Arfken, G.; Weber, H.; Harris, F.E. Mathematical Methods for Physicists; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Yuan, Y. Recent advances in trust region algorithms. Math. Program. 2015, 151, 249–281. [Google Scholar] [CrossRef]
- Saini, R. Optical detection of hairs. Int. J. Trichol. 2011, 3, 128–129. [Google Scholar] [CrossRef] [PubMed]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taleb, S.I.; Neipp, C.; Francés, J.; Márquez, A.; Alvarez, M.L.; Hernández, A.; Gallego, S.; Beléndez, A. Validation of Fresnel–Kirchhoff Integral Method for the Study of Volume Dielectric Bodies. Appl. Sci. 2021, 11, 3800. https://doi.org/10.3390/app11093800
Taleb SI, Neipp C, Francés J, Márquez A, Alvarez ML, Hernández A, Gallego S, Beléndez A. Validation of Fresnel–Kirchhoff Integral Method for the Study of Volume Dielectric Bodies. Applied Sciences. 2021; 11(9):3800. https://doi.org/10.3390/app11093800
Chicago/Turabian StyleTaleb, Soumia Imane, Cristian Neipp, Jorge Francés, Andrés Márquez, Mariela L. Alvarez, Antonio Hernández, Sergi Gallego, and Augusto Beléndez. 2021. "Validation of Fresnel–Kirchhoff Integral Method for the Study of Volume Dielectric Bodies" Applied Sciences 11, no. 9: 3800. https://doi.org/10.3390/app11093800
APA StyleTaleb, S. I., Neipp, C., Francés, J., Márquez, A., Alvarez, M. L., Hernández, A., Gallego, S., & Beléndez, A. (2021). Validation of Fresnel–Kirchhoff Integral Method for the Study of Volume Dielectric Bodies. Applied Sciences, 11(9), 3800. https://doi.org/10.3390/app11093800









