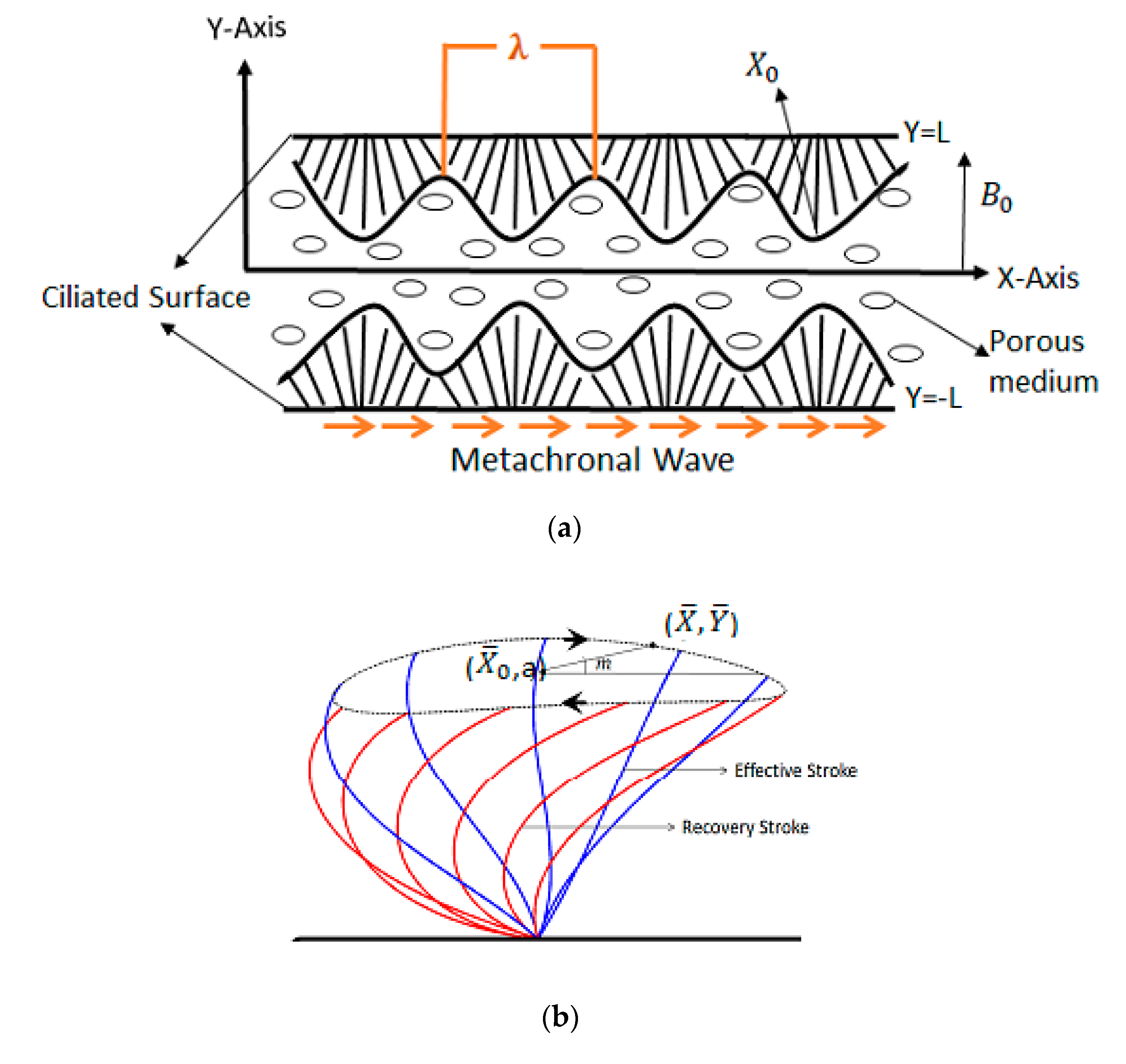
1. Introduction
Cilia are small hair-like structures found in most microorganisms, human and animals. Cilia play a key role in the respiratory system, but also in the reproductive and digestive systems of humans and for the locomotion of small animals in biofluids. Motile cilia responsible for the transport of biofluids exhibit a rhythmic waving motion that forms metachronal waves. Metachronal waves produced by the motion of ciliary organs spread along out of phase in a distensible conduit. The key role of metachronal waves is to regulate the continuity of the flow. Ciliated surfaces can exhibit various beating patterns and generate multiple types of metachronal waves, of which, the two most frequent ones are symplectic and antiplectic metachronal waves, considered for the first time by Knight [
1]. Later, few authors explored the motion of cilia forming symplectic wave patterns with numerous biotic fluids using analytical and numerical techniques, including Siddiqui et al. [
2], who found an analytic solution for a Newtonian fluid flow through a ciliated channel, or Maiti and Pandey [
3], who explored a viscous fluid flow through a ciliated tube. Periciliary dyskinesia disease is mainly due to defects in the airway cilia beating pattern and/or ciliary mortality. The main causes for that are related to the excessive mucus layer thickness and its excessive dynamic viscosity due to a default in the transmembrane transport of ions, inducing both a stagnation of mucus and inflammation. The most common respiratory diseases related to cilia alterations are sinusitis and chronic bronchitis, asthma [
4], infection and inflammation, bronchopneumonia and acute trachea bronchitis [
5].
Since the viscous fluid plays a key role in the ciliary flow, different authors studied mucus flow by taking different non-Newtonian fluid models. For example, Liron and Rozenson [
6] considered mucus (viscous fluid) as a linearized Oldroyd-B fluid. They represented the action of forces exerted by the cilia tip by impulsive forces. Mathematical equations were modelled and solved by the Fourier transform method. They confirmed that cilia penetration is necessary for an efficient transport. King et al. [
7] studied the bio rheological effect of mucus due to ciliary motion and found that the reduction in the shear stress leads to an increase of mucus transport.
Smith et al. [
8] presented a new mathematical model in which mucus is considered as a linear Maxwell fluid, and cilia are considered as an active porous medium. The periciliary layer (PCL) and mucus layer are separated by a thin layer. The system is solved by the Fourier series expansion method. The pressure gradient at the mucus–PCL interface and the cilia beating frequency are two key components for efficient mucus transport. Lee et al. [
9] measured mucociliary transport by considering a Newtonian fluid for both PCL and mucus and investigated the factors affecting their transport and underlying diseases related to the respiratory tract, related to defects in the mucociliary clearance process. Results were obtained numerically and compared with those of the projection method. The main features affecting mucociliary transport are the number of cilia, the cilia beating frequency and the PCL depth. Sedaghat et al. [
10] considered mucus as an Oldroyd-B fluid and demonstrated, using the lattice Boltzmann method, that the viscoelastic property of mucus has a significant impact on the deformation of the interface between the mucus and the periciliary layer. Recently, Chateau et al. [
11] studied the transportation and mixing induced by ciliary beating through a combined Lattice Boltzmann/Immersed Boundary method in a two-fluid environment. Both mucus and PCL were assumed as Newtonian fluids. They highlighted the superiority of antiplectic metachronal waves over symplectic ones to transport mucus. This was later confirmed by Mann et al. [
12], using the fractional Adomian decomposition method. These authors modelled the fractional Burgers fluid through a ciliated channel with the periciliary layer and mucus, also velocity profiles had obtained for both types of wave pattern and concluded that antiplectic waves are more efficient for the transportation of a viscous fluid. Most bionic fluids are viscoelastic in nature [
13]. Viscoelasticity is besides the essential rheological property of bronchial mucus [
14,
15]. Therefore, it is of prime importance to consider the non-Newtonian behaviour of mucus when investigating mucociliary transport. For the first time, the viscoelastic second-grade fluid flow due to the ciliary motion [
16,
17] is considered here under the effect of a magnetic field and inertial forces.
Furthermore, the interest in magnetohydrodynamics flows (MHD) has grown because of their broad industrial and health applications [
18,
19,
20,
21]. Ally et al. [
22] investigated the application of mucolytics (i.e., the process of reducing elasticity, rigidity and viscosity of mucus by breaking down the chemical bonds in mucus) to enhance particle retention under moderate magnetic fields. For this, they used the frog plate model to compare the two different mucolytics and found that N-acetylcysteine and dextran sulphate are effective for moderate and sufficiently large particle concentrations, respectively.
Some other investigators considered the MHD flow of linear and nonlinear fluids due to ciliary motion. Manzoor et al. [
23] studied the influence of magnetohydrodynamics (MHD) for a non-Newtonian Jeffrey fluid flow produced by ciliary motion in a porous medium. The results were obtained by a semi-analytical Adomian decomposition method. Bhatti et al. [
24] considered the Casson fluid model to study the influence of MHD for solid–liquid suspensions on the ciliary motion in a porous medium. For the same configuration, Elkhair et al. [
25] modelled the problem without applying the longwave length and low Reynolds number approximation. A series solution by the Adomian Decomposition Method was obtained, and the results showed that the magnetic field and Darcy’s resistance reduced the magnitude of the velocity field. Siddiqui et al. [
26] studied the MHD viscous flow for a ciliated planar channel embedded in a porous medium and concluded that mucus congestion in the respiratory tract can be cleaned by drugs containing magnetic nanoparticles.
A magnetic field has been widely used together with artificial cilia in microfluidic devices for mixing applications. These cilia can also be used for cell transportation, antifouling surfaces, biochemical targets such as proteins and chemical agent sensing. Vilfan et al. [
27] investigated fluid motion due to self-assembled artificial cilia using chains of super-paramagnetic beads. The use of a magnetic field to actuate beating cilia in a simple non-reciprocal beating manner caused a uniform motion above the cilia tips. Gauger et al. [
28] developed a numerical model of fluid transport due to the motion of artificial cilia made by super-paramagnetic elastic filaments that are actuated by an applied magnetic field. A better control of artificial cilia was obtained by driving them externally, using either a magnetic or an electric field. Sajid et al. [
29] studied the inertial flow by considering flagellated micro-organisms swimming in an MHD viscoelastic second-grade fluid. They demonstrated that propulsion in the presence of a magnetic field surges for low inertial forces and drops for higher ones.
Fluid flows through a porous medium have numerous real-world applications in nature, e.g., natural flows in porous medium can be observed under pathological conditions of gallstones when they drop into the bile tubes and close them incompletely or fully. Darcy’s law has also been used to study the ciliary flow of a biofluid assuming the ciliated carpet as a porous medium. Saleem et al. [
30] considered a compressible flow of Jeffrey fluid through a porous medium and concluded that the average velocity of a viscoelastic fluid flow increases in the presence of a magnetic field through the porous medium.
The flow of a second-grade fluid under the low Reynolds number approximation has been recently addressed by Hina et al. [
31], who concluded that viscoelastic effects are responsible for a drastic change in the flow field. Shaheen et al. [
32] analysed the magnetically actuated mucociliary pumping in a bronchial tube due to ciliary motion. They noticed that the ciliary beating frequency can be controlled by the application of a magnetic field. However, the MHD flow of a second-grade fluid induced by ciliary motion in a porous medium with inertial forces has not been studied yet. This is of particular interest for the diagnosis of respiratory diseases by magnetic resonance imaging [
32]. Therefore, the present study addresses the role of a magnetic field and inertial forces on second-grade fluid flow through a porous medium surrounded by ciliated walls.
In the present work, the flow of a second-grade fluid due to metachoronal motion of cilia is investigated, and the influence of moderate Reynolds number, magnetic field and porous medium on the velocity, pressure and stream functions is studied in detail. The momentum equations include inertial effects, which were always ignored in former studies [
31,
33]. The presence of a magnetic field and inertial forces reduces the momentum equations into a system of fourth-order non-linear partial differential equations with moving boundary conditions. Obtaining the solution of the highly nonlinear partial differential equations with nonhomogeneous boundary conditions is very challenging for researchers. Therefore, one attempts to solve this system by the analytical technique HPM [
33] together with the software Mathematica. The resulting expressions for the pressure gradient, stream function and velocity profile are portrayed, and the influences of the Hartmann number (magnetic field), Reynolds number (inertial force), porosity parameter (porous medium) and viscoelastic parameter (second-grade fluid) are discussed in detail. Antiplectic and symplectic metachronal wave patterns are observed, and the results show that the antiplectic wave pattern produces high speed compared with the symplectic wave pattern. To the best of the authors’ knowledge, such a comprehensive analysis has never been proposed so far in the literature.
3. Results and Discussion
Table 1 shows the results of horizontal and vertical velocity for a second-grade and Newtonian fluid in the upper half of channel under the effect of inertial force, magnetic field and porous medium. The negative and positive values of the velocity profile show that ciliary flow is generated by the to-and-fro motion of cilia. Numerical results show that horizontal velocity is maximum at the centre of the channel, and vertical velocity shows increasing and decreasing effects, which generates the wavy movement. It is also observed that the horizontal flow of the Newtonian fluid is larger than that of the second-grade fluid because the second-grade fluid has high viscosity compared with the Newtonian fluid.
In this section, the effects of the Hartmann number
, porosity parameter
, fluid parameter
and Reynolds number
on the velocity field, pressure gradient and stream function are investigated by fixing the values as mentioned in [
2,
31]. Note that the fluid parameter
could be used instead of
, as the second-grade fluid model satisfies the thermodynamic condition
+
= 0. Thus, one will quantify the effect of
on the velocity profile, pressure distribution and stream function. The implementation of the HPM solution can be validated by looking at the graphs: the horizontal velocity component is high at the centre of the channel because the flow is along the direction of the metachronal waves, and the vertical velocity component exhibits a sinusoidal behaviour which is assumed in the boundary conditions.
Figure 2a,d illustrate the effects of the operating parameters
and
on the horizontal velocity component. Their effects on the ciliated flow are prominent in the middle of the channel and insignificant nearby the channel walls, which generates the parabolic behaviour of the flow due to the force caused by the tips of the cilia bed.
Figure 2a shows that the Hartmann number
, which is the ratio of the electromagnetic to the viscous forces, weakens the horizontal velocity because the electromagnetic force is applied in the transverse direction of the flow. In the present study, the magnetic force is dominant over the viscous one, which helps to slow the ciliary flow and can be used to observe the activity of ciliary motion by resonance imaging for diagnostic purposes.
Figure 2b shows that the porosity parameter
helps to assist the axial flow. The porosity parameter is the ratio of the pore volume to the bulk volume, which is generally less than one. It shows that if the bulk volume of dense cilia reduces and the pore volume grows, then a parallel flow rises near the middle of the channel, because the fluid has more space to flow through the pores.
Figure 2c shows that the velocity profile in the horizontal direction increases with the increasing value of the second-grade fluid parameter
because of the presence of a magnetic field and the Reynolds number, which causes a reduction in fluid viscosity.
Figure 2d displays that the Reynolds number supports the accelerating flow of the second-grade viscous fluid.
The behaviour of the vertical velocity component is displayed in
Figure 3a,d. It vanishes in the centre of the channel and behaves like a sinusoidal wave. The vertical velocity rises by increasing the strength of the magnetic field (
M), the ratio of the pores volume to the bulk volume (
K), the viscosity of the fluid (
) and the Reynolds number
in the upper part of the conduit. The same behaviour is observed in the lower part of the channel in the opposite direction, due to the symmetry of the ciliated conduit.
Figure 4a,d illustrate that the horizontal pressure gradient along the flow exhibits a periodic behaviour. A favourable pressure gradient (
) surges when the intensity of the magnetic field and/or the porosity increase. The cilia require more pressure to induce the fluid flow in the presence of a magnetic field applied in the transverse direction. On the contrary, the porous medium assists the fluid flow in the flow direction; therefore, the horizontal pressure gradient is a reducing function of the porosity parameter.
Figure 4c,d show the dual behaviour of the horizontal pressure gradient by developing fluid viscosity
and inertial forces
. The pressure gradient decays in the regions
and
, while it rises in the regions
and
by increasing
and
.
The behaviour of the vertical pressure gradient is presented in
Figure 5a,d. It is symmetric about the centreline and behaves like a sinusoidal wave. The vertical pressure gradient is favourable (negative pressure gradient) in the region
and adverse (positive pressure gradient) in the region
. Increasing the values of
and
K leads to an increase of the pressure gradient amplitude, the Hartmann number
M having an opposite influence. It is also observed that near the upper wall
, the pressure gradient amplitude increases in the flow direction due to the recovery and effective stroke of the cilia beating.
The streamlines are displayed in
Figure 6,
Figure 7,
Figure 8 and
Figure 9 for different values of the Hartmann number
, porosity parameter
, fluid parameter
and Reynolds number
.
Figure 6a–c demonstrate that increasing the Hartmann number
M leads to more resistance for the inertial flow; therefore, the bolus size reduces. It can be observed from
Figure 7a–c that the bolus size rises with increased values of the porosity parameter
, as it allows the fluid to flow more easily through the pores.
Figure 8a–c indicate that, by increasing the fluid parameter
, the size of the trapped bolus rises. As shown in
Figure 9a–c, the bolus size and the number of streamlines become larger when the inertial forces are dominant over the viscous forces (increasing the Re number).
Comparisons of the velocity profiles for both symplectic and antiplectic metachronal waves are shown in
Figure 10a,b. It is noteworthy that the same behaviour is observed for both symplectic and antiplectic waves: if the length of the cilium increases, the amplitude of the velocity profiles becomes larger. However, the most important conclusion is that the horizontal velocity component (
Figure 10a) is much higher for the antiplectic waves. Therefore, antiplectic waves are more efficient to transport a second-grade fluid in the presence of a magnetic field than symplectic waves, which confirms former results in the literature for a Newtonian fluid obtained by more complex numerical simulations [
13]. The larger magnitude of the vertical velocity profiles for the antiplectic waves (
Figure 10b) is in line with the blowing–suction mechanism highlighted by Chateau et al. [
34] using a lattice Boltzmann solver. The authors showed that this mechanism is responsible for the enhanced transport capability of antiplectic waves over symplectic ones.
Figure 11 displays the skin friction coefficient as a function of the second-grade parameter
for different values of the cilia length
. It shows the linear relation between the skin friction coefficient, which is a measure of the fluid resistance on the wall, and
through the straight line when
= 0.1, which becomes nonlinear when
= 0.2 and 0.3.
Numerical results of velocity, pressure, stream function and shear stress are calculated by the Homotopy perturbation method (HPM) and shown through graphs. The distributions of velocity, pressure and shear stress are smooth. They also satisfy the boundary conditions defined for the velocity profile with decreasing coefficients of higher-order solutions, which guarantees that the series solution obtained with the HPM converges in the region −h < y < h and provides the best results of the present study.
4. Conclusions
In this study, we investigated, for the first time, the effect of inertial forces (Re ≠ 0) on the magneto-hydrodynamic flow of a second-grade fluid through a ciliated conduit. The nonlinear system of partial differential equations was solved by the Homotopy Perturbation Method and the software Mathematica. The combined influences of the Reynolds number , Hartmann number , fluid parameter and porosity parameter on the velocity profiles, pressure gradient and stream function were quantified and discussed in detail. The main results gained from this analysis can be summarized as follows:
The horizontal velocity component decreases with increasing values of the Hartmann number in the centre of the channel. On the contrary, it increases with increasing values of the Reynolds number , the porosity parameter , and the fluid parameter . The vertical velocity component vanishes in the centre of channel and behaves like a sinusoidal wave.
A favourable pressure gradient in the axial direction uniformly increases with the Hartmann number and decreases with the porosity parameter . It shows a dual behaviour for the fluid parameter and the Reynolds number , whereas a favourable pressure gradient in the vertical direction is symmetric around the channel centre. It decreases for large values of the Hartmann number , while it increases for larger values of the fluid parameter and the Reynolds number .
The size of the trapped bolus reduces by increasing the Hartmann number and expands by increasing the porosity parameter and the fluid parameter However, both the size and the number of trapped boluses of a second-grade fluid in a ciliated channel increase by increasing the Reynolds number.
The skin friction coefficient (or shear stress) of the second-grade fluid exhibits a linear relation for , whereas this relation becomes nonlinear for increasing values of the cilia length.
The results are useful to detect the frequency and motion of motile cilia under diseased conditions such as cystic fibrosis or bronchopneumonia. The application of a magnetic field for magnetic resonance imaging can detect a viscous fluid flow induced by ciliary motion. For future perspectives, the study will be extended to consider the influence of the temperature and surrounding environment on fluid transport.