Abstract
The aim of the study was to increase the speed, quantity and quality of solutions in intelligent systems aimed at solving the problem of structural–parametric synthesis of models of large discrete systems with a given behavior. As a hypothesis, it was assumed that the adapted model of an artificial neural network is able to control changes in the parameters of the functioning of the operators of the genetic algorithm directly in the process of solving the problem of intelligent structural–parametric synthesis of models of large discrete systems. To solve the problem of managing the process of intelligent search for solutions based on a genetic algorithm, an artificial neural network, which is used as an add-in, must dynamically change the “destructive” ability of operators based on data about the current and/or historical state of the population. In the article, the theory of Petri nets is used as a single mathematical device capable of modeling the work of evolutionary procedures. This mathematical tool is able to simulate the operation of a genetic algorithm adapted to solving the problem of structural–parametric synthesis of models of large discrete systems with a given behavior; simulate the operation and training of an artificial neural network; combine the genetic algorithm with a control add-in based on an artificial neural network to prevent attenuation and premature convergence; simulate the process of recognizing the state of the population; and simulate the operation of the models obtained as a result of the synthesis. As an example of the functioning of the proposed approach, the article presents the results of a computational experiment, which considers the problem of structural–parametric synthesis of computer technology based on the developed models of the element base-RS, D and T triggers that are capable of processing a given input vector into the required (reference) output. In the software implementation of the proposed approach, calculations on the CPU and CPU+GPGPU technologies were used.
1. Introduction
Modern computer-aided design systems contain parametric optimization modules that allow for a given structure of the designed system to select such values of the parameters of the functioning of its elements, at which the designed system is able to satisfy the user. Automation of the process of searching and optimizing the structure of the synthesized system is also a non-trivial task, and the more elements, connections between them and parameters of their functioning included in the structure of the synthesized system, the greater the amount of computing power required by modern automated systems to solve the problem.
At present time, many studies are aimed at solving the problem of improving the performance of computer technology: increasing the speed of computers; increasing the number of computers within a single device and synchronizing computers of one or more devices. However, this problem cannot be solved only with the help of hardware, so it is important to improve mathematical methods for finding solutions to the problem of structural–parametric synthesis.
One approach that has proven itself well in various subject areas is the use of intelligent methods. This class usually includes such mathematical tools as evolutionary strategies, differential evolution, genetic algorithms, programming of gene expression, artificial neural networks, etc.
In this paper, the use of a genetic algorithm is proposed as the main mathematical tool for solving the problem of structural–parametric synthesis of models of large discrete systems with a given behavior.
This mathematical apparatus belongs to the class of heuristic methods, the use of which is due to the solution of optimization and modeling using random selection, combination and variation of the desired structures of the synthesized system and the parameters of the functioning of the components. The adaptation of the genetic algorithm was carried out using the theory of Petri nets. In general, the proposed model is able to solve the problem, but directly in the genetic algorithm, taking into account the specifics of this tool, during the synthesis of solutions, such situations may arise in which the population is in a local extremum, premature convergence is observed, etc. The way out of this situation can be restarting the search procedure or manual correction of the parameters of the functioning of the operators of the genetic algorithm by the operator of the intelligent system. The use of such approaches affects not only the search time for solutions, but also the quality of the solutions obtained as a result of intelligent synthesis, so it is advisable to adjust the parameters of the operators of the genetic algorithm directly in the process of its operation, in order to avoid the above problems.
Modern research suggests the relevance of solving this problem, as researchers in this subject area develop adaptive methods for correcting the parameters of the functioning of genetic algorithms. The development of new approaches to the implementation of the genetic algorithm, which is able to adapt to the solution of the task directly in the process of finding solutions, is relevant. This approach was considered in the papers [1,2].
One of the promising methods in this field is the synergy of artificial neural networks and genetic algorithms [3], because the mathematical apparatus of artificial neural networks has proven itself well in solving control problems.
When using an artificial neural network as a control add-in over a genetic algorithm, it is advisable to apply a change in the destructive ability of its operators, the more expressed is the destructive ability, the greater the dispersion of individuals in the population over the solution space, which allows to knock the population out of the local extremum, with a decrease in the destructive ability, the population is able to conduct a more thorough study of the solution area in which it is currently located. Therefore, it is advisable to classify the parameters of the functioning of operators, in accordance with their destructive capacity. This classification will allow an artificial neural network to control the movement of the population in the decision space.
To simulate the operation of a genetic algorithm and an artificial neural network, it is advisable to use a single mathematical apparatus that will describe the operation of the selected intelligent methods, control the procedure of intelligent structural–parametric synthesis, and describe the structure and parameters of the synthesized models. The use of the theory of Petri nets is proposed as such a mathematical device. This mathematical apparatus has been widely used in various subject areas and a large number of extensions that allow users to model not only discrete, but also continuous systems.
On the basis of a single obtained model (Petri net) of a genetic algorithm under the control of an artificial neural network, a number of computational experiments are conducted, the task of which is to evaluate the increase in the convergence rate of the genetic algorithm, calculate the number of solutions found and determine whether it is possible to reduce the number of attenuations of the genetic algorithm. At the same time, for the experiment, a software implementation was carried out, using devices with a different number of computers: CPU and CPU+GPGPU. This allowed us to test the proposed model based on the Petri net for adequacy when working with the GPGPU technology, because this technology cannot provide an increase in performance if the branch block is used incorrectly, which is a “bottleneck” in the software implementation of many models and methods.
2. Literature Review for the Research Area
In the field of development of methods of structural–parametric synthesis, a large number of studies are conducted, since the solution of this problem is in demand in various subject areas: search for solutions in socio-economic systems, technological systems, energy systems, synthesis and reengineering of business processes, etc. This is due to the wide spread of specialized software tools and design automation services, and a logical requirement for a new generation of automation systems is the availability of specialized automation models for structural and parametric synthesis of developed systems, which will be able to synthesize a system based on the existing element base, and a given behavior (input and output vector) will be able to synthesize a solution within an adequate time.
Since the task of structural synthesis is quite time-consuming, it requires the improvement of existing methods and the development of new ones. In the field of parametric synthesis, the following methods are commonly used: heuristic methods, search methods, diagonal method, finite state machine synthesis method, etc. For the most part, these methods are based on a pre-known structure of the synthesized system, and the task is to find a parameterized structure that can transform the input set X into the set Y formed at the output of the system.
When solving the problem of structural synthesis, researchers use analytical methods, methods based on graph theory, heuristic methods, etc. In this case, the task is reduced to the synthesis of the system structure, that is, the selection of components and connections between them. The listed methods can be classified into standard ones: selection from ready-made prototype structures; construction of a private structure from a general one; directed search in the “AND-OR” tree; directed search in the state tree.
Usually, structural synthesis is associated with parametric synthesis, because the elements that make up the structure of the synthesized system function in accordance with the specified parameters. An exception may be cases in which the structure obtained as a result of the synthesis ensures the operability of the system, and the parameters of the functioning of the system elements are designed to improve the quality of the system functioning. Thus, we can talk about the relevance of the problem of structural–parametric synthesis of systems [4,5].
In the structural–parametric synthesis of a large discrete system with a given behavior, the number of elements and parameters of their functioning is so large that the solution of this problem by iteration is impossible even with the use of modern computing systems. Therefore, it is advisable to use the methods of directed search. The range of such methods is quite wide:
- -
- Genetic algorithms;
- -
- Simulated annealing method;
- -
- A set of algorithms based on the ant colony method;
- -
- Algorithm with a pair breakdown;
- -
- Algorithm with a return on a failed step;
- -
- Algorithm with recalculation in case of an unsuccessful step;
- -
- Search with bans, etc.
In recent times, a large number of studies in the field of structural–parametric synthesis have been aimed at the use of artificial intelligence methods, among which the genetic algorithm is widely used.
Genetic algorithms are commonly referred to as heuristic methods that are used in the following tasks: solution search, optimization and modeling. To solve the problem, the genetic algorithm uses random selection and combination based on mechanisms similar to natural selection. At the same time, this algorithm does not guarantee an accurate or optimal solution, but this solution is sufficient to solve the problem [6].
The application of this algorithm is associated with a number of difficulties, among which it is worth noting the possibility of damping, premature convergence, population concentration in the area of the local extremum, etc. Therefore, many studies are aimed at solving this problem. Modern approaches to solving the problem of increasing the convergence of a genetic algorithm can be classified as follows: creating new operators of the genetic algorithm; upgrading existing operators; changing the number and order of operation of operators; adjusting the number of individuals in the initial population; and development of an adaptive genetic algorithm that can change the parameters of functioning in the process of operation.
The most promising direction in solving time-consuming tasks is the development of a genetic algorithm that can adapt to the solution of the problem in the process of work. For this purpose, it is customary either to combine evolutionary procedures, for example, to use an ant algorithm or an artificial neural network [3], or to use methods of changing the settings of the parameters of the operator’s functioning by using fuzzy logic methods or elitism strategies, or to create a structure of two genetic algorithms [7,8], one of which solves the problem of configuring the parameters of the operators functioning of the second.
In general, setting up a genetic algorithm in a specific subject area is quite complex, and optimizing the parameters of the functioning of operators in one subject area for a specific problem cannot guarantee the efficiency of work when solving a similar problem [9]. Thus, the application of this evolutionary procedure in solving the problem of structural–parametric synthesis of large discrete systems with a given behavior requires the choice of a control add-in that can change the parameters of the operators ‘functioning directly in the process of the evolutionary procedure.
In this paper, we propose the use of an artificial neural network to solve the problem of structural–parametric synthesis of models of large discrete systems with a given behavior.
3. Materials and Methods
To achieve the goal of research to improve speedwork, quantity and quality of synthesized models of large discrete systems with a given behavior of solutions in intelligent information systems based on genetic algorithms, the paper proposes the use of artificial neural networks.
At the same time, the problem of determining the mathematical apparatus, that combines the selected evolutionary methods into a single model and support simulation modeling, arose. The apparatus would allow us to conduct computational experiments on the resulting models to assess their adequacy. For this purpose, the paper proposes the use of the mathematical apparatus of the theory of Petri nets.
The mathematical apparatus of the theory of Petri nets is widely used and has a large number of extensions (types), among which it is worth noting temporary networks, inhibitory networks, continuous networks, nested networks, color networks, information networks, etc. This variety allows you to model discrete systems in different subject areas.
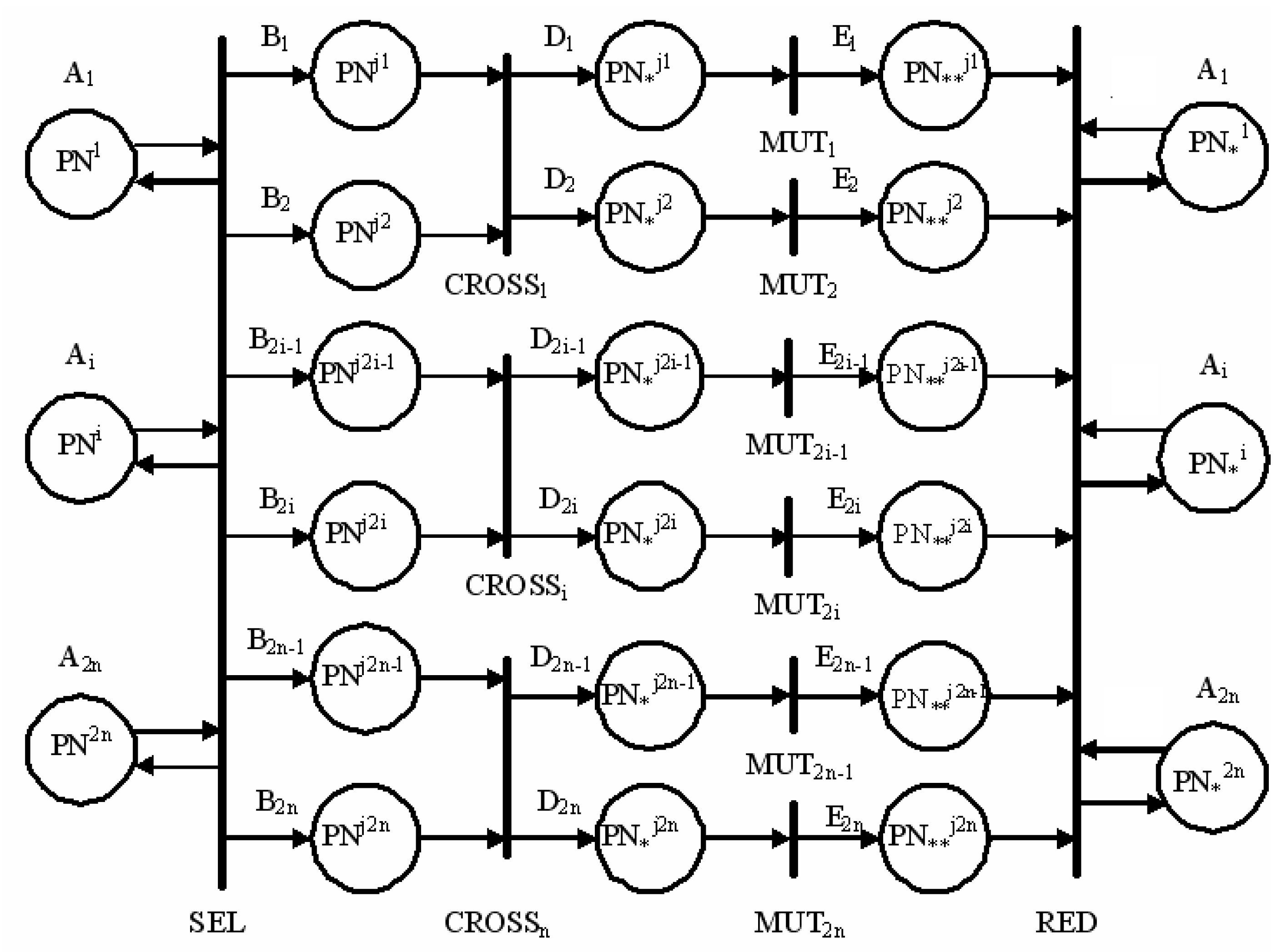
In Reference [10], it was proposed to use nested Petri nets to model the operation of a genetic algorithm (see Figure 1). Nested Petri nets allow using a multi-level approach, which consists in the fact that the top-level label of the model is a Petri net PN.
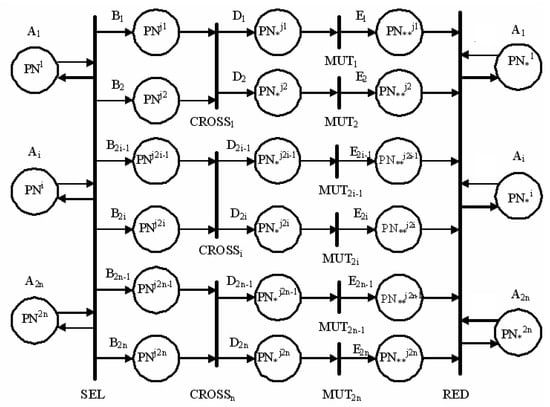
Figure 1.
Model of a genetic algorithm based on Petri nets.
The operation of the presented model is as follows:
- -
- It is required to create models of the element base based on the theory of Petri nets;
- -
- Encode each of the elements with a binary string;
- -
- Perform encoding of the types of inter-element relationships with a binary string;
- -
- Form the initial population in the form of a binary string that contains information about the elements and the relationships between them, while being a second-level model based on the Petri net, and place it in the positions of layer A;
- -
- Calculate the fitness function for each individual of the population (to calculate the fitness function, the input vector is given to the input of the second-level model, the model operation is simulated, the resulting output vector is compared with the reference output vector by the Hamming distance. The resulting values of the target function are written to the label);
- -
- The SEL transition performs the function of a selection operator, selects pairs for crossing based on the target function, and moves the population to the positions of layer B;
- -
- CROSSi transitions perform the work of the crossing operator and moves the population to the positions of layer D;
- -
- MUTi transitions perform the work of the mutation operator and moves the population from the position of the E layer;
- -
- The RED transition performs the work of the reduction operator, i.e., it calculates the fitness function of the individuals in the population and destroys the individuals with the highest value of the fitness function in a given volume, after which it returns the population to the position of layer A;
- -
- Process the specified number of cycles with the population [10].
Let us consider an example of how the model used works; let us say that you need to find a configuration of triggers that converts the input vector (0, 1, 1, 0) to the output vector (1, 0, 1, 0).
We define the objective function by using the concept of a metric space and considering the resulting vector at the output of the synthesized model and the reference output vector as Euclidean elements with a distance as follows:
where y = (y1, …, yn).
The smaller ρ1 is, the closer the PN model is to the specified property. If ρ1 = 0, then the model PN has the specified property.
Step 1. A population of four individual configurations is randomly formed (Table 1).

Table 1.
Example of an initial population.
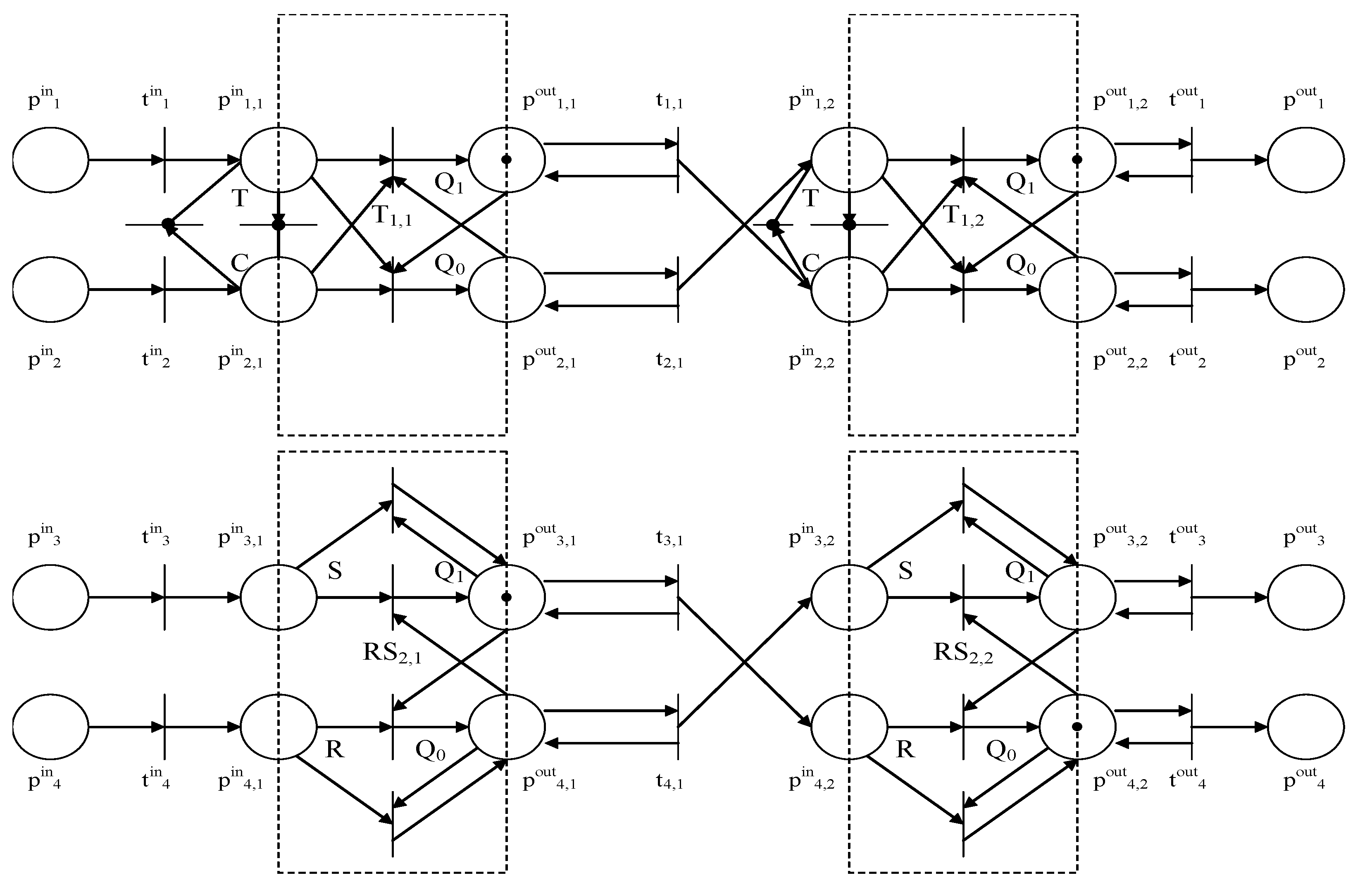
An image of an individual population represented by a network top-level label and simulating the operation of the configuration (T, T, RS, RS) in the initial state (1, 1, 1, 0) is shown in Figure 2.
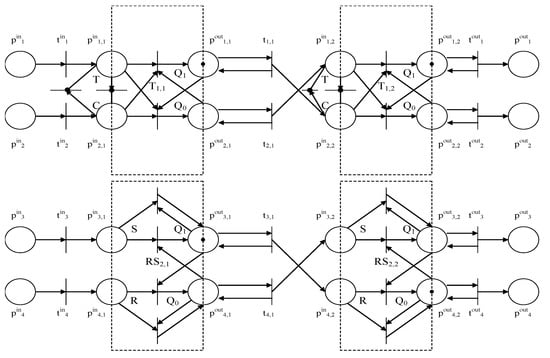
Figure 2.
Configuration 1 based on Petri net.
Step 2. Choose the two best configurations.
The input vector (0, 1, 1, 0) is fed to the input of each configuration and the distance (the sum of the modules of the coordinate differences) between the resulting output vector and the required output vector is calculated (1, 0, 1, 0). The smaller the distance, the better the configuration (see Table 2).

Table 2.
The value of the fitness function of individuals of the initial population.
The best configurations are 1, 2 and 4. Configurations 1 and 4 are randomly selected.
Step 3. Crossing configurations.
A split point is randomly selected—in the middle of the individual (see Table 3).

Table 3.
Split point.
As a result of crossing, Configurations 5 and 6 are obtained. The substitutions do not change (F1 = F5, F4 = F6) (see Table 4).

Table 4.
Crossing result.
Step 4. Mutation of the descendant configuration.
Configuration 6 is randomly selected. The last RS trigger is randomly selected and randomly changed to the D trigger. The result is Configuration 7 (see Table 5).

Table 5.
Mutation of the descendant configuration.
Step 5. Reduction of configurations.
The input vector (0, 1, 1, 0) is fed to the input of the descendant configurations and the distance (the sum of the modules of the coordinate differences) between the resulting output vector and the required output vector is calculated (1, 0, 1, 0) (see Table 6).

Table 6.
The value of the fitness function for Configuration 5 and Configuration 7.
The two weakest configurations must be removed from the population (see Table 7).

Table 7.
Reduction of configurations.
Configuration 3 is the weakest. From the four configurations that are in the penultimate place, Configuration 2 is randomly selected.
Step 6. Checking the algorithm shutdown criterion (see Table 8).

Table 8.
Population after reduction.
Configuration 7 is the required configuration.
Thus, the work of the model of the genetic algorithm based on nested Petri nets is performed.
To simulate the operation of an artificial neural network, it is also advisable to use the mathematical apparatus of the theory of Petri nets. At the same time, it is necessary to provide for the possibility of training the network. Therefore, as a means of storing information about the weight of synapses, it is necessary to use labels that can be changed during network training without compromising the structure of the artificial neural network.
The model of the genetic algorithm (shown in Figure 1) based on nested Petri nets should be modified to take into account the task of controlling the genetic algorithm. As the work of operators in the top-level network is modeled by transitions, accordingly, it is necessary to adapt this model by adding a transition layer for each operator, each transition in the operator layer models the work with certain functioning settings.
When forming a single model, it is necessary to provide for the connection of an artificial neural network model and a genetic algorithm. For this purpose, it is advisable to use positions, the presence of labels in the positions allows you to change the trajectory of the population according to the model of the genetic algorithm, thereby ensuring changes in the parameters of the operators.
The mathematical apparatus of Petri net theory has the property of parallelism, which is supported by the selected artificial intelligence methods and GPGPU technology. This feature allows us to apply parallel computing in the software implementation of the developed model and evaluate the increase in performance, taking into account the use of this technology.
4. Results
In this paper, we consider the simulation of the perceptron using the theory of Petri nets with further integration with the model of the genetic algorithm for solving the problem of structural–parametric synthesis of large discrete systems.
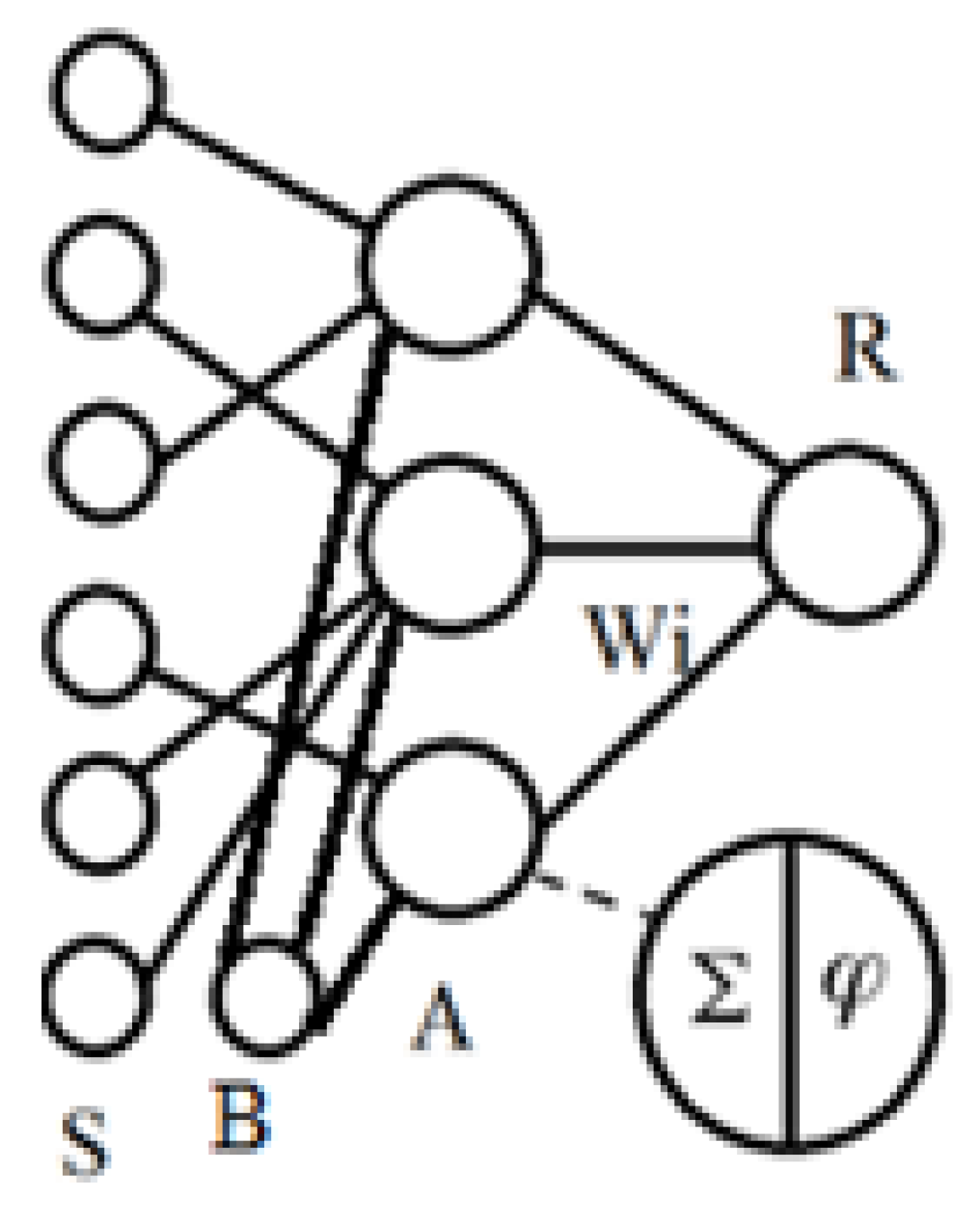
Figure 3 shows a logical model of an elementary perceptron.
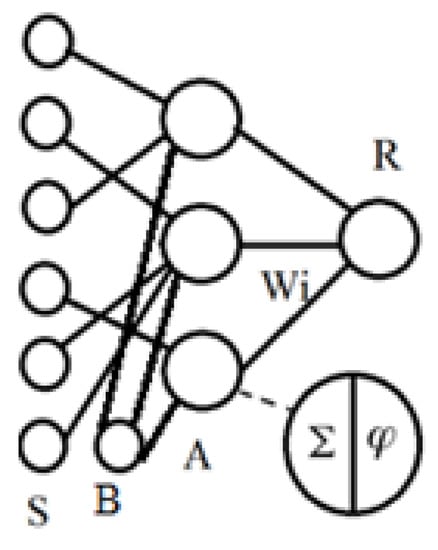
Figure 3.
Diagram of the elementary perceptron.
The structure of this model consists of the following elements:
- -
- S-elements, the purpose of which is to model the receptor layer or the input layer of an artificial neuron;
- -
- A-elements intended for association modeling (hidden layer);
- -
- R-elements are used to model the response of an artificial neural network (the output layer of the neural network);
- -
- W is the interaction matrix, i.e., the weights of the synapses connecting the layers of the artificial neural network;
- -
- B is the displacement neuron [11].
Then the perceptron can be represented in the following form:
where Si is the i-th perceptron receptor.
where Ai is the i-th association of the perceptron.
where Ri is the i-th perceptron reaction.
where Wi is the i-th weight of the connection between the layers S, A, and R of the perceptron.
where Bi is the i-th displacement neuron with the corresponding weight.
When modeling an artificial neural network using the mathematical apparatus of Petri net theory, Formula (1) can be represented as follows:
where PNNS is a Petri net that simulates the operation of a perceptron;
PS—positions simulating the perceptron receptor (the set of input positions of the artificial neural network model):
where n is the number of inputs to the artificial neural network.
PNA is a Petri net that simulates the operation of the association (provided by ):
where G is the number of neurons in the layer.
PR—positions that preserve the perceptron response (the set of output positions of the artificial neural network model):
PW—position that stores the weight factor value:
where Q is the number of W-type connections in the artificial neural network.
PB—position that stores the value of the weight coefficient of the connection of the correcting neuron and the PNA:
where D is the number of connections of the correcting neuron layer with the PNA.
PNcontr—a Petri net that provides the sequence of triggering layers of the artificial neural network model:
M0—initial network marking;
L—arcs that connect components into a single network;
T—junctions that connect components to a single network;
Pout—output positions.
where e is the number of neurons in the output layer of the artificial neural network.
The Petri net is usually displayed as positions P, transitions T, arcs L, and the initial marking M0 [12,13]:
Then, we have the following:
Accordingly, Formula (7) can be presented in the following form:
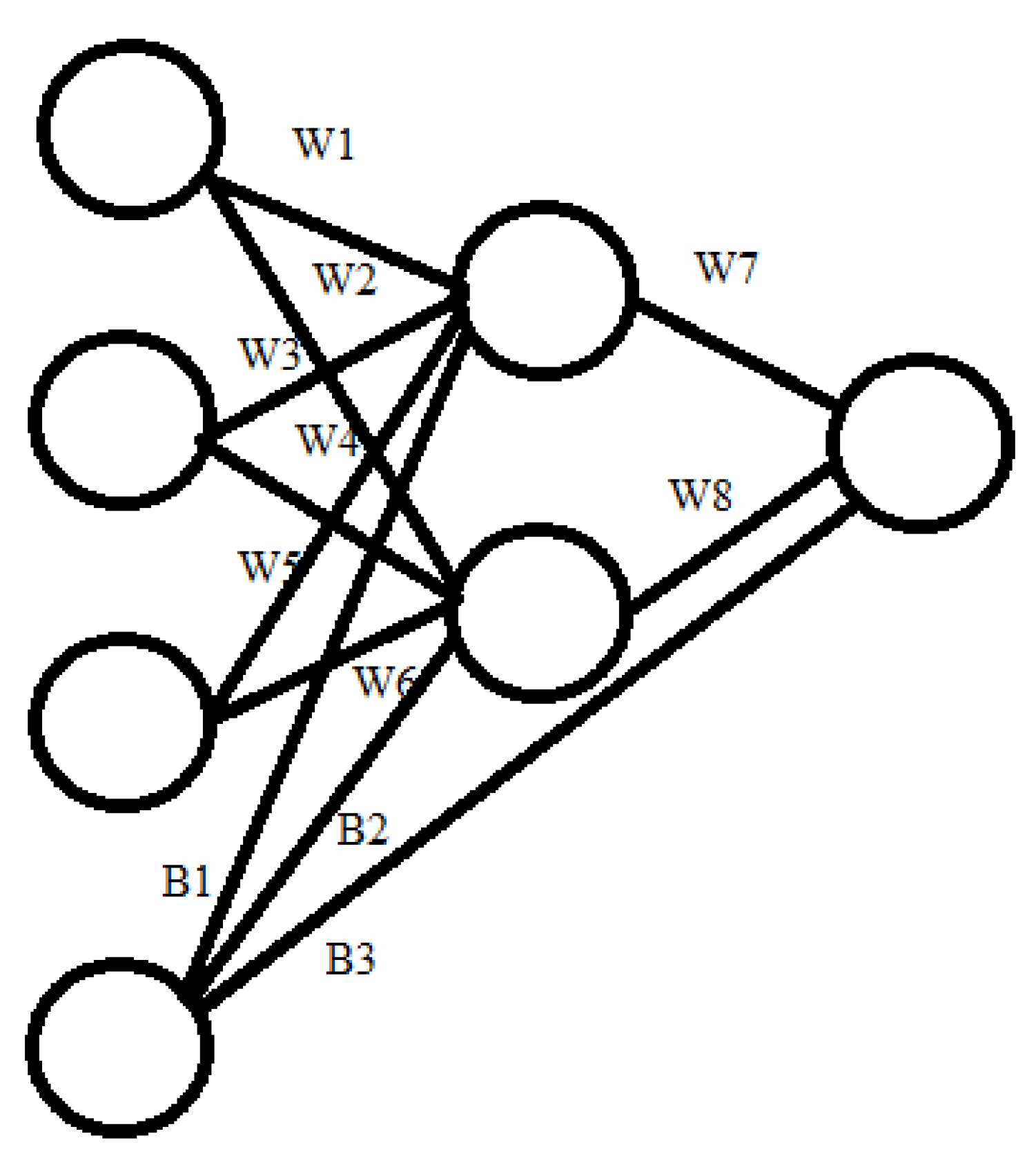
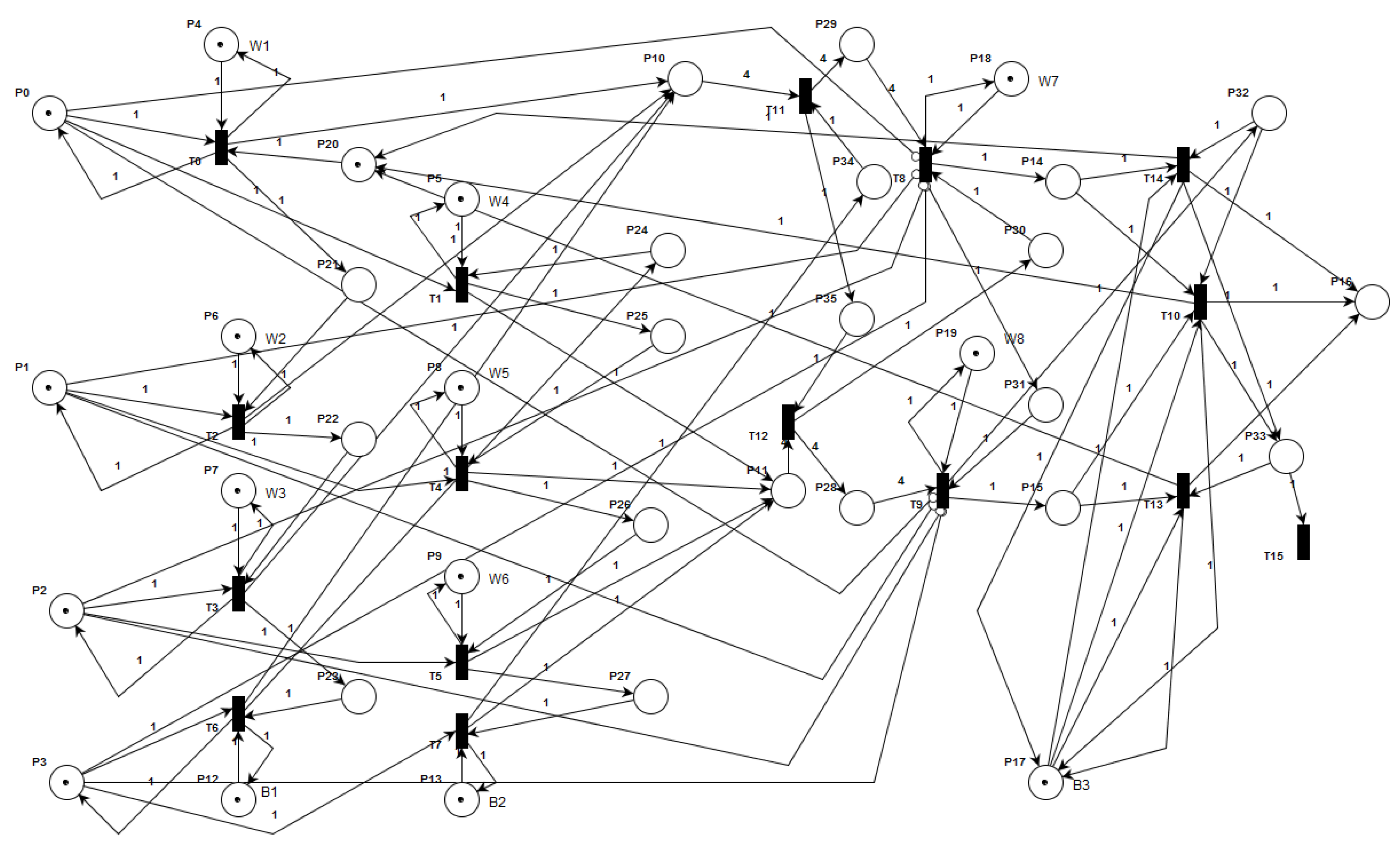
Figure 4 shows an example of an artificial neural network of direct distribution, the model of which is required to be built using the mathematical apparatus of the theory of Petri nets.
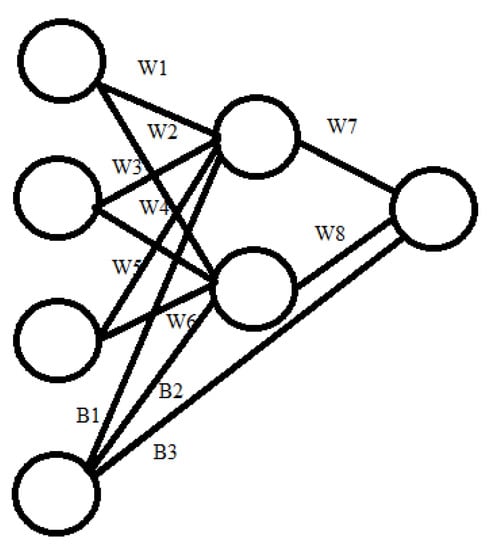
Figure 4.
Example of an artificial neural network.
Based on the representation (16) and Figure 4, the model of an artificial neural network based on a Petri net can be represented as follows (see Figure 5).
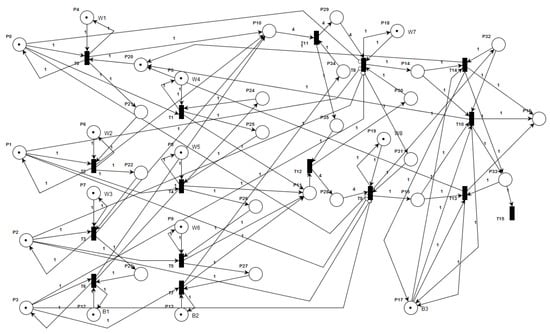
Figure 5.
Example model of an artificial neural network based on Petri nets.
According to (16), we have the following:
- -
- Ps = {P0, P1, P2, P3} (P3—correction neuron);
- -
- PR = {P10, P11};
- -
- PW = {P4, P5, P6, P7, P8, P9, P18, P19};
- -
- PB = {P12, P13, P17};
- -
- Pout = {P16};
- -
- PNcont = <{P20, P21, P22, P23, P24, P25, P26, P27, P31, P32, P33, P34, P35}, {T0, T1, T2, T3, T4, T5, T6, T7, T8, T9, T10, T11, T12, T13, T14, T15}, {Ling, Lf}, M0,Pcont>;
- -
- M0 = {1,1,1,1,1,1,1,1,1,1,0,0,1,1,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}.
Since in the proposed model the labels simulate the input data and the weights of the synapses, it is advisable to modernize their representation (see Table 9)

Table 9.
Representation of the initial marking in the developed model.
Mi—i-th marking of the Petri net;
Po—position in the artificial neural network model based on the Petri net;
K—the number of labels in Po (from 0 to n);
Kn—the ordinal number of the placemark in the Po position;
Wn (or Bn) is the weight of the label, where n is the ordinal number of the label.
Then, for the presented model of the artificial neural network in Figure 4, the initial marking of the Petri net can be represented in the following way (see Table 10).

Table 10.
Example of the initial marking.
Thus, the model of an artificial neural network based on the mathematical apparatus of the Petri net theory fully corresponds to the model presented in Figure 5.
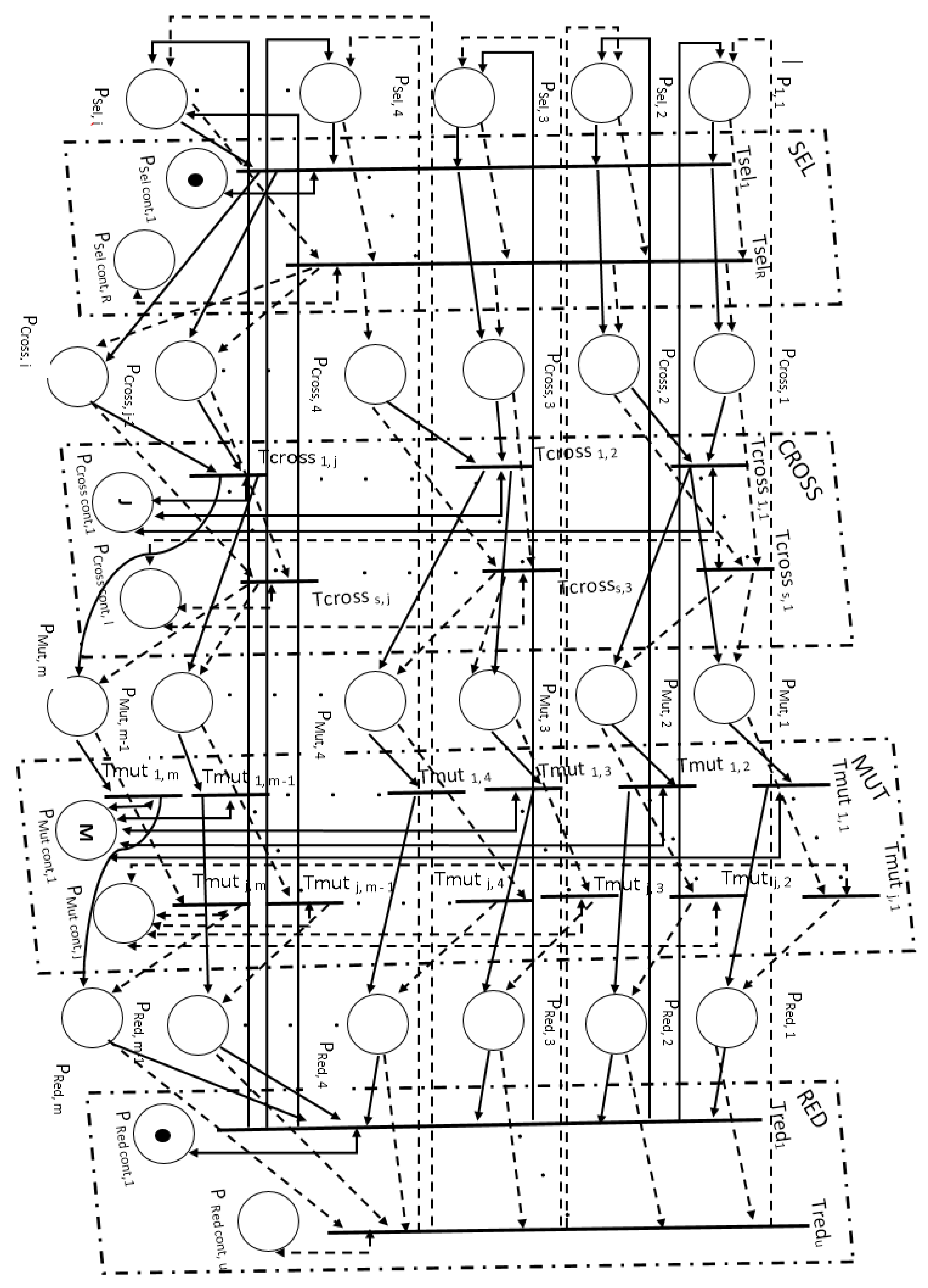
To control the genetic algorithm, it was necessary to develop a model of an artificial neural network using the proposed approach. For this purpose, the genetic algorithm presented in Figure 1 (see Figure 6) was adapted.
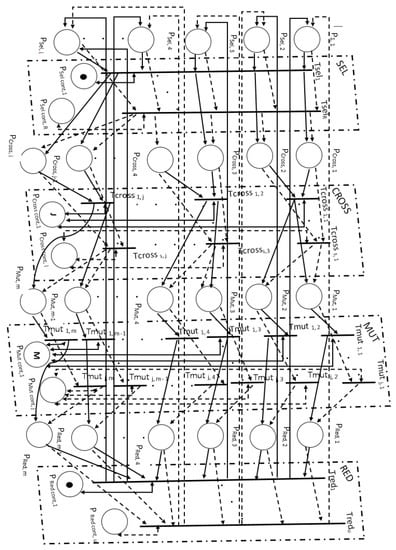
Figure 6.
Adaptation of the genetic algorithm to the solution of the problem of structural–parametric synthesis and control of the search procedure using an artificial neural network model.
Let us consider in more detail the use and application of the upgraded model of the genetic algorithm.
When solving the problem of controlling a genetic algorithm in the process of solution synthesis, it is advisable to consider the work of operators:
where we have the following:
- -
- SEL is the selection operator;
- -
- CROSS is the crossing operator;
- -
- MUT is the mutation operator;
- -
- RED is the reduction operator.
Each operator has different operating parameters. Under the parameters of the operators, we can understand the following:
SEL operator:
- -
- Tournament selection;
- -
- Roulette selection;
- -
- Combined (based on tournament and roulette), etc.
CROSS operator:
- -
- Single-point;
- -
- Two-point;
- -
- Multipoint, etc.
MUT operator:
- -
- Single-position mutation;
- -
- Multi-position mutation
- -
- Probability of triggering the mutation operator, etc.
RED operator:
- -
- Leave a certain number of individuals in the population with the fitness function value not lower than the specified threshold;
- -
- Leave all individuals in the population regardless of the value of the target function, etc.
Depending on the selected parameter of the operator’s performance, its resolution, i.e., the ability to change the binary string of the chromosome, changes, which in turn affects the movement of the population in the solution space.
In this case, the operators can be represented as follows:
where —i-th parameter of SEL operator’s functioning;
where —j-th parameter of CROSS operator’s functioning;
where —k-th parameter of MUT operator’s functioning;
where —o-th parameter of RED operator’s functioning.
Then the genetic algorithm can be represented as a combination of the parameters of its operators:
In this case, the operators can be represented as follows:
The use of the theory of Petri nets is proposed as an instrumental simulation of the genetic algorithm and artificial neural networks. A Petri net is a bipartite directed graph consisting of two types of vertices—positions and transitions connected by arcs. , where P is the positions, T is the transitions, and L is the relation between the vertices corresponding to the arcs of the graph. The marking of the network is also used—the function M, which matches each position with a non-negative integer. The marking can be characterized by the vector , where n is the number of positions in the network. In the graphical representation, the marking M corresponds to the number of marks in the positions of the Petri net.
As in the model shown in Figure 1, the top-level transitions model the operation of the operators of the evolutionary procedure, and the positions serve to store labels, which in turn are models of individuals in the population.
Then the simulation model of the genetic algorithm can be represented as follows:
where we have the following:
P—network positions;
T—network transitions;
L—connecting arcs;
M0—initial marking of the network.
Positions need to be divided into two types: positions for storing the population and positions for managing the parameters of the operators.
where the positions for storing the population are as follows:
set of positions for storing the population of individuals in the SEL layer;
set of positions for storing the population of individuals in the CROSS layer;
set of positions for storing the population of individuals in the MUT layer;
the set of positions for storing the population of individuals in the RED layer.
Transitions T can simulate the operation of operators with different functioning parameters.
where —transitions that simulate the operation of the SEL operator with a certain function parameter R;
—transitions that simulate the operation of the CROSS operator in the connected layer S with a certain function parameter J;
transitions that simulate the operation of the MUT operator in the connected layer J with a certain function parameter M;
transitions that simulate the operation of the RED operator with a certain U function parameter.
In addition to the positions and transitions in the simulation model of the genetic algorithm based on Petri nets, it is necessary to determine the connecting arcs of L.
where –the included arcs along which the labels pass (achieved by “exciting” the transition by placing the label from the control neural network in the corresponding control position);
—disabled arcs (connected to the control position where there are no labels).
The value M0 corresponds to the initial marking of the developed model based on Petri nets.
Operating is performed as follows:
At the beginning, the model of an artificial neural network based on Petri nets, built according to the principle shown in Figure 5, is connected to the one presented at the selected control positions (at the beginning of the work, the transitions with operator functions defined by the expert in Figure 6 are connected , , , . The connection uses a different number of labels, since the number of transitions in the layers is different). Secondly, search criteria are entered. In the end the model is being launched.
The neural network model analyzes the state of the population and the genetic algorithm. In the proposed model, the following positions are highlighted: Psel, Pcross, Pmut and Pred, which are connected to the corresponding outputs of the artificial neural network model. The presence of labels in these positions activates a transition with a given parameter of the functioning of the genetic algorithm operator.
To solve the problem of increasing the speed and number of solutions found in an intelligent system of structural–parametric synthesis, it is necessary to develop a model of an artificial neural network based on the mathematical apparatus of Petri nets, that provides recognition of the state of the population and, if necessary, changes the parameters of the functioning of operators.
As an example, consider a population of 250 individuals. The model of a fully connected neural network can consist of the following:
- -
- 251 neurons of the input layer (250 neurons for input data and one correction neuron);
- -
- 250 neurons of the first hidden layer;
- -
- 100 neurons of the second hidden layer;
- -
- 5 neurons of the output layer (attenuation, attenuation, convergence, convergence and non-interference).
Training of the neural network is carried out by using the method of back propagation of the error. The activation function is f (x) = tanh(x).
The value of the fitness function of each individual in the population is used as input data:
For software implementation, we use the Python programming language and the Numba and PyCUDA modules.
For training, we used data obtained as a result of a computational experiment to find the configuration of a memory element (following the example of the genetic algorithm described earlier, but on a larger configuration):
- -
- Element base based on RS, D and T triggers (models of which are made using the mathematical apparatus of Petri nets);
- -
- The dimension of the configuration of the simulated device is 26X10;
- -
- Static inter-component connections;
- -
- Specified input vector—1010 0101 0101 0101 0101 0101 0101 0010 1010 1010 1010 1010 1001;
- -
- Specified output vector (the reference vector into which the synthesized device should process the specified input vector)—1000 1101 1001 0101 0001 1001 1111 1110 1010 1010 0000 1111 1001;
- -
- The value of the fitness function is calculated from the Hamming distance between the reference vector and the output vector obtained after running the synthesized models;
- -
- Number of training data for an artificial neural network—100 variants for each variant of the population state;
- -
- The number of populations to be processed for solution synthesis is 200.
An example of the data that were used to train a neural network in a graphical representation is shown in Figure 7.
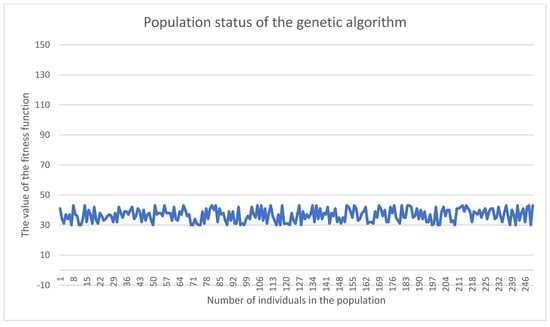
Figure 7.
Example of input data for training an artificial neural network.
As a result of the training, the values of the synapse weight coefficients were obtained, which were used in modeling an artificial neural network using Petri net theory.
Based on the approach proposed in this paper, two models (a genetic algorithm and a neural network) were combined, and two computational experiments were conducted, the task of which was to do the following:
(1) The first involved estimating the number of solutions found that meet the search criteria, using a model of a genetic algorithm without an artificial neural network (Figure 1): Table 11 column 2 calculation on the CPU, as well as using its INS to control the GA Table 11 column 3 calculation on the CPU. The second experiment was the use of GPGPU technology [14] in software implementation for a model of a genetic algorithm without an artificial neural network in Table 3 column 4 and a model of a genetic algorithm using an artificial neural network in Table 11 column 5. The estimation of the number of solutions found was carried out when processing 200 generations of the population, using GPGPU + CPU, as well as using CPU only (see Table 11).

Table 11.
Computational experiment 1.
(2) The second involved determining, according to the evaluation of the performance improvement, the estimate of the time it would take to synthesize the first solution that meets the criteria: the model of the genetic algorithm without the INS Table 12 column 2 calculation on the CPU, the model of the genetic algorithm with the INS Table 12 column 3 calculation on the CPU; the model of the genetic algorithm without the INS Table 12 column 4 calculation on the CPU + GPGPU; the model of the genetic algorithm with the INS Table 12 column 5 calculation on the CPU + GPGPU; the waiting time for the solution is set to 3000 s, in case of not finding solutions, and the number is 0 (see Table 12).

Table 12.
Computational experiment 2.
For the computational experiment, we used Lenovo IdeaPad L340 Gaming; Intel Core i5-9300H @ 2.4 GHz processor; 8 Gb RAM; 512 Gb SDD; Nvidia GEFORCE GTX 1650 4 GB video card. The initial setup of the genetic algorithm operators is as follows:
- -
- Selection operator-tournament selection;
- -
- Crossing operator—single-point;
- -
- Mutation operator—multipoint (mutation probability 0.3);
- -
- Reduction operator—50% of individuals with the best fitness function value remain in the population.
5. Discussion
In the course of the study, the model of a genetic algorithm based on nested Petri nets was modernized, aimed at solving the problem of structural–parametric synthesis of large discrete systems with a given behavior, in order to increase the speed, quantity and quality of solutions that meet the search criteria. For this purpose, it was proposed to implement a control add-in by using the mathematical apparatus of artificial neural networks. In order to use a single mathematical apparatus, an artificial neural network was modeled by using the theory of Petri nets.
When combining evolutionary procedures, it is proposed to use control positions that connect the desired transition with certain parameters of the functioning of the genetic algorithm operator. The transition is connected by moving the placemark to the desired position, which allows the population to change the trajectory of movement within the framework of the genetic algorithm model.
To control the procedure for synthesizing solutions based on a genetic algorithm, the resolution of the operators is used. When a population is found in a local extremum or the genetic algorithm fades, the artificial neural network increases the destructive capacity, thereby knocking the population out of the inefficient solution domain and scattering it across the solution space in order to find new extremes. Moreover, an artificial neural network can reduce the destructive ability of operators, which allows you to perform a thorough study of the area, if there is a convergence of the GA, thereby speeding up this process.
When modeling an artificial neural network with a Petri net, the use of labels as a storage of information about the weight of synapses of neurons is proposed. This approach makes it possible to simplify the process of functioning of the evolutionary procedure and will further simplify the modeling of the learning process.
The use of the mathematical apparatus of the theory of Petri nets made it possible to perform a software implementation using GPGPU technology, because this mathematical apparatus and the selected algorithms have the property of parallelism, which allows you to distribute the calculation flows to a large number of calculators.
Based on the results of computational experiments, we can say that the use of artificial neural networks as a control add-in over the genetic algorithm allows to increase the number of synthesized solutions for a given number of processed populations, but loses in time characteristics to the usual genetic algorithm (see the average time spent on processing 200 generations of the population and the average number of solutions found, Table 3, calculation on the CPU and CPU + GPGPU), this can be explained by an increase in computational load. It is worth noting. That the number of solutions found in the GA under the control of the INS is greater than that of a simple genetic algorithm.
The use of GPGPU technology in the software implementation practically eliminates the time required for an artificial neural network to make decisions and adjust the parameters of the functioning of the genetic algorithm operators.
However, it is worth noting that, when searching for the first solution that will meet the search criteria, the genetic algorithm under the control of the ANN shows significantly better time required to synthesize solutions, and it also has a larger number of solutions found. (See the average time spent searching for a solution and the average number of solutions found, Table 4, calculation on CPU and CPU + GPGPU.)
6. Conclusions
Recent research suggests that the development of artificial intelligence cannot be performed by using a single mathematical apparatus or an applied algorithm. Therefore, it is advisable to find new solutions by combining existing approaches. The synergy of the neural network approach and genetic algorithms is a promising direction that can be widely used. This kind of unification requires specialized synchronization methods, which can be achieved by choosing a universal and well-developed mathematical apparatus. In this paper, an approach based on the theory of Petri nets was first proposed. The use of this mathematical tool will allow you to fully reveal the properties of parallelism [15,16] that are inherent in the genetic algorithm and artificial neural network [17,18], and it will also allow you to use parallel computing in software implementation. We should remember that the mathematical apparatus of the theory of Petri nets was created as a tool aimed at modeling computer technology, which allows us to talk not only about the possibility of software implementation of the proposed models and methods, but also about the hardware implementation.
In the framework of further research, it is promising to conduct a thorough study of the influence of the destructive ability of the operators of the genetic algorithm on the distribution of individuals in the population in the solution space. This study will improve the performance of the genetic algorithm, as well as reduce the number of individuals in the initial population, which will reduce the load on the calculators, without losing quality, and will not increase the time it will take to synthesize solutions.
An adaptive genetic algorithm controlled by an artificial neural network will make it possible to synthesize solutions for large discrete systems with a given behavior not only on static inter-component connections but also to use a dynamic inter-component bus, in which the connections between the elements can change during the operation of the simulated system
Based on the above, we can conclude the practical significance, innovation and prospects of the proposed approach.
Author Contributions
Conceptualization, D.A.P.; methodology, D.A.P.; software, D.A.P. and N.V.P.; validation, D.A.P., N.V.P. and V.A.L.; formal analysis, D.A.P.; investigation, D.A.P.; resources, D.A.P. and V.A.L.; data curation, D.A.P. and V.A.L.; writing—original draft preparation, D.A.P., N.V.P. and V.A.L.; writing—review and editing, D.A.P.; visualization, D.A.P. and N.V.P.; supervision, D.A.P.; project administration, D.A.P.; funding acquisition, this research received no external funding. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Park, K.-M.; Shin, S.-H.; Shin, D.; Chi, S.-D. Design ofWarship Simulation Using Variable-Chromosome Genetic Algorithm. Appl. Sci. 2019, 9, 4131. [Google Scholar] [CrossRef]
- Park, K.; Shin, D.; Chi, S. Variable Chromosome Genetic Algorithm for Structure Learning in Neural Networks to Imitate Human Brain. Appl. Sci. 2019, 9, 3176. [Google Scholar] [CrossRef]
- Styrcz, A.; Mrozek, J.; Mazur, G. A neural–network controlled dynamic evolutionary scheme for global molecular geometry optimization. Int. J. Appl. Math. Comput. Sci. 2011, 21, 559–566. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdas, G.; Kayabekir, A.E.; Yucel, M. (Eds.) Advances in Structural Engineering—Optimization. Available online: https://www.springer.com/gp/book/9783030618476 (accessed on 18 March 2021).
- Barkalov, A.; Titarenko, L.; Mielcarek, K.; Chmielewski, S. Logic Synthesis for FPGA-Based Control Units. Available online: https://www.springer.com/gp/book/9783030382940 (accessed on 10 March 2021).
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Mutingi, M.; Mbohwa, C. Grouping Genetic Algorithms. Available online: https://www.springer.com/gp/book/9783319443935 (accessed on 10 March 2021).
- Agust, L.; Salcedo-Sanz, S.; Jiménez-Fernández, S.; Carro-Calvo, L.; Del Ser, J.; Portilla-Figueras, J.A. A new grouping genetic algorithm for clustering problems. Expert Syst. Appl. 2012, 39, 9695–9703. [Google Scholar]
- Cano, J.A. Parameters for a genetic algorithm: An application for the order batching problem. IBIMA Bus. Rev. 2019, 2019, 802597. [Google Scholar] [CrossRef]
- Petrosov, D.A.; Lomazov, V.A.; Mironov, A.L.; Klyuev, S.V.; Muravyov, K.A.; Vasilievna, F.M. Intellectual structural-parametric synthesis of large discrete systems with specified behavior. J. Eng. Appl. Sci. 2018, 13, 2177–2182. [Google Scholar]
- Poznyak, T.I.; Chairez Oria, I.; Poznyak, A.S. Background on Dynamic Neural Networks. In Ozonation and Biodegradation in Environmental Engineering; Elsevier: Amsterdam, The Netherlands, 2019; pp. 57–74. [Google Scholar] [CrossRef]
- Girault, C.; Valk, R. Petri Nets for Systems Engineering: A Guide to Modeling, Verification, and Applications. Available online: https://www.springer.com/gp/book/9783540412175 (accessed on 1 March 2021).
- René, D.; Hassane, A. Discrete, Continuous, and Hybrid Petri Nets; Springer: Berlin/Heidelberg, Germany, 2010; 550p. [Google Scholar]
- NVIDIA Launches the World’s First Graphics Processing Unit: GeForce 256, NVIDIA. Available online: https://www.nvidia.com/object/IO_20020111_5424.html (accessed on 18 March 2021).
- Dworzański, L.W.; Lomazova, I.A. On compositionality of boundedness and liveness for nested petri nets. Fundam. Inform. 2012, 120, 275–293. [Google Scholar] [CrossRef]
- Petrosov, D.A.; Vashchenko, R.A.; Stepovoi, A.A.; Petrosova, N.V. Application of artificial neural networks in genetic algorithm control problems. Int. J. Emerg. Trends Eng. Res. 2020, 8, 177–181. [Google Scholar] [CrossRef]
- Kojecký, L.; Zelinka, I. On the Similarity between Neural Network and Evolutionary Algorithm. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing; Available online: https://www.springerprofessional.de/on-the-similarity-between-neural-network-and-evolutionary-algori/18504684 (accessed on 7 March 2021).
- Saikia, P.; Baruah, R.D.; Singh, S.K.; Chaudhuri, P.K. Artificial Neural Networks in the Domain of Reservoir Characterization: A Review from Shallow to Deep Models. Comput. Geosci. 2019, 135, 104357. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).