Coupled Mode Sound Propagation in Inhomogeneous Stratified Waveguides
Abstract
1. Introduction
2. Method
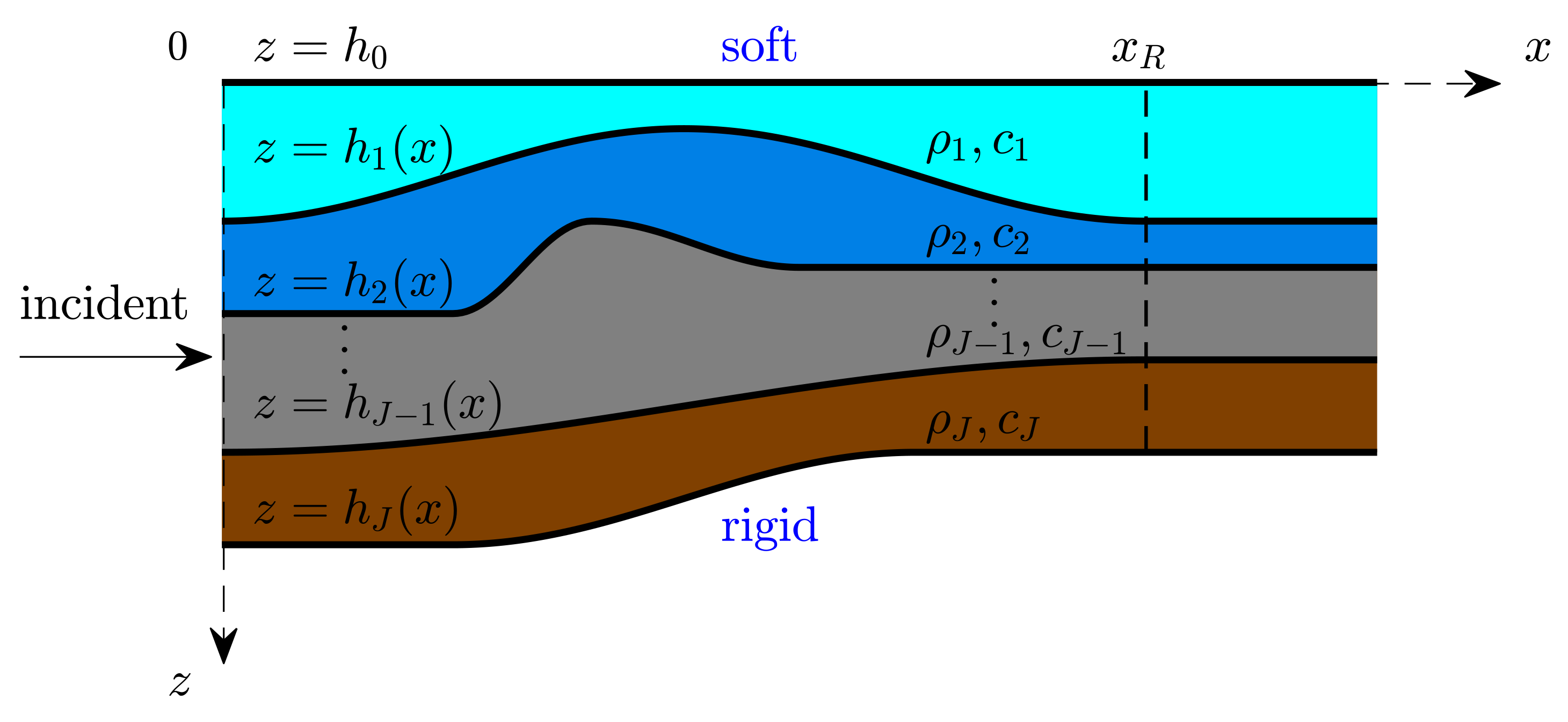
2.1. Two-Dimensional Two-Way Coupled Mode Equations
2.2. Two-Dimensional One-Way Coupled Mode Equations
2.3. Optimal Incident Waves for Sound Focusing
3. Numerical Results
4. Application to Waveguides with Penetrable Infinite Half Space and Internal Wave
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Interface Matrices D and E
Appendix B. Energy Conservation
Appendix C. Radiation Condition
References
- Pierce, A.D. Extension of the Method of Normal Modes to Sound Propagation in an Almost-Stratified Medium. J. Acoust. Soc. Am. 1965, 37, 19–27. [Google Scholar] [CrossRef]
- Milder, D.M. Ray and Wave Invariants for SOFAR Channel Propagation. J. Acoust. Soc. Am. 1969, 46, 1259–1263. [Google Scholar] [CrossRef]
- Evans, R.B. A coupled mode solution for acoustic propagation in a waveguide with stepwise depth variations of a penetrable bottom. J. Acoust. Soc. Am. 1983, 74, 188–195. [Google Scholar] [CrossRef]
- Luo, W.; Schmidt, H. Three-dimensional propagation and scattering around a conical seamount. J. Acoust. Soc. Am. 2009, 125, 52–65. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Belibassakis, K.A.; Athanassoulis, G.A.; Papathanasiou, T.K.; Filopoulos, S.P.; Markolefas, S. Acoustic wave propagation in inhomogeneous, layered waveguides based on modal expansions and hp-FEM. Wave Motion 2014, 51, 1021–1043. [Google Scholar] [CrossRef]
- Rutherford, S.R.; Hawker, K.E. Consistent coupled mode theory of sound propagation for a class of nonseparable problems. J. Acoust. Soc. Am. 1981, 70, 554–564. [Google Scholar] [CrossRef]
- Fawcett, J.A. A derivation of the differential equations of coupled-mode propagation. J. Acoust. Soc. Am. 1992, 92, 290–295. [Google Scholar] [CrossRef]
- Abawi, A.T. An energy-conserving one-way coupled mode propagation model. J. Acoust. Soc. Am. 2002, 111, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Pierce, A.D. Augmented adiabatic mode theory for upslope propagation from a point source in variable-depth shallow water overlying a fluid bottom. J. Acoust. Soc. Am. 1983, 74, 1837–1847. [Google Scholar] [CrossRef]
- Chiu, C.S.; Miller, J.H.; Lynch, J.F. Forward coupled-mode propagation modeling for coastal acoustic tomography. J. Acoust. Soc. Am. 1996, 99, 793–802. [Google Scholar] [CrossRef]
- Pagneux, V. Multimodal admittance method in waveguides and singularity behavior at high frequencies. J. Comput. Appl. Math. 2010, 234, 1834–1841. [Google Scholar] [CrossRef]
- Pagneux, V.; Amir, N.; Kergomard, J. A study of wave propagation in varying cross-section waveguides by modal decomposition. Part I. Theory and validation. J. Acoust. Soc. Am. 1996, 100, 2034–2048. [Google Scholar] [CrossRef]
- Félix, S.; Pagneux, V. Sound propagation in rigid bends: A multimodal approach. J. Acoust. Soc. Am. 2001, 110, 1329–1337. [Google Scholar] [CrossRef]
- Félix, S.; Pagneux, V. Multimodal analysis of acoustic propagation in three-dimensional bends. Wave Motion 2002, 36, 157–168. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q. A coupled mode method for sound propagation in range-dependent waveguides. Acta Phys. Sin. 2021, in press. [Google Scholar] [CrossRef]
- Tsouvalas, A. Underwater Noise Emission Due to Offshore Pile Installation: A Review. Energies 2020, 13, 3037. [Google Scholar] [CrossRef]
- Westwood, E.K.; Koch, R.A. Elimination of branch cuts from the normal-mode solution using gradient half spaces. J. Acoust. Soc. Am. 1999, 106, 2513–2523. [Google Scholar] [CrossRef]
- Guo, W.; Yang, D.S. Sound focusing in inhomogeneous waveguides. Acta Phys. Sin. 2020, 69, 074301. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Guo, W. Sound propagation in inhomogeneous waveguides with sound-speed profiles using the multimodal admittance method. Chin. Phys. B 2020, 29, 14303. [Google Scholar] [CrossRef]
- Athanassoulis, G.A.; Belibassakis, K.A. Rapidly-Convergent Local-Mode Representations for Wave Propagation and Scattering in Curved-Boundary Waveguides; Springer: Berlin/Heidelberg, Germany, 2003; pp. 451–456. [Google Scholar]
- Maurel, A.; Mercier, J.F.; Pagneux, V. Improved multimodal admittance method in varying cross section waveguides. Proc. R. Soc. A 2014, 470, 20130448. [Google Scholar] [CrossRef]
- Mercier, J.F.; Maurel, A. Improved multimodal method for the acoustic propagation in waveguides with a wall impedance and a uniform flow. Proc. R. Soc. A 2016, 472, 20160094. [Google Scholar] [CrossRef]
- Bi, W.; Pagneux, V.; Lafarge, D.; Aurégan, Y. An improved multimodal method for sound propagation in nonuniform lined ducts. J. Acoust. Soc. Am. 2007, 122, 280–290. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.Y.; McLaughlin, J. The Riccati method for the Helmholtz equation. J. Acoust. Soc. Am. 1996, 100, 1432–1446. [Google Scholar] [CrossRef]
- Iserles, A.; Marthinsen, A.; Nørsett, S.P. On the Implementation of the Method of Magnus Series for Linear Differential Equations. BIT Numer. Math. 1999, 39, 281–304. [Google Scholar] [CrossRef]
- Maurel, A.; Mercier, J.F.; Félix, S. Wave propagation through penetrable scatterers in a waveguide and through a penetrable grating. J. Acoust. Soc. Am. 2014, 135, 165–174. [Google Scholar] [CrossRef]
- Pagneux, V.; Maurel, A. Lamb wave propagation in inhomogeneous elastic waveguides. Proc. R. Soc. A 2002, 458, 1913–1930. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Metrikine, A.V. Noise reduction by the application of an air-bubble curtain in offshore pile driving. J. Sound Vib. 2016, 371, 150–170. [Google Scholar] [CrossRef]
- Doc, J.B.; Félix, S.; Lihoreau, B. Coarse-grid computation of the one-way propagation of coupled modes in a varying cross-section waveguide. J. Acoust. Soc. Am. 2013, 133, 2528–2532. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Tsouvalas, A.; Stampoultzoglou, T.; Metrikine, A. A fast computational model for near- and far-field noise prediction due to offshore pile driving. J. Acoust. Soc. Am. 2021, 149, 1772–1790. [Google Scholar] [CrossRef]
- Knobles, D.P.; Stotts, S.A.; Koch, R.A. Low frequency coupled mode sound propagation over a continental shelf. J. Acoust. Soc. Am. 2003, 113, 781–787. [Google Scholar] [CrossRef] [PubMed]
- Shmelev, A.A.; Lynch, J.F.; Lin, Y.T.; Schmidt, H. Three-dimensional coupled mode analysis of internal-wave acoustic ducts. J. Acoust. Soc. Am. 2014, 135, 2497–2512. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, Q. Coupled Mode Sound Propagation in Inhomogeneous Stratified Waveguides. Appl. Sci. 2021, 11, 3957. https://doi.org/10.3390/app11093957
Liu J, Li Q. Coupled Mode Sound Propagation in Inhomogeneous Stratified Waveguides. Applied Sciences. 2021; 11(9):3957. https://doi.org/10.3390/app11093957
Chicago/Turabian StyleLiu, Juan, and Qi Li. 2021. "Coupled Mode Sound Propagation in Inhomogeneous Stratified Waveguides" Applied Sciences 11, no. 9: 3957. https://doi.org/10.3390/app11093957
APA StyleLiu, J., & Li, Q. (2021). Coupled Mode Sound Propagation in Inhomogeneous Stratified Waveguides. Applied Sciences, 11(9), 3957. https://doi.org/10.3390/app11093957





