Multi-Scale Convolutional Recurrent Neural Network for Bearing Fault Detection in Noisy Manufacturing Environments
Abstract
:1. Introduction
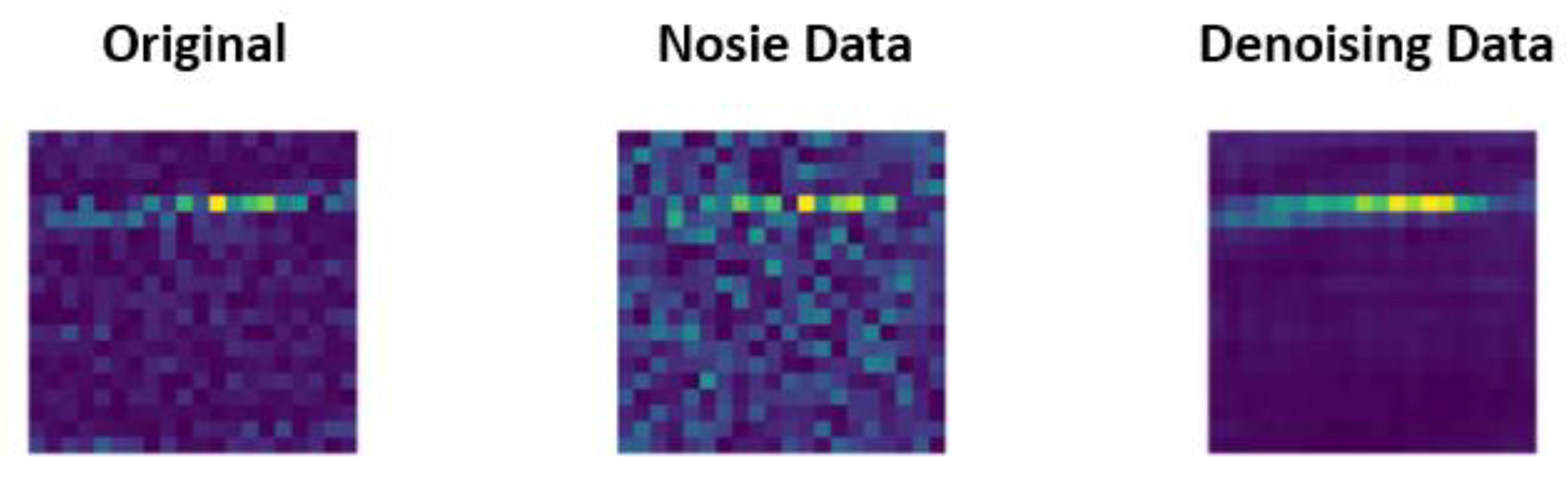
- The bearing vibration signal of strong noise in an environment such as the vibration signal extracted from an actual site can be removed through a DAE. In addition, it can be extracted by highlighting the characteristics of the vibration signal of the bearing.
- A multi-scale convolution neural network (MS-CNN) can effectively extend the extraction range of bearing vibration signals and extract complex spatial features. In addition, temporal features can be extracted using a recurrent neural network (RNN) with better temporal awareness. The temporal and spatial characteristics of bearing vibration signals can be effectively extracted through the MS-CRNN.
2. Background and Related Work
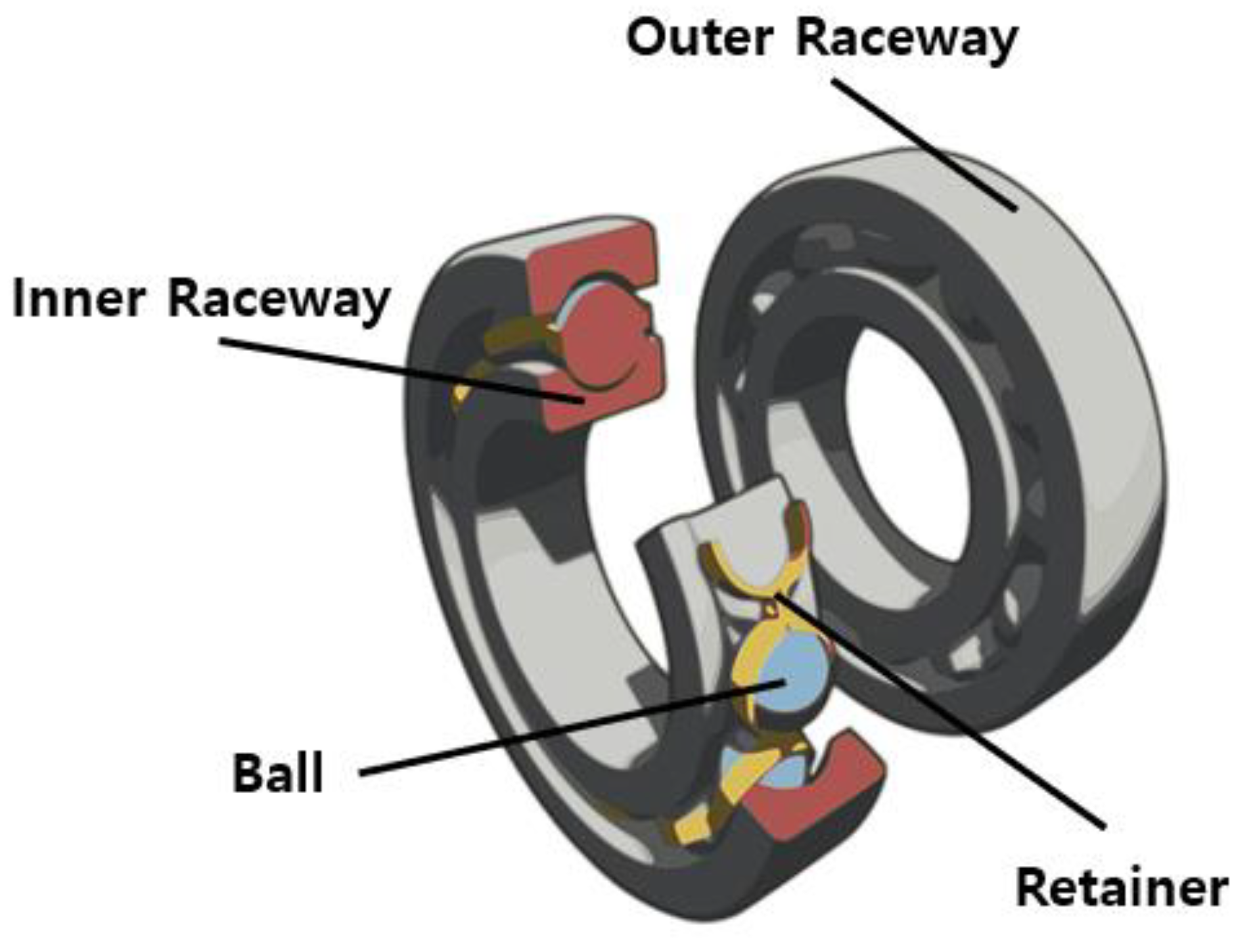
2.1. Defective Rolling Bearing
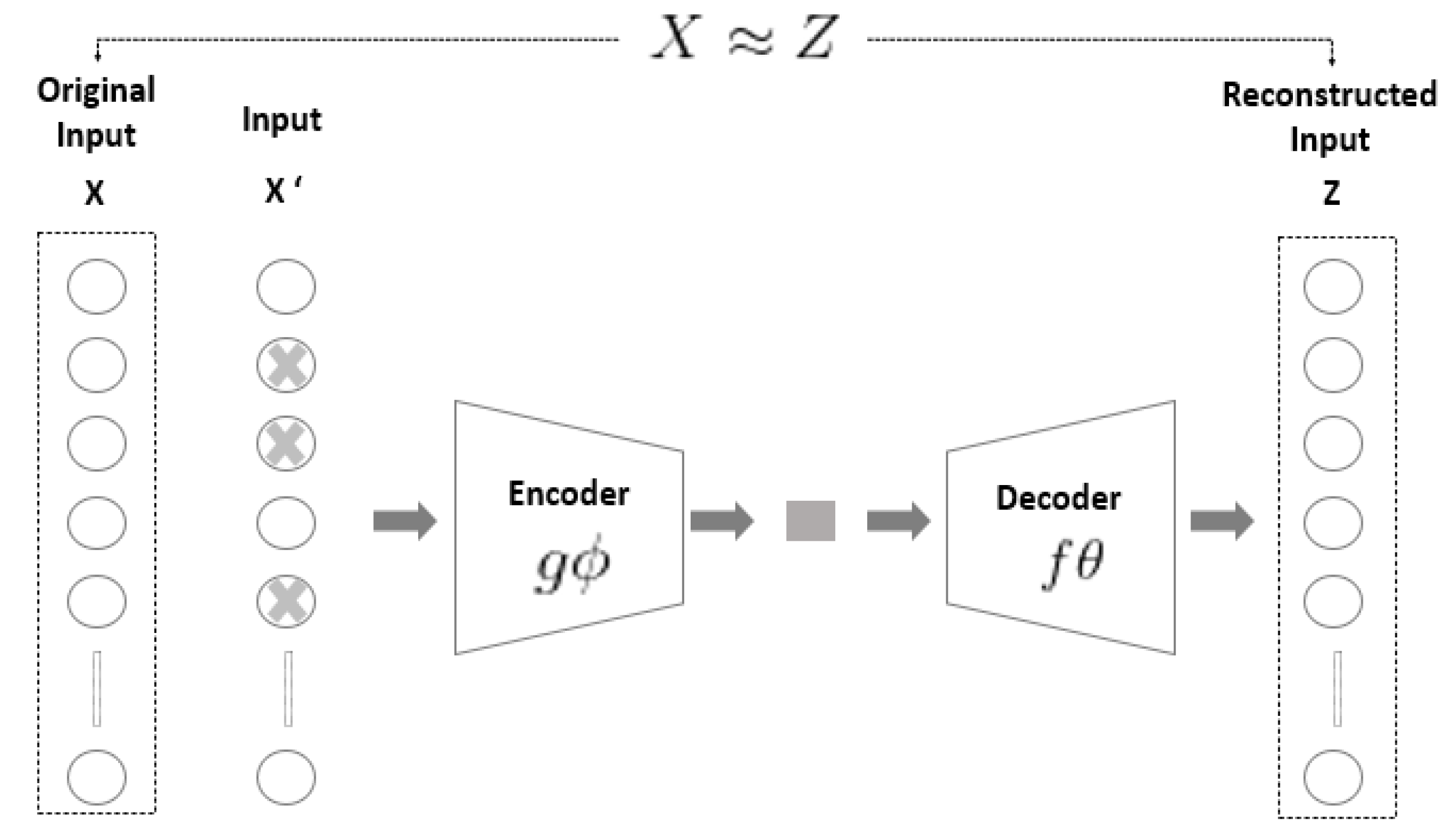
2.2. Denoising Autoencoder (DAE)
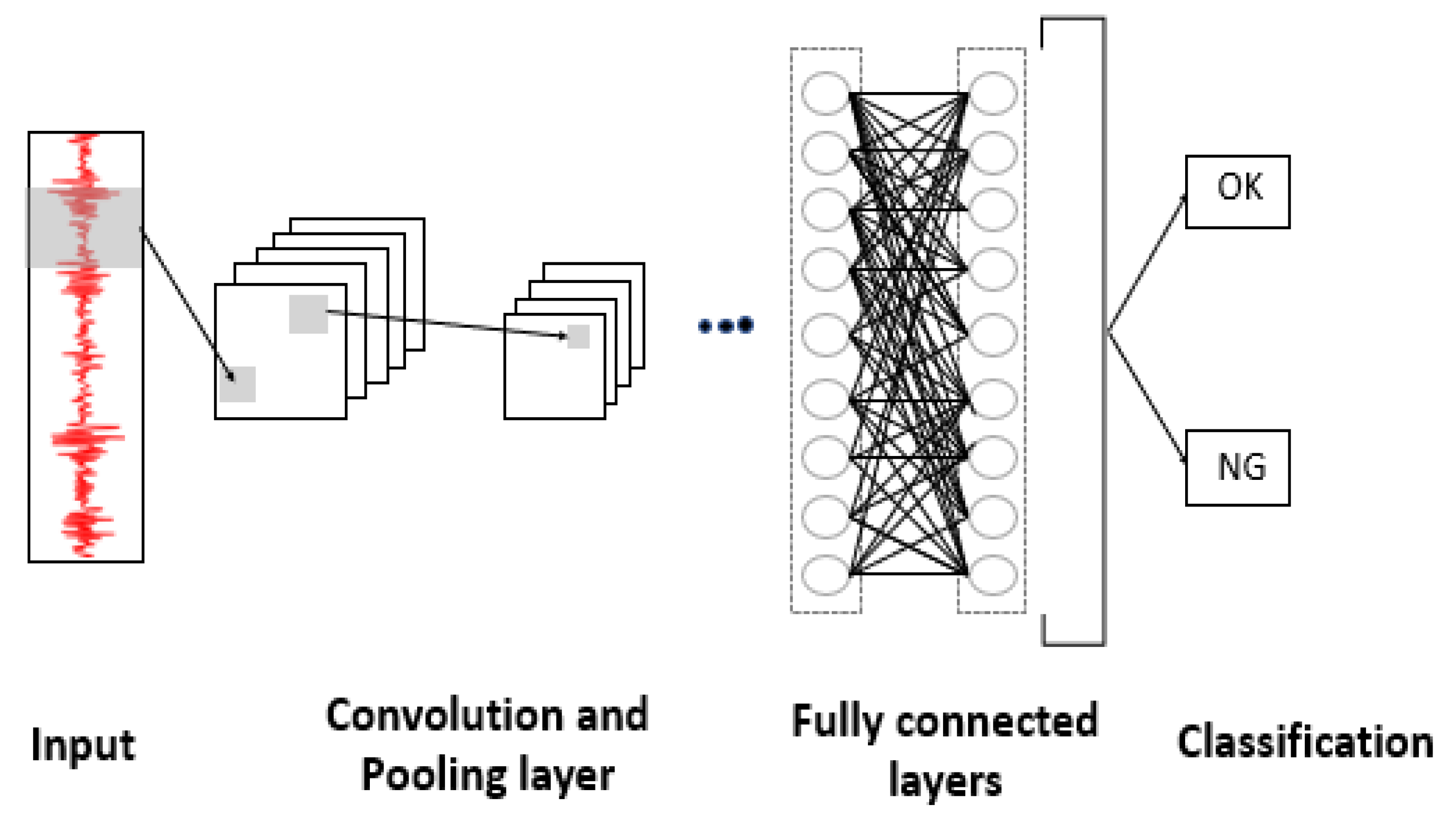
2.3. Convolution Neural Network (CNN)
2.4. Multi-Scale Convolution Neural Network (MS-CNN)
2.5. Long Short-Term Memory (LSTM)
3. MS-CRNN for DAE-Based Noise Removal and Fault Detection
3.1. DAE for Denoising
3.2. MS-CRNN for Bearing Fault Detection
4. Experiment and Result Analysis
4.1. Experiment Environment
4.2. Evaluation Metrics
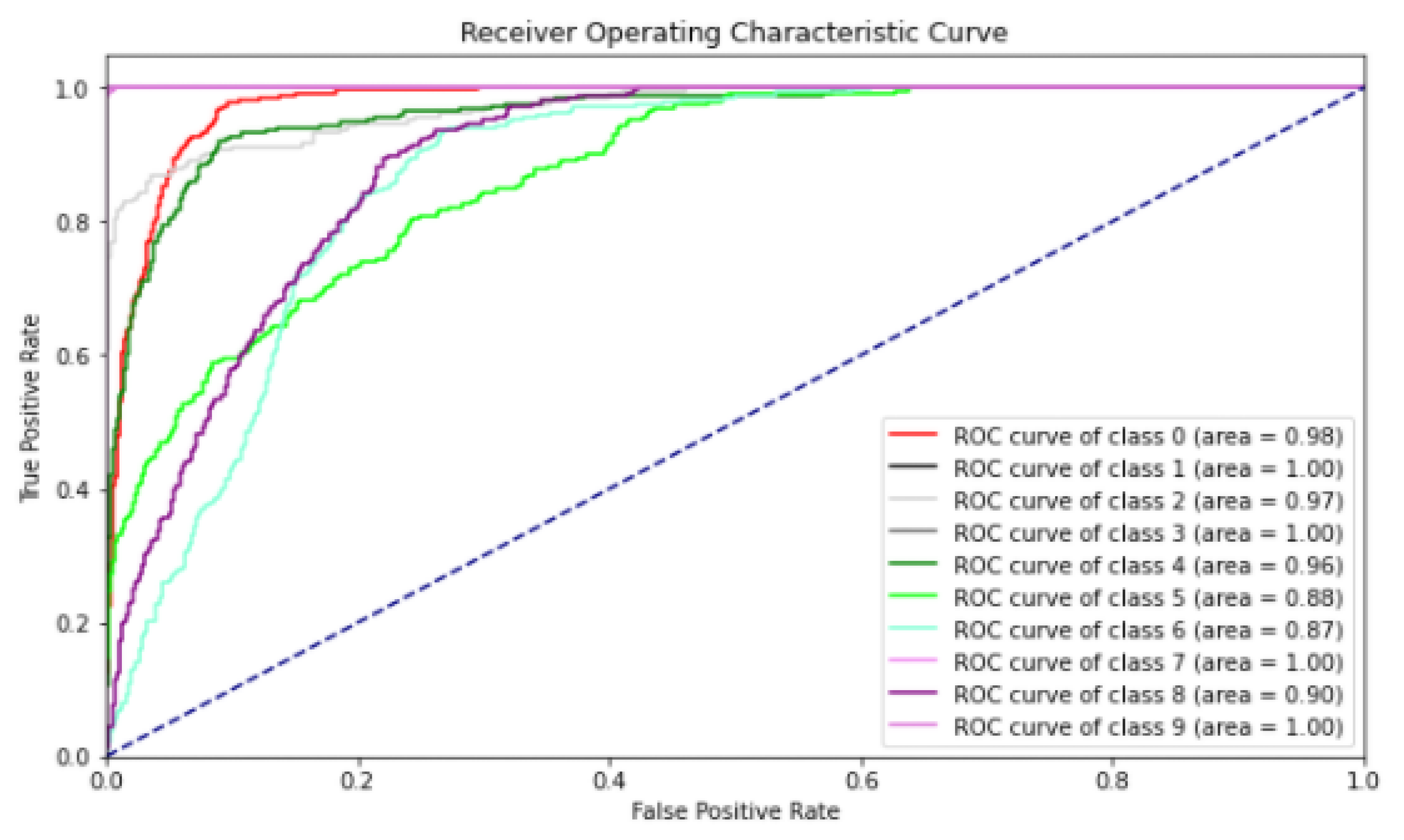
4.3. Experiment and Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dombrowski, U.; Wagner, T. Mental strain as field of action in the 4th industrial revolution. Procedia CIRP 2014, 17, 100–105. [Google Scholar] [CrossRef] [Green Version]
- Abramovici, M.; Göbel, J.C.; Neges, M. Smart engineering as enabler for the 4th industrial revolution. In Integrated Systems: Innovations and Applications; Springer: Cham, Switzerland, 2015; pp. 163–170. [Google Scholar]
- Nelson Raja, P.; Kannan, S.M.; Jeyabalan, V. Overall line effectiveness—A performance evaluation index of a manufacturing system. Int. J. Product. Qual. Manag. 2010, 5, 38–59. [Google Scholar] [CrossRef]
- Hashemian, H.M. State-of-the-art predictive maintenance techniques. IEEE Trans. Instrum. Meas. 2010, 60, 226–236. [Google Scholar] [CrossRef]
- Selcuk, S. Predictive maintenance, its implementation and latest trends. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 1670–1679. [Google Scholar] [CrossRef]
- Kotzalas, M.N.; Harris, T.A. Fatigue failure progression in ball bearings. J. Trib. 2001, 123, 238–242. [Google Scholar] [CrossRef]
- El Laithy, M.; Wang, L.; Harvey, T.J.; Vierneusel, B.; Correns, M.; Blass, T. Further understanding of rolling contact fatigue in rolling element bearings—A review. Tribol. Int. 2019, 140, 105849. [Google Scholar] [CrossRef]
- Zarei, J.; Poshtan, J. Bearing fault detection using wavelet packet transform of induction motor stator current. Tribol. Int. 2007, 40, 763–769. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Wu, T.; Guo, S.; Shao, T.; Malekian, R.; Li, Z. Development and trend of condition monitoring and fault diagnosis of multi-sensors information fusion for rolling bearings: A review. Int. J. Adv. Manuf. Technol. 2018, 96, 803–819. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Wang, H.; Liu, P.; Huang, S.; Fan, P. A sparse stacked denoising autoencoder with optimized transfer learning applied to the fault diagnosis of rolling bearings. Measurement 2019, 146, 305–314. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Wang, S.; Li, W.; Sarkodie-Gyan, T.; Feng, S. A hybrid deep-learning model for fault diagnosis of rolling bearings. Measurement 2021, 169, 108502. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Zhao, D.; Gelman, L.; Chu, F.; Ball, A. Novel method for vibration sensor-based instantaneous defect frequency estimation for rolling bearings under non-stationary conditions. Sensors 2020, 20, 5201. [Google Scholar] [CrossRef]
- Song, L.; Wang, H.; Chen, P. Vibration-based intelligent fault diagnosis for roller bearings in low-speed rotating machinery. IEEE Trans. Instrum. Meas. 2018, 67, 1887–1899. [Google Scholar] [CrossRef]
- Hao, Y.; Song, L.; Cui, L.; Wang, H. A three-dimensional geometric features-based SCA algorithm for compound faults diagnosis. Measurement 2019, 134, 480–491. [Google Scholar] [CrossRef]
- Shi, H.T.; Bai, X.T.; Zhang, K.; Wu, Y.H.; Yue, G.D. Influence of uneven loading condition on the sound radiation of starved lubricated full ceramic ball bearings. J. Sound Vib. 2019, 461, 114910. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset with Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Zhang, X.; Ye, B.; Wang, X. Aero-engine bearing fault detection: A clustering low-rank approach. Mech. Syst. Signal Process. 2020, 138, 106529. [Google Scholar] [CrossRef]
- Nivesrangsan, P.; Jantarajirojkul, D. Bearing fault monitoring by comparison with main bearing frequency components using vibration signal. In Proceedings of the 2018 5th International Conference on Business and Industrial Research (ICBIR), Bangkok, Thailand, 17–18 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 292–296. [Google Scholar]
- Ozcan, I.H.; Eren, L.; Ince, T.; Bilir, B.; Askar, M. Comparison of time-domain and time-scale data in bearing fault detection. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27–29 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 143–146. [Google Scholar]
- Shijie, S.; Kai, W.; Xuliang, Q.; Dan, Z.; Xueqing, D.; Jiale, S. Investigation on Bearing Weak Fault Diagnosis under Colored Noise. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5097–5101. [Google Scholar]
- Shi, H.; Guo, L.; Tan, S.; Bai, X. Rolling bearing initial fault detection using long short-term memory recurrent network. IEEE Access 2019, 7, 171559–171569. [Google Scholar] [CrossRef]
- Li, C.; Zhang, W.E.I.; Peng, G.; Liu, S. Bearing fault diagnosis using fully-connected winner-take-all autoencoder. IEEE Access 2017, 6, 6103–6115. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Mayes, I.W.; Davies, W.G.R. Analysis of the Response of a Multi-Rotor-Bearing System Containing a Transverse Crack in a Rotor. J. Vib. Acoust. Stress Reliab. 1984, 106, 139–145. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fournier, Q.; Aloise, D. Empirical comparison between autoencoders and traditional dimensionality reduction methods. In Proceedings of the 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Sardinia, Italy, 3–5 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 211–214. [Google Scholar]
- Majeed, S.; Mansoor, Y.; Qabil, S.; Majeed, F.; Khan, B. Comparative analysis of the denoising effect of unstructured vs. convolutional autoencoders. In Proceedings of the 2020 International Conference on Emerging Trends in Smart Technologies (ICETST), Karachi, Pakistan, 26–27 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Lo, S.C.B.; Chan, H.P.; Lin, J.S.; Li, H.; Freedman, M.T.; Mun, S.K. Artificial convolution neural network for medical image pattern recognition. Neural Netw. 1995, 8, 1201–1214. [Google Scholar] [CrossRef]
- Mishkin, D.; Sergievskiy, N.; Matas, J. Systematic evaluation of convolution neural network advances on the imagenet. Comput. Vis. Image Underst. 2017, 161, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Liu, T.; Fang, S.; Zhao, Y.; Wang, P.; Zhang, J. Implementation of training convolutional neural networks. arXiv 2015, arXiv:1506.01195. [Google Scholar]
- Yu, D.; Wang, H.; Chen, P.; Wei, Z. Mixed pooling for convolutional neural networks. In International Conference on Rough Sets and Knowledge Technology; Springer: Cham, Switzerland, 2014; pp. 364–375. [Google Scholar]
- Traore, B.B.; Kamsu-Foguem, B.; Tangara, F. Deep convolution neural network for image recognition. Ecol. Inform. 2018, 48, 257–268. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Yu, Y. Visual saliency detection based on multiscale deep CNN features. IEEE Trans. Image Process. 2016, 25, 5012–5024. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhuang, J.; Duan, L.; Cheng, W. A multi-scale convolution neural network for featureless fault diagnosis. In 2016 International Symposium on Flexible Automation (ISFA); IEEE: Piscataway, NJ, USA, 2016; pp. 65–70. [Google Scholar]
- Koutnik, J.; Greff, K.; Gomez, F.; Schmidhuber, J. A clockwork rnn. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; PMLR: New York, NY, USA, 2014; pp. 1863–1871. [Google Scholar]
- Williams, G.; Baxter, R.; He, H.; Hawkins, S.; Gu, L. A comparative study of RNN for outlier detection in data mining. In Proceedings of the 2002 IEEE International Conference on Data Mining, Maebashi City, Japan, 9–12 December 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 709–712. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks: ICANN’99, Edinburgh, UK, 7–10 September 1999; pp. 850–855. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: Piscataway, NJ, USA, 2016; Volume 28, pp. 2222–2232. [Google Scholar]
- Bearing Data Center Seeded Fault Test Data. Available online: https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 28 October 2016).




| Layer | Output Size |
|---|---|
| Conv2D | 20 × 20 |
| BatchNormalization | 20 × 20 |
| MaxPooling | 10 × 10 |
| Conv2D | 10 × 10 |
| MaxPooling | 5 × 5 |
| Conv2D | 5 × 5 |
| UpSampling2D | 10 × 10 |
| BatchNormalization | 10 × 10 |
| Conv2D | 10 × 10 |
| UpSampling2D | 20 × 20 |
| Conv2D | 20 × 20 |
| Layer Name | Output Size | Network | Connected to |
|---|---|---|---|
| Input_Layer | (20 × 20) | Conv2D | |
| 1Conv_Layer1 | (20 × 20) | Conv2D, kernel size = 1 × 1 | Input_Layer |
| 1Pool_Layer1 | (10 × 10) | Maxpooling2D size = 2 × 2 | 1C_L1 |
| 2Conv_Layer1 | (20 × 20) | Conv2D, kernel size = 3 × 3 | Input_Layer |
| 1Conv_Layer2 | (10 × 10) | Conv2D, kernel size = 1 × 1 | 1P_L1 |
| 2Conv_Layer2 | (20 × 20) | Conv2D, kernel size = 3 × 3 | 2C_L1 |
| 1Pool_Layer2 | (5 × 5) | Maxpooling2D, size = 2 × 2 | 1C_L2 |
| 2Pool_Layer1 | (5 × 5) | Maxpooling2D, size = 4 × 4 | 2C_L2 |
| 1Conv_Layer3 | (5 × 5) | Conv2D, kernel size = 1 × 1 | 1P_L2 |
| 2Conv_Layer3 | (5 × 5) | Conv2D, kernel size = 3 × 3 | 2P_L1 |
| 3Conv_Layer1 | (20 × 20) | Conv2D, kernel size = 5 × 5 | Input_Layer |
| 1Pool_Layer3 | (2 × 2) | Maxpooling2D, size = 2 × 2 | 1C_L3 |
| 2Pool_Layer2 | (2 × 2) | Maxpooling2D, size = 2 × 2 | 2C_L3 |
| 3Pool_Layer1 | (2 × 2) | Maxpooling2D, size = 8 × 8 | 3C_L1 |
| Merge_Layer | (2 × 2) | Concatenate | 1P_L3, 2P_L2, 3P_L1 |
| LSTM_Layer | 64 | LSTM | M_L |
| Flatten_Layer | 120 | - | LSTM_L |
| FC_Layer1 | 64 | Fully connected layer | Flatten_L |
| FC_Layer2 | 32 | Fully connected layer | FC_L1 |
| Output Layer | 10 | Softmax | FC_L2 |
| Hardware Environment | Software Environment |
|---|---|
| CPU: Intel Core i7-8700K, 3.7 GHz, six-core twelve threads, 16 GB GPU: Geforce GTX 1080 Ti | Windows TensorFlow 2.0 framework Python 3.7 |
| Fault Type | Fault Diameters | Class Num |
|---|---|---|
| Normal | - | 0 |
| Ball | 0.007 | 1 |
| Ball | 0.014 | 2 |
| Ball | 0.021 | 3 |
| Inner race | 0.007 | 4 |
| Inner race | 0.014 | 5 |
| Inner race | 0.021 | 6 |
| Outer race | 0.007 | 7 |
| Outer race | 0.014 | 8 |
| Outer race | 0.021 | 9 |
| Model | 1D-CNN | MS-CNN | CNN-LSTM | MS-CRNN |
|---|---|---|---|---|
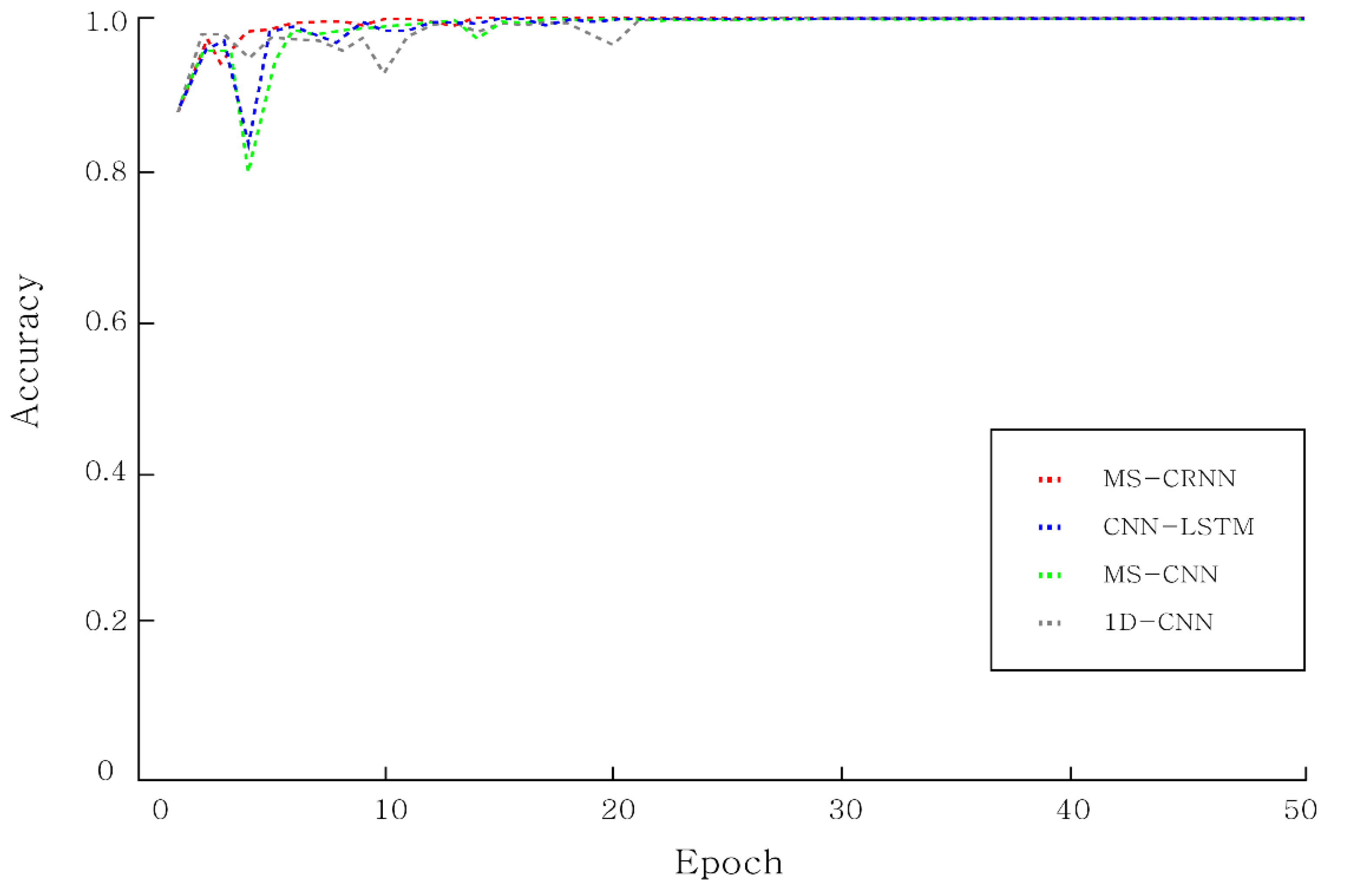
| Accuracy | 99.53% | 99.66% | 99.99% | 100% |
| F1 Score | 99.42% | 99.59% | 99.94% | 100% |
| Model | 1D-CNN | MS-CNN | CNN-LSTM | MS-CRNN |
|---|---|---|---|---|
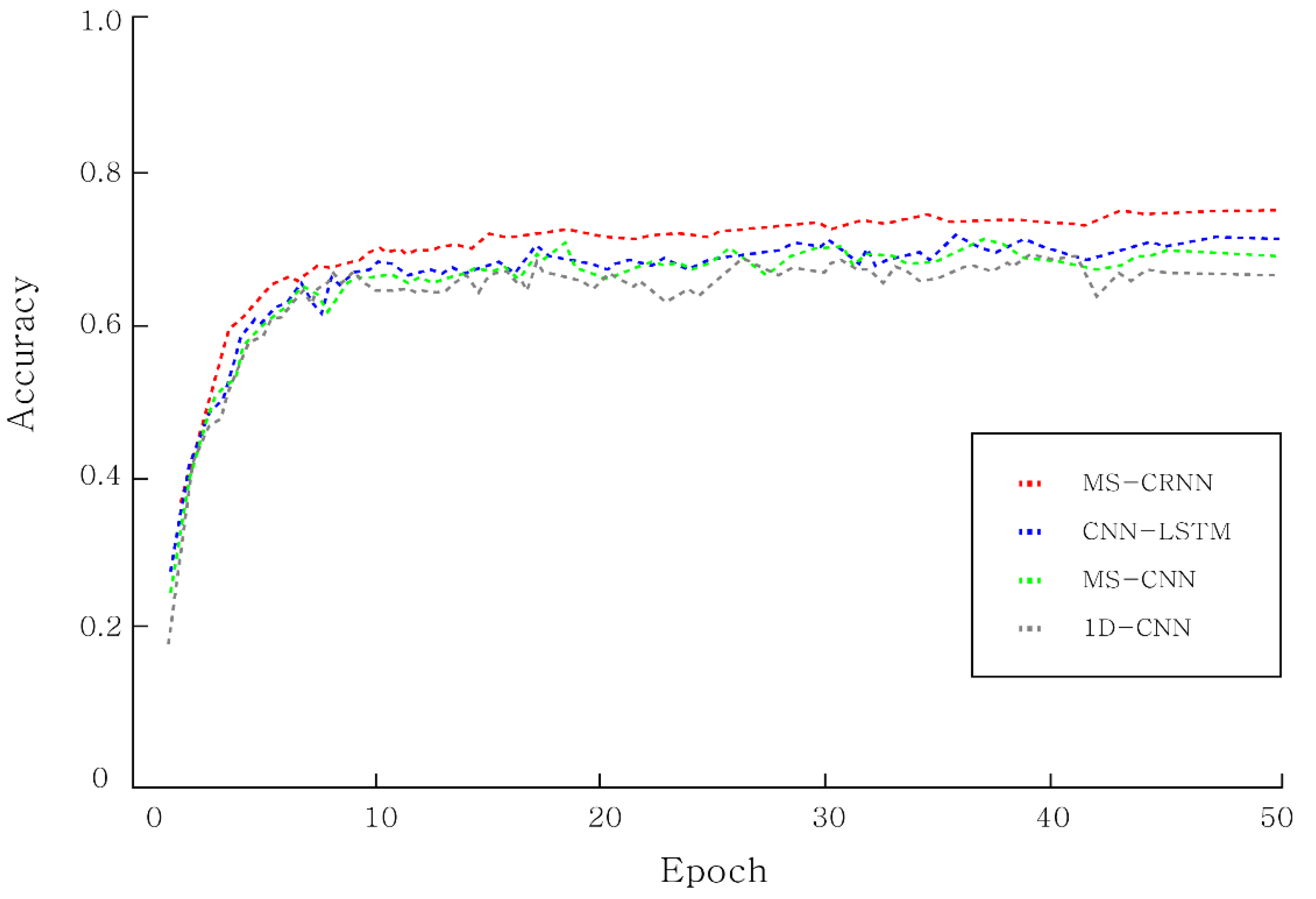
| Accuracy | 65.77% | 68.52% | 70.68% | 76.15% |
| F1 Score | 64.96% | 67.70% | 69.90% | 75.54% |
| Model | DAE + 1D-CNN | DAE + MS-CNN | DAE + CNN-LSTM | DAE + MS-CRNN |
|---|---|---|---|---|
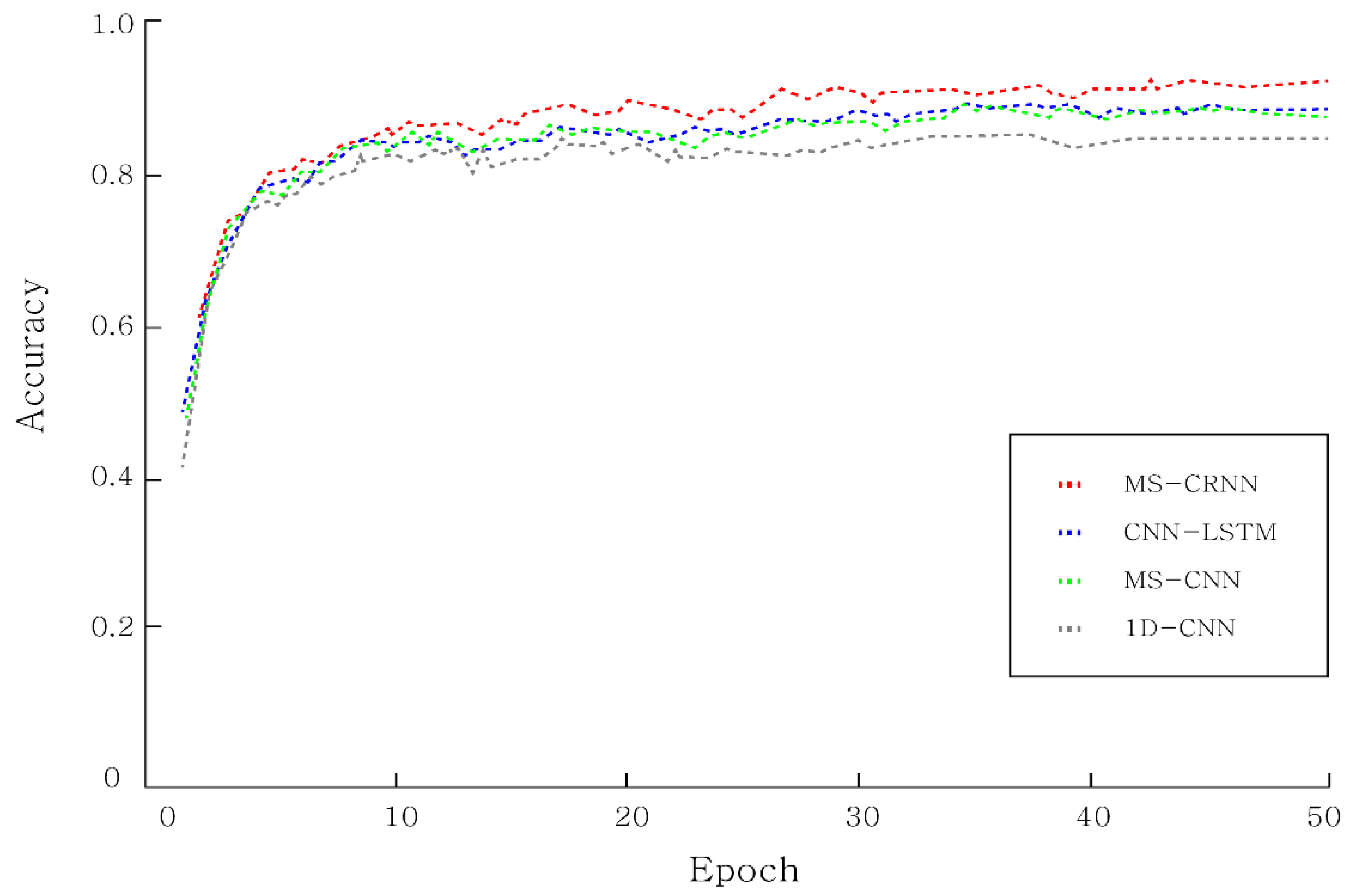
| Accuracy | 83.43% | 86.76% | 87.10% | 92.71% |
| F1 Score | 82.79% | 86.12% | 86.50% | 91.92% |
| Model | DAE + 1D-CNN | DAE + MS-CNN | DAE + CNN-LSTM | DAE + MS-CRNN |
|---|---|---|---|---|
| MCC | 0.81% | 0.86% | 0.87% | 0.91% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, S.; Han, S.; Jeong, J. Multi-Scale Convolutional Recurrent Neural Network for Bearing Fault Detection in Noisy Manufacturing Environments. Appl. Sci. 2021, 11, 3963. https://doi.org/10.3390/app11093963
Oh S, Han S, Jeong J. Multi-Scale Convolutional Recurrent Neural Network for Bearing Fault Detection in Noisy Manufacturing Environments. Applied Sciences. 2021; 11(9):3963. https://doi.org/10.3390/app11093963
Chicago/Turabian StyleOh, Seokju, Seugmin Han, and Jongpil Jeong. 2021. "Multi-Scale Convolutional Recurrent Neural Network for Bearing Fault Detection in Noisy Manufacturing Environments" Applied Sciences 11, no. 9: 3963. https://doi.org/10.3390/app11093963
APA StyleOh, S., Han, S., & Jeong, J. (2021). Multi-Scale Convolutional Recurrent Neural Network for Bearing Fault Detection in Noisy Manufacturing Environments. Applied Sciences, 11(9), 3963. https://doi.org/10.3390/app11093963







