Sliding Balance Control of a Point-Foot Biped Robot Based on a Dual-Objective Convergent Equation
Abstract
:1. Introduction
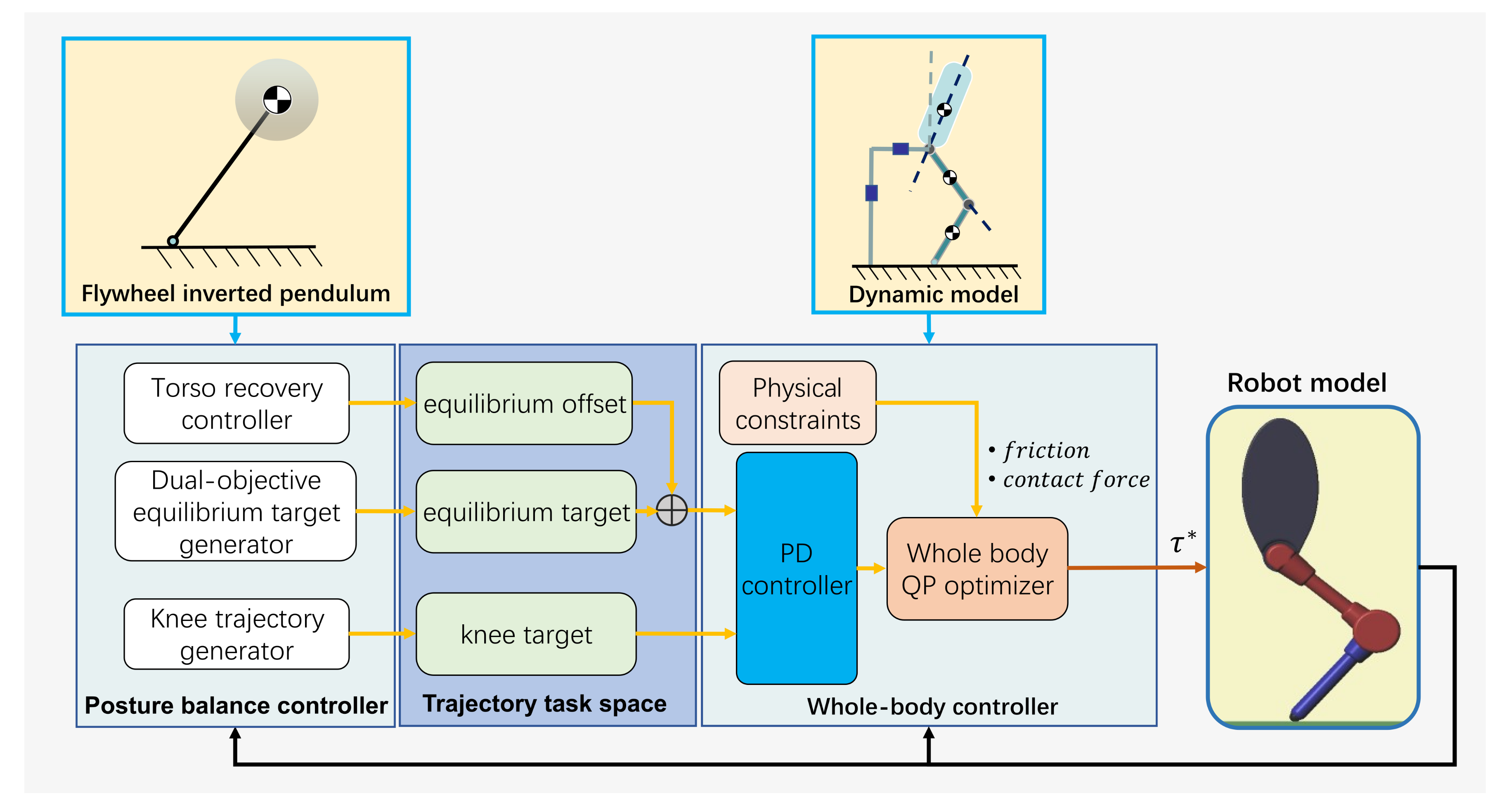
2. Dual-Objective Convergence Equation for the Biped Robot
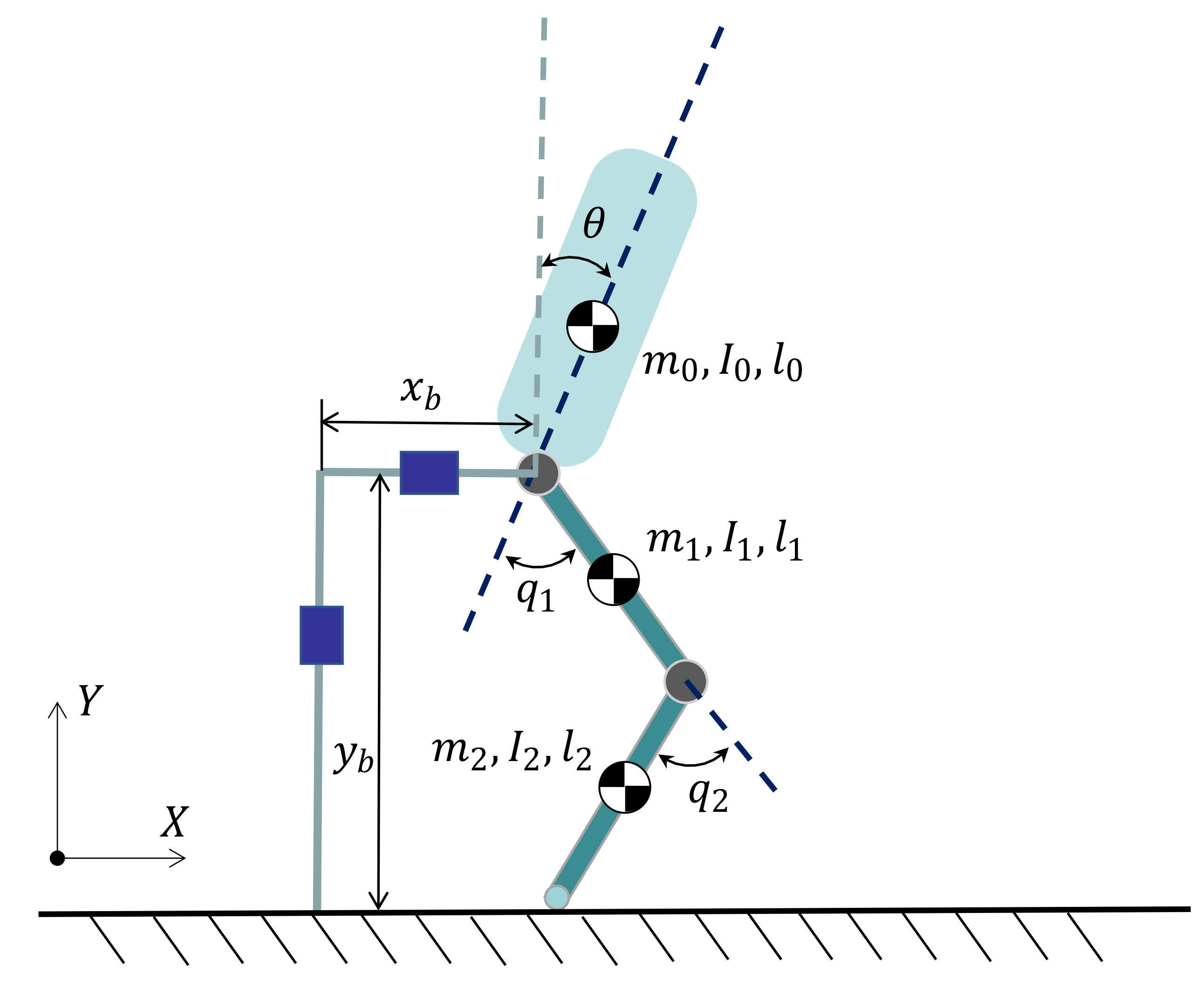
2.1. Model Configuration
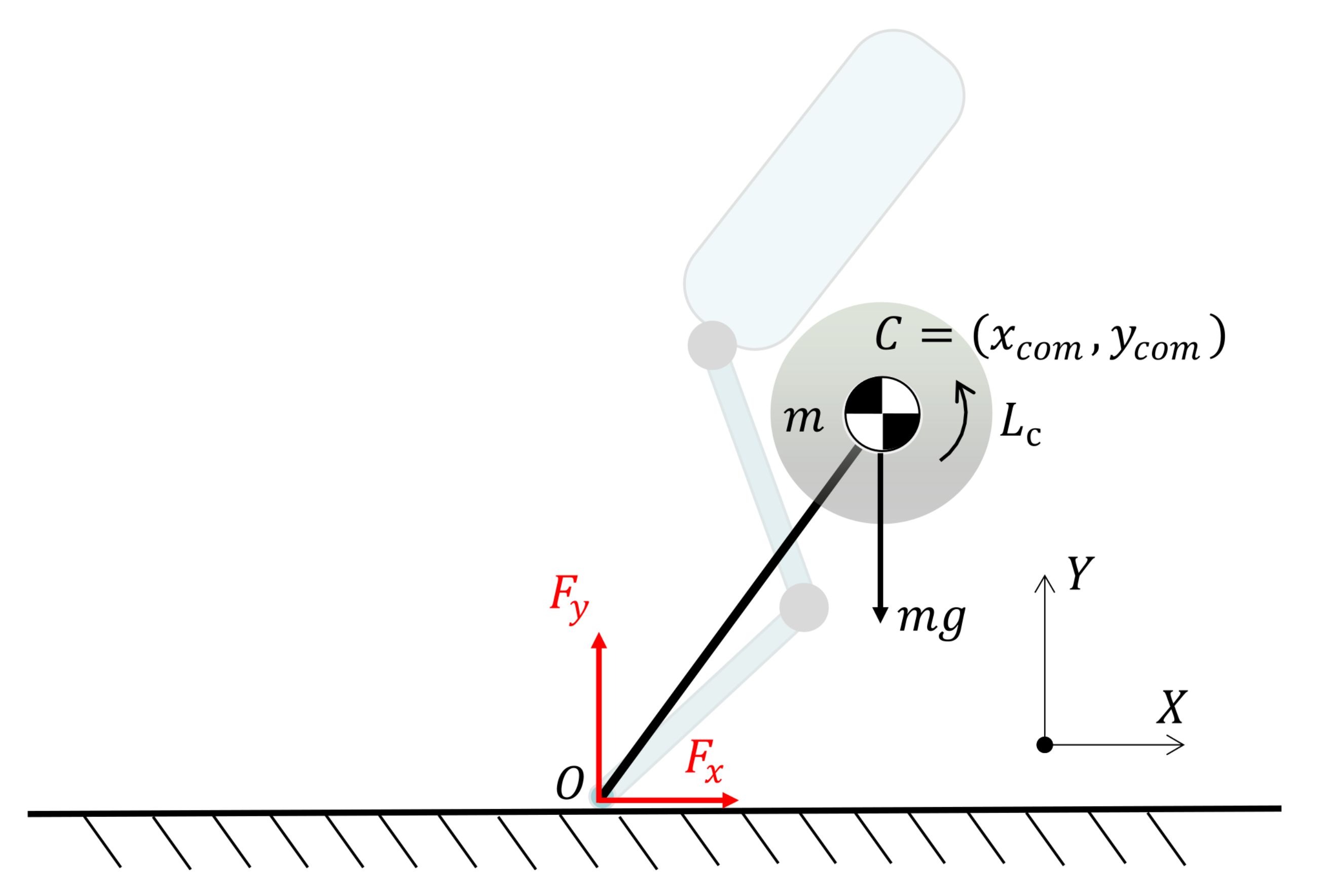
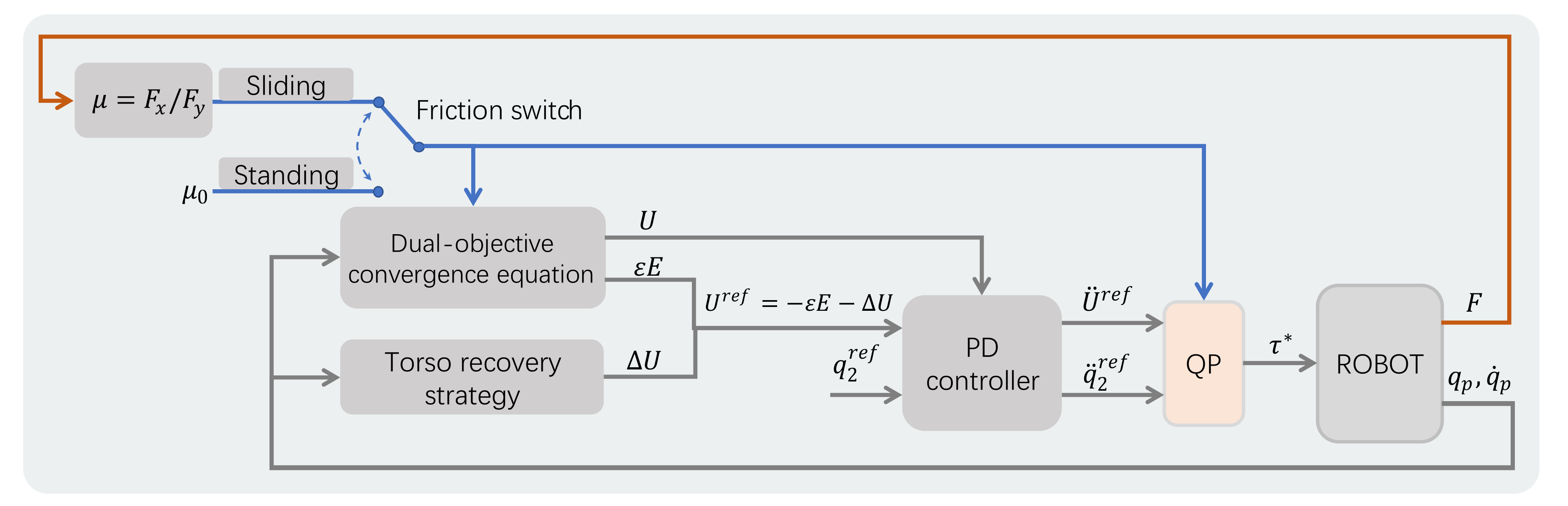
2.2. Dual-Objective Convergence Equation
2.3. Convergence Equation for Sliding
2.4. Convergence Equation for Standing
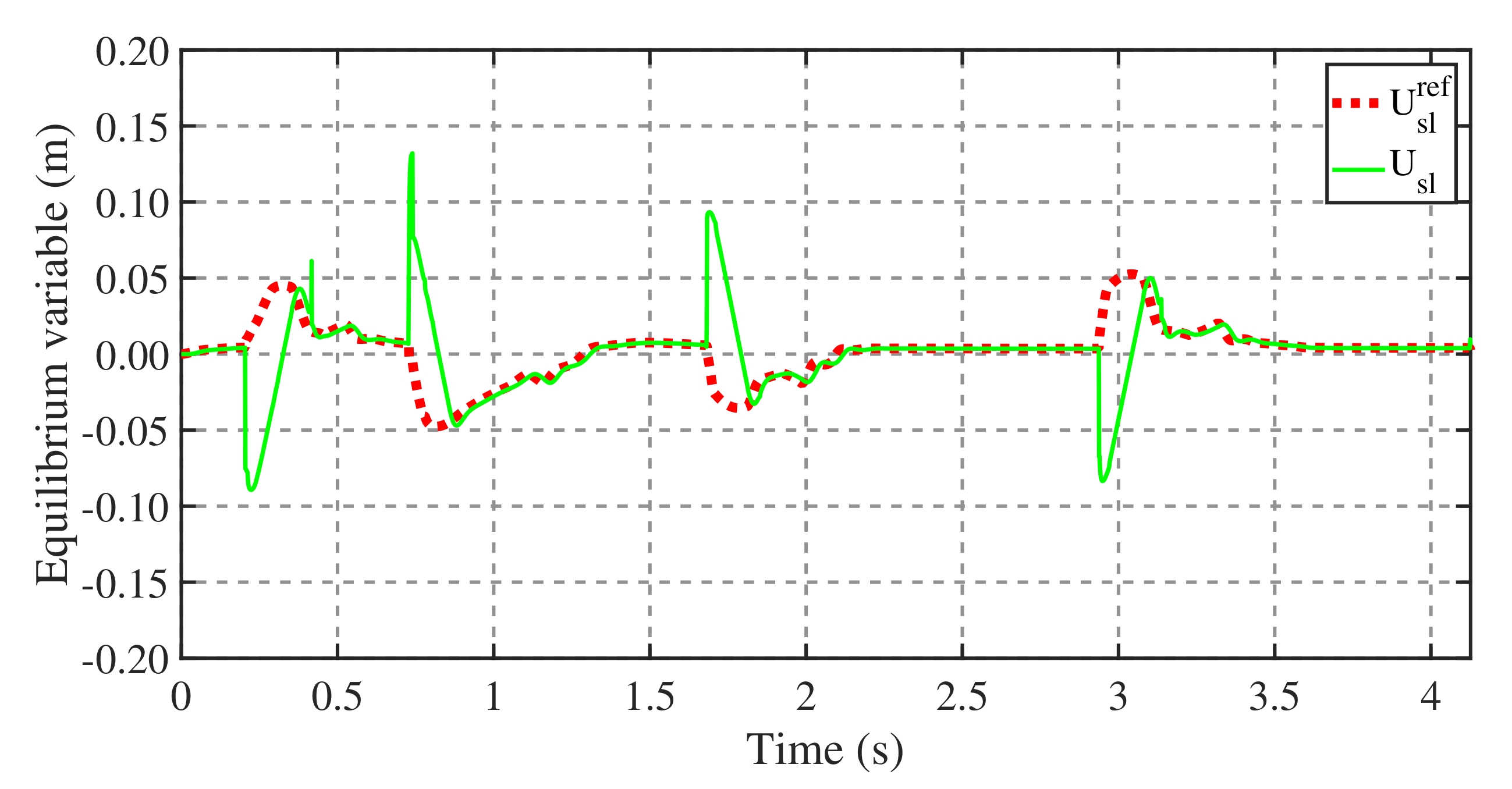
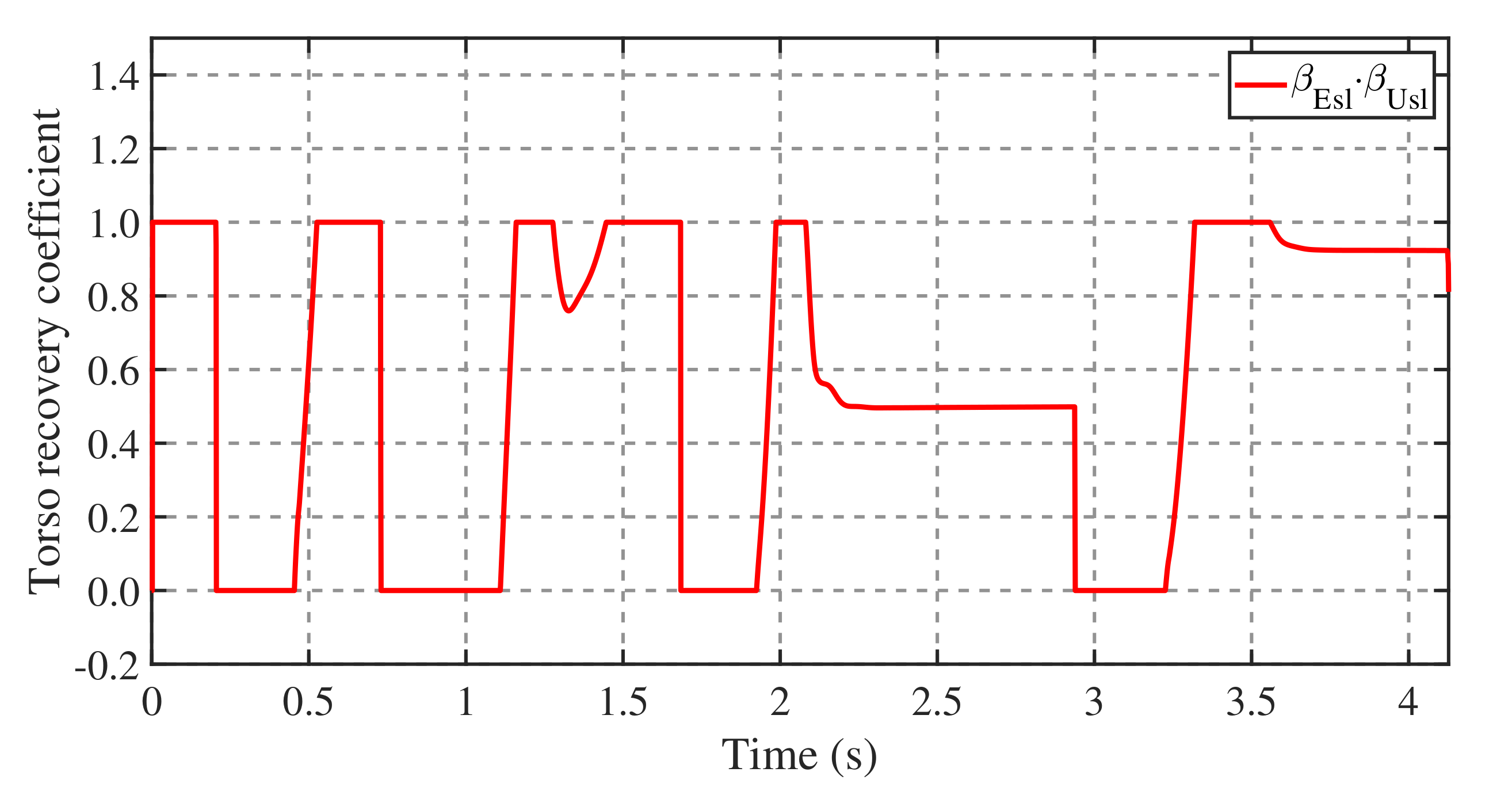
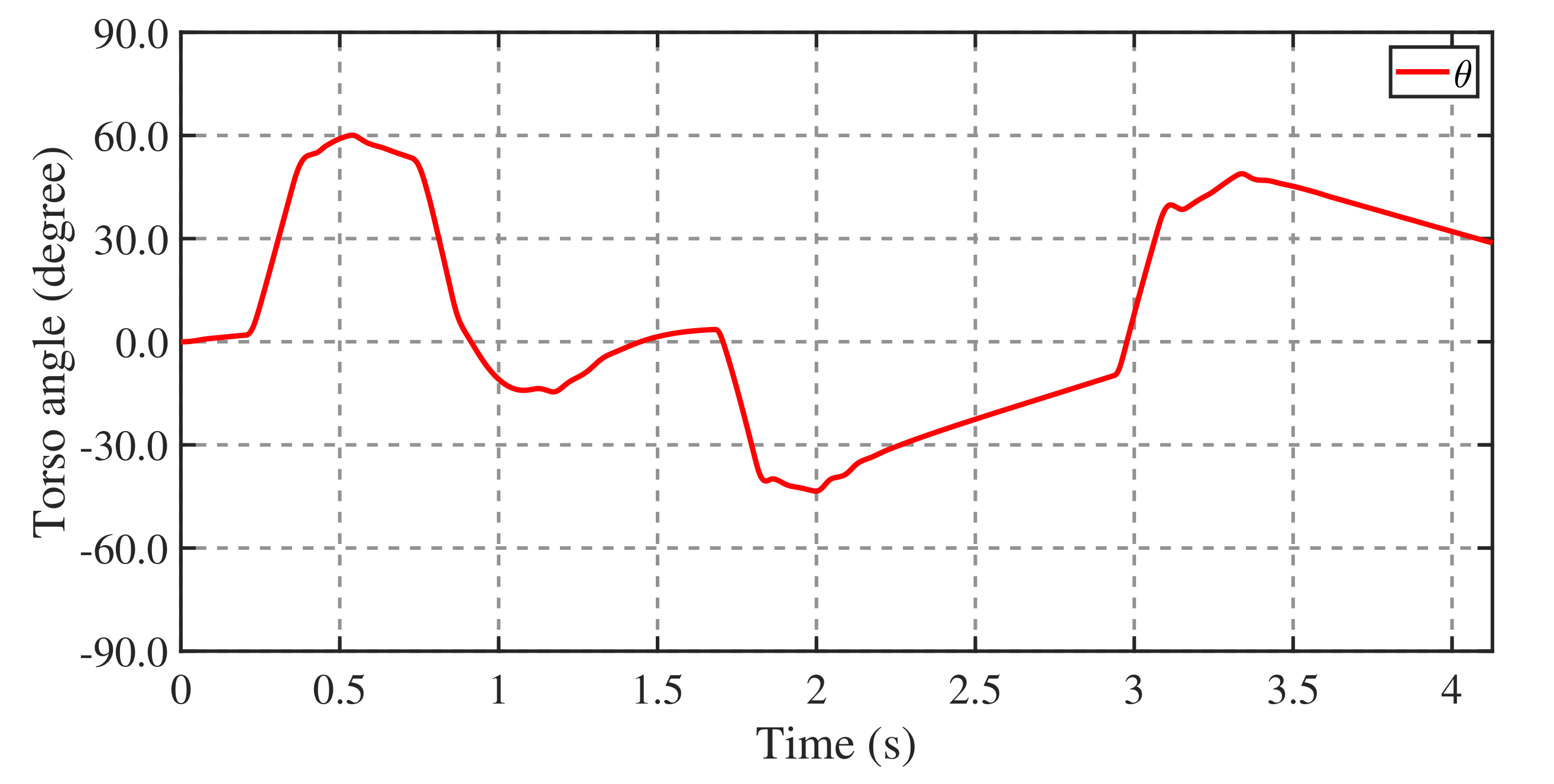
2.5. Torso Recovery Strategy
- First, reduce the difference (i.e., error) between U and so that E begins to converge in the desired way.
- Then, wait for the amplitude of E to gradually decrease to within a permissible range, which indicates that the robot enters a stable state.
- Finally, add an equilibrium offset to the desired equilibrium target according to the feedback states of the torso. Therefore, the angle of the torso gradually recovers to the reference value.
3. QP Controller with Multiple Constraints
3.1. Qp Process
3.2. PD Controller
3.3. Dynamic Constraints
3.4. Contact Constraints
3.4.1. Contact Constraint in Sliding
3.4.2. Contact Constraint in Standing
4. Results
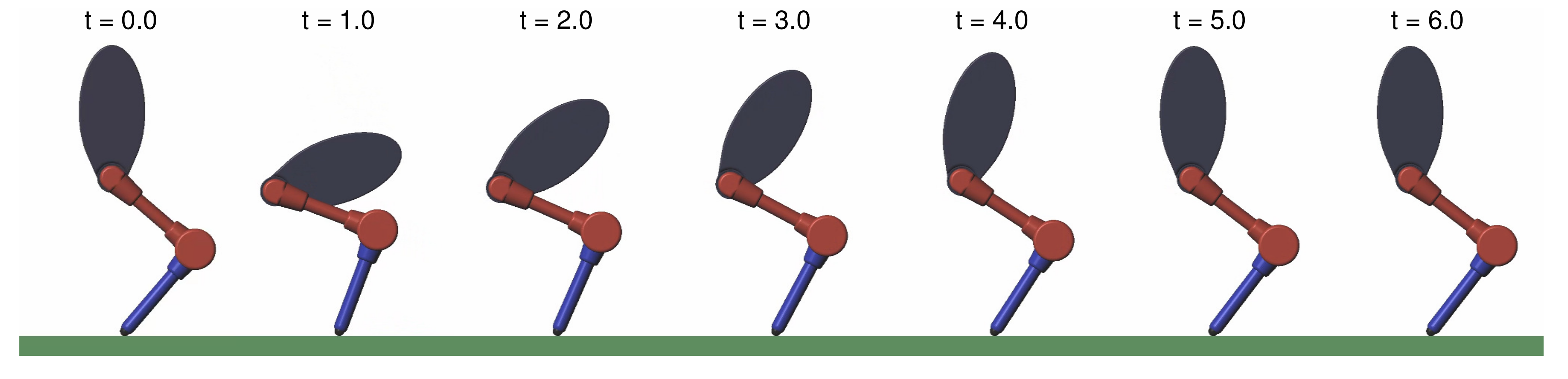
4.1. Balance in Sliding on Uneven Terrain
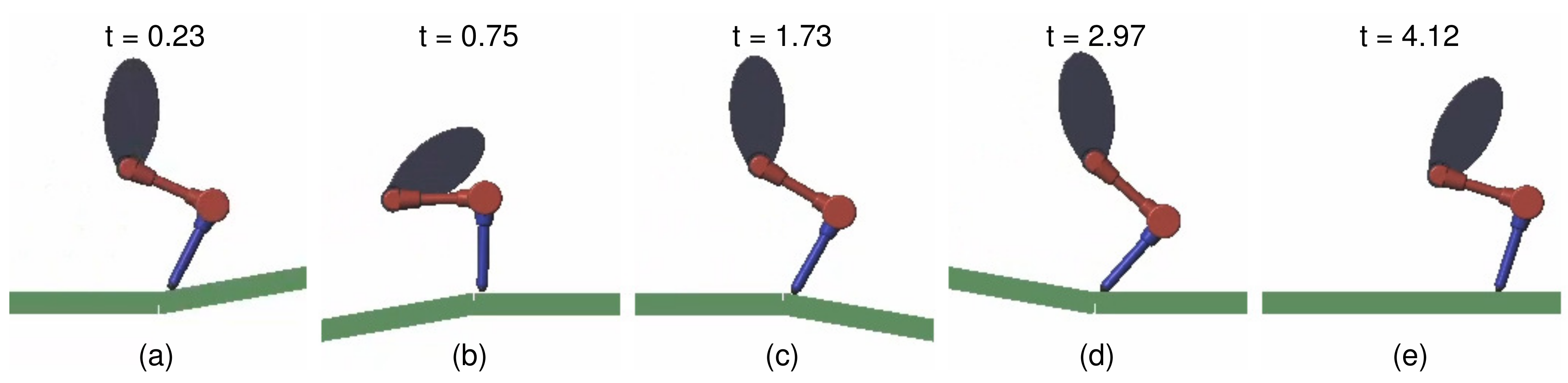
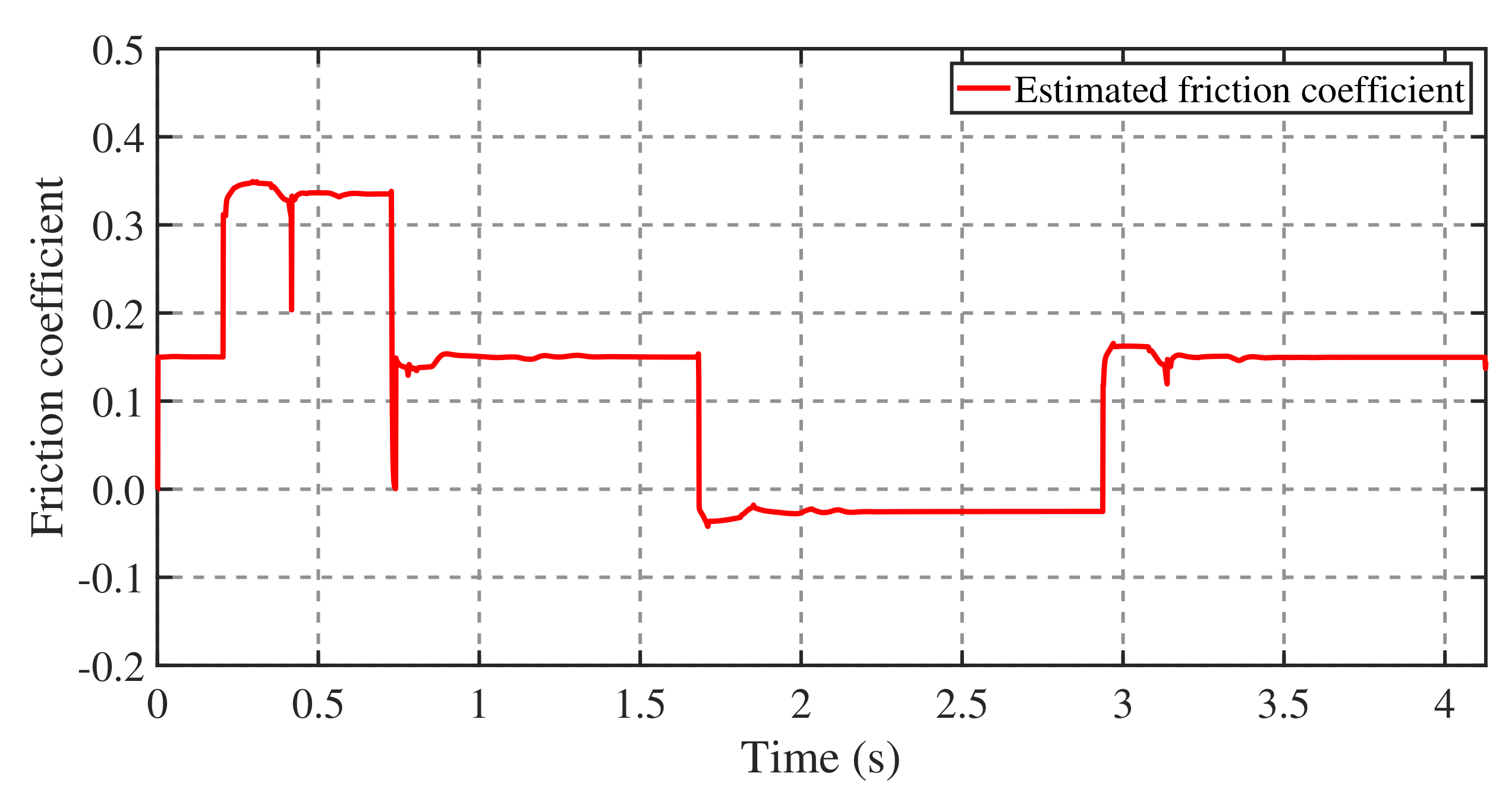
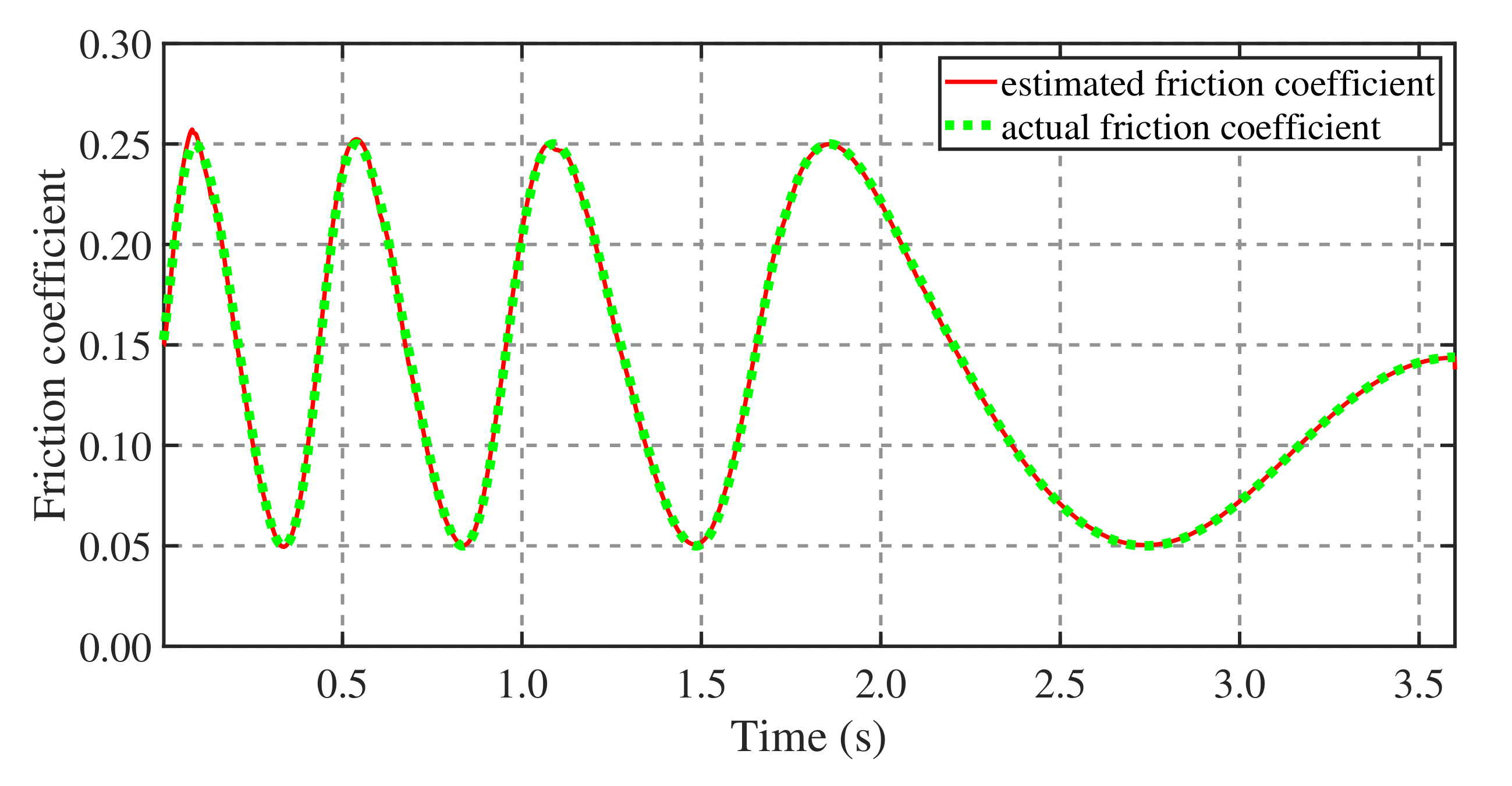
4.2. Balance Recovery on Terrain with a Variable Coefficient of Friction
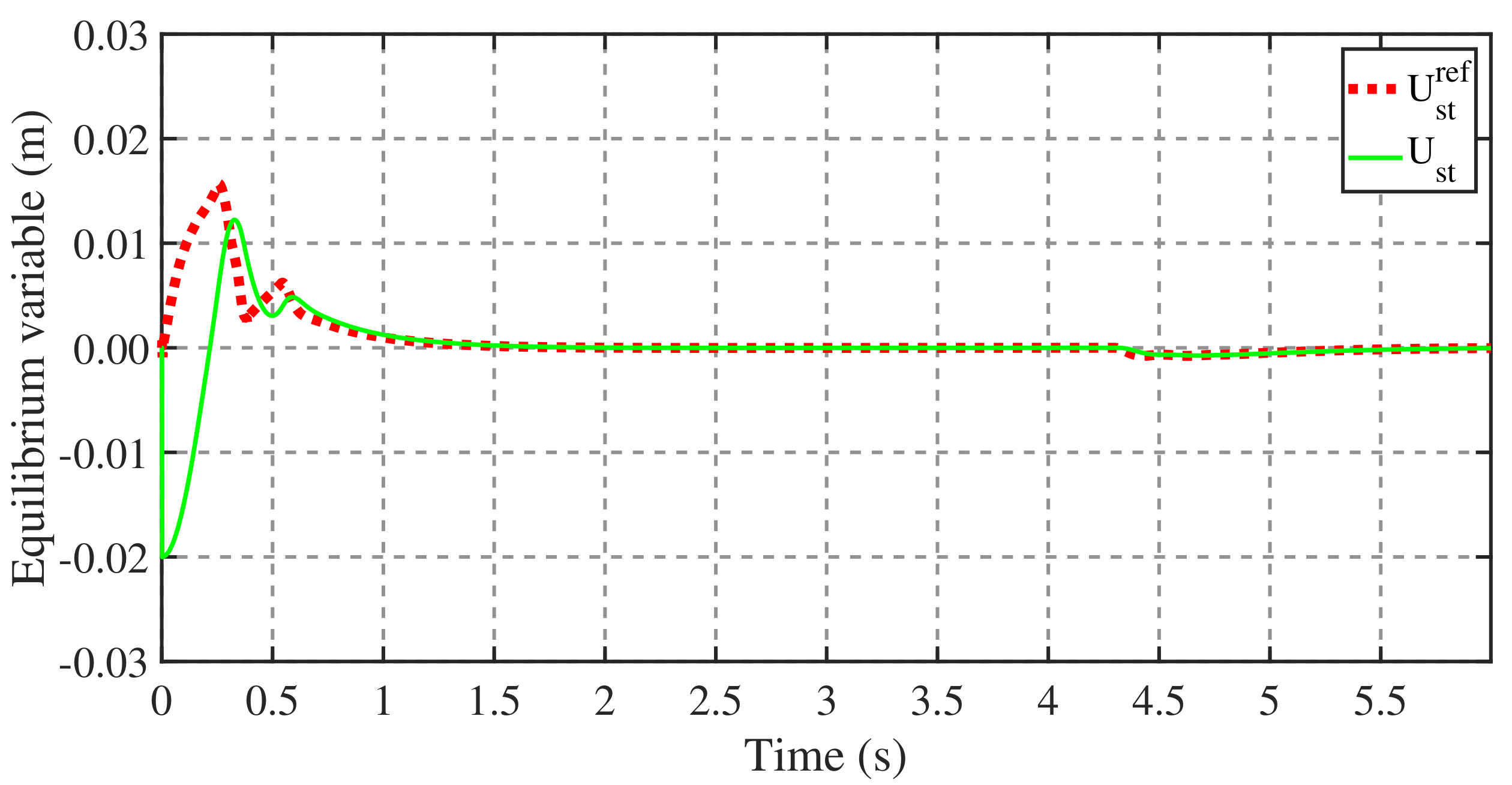
4.3. Balance Recovery in Standing
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Westervelt, E.R.; Grizzle, J.W.; Chevallereau, C.; Choi, J.H.; Tokyo, L. Feedback Control of Dynamic Bipedal Robot Locomotion; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kajita, S.; Hirukawa, H.; Harada, K.; Yokoi, K. Introduction to Humanoid Robotics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-theory and basic experiment. In Proceedings of the Fifth International Conference on Advanced Robotics’ Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991. [Google Scholar]
- Zhao, J.; Gao, J.; Zhao, F.; Liu, Y. A search-and-rescue robot system for remotely sensing the underground coal mine environment. Sensors 2017, 17, 2426. [Google Scholar] [CrossRef] [Green Version]
- Waldron, K.J. Mobility and controllability characteristics of mobile robotic platforms. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985. [Google Scholar]
- Zheng, Y.; Wang, H.; Li, S.; Liu, Y.; Oh, P. Humanoid robots walking on grass, sands and rocks. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 22–23 April 2013. [Google Scholar]
- Quan, N.; Hereid, A.; Grizzle, J.W.; Ames, A.D.; Sreenath, K. 3D dynamic walking on stepping stones with control barrier functions. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016. [Google Scholar]
- Jo, S.H.; Chu, J.U.; Lee, Y.J. Motion planning for biped robot with quad roller skates. In Proceedings of the 2008 International Conference on Control, Automation and Systems, Seoul, Korea, 14–17 October 2008; pp. 1173–1177. [Google Scholar]
- Hashimoto, K.; Hosobata, T.; Sugahara, Y.; Mikuriya, Y.; Takanishi, A. Realization by Biped Leg-wheeled Robot of Biped Walking and Wheel-driven Locomotion. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2970–2975. [Google Scholar]
- Lahajnar, L.; Kos, A.; Nemec, B. Skiing robot-design, control, and navigation in unstructured environment. Robotica 2009, 27, 567–577. [Google Scholar] [CrossRef] [Green Version]
- Abdallah, M.E.; Goswami, A. A Biomechanically Motivated Two-Phase Strategy for Biped Upright Balance Control. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Mosadeghzad, M.; Li, Z.; Tsagarakis, N.G.; Medrano-Cerda, G.A.; Dallali, H.; Caldwell, D.G. Optimal ankle compliance regulation for humanoid balancing control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4118–4123. [Google Scholar]
- Stephens, B. Integral control of humanoid balance. IEEE/RSJ International Conference on Intelligent Robots and Systems. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Macchietto, A.; Zordan, V.; Shelton, C.R. Momentum control for balance. Acm Transactions on Graphics. ACM Trans. Graph. 2009, 28, 1–8. [Google Scholar] [CrossRef]
- Lee, S.H.; Goswami, A. A momentum-based balance controller for humanoid robots on non-level and non-stationary ground. Auton. Robot. 2012, 33, 399–414. [Google Scholar] [CrossRef]
- Yoshida, Y.; Takeuchi, K.; Sato, D.; Nenchev, D. Postural balance strategies for humanoid robots in response to disturbances in the frontal plane. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011. [Google Scholar]
- Goswami, A.; Kallem, V. Rate of change of angular momentum and balance maintenance of biped robots. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 3785–3790.
- Stephens, B. Humanoid push recovery. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 29 November–1 December 2007. [Google Scholar]
- Mayr, J.; Gattringer, H.; Bremer, H. Bipedal balancing control based on the centroidal momentum pivot and the best COM-CMP regulator. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 Novemeber 2013; pp. 4061–4066. [Google Scholar]
- Shafiee-Ashtiani, M.; Yousefi-Koma, A.; Mirjalili, R.; Maleki, H.; Karimi, M. Push Recovery of a Position-Controlled Humanoid Robot Based on Capture Point Feedback Control. In Proceedings of the 2017 5th RSI International Conference on Robotics and Mechatronics, Tehran, Iran, 25–27 October 2017; pp. 126–131. [Google Scholar]
- Zutven, P.V.; Kostiand, D.; Nijmeijer, H. Foot placement for planar bipeds with point feet. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 983–988. [Google Scholar]
- Kim, D.; Thomas, G.; Sentis, L. A method for dynamically balancing a point foot robot. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots, Seoul, Korea, 3–5 November 2015; pp. 901–907. [Google Scholar]
- Peng, S.J.; Shui, H.T.; Tao, S.; Ma, H.X. A novel stability criterion for underactuated biped robot. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics, Guilin, China, 19–23 December 2009; pp. 1912–1917. [Google Scholar]
- Grasser, F.; D’Arrigo, A.; Colombi, S.; Rufer, A.C. Joe: A mobile, inverted pendulum. IEEE Trans. Ind. Electron. 2002, 49, 107–114. [Google Scholar] [CrossRef]
- Ha, J.; Lee, J. Position control of mobile two wheeled inverted pendulum robot by sliding mode control. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, Jeju, Korea, 17–21 October 2012; pp. 715–719. [Google Scholar]
- Huang, C.; Wang, W.; Chiu, C. Design and Implementation of Fuzzy Control on a Two-Wheel Inverted Pendulum. IEEE Trans. Ind. Electron. 2011, 58, 2988–3001. [Google Scholar] [CrossRef]
- Jeong, S.; Takahashi, T. Wheeled inverted pendulum type assistant robot: Design concept and mobile control. Intell. Serv. Robot. 2008, 1, 313–320. [Google Scholar] [CrossRef]
- Khatib, O. A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE J. Robot. Autom. 1987, 3, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Hutter, M.; Hoepflinger, M.; Remy, C.; Siegwart, R. Hybrid Operational Space Control for Compliant Legged Systems. In Proceedings of the Robotics science and systems VIII, Sydney, Australia, 9–13 July 2012; pp. 129–136. [Google Scholar]
- Zafar, M.; Hutchinson, S.; Theodorou, E.A. Hierarchical optimization for Whole-Body Control of Wheeled Inverted Pendulum Humanoids. In Proceedings of the 2019 International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 7535–7542. [Google Scholar]
- Klemm, V.; Morra, A.; Gulich, L.; Mannhart, D.; Rohr, D.; Kamel, M.; Viragh, Y.; Siegwart, R. LQR-Assisted Whole-Body Control of a Wheeled Bipedal Robot With Kinematic Loops. IEEE Robot. Autom. Lett. 2020, 5, 3745–3752. [Google Scholar] [CrossRef]
- Ames, A.D.; Powell, M. Towards the unification of locomotion and manipulation through control lyapunov functions and quadratic programs. Lect. Notes Control. Inf. Sci. 2013, 449, 219–240. [Google Scholar]
- Steve, M. Simscape Multibody Contact Forces Library. 2020. Available online: https://github.com/mathworks/Simscape-Multibody-Contact-Forces-Library/releases/tag/20.2.5.0 (accessed on 20 November 2020).






| Description | Symbol | Value | Unit |
|---|---|---|---|
| torso mass | 15.6 | Kg | |
| thigh mass | 6.8 | Kg | |
| calf mass | 4.5 | Kg | |
| torso inertia | 0.49 | Kg · m | |
| thigh inertia | 0.11 | Kg · m | |
| calf inertia | 0.09 | Kg · m | |
| torso length | 0.40 | m | |
| thigh length | 0.33 | m | |
| calf length | 0.33 | m |
| Description | Symbol | Value |
|---|---|---|
| dual-objective proportion | 0.025 | |
| torso control parameter | [0.50, 0.25, 0.04, 0.02, 10/180, 500/180, 0.0125, 0.0156] | |
| equilibrium variable PD parameter | [2.5, 0.02, 3.0, 0.5, 50.0, 1.0] | |
| knee PD parameter | [, 10/180, 1.5, 0.5, 20, 200/180] | |
| equilibrium variable relaxations weight in QP | 1000 | |
| knee relaxations weight in QP | 1 | |
| max Vertical contact force proportion | 2.5 | |
| min Vertical contact force proportion | 0.5 |
| Description | Symbol | Value |
|---|---|---|
| dual-objective proportion | 0.01 | |
| torso control parameter | [1.0, 0.5, 0.02, 0.01, 10/180, 1000/180, 0.002, 0.003] | |
| equilibrium variable PD parameter | [1.0, 0.02, 1.5, 1.5, 9.8, 0.2] | |
| knee PD parameter | [, 10/180, 1.5, 0.5, 20, 200/180] | |
| equilibrium variable relaxations weight in QP | 1 | |
| knee relaxations weight in QP | 1 | |
| max Vertical contact force proportion | 2.5 | |
| min Vertical contact force proportion | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Gao, J.; Shi, X.; Tian, D.; Liu, Y. Sliding Balance Control of a Point-Foot Biped Robot Based on a Dual-Objective Convergent Equation. Appl. Sci. 2021, 11, 4016. https://doi.org/10.3390/app11094016
Lu Y, Gao J, Shi X, Tian D, Liu Y. Sliding Balance Control of a Point-Foot Biped Robot Based on a Dual-Objective Convergent Equation. Applied Sciences. 2021; 11(9):4016. https://doi.org/10.3390/app11094016
Chicago/Turabian StyleLu, Yizhou, Junyao Gao, Xuanyang Shi, Dingkui Tian, and Yi Liu. 2021. "Sliding Balance Control of a Point-Foot Biped Robot Based on a Dual-Objective Convergent Equation" Applied Sciences 11, no. 9: 4016. https://doi.org/10.3390/app11094016
APA StyleLu, Y., Gao, J., Shi, X., Tian, D., & Liu, Y. (2021). Sliding Balance Control of a Point-Foot Biped Robot Based on a Dual-Objective Convergent Equation. Applied Sciences, 11(9), 4016. https://doi.org/10.3390/app11094016





