Cavity Detection in Steel-Pipe Culverts Using Infrared Thermography †
Abstract
1. Introduction
2. Literature Review
3. Theoretical Basis
4. Method
4.1. Experiment Setup and Data Acquisition
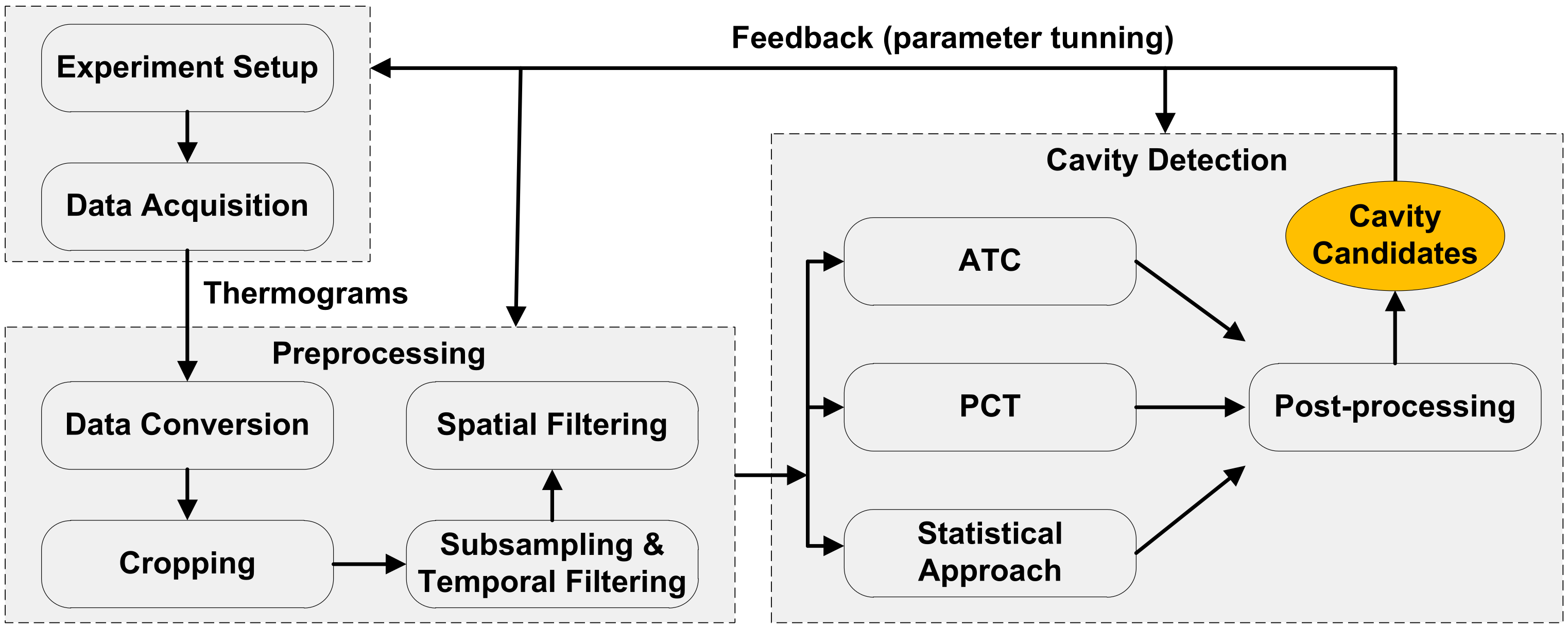
4.2. Processing Algorithm
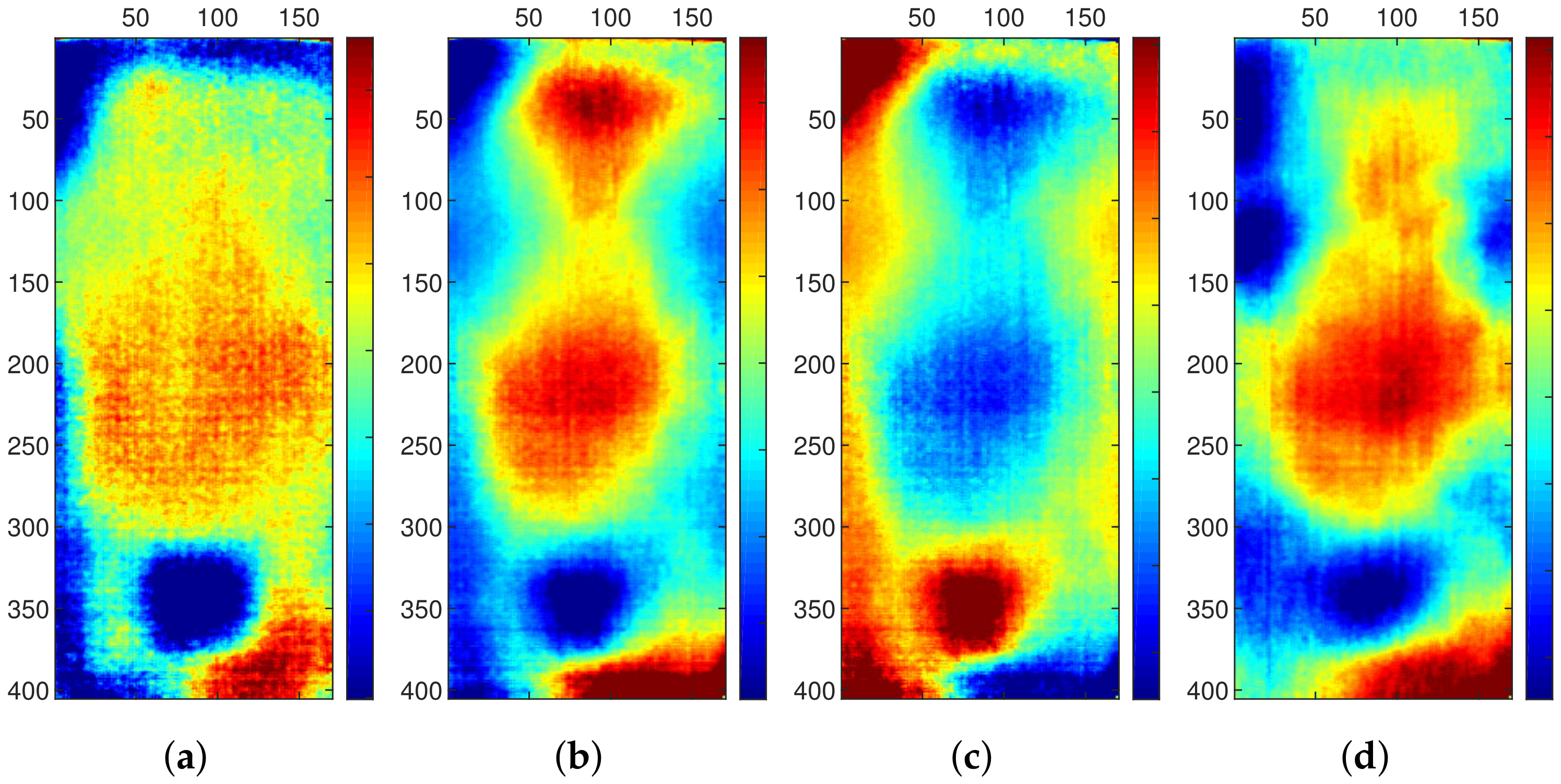
4.3. Principal Components Thermography
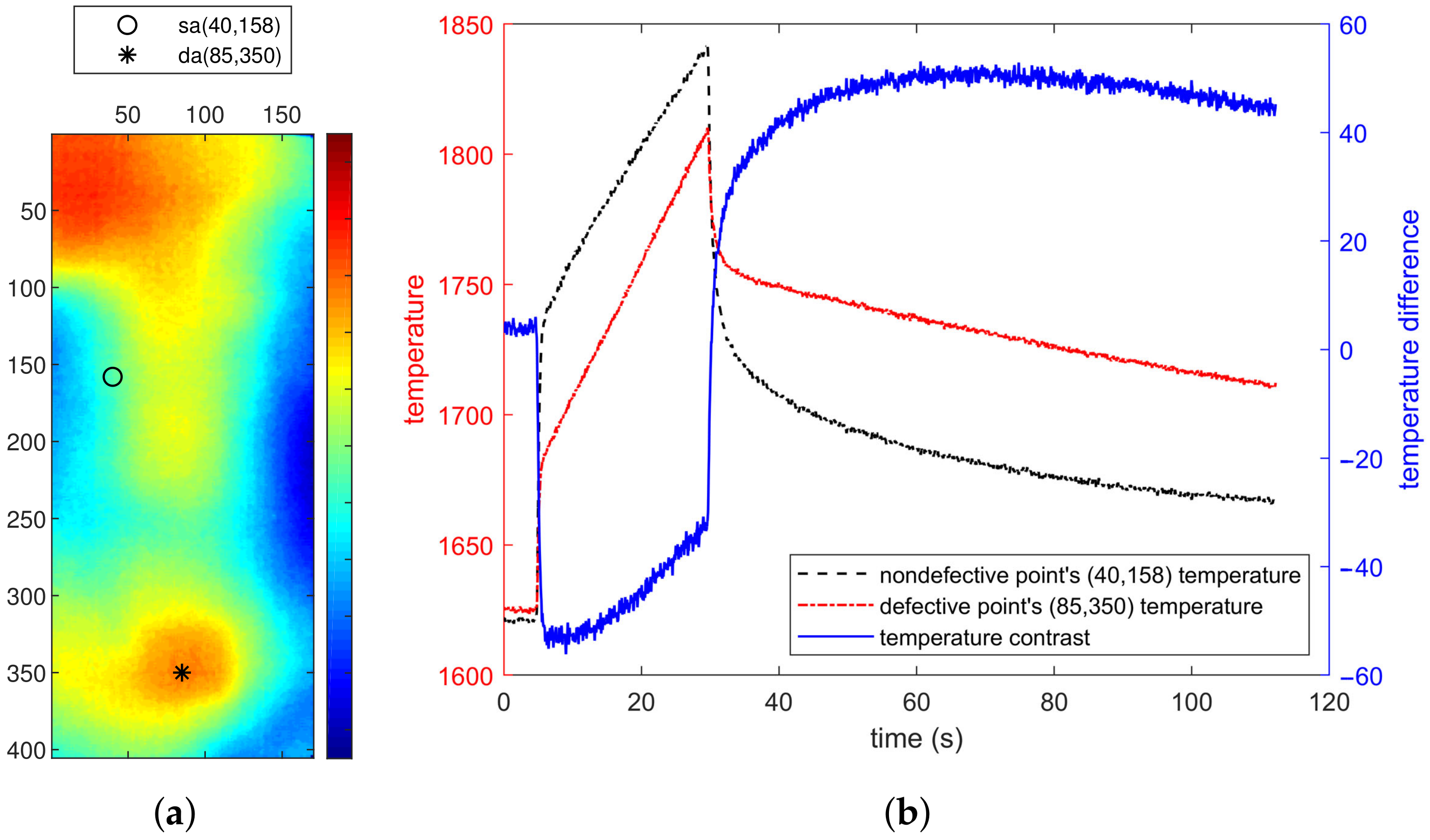
4.4. A Statistical Method for Cavity Identification
| Algorithm 1 The proposed statistical algorithm for cavity detection. |
 |
5. Experimental Results
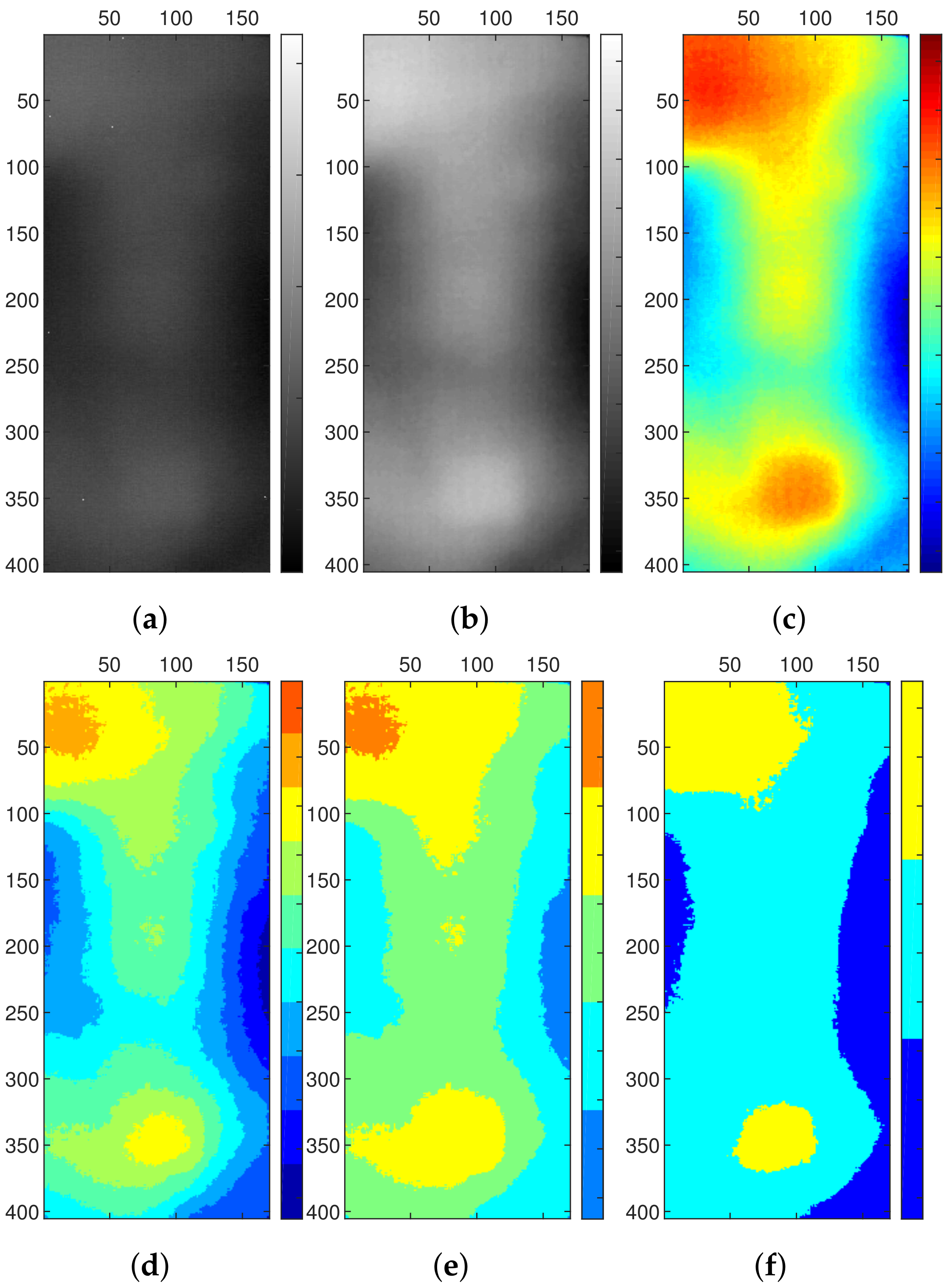
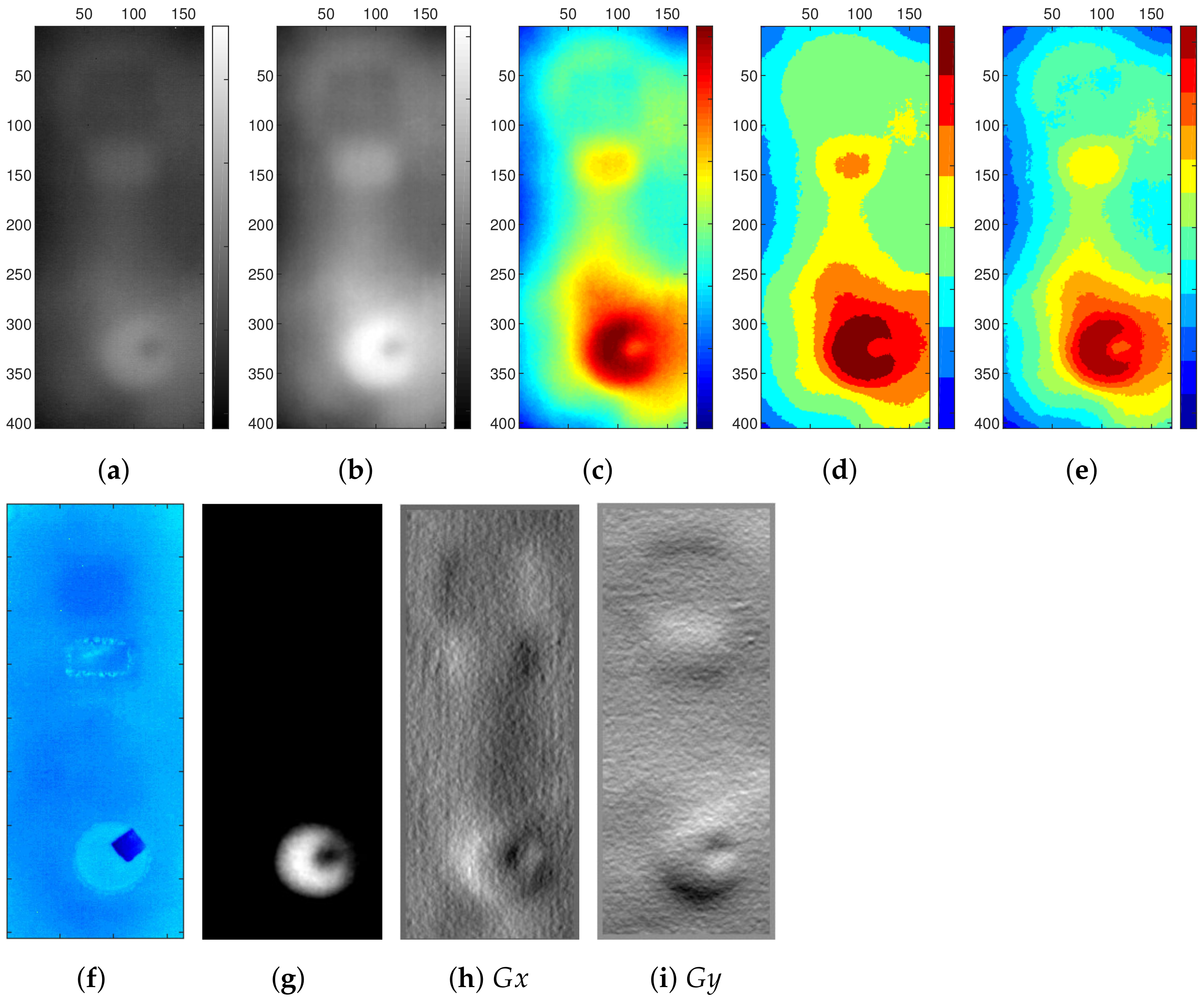
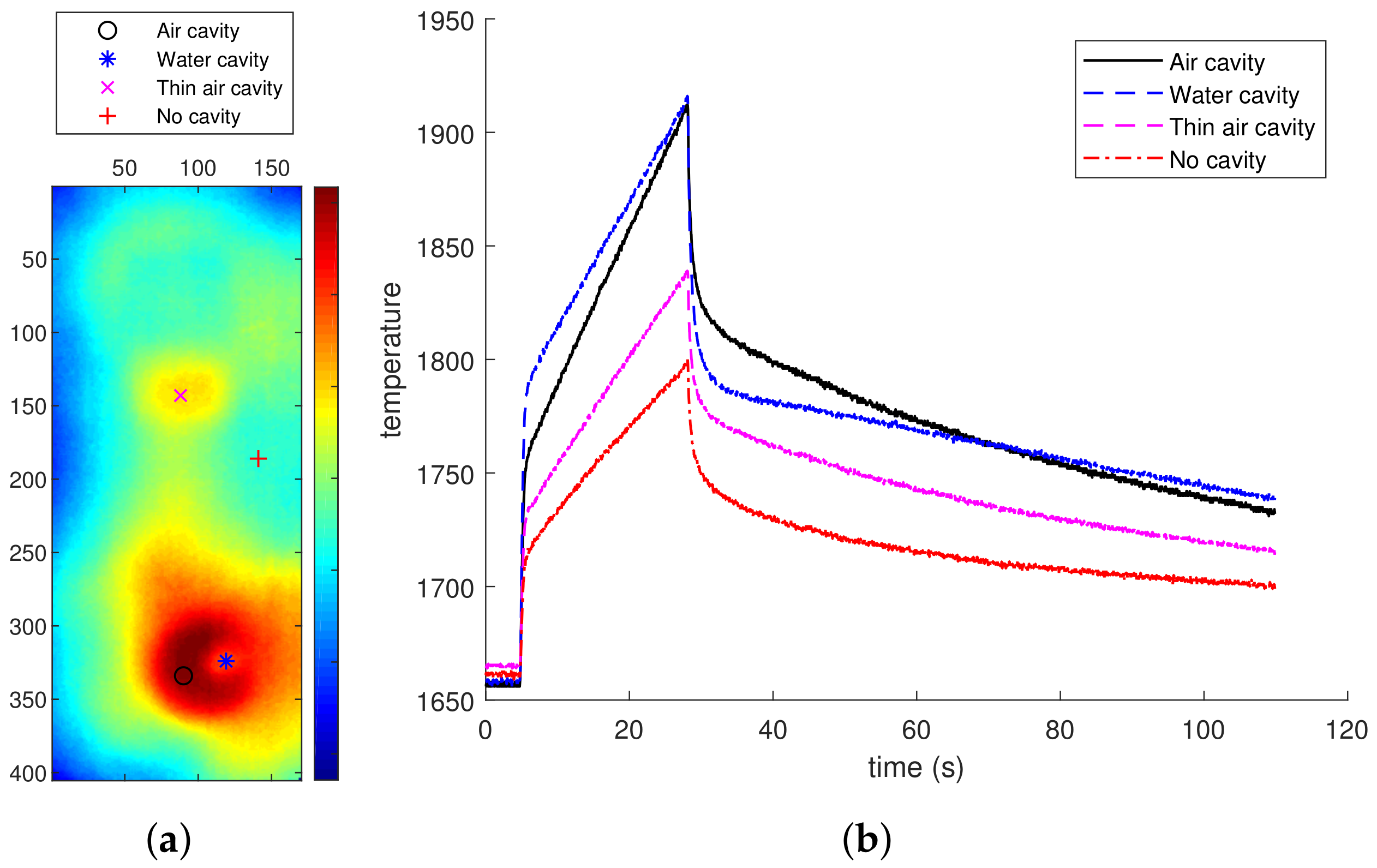
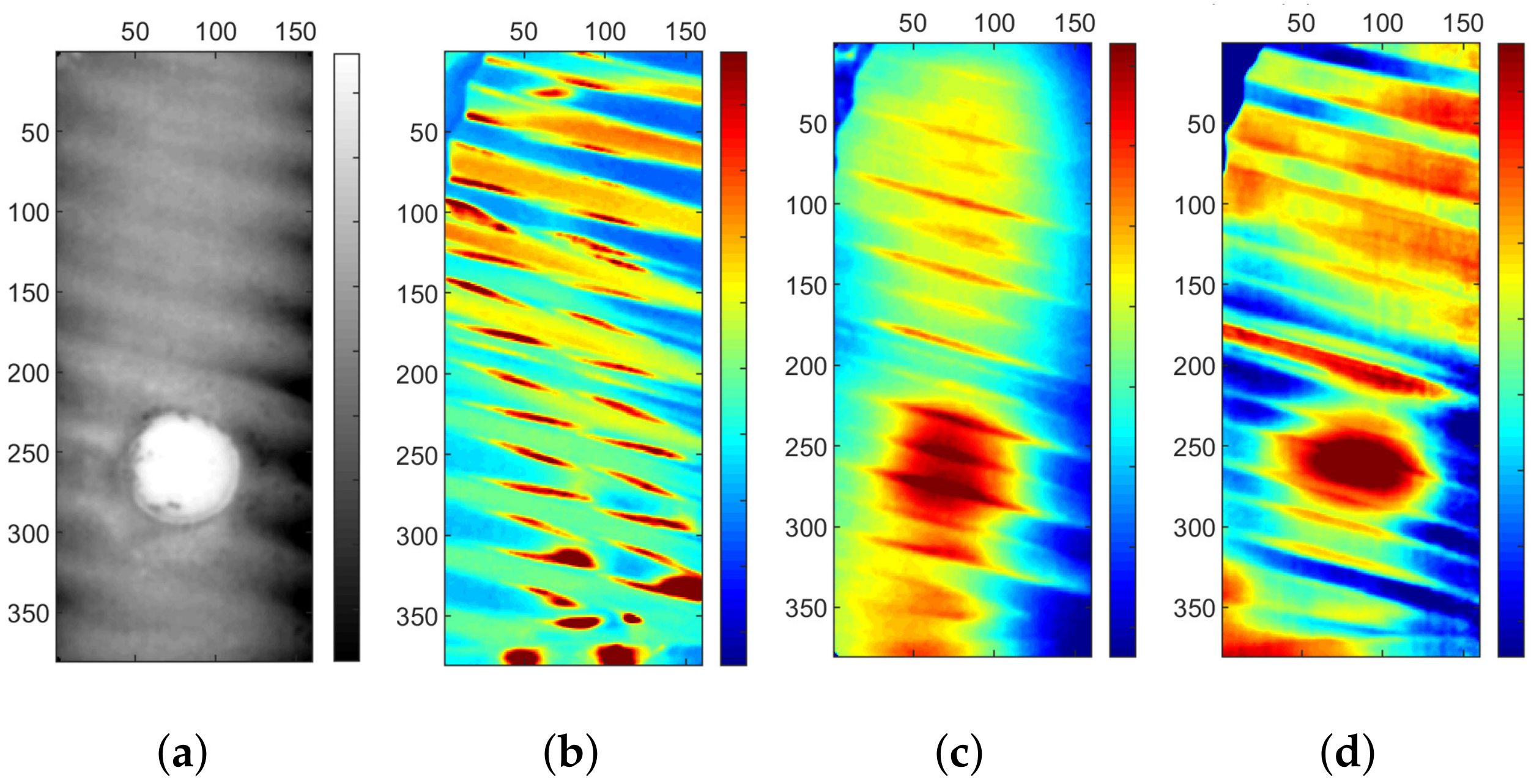
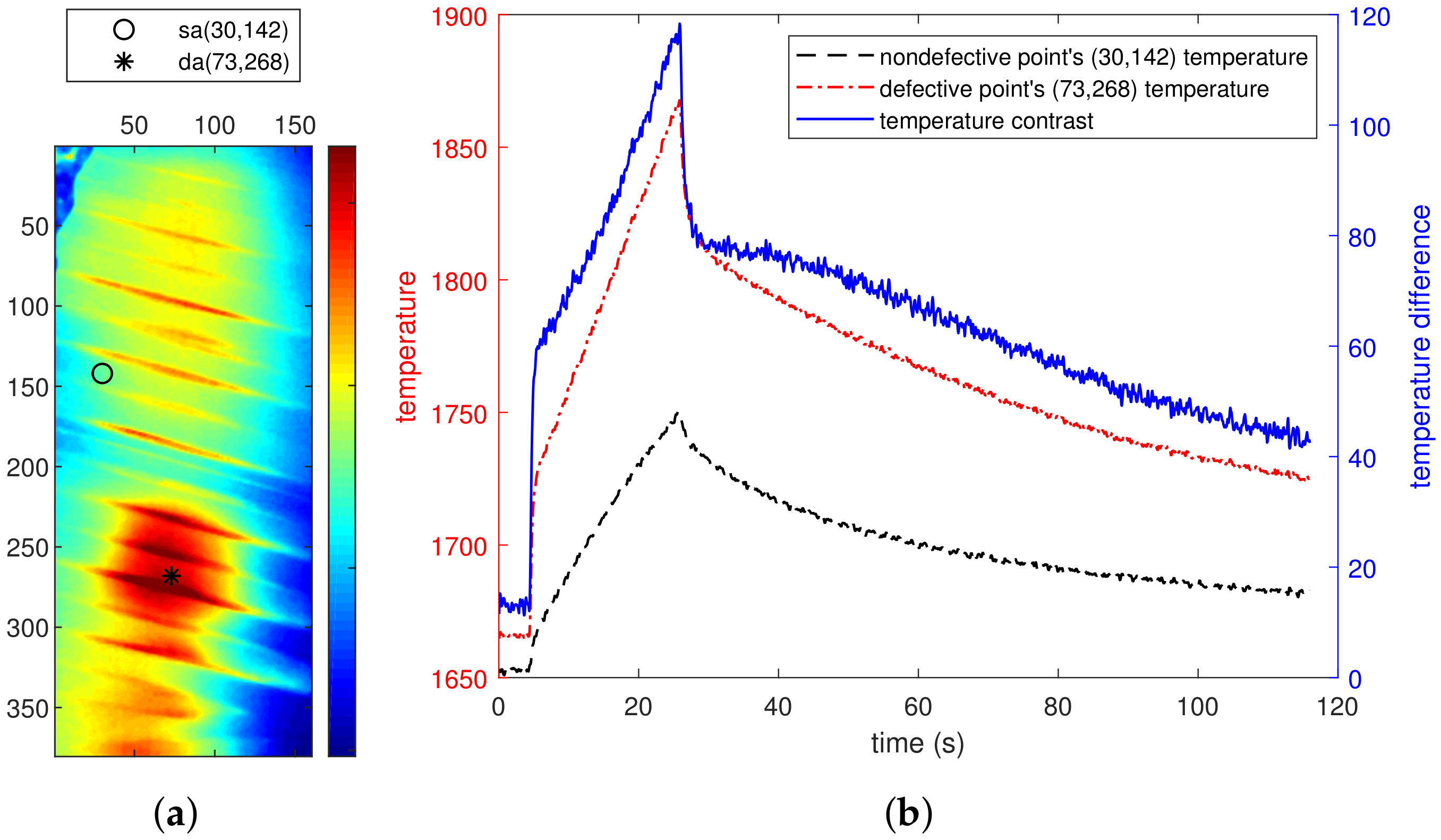
5.1. Experiment 1: Specimen 1, Cavity Configuration 1
5.2. Experiment 2: Specimen 1, Cavity Configuration 3
5.3. Experiment 3: Specimen 2, Cavity Configuration 4
5.4. Experiment 4: Specimen 2, Specific Configuration
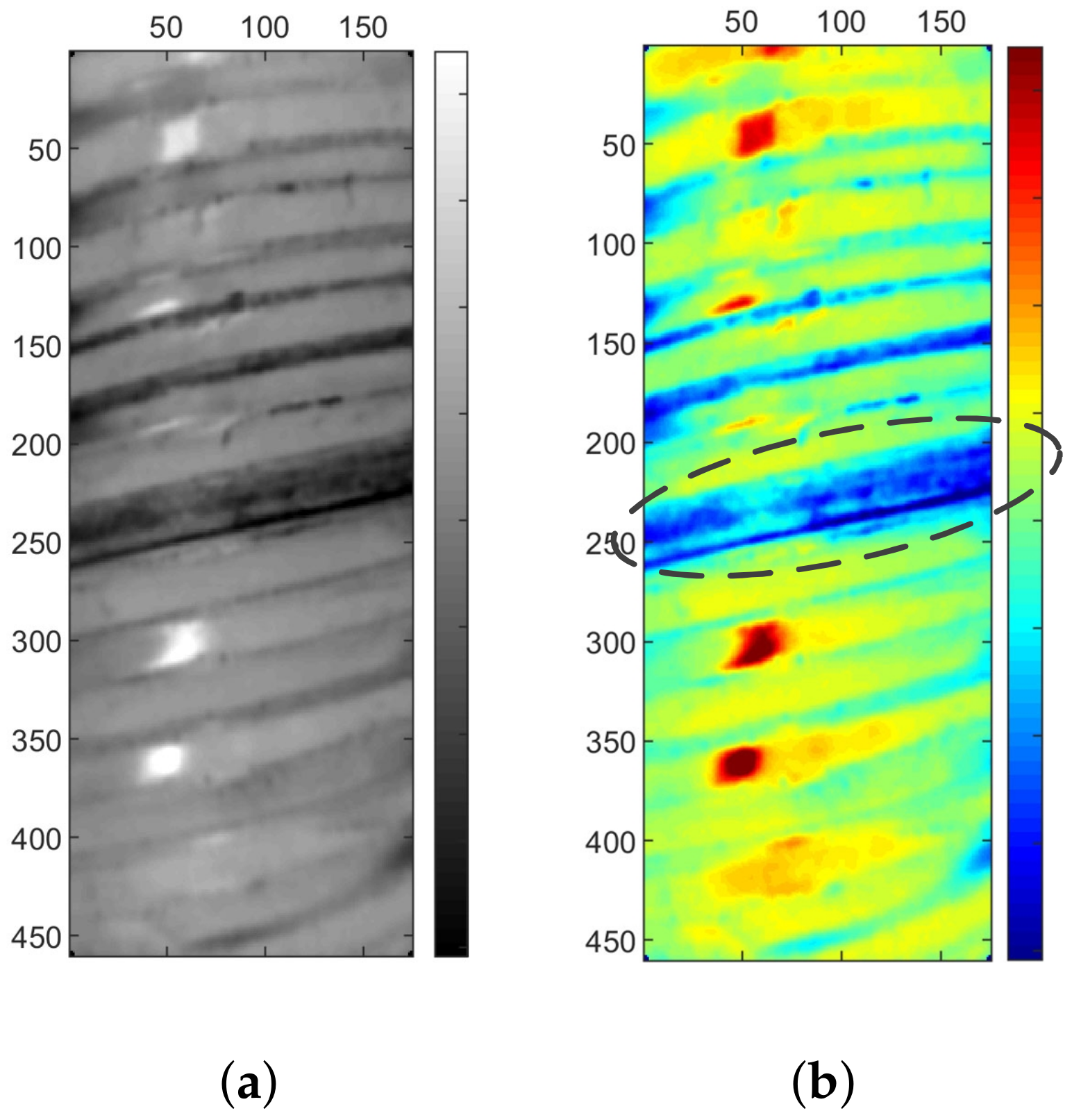
5.5. Result of the Statistical Approach
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACT | Absolute thermal contrast |
| APT | Absolute phase contrast |
| EOF | Empirical orthogonal function |
| LPT | Long pulse thermography |
| LT | Lock-in thermography |
| IRT | Infrared thermography |
| NDT | nondestructive testing |
| PCA | Principal components analysis |
| PCT | Principal components thermography |
| PT | Pulse thermography |
| PPT | Pulsed phase thermography |
References
- Cabonce, J.; Fernando, R.; Wang, H.; Chanson, H. Using small triangular baffles to facilitate upstream fish passage in standard box culverts. Environ. Fluid Mech. 2019, 19, 157–179. [Google Scholar] [CrossRef]
- Donaldson, B. Use of highway underpasses by large mammals and other wildlife in Virginia: Factors influencing their effectiveness. Transp. Res. Rec. 2007, 2011, 157–164. [Google Scholar] [CrossRef]
- TRB. Culverts and Soil–Structure Interaction: Fifty Years of Change and A Twenty-Year Projection; Technical Report E-C230; Transportation Research Board: Washington, DC, USA, 2018. [Google Scholar]
- Sheth, A.; Sinfield, J.V. Synthesis Study: Overview of Readily Available Culvert Inspection Technologies (Joint Transportation Research Program); Technical Report FHWA/IN/JTRP-2018/17; Lyles School of Civil Engineering, Purdue University: West Lafayette, IN, USA, 2018. [Google Scholar]
- Piratla, K.R.; Pang, W.; Jin, H.; Stoner, M. Best Practices for Assessing Culvert Health and Determining Appropriate Rehabilitation Methods: A Research Project in Support of Operational Requirements for the South Carolina Department of Transportation; Technical Report; South Carolina Department of Transportation, Office of Materials and Research: Clemson, SC, USA, 2016.
- Atef, A.; Zayed, T.; Hawari, A.; Khader, M.; Moselhi, O. Multi-tier method using infrared photography and GPR to detect and locate water leaks. Autom. Constr. 2016, 61, 162–170. [Google Scholar] [CrossRef]
- Stampolidis, A.; Soupios, P.; Vallianatos, F.; Tsokas, G. Detection of leaks in buried plastic water distribution pipes in urban places-a case study. In Proceedings of the 2nd International Workshop on Advanced Ground Penetrating Radar, Delft, The Netherlands, 14–16 May 2003; pp. 120–124. [Google Scholar]
- Thitimakorn, T.; Kampananon, N.; Jongjaiwanichkit, N.; Kupongsak, S. Subsurface void detection under the road surface using ground penetrating radar (GPR), a case study in the Bangkok metropolitan area, Thailand. Int. J. Geo-Eng. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Chen, D.H.; Wimsatt, A. Inspection and Condition Assessment Using Ground Penetrating Radar. J. Geotech. Geoenviron. Eng. 2010, 136, 207–214. [Google Scholar] [CrossRef]
- Lefebvre, G.; Karray, M. New developments in in-situ characterization using Rayleigh waves. In Proceedings of the 51st Canadian Geotechnical Conference, Edmonton, AB, Canada, 4–7 October 1998; pp. 821–828. [Google Scholar]
- Karray, M.; Lefebvre, G. Détection des cavités sous les pavages par l’analyse modal des ondes de Rayleigh (MASW). Can. Geotech. J. 2009, 46, 424–437. [Google Scholar] [CrossRef]
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Meola, C.; Carlomagno, G.M.; Giorleo, L. The use of infrared thermography for materials characterization. J. Mater. Process. Technol. 2004, 155–156, 1132–1137. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Maldague, X. Pulsed phase thermography reviewed. Quant. Infrared Thermogr. J. 2004, 1, 47–70. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Tarpani, J.R.; Maldague, X.P.V. Nondestructive testing with thermography. Eur. J. Phys. 2013, 34, S91–S109. [Google Scholar] [CrossRef]
- Qu, Z.; Jiang, P.; Zhang, W. Development and Application of Infrared Thermography Non-Destructive Testing Techniques. Sensors 2020, 20, 3851. [Google Scholar] [CrossRef]
- Maillard, S.; Cadith, J.; Bouteille, P.; Legros, G.; Bodnar, J.; Detalle, V. Non-destructive testing of forged metallic materials by active infrared thermography. Int. J. Thermophys. 2012, 33, 1982–1988. [Google Scholar] [CrossRef]
- Chaki, S.; Marical, P.; Panier, S.; Bourse, G.; Mouftiez, A. Interfacial defects detection in plasma-sprayed ceramic coating components using two stimulated infrared thermography techniques. NDT E Int. 2011, 44, 519–522. [Google Scholar] [CrossRef]
- Almond, D.P.; Peng, W. Thermal imaging of composites. J. Microsc. 2001, 201, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Ibarra-Castanedo, C.; Piau, J.M.; Guilbert, S.; Avdelidis, N.P.; Genest, M.; Bendada, A.; Maldague, X.P.V. Comparative Study of Active Thermography Techniques for the Nondestructive Evaluation of Honeycomb Structures. Res. Nondestruct. Eval. 2009, 20, 1–31. [Google Scholar] [CrossRef]
- Sakagami, T.; Kubo, S. Development of a new non-destructive testing technique for quantitative evaluations of delamination defects in concrete structures based on phase delay measurement using lock-in thermography. Infrared Phys. Technol. 2002, 43, 311–316. [Google Scholar] [CrossRef]
- Bison, P.; Marinetti, S.; Cuogo, G.; Molinas, B.; Zonta, P.; Grinzato, E. Corrosion detection on pipelines by IR thermography. In Thermosense: Thermal Infrared Applications XXXIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8013, pp. 116–125. [Google Scholar]
- Rodríguez-Martin, M.; Lagüela, S.; González-Aguilera, D.; Arias, P. Cooling analysis of welded materials for crack detection using infrared thermography. Infrared Phys. Technol. 2014, 67, 547–554. [Google Scholar] [CrossRef]
- Milovanović, B.; Banjad Pečur, I. Review of active IR thermography for detection and characterization of defects in reinforced concrete. J. Imaging 2016, 2, 11. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Lin, G.; Li, Q.; Sun, Y.; Sun, Y. Infrared Thermal Imaging-Based Crack Detection Using Deep Learning. IEEE Access 2019, 7, 182060–182077. [Google Scholar] [CrossRef]
- Costello, S.; Chapman, D.; Rogers, C.; Metje, N. Underground asset location and condition assessment technologies. Tunn. Undergr. Space Technol. 2007, 22, 524–542. [Google Scholar] [CrossRef]
- Yang, C.; Allouche, E. Evaluation of non-destructive methods for condition assessment of culverts and their embedment. In Proceedings of the ICPTT 2009: Advances and Experiences with Pipelines and Trenchless Technology for Water, Sewer, Gas, and Oil Applications, Shanghai, China, 18–21 October 2009; pp. 28–38. [Google Scholar]
- Meola, C. Infrared Thermography Recent Advances and Future Trends; Bentham Science Publishers: New York, NY, USA, 2012. [Google Scholar]
- Osornio-Rios, R.A.; Antonino-Daviu, J.A.; de Jesus Romero-Troncoso, R. Recent industrial applications of infrared thermography: A review. IEEE Trans. Ind. Inform. 2018, 15, 615–625. [Google Scholar] [CrossRef]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent advances in active infrared thermography for non-destructive testing of aerospace components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef] [PubMed]
- Breitenstein, O.; Warta, W.; Schubert, M.C. Lock-in Thermography: Basics and Use for Evaluating Electronic Devices and Materials; Springer: Berlin, Germany, 2019; Volume 10. [Google Scholar]
- Giorleo, G.; Meola, C. Comparison between pulsed and modulated thermography in glass–epoxy laminates. Ndt E Int. 2002, 35, 287–292. [Google Scholar] [CrossRef]
- Dillenz, A.; Zweschper, T.; Riegert, G.; Busse, G. Progress in phase angle thermography. Rev. Sci. Instrum. 2003, 74, 417–419. [Google Scholar] [CrossRef]
- BuSSe, G.; Wu, D.; Karpen, W. Thermal wave imaging with phase sensitive modulated thermography. J. Appl. Phys. 1992, 71, 3962–3965. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C. Quantitative Subsurface Defect Evaluation by Pulsed Phase Thermography: Depth Retrieval with the Phase. Ph.D. Thesis, Laval University, Quebec, QC, Canada, 2005. [Google Scholar]
- Carlomagno, G.M.; Meola, C. Comparison between thermographic techniques for frescoes NDT. NDT E Int. 2002, 35, 559–565. [Google Scholar] [CrossRef]
- Gleiter, A.; Spiessberger, C.; Busse, G. Lockin thermography with optical or ultrasound excitation. Stroj. Vestn. J. Mech. Eng. 2010, 56, 619–624. [Google Scholar]
- Jia, Y.; Tang, L.; Ming, P.; Xie, Y. Ultrasound-excited thermography for detecting microcracks in concrete materials. NDT E Int. 2019, 101, 62–71. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.; Zhou, X.; Tan, Y. Experimental studies on void detection in concrete-filled steel tubes using ultrasound. Constr. Build. Mater. 2016, 128, 154–162. [Google Scholar] [CrossRef]
- Lin, S.; Shams, S.; Choi, H.; Azari, H. Ultrasonic imaging of multi-layer concrete structures. NDT E Int. 2018, 98, 101–109. [Google Scholar] [CrossRef]
- Sophian, A.; Tian, G.; Fan, M. Pulsed eddy current non-destructive testing and evaluation: A review. Chin. J. Mech. Eng. 2017, 30, 500–514. [Google Scholar] [CrossRef]
- Xu, X.; Ji, H.; Qiu, J.; Takagi, T. Detection of delamination in laminated CFRP composites using eddy current testing: Simulation and experimental study. Int. J. Appl. Electromagn. Mech. 2018, 57, 177–192. [Google Scholar] [CrossRef]
- Yin, A.; Gao, B.; Yun Tian, G.; Woo, W.L.; Li, K. Physical interpretation and separation of eddy current pulsed thermography. J. Appl. Phys. 2013, 113, 064101. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Tian, G.; Ciampa, F. Comparative analysis of eddy current pulsed thermography and long pulse thermography for damage detection in metals and composites. NDT E Int. 2019, 107, 102155. [Google Scholar] [CrossRef]
- Lau, S.; Almond, D.; Patel, P. Transient thermal wave techniques for the evaluation of surface coatings. J. Phys. D Appl. Phys. 1991, 24, 428. [Google Scholar] [CrossRef]
- Almond, D.P.; Angioni, S.L.; Pickering, S.G. Long pulse excitation thermographic non-destructive evaluation. NDT E Int. 2017, 87, 7–14. [Google Scholar] [CrossRef]
- Kalyanavalli, V.; Ramadhas, T.A.; Sastikumar, D. Long pulse thermography investigations of basalt fiber reinforced composite. NDT E Int. 2018, 100, 84–91. [Google Scholar] [CrossRef]
- Krapez, J.C.; Cielo, P. Thermographic nondestructive evaluation: Data inversion procedures Part I: 1-D analysis. Res. Nondestruct. Eval. 1991, 3, 81–100. [Google Scholar] [CrossRef]
- Maldague, X.; Marinetti, S. Pulse phase infrared thermography. J. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Pearson: London, UK, 2008. [Google Scholar]
- Krapez, J.C.; Maldague, X.; Cielo, P. Thermographic nondestructive evaluation: Data inversion procedures Part II: 2-D analysis and experimental results. Res. Nondestruct. Eval. 1991, 3, 101–124. [Google Scholar] [CrossRef]
- Avdelidis, N.; Almond, D.P. Through skin sensing assessment of aircraft structures using pulsed thermography. NDT E Int. 2004, 37, 353–359. [Google Scholar] [CrossRef]
- González, D.; Ibarra-Castanedo, C.; Pilla, M.; Klein, M.; López-Higuera, J.; Maldague, X. Automatic interpolated differentiated absolute contrast algorithm for the analysis of pulsed thermographic sequence. In Proceedings of the 7th Conference on Quantitative InfraRed Thermography (QIRT), Rhode Saint Genèse, Belgium, 5–8 July 2004; pp. 1–6. [Google Scholar]
- Benítez, H.D.; Ibarra-Castanedo, C.; Bendada, A.; Maldague, X.; Loaiza, H.; Caicedo, E. Definition of a new thermal contrast and pulse correction for defect quantification in pulsed thermography. Infrared Phys. Technol. 2008, 51, 160–167. [Google Scholar] [CrossRef]
- Bai, W.; Wong, B. Evaluation of defects in composite plates under convective environments using lock-in thermography. Meas. Sci. Technol. 2001, 12, 142. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Milovanović, B.; Gaši, M.; Gumbarević, S. Principal Component Thermography for Defect Detection in Concrete. Sensors 2020, 20, 3891. [Google Scholar] [CrossRef]
- Gauci, J.; Camilleri, K.P.; Falzon, O. Principal component analysis for dynamic thermal video analysis. Infrared Phys. Technol. 2020, 109, 103359. [Google Scholar] [CrossRef]
- Winfree, W.P.; Cramer, K.E.; Zalameda, J.N.; Howell, P.A.; Burke, E.R. Principal component analysis of thermographic data. In Thermosense: Thermal Infrared Applications XXXVII; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9485, pp. 211–221. [Google Scholar]
- Liang, T.; Ren, W.; Tian, G.Y.; Elradi, M.; Gao, Y. Low energy impact damage detection in CFRP using eddy current pulsed thermography. Compos. Struct. 2016, 143, 352–361. [Google Scholar] [CrossRef]
- D’Accardi, E.; Palumbo, D.; Tamborrino, R.; Galietti, U. Quantitative analysis of thermographic data through different algorithms. Procedia Struct. Integr. 2018, 8, 354–367. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Number BOOK; Clarendon Press: Oxford, UK, 1992. [Google Scholar]
- Flir. Cooled or Uncooled? Available online: https://www.flir.ca/discover/rd-science/cooled-or-uncooled/ (accessed on 31 March 2021).
- Zhang, Z.; Moore, J.C. Chapter 6—Empirical Orthogonal Functions. In Mathematical and Physical Fundamentals of Climate Change; Elsevier: Boston, MA, USA, 2015; pp. 161–197. [Google Scholar]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography, 3rd ed.; Elsevier: Boston, MA, USA, 2014. [Google Scholar]
- Thermtest. Materials Thermal Properties Database. Available online: https://thermtest.com/materials-database (accessed on 8 April 2021).






| Feature | FLIR Phoenix | Jenoptik VarioCAM |
|---|---|---|
| IR detector | Cooled Indium Antimonide (InSb) | Uncooled microbolometer array (FPA) |
| Image resolution | 640 × 512 | 640 × 480 |
| Spectral range | 3–5 m | 7.5–14 m |
| Thermal sensitivity | <25 mK | <70 mK; <30 mK at 30 C object |
| Frame rate | 50 Hz | 50 Hz (PAL), 60 Hz (NTSC) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalhor, D.; Ebrahimi, S.; Tokime, R.B.; Mamoudan, F.A.; Bélanger, Y.; Mercier, A.; Maldague, X. Cavity Detection in Steel-Pipe Culverts Using Infrared Thermography. Appl. Sci. 2021, 11, 4051. https://doi.org/10.3390/app11094051
Kalhor D, Ebrahimi S, Tokime RB, Mamoudan FA, Bélanger Y, Mercier A, Maldague X. Cavity Detection in Steel-Pipe Culverts Using Infrared Thermography. Applied Sciences. 2021; 11(9):4051. https://doi.org/10.3390/app11094051
Chicago/Turabian StyleKalhor, Davood, Samira Ebrahimi, Roger Booto Tokime, Farima Abdollahi Mamoudan, Yohan Bélanger, Alexandra Mercier, and Xavier Maldague. 2021. "Cavity Detection in Steel-Pipe Culverts Using Infrared Thermography" Applied Sciences 11, no. 9: 4051. https://doi.org/10.3390/app11094051
APA StyleKalhor, D., Ebrahimi, S., Tokime, R. B., Mamoudan, F. A., Bélanger, Y., Mercier, A., & Maldague, X. (2021). Cavity Detection in Steel-Pipe Culverts Using Infrared Thermography. Applied Sciences, 11(9), 4051. https://doi.org/10.3390/app11094051








