Experimental and Numerical Study on the Performance Change of a Simple Propeller Shape Using the Coanda Effect

Abstract

In this study, a jet injection propeller was designed to increase its efficiency, and the results were compared by open water tests and numerical computations. Also, the change in shape of the slit and injection volume conditions, which are difficult to perform experiments with, were analyzed through computations. The jet injected from the blade surface generates additional thrust due to the Coanda effect, and the jet injection generates a moment in the direction of propeller rotation, resulting in a decrease in the total torque. Computations were performed for three slit heights. When the height of the slit is high, the efficiency of the propeller increases, even if the power of the pump required for jet injection is considered. The result was found to increase the efficiency by about 8.7%, even when the efficiency was compared under the condition of generating the same thrust by controlling the injection volume of the jet by designing a normal propeller that does not inject a jet.

1. Introduction

The International Maritime Organization (IMO) institutionalized the Energy Efficiency Design Index (EEDI) in 2013 to reduce the greenhouse gas (GHG) emissions of ships and is strengthening regulations. The goal is reducing the annual amount of GHG generated by international shipping by 2050 by at least 50% compared to 2008, so ships built after 2025 should reduce the amount of GHG by 30% compared to the standard value [1]. Methods to reduce the EEDI to satisfy the regulations include reducing the CO₂ conversion factor, the designed fuel consumption rate, or the designed engine power rate, as well as increasing the designed speed and the designed capacity volume [2]. In phase 2, the EEDI should be reduced by 20% compared to the initial value. The EEDI regulation could be satisfied by reducing engine power obtained through slow operation. In phase 3, additional technology development is required to improve fuel economy. In order to satisfy the currently strengthened EEDI regulations, many studies are being conducted to reduce the required power of ships.

In this study, attention is paid to a method of increasing propeller propulsion efficiency as a way to increase a ship’s efficiency. In order to increase the efficiency of propellers, we tried to apply the Coanda effect to screw propellers that are currently used in most ships. The Coanda effect refers to a phenomenon in which the jet flows along the curvature of a curved surface. When the jet flows along the curved surface, the flow direction changes to induce the flow direction of the surrounding fluids, and a force is generated in the opposite direction of the fluid flow by the law of action and reaction. We devised a propeller that converts the force generated through the Coanda effect into the thrust of the propeller.

The Coanda effect is currently widely applied in the aeronautical field. Chng et al. [3] confirmed that the jet on an airfoil surface is effective in increasing the lift and controlling stall by designing an airfoil surface to allow injection and suction, as well as performing experiments and a numerical analysis. In addition, after applying a flap and droop nose to the airfoil, the effect of the jet on the airfoil was analyzed through experiments [4,5] and numerical analysis [6]. Model tests [7] and a numerical analysis [8] were performed using plasma actuators to analyze changes in airfoil performance. Slomsk et al. [9] compared the behavior of jet injection according to the turbulence model in a circulation control airfoil.

In order to apply the Coanda effect to ships, there are many studies in which a hydrofoil is applied. Maltsev et al. [10] designed a hydrofoil capable of jet injection and performed a model experiment in a cavitation tunnel. They showed that the lift increased by up to three times through jet injection. Also, experiments [11] and a numerical analysis [12] were performed by attaching a rotor to the trailing edge of a hydrofoil, and it was found that the lift force was increased by reinforcing the circulation flow as the rotor rotated.

Seo et al. [13] designed a three-dimensional Coanda horn rudder, performed experiments and computations, and compared the lift increase in jet flow for various rudder angles. In addition, by incorporating the Coanda effect into a stabilizer fin, the performance of the fin stabilizer was improved by increasing the lift. At the same time, the effect of power reduction was confirmed by comparing the required power with that of a fixed stabilizer fin [14]. According to previous studies, both airfoils and hydrofoils showed the same tendency of increased lift when jet injected from the surface. To apply the tendency of increased lift to a propeller, Eom et al. [15] proposed a hydrofoil shape that not only increases lift during jet injection, but also reduces cavitation compared to a circulation-type shape.

In this study, a jet injection propeller was designed based on the research of Eom et al. [15], and we tried to examine whether the jet on the hydrofoil surface could increase the efficiency of the propeller. Basic research was conducted prior to optimizing the shape of the jet by analyzing the efficiency according to the shape of the jet injection [16]. By applying the optimized jet-injection hydrofoil to a propeller, the performance change of the propeller according to jet injection was studied. In order to find out the effect of jet injection on the propeller performance, a simple propeller shape and experimental equipment capable of jet injection were designed and tested, and the results were compared with computations. Additionally, through numerical computations, the change in performance was analyzed according to the shape of the injection hole and the injection volume, which are difficult to perform an experiment on. Finally, considering the power of the pump required for jet injection, the efficiency as an energy saving device (ESD) was examined by comparing the efficiency with a simple screw propeller shape.

2. Experimental and Numerical Method

2.1. Propeller Modelling

The profile of the propeller blade in this study is based on a NACA66 airfoil, which is widely used as a section of ship propellers such as the KP505 [17] and KP632 [18]. The section of NACA66 (MOD) used in this study is shown in Figure 1. Additional structures were added inside the hydrofoil to inject a jet. In order to secure the strength of the experimental equipment, the thickness of the NACA66 (MOD) is set to 24% of the chord length.

In Figure 1, the tunnel is the passage through which water flows from the shaft to the propeller blades to inject a jet. The slit is the jet opening in the hydrofoil, and the round tunnel is the passage connecting the tunnel and the slit. In the case without a jet section, since a jet is not injected, only the tunnel exists inside the hydrofoil. In the geometry with a jet section, the slit, round tunnel, and tunnel exist inside the hydrofoil to inject the jet. This section is designed without an angled part as possible in the hydrofoil after the slit so that the jet injected from the slit can flow along the hydrofoil.

In addition, in the case with a jet section, all hydrofoil geometry except around the slit was made with the same geometry as without a jet section. The shape and location of the slit and tunnel were selected based on Eom et al. [16], who optimized the shape of the jet nozzle through 2D and 3D hydrofoil studies that injected a jet. The position of the slit is in the center of the chord, and the height of the tip was selected as 25% of the slit height.

Based on the NACA66 (MOD, t/c = 0.24) section in Figure 1, a Coanda propeller that injects a jet from the propeller blade surface was manufactured. The specifications of the propeller are shown in

Table 1. Parameters of the Coanda propeller used in the experiment.

Parameter	Value
Diameter, $D$(mm)	250
Pitch ratio, $P/D$	0.777
Hub ratio, $d/D$	0.250
Inner tunnel ratio, $d_{inner}/D$	0.144
No. of Blades	2
Section	NACA66 (MOD, t/c = 0.24)
Slit position (r/R)	0.5–0.9
Slit height, $h_S$ (mm)	1.0
Slit area, $A_S$ (mm2)	48.663
Expanded area ratio	0.186

. The diameter of the propeller $\left(D\right)$ is 250 mm, which is relatively large compared to other propellers to make inner structure, and the length of the chord $\left(c\right)$ is 50 mm. The geometry of the propeller was designed as a simple shape with only pitch without rake and skew as a basic study.

Figure 2 shows the propeller used in the experiment and the modeled propeller. It also shows the shape of the inner structure. The Coanda propeller used in the experiment was manufactured through 3D printing using acrylic material to secure the strength of the propeller. When manufacturing the propeller, the height of the slit was selected as 1.0 mm in consideration of the manufacturing limit of the 3D printer equipment. Slit smaller than 1.0 mm could not be manufactured through 3D printing, so the performance change according to the slit height was studied through numerical computations.

The propeller shaft was designed as a hollow shaft so that the water required for jet injection could have a passage through which it can move. The hollow shaft is called the inner tunnel, and its diameter is 0.144 $D$, which is about 57% of the entire hub diameter.

From the inner tunnel to the propeller r/R = 0.5, it consists of the without a jet section, allowing water to rise up to the slit. From r/R = 0.5 to 0.9, the propeller is composed of with a jet section, and jets are injected through a lit. There is no tunnel inside the section above r/R = 0.9 because water does not need to move there.

2.2. Experimental Setup

A model test was carried out in Inha university towing tank. It has a length of 50 m, a width of 4 m, and a depth of 1.5 m. The maximum allowable capacity of the measuring equipment for a propeller open water test (POW) possessed by Inha university is 50 N of thrust and 2 N∙m of torque. Until now, experiments using propellers that inject a jet have never been carried out, so a new type of experimental equipment was manufactured using the existing POW equipment. Figure 3 shows a diagram of the experimental equipment used in this study.

To inject water with a propeller, a pump was attached to the back of a towing carriage to suck in water. The position of the pump is as far behind the propeller as possible to minimize the influence on the propeller. A flow-rate control valve was attached between the pump and the propeller to control the flow rate injected from the propeller. In order to measure the adjusted flow rate, a pressure sensor was added to the passage through which water flows through the propeller to measure the pressure inside the pipe. The flow rate injected from the propeller was obtained by calibrating the pressure and flow rate.

Since it was impossible to put water directly into the rotating propeller, a chamber was created to puts water through the propeller. The chamber was filled with water in POW equipment with two oil seals. There were total of four holes in the propeller shaft, two holes in the chamber and others in the propeller position. As the propeller rotates, the shaft also rotates, thrust and torque are measured by sensors connected to the shaft. Water enters the hole in the rotating shaft in the chamber and is directed to the propeller along the shaft due to the pressure in the chamber.

In the chamber, the two oil seals not only withstand the pressure in the chamber but also enclasp the rotating shaft properly so that it does not interfere with measuring the thrust and torque. Finally, the water moving along the shaft is put into the propeller through the remaining two holes mentioned above and injected through the slit of the propeller through the tunnel.

2.3. Experimental Conditions

Using the mass flow rate measured using a pressure gauge and the jet velocity, the jet momentum injected from the slit is expressed as the jet momentum coefficient (C_j) as shown in Equation (1).

$$C_j=\frac{\dot{m}{V}_{jet}}{\frac{1}{2}\rho S{V}_R^2}$$

(1)

$\dot{m}$ is the mass flow rate, $V_{jet}$ is the velocity of the jet injected from the slit, $\rho$ is the density, $S$ is the surface area of the propeller, and $V_R$ is the relative velocity at r/R = 0.7 of the propeller. The jet velocity from the slit can be obtained through the flow rate.

Since the pump is attached to the towing carriage and moved together, the volume of water entering the pump varies depending on the towing speed. As a result, the jet momentum coefficient changes for each advance coefficient. The average jet momentum coefficient of the experimental conditions is 0.00420, and the jet momentum coefficient obtained using a pressure gauge is set equal to the computation conditions.

Table 2. Experimental conditions.

JA	RPS	U(m/s)	${\mathit{C}}_{\mathit{j}}$	Re
0.1	8	0.2	0.0/0.00429	2.471 × 105
0.2		0.4	0.0/0.00428	2.479 × 105
0.3		0.6	0.0/0.00424	2.591 × 105
0.4		0.8	0.0/0.00418	2.509 × 105
0.5		1.0	0.0/0.00415	2.531 × 105
0.6		1.2	0.0/0.00407	2.559 × 105

shows the experimental conditions. The experimental conditions were selected to increase the Reynolds number as much as possible within the allowable measurement range of the POW equipment. The Reynolds number used in this paper can be defined as Equation (2).

$$Re=\frac{c\sqrt{U^2+{\left(2\pi n{r}_{0.7R}\right)}^2}}{\nu }$$

(2)

$U$ is the advance speed of propeller, $n$ is the rate of rotation (in RPS) and $\nu =\rho /\mu$ the kinematic viscosity. In this study, RPS was fixed at 8 RPS, and the advance coefficient ($J_A=U/nD)$ was changed by the advance speed. Due to the simple shape of the propeller, the thrust is a negative value after $J_A$ = 0.6. Therefore, the experiment was performed only up to $J_A$ = 0.6.

2.4. Numerical Modeling

In this study, computation was performed using commercial CFD software, STAR-CCM+ v13.06. Implicitly unsteady, incompressible flow was selected as the physical model for computations. The continuity equation and Reynolds average Navier-Stokes (RANS) equations were used as the governing equations and can be expressed in the form of integral equations, as shown in Equations (3) and (4).

$$\frac{d}{dt}{{\displaystyle \int }}_{\mathsf{\Omega }}^{}\rho d\mathsf{\Omega }+{{\displaystyle \int }}_{\mathrm{S}}^{}\rho u_i{n}_{i}dS=0$$

(3)

$$\frac{d}{dt}{{\displaystyle \int }}_{\mathsf{\Omega }}^{}\rho d\mathsf{\Omega }+{{\displaystyle \int }}_{\mathrm{S}}^{}\rho u_i{n}_{i}dS={{\displaystyle \int }}_S^{}({\tau }_{ij}{n}_j-p{n}_i)dS+{{\displaystyle \int }}_{\mathsf{\Omega }}^{}\rho b_{i}d\mathsf{\Omega }$$

(4)

$u_i$ and $b_i$ represent the tensors of velocity and volume, respectively. $p$ is the pressure and ${\tau }_{ij}$ is defined in Equation (5) as the effective stress due to viscosity and turbulence.

$${\tau }_{ij}={\mu }_e\left[\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\frac{2}{3}{\delta }_{ij}\frac{\partial u_k}{\partial x_k}\right]$$

(5)

Model-scale propellers cannot use turbulence simulators in resistance tests, so turbulent and laminar flow areas coexist. As a result, it is difficult to analyze a fully turbulent model, so there are many studies that apply a transition model. Baltazar et al. [19] used a fully turbulent model and transition model for the $SST k-\omega$ model and compared them with paint-test results. It was confirmed that the flow pattern was improved when the transition model was used. After that, Baltazar et al. [20] analyzed the turbulence behavior of the turbulence model and the transition model for several Reynolds number. Taranov et al. [21] and Bhattacharyya et al. [22] showed that the result of the transition model was more similar to the experiment by comparing the POW test result corresponding to the Reynolds number of the transition region and the computation result using the fully turbulent model and the transition model.

Considering the Reynolds number of the experimental conditions performed in this study, it corresponds to the transition region. Considering the results of previous studies, it is judged that the calculation of this study is appropriate to use the transition model. Therefore, the computations were performed by additionally setting a transition model, and the $SST k-\omega$ model and gamma transition model were used.

Figure 4 shows the domain and boundary conditions used in the computation. The inlet condition is set to a velocity inlet, and the outlet condition is set to a pressure outlet. Except for the inlet and outlet conditions, all of the surfaces are far enough away from the propeller so as not to affect the calculation, and a slip-wall boundary condition was applied. In the same method as in experimental conditions, the modeling was performed so that the water for jet injection could flow into the propeller through the shaft. A mass flow inlet boundary condition was given to the end of the propeller shaft, and the mass flow rate measured in the experiment was set equally in computations. Figure 5 shows the grid system used in the numerical simulations of this study. A Self-propelled method where the propeller and grid around the propeller rotate together was used for propeller rotation and the timestep of the simulations was set to the time of the propeller rotating 2°.

A grid dependency test was conducted to determine the reliability of the numerical analysis. A total of 4 grid sizes were considered, and each grid size is shown in

Table 3. Grid size for grid dependency test.

Grid Type	Grid Size
Coarse	1,315,159
Medium	2,119,080
Fine	3,020,276
Very fine	5,938,176

. The test was operated at an advance coefficient of 0.1 and the convergence of $K_T$ and $10K_Q$ was compared. $K_T$ and $10K_Q$ can be defined as:

$$K_T=\frac{T}{\rho n^2{D}^4}$$

(6)

$$10K_Q=\frac{10Q}{\rho n^2{D}^5}$$

(7)

where $T$ is the total thrust of the propeller, and $Q$ is the total torque of the propeller. Since there are too many variables to be considered when describing the inner structures, it is difficult to accurately test them, so a grid dependency test was conducted using a propeller with only a blade without internal structures (a normal propeller).

The grid dependency test results are shown in

Table 4. Numerical uncertainty analyses from grid convergence at J_A = 0.1.

	${\mathit{K}}_{\mathit{T}}$	$10{\mathit{K}}_{\mathit{Q}}$
$GC{I}_{fine}$	0.54%	0.14%
$GC{I}_{very fine}$	0.06%	0.02%

and Figure 6. The Grid Convergence Index (GCI) can be found in the study by Celik et al. [23]. Both the fine grid and very fine grid showed high convergence, but the fine grid was adopted in consideration of the computation efficiency. Therefore, all subsequent computations used the fine grid system. An additional grid was required to model inner structures, and about 4.1 M grid elements were used for the computations.

3. Results

3.1. Comparison of Experimental and Computation Results

Figure 7 shows a comparison of the results of the experiment and numerical computations under the condition of jet injection and the condition without jet injection. As described above, since the flow rate injected from the propeller cannot be controlled, $C_j$ is not constant for each advance coefficient. In Figure 7a, it can be seen that the results of the experiment and computation are generally similar. Compared with the experimental results at high advance coefficient, the agreement is relatively high, whereas at low advance coefficient, the error tended to increase. As can be seen in Table 2, this appears to be an error that happens when an experiment is performed at low speed.

In the case of jet injection, the thrust and torque tend to decrease in both the experiment and computation. As can be seen in Figure 7b, the higher the advance coefficient, the lower the efficiency is. Although the error is relatively large at the low advance ratio, the overall trend of the $K_T$ and $10K_Q$ curves are similar. When the trends of the jet-injected thrust and torque reduction are compared, the numerical analysis and the experiment shows similar trends. After that, through computation results, the cause of the decrease in thrust and torque during jet injection was analyzed.

In general, when analyzing propeller performance through numerical analysis, the changes in thrust and torque are compared using pressure and wall shear stress contours. However, when a jet is injected, the flow distribution is different from that of a general propeller. Therefore, there is a limit to analyzing the performance change of a propeller using pressure and wall shear stress as in the existing method. Thus, in this study, a function of thrust and torque was created by separating the pressure and wall shear stress into x, y, and z components and superposing them. This function means the thrust and torque acting on each surface mesh. For all surface meshes, this function multiplied by the surface area $\left(\mathsf{\Delta }\mathrm{s}\right)$ of each surface mesh is summed to become the thrust and torque acting on the entire propeller. This function was expressed by the thrust per unit area (PUA) and torque PUA, thrust PUA $\left(T_{PUA}\right)$ and torque PUA $\left(Q_{PUA}\right)$ can be defined by Equations (8) and (9) as follows.

$$T={\displaystyle \sum }{T}_{PUA}\mathsf{\Delta }\mathrm{s}$$

(8)

$$Q={\displaystyle \sum }{Q}_{PUA}\mathsf{\Delta }\mathrm{s}$$

(9)

Figure 8 and Figure 9 compare the thrust PUA and torque PUA with jet injection or without it at an advance coefficient of 0.4, at which the propeller efficiency is the highest. Changes in thrust and torque are clearly shown on the suction side where the jet is injected, while there is almost no change on the pressure side. It can be confirmed that the jet injected on the suction side does not affect the pressure side.

The change in thrust and torque with and without jet injection is the largest around the slit, and the change is particularly large above r/R = 0.6. When not injecting a jet, high thrust and torque occurred behind side of the slit (between the slit and the trailing edge). When injecting a jet, the area where the thrust and torque occur increased, but the maximum result has a decrease in value. Not only that, but the same tendency is also shown on the front side of the slit (between the slit and the leading edge). When not injecting a jet, the thrust and torque PUA were high on the front side of the slit, while when injecting a jet, their values were reduced. To analyze the causes, the velocity distributions in the center of the slit were compared.

Figure 10 shows the tangential velocity distribution from the center of the slit from r/R = 0.5 to 0.9, where the slit exists. The positive tangential velocity is the velocity in the direction of rotation. It can be confirmed that at all r/R, there is a positive velocity distribution when the jet is not injected. This means that when the propeller rotates, absorbed flow is generated through the slit of the propeller into the inner structure. When injecting a jet, the velocity distribution appears similar to not injecting jet until r/R = 0.6. After r/R = 0.6, the velocity decrease but still shows a positive velocity component. After r/R = 0.82, a negative velocity component appears.

The reason why these velocity distributions are displayed can be found in the direction of rotation of the propeller and the shape of the slit. Since the slit of the propeller faces in the opposite direction to the rotation direction, when the propeller rotates, low pressure is generated in the inner structure. Therefore, a flow of relatively high pressure absorbed from the outside to the inside is generated. With a jet, the speed is reduced by offsetting the velocity of suction due to the flow generated in the internal structure. It can be confirmed that these velocity changes are mainly displayed at high r/R due to the centrifugal force generated by the rotation of the propeller. The flow around the blade section was compared in order to analyze the cause of the change in thrust and torque due to jet injection in detail.

Figure 11 shows the nondimensionalized tangential velocity divided by the relative velocity at r/R = 0.73, where the changes in thrust and torque are large. Looking at Figure 11a, it can be confirmed that when the jet is not injected, an absorbed velocity distribution is generated in the slit. High thrust and torque appeared in a small area just in front of the slit where water is rapidly drawn in.

But looking at Figure 11b, not only did the velocity of suction decrease when injecting a jet, but the effect of the jet caused a change in the slit’s rear velocity distribution. This is a phenomenon that is displayed when pushing out the flow that is locally absorbed by the flow injected inside the propeller, which causes thrust and torque to occur over a wide area. In addition, the flow velocity decreased immediately in front of the slit, the downwash could not be guided, the velocity of the flow on the hydrofoil became relatively slow, so the thrust and torque at the front side of the slit decreased.

The injection volume of the experimental conditions is the maximum volume allowed by the experimental equipment and propellers with lower slit height than 1.0 mm are hard to manufacture, so additional experiments are difficult. In addition, when comparing the results of the experiment and computation, an error occurs at low advance coefficient, but the tendency of the decrease in thrust, torque, and efficiency generated during jet inject is similar, so it judged that the results of computations can be trusted. Therefore, the higher injection volume and the changed according to the slit height was performed only by computations.

3.2. Performance Variation with Slit Height and Jet Injection Volume

Propellers with the slit heights of 0.2 mm and 0.6 mm were designed to analyze the change in performance according to the slit height. Figure 12 shows the geometry of the hydrofoil for each slit height. The injection range is the same for all three propellers at r/R = 0.5 to 0.9, and the shape of the propeller is slightly different around the slit depending on the height of the slit. The remaining shapes are all the same. The computations were performed while changing $C_j$ in order to evaluate the change in performance according to the injection volume.

Table 5. Computation conditions according to the slit height.

$h_S$ (mm)	1.0		0.6		0.2
$A_S$ (mm2)	48.663		29.199		9.733
$C_j$	$\dot{m}$ (kg/s)	$V_{jet}$ (m/s)	$\dot{m}$ (kg/s)	$V_{jet}$ (m/s)	$\dot{m}$ (kg/s)	$V_{jet}$ (m/s)
0.000	-	-	-	-	-	-
0.050	0.66	6.85	0.52	8.84	0.29	15.31
0.125	1.05	10.83	0.81	13.98	0.47	24.21
0.200	1.33	13.70	1.03	17.68	0.59	30.63

shows the computation conditions for each slit height. Since the injection range is constant even if the height of the slit changes, the slit area is proportional to the scale of the slit height ($\lambda$). $C_j$ is the product of $\dot{m}$ and $V_{jet}$ in Equation (1), so $V_{jet}$ is proportional to $1/\sqrt{\lambda }$, and $\dot{m}$ is proportional to $\sqrt{\lambda }$.

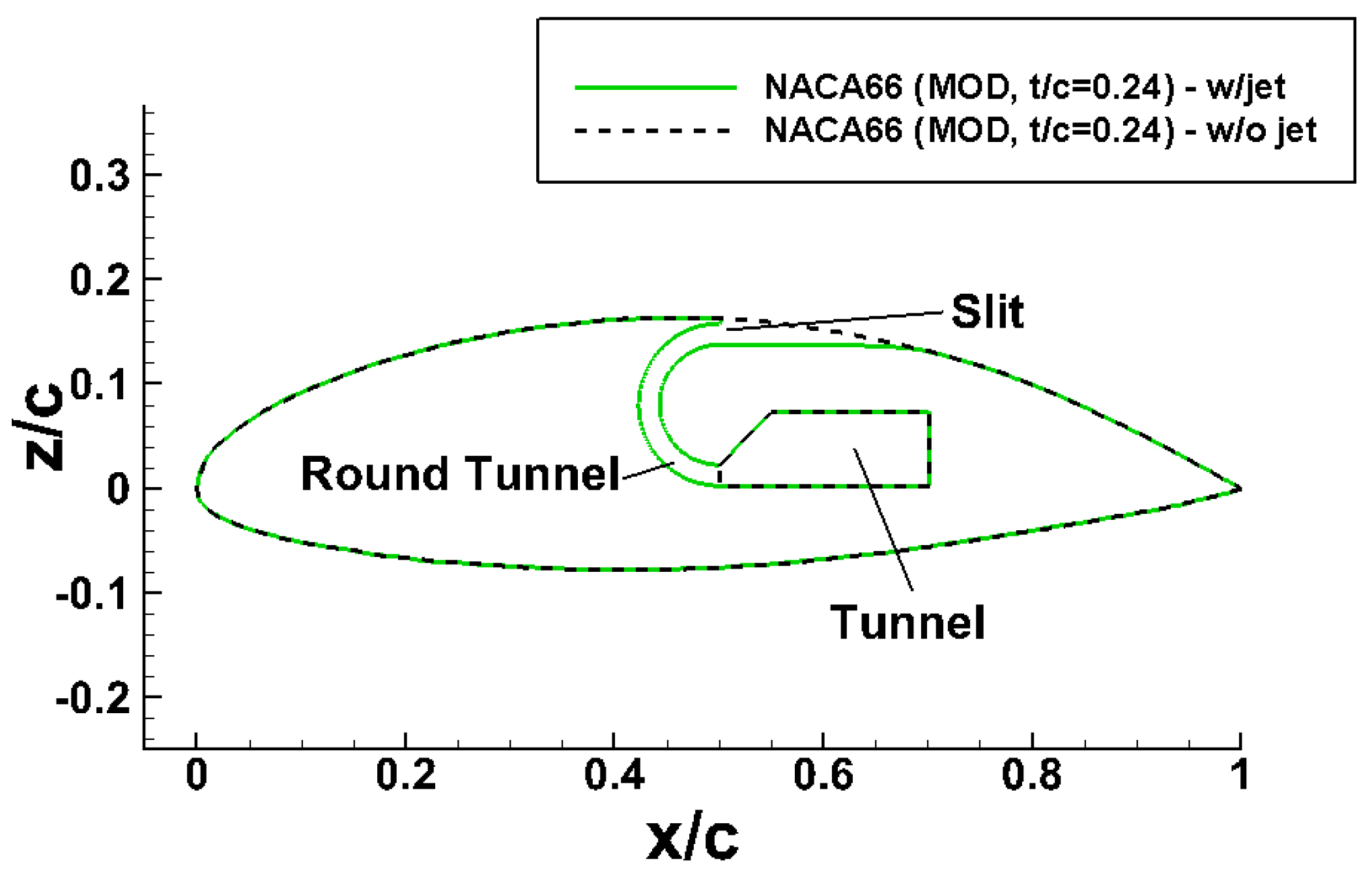
Figure 13 shows the names of each part of the Coanda propeller. The slit, round tunnel, and tunnel are combined into an inner structure, and all the remaining parts of the propeller except the inner structure are called a blade. We compared the thrust and torque for each. Figure 14 shows $K_T$ according to $C_j$ for each slit height. It can be confirmed that the thrust increases for all the slit heights as $C_j$ increases. In the case of the inner structure, the thrust does not differ greatly depending on the height of the slit. Naturally, most of the thrust generated by the propeller occurs from the blade.

When the jet is not injected, the highest thrust is displayed at $h_S$ = 0.2 mm, which is a phenomenon manifested by the hydrofoil shape. Looking at Figure 12, there is a part where the hydrofoil is cut by the slit in the with jet section. The lower the slit height, the more the existing hydrofoil shape will be maintained, so most will appear when the jet is not injected in the lowest slit height. However, although the thrust increase appears differently depending on the slit height, most thrust appears when $C_j$ = 0.2 and $h_S$ = 1.0 mm.

Figure 15 shows the thrust PUA and velocity distribution of the propeller surface by $C_j.$ Only the negative tangential velocity contour is shown for convenience to see the jet distribution. The jet injection distribution is different according to the slit height. When $h_S$ = 0.2 mm, it can be confirmed that the jet injected from the slit is generated in a narrow ad fast flow, and the jet rides to the end of the blade, where it does not separate due to the Coanda effect. In addition, the small slit area increases the pressure of the inner structure, resulting in a pattern in which jets are injected from the entire slit. In contrast, when the height of the slit is increased, the area of the slit is increased, and the jet injection velocity is reduced. As a result, the Coanda effect causes the jet to flow on the blade, but it is relatively separated and disappears quickly. The jet injection pattern is also concentrated at high r/R due to the centrifugal force caused by the rotation of the propeller.

It can be confirmed that the lower the height of the slit, the closer the region where the thrust is generated is to the slit. Looking at Figure 12, there is a surface that is cut so that the jet injected from the slit can flow on the hydrofoil surface. This surface has a larger curvature as the height of the slit increases. When a jet is injected, downwash is induced at this part due to the Coanda effect, thrust is generated at the surface that is cut. It can be seen that the downwash induced in the front of this slit increases as $C_j$ increases.

Due to hydrofoil geometry and the pattern of the jet, which is displayed differently according to the height of the slit, the tendency of thrust increment also appears differently according to the height of the slit. Comparing the thrust generated at the same $C_j$, when $h_S$= 1.0 mm, high thrust is concentrated in a narrow at high r/R, and when $h_S$ = 0.2 mm, it is distributed over the entire slit. When $h_S$ = 0.6 mm with a medium slit height, the thrust appears in the entire slit, and at the same time, the thrust is partially concentrated at high r/R. This can be analyzed by the effect of jet thickness due to the centrifugal force as in the previous case.

When $h_S$ = 0.2 mm, the speed of the jet is very high, but the thickness of the jet is thin, so it does not induce a large downwash when flowing on a curved surface. On the other hand, when $h_S$ = 1.0 mm, when jet is thick and flow on a curved surface, the downwash is greatly guided, and high thrust is generated at the same time. Such a tendency appears at the same time even when $h_S$ = 0.6 mm. Therefore, as shown in Figure 14, the thrust is the highest at low $C_j$, because the jet induces the downwash of the entire slit at $h_S$ = 0.2 mm. But the higher the mass flow rate, the greater the amount of induced downwash is at $h_S$ = 0.6 mm and $h_S$ = 1.0 mm because of the jet thickness and large curvature, the thrust is higher than at $h_S$ = 0.2 mm.

Figure 16 shows the velocity distribution at the center of the slit for each $C_j$. When $h_S$ = 0.2 mm, it can be confirmed that the velocity change is not largely based on r/R, and the jet with the fastest velocity is injected in the entire slit. However, when $h_S$ = 0.6 mm, the jet is injected over the entire slit like at h_S = 0.2 mm, but there is a flow that is absorbed into the inner structure at low r/R. In addition, due to the centrifugal force generated by the rotation of the propeller, the flow velocity of the jet increases as r/R increases. Similarly, when $h_S$ = 1.0 mm, the velocity change due to r/R appears the largest. A high r/R, a jet with a faster speed is generated compared to $h_S$ = 0.6 mm, and there is a flow that is induced into the inner structure until r/R = 0.6. These jet injection patterns are shown in the same way as $C_j$ increases.

Figure 17 shows the change of torque by $C_j$. It can be confirmed that the torque on the blade tended to increase at all slit heights as $C_j$ increased in Figure 17b. However, a large decrease in torque appeared in the inner structure, and the total torque tended to decrease as $C_j$ increased. It can be seen that the jet is injected in the direction opposite to the direction of rotation of the propeller, and a moment is generated in the direction of the rotation of the propeller. Therefore, a decrease in torque appears in the inner structure. The decrease in these torques appeared most at $h_S$ = 1.0 mm, and it was analyzed by the jet injection pattern. This phenomenon appeared because the jets are concentrated at high r/R, so the jet moment arm is largest.

In Figure 18, the torque PUA distribution by jet injection becomes almost the same as the thrust distribution. Similar to the thrust, behind the slit, a large torque increase is shown when jet injection guides the downwash, and the mass flow is concentrated. The jet injected from the slit generates thrust from the surface of the blade while guiding the downwash by the Coanda effect, and at the same time, higher wall shear stress is generated by the jet, so the distribution of thrust and torque is similar. However, in the case of wall shear stress, the flow near the wall is dominated by the influence of velocity particular. Therefore, as $C_j$ increased at all slit heights, so did the wall shear stress. Therefore, unlike Figure 14b, it can be confirmed in Figure 17b that the lower the slit height, the more the torque on the blade tended to increase.

Figure 19 shows the distribution of torque PUA generated in the inner structure. The surface in the leading edge direction is defined as “outside,” and the surface in the trailing edge direction is defined as “inside.” When $h_S$ = 1.0 mm, the jets are concentrated at high r/R, as described above, which greatly reduces the torque in the round tunnel at outside. However, in the case of the tunnel, the torque generation area is not large compared to other propellers. At $h_S$ = 0.6 mm, compared to $h_S$ = 1.0 mm, the jet injection is dispersed throughout the slits, and the torque does not decrease significantly in the round tunnel. Even in the case of tunnels, torque appears in a relatively large area compared to $h_S$ = 1.0 mm. At $h_S$ = 0.2 mm, as explained earlier, the slit area is narrow, and the pressure inside the inner structure increases. As a result, depending on the direction of the round tunnel, negative torque is generated in the round tunnel at outside, and positive torque generated in the inner round tunnel, which cancel each other out.

In order to inject a jet, additional power is required from the pump. In order to calculate the power of the pump, the head ($H$) of the pump must be considered. The head is the energy of a fluid of unit weight and can be expressed as in Equation (10).

$$H=H_p+H_v+H_l$$

(10)

The potential head ($H_p$) is the difference between the potential energy of the inlet and the potential energy of the outlet in the propeller structure, which is the same as the difference in the depth of the inlet and outlet. The velocity head ($H_v$) also is the difference in kinetic energy between the inlet and outlet. Finally, the head loss ($H_l$) is the energy that the fluid flowing in the internal structure loses by friction or collision with the wall surface.

In this study, for simple comparison, it is assumed that the depths of the inlet and outlet in the propeller structure are the same, and the there is no energy loss due to friction or collision with the wall surface. Therefore, the head of the pump required to inject the jet is considered only with the velocity head and can be calculated by Equation (11).

$$H=\frac{V_{jet}^2}{2g}$$

(11)

$$P_{Pump}=\dot{m}gH\frac{1+\alpha }{{\eta }_{Pump}}$$

(12)

Using the head of pump obtained in Equation (11), the power of the pump can be obtained as in Equation (12). $\alpha$ is the margin ratio, and ${\eta }_{Pump}$ is the efficiency of the pump. In this study, the margin ratio is assumed to be 0, and the pump efficiency is assumed to be 1 for simple comparison. The efficiency of the propeller considering the power of the pump is the same as in Equation (13).

$${\eta }_O=\frac{TU}{2\pi nQ+P_{Pump}}$$

(13)

Table 6. The comparison of propeller performance change according to C_j at each slit height.

${\mathit{h}}_{\mathit{S}}\left(\mathbf{mm}\right)$	${\mathit{C}}_{\mathit{j}}$	${\mathit{K}}_{\mathit{T}}$	$\mathbf{\Delta }{\mathit{K}}_{\mathit{T}}/{\mathit{C}}_{\mathit{j}}$	$10{\mathit{K}}_{\mathit{Q}}$	$\mathbf{\Delta }10{\mathit{K}}_{\mathit{Q}}/{\mathit{C}}_{\mathit{j}}$	${\mathit{P}}_{\mathit{P}\mathit{u}\mathit{m}\mathit{p}}\left(\mathbf{W}\right)$	${\mathit{\eta }}_{\mathit{O}}$
1.0	0.0	0.055	-	0.077	-	-	0.454
	0.05	0.081	0.518	0.037	−0.797	15.60	0.591
	0.125	0.113	0.467	−0.067	−1.153	61.64	0.556
	0.2	0.138	0.414	−0.170	−1.237	124.76	0.385
0.6	0.0	0.060	-	0.079	-	-	0.487
	0.05	0.086	0.524	0.069	−0.192	20.13	0.412
	0.125	0.117	0.453	0.020	−0.466	79.58	0.271
	0.2	0.137	0.387	−0.039	−0.590	161.56	0.184
0.2	0.0	0.063	-	0.079	-	-	0.507
	0.05	0.091	0.566	0.076	−0.066	34.87	0.311
	0.125	0.114	0.412	0.038	−0.328	137.84	0.152
	0.2	0.132	0.346	−0.011	−0.451	278.96	0.096

shows the change in propeller performance due to the slit height and $C_j$. Compared with the condition not injecting a jet, the difference of $K_T$ and $10K_Q$ at each $C_j$ is compared. Low $C_j$ has the highest increases in thrust by inducing a downwash across the slit at high jet speed. However, as the results confirmed earlier, as $C_j$ increases, $\mathsf{\Delta }{K}_T/C_j$ increases when the jet thickness is thick ($h_S$ = 0.6 mm and $h_S$ = 1.0 mm). Even with the same $C_j$ (that is, the momentum of the jet injected from the slit is the same), the thrust increase appears different depending on the hydrofoil geometry of high curvature and thickness of the jet.

The decrease in torque appeared larger when the slit height was higher for all $C_j$, and it was confirmed by previous results that this due to the injection pattern of the jet. The increase in thrust and the decrease in torque are not linear based on $C_j$ for all slit heights, and the higher $C_j$ is, the smaller the increase in thrust is, and the larger the decrease in torque is. At the same $C_j$, the power of the pump is the highest at $h_S$ = 0.2 mm. As can be seen in Table 5, the slit area is small, and the jet speed is the fastest, which lead to increase in the required power of the pump. Not only that, due to the injection pattern, but the reduction in torque is also not very large, so the efficiency considering the power of the pump is reduced for all $C_j$. However, when $h_S$ = 1.0 mm, the efficiency of the propeller increased when injecting a jet. This result is found not only because the torque is greatly reduced through jet injection, but also because the jet speed is relatively slow, and the required power of the pump is small.

3.3. Comparison with Normal Propeller

In order to examine the potential of a jet injection propeller as an ESD, it is necessary to make a comparison with a conventional screw propeller that does not inject a jet. Since the design speed of a ship is fixed, the thrust that a propeller must have is fixed, so the thrust was identified in a normal propeller to compare the efficiency. From the previous results, it was confirmed that when injecting a jet, the jet induces a downwash flow, and thrust is generated. Therefore, the pitch distribution of a normal propeller is changed so that the actual angle of attack is larger than that of Coanda propeller. The actual angle of attack is 3° at r/R = 0.25 to 0.5 and 4° at r/R = 0.5 to 1.0 in the Coanda propeller, but it is 4° at all r/R in the normal propeller. After that, the jet injection volume of the Coanda propeller was adjusted to identify the thrust with the normal propeller, and the results were compared.

3.3.1. NACA66 (MOD, t/c = 0.24) Propeller

By adjusting the jet injection volume for the height of each slit, the difference from the thrust produced by the normal propeller was identified within 1%.

Table 7. Performance comparison of Coanda propeller with thrust identify of normal propeller (NACA66 (MOD, t/c = 0.24)).

$\mathit{T}\mathit{y}\mathit{p}\mathit{e}$	${\mathit{C}}_{\mathit{j}}$	${\mathit{K}}_{\mathit{T}}$	$\mathbf{\Delta }{\mathit{K}}_{\mathit{T}}/{\mathit{C}}_{\mathit{j}}$	$10{\mathit{K}}_{\mathit{Q}}$	$\mathbf{\Delta }10{\mathit{K}}_{\mathit{Q}}/{\mathit{C}}_{\mathit{j}}$	$\dot{\mathit{m}}(\mathbf{kg}/\mathbf{s})$	${\mathit{V}}_{\mathit{j}\mathit{e}\mathit{t}}(\mathbf{m}/\mathbf{s})$	${\mathit{P}}_{\mathit{P}\mathit{u}\mathit{m}\mathit{p}}\left(\mathbf{W}\right)$	${\mathit{\eta }}_{\mathit{O}}$
Normal	-	0.073	-	0.087	-	-	-	-	0.534
$h_S$ = 1.0 mm	0.0	0.055	-	0.077	-	-	-	-	0.454
	0.034	0.073	0.505	0.057	−0.602	0.55	5.69	8.94	0.543
$h_S$ = 0.6 mm	0.0	0.060	-	0.079	-	-	-	-	0.487
	0.030	0.073	0.408	0.073	−0.181	0.40	6.89	9.54	0.446
$h_S$ = 0.2 mm	0.0	0.063	-	0.079	-	-	-	-	0.507
	0.013	0.073	0.809	0.081	0.184	0.15	7.77	4.56	0.487

shows a comparison between the computation results of the normal propeller and the change in performance after and before jet injection of the Coanda propeller. A comparison of the propeller performance changes through jet injection showed an increase in thrust and a decrease in torque at $h_S$ = 1.0 mm and $h_S$ = 0.6 mm, similar to the previous results. At $h_S$ = 0.6 mm, the efficiency increased by about 1.7% compared to the efficiency of the normal propeller.

However, when $h_S$ = 0.2 mm, the thrust increased, but the torque also increased. The reason for this result is that the thrust that have to be increased to identify the normal propeller is small, so the thrust can be identified even with a low injection volume. Therefore, the increase of the blade surface torque caused by the jet is larger than the moment generated by the jet. However, in the case of $h_S$ = 0.6 mm, the thrust increases, and the torque decreases, as in the case of $h_S$ = 1.0 mm, but $\mathsf{\Delta }{K}_T/C_j$ is the lowest compared to other propellers. As a result, the required power of the pump was also the largest, and the efficiency of the propeller was reduced the most.

In order to inject a jet and increase the thrust by the Coanda effect, it is necessary for the jet speed to be higher than the relative speed of the propeller. From the previous results, it was confirmed in Figure 7 and Figure 10 that the thrust decreases when the jet velocity is less than the propeller’s inflow velocity. Looking at Table 7 and Figure 20a, it can be seen that the jet velocity is injected faster the relative velocity of the propeller even at low $C_j$ when $h_S$ = 0.2 mm, and it is injected all over the slit. That is, the area of the slit is small, and it is easy to increase the speed of the jet, so the effect of improving the thrust through the jet can be seen even at al low injection volume.

However, in the case of $h_S$ = 1.0 mm and $h_S$ = 0.6 mm with high slit height, it can be expected that there is an injection volume range in which the thrust decreases because the jet velocity is less than the relative velocity of the propeller. In the case of $h_S$ = 0.6 mm, as in the case of $h_S$ = 0.2 mm, a jet is injected across the slit to generate thrust. However, looking at Figure 20a, jet injection hardly occurs around r/R = 0.5. That is, in the case of $h_S$ = 0.6 mm, the propeller efficiency is the lowest at low $C_j$, because the slit area is relatively large, and the additional injection volume is required to increase the jet injection speed at low r/R.

In the case of $h_S$ = 1.0 mm, the area of the slit is large, so the required power of the pump is low, and high thrust is generated due to the large thickness of the jet and hydrofoil geometry with high curvature, and the torque is greatly reduced due to the jet injection pattern. As a result, $C_j$ is the highest compared to the others, but the power of the pump is less than at $h_S$= 0.6 mm, and the efficiency of the propeller is also increased.

Figure 20b,c show the distribution of torque PUA and $-C_P$ of the propellers. Torque PUA appears to be concentrated in the area where jet injection is concentrated, like the thrust, as confirmed previously. Since thrust is mostly caused by the pressure difference between the pressure side and the suction side, the $-C_P$ distribution is generally similar to that of the thrust PUA. In the case of the Coanda propeller, the angle of attack is smaller than that of the normal propeller, so the pressure drop in front of the slit is relatively small. But a pressure drop appears at high r/R, in the area where the jet is concentrated and induces downwash flow.

As the height of the slit decreases, the area that induces the downwash flow is closer to the slit due to the hydrofoil shape. In the case of $h_S$ = 0.2 mm, the downwash flow is induced in front of the slit, and a pressure drop appeared in front of the slit. The jet velocity is high, but the maximum pressure drop is relatively small due to the low thickness. There are various variables in designing propellers, but in this study, an analysis was performed after reducing the thickness to examine the effect on the thickness.

3.3.2. NACA66 (MOD, t/c = 0.12) Propeller

Figure 21 shows the hydrofoil geometry with reduced thickness compared with the NACA66 (MOD, t/c = 0.24) hydrofoil used in this study. The NACA66 (MOD, t/c = 0.12) has a thickness reduced by 1/2 from the previously used hydrofoil (NACA66 (MOD, t/c = 0.24)), and an internal structure was added. The location of the slit and the tunnel in the x-axis direction, and the area of the tunnel are the same. The size of the round tunnel decreases as the gap between the tunnel and the slit decreases. All other particulars except the thickness are the same. As in the previous method, the injection volume of each slit height was adjusted to identify the thrust of the normal propeller, and the performance change of the propeller was studied.

Table 8. Performance comparison of Coanda propeller with thrust identify of normal propeller (NACA66 (MOD, t/c = 0.12))

$\mathit{T}\mathit{y}\mathit{p}\mathit{e}$	${\mathit{C}}_{\mathit{j}}$	${\mathit{K}}_{\mathit{T}}$	$\mathbf{\Delta }{\mathit{K}}_{\mathit{T}}/{\mathit{C}}_{\mathit{j}}$	$10{\mathit{K}}_{\mathit{Q}}$	$\mathbf{\Delta }10{\mathit{K}}_{\mathit{Q}}/{\mathit{C}}_{\mathit{j}}$	$\dot{\mathit{m}}(\mathbf{kg}/\mathbf{s})$	${\mathit{V}}_{\mathit{j}\mathit{e}\mathit{t}}(\mathbf{m}/\mathbf{s})$	${\mathit{P}}_{\mathit{P}\mathit{u}\mathit{m}\mathit{p}}\left(\mathbf{W}\right)$	${\mathit{\eta }}_{\mathit{O}}$
Normal	-	0.060	-	0.064	-	-	-	-	0.601
$h_S$ = 1.0 mm	0.0	0.043	-	0.053	-	-	-	-	0.517
	0.052	0.060	0.330	0.005	−0.908	0.68	7.01	16.75	0.653
$h_S$ = 0.6 mm	0.0	0.045	-	0.052	-	-	-	-	0.550
	0.048	0.060	0.325	0.029	−0.476	0.50	8.64	18.79	0.431
$h_S$ = 0.2 mm	0.0	0.049	-	0.053	-	-	-	-	0.580
	0.036	0.060	0.322	0.040	−0.377	0.25	12.99	21.29	0.356

shows the performance comparison between the NACA66 (MOD, t/c = 0.12) propeller and the normal propeller. As the thickness of the hydrofoil decreased, its geometry changed, and $K_T$ decreased for the Coanda propeller and the normal propeller. The thrust that needs to be increased to identify the normal propeller is similar when compared to Table 7, but $C_j$ has increased overall. In Figure 21, the curvature of the hydrofoil decreases as the hydrofoil thickness decreases. Therefore, the curvature that the jet can follow is reduced, the induced downwash is reduced, and the jet injection volume to the thrust is increased.

In the case of the NACA66 (MOD, t/c = 0.24), the volume of jet injection is small, and at $h_S$ = 0.6 mm, the required pump power to inject a jet with a velocity faster than the relative velocity of the propeller is relatively large. But in the case of the NACA66 (MOD, t/c = 0.12) propeller, the required power of the pump is the highest at $h_S$ = 0.2 mm, where the jet speed is fast due to high injection volume. In addition, the increase in thrust and decrease in torque compared to the jet injection volume are also smallest, and the propeller efficiency was the lowest. However, in the case of $h_S$ = 1.0 mm, the efficiency increases by about 26.4% compared to the case without a jet, and by about 8.6% compared to the normal propeller. As the jet injection volume increased, not only did the thrust increase, but the moment generated by the jet was also large, resulting in a relatively large increase in efficiency.

In Figure 22, the thrust PUA, torque PUA, and $-C_P$ contour of the normal propeller and Coanda propeller with reduced thickness are compared. As the propeller thickness decreases, the overall curvature of the hydrofoil decreases. As a result, it can be seen that the inflow velocity at the front of the propeller is reduced. In addition, the area where the thrust is generated has moved toward the trailing edge of the propeller compared to Figure 20. This phenomenon is caused by the movement of the curved surface of the hydrofoil, which induces downwash flow in the process of manufacturing the hydrofoil, as shown Figure 21.

The $-C_P$ distribution also shows a pressure drop in the region where the mass flow is concentrated and downwash flow is strongly induced. However, compared to Figure 20c, the pressure drop in front of the slit is relatively small. Likewise, the curvature of the hydrofoil decreases, and the downwash induction of the jet increases. As in the previous results, even if the thickness decreased, the area where the pressure drop appeared decreased as the slit height decreased.

4. Conclusions

This study attempted to present the concept of a propeller that injects jets the propeller surface and predict its performance through experiments and computations. Experimental equipment including propellers was directly designed for jet injection, and we performed model tests and computations to compare the results. Experiments were performed with advance coefficients of 0.1 to 0.6, and in the results, it appeared that the thrust and torque decreased for all advance coefficients. When the jet injected, a flow that is induced into the internal structure from the suction side of the propeller occurs, appearing in thrust and torque. However, the jet injection velocity does not reach a higher value than the relative velocity of a propeller in experiment conditions, resulting in relatively reduced thrust and torque. This trend was observed similarly in both the computation and experiment, so it is judged that the result of computations can be reliable.

After that, the performance change according to the height of the slit was analyzed through computation. For all slit heights, the thrust tended to increase as the jet injection volume increased. This is the result of changing the pressure distribution on the blade surface due to the Coanda effect when jetting from the blade surface. According to the height of the slit, the pattern of jets injected from the slit was different. When the height of the slit was low, a jet with high speed was injected throughout the slit, and the increase in thrust was high at low $C_j$. However, due to the inject pattern, the moment generated by the jet was small, and the torque reduction was small.

When the height of the slit was high, the injected jet was concentrated at high r/R. In addition, the jet concentrated at high r/R led to an effect of increasing the moment arm, resulting in a significant decrease in torque. Also due to wide area of the slit, the jet speed was relatively small, and thus, the power required of the pump was small, resulting in an increase in the efficiency of the propeller, even when considering the efficiency of the pump. Comparing the change in lift and drag according to $C_j$, as $C_j$ increased, the decrease in torque increased, and the increase in thrust decreased. In other words, considering the power of the pump, it can be expected that if $C_j$ is too high, it will not be efficient.

The efficiency was compared by identifying thrust with the normal propeller for two cases of thickness. In the case of the NACA66 (MOD, t/c = 0.24) propeller with a relatively high thickness, the volume of the jet required to identify the thrust was small because the curvature of hydrofoil was large. In the case of $h_S$ = 1.0 mm, it was confirmed that the efficiency increases compared to the normal propeller, even when the power of the pump is included.

In the case of the NACA66 (MOD, t/c = 0.12) propeller with reduced thickness, the behind side of the hydrofoil has to be cut out due to the inner structure geometry of the hydrofoil, and as a result, the curvature decreased, and the induced downwash flow decreased due to the jet. As a result, the required jet injection volume was increased, but the torque reduction was larger at $h_S$ = 1.0 mm, which greatly increases the efficiency in (MOD, t/c = 0.06) propeller. Through these results, the possibility of improving the efficiency through jet injection on the propeller surface was confirmed.

Limitations of this study also exist. The computation results of this study will be less than the expected propeller efficiency when considering the margin or efficiency of the pump. In addition, the jet injection creates region where the pressure drop appears larger than that of the normal propeller in area with high curvature, and the cavitation performance is expected to decrease significantly. Also, as the propeller curvature changes according to the slit height, it is difficult to directly compare the performance change by jet injection alone, since it shows a correlated effect between jet injection and propeller in high curvature. However, through this study, it was possible to confirm the possibility of increasing the efficiency of the propeller when jets are injected from the surface of the propeller. In the future, research on hydrofoil geometry that can reduce the large pressure drop that appears during jet injection and research to optimize the geometry of the propeller and slit will be conducted to improve the cavitation and propeller performance.