Towards Productive and Ergonomic Order Picking: Multi-Objective Modeling Approach

Abstract

The logistics sector should strive for sustainability alongside productivity by protecting its order pickers’ health and welfare. Existing storage assignment models are mainly based on the criterion of order picking time and, to a lesser extent, the human factor. In the paper, a solution to a storage assignment problem using a multi-objective model based on binary integer linear programing is presented by developing a solution that considers order picking time, energy expenditure and health risk. The Ovako Working Posture Assessment System (OWAS) method was used for health risk assessment. The downside of solely health risk-optimization is that the average order picking time increases by approximately 33% compared to solely time-optimization. Contrary to this, the developed multi-objective function emphasizing time has proven to be promising in finding a compromise between the optimal order picking time and eliminating work situations with a very-high risk for injuries. Its use increases the time by only 3.8% compared to solely time-optimization while significantly reducing health risk.

1. Introduction

Our lives, work and development are primarily driven by trends, concepts and regional or global policies. In the fields of production and intra-logistics, among the most influential concepts are the lean approach, industry 4.0 and sustainability. In addition to these listed, due to the aging population, the increase in the number of musculoskeletal disorders (MSDs) and, last but not least, the pandemic events, the human factor is slowly coming to the fore. Therefore, there is a need to incorporate more aspects into systems modeling besides productivity and economic aspect. In manual work, there is a growing need to add at least the aspect of caring for workers’ physical health besides productivity. This can be beneficial for the most labor- and time-intensive operations like manual man-to-goods order picking [1,2], which is the central focus of this paper. The solution lies in development of a storage assignment model to minimize factors that noticeably influence on key performance indicators. The storage assignment method is a series of rules determining how items are assigned to storage locations [3].

In the following, we explain drivers for multi-objective optimization development, manual man-to-goods order picking, decision support models for storage assignment, the OWAS method in order to set the goals and structure of research work and the reasons for them.

1.1. Lean and Sustainability as Drivers for Multi-Objective Optimization Development

A lean approach is being introduced to production environments to decrease costs and increase productivity, which creates an intensified work pace and demands [4]. However, this does not increase the need for workers’ decision-making and self-organization in the workplace. Work becomes standardized, movements prescribed. Such work can become more or less burdensome. In a society where more and more companies are introducing lean, intensive work, this can be reflected in increased MSDs [5,6,7]. In Germany, for example, musculoskeletal and connective tissue disorders accounted for EUR 17.2 billion (EUR 17,200 million) of production loss (production loss costs based on labor costs) in 2016 and EUR 30.4 billion in loss of gross value added (loss of labor productivity), representing 0.5% and 1.0% of Germany’s gross domestic product, respectively [8]. Despite that, the main objective of decision support models and Warehouse Management Systems remains the reduction of the average distance the order picker needs to travel, thus lowering the order picking time [9] and increasing the number of picks per order picker.

We can achieve nearly the same order picking time with different proportions of overall traveling, searching and picking times for identical customer orders from different item layouts at storage locations. We assume that viable alternatives differ in contribution to order picker’s fatigue, workload, and proportions of postures with a negative impact on the worker’s physical health. Manual “man-to-goods” order picking requires manual material handling tasks, such as stretching, turning, lifting, lowering, squatting and carrying, and is considered highly repetitive because the cycle times are usually measured in seconds. Manual lifting and exposure to other ergonomic stressors are proven to be linked to low back pain [10,11,12,13]. Up to 80% of the population experiences low back pain approximately at least once in their lifetime [14,15,16]. The cost of temporary and permanent incapacity for work associated with manual material handling is an important, influential element for the industry [17].

Although this is often overlooked, the lean concept is not just about increasing productivity but also about improving safety. In some areas, like order picking, it is challenging to achieve productivity and safety simultaneously. Today, when the interaction of productivity and ergonomic suitability is still relatively unexplored, managers prefer not to talk about the potential detrimental impact of order picking on people’s wellbeing and even encourage overloading through the variable part of pay [18]. However, this problem cannot be omitted because the implemented optimization strategy within a logistic system must be consistent with workers’ consent and commitment for whole system efficiency [19]. Order picking activities can be seen in optimization aspects as one of the steps towards a sustainable organization without a waste of time [20] but still friendly to workers’ wellbeing. It is difficult to achieve consistent and conscious efforts toward successful lean implementation in a warehouse environment due to the diversity and high frequency of tasks with the differing workload, but not impossible when considering industry 4.0 based on digitalization. Research has already proven a positive correlation between lean manufacturing and industry 4.0 [21,22] with its essential information technology (IT) element. A warehouse management system could then be seen as a lean and sustainable solution all at once. It could inform order pickers about the achieved level of safe daily workload, load them with ergonomically acceptable sequences of tasks, and among others, propose a more ergonomically favorable picking sequence outside the rush periods. Therefore, it makes sense to explore the possibility of a multi-objective assignment model, which will help managers achieve high productivity while preserving order pickers’ physical health and have the potential to upgrade the warehouse management system’s optimization component.

1.2. Manual Man-to-Goods Order Picking

Over the last decade, we have witnessed the growth of e-commerce driven by digitalization, and more recently, a pandemic. Accordingly, the need for picking items listed on customers’ orders from locations in storage racks is growing and has become omnipresent. This activity is in 80% of warehouse environments performed manually by order pickers [23,24]. Most warehouses and distribution centers use a man-to-goods picking model according to which order pickers travel around the warehouse and collect items sequentially. The costs of these processes are relatively high. Some authors [25,26] report that they can account for more than 50% of warehouse operating costs. Today, order picking is mainly recognized as a cost, not adding value for the final customers. The key checked daily performance indicator for order picking is the cost per line ordered. This mindset is reflected in the managerial treatment of order picking, where concern for efficiency and searching for new workers to replace the absentees and those with burnout are at the forefront. With rising labor costs, an aging population, increasing sick leave costs and increasing efforts to motivate for quality work, the focus from the economy is slowly shifting to caring for the physical health of employees.

The research stream in the field of order picking optimization is mainly concerned with time optimization. It is generally acknowledged that the amount of time spent depends mainly on factors related to the work environment (job factors) and factors related to the individual worker (order picker’s factors). Figure 1 highlights the most frequently mentioned factors, which, however, also affect energy expenditure and health risk. The use of time optimization benefits in the increase in picks per time unit, as the same time order pickers spend more energy and repeat movements more frequently. Time optimization without built-in restrictions leads to workers’ burnout and/or MSDs occurrence. Energy consumption must not exceed the permanent capacity limit or the load at which even at 8 h of exposure, no harmful conditions occur. No postures should represent a high health risk for MSDs occurrence.

The turnaround occurs in 2016, when [9] integrated energy expenditure into the bi-objective optimization model in addition to time [27]. New scientific contributions [28,29] in solving the storage assignment problem in the last five years propose, justify, and take into account order picking time and additionally also energy expenditure and health risk. Adding energy expenditure and health risk results from the fact that they are dependent on many interrelated factors occurring during order picking. On the other hand, they are relatively measurable and resultant. The number of published scientific works including only order picking time in modeling leads before works combining order picking time and energy expenditure, which, however, are also no longer rare. Since 2016, a growing trend of scientific contributions that have added health risk to order picking time and energy expenditure in decision support models for storage assignment is emerging.

1.3. Decision Support Models for Storage Assignment

A recent literature review on picker routing revealed that in 83% of considered papers, straight or parallel shelves, which may be intersected by one or multiple cross aisles, were the subject of research [27,30]. This indicates the popularity and prevalence of such layouts in practice. The number of items collected per unit time, fatigue, and physical health of order pickers are greatly influenced by determining storage positions for individual types of goods, determining the sequence of picking items from storage racks and layout. In the literature on order picking, there is a noticeable trend towards developing decision support models focusing on the assignment of items to storage positions [1,30]. The assignment can be either random or based on specific criteria but always chosen to support an increase in the number of items picked per particular time unit or minimization of travel distance. Researchers have developed several storage assignment methods to shorten total fulfillment time. Three frequently in practice implemented examples are:

• An ergonomic storage assignment method by classifying items at different heights in storage locations using flow racks [31];
• A concept of golden zone storage, where high-demand items are stored in the area between a picker’s waist and shoulders [23,32];
• Modeling order picker’s fatigue/recovery level based on predicted energy expenditure rate calculated from results of monitoring heart rate [33].

The literature on storage assignment is focused on developing methods that reduce travel distance and order picking time which put warehouse managers in a precarious position because the results of the methods used do not inform them about health risks for operators [31]. Other objectives, such as minimizing order picker’s discomfort or the prevention of MSDs, have been mainly overlooked in managerial decision support models for the storage assignment problem [23] or have only very infrequently been discussed [34]. In contrast to the management-oriented literature, order pickers’ wellbeing has been studied in the ergonomics literature [9]. Several scientific works describe the manual order picking process as work in an environment that puts workers at risk of developing MSDs (e.g., [35,36]). Order picking activities require the use of all order picker’s body parts and thus creating a risk of various MSDs.

The recognized need to incorporate ergonomics or human factors issues into planning models for order picking in the scientific literature in 2015 [23] was followed by a growing number of published works in this area in recent years. Works on ergonomics can be divided into three research streams. First is oriented on physical ergonomics, second on cognitive ergonomics and third on organizational ergonomics. Because of the topic discussed in this paper, our research is limited to physical ergonomics. It studies human anatomical, anthropometric, physiological and biomechanical characteristics and their links to physical activity. Research works on order picking, including a focus on physical ergonomics, observe the handling of loads and postures.

Some multi-objective models, including time and health risk dimensions, are already proposed. A few of them are discussed in more detail in the following [9,27,28,29,37].

In [9], the authors analyzed the optimal allocation of items to storage locations to minimize total picking times and ergonomic strains, the latter based on the energy expenditure prediction model developed by [38]. In the next step, the rest allowance formulation of [38] is used to develop an integrated approach that considers both order picking time and energy expenditure. Researchers’ recommendations are valid for a specific order picking environment: a single-aisle consisting of a single shelf at a time, each item is stocked in a unique location, fixed and equally dimensioned storage locations, six different vertical and horizontal storage levels (0.25, 0.58, 0.94, 1.30, 1.63, 1.96 m), the depot (I/O point) at one end of the shelf, a return routing policy, walking speed 1 m/s, male operator: 75 kg, load of 0.2 kg per picked item. As authors already discover, further analyses of the impact of order profiles, especially the number of items (mass) to be picked per line of an order, on the relative efficiency of different storage assignment policies are required.

Harari et al. [17] found out in the laboratory experiment that the mass of the handled box, the initial lifting height, and the final lowering height significantly affected the lifting, carrying, lowering, and returning task times, and as such should be considered in the development of time prediction methods. In both the field and the laboratory experiments, the workers carried the box faster as the box mass increased. Further, the walking velocity for returning without a box was lower than the velocity for carrying the box in the laboratory experiment. Surprisingly, in their laboratory experiment, the worker’s height and weight did not significantly influence the task times. Konz and Rode [39] concluded similarly. That is why we think it makes sense to introduce several different masses and even sizes of loads into modeling.

Larco et al. [40] researched trade-off analysis between time-based function and ergonomics-based function. If [9] studied human factors through energy expenditure, ref. [40] studied workers’ discomfort using the Borg CR-10 scale [41] based on self-reporting. The authors propose a unified methodology to quantify and balance two potentially conflicting criteria at order picking. The first is the short-term economic criterion of minimizing total order-picking time (considering a location in an aisle, shelf height, quantity of a specific item to be picked, volume). The second is a human wellbeing criterion of minimizing average discomfort ratings. The recommendations are similar to [9], tied to a specific warehouse environment: order-picking, “pick-by-light”, zones, limited walking distances, retrieving time is dominant in the cycle time, items are picked from totes on shelves at three levels (from 0.2 to 1.90 m), the maximal mass of loads is 3 kg, and most picks involve single order lines. Numerical data were collected from WMS, and workers reported discomfort rate. The authors propose a simple heuristic that combines two criteria and the popularity of an item. The item should be preferably stored close to the depot and in the golden zone, whereby more frequent items are preferred for more favorable locations. The authors in [40] excluded the influence of mass from the model, which becomes less suitable for warehouses where heavier loads are manipulated. In their specific case, the results showed that volume is a better proxy than mass to handle complexities such as easiness to grab a product or ease retrieving a product from its location. The authors confirmed that picking outside the golden zone requires additional retrieving time.

These approaches [9,40] are valuable and beneficial but do not reveal how often an employee has been exposed to situations with medium or high risk for injuries like MSDs.

The missing aspect of the health risk was included in the analytical model [29] to assess metabolic cost using the energy expenditure concept and critical postures using the Ovako Working Posture Analysis System (OWAS) index. The model is one of the first attempts to integrate health risks and covers different warehouse racks for storing pallets. It does not respond to the challenges of picking small boxes in various dimensions and masses from a multi-shelf warehouse rack and the cost viewpoint is missing.

Another solution, including health risk, was proposed in the form of a heuristic storage assignment model [27], suggesting to minimise health risks based on the NIOSH lifting equation. The limitation of the proposal is that the NIOSH method is used in cases where more time is spent on manual material handling than on walking between items positions, which is a rarity in classical man-to-goods order picking. The NIOSH method is suitable for assessing health risk in zones rather than picking along long straight racks. An important contribution of [27] is that neglecting human factors and focusing primarily on time minimization can cause significant health risks.

The most novel and comprehensive work in the field under consideration introduced an integrated storage assignment method for man-to-goods order picking considering cost and human factors objectives [28]. The model includes three different pallet racks layouts and so still leaves an open research gap on the challenges of picking small boxes in various dimensions and masses from a multi-shelf warehouse rack. This model supports the correctness of using the OWAS method for health risk assessment in man-to-goods order picking environments in this paper.

Literature reviews (ours and [23,30,42]) suggest that efforts to establish a productive and at the same time safe order picking environment are emerging, but there is still a need for research. Previous research works do not answer when to use which type of optimization, how to balance weights of the individual objective functions in multi-objective models, do not explore the influence of different masses and sizes of loads, and models for different layouts are missing. We refer to the recent survey [43] for further readings on storage assignment.

1.4. The OWAS Method

When performing work, we strive to keep the local loads on the body segments as small as possible and to be within the permissible body loads. An objective assessment of physiological wellbeing can only be obtained with the help of established methods for assessing exposure to risk factors in the normal functioning of the human musculoskeletal structure. The impact of the performed movements on the occurrence of injuries is studied with ergonomics evaluation methods, including OCRA, the NIOSH lifting equation, OWAS, and the Borg-Scale [41,43,44], and others. The methods differ according to the data acquisition method, namely self-report, observation, and direct measurement [45]. In the Scopus database, we searched for scientific papers in the field of order picking to identify which ergonomic evaluation methods were already used and which method predominates in the frequency of use (

Table 1. Use of ergonomic evaluation methods in order picking.

Evaluation Method	Number of Categories Assessed	Scoring Scale	Scoring Range	Number of Risk Levels	Number of Papers in the Scopus Database	Sources
OWAS	4	discrete	1–4	4	6	[29,45,46,47,48,49]
REBA	9	discrete	1–15	5	4	[50,51,52,53]
RULA	10	discrete	1–7	4	5	[53,54,55,56,57]
NIOSH LI	8	continues	0< *	3	3	[45,48,58]

* In the NIOSH Lifting Index model, there is no theoretical limitation of the upper value of the lifting index level, nevertheless above results of 3, the risk level is considered the highest risk level.

).

We observed the use of four ergonomic evaluation methods. Between them, RULA and NIOSH LI are less appropriate for use in an analyzed working environment in this paper. OWAS is the most known and widely used in the scientific literature on order picking, although its authors initially did not envisage such an application. The OWAS method allows testing the optimization of order picking activities with a relatively simple biomechanical assessment model. Therefore, a simplified evaluation scheme can be advantageous when the method is used as a support in a complex optimization model. It is necessary to be aware that implementation is time consuming and that quality depends on the knowledge and training of the observer [3].

In the paper, the OWAS method was chosen according to the frequency of previous use in order picking, the description of the method and our positive experience in evaluating the work of order pickers.

Gomez-Galan and co-authors [46] reviewed OWAS. OWAS, an abbreviation for The Ovako Working Posture Assessment System, originates from Finland. Its reliability was confirmed on real examples from the industrial environment by a group of engineers. Afterward, the experts defined four health risk categories, the first related to normal postures without corrective activity recommendations. The second and third categories concerned postures with some risk with recommendations for corrective actions to be taken. The fourth category referred to unacceptable postures; immediate corrective measures are required [59].

The OWAS method has several purposes. An observer, with its help, identifies the frequency and time spent in the positions of the observed task. According to the standard procedure, the obtained assessment is a valuable starting point to make recommendations for corrective measures [59]. The OWAS identifies the four most common back postures, three arm postures, seven leg postures, and three handled load mass categories [59]. Each worker’s posture was assigned a four-digit code that depended on the classification regarding previously mentioned postures and the load [60]. The process of implementing OWAS consists of observing work tasks, codifying postures, assigning risk categories and proposing corrective actions [46]. OWAS is a simple and useful method, can be used by personnel from different fields, such as health, engineering, industry, etc., without specialized training [59] and is well documented [60]. Gomez-Galan and co-authors [46] draw attention to the limitations of the method. Several authors neither differentiated the right from left upper limbs, nor evaluated the parts of the body such as the neck, elbows, and wrists, had crude posture coding for the shoulders, took too much time to apply, and did not take into account repetition or duration of the sequential postures [60].

1.5. Goal and Structure

In the present paper, we consider the overall manual man-to-goods order picking activity of small boxes in various dimensions and masses from a multi-shelf warehouse rack through time, energy expenditure and health-risk viewpoints. It is an environment that has not yet been covered by previous research in terms of a comprehensive approach from economic and ergonomics perspectives. For health risk modeling OWAS method is used as it has already been shown to be appropriate in previous research.

We extend research work in the area of storage assignment models and contribute to the literature by:

• Considering overall order picking activity of small boxes in various dimensions and masses from a multi-shelf warehouse rack through time, energy expenditure and health-risk viewpoints. The inclusion of boxes with different masses and dimensions and different stock structures in terms of the share of light and heavy boxes in the total stock is original and provides managerial insight into the effects of using distinctive objective optimization functions;
• Developing a solution to a storage assignment problem using a multi-objective model including time, energy expenditure and health risk based on binary integer linear programing with the possibility of a different weighting of individual optimization criteria;
• Comparing the results of the popular with managers time based-objective function with the newly developed multi-objective function including time, energy expenditure and health risk in terms of the occurrence of situations that may endanger the physical health of order picker;
• Considering the applicability of the developed one- and multi-objective functions.

The paper structure is as follows: Section 2 defines the problem and develops the multi-objective model. The case study is described in Section 3, and the methodology for the experiment in Section 4. Section 5 is organized around results. The paper ends with a discussion in Section 6 and conclusions in Section 7.

2. Problem Description and Models Development

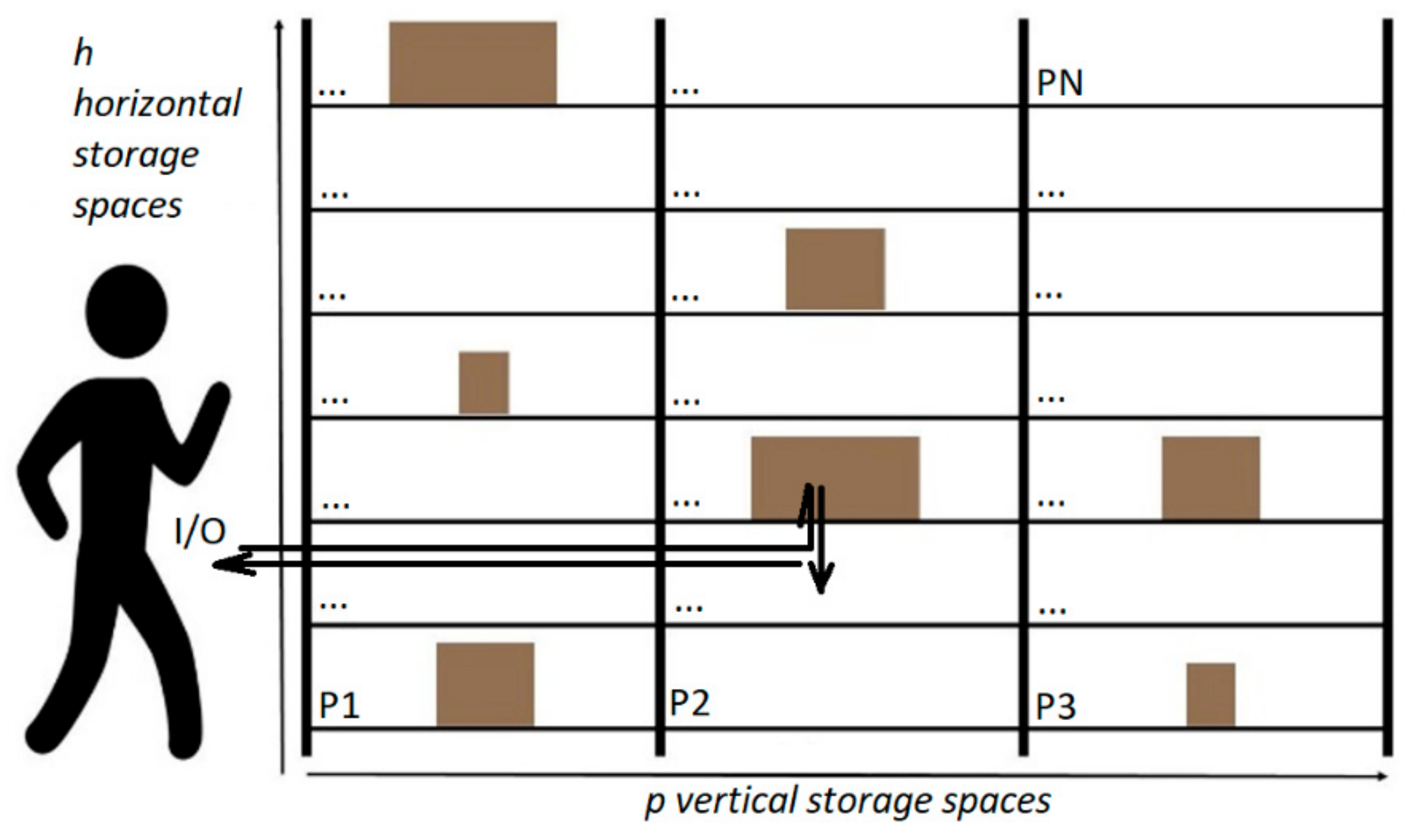
This paper studies the storage assignment problem for a manual man-to-goods order picking system. The purpose is to fill a theoretical warehouse with m different types of boxes. The theoretical warehouse consists of one arbitrarily long storage rack with h shelves on various heights and p horizontally positioned storage spaces (Figure 2). The depot (I/O point) is located at one end of the storage rack. The order picker picks orders using a return routing policy, where order pickers leave the aisles on the side where they entered it [61]. The goal is to achieve such an arrangement of boxes that the time, energy expenditure and health risk for the order picker in the process of order picking would be minimal.

The following restrictions must be observed during the order picking and assigning boxes to storage spaces:

• Every storage space accepts only one box at a time;
• The order picker starts on the depot, takes a walk to the storing space, takes out the required box and puts it on the conveyor belt behind him/her. After picking and placing the box, he/she returns to the depot;
• We can assign any number of different types of boxes, each with its frequency. If the sum of frequencies is larger than the number of storage spaces in the warehouse, some of the boxes will not be assign.

The paper introduces three storage assignment solutions, the first according to order picking time, the second according to energy expenditure, and the third according to health risk, presented with three one-objective functions. In this way, we create a basis for researching how optimization according to only one criterion affects the other two criteria not included in the optimization.

Later we develop a multi-objective model capable of determining storage assignments for boxes based on the three criteria mentioned above. Multi-objective optimization is applied when the optimization problem has more than one objective [62], which conflict. The advantage of the multi-objective function is the ability to weigh each objective function, where the size of an individual weight depends on business policies and needs. In this way, we create a basis for researching how results from multi-objective optimization differ/are the same as in the case optimization according to only one criterion. We are particularly interested in comparing the results of multi-objective optimization and time-objective optimization.

2.1. Development of a Model with a Single Objective

The decision variable $x_{ij}$ in the arrangement of the boxes in the warehouse represents the combination of a specific box $i$ in a storage place $j$. The decision variable $x_{ij}$ occupies the value 1 when the box $i$ is placed on the storage place $j$ and 0 if the box $i$ is not placed on the storage place $j$ (1).

The first step of model development begins with defining different types of boxes that need to be stored (2). Boxes are unambiguously marked with a number from 1 to $M$ and with the frequency for each box type $f_i$. $M$ is an index for the last box, which is the same as the number of different boxes.

$$x_{ij}=\left\{\begin{array}{l}1;\mathrm{if} \mathrm{the} \mathrm{box} \mathrm{positioned} \mathrm{on} \mathrm{storage} \mathrm{space} j\\ 0;\mathrm{otherwise}\end{array}\right.$$

(1)

The second step of model development determines the capacity of storage spaces in the considered warehouse. The number of storage place $N$ is calculated with the Formula (3). $N$ represents the $j$ index in the decision variable (2), where each storage place has its index determined with the number from 1 to $N$. $N$ is the index for the last storage space and is the same as the number of different storage spaces. After this, the determination of the binary decision variable follows.

$$i=1,2,3,\dots ,M$$

(2)

The third step of model development defines the decision variable $x_{ij}$ as a binary decision variable (3).

$$j=1,2,3,\dots ,N$$

(3)

The fourth step of model development constructs the objective function (4), where we define the minimization of the sum of the product between coefficient $c_{ij}$ and decision variable $x_{ij}$.

$${\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{c}_{ij}\cdot x_{ij}}}$$

(4)

The coefficient $c_{ij}$ in the objective function could present a wide range of factors that impact the decision (for example, order picking time, energy expenditure for picking, the weight of boxes, etc.). However, in the case where order picking is optimized for one objective, the meaning of the coefficient $c_{ij}$ is uniquely determined.

The last step of model development defines the constraints of the optimization problem, which define the restriction of the problem. When determining storage assignments for boxes in the warehouse rack, there are two restrictions. With the first type of constraint (5), we define the frequency of the individual type of box stored in the warehouse (where $f_m$ represents the frequency of the specific box type). With the second type of constraint (6), we limit the number of stored boxes in one storage space inside the storage rack, where $l_n$ represents the space restriction for each specific box type in one storage space.

$$\begin{array}{c}\forall m,n\in \mathbb{N},n=1,2,\dots ,N,m=1,2,\dots ,M\\ \hfill \mathrm{and}\hfill \\ {\mathrm{x}}_{m,j},x_{i,n}\in \left\{0,1\right\}\\ \mathrm{we} \mathrm{define}:\\ {\displaystyle \sum _{j=1}^N{x}_{m,j}=f_m}\end{array}$$

(5)

$${\displaystyle \sum _{i=1}^M{x}_{i,n}=l_n}$$

(6)

2.2. Development of a Model with Multiple Objectives

However, when storage assignment is optimized for more than one objective, we have to consider all of the single objective function’s desired variables. Let us assume that $K$ different objectives are included in the optimization process (7).

$$w_{o_1}\cdot ({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{o}_{1_{ij}}\cdot x_{ij}}),} w_{o_2}\cdot ({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{o}_{2_{ij}}\cdot x_{ij}}),} \dots ,w_{o_K}\cdot ({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{o}_{K_{ij}}\cdot x_{ij}})}$$

(7)

Each objective function has its priority weight ($w_{o_1},w_{o_2} \mathrm{and}\hspace{0.17em}{w}_{o_K}$ present different priority weights for different objectives). Determining the value for the priority weights is left to the decision-maker in the company. Multi-objective function user can weigh the individual coefficient on the basis of preliminary calculations, practical experiences or depending on which objectives are important for him/her at a given moment. In the below-described case study, we weighted the most important coefficient with 0.8 and remining two each with weigh 0.1. This weigh distribution indicates the priority of the selected coefficient and at the same time does not negate the importance of taking into account other coefficients. All of the coefficients in objective functions have to be normalized ($o_{1_{ij}},o_{2_{ij}} \mathrm{and} o_{K_{ij}}$ present the normalized data based on different objectives). The constraints (5) and (6) from the single objective model are also included in the multi-objective model.

3. Case Study

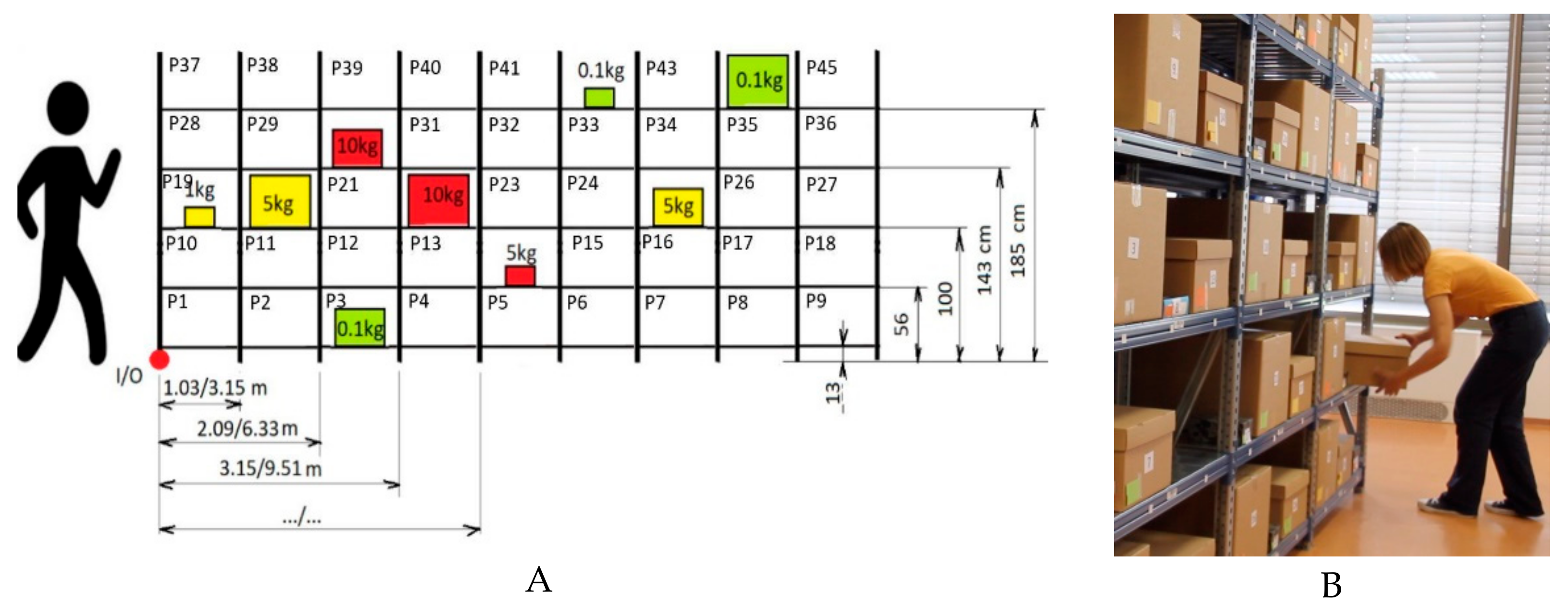
For a simple validation of our models, we analyzed a warehouse that consists of a single storage rack with five vertical and nine horizontal storage levels (Figure 3B). On that storage rack, boxes are stocked in 45 storage spaces (Figure 3A). Storage spaces have fixed and equal dimensions. The box is positioned in the middle of the front width of the storage space. The order pickers can pick items from each of them one at a time.

Two different lengths of storage rack are analyzed—the first one with 1.06 m spacing between rack holders and the other with 3.18 m spacing. The box is always stocked in the middle of two rack holders. Distances between the depot (I/O) and the end of a specific position from P1 to P9 are also shown in (Figure 3A).

The order picker handles nine types of cardboard boxes without handles in the above-described warehouse (

Table 2. Types and masses for the boxes.

Box Type/Mass	Label	Box Type/Mass	Label	Box Type/Mass	Label
Large/0.1 kg	L	Medium/0.1 kg	M	Small/0.1 kg	S
Large/5 kg	L	Medium/5 kg	M	Small/5 Kg	S
Large/10 kg	L	Medium/10 kg	M	Small/1 kg	S

). Boxes appear in three sizes: Large (31 cm × 37 cm × 45 cm), Medium (20 cm × 30 cm × 40 cm), and Small (7 cm × 11 cm × 18 cm). Each box size is represented in three different masses: Large (0.1 kg, 5 kg, 10 kg), Medium (0.1 kg, 5 kg, 10 kg), and Small (0.1 kg, 1 kg, 5 kg).

In the described working laboratory environment (Figure 3A), which is an excellent approximation to the actual storage environment of smaller dimensions, it was necessary to obtain data on the picking time for each box type/mass at all five possible shelf heights.

Nine men with a mean age of 42 (SD 17.8) years, the height of 179 (SD 5.2) cm, weight of 86 (SD 9.4) kg, and eight women with a mean age of 40 (SD 15.2) years, the height of 163 (7.4) cm, the weight of 62 (12.4) kg participated in the experiment. The participants were of different professions. Five men and four women are physical workers, two male and three female are students, and the rest are office workers. None of them have ever worked as an order picker in a warehouse. They all signed a consent form approved by the Senate of the Faculty of logistics at the University of Maribor.

The participants picked cardboard boxes without handles in three different volumes and with four different loadings from shelves on five different heights in the steel warehouse rack.

During the experiment, each participant picked the ordered box from a rack and lowered or lifted the box on a surface for disposal, using a grip of the box’s side surfaces between the palms (Figure 4).

A sequence of boxes on the picking list was determined randomly and was the same for all participants. The participants did not know how heavy the box they should pick is. After unloading the box on the surface for disposal, the assistant immediately read the new number of the box for picking and removed the box from improvised surface for disposal. A video camera with a rate of 60 frames per second recorded the participants while they were performing the tasks. Later a time study was conducted by measuring picking times directly from the video recordings (

Table 3. Average picking times from different heights.

Type/Mass	Average Picking Time at the Height of … [s]
	13 cm	56 cm	100 cm	143 cm	185 cm
Large 0.1 kg	2.71	2.62	2.71	2.80	3.04
Large 5 kg	3.77	3.57	3.13	3.30	4.54
Large 10 kg	4.37	3.85	3.99	4.15	5.57
Medium 0.1 kg	2.50	2.30	2.26	2.19	2.73
Medium 5 kg	3.70	3.44	3.21	3.81	4.23
Medium 10 kg	4.03	3.70	3.77	4.16	5.39
Small 0.1 kg	1.95	1.74	1.71	1.79	2.00
Small 5 kg	2.91	2.73	2.78	3.14	3.45
Small 1 kg	2.21	1.95	2.00	2.15	2.61

).

The laboratory-derived average times from Table 3 were later used as input data for model validation and for use in simulated scenarios. We designed four different scenarios with a different frequency of individual boxes:

• Scenario 1 (S1)—all types of boxes are presented randomly (frequency of individual boxes is between 1 and 6);
• Scenario 2 (S2)—all types of boxes are equally represented (all types of boxes have a frequency of 4);
• Scenario 3 (S3)—heavy boxes predominate (heavy boxes have a frequency of 9 and all others a frequency of 2);
• Scenario 4 (S4)—light boxes predominate (light boxes have a frequency of 9 or 8 and the heaviest have a frequency of 2 or 1).

In all four scenarios, there are 36 boxes in order to achieve comparability of results.

4. Methodology for the Experiment

As mentioned, the storage space assignments of boxes were made:

• With a time-based objective model;
• With an energy expenditure-based model;
• With a health-risk based model;
• With a multi-objective model (all described in Section 4).

Three single-objective models and one multi-objective model were developed. We choose three factors that significantly impact the decision-making process about storage assignment: picking time, energy expenditure and health risk.

The first single-objective function is time-based, where the objective is to minimize the total time needed for order picking ($T$). The second single-objective function is an energy-based objective function ($E$), where the rack locations are determined based on the minimum energy expenditure for order picking. As a novelty, the third single-objective function is a health risk-based objective function ($O$), where the objective is to minimize the health risk for the order picker. The following Formulas (8)–(10) define single-objective models for the presented case (where we use the corresponding objective function for the selected optimization):

$$\min (T)=\min {\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}{t}_{ij}\cdot x_{ij}}}$$

(8)

$$\min (E)=\min {\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}{e}_{ij}\cdot x_{ij}}}$$

(9)

$$\min (O)=\min {\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}{o}_{ij}\cdot x_{ij}}}$$

(10)

where $t_{ij}$ represents the time needed for the whole process of picking the $i$-th box from the $j$-th storage space, $e_{ij}$ represents the energy usage for the entire process of picking the $i$-th box from the $j$-th storage space, and $o_{ij}$ represents the value of health risk for the whole process of picking the $i$-th box from the $j$-th storage space.

All three single-objective functions are subject to the same following constraints (11):

$$\begin{array}{c}\forall m,n\in \mathbb{N},n=1,2,\dots ,N,m=1,2,\dots ,M\\ \mathrm{and}\\ {\mathrm{x}}_{m,j},x_{i,n}\in \left\{0,1\right\}\\ \mathrm{we} \mathrm{define}:\\ {\displaystyle \sum _{j=1}^N{x}_{m,j}=f_m}\\ {\displaystyle \sum _{i=1}^9{x}_{i,n}\le 1}\end{array}$$

(11)

$f_m$ refers to the frequency of individual boxes which need to be picked in each scenario.

The last is the multi-objective function where optimization of arrangements is based on all three objective factors (12):

$$\min (T,E,O)=\min ({\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}{w}_t(t_{ij}\cdot x_{ij}})},{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}{w}_e(e_{ij}\cdot x_{ij}})},{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}{w}_o(o_{ij}\cdot x_{ij}})})$$

(12)

where $w_t$ represents the weight of time function, $w_e$ represents the weight of energy function, and $w_o$ represents the weight of health risk function.

Further, we analyze four differently weighted scenarios (

Table 4. Differently weighted scenarios.

Type of Situation	Objective Function
All three decision factors are equally important	$\min ({\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}(t_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}(e_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}(o_{ij}}\cdot x_{ij})})$
The health risk is the most important decision factor	$\min ({\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.1\cdot (t_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.1\cdot (e_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.8\cdot (o_{ij}}\cdot x_{ij})})$
Time is the most important decision factor	$\min ({\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.8\cdot (t_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.1\cdot (e_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.1\cdot (o_{ij}}\cdot x_{ij})})$
Energy is the most important decision factor	$\min ({\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.1\cdot (t_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.8\cdot (e_{ij}}\cdot x_{ij}),}{\displaystyle \sum _{i=1}^9{\displaystyle \sum _{j=1}^{45}0.1\cdot (o_{ij}}\cdot x_{ij})})$

). The advantage of the multi-objective function is that the decision-maker can determine the importance of specific criteria in a particular situation. The constraints are the same as (11).

Before single- and multi-objective functions were used for storage assignment purposes, all data ware normalized. Section 4.1, Section 4.2 and Section 4.3 explain how we calculated total time, total energy expenditure, and overall health risk values in the minimization functions. All linear programing results were obtained using the MATLAb software tool.

4.1. Calculation of Total Time, Used for the Time-Based Minimization Function

We calculated the total time used for the minimization function with the Formula (13):

$$T_{total}=T_{walking}+T_{picking}$$

(13)

where $T_{picking}$ represents the average time, measured by multiple experiments (described in [63]), for each box and storage place. $T_{walking}$ is calculated by the Formula (14):

$$T_{walkin{g}_i}=\frac{s_i}{v_{walking}}$$

(14)

where for $v_{walking}$ the value $0.83\frac{\mathrm{m}}{\mathrm{s}}$ is taken into account and $s_i$ is defined by the middle of the storing place (Figure 4).

4.2. Calculation of Total Energy Consumption, Used for the Minimization Function

Total energy consumption, used for the minimization function, was calculated with the Formula (15):

$$E_{total}=E_{walking}+E_{picking}$$

(15)

where $E_{picking}$ represents the average energy consumption [37] calculated based on the Formula (16):

$$E_{job}^{·}=\frac{{\displaystyle \sum _{i=1}^{n_l}{E}_{post}^{·}\cdot t_i}+{\displaystyle \sum _{i=1}^n△E_{tas{k}_i}}}{T}$$

(16)

where [37]:

• $E_{job}^{·}$ = average energy expenditure rate of the job (Kcal/min),
• $E_{post}^{·}$ = metabolic energy expenditure rate due to the maintenance of the $i^{th}$ posture (Kcal/min),
• $t_i$ = time duration of $i^{th}$ posture (min),
• $n_l$ = total number of body postures employed in the job,
• $△E_{task}$ = net metabolic energy expenditure of the $i^{th}$ task in a steady-state (Kcal).

$E_{walkin{g}_i}$ is calculated by the Formula (17):

$$E_{walkin{g}_i}=T_{walkin{g}_i}\cdot BMR$$

(17)

where for BMR the value of $3.39\frac{\mathrm{Kcal}}{\min }$ was used, which coincides with the velocity of walking $v_{walking}=0.83\frac{\mathrm{m}}{\mathrm{s}}$ [37].

4.3. Calculation of the Overall Level of Health Risk Based on OWAS Coding, Used for the Minimization Function

To use the OWAS method in the minimization function, we needed to determine numerical values that will unequivocally communicate health risks for specific boxes on specific storage spaces because the OWAS codes did not prove useful. In the first step, which followed the standard OWAS procedure, work postures during order picking in the case study warehouse rack [63] were observed and recorded (Figure 5). The observation was followed by codifying. We assigned a 4-digit code to each posture that appeared in the order picking process. The resulting codes depend on the classification for different parts of the body. The first numeric value in the 4-digit code refers to the back (4 postures), the second to arms (3 postures), the third to legs (7 postures), and the fourth to the mass of the load handled (3 categories). Codes were a prerequisite for calculating the overall level of health risk for a specific box at a specific storage space, taking into account the box’s frequency in the entire scenario. In a particular case study (1 storage rack and four different scenarios), 405 calculations were needed (9 different boxes with their frequencies, five different heights above the ground). For each numerical value in the 4-digit code, a reasonably thought-out numerical value was assigned to indicate the health risk level for a specific group of postures/categories (back, arms, legs, mass). The overall level of health risk for a specific box at a specific storage space, taking into account the frequency of the box in the entire scenario, is a sum of 4 selected health risk values according to the baseline four-digit code.

The numerical health risk values describing the health risk level for a specific group of postures/categories (back, arms, legs, mass), were reasonably thought-out in a way that the sum of all numerical health risk values for a specific scenario could never exceed the health risk value determined for the next health risk.

We use three different health risk values based on postures/categories and repetition frequencies:

• Health risk value 1: negligible risk—normal postures without recommendations for any corrective activity;
• Health risk value 200: some risk—one or more postures with recommendation(s) for corrective action(s) to be taken;
• Health risk value 30,000: very-high risk—one or more unacceptable postures with recommendation(s) for immediate corrective measure(s).

5. Results

Based on the calculation of the overall level of health risks based on OWAS coding, we got 405 different calculation results for a specific combination of the $i$-th box and the $j$-th positions.

Table 5. Frequency of occurrence of a specific health risk level.

Health Risk Level (HRL)		(HRL) Occurrence Frequency for Specific Rack Type
Type	Number of Cases	Short Rack		Long Rack
Very-high risk	9	1	0.25%	0	0%
	2	12	2.96%	8	1.98%
	1	4	0.99%	5	1.23%
Some risk	4	7	1.73%	0	0%
	3	13	3.21%	13	3.21%
	2	71	17.53%	37	9.14%
	1	122	30.12%	133	32.84%
Negligible risk	one to several	175	43.21%	209	51.60%
Sum		405	100%	405	100%

presents the frequency of a specific health risk level occurring for order pickers in the case study environment.

The calculation revealed the smallest percentage of cases with very-high health risk levels among 405 possible combinations of box type, box frequency, and different heights above the ground. A very-high health risk level stands for one or more unacceptable postures that need immediate corrective measures. Such cases should not occur in practice, as each occurrence poses a direct threat of immediate injury. The percentage of $HRL$ occurrence frequency with very-high health risk is slightly higher in a shorter storage rack (4.2%) than in a longer one (3.2%). We counted 37 cases (6.81% of all cases) with a direct threat in the short storage rack and 21 cases (4.41% of all cases) with a direct threat in the long storage rack. In our specific case study, the risk that the order picker will be injured is 43.2% higher in the case of shorter routes than in the case of longer routes between storage spaces. In both types of racks, cases representing some risk predominate. In such cases, immediate injuries are very unlikely, but the likelihood increases in the long run. The percentage of $HRL$ occurrence frequency with some health risk is slightly higher in a shorter storage rack (52.6%) than in a longer one (45.2%). We counted 331 cases (81.72% of all cases) with a long-term threat in the short storage rack and 246 cases (60.74% of all cases) with a long-term threat in the long storage rack. In our specific case study, the risk that the order picker will be injured in the long term is 25.7% higher in the case of shorter routes than in the case of longer routes between storage spaces. We revealed that order picking in our specific case study is safer in the case of longer distances between storage spaces than in the shorter one.

5.1. Comparisons between Results of Minimization Functions with One Optimization Factor

As described, we used all three single-objective minimization functions on four different scenarios in two different warehouses, differing in length of storage spaces. Below we present the results for the short rack and scenario 3 in which heavy boxes predominate.

When optimization considers just time, we can see (Figure 6) that heavier boxes (10 kg, colored orange) are placed close to the depot (I/O) and in a golden zone, where picking times are shorter. Walking time has an impact but only in a limited way due to the short distances between storage spaces in a rack. As the number of boxes for storing is smaller than the number of available storage spaces, empty storage spaces expectedly appear on the rack’s remote part (according to the depot I/O). The best solution in a time-based manner encompasses two cases with a very-high health risk, which makes the proposal unsuitable from the point of view of safety (the $HR$ value is 67,107). On the other hand, the proposal is excellent in terms of employee productivity (calculated time is 495.95 s and energy consumption is 57.43 Kcal).

When optimization considers just energy, we can see (Figure 7) that heavier boxes (10 kg, colored orange) are placed in a golden zone, and below it, in storage spaces where picking energy expenditures are small. Walking time has an impact but only in a limited way due to the short distances between storage spaces in a rack. As the number of boxes for storing is smaller than the number of available storage spaces, empty storage spaces expectedly appear in the last remote column (according to the depot (I/O) and on the lowest and highest shelves due to significant picking energy expenditures. The best solution in an energy-based manner encompasses four cases with a very-high health risk, which makes the proposal even more unsuitable from the point of view of safety than the time-based proposal ($HR$ value is 126,508). The proposal is also worse in terms of employee productivity (calculated time is 505.93 s and energy consumption is 57.11 Kcal).

When optimization considers just health risk, we can see (Figure 8) that heavier boxes (10 kg, colored orange) are placed in a golden zone and below and above it, in storage spaces far from the depot (I/O). Unlike in the previous two storage assignment proposals, empty storage spaces are now located closer to the depot (I/O). Placing boxes on the end of the rack corridor reduces the share of time spent performing a certain posture in the total time spent for picking boxes out of the shelves, thus reducing the health risk. As the number of boxes for storing is smaller than the number of available storage spaces, empty storage spaces appear closer to the depot (I/O), above and below the golden zone due to some or very-high health risks. The result matches expectations before the use of the health-risk minimization function. The best solution in the health risk-based manner encompasses no cases with a very-high health risk, making the proposal excellent from the point of view of safety ($HR$ value is 1935). The proposal is the worst in terms of employee productivity between one-objective solutions (time needed to complete the scenario is 657.84 s and energy consumption is 75.16 Kcal).

The best solution for the order picker’s physical health is the minimization of the health risk-based objective function, where we note that no box is placed in a storage space with a very-high health risk. Nine boxes are positioned in storage spaces with some health risk and others in spaces with negligible risk. On the other hand, this increases the time by 32.65% in comparison with time-objective optimization. A summary of the results for scenario 3 (short rack) and the other three scenarios described in the case study section is given in

Table 6. Comparison of results for different scenarios, rack type and single-objective function.

Scenario (Rack Type)	Observed Factor	Time-Based Optimization 4	Energy-Based Optimization 5	HR-Based Optimization 6
Scenario 1 (Short rack)	$T {}^1$ (s)	478.71	488.39	642.2
	$E {}^2$ (Kcal)	55.09	54.83	72.93
	$HR {}^3$ (value)	64,321	154,416	2183
Scenario 2 (Short rack)	$T$ (s)	480.1	491.35	643.14
	$E$ (Kcal)	55.32	55.0	73.17
	$HR$ (value)	65,913	155,910	2183
Scenario 3 (Short rack)	$T$ (s)	495.95	505.93	657.84
	$E$ (Kcal)	57.43	57.11	75.16
	$HR$ (value)	67,107	126,508	1935
Scenario 4 (Short rack)	$T$ (s)	464.67	477.28	626.88
	$E$ (Kcal)	53.68	53.4	71.14
	$HR$ (value)	45,316	65,166	2532
Scenario 1 (Long rack)	$T$ (s)	970.68	973.42	1294.9
	$E$ (Kcal)	110.79	110.49	146.42
	$HR$ (value)	66,704	96,906	3718
Scenario 2 (Long rack)	$T$ (s)	973.07	976.32	1301.28
	$E$ (Kcal)	111.02	110.7	147.19
	$HR$ (value)	64,658	94,256	3224
Scenario 3 (Long rack)	$T$ (s)	988.92	991.49	1239.97
	$E$ (Kcal)	113.13	112.67	140.29
	$HR$ (value)	64,906	94,905	2924
Scenario 4 (Long rack)	$T$ (s)	902.43	907.88	1234.55
	$E$ (Kcal)	103.15	102.93	139.51
	$HR$ (value)	65,653	65,803	2425

¹$T$—time in seconds; ²$E$—energy expenditure in Kcal; ³$HR$—health risk; ⁴ time-based optimization is expressed in (s) for $T$, in (Kcal) for $E$, and (numerical value) for $HR$; ⁵ energy-based optimization is expressed in (s) for $T$, in (Kcal) for $E$, and (numerical value) for $HR$; ⁶ HR-based optimization is expressed in (s) for $T$, in (Kcal) for $E$, and (numerical value) for $HR$.

.

The average results of three one-objective optimizations (time-, energy-, health risk-based) are compared according to the type of rack (short, long) in

Table 7. Comparisons of the average results from the perspective of time-based optimization.

Observed Factor	Rack Type	Time-Based Optimization	Energy-Based Optimization	HR-Based Optimization
Average time (s)	Short rack	100%	+2.32%	+33.97%
	Long rack	100%	+0.37%	+32.2%
Average energy (Kcal)	Short rack	100%	−0.53%	+32.0%
	Long rack	100%	−0.3%	+30.89%
Average HR (value)	Short rack	100%	+106.88%	−96.34%
	Long rack	100%	+34.34%	−95.31%

. As a starting point of the comparison, we took the average results of time-based optimization and determined the percentage deviations of the average results of energy- and health risk-based optimizations.

As presented in Table 7, when comparing average picking times, energy-based and health risk-based optimizations give on average longer order picking times than time-based. The only difference is that in the case of energy-based optimization the difference is much smaller than in the case of health risk-based optimization. The value of average energy expenditure logically drops when comparing the energy-based optimization with time-based, but the difference is relatively small, less than 1%. A comparison of average health risk values shows that in time-based optimization the order picker is on average more often exposed to the very-high health risk. If in time-based optimization the order picker is on average twice exposed to a very-high health risk (with the minimum of once and the maximum of twice), in energy-based optimization it is three times (with the minimum of once and the maximum of five times). On the other hand, with the health risk-optimization function the order picker is never exposed to very-high risk.

5.2. Comparisons between Results from Differently Weighted Multi-Objective Minimization Functions

A comparative analysis on four different scenarios in two different warehouses, differing in length of storage spaces, was made based on three differently weighted multi-objective functions. In the first, time, energy expenditure and health risk are equally weighted. In the second, the health-risk is the most weighted and in the third, time-risk is the most weighted. Results are presented in

Table 8. Comparison of results for different scenarios, rack type, and minimization based on differently weighted multi-objective functions.

Scenario (Rack Type)	Observed Factor	Weighted Multi-Objective Minimization Function
		t + e + o	0.1t + 0.1e + 0.8o	0.8t + 0.1e +0.1o	0.1t + 0.8e +0.1o
Scenario 1 (Short rack)	$T$ (s)	498.36	579.85	495.74	475.24
	$E$ (Kcal)	56.45	64.33	56.55	54.07
	$HR$ (value)	3328	1338	3527	5314
Scenario 2 (Short rack)	$T$ (s)	501.57	583.47	498.04	500.27
	$E$ (Kcal)	56.78	64.67	56.77	56.79
	$HR$ (value)	3328	1338	3726	65,316
Scenario 3 (Short rack)	$T$ (s)	519.95	601.70	515.38	518.50
	$E$ (Kcal)	59.26	67.10	59.24	58.99
	$HR$ (value)	3328	1338	3925	65,515
Scenario 4 (Short rack)	$T$ (s)	486.81	566.03	483.87	486.79
	$E$ (Kcal)	54.94	62.64	55.23	55.26
	$HR$ (value)	3328	1338	3527	5517
Scenario 1 (Long rack)	$T$ (s)	1032.50	1211.3	1024.33	1023.95
	$E$ (Kcal)	116.75	136.45	116.45	116.04
	$HR$ (value)	3420	2624	3319	5116
Scenario 2 (Long rack)	$T$ (s)	1034.72	1213.52	1026.63	1026.44
	$E$ (Kcal)	117.00	136.7	116.66	116.25
	$HR$ (value)	3570	2624	3469	4317
Scenario 3 (Long rack)	$T$ (s)	1033.04	1212.89	1024.9	1044.67
	$E$ (Kcal)	117.21	137.07	116.92	114.45
	$HR$ (value)	3120	2474	3769	3916
Scenario 4 (Long rack)	$T$ (s)	1019.24	1198	1011.32	1012.96
	$E$ (Kcal)	115.24	134.85	114.83	114.72
	$HR$ (value)	3968	3622	3766	4919

t: time, e: energy and o: health risk value (due the fact that HR is calculated with the OWAS).

.

The average results of the differently weighted multi-objective minimization functions are compared according to the type of rack (short, long) from the perspective of time-based optimization in

Table 9. Comparisons of the average results from a perspective of time-based objective minimization function.

Observed Factor	Rack Type	Time-Based Optimization	Weighted Multi-Objective Minimization Function
			t + e + o	0.1t + 0.1e + 0.8o	0.8t + 0.1e + 0.1o	0.1t + 0.8e + 0.1o
Time (s)	Short rack	100%	+4.55%	+21.45%	+3.83%	+3.20%
	Long rack	100%	+7.42%	+26.09%	+6.57%	+7.12%
Energy (Kcal)	Short rack	100%	+2.67%	+16.80%	+2.83%	+1.62%
	Long rack	100%	+6.42%	+24.42%	+6.11%	+5.33%
HR (value)	Short rack	100%	−94.51%	−97.79%	−93.94%	−41.62%
	Long rack	100%	−94.69%	−95.72%	−94.59%	−93.03%

t: time, e: energy and o: health risk value (due the fact that HR is calculated with the OWAS).

.

As presented in Table 9, it is important to emphasize that the order picker is never exposed to very-high health risk in the first three analyzed situations (t + e + o, 0.1t + 0.1e + 0.8o, 0.8t + 0.1e + 0.1o), even in a situation where time is the most crucial decision factor. In the equal importance of all factors, the order picker is exposed 19 times to some risk and 58 times when the time is the most important factor. The order picker is exposed to some risk only 12 times when health risk is the most weighted factor.

Different behavior was found only in the multi-objective emphasizing energy minimization function (0.1t + 0.8e + 0.1o) for the short rack. There, the HR value also decreases, but more than 50% less than with other multi-objective minimization functions. Scenarios S2 (all types of boxes are equally represented) and S3 (heavy boxes predominate) each contain one situation with very-high risk.

6. Discussion

The developed general model supports manual man-to-goods order picking in arbitrarily long racks with several shelves and one entry and exit point. As this is manual order picking, the highest shelf should not be placed higher than 177 cm. As a novelty in the paper, we develop three single-objective functions and one multi-objective function to support decision-making on storage assignment in a described warehouse environment. They allow minimization of time, energy expenditure and health risk individually or in a weight-adjusted trinity. In addition to developing individual models, we are interested in comparisons between results from the use of functions from a decision-maker perspective. For them, the most important is time-saving and consequently lowering costs. The cost of order picking largely depends on the number of items collected per unit time.

The introduction mentioned authors that have already experimented with time, energy expenditure, and health risk objective functions, but in different environments or by addressing less influential factors. This paper addresses order picking of smaller boxes in various dimensions and masses, which is a daily practice in packet distribution for the retail sector’s needs.

Including only time and energy expenditure would represent a sound basis for safer order picking. Still, it would not protect against MSDs due to the unanalyzed presence of situations with a high risk for injuries. Therefore, it makes sense to explore the possibility of a multi-objective assignment model and check if it is possible to achieve increased productivity while preserving the order pickers’ physical health.

Our experiment shows that less strenuous and safer work requires longer operating times and results in lower productivity. This result was logical and expected. The question is, what is the magnitude of this deviation. Focusing only on lower energy expenditure is reflected in a less than 3% increase in the order picking time, which is not much, and the benefits are questionable. A 3% time savings in one shift equals a 15-min break. Similar results were already observed by authors [9], who proposed a bi-objective model, including time and energy expenditure. They calculated that the maximum difference is about 2% in time and 2.5% in energy. In their case, the order fulfillment time in employing the energy-based storage assignment was 2% higher than the total time that results if the time-based assignment was used. Comparable results from the previous study contributed to the validation of our model. By extending the model to a multi-objective one, we find another concern about energy-based assignment usability, which was not previously understood from the mentioned bi-objective model. A comparison of average health risk values shows that the order picker is on average more often exposed to very-high health risks (unacceptable, immediate action required) in energy-based assignments than in time-based assignments. Scientific literature suggests a dynamic determination of breaks according to energy expenditure amounts. Still, even in this case, we cannot guarantee the absence of individual pick activities with a high risk of injury without additional modeling. Ergonomic assessment needs to be built into decision models, as it is not enough to protect workers from overwork; they also need to be protected from injury and MSDs. It has been revealed that with the health-risk optimization function, the order picker is never exposed to very-high risk (unacceptable, immediate action required). Only some boxes are positioned in storage spaces with some health risk, and the majority of them in spaces with negligible risk. On the other hand, this increases the average time by approximately 33% compared to single-objective time-objective optimization. A single-objective health risk-based assignment is suitable from a managerial perspective for a time frame when the number of customer orders is low. It is also ideal for warehouses where rush hour traffic can be rescheduled throughout the working day.

To mitigate the extremes of single-objective functions’ results, we have developed a multi-objective one with the possibility of a different weighting of individual optimization criteria. The multi-objective order picking time-weighted function (the weight is 0.8) has proven to be promising to find a compromise between optimal time and elimination of situations with a very-high risk for injuries. 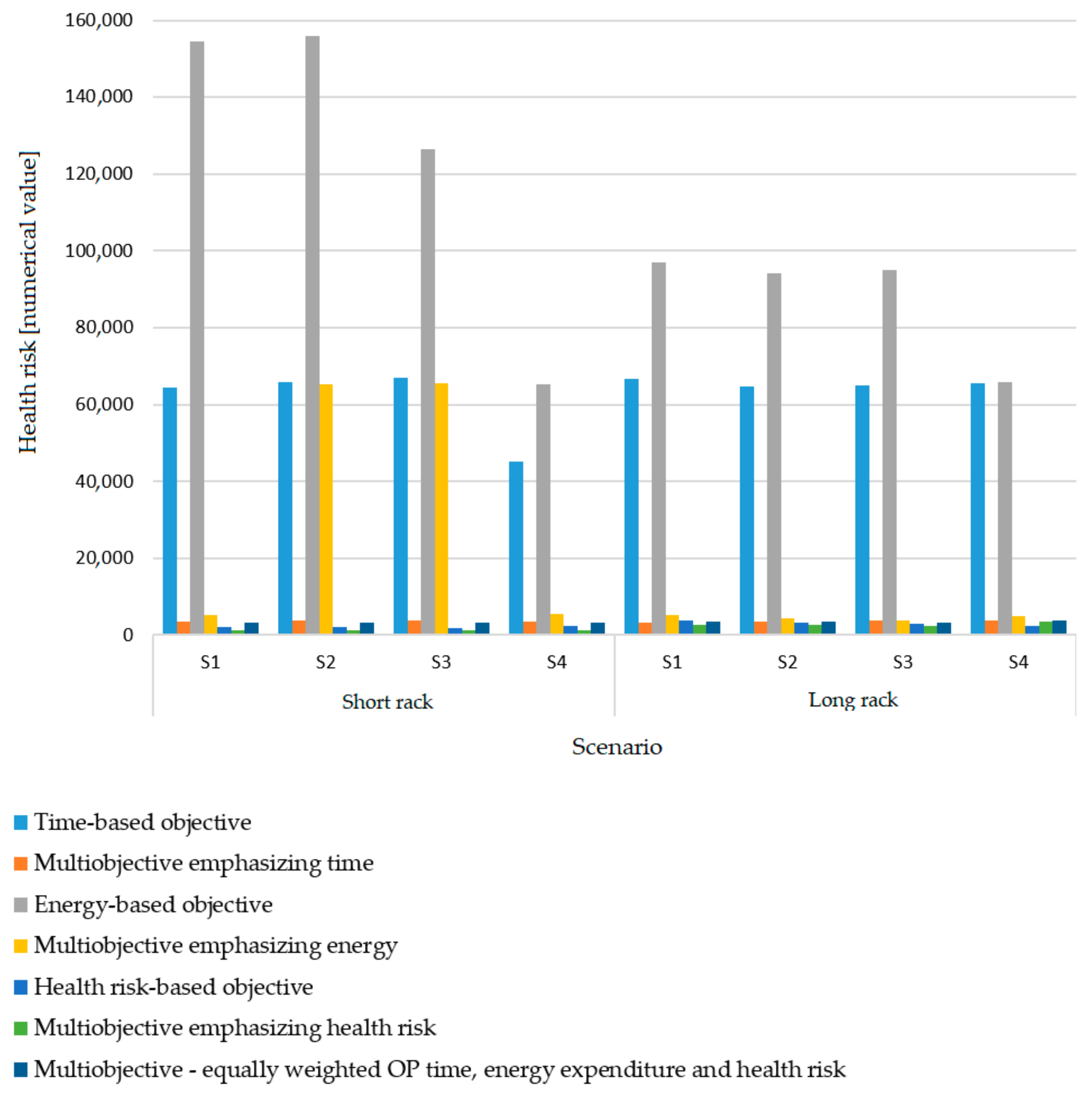Figure 9 visualizes results from different single- and multi-objective functions. Their use resulted in different assignment scenarios and different overall picking times needed to prepare orders. Overall picking time is one of the most interesting aspects for managers who are most inclined to organize work in a way that it is performed in the shortest possible time. They would be willing to do something more for their employees’ physical health, as long as it does not prolong the overall picking times too much.

In scenario 4 (S4) we achieve the shortest overall order picking time because we move mostly light boxes weighing about a tenth of a kilogram. For scenario 3 (S3) we achieve the longest overall order picking time because we move mostly heavy boxes weighing 5 or 10 kg. The time achieved in scenario 2 (S2) is somewhat in the middle because heavy and light boxes were equally frequent. In Figure 9, of course, this is hard to see, however, it can be read from Table 6, Table 7, Table 8 and Table 9. We were more interested in the visualization of the results of single-objective functions and differently weighted multi-objective functions to show that the relationship between the results of different functions does not strongly depend on the structure of the goods in terms of weight and dimensions. The characteristics of boxes in terms of mass and dimensions affect the overall order picking time to some smaller extent. At short storage racks, the impact comes to the fore less than with long racks. This aspect was not further analyzed in the present paper but is an interesting topic for future research. We know that sole time optimization does not have the best effect on people’s wellbeing and can cause injuries. Figure 9 visualizes which objective function is closest in the result (overall order picking time) to the optimal single-objective time-based function, which is the most popular with managers. Results reveal, for example, that solely energy-based optimization, although very close in time and less tiring for the worker, is not a suitable replacement for solely time-based optimization because it contains more health risky situations that can cause injuries. A long rack significantly increases the differences in overall order-picking times between individual functions due to long distances.

According to Figure 9, the best order picking times are expectedly achieved by using a time-based objective function. In the short storage rack, a time emphasizing multi-objective function, an energy-based single-objective function and an equally weighted multi-objective function give a minimal increase in overall order picking time compared to a time-based single-objective function. In contrast, minimal time differences are observed between the time-based single-objective function and the energy-based single-objective function at a long storage rack. The overall order picking times are most increased when using the health risk-based single-objective function and the multi-objective function emphasizing health risk. The multi-objective function emphasizing time achieves promising results in terms of a minimal increase in time consumption. Simultaneously, the multi-objective function emphasizing time is also excellent in terms of a slight increase in health risk without the presence of situations with a high health risk. Health risk increases in the multi-objective function emphasizing time, only 10% on average in the short rack and 1.74% on average in the long rack. In contrast, in the health risk-based objective function, the increase was around 33% for both types of racks.

Figure 10 visualizes results from different single- and multi-objective functions. Their use resulted in different assignment scenarios and different energy expenditures needed to prepare orders.

Maximum energy consumption is the result of optimization with health risk-based objective function and multi-objective emphasizing health risk. As expected, energy consumption is higher in longer storage corridors and scenario 3 (S3) where heavy boxes predominate.

Figure 11 visualizes results from different single- and multi-objective functions. Their use resulted in different assignment scenarios and different health risks values.

The health risk value is calculated so that it has a message value, which has not been found in the scientific literature so far. Attention should be paid to scenarios where the health risk value exceeds 30,000. This means that it demands one or more unacceptable postures with recommendations for immediate corrective measures. The health of order pickers is more endangered in short racks than in long ones, especially in the case of energy optimization.

One of the more important findings is concluded from the results in Table 9. Regardless of which differently weighted multi-objective function is used, we consistently achieve a considerable reduction in health risks compared to the solely time-based single-objective function.

The theoretical contribution of this study is in a developed solution to a storage assignment problem using a multi-objective model including time, energy expenditure and health risk based on binary integer linear programing with the possibility of a different weighting of individual optimization criteria. By counting the number of very risky postures for employee injuries, we determined a new view on the inclusion of health risk in treating warehouse assignment problem. We can give practice recommendations based on comparing several different optimization models or changing weights within the multi-objective model. The practical contributions of this study can be described with managerial insights:

• Managerial insight #1. Less strenuous and safer work requires longer operating times and results in lower productivity. To overcome this issue, managers should use multi-objective optimization models to reduce health risk significantly at the cost of a small increase in time consumption, below 5% in short racks and below 10% in long racks. A single-objective health risk-based assignment is suitable from a managerial perspective for a time frame when the number of customer orders is low. It is also ideal for warehouses where rush hour traffic can be rescheduled throughout the working day.
• Managerial insight #2. Energy optimization is less tiring for employees, but solely energy optimization or multi-objective optimization emphasizing energy has not proven very suitable in practice. They both increase the number of very risky postures for employee injuries. A very-high health risk level stands for one or more unacceptable postures that need immediate corrective measures. Such cases should not occur in practice, as each occurrence poses a direct threat of immediate injury.
• Managerial insight #3. Employee health is becoming increasingly important. When buying a warehouse management system (WMS), pay attention to the possibility of taking order picker’s factors into account when optimizing work in the warehouse.

Study Limitations

This experiment was conducted in a laboratory environment. Although this is a study limitation, it does not diminish the credibility of the results. Picking times were measured based on measuring the actual picking performed by people. Order pickers were using properly weighted cartoon boxes stored in a real warehouse rack. The OWAS method was performed by posture observation during order picking in a replica of a real environment. The same positions would also be observed in the real warehouse. OWAS method is not based on the automatic capture of work data, which in the case of a good knowledge of the real process eliminates the need to intervene in the industrial environment.

The order picking in the laboratory environment was carried out at room temperature, under standard office lighting, without noise, with properly rested and healthy people, unburdened by the required amount of picking items per working day. However, the inability to generalize results in terms of different working conditions is also a limitation of studies performed in specific industrial environments.

The developed approach does not account for pick correlations of items and does not strive to place near items that are frequently picked together like [64,65].

7. Conclusions

The lean concept is not just about increasing productivity but also about improving safety. The logistics sector should strive for sustainability by protecting its order pickers’ health and welfare and treating them as its most vulnerable resource, as most order picking worldwide is still done manually. In order picking processes, safety requirements ensure order pickers’ physical health maintenance with an ergonomically appropriate workload and elimination of situations with a high risk for immediate and long-term injuries. This paper contributes to these efforts by comparing results from the use of several single-objective and multi-objective functions taking into account the criteria of time, energy expenditure, and health risk. In doing so, we are aware that the practice is not always in favor of introducing care for employees’ physical health, which is especially true for less developed countries with cheap and relatively young labor. By entering a smart society, however, our efforts are welcome, as we help build smart systems that will allow for the dynamic adaptation of the operation of warehouse systems for the benefit of all stakeholders involved, including employees. We certainly see a multi-objective decision model as part of modern warehouse management systems.

The paper represents only the first attempt to create a multi-objective model, which, however, can inspire the broader scientific community. We notice some opportunities for future research work, such as the need to improve the methodology of integrating the 4-digit OWAS codes into the overall health risk assessment system for different order picking scenarios. An important piece of information is the number of situations with a high risk of injury.

We further note that it makes sense to focus future research efforts on finding the optimal balance between weights for time, energy expenditure and health risk in a multi-objective function. Goal programing should be applied. Thanks to our study, we have now come closer to the optimal choice using the multi-objective function emphasizing the time. A promising direction is to increase the number of objectives and their ranking/determination of weight coefficients.

Although input data adequately represent the real situation, we want to use optimization models on the real data as well.