1. Introduction
The demand for improving energy efficiency to battle with the shortage of energy supply, volatile oil prices, and climate change is increasing [
1]. Some energy production processes, such as renewable energy generation and waste heat recovery, face the issues of mismatch between demand and supply. Thermal energy storage (TES) provides a promising solution to bridge this mismatch by storing and releasing heat or cold at given conditions, thus upgrading the system efficiency [
2,
3].
Common TES technologies include sensible heat thermal energy storage (SHTES), latent heat thermal energy storage (LHTES), and thermochemical storage (TCS) [
4,
5]. Among them, LHTES demonstrates unique advantages over the others by providing a large storage density while being chemically stable [
5,
6]. LHTES uses phase change materials (PCMs) to absorb and release the latent heat during phase transition at a nearly constant temperature, making it a good fit for the temperature management services [
7,
8]. Previous studies have reported design integration of LHTES in an extensive range of applications, including concentrating solar power plants (CSP) [
9], solar-absorption chilling systems [
10], buildings [
11,
12], waste thermal energy recovery [
13], and thermal management of electronics [
14].
Among various LHTES configurations, the shell-and-tube type is widely studied [
15]. Due to its advantages, such as simple design, low cost, low pressure drop [
16,
17], large heat transfer area, high discharging power, and high effectiveness [
5], the shell-and-tube type of LHTES is the most employed configuration [
18].
The design of a shell-and-tube LHTES unit encompasses a wide range of topics. Many past studies have been dedicated to heat transfer enhancement by inclusions of material additives or metal objects into the PCMs [
19,
20]. Others focused on the refinement of storage configuration to achieve satisfactory melting and solidification performance [
21,
22]. However, very few studies have been found to answer the question of what specific steps to follow in searching for both the best storage material and the corresponding schematic design of a shell-and-tube LHTES unit.
Regin et al. [
23] proposed a flowchart that describes different design stages of LHTES, from material research to commercial product. However, since this flowchart involves the full life span of the design process, it does not specify the detailed design method, for example, how to obtain material and geometrical properties. No optimization was mentioned in the flowchart. Tehrani et al. [
24] described the design process of the shell-and-tube LHTES system for CSP tower plants, as illustrated in
Figure 1. The design process covers PCM selection, storage volume estimation, selection of geometric parameters, and optimizing storage volume with the given design alternatives. It pioneers the design methodology of the shell-and-tube LHTES system even though a few limitations still exist. The PCMs selection, according to this study, adopts the melting temperature and the availability of detailed properties of the materials to filter the database. This practice is commonly seen in most studies and engineering cases. For example, in the methodology developed by Liu et al. [
18] to design a cascade PCM storage unit, three PCMs were selected based on the temperature restrictions and material properties. However, when dealing with a broad spectrum of materials with detailed property data available, researchers should spend a significant amount of effort choosing the best alternatives.
Another limitation found in this design process and other commonly used design processes is the employment of numerical simulations, which is complicated by the high demand for computational resources, especially for optimizing many geometric parameters that need dozens to hundreds of iterations. To replace the time-consuming computational fluid dynamics (CFD) simulations, Raud et al. [
25] developed an analytical approximation of a shell-and-tube LHTES unit’s melting time. The analytical approximation was validated by CFD with modest errors (from 10.9% to 13.6%). However, this method lacks adequate flexibility when dealing with varying working conditions by determining the heat transfer fluid (HTF) mass flow rate—a key parameter for a TES unit operation—as a function of the HTF inlet temperature instead of an independent variable. Nonetheless, these studies provide a possibility with more effective, comprehensive, flexible, and computationally available approaches for shell-and-tube LHTES design.
Recently, we reported a multi-criteria material assessment methodology which systematically selects the most suitable material for intended applications [
26,
27]. In this method, not only will the individual properties be assessed, but also the collective performance which reflects the system requirements. Though the methodology provides adequate material assessment, it does not include any discussion of the geometry or containment.
Therefore, in this study, we present a comprehensive methodology for the design of shell-and-tube LHTES units which is based on the multi-criteria material assessment methodology but also includes geometric configuration and material-geometry optimization. The multi-criteria material assessment is used to automatically assess the material properties from a wide range of candidates. An ε-NTU method is adopted to approximate the TES performance with high flexibility and modest error. A single cost reduction objective function lumps all the parameters together to optimize the materials and geometry. In the end, the study validates the model with real-world cases. An optimization case study is also introduced to showcase the applicability of this methodology.
2. Methodology
The workflow of this comprehensive methodology is illustrated in
Figure 2. The procedure begins with the input of the PCM database and fulfills a systematic material assessment procedure, proposed based on the multi-criteria decision-making methods. Here the top-performing PCMs will be concluded. Then the geometric design procedure will be performed based on the design engineer preferences of known storage unit parameters. The ε-NTU method, cost minimization, and the optimization algorithm will help the engineer implement the designing process to obtain a final design. The detailed workflow will be elaborated on in the following sections.
2.1. Material Assessment
The material assessment comprises the steps of preliminary screening, ranking by attributes, and performance checking by objective functions. The selected materials will be provided to the later geometry assessment.
2.1.1. Prescreening of PCM Database Based on System Goals and Scopes
First of all, the goals and requirements of the energy system that uses the LHTES unit shall be clearly defined and translated into PCM selection objectives. After determining the selection objectives, PCM candidates are prescreened based on their “Boolean” properties with a value of either 1 for “Yes” or 0 for “No”. For example, if the material’s melting point does not fall in the desired temperature range of the application, its value will be 0 and the material will be screened out. Other Boolean properties can also be considered during the prescreening process, including congruent melting, non-corrosive, non-toxic, and non-hazardous.
2.1.2. Multi-Attribute Decision Making (MADM) Ranking
In the second step, Multi-Attribute Decision Making (MADM) tools—Techniques for Order Preference by Similarity to Ideal Solutions (TOPSIS) and the Analytic Hierarchy Process (AHP)—are combined to rank the prescreened material candidates.
Table 1 illustrates a typical MADM performance matrix composed of a series of alternatives, their attributes, and the weights of each attribute.
Xij is the rating of alternative
i with respect to its attribute
j, while
Wj is the weight of attribute
j denoting its relative importance to the other attributes [
28].
In this study, the material candidates are regarded as the alternatives, and the attributes are the PCM’s quantitative properties, including the latent heat of fusion,
dH [kJ·kg
−1], specific heat,
cp [kJ·kg
−1·K
−1], thermal conductivity,
[W·m
−1·K
−1], and the material density,
ρ [kg·m
−3]. For the weights, AHP in subjective weighting is employed to take the designers’ preferences into consideration [
26,
27].
The TOPSIS algorithm is then used to seek the best material alternatives closest to the “ideal solution.” It comprises six steps [
27,
30]:
2.1.3. Multiple Objective Decision Making (MODM) Examinations
After the MADM step, two conflicting objective functions of Ashby’s approach [
31,
32] are used to examine whether the ranking goals agree with two primary LHTES performance objectives: high energy density and fast heat transfer.
To maximize the thermal energy stored in a certain volume and minimize the thermal inertia, the volumetric energy density and equivalent diffusivity of the PCM are selected as the objective functions
and
,
where Δ
T [K] is the temperature change during charging/discharging.
High
value indicates that the LHTES unit stores more thermal energy by using this material, while high
allows for faster charging and discharging of the LHTES unit. The
and
values of the materials are plotted in an objective map with the conflicting objectives
and
being the
x and
y axes. Preferred material alternatives should perform better than nonpreferred materials for both
and
, indicating that they have relatively higher
,
, and
at the same time, which are the key desired properties of PCMs [
3,
33,
34]. An illustration about how to plot the properties of PCMs in an objective map is provided in
Figure 3.
If the MADM ranking results mostly overlap with the MODM examination results, the best material alternatives will serve as the material candidates for the geometrical assessment. Otherwise, the designer should adjust the weights of the MADM ranking. After several rounds of iteration, the final decision will be a combination of both the engineers’ preference and the LHTES performance objectives [
26].
Detailed explanation and illustration of how the MADM ranking and MODM examination work jointly to rank the PCMs can be found in Xu et al. [
26,
27].
2.2. Shell-and-Tube LHTES Design Method
With the top PCMs produced by the material assessment, the ε-NTU method is adopted to produce the design configuration that will serve the LHTES unit’s needs. The configuration is later optimized to minimize the production cost of the LHTES unit as a whole. The typology of shell-and-tube is used in this study, but the same methodology can be extended to cover a wider range of configurations, including packed-bed and plate type LHTES.
Several assumptions are considered in the ε-NTU method of this methodology:
The HTF is on the tube side and PCM on the shell side.
The tubes are aligned parallelly and distributed evenly in the shell space, regardless of the number of the tubes and passes.
The phase change process happens when the temperature of the PCM is fixed at the phase change temperature without supercooling, and the natural convection of the HTF during the phase change is neglected. The ε-NTU method is designed to be temperature independent, while the effect of natural convection increases with the temperature difference between the HTF and the PCM. Neglecting the natural convection may lead to underestimating the heat transfer coefficient, especially during the melting process. However, this effect will not significantly affect the accuracy of the ε-NTU method according to Tay et al. [
35]. Therefore, this method approximates the “worst-case scenario” of an LHTES unit since the PCM sensible heat is not utilized to ensure a constant HTF outlet temperature during cyclic operations, and the phase change process is conduction-dominated.
The designs are optimized for cost reduction purposes. Since the operational cost depends primarily on the application, only the initial cost of the entire LHTES unit is considered here, including the material cost of both PCMs and containment, as well as the production cost of the designed configuration.
Finned tube designs or rough heat exchanging surfaces are not discussed within this study. However, future arrangements can be made to accommodate certain types of finned or surface designs.
The mathematical models are introduced based on the basic shell-and-tube LHTES configuration shown in
Figure 4.
Figure 4a illustrates the 3D model, in which the PCMs resides on the shell side, and HTF flows inside the pipe.
Figure 4b shows the single pipe configuration in 2D, while
Figure 4c presents the storage unit configuration with multiple tubes or passes.
Dt is the tubes’ outer diameter,
Do stands for the shell’s inner diameter, and
P is the pitch distance between the tubes.
The effectiveness of a heat exchanger used for the ε-NTU method is defined as:
where
DT [K] is the temperature difference between the outlet and inlet of HTF,
Tmp [K] is the melting temperature of PCM, and
Tin [K] is the inlet temperature of the HTF. The definition of the number of transfer units (
NTU) is given below, as well as the correlation between effectiveness and
NTU:
where
UA [W·K
−1] stands for the heat transfer capacitance, which is the invert of the total thermal resistance.
The thermal resistances of the HTF, wall, and PCM are given by Tay et al. [
35] as:
where
ri and
ro [m] are the internal and outer radius of the tubes;
rmax [m] is defined as the maximum distance where the phase change front from one tube meets the phase change front of another tube, which equals half of the pitch distance
P [m];
L [m] is the total tube length;
kw and
kPCM [W·m
−1·K
−1] are the thermal conductivity of the tube wall and the PCM; and δ is the fraction of the PCM that has yet to change the phase.
hf is the heat transfer coefficient defined as:
where
kHTF [W·m
−1·K
−1] is the thermal conductivity of the HTF and the Nusselt number
Nu is given by:
and
where
n = 0.3 for cooling and 0.4 for heating. With all of the above information, the average effectiveness can be calculated from:
The accuracy and application range of the ε-NTU method is discussed and validated in
Section 3.1.
2.3. Cost Optimization
For an LHTES unit, the ε-NTU method approximates the performance of one set of design parameters at a time, but it does not guarantee an optimized design combination. Here we propose an optimization algorithm based on cost reduction to examine various design combinations and quickly produce the choice with minimized cost. The benefits of this optimization algorithm include: (1) it ensures the flexibility to deal with any number of variables; (2) users can define the boundaries and constraints of variables according to their interest and objectives; and (3) it saves time and computational resources in the preliminary design stage before complicated computational fluid dynamic and experimental studies.
Since the levelized cost of the storage unit depends on the operational years, which are not certain at the design stage, here we consider minimizing the f.o.b. purchase cost of the storage unit. The f.o.b. purchase cost of a shell-and-tube LHTES contains two parts: the cost of the PCM, CPCM, and the cost of the containment. The latter is assumed to be equal to that of a conventional shell-and-tube heat exchanger with the same configuration, CHEX. Therefore, the total purchase cost is Ctot = CPCM + CHEX. It is worth mentioning that this methodology may overestimate the Ctot if the LHTES unit also uses the PCM’s sensible heat to store and release the thermal energy. It may also underestimate the Ctot if the LHTES unit has some “dead volume” in which some of the PCM in the LHTES unit does not participate in the energy storage, which is neglected in this methodology.
For shell-and-tube heat exchanger units, the f.o.b. purchase cost can be estimated using the method developed by Seider et al. [
36] based on various references as:
where
CB is the cost of a base-case heat exchanger with a shell-side pressure lower than 700 kPa, which can be calculated in the following equations:
and for U-tube design,
where
A [m
2] is the tube outside surface area,
FP,
FM,
FL are the pressure, material, and length factor. For TES units operating at no or low gauge pressures, the pressure factor
FP can be considered as equal to unity.
FM is given as:
where
a and
b are two constants, of which the values depend on the construction material.
Table 2 briefly summarises the constant values for
a and
b with respect to some common construction materials. The extensive list is accessible in Seider et al. [
36].
Some of the length factors,
FL, are listed in
Table 3 for different tube lengths.
The cost minimization is realized with a given set of variables using the
Matlab Generic Algorithm (GA) solver [
37]. The GA solver generates a population of points in each of the iterations and searches for the local minimum within the population. Then, with random number generators, the GA solver selects the next population and compares the local optimal with the previous optimal until a global optimal is found. For the shell-and-tube LHTES cost optimization, to speed up the search, users are allowed to specify the boundaries and constraints of the variables. The variables involved in the optimization can be categorized into material properties, geometric parameters, and operational parameters, as listed in
Table 4.
Some of them can be set as fixed values, depending on the setup and operational limitations, while the others will be subject to constraints within certain boundaries. In
Section 3.2, the detailed execution procedure using the optimization algorithm is introduced to present how the cost minimization is achieved.
3. Results and Discussion
The material assessment part of the methodology in
Section 2.1 has been previously validated and applied [
26,
27]. Hence, this section seeks to validate the ε-NTU method with experimental results for different types of shell-and-tube LHTES designs mentioned in the literature, as well as apply the cost optimization in a real application.
3.1. Design by ε-NTU Method (Validation Using Experimental Data)
This section employs the published data of several LHTES units to validate the ε-NTU method.
According to the applicable requirements of the ε-NTU method:
HTF on the tube side and PCM on the shell side,
phase change takes place at or near the melting temperature range with no obvious supercooling,
smooth tubes evenly and parallelly distributed,
The lab-scale LHTES units developed by Gasia et al. at the University of Lleida [
38], Fadl and Eames at Loughborough University [
39], as well as Tay et al. [
35] at the University of South Australia based on which the ε-NTU method was proposed, are selected and used to validate the accuracy and applicable range of the ε-NTU method.
These units represent a wide range of shell-and-tube LHTES designs and operation conditions by covering different tank geometries, tube arrangements (number of tubes and passes, tube diameter and length), HTFs, PCMs, temperature ranges, and flow schemes (laminar or turbulent). The configurations and key parameters of these shell-and-tube LHTES units are presented in
Table 5.
The calculated results generated by the ε-NTU method and the experimental results are compared and presented in
Table 5. The average absolute error of the three cases ranges from 2.2% to 13%. The Gasia et al. [
38] and Fadl and Eames [
39] cases have lower discrepancies probably because of lower temperature differences between the HTF and the PCM, hence smaller heat transfer enhancement due to natural convection. Despite the highest temperature differences, the average error of the Tay et al. [
37] case is still limited. Therefore, the conclusion can be drawn that the ε-NTU method provides modest errors on a broad range of shell-and-tube LHTES designs and operating conditions. It can be used to calculate the performance of a shell-and-tube LHTES unit as long as the applicable requirements are met.
Future research can try to include the influence of the natural convection during the phase change into the design methodology, as well as develop similar methods for finned units and other types of TES designs, for example, packed-bed and plate type.
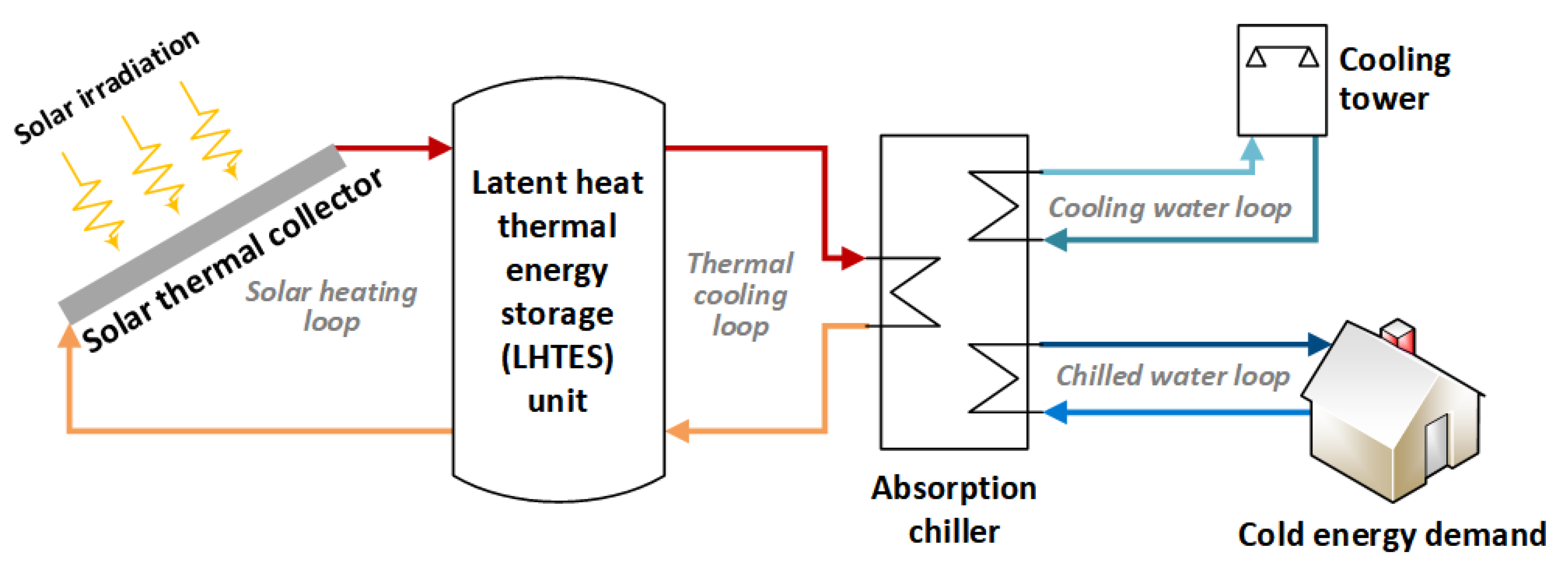
3.2. Optimization of the LHTES Geometries for a Solar Absorption Chiller Application
In order to showcase how the optimization algorithm aids the selection of design parameters, this study adopts the design parameters of the shell-and-tube LHTES unit developed by Gasia et al. at the University of Lleida [
38] for the optimization case study and assumes that this unit is used to buffer the fluctuation of a solar-absorption cooling system (as illustrated in
Figure 5). Therefore, the operational parameters such as discharging power, the mass flow rate of the HTF (Syltherm 800), and the inlet temperature of HTF are fixed due to operational constraints.
The solar-absorption cooling system provides 1 kW of cold energy to the end-users. The solar thermal collector supplies the heat to a single effect absorption chiller with a COP of 0.7. In order to avoid overheating and supply heat during the nighttime, an LHTES unit is deployed between the solar thermal collector and the absorption chiller. The LHTES unit is charged by excess irradiance during the daytime and uses the stored heat to drive the absorption chiller when there is a lack of solar irradiance or during the nighttime. Operation conditions of the LHTES unit are listed in the first part of
Table 6 as the fixed variables.
Three cases with three different PCMs selected by the material assessment process are presented. The costs of the PCMs are assumed to be USD 10 per kilogram according to the average market price. The geometric parameters are optimized for each case with minimized cost with respective PCMs, and the results are shown in the third part of
Table 6 as the optimized geometric variables.
The three cases receive the same amount of heat from the solar thermal collector and produce the same amount of driving heat for the downstream absorption chiller. The optimization algorithm found different global optimum LHTES geometries for different PCMs, resulting in the PCM costs ranging from around USD 850–1600 per unit, while the total cost ranges from around USD 31,000–38,000 per unit.
Since the design parameters for operation are fixed, the containment materials’ selection has the most significant impact on the total f.o.b. cost. The major cause of the high total cost listed in
Table 6 is due to the using of high-cost stainless steel for both the shell and tubes.
As shown in
Figure 6, the costs of four shell and tube material combinations are calculated. If changing the shell/tube materials from the high corrosion resistance stainless steel/stainless steel to other material combinations, the total cost decreases significantly. If using the low corrosion resistance carbon steel/carbon steel, the total cost can be reduced by around 3/4 due to much lower material costs, ranging from around USD 8400 to 10,200 per unit. It is worth mentioning that, for each selected PCM, the optimized geometry (tube lengths and the number of tubes) varies only in a limited range for each shell and tube material combination, and the PCM costs remain the same. Therefore, using low or non-corrosive PCMs can significantly decrease the containment material cost. Selecting the correct PCMs in the prescreening to make sure that it does not corrode the containment materials not only increases the lifespan of the LHTES unit, but also saves the investment cost. Users can also try to freeze more fixed variables, for example, the tube diameter, to decrease the costs.
Moreover, this methodology has been found to be considerably faster compared with CFD-based methodologies. The average computing time using this methodology to finish the design of one shell-and-tube LHTES unit, from the material assessment to the cost output, is around 5–10 s. Depending on the quality of the mesh, CFD simulation-based methodologies can cost up to several hours to finish one optimization due to the dozens and hundreds of rounds of iterations that are needed for the GA solver. Therefore, this methodology is ideal for generating a quick and reliable preliminary design before running into detailed CFD simulations and mechanical assessments.
Future work could evaluate the operational cost of an LHTES unit together with the energy system that is equipped with the LHTES unit, and analyze the effect of different designs on the overall performance of the downstream equipment and the whole energy system.
4. Conclusions
The design of shell-and-tube LHTES is a complicated process encompassing a wide range of issues such as material selection, geometric design, and numerical and experimental study. So far, limited all-inclusive design methodology has been found in the literature to guide design engineers step by step from the material selection to a valid geometrical design and at the same time optimize the design with cost minimization. This study proposes a comprehensive design methodology that aims to overcome this issue.
The methodology proposed comprises a material assessment step to examine the competencies of the PCM choices and a geometrical assessment step to produce the geometric parameters that minimize the storage unit’s purchase cost with user-specified boundaries and constraints. The material assessment step adopts the multi-criteria decision-making tools to evaluate the database of PCMs based on their properties and collective competencies and suggests the best choices. The LHTES unit is evaluated by the ε-NTU method for quick and accurate performance approximation. The optimization step employs the Genetic Algorithm, which varies all open parameters with user-specified constraints, and compares the costs from each step with the parent step until the minimum cost is found.
Two case studies have been presented to explain the applicability of the methodology. The first case uses real storage units produced and reported in the literature to validate the ε-NTU method. In the second case study, design optimizations based on cost minimization are realized for the solar absorption chilling application. The minimized costs for different scenarios such as different PCMs and different geometric variables are presented. The total purchase cost of as low as USD 8396 per unit is reported for a 1.42 kW shell-and-tube LHTES unit.
The methodology is a systematic and flexible procedure to generate a reliable preliminary design of the storage unit without occupying too many numerical resources such as the computational fluid dynamics tools. It can also be used for parametric studies when the engineers are in search of the parameters that influence the performance or the cost of the storage unit the most.
To make the design methodology more accurate, future research can consider natural convection for LHTES performance approximation. The methodology can also include other storage types and the interaction between the storage unit to the downstream energy system.