Abstract
Offline changepoint detection (CPD) algorithms are used for signal segmentation in an optimal way. Generally, these algorithms are based on the assumption that signal’s changed statistical properties are known, and the appropriate models (metrics, cost functions) for changepoint detection are used. Otherwise, the process of proper model selection can become laborious and time-consuming with uncertain results. Although an ensemble approach is well known for increasing the robustness of the individual algorithms and dealing with mentioned challenges, it is weakly formalized and much less highlighted for CPD problems than for outlier detection or classification problems. This paper proposes an unsupervised CPD ensemble (CPDE) procedure with the pseudocode of the particular proposed ensemble algorithms and the link to their Python realization. The approach’s novelty is in aggregating several cost functions before the changepoint search procedure running during the offline analysis. The numerical experiment showed that the proposed CPDE outperforms non-ensemble CPD procedures. Additionally, we focused on analyzing common CPD algorithms, scaling, and aggregation functions, comparing them during the numerical experiment. The results were obtained on the two anomaly benchmarks that contain industrial faults and failures—Tennessee Eastman Process (TEP) and Skoltech Anomaly Benchmark (SKAB). One of the possible applications of our research is the estimation of the failure time for fault identification and isolation problems of the technical diagnostics.
1. Introduction
Changepoint detection (CPD), being one of the stated major challenges for big data applications [1], is a particular part of an anomaly detection in time series data problem presented in detail in the fundamental works [2,3]. In terms of the number of points, the anomalies are divided into a single point and collective ones. The changepoint detection problem mostly relates to the collective anomalies type. A common definition of the changepoint detection is proposed in [4]:
Changepoint detection is a study of methods for identification of changes in the probability distribution of an observed stochastic process.
Changepoint detection problems can be applied in many applications, such as computer network intrusions [5], power plant failures [6], finances [7], climate changing [8], and illness indication in medicine, including heart attack recognition [9] and arrhythmias detection [10].
All algorithms used for changepoint detection can be split into two main classes: “online” and “offline” algorithms. Most of the algorithms and approaches from these classes differ significantly. Online algorithms try to find changepoints as soon as they occur, and they are often applicable for real-time anomaly detection and online process monitoring. Offline algorithms appropriately deal with signal segmentation or delayed analysis of the whole process realization. Moreover, they try to solve the changepoint detection problem as accurately as possible. Some of the offline algorithms can be used in real-time batch processing. However, the offline algorithms usually lose accuracy in this case because they work only with a part of the signal and can not solve the problem for the entire signal in an optimal way. The scope of this paper is specifically an offline changepoint detection problem.
Anomalies of various nature may cause different statistical changes—mean, standard deviation, autoregression dependence, seasonality, etc. To detect such changes, various specific models may be applied. One of the biggest challenges for this problem is to select either the most robust model or several better-performing ones, each for the specific statistical change. Moreover, the selection of the best model depends on the search method and selection criterion. The details regarding the model selection challenges and single-best-model paradigm are presented in [11] and references therein. Ensembles of models allow avoiding using a high number of separate models, improve the robustness of the resulting changepoint detection procedure, and reduce the dependence of the resulting procedure to the particular set of data or type of anomaly [12].
Ensemble approach in classification and clustering problems is widely studied, applied to, and formalized well [12]. In recent years, the popularity and achieved results of the ensemble approach in the outlier detection problem have grown as well. The current state of the ensemble analysis and various ensemble procedures for the outlier detection problem are represented in the following papers [12,13,14,15,16,17]. Although outlier detection and changepoint detection problems are often considered subproblems of general anomaly detection problem, the ensemble approach in the changepoint detection problem is weakly formalized and much less highlighted. The reasons why ensemble analysis for anomaly detection subproblems is quite challenging and hence not so widely explored are well described in the mentioned paper [12]. It is worth noting that event detection in temporal data [14,18] looks like a similar problem to changepoint detection. Nevertheless, it mainly aims at finding a single anomalous point followed by the normal points making the problem closer to the outlier detection problem.
The paper [19] is the first work in the direction of changepoint detection ensembles (CPDE) for time series data according to the paper itself and to our best knowledge. We found just a few relevant papers published since 2013 [4,11,20,21] that represent the current state in this field of knowledge. None of these papers focus on the analysis of various scaling functions and just two of them ([4,19]) have compared more than one aggregation function. Moreover, just two of the works ([19,20]) relate to the offline CPD problem, but they select only one base detector for the ensembles—the Lepage nonparametric test is able to assess changes in the mean or the variance. Among the papers, just one [21] uses a technical-related benchmark—KDD Cup 1999 network intrusion detection dataset—while others either use synthetic data or ecology-related data. Finally, all of the works in the CPDE field of knowledge lack generalizing ideas. They do not aim to formulate a framework for various detectors (models), search methods, aggregation, and combination functions for use and analysis.
This paper proposes a novel model-centered, independent, scaled (normalized) ensemble approach for the offline changepoint detection problem. Moreover, we select and study various common aggregation functions from outlier, cluster, and classification ensembles and their applicability in CPD ensembles. The pseudocode of the particular suggested ensemble algorithms is presented in Appendix A. Our ensemble approach is based on and extends the famous changepoint detection procedure formulated in [22]. Additionally, we compare the proposed ensemble and original non-ensemble approaches and the various scaling and aggregation functions. For the comparison, we conducted numerical experiments on the two technical benchmarks that contain industrial faults and failures—Tennessee Eastman Process (TEP) benchmark and Skoltech Anomaly Benchmark (SKAB). The algorithms are applied in an unsupervised way without any fitting stage but for a known number of changepoints to look for. We also provide links to the Python source code with the implemented ensemble algorithms and experiment results. The proposed source code is based on the ruptures Python scientific library, presented and described in [22] as well.
Our work differs from previous in three key aspects. Firstly, most works focus on the single CPD algorithm and a few situational aggregation functions, not paying attention to the scaling functions. At the same time, we tried to embrace the most common CPD algorithms, scaling and aggregation functions, comparing them during the numerical experiment. Secondly, we work with several cost functions (models), aggregating their results. Just one of the works deals with various base detectors, while the closest to our work [19] not only uses a single model as the base detector but also highlights the aggregation of different test statistics (base detectors) in the ensemble as the possible future research direction. Third, none of the works focus on detecting changepoints in the industrial data. Still, one of the works [20] considers complex embedded systems modeled by an autoregressive moving-average (ARMA) process. One more [21] shows the results on the intrusion detection dataset. Therefore, our work is the first to apply CPDE on the benchmarks with industrial faults and failures, showing the possible applicability in technical diagnostics. Additionally, ensemble analysis for the CPD problem lacks research works, especially when compared with outlier detection, clustering, or classification problems.
One of the possible applications of our research is the estimation of the failure time [20] for fault diagnosis, and isolation phases of the technical diagnostics or process monitoring loop [23]. It can help to determine which fault occurred. Accurate models and solutions for fault detection and diagnosis (FDD) make process monitoring systems more efficient and retrospective analysis more correct. Improving the FDD process can help to move to condition-based maintenance, which can be less expensive than other maintenance strategies [24]. Moreover, improving process monitoring develops smart manufacturing and industrial big data environment technologies helping managers to fit industry into the concept of Industry 4.0 [25]. Additionally, a thorough analysis of the historical data can help in predicting and avoiding some threats in the future [26].
2. Materials and Methods
2.1. Ensembles of Offline Changepoint Detection Procedures
2.1.1. Time Series
A time series y is a sequence of points or samples representing process characteristics , where —sample at a time moment t, —time moment or index of the time series, T—length of a time series.
is a subsequence or part of the time series y, where .
and also refer to univariate and multivariate problems, respectively.
2.1.2. Changepoint
An accepted definition of a changepoint is as follows: is considered as a changepoint if at a time some characteristics of a process y abruptly change. is a particular partition of y for subsequences, where K is a total number of changepoints, which may be known or unknown for a specific changepoint detection problem. Generally, a partition is a set of indices or timestamps that indicate a specific segment of a time series y. We define segmentation as a process of finding a particular partition for a time series y. A subsequence can be called a segment of y for a partition .
2.1.3. Changepoint Detection Procedure
We call a changepoint detection (CPD) procedure if finds the “best partition” by minimizing the quantitative criterion , where is a cost function which measures for each point of the partition or for each subsequence a “quality of partition”. To find the “best partition” , a discrete optimization problem of minimizing the criterion must be solved. If a number of changepoints K is known beforehand, an optimization problem is as follows:
where is a cardinality of a .
For an unknown K, an optimization problem looks like:
where is a constraint to balance a number of found changepoints. Additional penalty allows to choose if a few most highly ranked points (or even none) or a lot of candidates of a changepoint will be selected as a final decision of a “best partition” .
It is important to mention that in the case of a multivariate problem (), we need to aggregate criteria for each of the D time series inside the (in this case, we can call an ensemble already according to the further definition of the ensemble procedure). To avoid dealing with ensembling of individual univarite time series, considered criterion is then defined in our case in a common way as a sum of the criteria calculated for each univariate time series and looks like:
Though dealing with univariate time series and following aggregating looks like a simpler approach against using multivariate models from the first, the paper [21] clearly shows how aggregation of the univariate models outperforms multivariate models.
A CPD procedure in a general way may consist of three main parts:
- A cost function, also called a model,
- A search method for finding , also called an optimization or detection algorithm,
- A constraint on the number of changepoints if the exact number of changepoints K is unknown.
The scheme of the CPD procedure used in our work is shown in Figure 1.
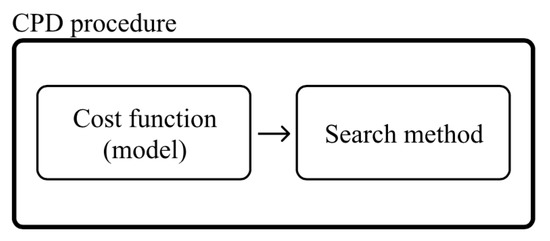
Figure 1.
Components of a typical non-ensemble changepoint detection (CPD) approach.
For a comprehensive review of cost functions and search methods, the theoretical foundation behind them as well as the intuition behind the selection of a constraint, an interested reader may refer to [22]. The number of changepoints K or a constraint are usually set in a problem statement or can be defined during the experiment process, and the search method only determines the way of changepoint finding. A cost function determines the particular function for minimizing. Therefore, it is vital to select the right cost function for each specific changepoint detection case since different cost functions usually represent different statistical properties of a signal. For example, changes in a mean can hardly be detected through standard deviation calculation. It also means that proper cost function selection can become a laborious and time-consuming process with an uncertain result.
2.1.4. CPD Ensemble Procedure
Let us denote N CPD procedures as and an aggregation or combination function as . We call A a CPD Ensemble (CPDE) if the “best partition” is a result of solving the problem for a fixed K:
and for an unknown K:
We propose a novel way to find changepoints by aggregating several cost functions inside the CPD procedure, as is shown in Figure 2.

Figure 2.
Components of a proposed CPD ensemble (CPDE) approach.
A procedure A is a particular case of an Ensemble method defined by an aggregation function . The proposed Ensemble approach implies using several cost functions and aggregating afterward during the single CPD procedure running. The result of each cost function applied is a univariate time series. Altogether they form an -dimensional array of scores, , where , , , N is the number of applied cost functions, and M is a length of single cost function results. Generally, M depends on the search method. Therefore, using N cost functions results in getting a multivariate time series of scores with the to which the aggregation function applied. The search method is only applied to the aggregation result. Such an approach solves the problem of proper cost function selection and improves the robustness of the CPD procedure. The robustness is achieved by making the CPD procedure invariant to a particular statistical change considering outputs of various statistical models (cost functions). The intuition behind the aggregation of several cost functions through using base detectors score combinations is mainly related to the classification and outlier ensembles. Such an approach allows:
- Avoiding losing useful information as it could be if the outputs of the whole CPD procedure are aggregated. Our approach works with scores representing confidence and many time-related characteristics, while for the second approach, only the sets of changepoints are available for combining.
- Borrowing some useful and interesting ideas from the classification and outlier ensembles where combining scores of the base detectors is the most common approach;
- Getting more opportunities when working with the multivariate time series of scores by applying some classical techniques from the time series analysis;
- Constructing a framework with four main parts (cost function, scaling function, aggregation function, search method). It simplifies the experiments currently conducted or for further research and allows to improve the results by various minor changes added for the best-working methods.
An illustrative example of the cost functions aggregation procedure is shown in Figure 3.

Figure 3.
An illustrative example of the cost functions aggregation procedure.
Characteristics of the proposed CPDE procedure in terms of the categorization according to [12] (shown in Figure 4) are as follows:
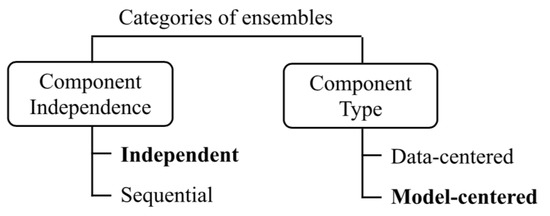
Figure 4.
Categorization of ensemble techniques.
- Model-centered: these are the models that we use to create an ensemble, but we do not pick subsets of data points or data features (data-centered).
- Independent: we calculate the ensemble components (cost function scores) before the aggregation independently from each other and not in a sequential way.
- Scaled (normalized): aggregation function should include a scaling procedure for each argument (cost function application result), since different cost functions may generate differently scaled outputs. Scaling avoids favoring one or more cost functions.
A variety of scaling and aggregation functions for outlier, changepoint, classification ensembles, as well as the related issues can be found in papers [12,13,14,16,18,19,20,27,28]. Though scaling can be included in and considered part of aggregation procedure [4], we treat it separately from the aggregation function. Common scaling procedures are as follows:
- MinMax: normalizing all values to the range , also known as MinMax scaling;
- Znorm: zero mean, unit variance scaling, also known as Z-normalization or standard scaling;
- MaxAbs (MinAbs): scaling by maximum (minimum) absolute value, also known as MaxAbs (MinAbs) scaling;
- Rank: using ranks of the criterion points from minimum to maximum value.
All procedures translate each criterion individually. Among aggregation functions, also called combination functions, combination methods, or combination algorithms, the popular ones are as follows:
- Average: averaging scores of all cost functions;
- WeightedAverage: weighting cost functions and then averaging weighted scores. Difference between static and dynamic weighting is presented in [29]. Commonly, the weights for various models or cost functions are predetermined [16,29]. For unsupervised offline ensembles, the weights can show the degree of confidence of each separate detector.
- MajVote: the point that the majority of all cost functions has selected is a changepoint. Though majority voting is primarily used in classification ensembles [28,29], it can be applied for CPDE, for example, together with Rank scaling or using the threshold [4];
- Max (Min): selecting maximum (or minimum) among scores of various cost functions;
- Sum: summarizing scores of various cost functions;
- ThresholdSum: discarding (pruning) scores below the selected threshold and then summarizing scores. Pruning can be applied either to the scores of every single model by using the threshold or to the scores at each point by selecting only the top models [12];
- AverageOfMax: dividing cost functions into groups, taking maximum of scores of each group, and then averaging;
- MaxOfAverage: dividing cost functions into groups, averaging scores of each group, and then taking maximum of averages;
- FeatureBagging: applying cost functions to feature subsets and averaging of the obtained scores.
The exact formulations of the scaling and aggregation functions selected for the experiment are presented in the next subsection.
2.2. Numerical Experiment
During the experiment, we compare the CPD procedure with a single cost-function inside (non-ensemble approach) and the proposed CPDE procedure (ensemble approach). The experiment setup in parts of cost functions, scaling functions, aggregation functions, and search methods is shown in Figure 5. We selected for the experiment not all common aggregation functions because some of them are not suitable for the provided algorithms or relate to data-centered ensembles (FeatureBagging), some need more cost functions to be used or at least more scores to be generated for proper use (AverageOfMax, MaxOfAverage), and some duplicate the result of selected ones (Average, WeightedAverage, MajVote). Selection of cost functions was based on the recommendations from [19,22]. The motivation for using selected cost functions under a single ensemble comes from a desire to avoid the time-consuming and laborious process of proper model selection. Furthermore, in most engineering applications, various signals are generated from various statistical models. Likewise, a single signal may have various normal operation states generated by various models. We find a combination of different cost functions useful for diagnostics tasks in technical engineering systems that is one of the possible applications of our research. We do not use a constraint because the number of changepoints for the experiment is assumed to be known. For our experiment, the number of changepoints is equal to 1 for TEP and 4 (for most datasets) for SKAB.

Figure 5.
The numerical experiment setup for CPD ensemble and non-ensemble approaches.
2.2.1. Benchmarks
Tennessee Eastman Process (TEP) Benchmark
The original paper [30] presented a model of the industrial chemical process named Tennessee Eastman Process and model-based TEP simulator for data generation. The most widely used benchmark based on TEP is presented in [31]. The benchmark consists of 22 datasets, 21 of which (Fault 1–21) contain faults and 1 (Fault 0) is a fault-free. All datasets have training (500 samples) and testing (960 samples) parts: training part has healthy state observations, testing part begins right after training, and contains faults which appear after 8 h since the training part. Each dataset has 52 features or observation variables with a 3 min sampling rate for most of all. Description of the process and related aspects, graphical diagram of the TEP, simulation code, benchmark simulation conditions, benchmark downloading links are presented in [31] and references therein. We do not use the Fault 0 (fault-free) dataset in our experiment due to the unsupervised manner of our approaches. The example of the time series representing a single feature in the dataset is shown in Figure 3. It is worth noting that we applied Z-normalization to the data before the experiment running because of the different scales of the separate features.
Skoltech Anomaly Benchmark (SKAB)
SKAB [32] is designed for evaluating algorithms for anomaly detection. SKAB includes 34 datasets and Python modules for algorithms’ evaluation. Each dataset represents a multivariate time series collected from the sensors installed on the testbed. All instances are labeled for evaluating the results of solving both outlier and changepoint detection problems. The data and detailed description of the SKAB are available at https://github.com/waico/SKAB (accessed on 8 May 2021). For SKAB, we have also used the Z-normalization procedure because the data are differently scaled as well.
2.2.2. Search Methods
The “forward dynamic programming” algorithm for optimal signal segmentation is initially presented in [33]. This algorithm provides finding the exact solution for the optimization problems stated earlier by calculating all possible partitions of the signal. Some of the observations about the algorithm and its extensions, as well as the computational complexity and other characteristics, are presented in [22].
The window-based algorithm provides an approximate solution to the mentioned problems. It is based on calculating the dissimilarity of the two following each other window. The details are presented in [22].
The binary segmentation algorithm also provides an approximate solution to the problems. The signal is split into two parts for each step of this algorithm. For the details and additional information about the algorithm, an interested reader may refer to [34].
Extension
Our extension of the above-mentioned algorithms is as follows: in the part of cost function calculation, we simultaneously calculate costs for all partitions using each cost function separately, resulting in an -dimensional array of scores. Then all the scores are scaled independently across the Nth dimension, and, finally, they are aggregated into a single result of size. Finally, a search method is applied to the aggregated time series of without any changes. Pseudocode of the proposed , , and search methods is presented in the Appendix A.
2.2.3. Cost Functions
As well, we selected several well-known cost functions for the experiment (Figure 5).
Median-Shift through Least Absolute Deviation—l1
It allows to detect changes in median of the signal [35]. The cost function is defined by the formula:
where is the median of a subsequence . Generally, the shift of any central point (mean, median, mode) in a numerical data set can be detected.
Mean-Shift through Least Squared Deviation—l2
Allows to detect changes in mean of the signal [22]. The cost function is defined by the formula:
where is the mean of a subsequence .
Mahalanobis-Type Metric—Mahalanobis
It allows to detect changes in the pseudo-metric of the signal [36]. We use Mahalanobis distance [37] as the pseudo-metric in our experiment. The cost function is defined by the formula:
where is the mean and is the inverse of the empirical covariance matrix of a subsequence . Generally, instead of , any symmetric positive semi-definite matrix can be used.
Piecewise Linear Model—Linear
It allows to detect changes in a linear relationship between an observed variable and a covariate [38]. Let us assume that the process is defined by the model , where is a covariate vector, u is a vector of regression parameters, p is an order of the model and is a noise. Then the cost function is defined by the formula:
In the other words, a linear regression is fitted for each subsequence .
Piecewise Autoregressive Model—ar
If the observed variable depends linearly on its previous states, a piecewise autoregressive model can be used [39]. The cost function is defined by the formula:
where . For the experiment, we chose from the grid search procedure.
2.2.4. Scaling Functions
The following scaling functions are used during the experiment:
where is a result of the nth cost function applied, being a 1-dimensional array of M elements, is the mean of , and is the standard deviation of . The outputs of , , , and functions are single values calculated over the input array. The function transforms the input array into a set of ranks of the values in “ascending” order.
2.2.5. Aggregation Functions
The following aggregation functions are used during the experiment:
where is the mean of the sample, —weighting coefficient. The idea behind the weighting coefficient is based on the calculating the confidence of each cost function in its extremum, so when the output does not have any outstanding extremums, its weight will go to zero vanishing the related scores.
2.2.6. Performance Measures
Community commonly applies TEP benchmark for comparing various algorithms [31,40,41,42] using mostly several metrics: detection delay, missing alarm rate, fault detection rate (FDR), and false alarm rate. Usually, in papers with the TEP benchmark, FDR is calculated by using labels of all single instances in each dataset for TP and FN counting. Obviously, such an approach does not give representative results for the CPD problem. That is why for performance scoring, we use the NAB scoring algorithm and metrics from [43]. It was initially proposed for the Numenta Anomaly Benchmark but it can be also used for other datasets [44]. The main features of this algorithm are rewarding early detection and penalizing false positives and false negatives. This is achieved with a special scoring function (19) that is applied to the detection window (Figure 3).
where x is the position of the detected anomaly relative to the right border of the window measured by points. and are weight coefficients from the application profiles for true positives and false positives, respectively. The width of the window is heuristically determined as 10% of the dataset length for TEP benchmark and for SKAB. It follows from the assumption that this window size is appropriate for the domain problem. The NAB scoring algorithm is also parameterized by application profiles, that allow us to better understand the properties of each specific anomaly detection algorithm. For our paper, we take application profiles, provided in [45]. They are shown in Table 1.

Table 1.
Application profile for NAB scoring algorithm.
3. Results
We provide in Table 2 and Table 3 the results of the numerical experiments, in which CDP and CPDE procedures were run on the TEP and SKAB benchmarks. Negative or zeroed results mean that none of changepoints were found. Bold numbers refer to the best results among the procedure (CPD or CPDE) and search method. Dashes mean unapplicability of the cost function to the search method. It is relevant to the linear cost function and search method. The window-based algorithm when used in CPD and CPDE procedures needs an additional window width selection stage. The window width was selected from the classical grid search procedure for various values. The results are presented under the assumption that better-performed windows are found. The results for various windows are presented at https://github.com/YKatser/CPDE (accessed on 8 May 2021). One more assumption on the experiments is that various features in the datasets (signals) are generated from the various models.

Table 2.
NAB scoring algorithm (higher is better) results of the CPD algorithms on the TEP benchmark.

Table 3.
NAB scoring algorithm (higher is better) results of the CPD algorithms on SKAB.
The best overall NAB (standard) score for TEP benchmark is equal to . This score is achieved by four algorithms at once:
- + aggregation + scaling;
- + aggregation + scaling;
- + aggregation + scaling;
- + aggregation + scaling.
The best score among non-ensemble procedures equals to and refers to and search methods with cost function.
The best overall NAB (standard) score for SKAB is equal to . This score is achieved by the search method with cost function. The best score among ensemble procedures equals to and refers to the search method with aggregation function and scaling function.
LowFP and LowFN profiles indicate that all of the procedures generate more false positives for SKAB, whereas the gap between profiles for TEP benchmark is diminutive.
3.1. CPD and CPDE Procedures
For TEP, shows exact results as , while shows quite similar results to . As for SKAB, the difference between and is minor as well, while the difference between and is already significant in favor of the first. It is interesting that improves for both benchmarks, and improves just for TEP. Especially interesting is that shows excellent results for TEP, demonstrating much better performance than and has great results in general, but for SKAB loses against the algorithm as well as generally among all CPDE procedures. We can explain it by benchmark differences and fitting of the specific algorithms to the data.
algorithm is the only algorithm among non-ensemble ones that outperforms ensemble procedures for the TEP benchmark. Even so, for SKAB, outperforms the algorithm quite confidently, which can also be explained by the overfitting to the data. Eventually, and display the weakest performance among all CPD and CPDE procedures.
Finally, in four out of six cases, the ensemble approach shows better results than the non-ensemble one, and one of the other two cases is comparable. Therefore, there is just one (out of six) considerable loss of the ensemble approach against the non-ensemble ones. demonstrates the best overall performance regardless of the benchmark, aggregation, or scaling function.
3.2. Cost Functions (Models)
Among five selected for experiment cost functions, the noticeably better result was achieved by the cost function. Just once, it has shown the second-best score ( search method on SKAB). , , models achieved about the same results, while the model was significantly worse than others. Obviously, cost function results depend on the data properties and anomaly nature, though experimentally, the cost function shows the best result regardless of the dataset.
3.3. Aggregation Functions
and act quite similar for all search methods. Still, performs slightly better. significantly losses to them with , failing with and scaling functions regardless of search method. aggregation function, in general, has worse results, but it also has the best results with some scaling functions for the TEP benchmark. Nevertheless, it looks like a data-based pattern and not a general case.
3.4. Scaling Functions
It was unexpected to us that it is the scaling function that shows the best results in 4 out of 6 cases ( and for both benchmarks). In general, among all aggregation functions and ensemble procedures, shows the worst results. Excluding aggregation and search algorithm from the analysis, the results of all scaling functions are quite indistinguishable, except for just a few winning scores that rater looks like outliers.
3.5. CPD and CPDE Procedures vs. SOTA Changepoint Detection Algorithms
We should note that in our work CPD procedures from [22] are sometimes considered as state-of-the-art (SOTA) for changepoint detection problem. Moreover, existing algorithms and approaches in the CPDE field are not systematized, and it is questionable to consider any of them as SOTA. Quite noteworthy is that all of the added-to-compare algorithms except for unsupervised ARIMAFD [46] are semi-supervised since they need a training set with the healthy operation mode, while all algorithms tested in our work are unsupervised. Therefore, compared algorithms are applicable in different situations and are not competing.
In Table 4, we compared our results with some other SOTA results achieved on TEP and SKAB benchmarks. We have found only one work [47] where CPD algorithms were applied to TEP benchmark with NAB metric. We provide here the results from this work. It is worth noting that the TEP benchmark in this work differs from ours since the authors synthesized datasets from the TEP model themselves, while we used the most common previously generated benchmark. This fact makes the comparison for the TEP benchmark not fully reliable. For the details about the dataset and differences from our version of the TEP benchmark, an interested reader can refer to [47]. For SKAB, we used the results presented in the related repository https://github.com/waico/SKAB (accessed on 8 May 2021). Multi-Scale Convolutional Recurrent Encoder-Decoder (MSCRED) from [48] is positioned as the state-of-the-art in technical diagnostics. Under the LSTM, anomaly detection algorithm based on the LSTM-based forecasting algorithm is meant.

Table 4.
Comparison of the CPD and CPDE procedures with SOTA changepoint detection algorithms.
It is clear from the table that CPD and proposed CPDE procedures show slightly worse results than Neural Networks-based SOTA approaches while confidentially overperforming classical (Hotelling’s ) and situational (ARIMAFD) algorithms.
4. Discussion
We provide here our recommendations based on the experiment results.
- According to the experiment results, the ensemble approach almost always is a priority option. Among non-ensemble procedures, the favorite ones are and methods but only with cost function. Among ensemble search algorithms, we recommend to use .
- The question of what combination function to select is mentioned in [13]. Averaging and maximum aggregation functions are the only methods compared by authors from a bias-variance trade-off perspective. None of these functions were declared as a clear winner. The experiments indicated that maximization achieved better results than averaging for larger datasets, while the opposite picture was for smaller datasets.Our experiment revealed that selecting either or is a confident strategy for steadily achieving high scores. aggregation function may lead as to the best or the worst score, while it still can be used in combination with and or functions without major losses in a score. After all, we either cannot highlight the best combination strategy.
- Regarding the scaling functions, we can recommend avoiding the to maximize the results for most cases, even though it sometimes allows a high score. All of the other scaling functions get similar results.
The limitations of the study are mainly connected with the data properties and generalizability of the results. Our research is mainly focused on the technical domain and industrial data, hence industrial faults and failures. Not only do the datasets used in our numerical experiment not allow generalizing results to any domain of knowledge, but the bias in the data in some specific domain may lead to the inconsistency of the results. Differences in the real-world data are forcing researchers to test the methods when expanding the proposed ensembles to the new application. One more limitation is connected with the NAB scoring algorithm used for the evaluation of various methods results. The way of applying the NAB algorithm may differ from varying the window size and location around the changepoint to application profile tunning, and no recommendations or algorithm limitations are provided. The major limitation of the work is that the CPDE approach was not studied for the unknown number of changepoints. The last limitation is connected with some algorithm parameters selected from the grid search procedures. They are the number of lags for the autoregressive model equal to 1 and the window size equal to 20 points for the and search methods. We assumed that the grid search procedure provides optimal results for these parameters. Nevertheless, the limitations were known during the study’s design, and we consider that they did not affect the principal results of the numerical experiment.
5. Conclusions
We proposed a novel, although quite intuitive, way of ensembling unsupervised offline changepoint detection procedures in this work. An ensemble approach for the CPD procedure allows us to avoid the time-consuming process of algorithm selection and decreases the uncertainty of the results. Generally, the robustness of the ensemble algorithms assists in the automatization of the signal segmentation process, which is useful in numerous engineering applications. Our study showed that the proposed CPDE procedure is at least promising. Additionally, we compared various common scaling (MinMax, Z-norm, MinAbs, Rank), and aggregation (Min, Sum, WeightedSum, ThresholdSum) functions. The comparison results formed the basis for the recommendations on scaling and aggregation functions selection for CPDE. Moreover, the proposed approach can act as a framework allowing putting together many methods, algorithms, and cost functions. It positively affects the existing problem of lack of systematization in the CPDE field of knowledge. Both CPD and CPDE procedures were applied in an unsupervised way without fitting phase but for a predefined number of changepoints. The results were obtained on the technical anomaly detection benchmarks—Tennessee Eastman Process and Skoltech Anomaly Benchmark using the NAB scoring algorithm. We also presented pseudocode of the proposed , , and algorithms (search methods) and the link to their Python realization.
As for the future work ensemble, the approach may be extended over some other search methods. Altogether with the proposed algorithms, they can form a programming framework of state-of-the-art CPDE algorithms similar to the ruptures library. Additionally, more aggregation and scaling (normalizing) functions may be explored and compared. It can expand the proposed recommendation list for selection normalizing and aggregation functions in the technical domain or regardless of the domain at all. Presented algorithms can also be applied to various application domains using the proposed pseudocode and python code from the repository. Applying the algorithms to more datasets and benchmarks, including synthetic ones, may help to generalize results and avoid overfitting to the particular dataset. One more interesting direction is automizing window width selection for and procedures, which can be based on the presented algorithms and code. Generally, the proposed solution forms the framework for changepoint detection ensembles. It can be the base for various search methods, scaling, aggregation functions, and cost functions (models) applicable in offline CPD in numerous applications—from computer networks intrusion analysis and power plant failures diagnostics to ecological changes analysis and various medical applications. Our proposed solution fits the best in unsupervised offline or retrospective analysis applications where the most accurate changepoint detection is required, and models from which the analyzed signals being generated are unknown.
Author Contributions
Conceptualization and methodology, I.K., V.K., and V.L.; software, I.K. and V.K.; validation, V.L. and I.M.; formal analysis, I.K. and V.K.; investigation, V.K.; resources, I.M.; data curation, I.K.; writing—original draft preparation, I.K.; writing—review and editing, V.L. and I.M.; visualization, V.K.; supervision, V.L.; project administration, I.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. The first dataset (TEP) can be found here: https://github.com/YKatser/CPDE/tree/master/TEP_data (accessed on 8 May 2021). The second dataset (SKAB) is openly available at https://doi.org/10.34740/KAGGLE/DSV/1693952 (accessed on 8 May 2021), reference number [32], while the detailed description is available in the SKAB repository at https://github.com/waico/SKAB (accessed on 8 May 2021). Implemented search methods, experiment pipeline, and supplementary materials are available at https://github.com/YKatser/CPDE (accessed on 8 May 2021). All information about experiment repeatability is also provided in the repository. All code in the repository is made available under the GNU General Public License v3.0. For the experiment, we also used ruptures Python package which is being distributed under the BSD License. The package is available at https://github.com/deepcharles/ruptures (accessed on 8 May 2021).
Acknowledgments
The authors would like to thank Dmitry Lakontsev from Skolkovo Institute of Science and Technology for the support and critical reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Pseudocode of the Ensemble Algorithms
Here the pseudocode of the proposed ensemble algorithms is shown, including:
- (Algorithm A1) based on the algorithm;
- (Algorithm A2) based on the algorithm;
- (Algorithm A3) based on the algorithm.
| Algorithm A1 |
Input: signal , cost functions , number of regimes . for all , do for do Initialize end for end for . for do for all do end for end for Initialize L, a list with K elements. Initialize the last element: . Initialize . while do . end while Remove T from L. Output: set L of estimated breakpoint indexes. |
| Algorithm A2 |
Input: signal , cost functions , half-window width w, peak search procedure . Initialize NT-long arrays filled with 0: , . ▹Score list. for do . . . for do . end for . end for . ▹Peak search procedure. Output: set L of estimated breakpoint indexes. |
| Algorithm A3 |
Input: signal , cost functions , stopping criterion. Initialize . ▹Estimated breakpoints. repeat . ▹Number of breakpoints. ▹Dummy variables. if then Denote by the elements (in ascending order) of L, ie . end if Initialize G a -long array. ▹list of gains for do for do end for . end for . until stopping criterion is met. Output: set L of estimated breakpoint indexes. |
References
- Fearnhead, P.; Rigaill, G. Changepoint Detection in the Presence of Outliers. J. Am. Stat. Assoc. 2018, 114, 169–183. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier analysis. In Data Mining; Springer: Berlin/Heidelberg, Germany, 2015; pp. 237–263. [Google Scholar]
- Artemov, A.; Burnaev, E. Ensembles of detectors for online detection of transient changes. In Proceedings of the Eighth International Conference on Machine Vision (ICMV 2015), Barcelona, Spain, 19–21 November 2015; Verikas, A., Radeva, P., Nikolaev, D., Eds.; SPIE: Bellingham, WA, USA, 2015. [Google Scholar] [CrossRef]
- Tartakovsky, A.G.; Rozovskii, B.L.; Blazek, R.B.; Kim, H. A novel approach to detection of intrusions in computer networks via adaptive sequential and batch-sequential change-point detection methods. IEEE Trans. Signal Process. 2006, 54, 3372–3382. [Google Scholar] [CrossRef]
- Banerjee, T.; Chen, Y.C.; Dominguez-Garcia, A.D.; Veeravalli, V.V. Power system line outage detection and identification—A quickest change detection approach. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 3450–3454. [Google Scholar]
- Bai, J. Estimation of a change point in multiple regression models. Rev. Econ. Stat. 1997, 79, 551–563. [Google Scholar] [CrossRef]
- Reeves, J.; Chen, J.; Wang, X.L.; Lund, R.; Lu, Q.Q. A review and comparison of changepoint detection techniques for climate data. J. Appl. Meteorol. Climatol. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Rad, M.Z.; Ghuchani, S.R.; Bahaadinbeigy, K.; Khalilzadeh, M.M. Real time recognition of heart attack in a smart phone. Acta Inform. Med. 2015, 23, 151. [Google Scholar] [CrossRef]
- Shvetsov, N.; Buzun, N.; Dylov, D.V. Unsupervised non-parametric change point detection in electrocardiography. In Proceedings of the 32nd International Conference on Scientific and Statistical Database Management, Vienna, Austria, 7–9 July 2020; pp. 1–4. [Google Scholar]
- Zhao, K.; Wulder, M.A.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote. Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier ensembles: Position paper. ACM SIGKDD Explor. Newsl. 2013, 14, 49–58. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Sathe, S. Theoretical foundations and algorithms for outlier ensembles. ACM Sigkdd Explor. Newsl. 2015, 17, 24–47. [Google Scholar] [CrossRef]
- Rayana, S.; Akoglu, L. Less is more: Building selective anomaly ensembles. ACM Trans. Knowl. Discov. Data (TKDD) 2016, 10, 1–33. [Google Scholar] [CrossRef]
- Chen, J.; Sathe, S.; Aggarwal, C.; Turaga, D. Outlier detection with autoencoder ensembles. In Proceedings of the 2017 SIAM International Conference on Data Mining, Houston, TX, USA, 27–29 April 2017; pp. 90–98. [Google Scholar]
- Smolyakov, D.; Sviridenko, N.; Ishimtsev, V.; Burikov, E.; Burnaev, E. Learning ensembles of anomaly detectors on synthetic data. In Proceedings of the International Symposium on Neural Networks, Moscow, Russia, 10–12 July 2019; pp. 292–306. [Google Scholar]
- Zhao, Y.; Nasrullah, Z.; Hryniewicki, M.K.; Li, Z. LSCP: Locally selective combination in parallel outlier ensembles. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019; pp. 585–593. [Google Scholar]
- Gao, J.; Fan, W.; Turaga, D.; Verscheure, O.; Meng, X.; Su, L.; Han, J. Consensus extraction from heterogeneous detectors to improve performance over network traffic anomaly detection. In Proceedings of the 2011 Proceedings IEEE Infocom, Shanghai, China, 10–15 April 2011; pp. 181–185. [Google Scholar]
- Alippi, C.; Boracchi, G.; Roveri, M. Ensembles of change-point methods to estimate the change point in residual sequences. Soft Comput. 2013, 17, 1971–1981. [Google Scholar] [CrossRef]
- Alippi, C.; Boracchi, G.; Puig, V.; Roveri, M. An ensemble approach to estimate the fault-time instant. In Proceedings of the 2013 Fourth International Conference on Intelligent Control and Information Processing (ICICIP), Beijing, China, 9–11 June 2013; pp. 836–841. [Google Scholar]
- Faithfull, W.J.; Rodríguez, J.J.; Kuncheva, L.I. Combining univariate approaches for ensemble change detection in multivariate data. Inf. Fusion 2019, 45, 202–214. [Google Scholar] [CrossRef]
- Truong, C.; Oudre, L.; Vayatis, N. Selective review of offline change point detection methods. Signal Process. 2020, 167, 107299. [Google Scholar] [CrossRef]
- Katser, I.; Kozitsin, V.; Maksimov, I. NPP Equipment Fault Detection Methods. Izvestiya vuzov. Yadernaya Energetika 2019, 4, 5–27. [Google Scholar] [CrossRef]
- Advanced Surveillance, Diagnostic and Prognostic Techniques in Monitoring Structures, Systems and Components in Nuclear Power Plants; Number NP-T-3.14 in Nuclear Energy Series; International Atomic Energy Agency: Vienna, Austria, 2013.
- Lu, Y. Industry 4.0: A survey on technologies, applications and open research issues. J. Ind. Inf. Integr. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Vaidya, S.; Ambad, P.; Bhosle, S. Industry 4.0—A Glimpse. Procedia Manuf. 2018, 20, 233–238. [Google Scholar] [CrossRef]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Nguyen, V.L.; Hüllermeier, E.; Rapp, M.; Mencía, E.L.; Fürnkranz, J. On Aggregation in Ensembles of Multilabel Classifiers. In Proceedings of the 23rd International Conference, DS 2020, Thessaloniki, Greece, 19–21 October 2020; pp. 533–547. [Google Scholar]
- Costa, V.S.; Farias, A.D.S.; Bedregal, B.; Santiago, R.H.; Canuto, A.M.d.P. Combining multiple algorithms in classifier ensembles using generalized mixture functions. Neurocomputing 2018, 313, 402–414. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Chiang, L.H.; Russell, E.L.; Braatz, R.D. Fault Detection and Diagnosis in Industrial Systems; Springer: London, UK; Science & Business Media: Berlin, Germany, 2000. [Google Scholar]
- Katser, I.D.; Kozitsin, V.O. Skoltech Anomaly Benchmark (SKAB). 2020. Available online: https://www.kaggle.com/dsv/1693952 (accessed on 8 May 2021).
- Guédon, Y. Exploring the latent segmentation space for the assessment of multiple change-point models. Comput. Stat. 2013, 28, 2641–2678. [Google Scholar] [CrossRef]
- Fryzlewicz, P. Wild binary segmentation for multiple change-point detection. Ann. Stat. 2014, 42, 2243–2281. [Google Scholar] [CrossRef]
- Bai, J. Least absolute deviation estimation of a shift. In Econometric Theory; Cambridge University Press: Cambridge, UK, 1995; pp. 403–436. [Google Scholar] [CrossRef]
- Xing, E.P.; Jordan, M.I.; Russell, S.J.; Ng, A.Y. Distance metric learning with application to clustering with side-information. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2003; pp. 521–528. [Google Scholar]
- Mahalanobis, P.C. On the Generalized Distance in Statistics. In Proceedings of the National Institute of Sciences of India, Calcutta, India, 16 April 1936; Volume 2, pp. 49–55. [Google Scholar]
- Bai, J.; Perron, P. Critical values for multiple structural change tests. Econom. J. 2003, 6, 72–78. [Google Scholar] [CrossRef]
- Bai, J. Vector Autoregressive Models with Structural Changes in Regression Coefficients and in Variance-Covariance Matrices; Technical Report; China Economics and Management Academy, Central University of Finance: Beijing, China, 2000. [Google Scholar]
- Shao, J.D.; Rong, G.; Lee, J.M. Generalized orthogonal locality preserving projections for nonlinear fault detection and diagnosis. Chemom. Intell. Lab. Syst. 2009, 96, 75–83. [Google Scholar] [CrossRef]
- Odiowei, P.E.; Cao, Y. Nonlinear Dynamic Process Monitoring Using Canonical Variate Analysis and Kernel Density Estimations. IEEE Trans. Ind. Inform. 2010, 6, 36–45. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process. Control. 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Lavin, A.; Ahmad, S. Evaluating Real-Time Anomaly Detection Algorithms—The Numenta Anomaly Benchmark. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015. [Google Scholar] [CrossRef]
- Safin, A.M.; Burnaev, E. Conformal kernel expected similarity for anomaly detection in time-series data. Adv. Syst. Sci. Appl. 2017, 17, 22–33. [Google Scholar]
- Ishimtsev, V.; Bernstein, A.; Burnaev, E.; Nazarov, I. Conformal k-NN Anomaly Detector for Univariate Data Streams. In Proceedings of the Machine Learning Research, Stockholm, Sweden, 13–16 June 2017; Volume 60: Conformal and Probabilistic Prediction and Applications, pp. 213–227. [Google Scholar]
- Kozitsin, V.; Katser, I.; Lakontsev, D. Online Forecasting and Anomaly Detection Based on the ARIMA Model. Appl. Sci. 2021, 11, 3194. [Google Scholar] [CrossRef]
- Filonov, P.; Kitashov, F.; Lavrentyev, A. Rnn-based early cyber-attack detection for the tennessee eastman process. arXiv 2017, arXiv:1709.02232. [Google Scholar]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumezanu, C.; Cheng, W.; Ni, J.; Zong, B.; Chen, H.; Chawla, N.V. A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1409–1416. [Google Scholar]
- Filonov, P.; Lavrentyev, A.; Vorontsov, A. Multivariate industrial time series with cyber-attack simulation: Fault detection using an lstm-based predictive data model. arXiv 2016, arXiv:1612.06676. [Google Scholar]
- Hotelling, H. Multivariate Quality Control Illustrated by Air Testing of Sample Bombsights. In Techniques of Statistical Analysis; Eisenhart, C., Hastay, M.W., Wallis, W.A., Eds.; McGraw-Hill: New York, NY, USA, 1947; pp. 111–184. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).