Enhanced Quasi Type-1 PLL-Based Multi-Functional Control of Single-Phase Dynamic Voltage Restorer
Abstract
:1. Introduction
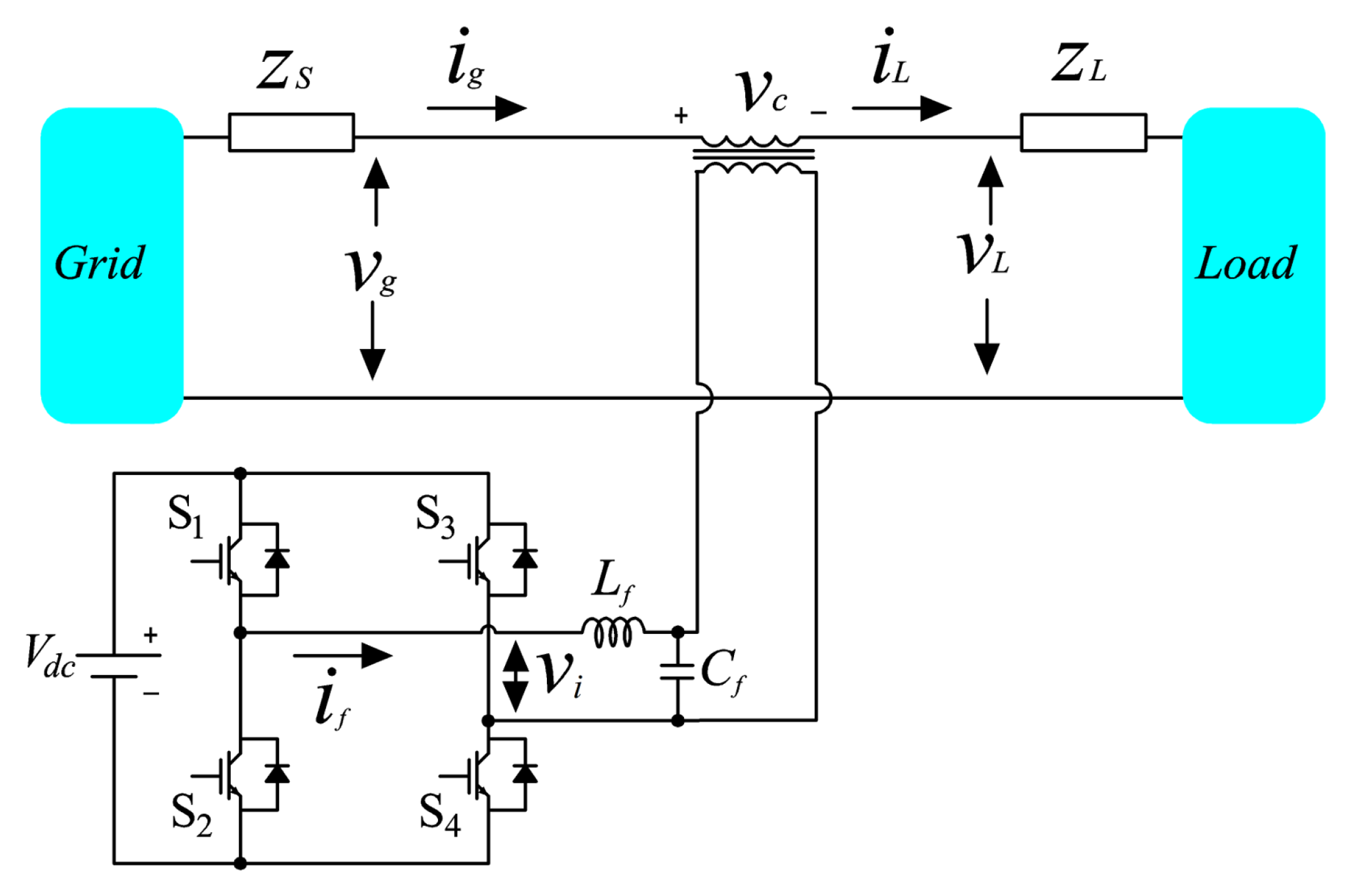
2. DVR Modeling and Problem Formulation
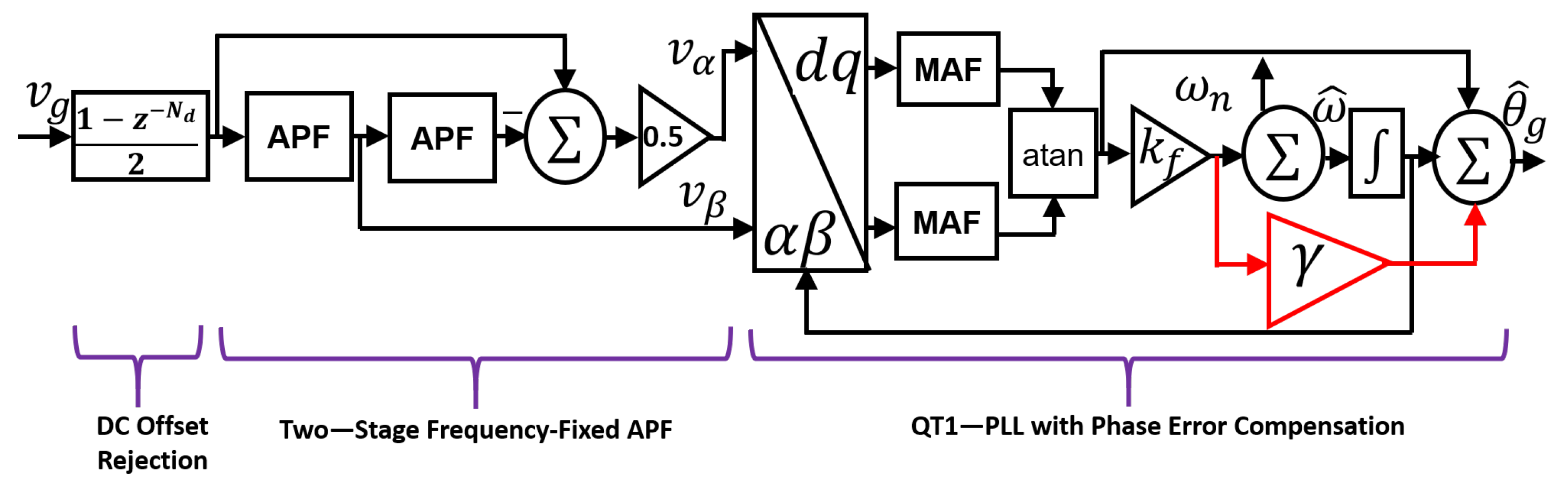
3. Reference Signal Generator
3.1. DC Offset Rejection
3.2. Tuning-Free Fixed-Frequency Orthogonal Signal Generator
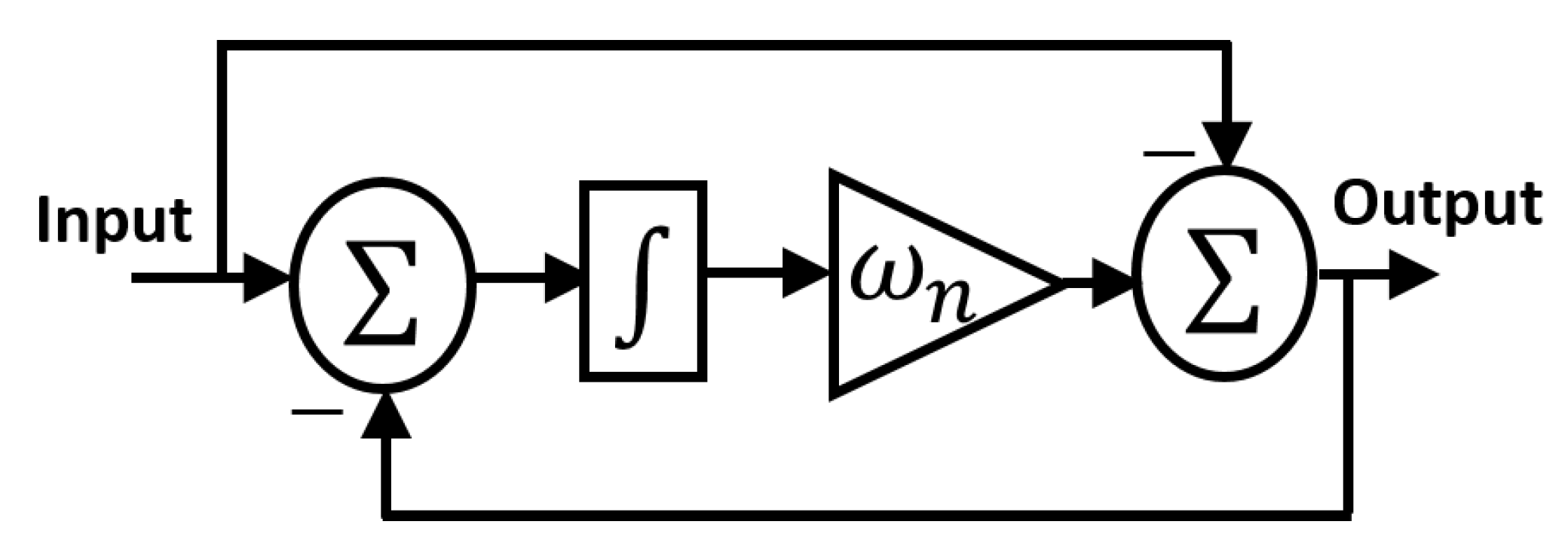
3.3. Implementation in PLL
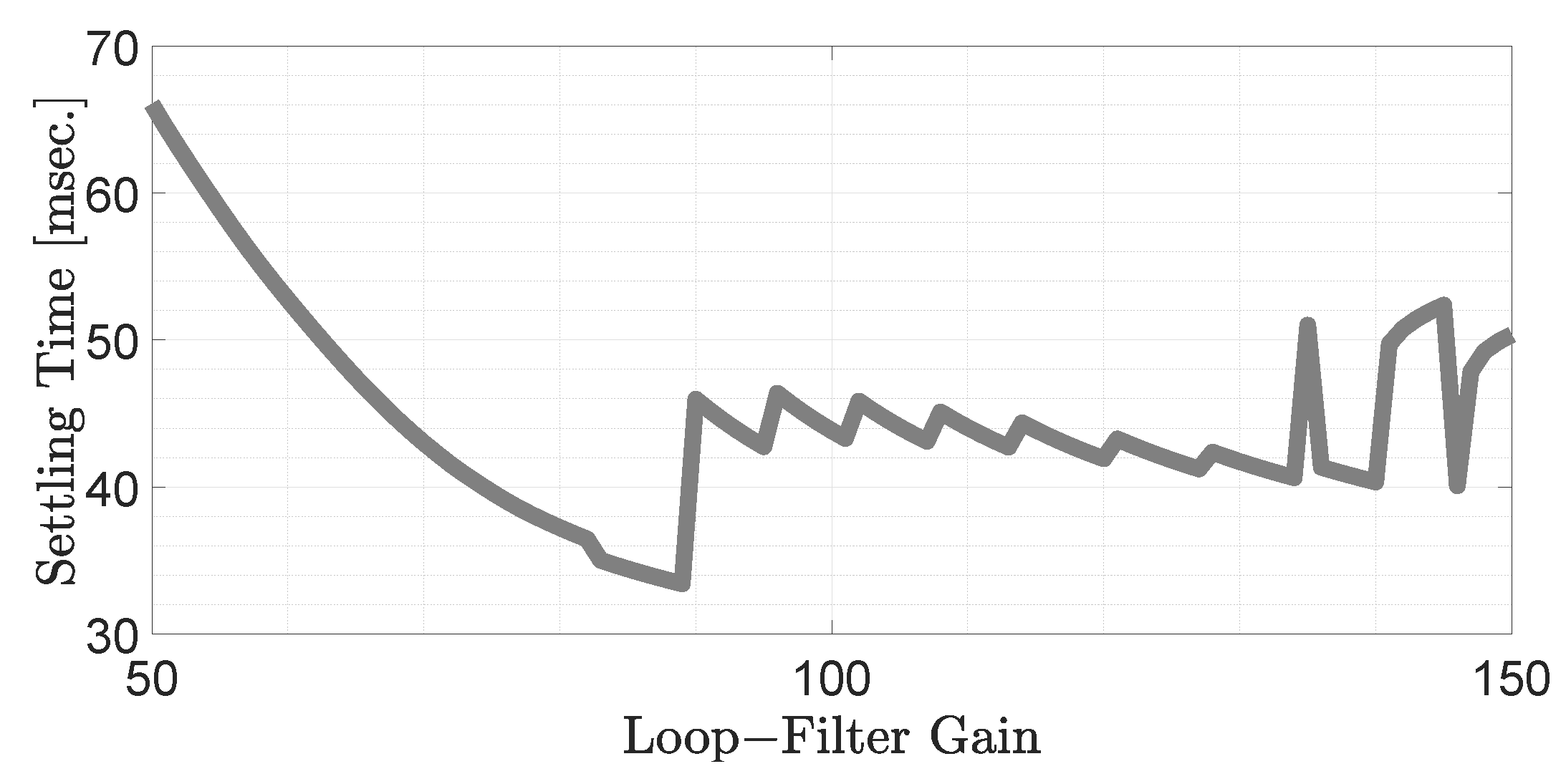
3.4. Small-Signal Modeling and Tuning
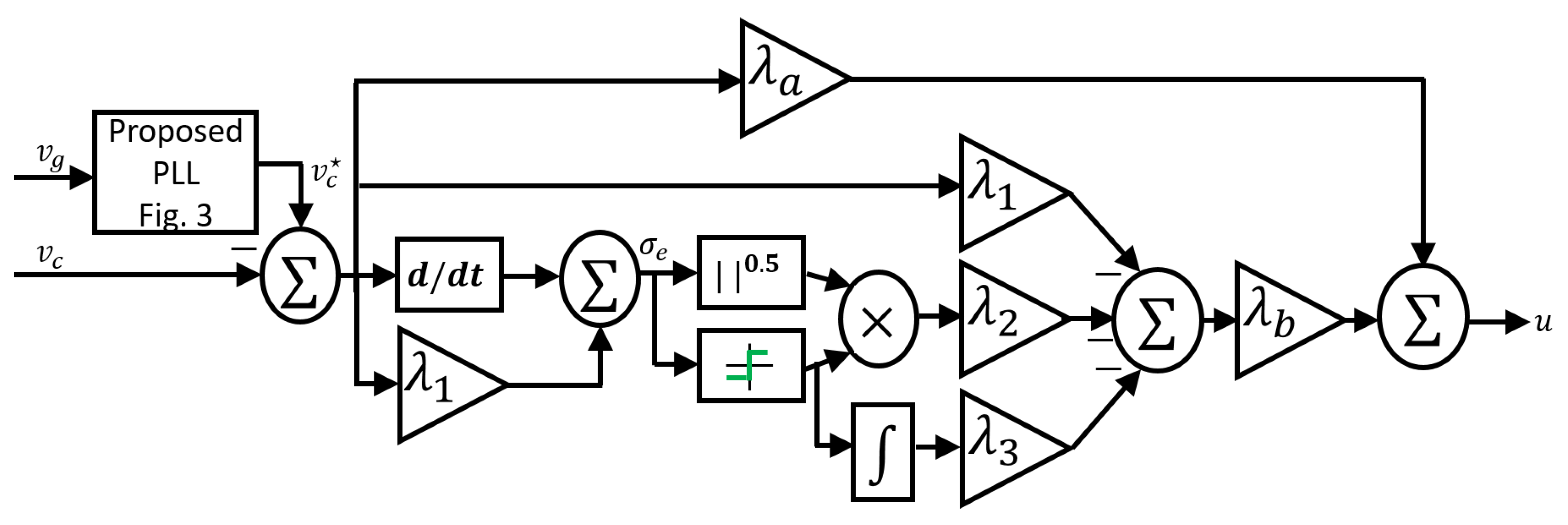
4. Super Twisting Sliding Mode Controller Design
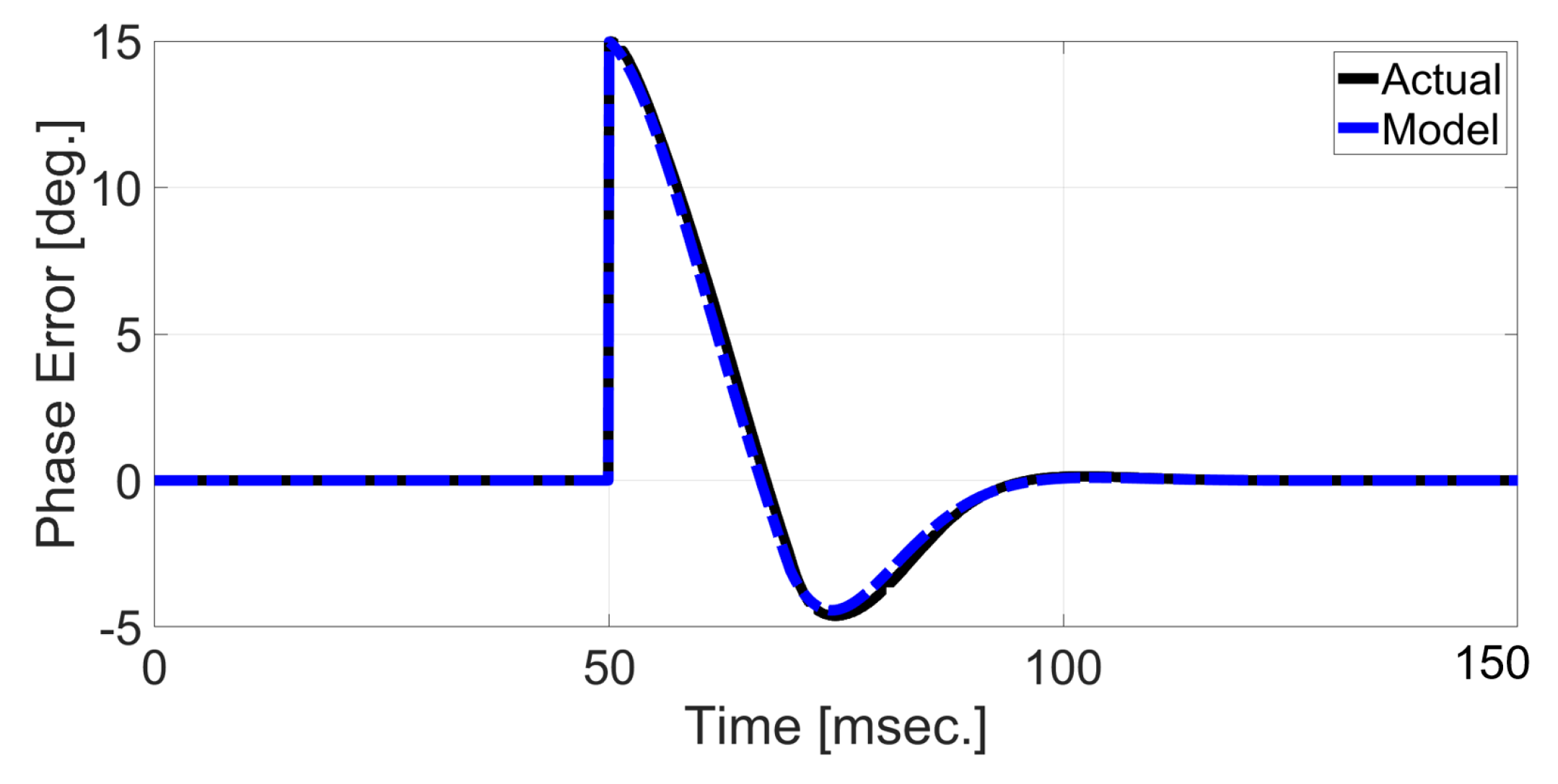
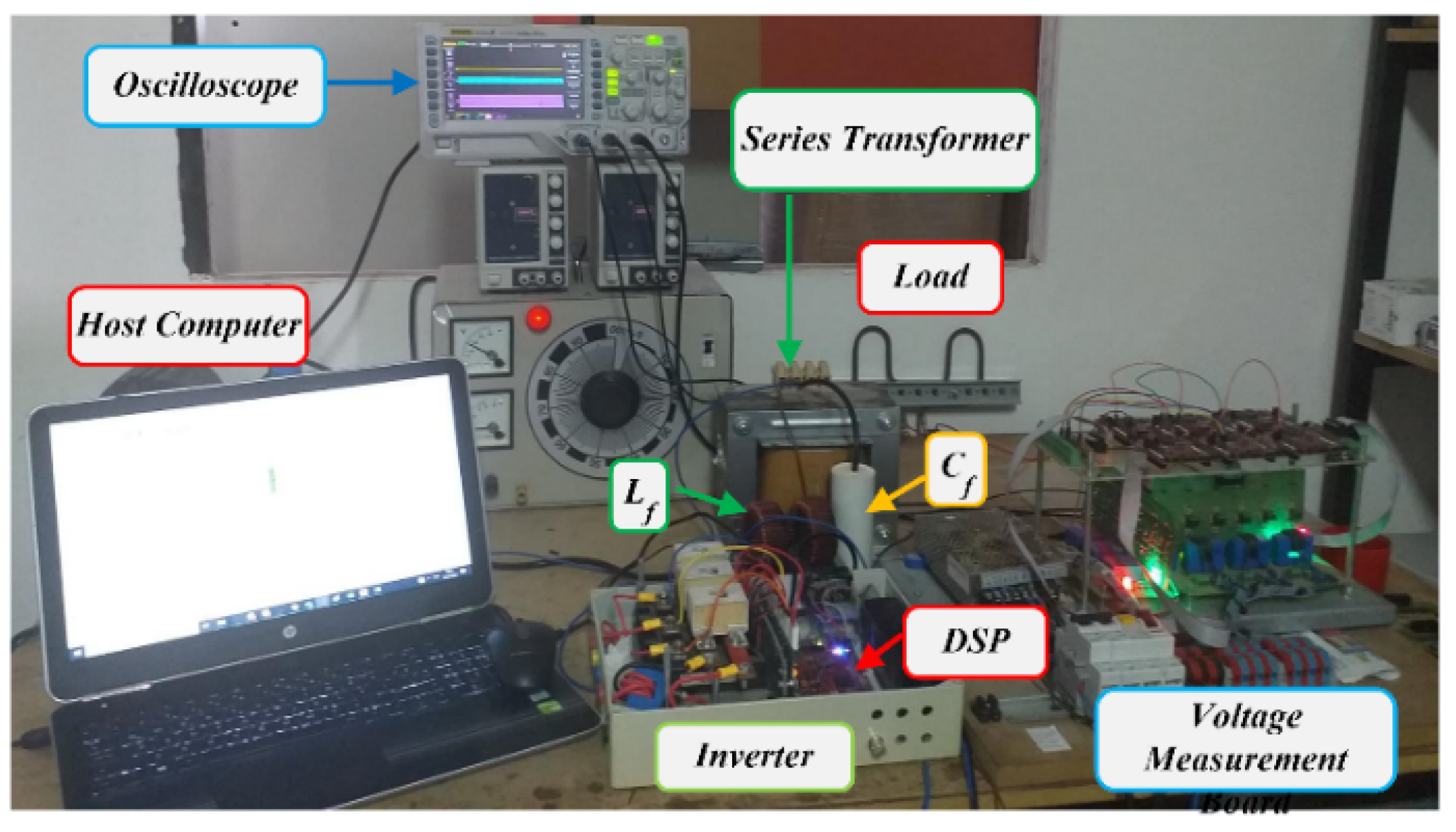
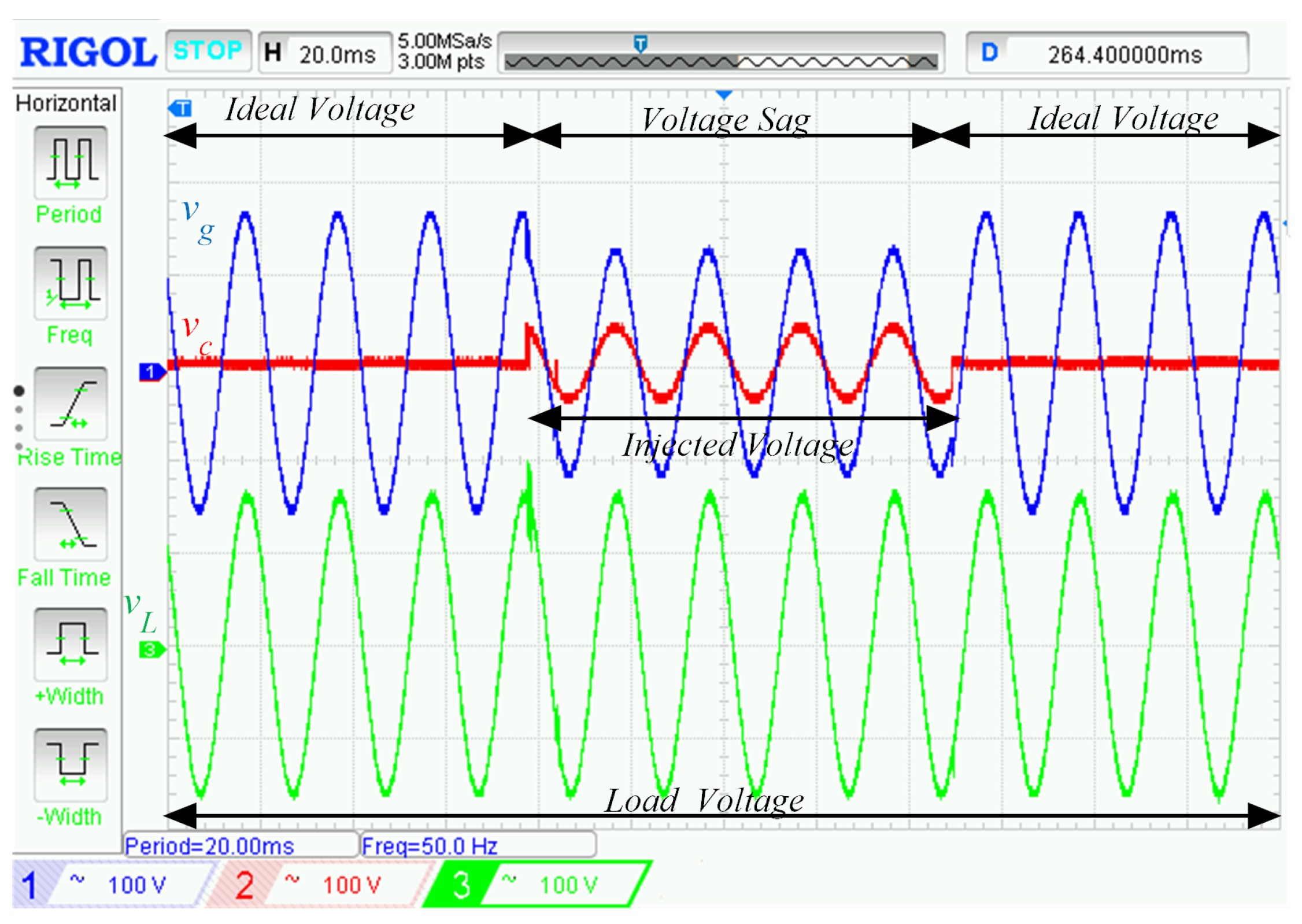
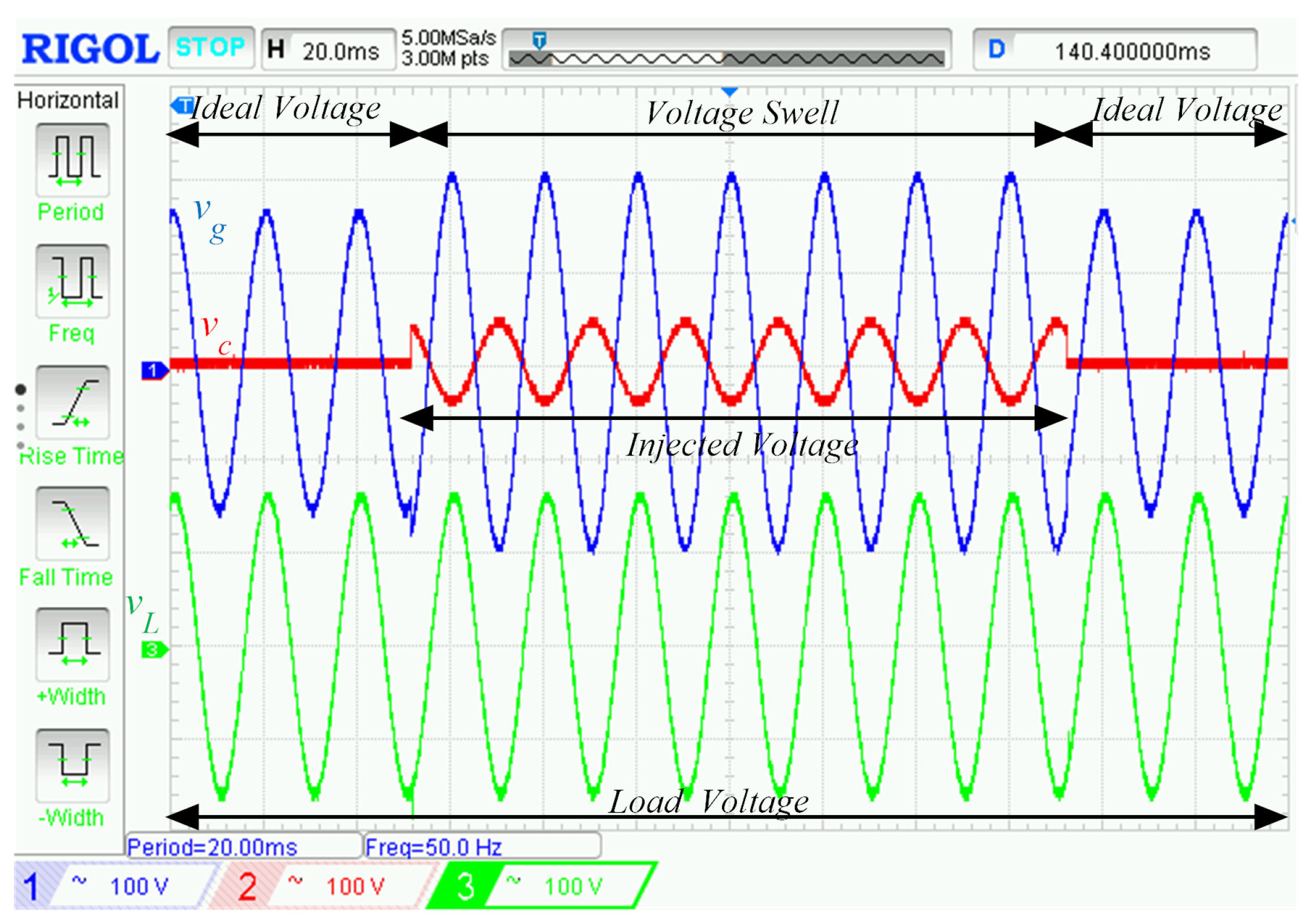
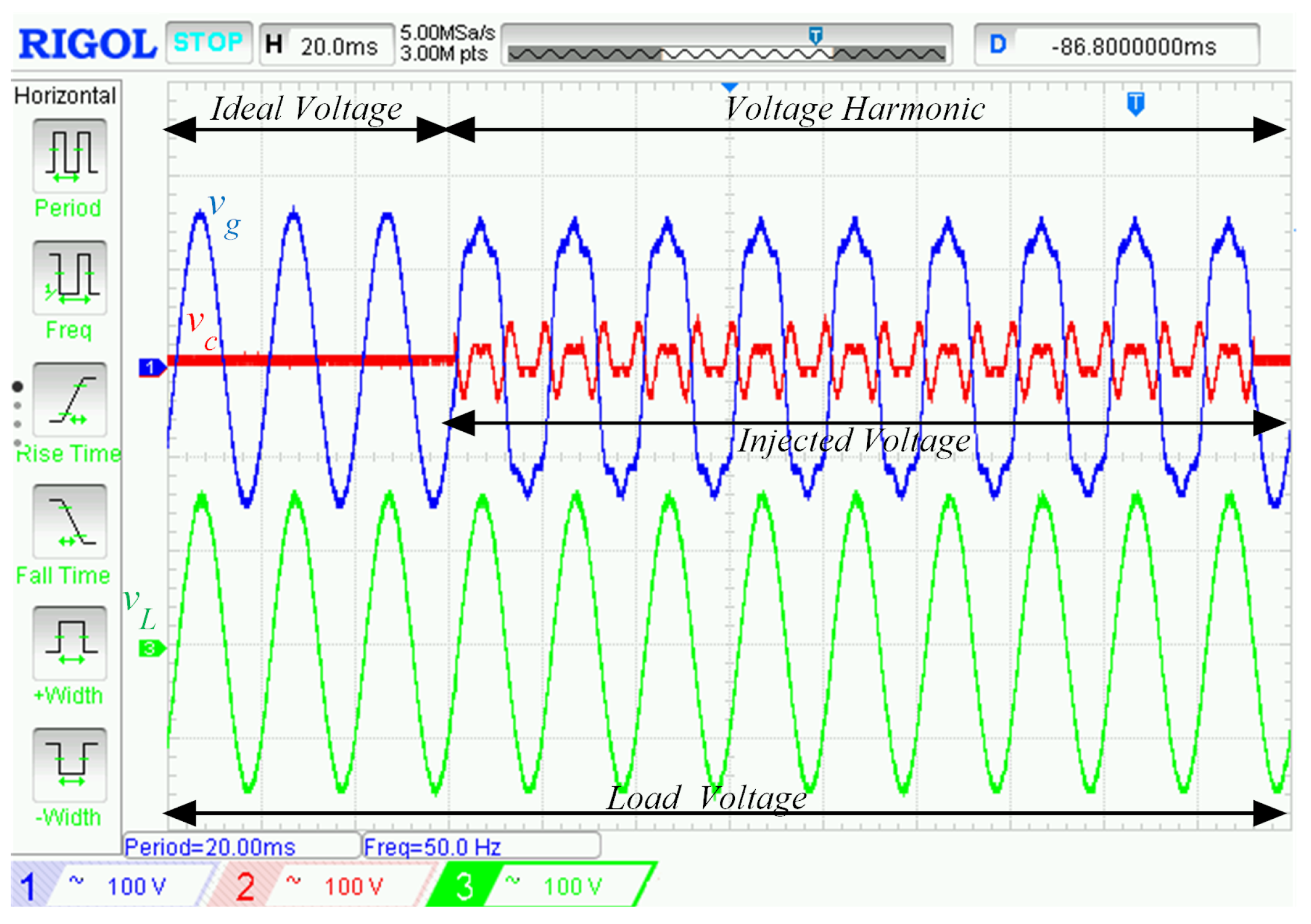
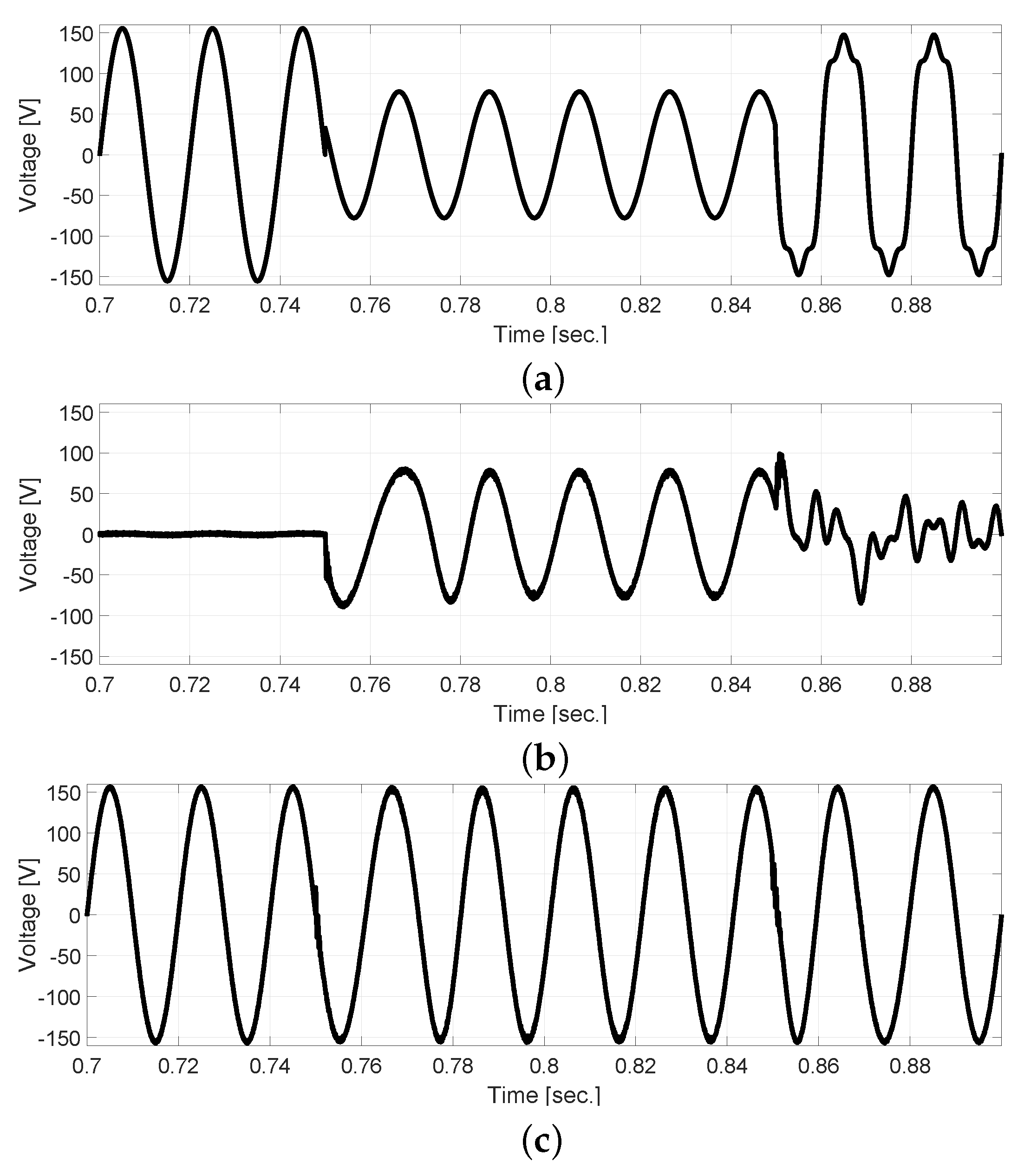
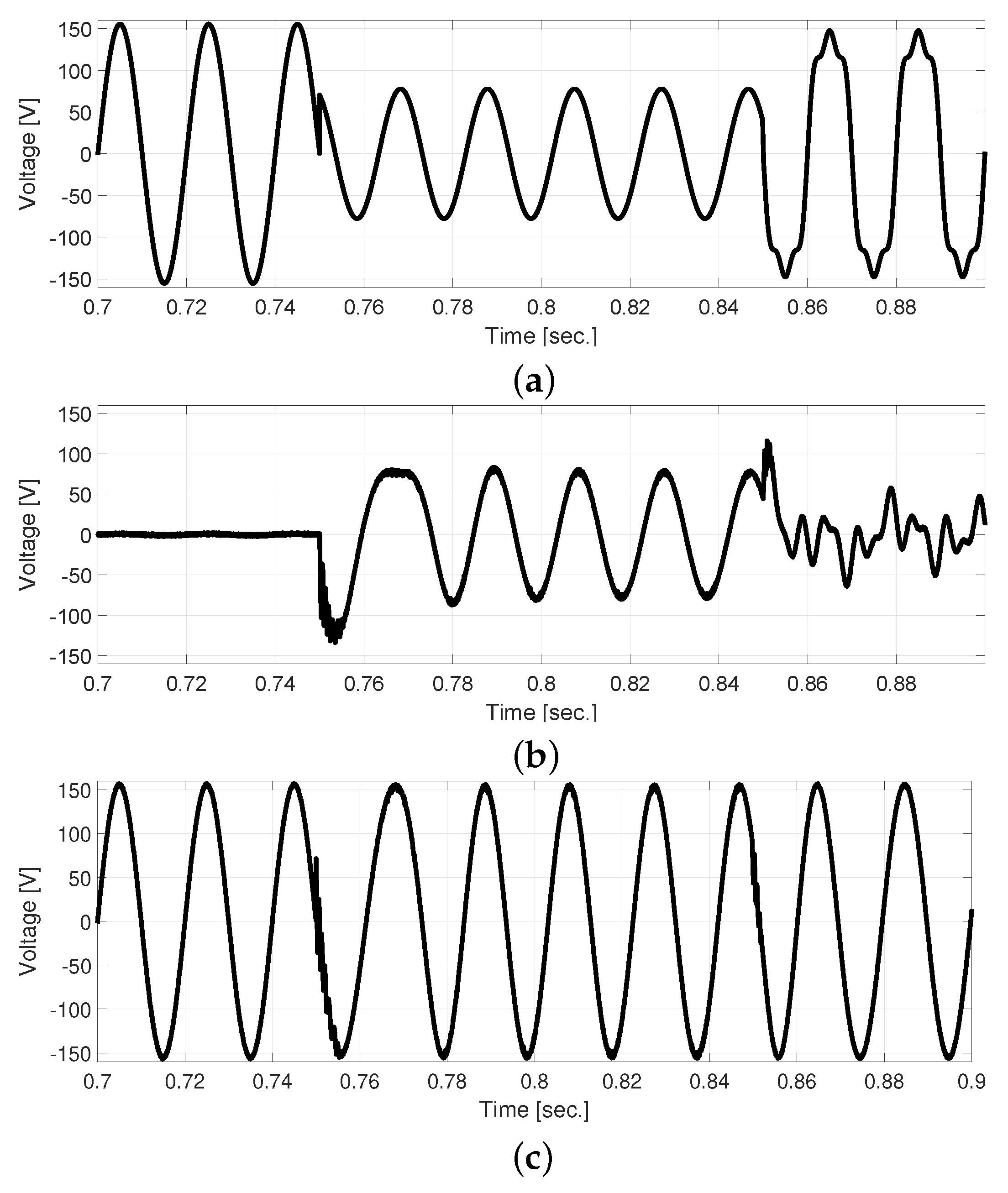
5. Simulation and Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Moghassemi, A.; Padmanaban, S. Dynamic voltage restorer (DVR): A comprehensive review of topologies, power converters, control methods, and modified configurations. Energies 2020, 13, 4152. [Google Scholar] [CrossRef]
- Yáñez-Campos, S.C.; Cerda-Villafaña, G.; Lozano-García, J.M. A Two-Grid Interline Dynamic Voltage Restorer Based on Two Three-Phase Input Matrix Converters. Appl. Sci. 2021, 11, 561. [Google Scholar] [CrossRef]
- Abas, N.; Dilshad, S.; Khalid, A.; Saleem, M.S.; Khan, N. Power quality improvement using dynamic voltage restorer. IEEE Access 2020, 8, 164325–164339. [Google Scholar] [CrossRef]
- Toumi, T.; Allali, A.; Abdelkhalek, O.; Abdelkader, A.B.; Meftouhi, A.; Soumeur, M.A. PV Integrated single-phase dynamic voltage restorer for sag voltage, voltage fluctuations and harmonics compensation. Int. J. Power Electron. Drive Syst. 2020, 11, 547. [Google Scholar] [CrossRef] [Green Version]
- IEEE Standard 1346-1998; IEEE Recommended Practice for Evaluating Electric Power System Compatibility with Electronic Process Equipment. IEEE: Piscataway Township, NJ, USA, 1998. [CrossRef]
- Lucas, A. Single-phase PV power injection limit due to voltage unbalances applied to an urban reference network using real-time simulation. Appl. Sci. 2018, 8, 1333. [Google Scholar] [CrossRef] [Green Version]
- Trabelsi, M.; Komurcugil, H.; Refaat, S.S.; Abu-Rub, H. Model predictive control of packed U cells based transformerless single-phase dynamic voltage restorer. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 1926–1931. [Google Scholar]
- Kumar, C.; Mishra, M.K. Predictive voltage control of transformerless dynamic voltage restorer. IEEE Trans. Ind. Electron. 2015, 62, 2693–2697. [Google Scholar] [CrossRef]
- Ahmed, H.; Salgado, I.; Chairez, I.; Benbouzid, M. Robust gradient estimator for unknown frequency estimation in noisy environment: Application to grid-synchronization. IEEE Access 2020, 8, 70693–70702. [Google Scholar] [CrossRef]
- Ahmed, H.; Biricik, S.; Benbouzid, M. Enhanced Frequency Adaptive Demodulation Technique For Grid-Connected Converters. IEEE Trans. Ind. Electron. 2021, 68, 11053–11062. [Google Scholar] [CrossRef]
- Remya, V.; Parthiban, P.; Ansal, V.; Nandakumar, A. Single-phase DVR with semi-Z-source inverter for power distribution network. Arab. J. Sci. Eng. 2018, 43, 3135–3149. [Google Scholar] [CrossRef]
- Satputaley, R.J.; Borghate, V.B. Performance analysis of DVR using “new reduced component” multilevel inverter. Int. Trans. Electr. Energy Syst. 2017, 27, e2288. [Google Scholar] [CrossRef]
- Ahmed, H.; Biricik, S.; Benbouzid, M. Linear Kalman Filter-Based Grid Synchronization Technique: An Alternative Implementation. IEEE Trans. Ind. Inform. 2021, 17, 3847–3856. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M. Simplified Second-Order Generalized Integrator - Frequency-Locked Loop. Adv. Electr. Electron. Eng. 2019, 17, 405–412. [Google Scholar] [CrossRef]
- Ahmed, H.; Pay, M.L.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E. Hybrid estimator-based harmonic robust grid synchronization technique. Electr. Power Syst. Res. 2019, 177, 106013. [Google Scholar] [CrossRef]
- Meena, A.; Islam, S.; Anand, S.; Sonawane, Y.; Tungare, S. Design and control of single-phase dynamic voltage restorer. Sādhanā 2017, 42, 1363–1375. [Google Scholar] [CrossRef]
- Nielsen, J.G.; Newman, M.; Nielsen, H.; Blaabjerg, F. Control and testing of a dynamic voltage restorer (DVR) at medium voltage level. IEEE Trans. Power Electron. 2004, 19, 806–813. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H. Optimized sliding mode control to maximize existence region for single-phase dynamic voltage restorers. IEEE Trans. Ind. Inform. 2016, 12, 1486–1497. [Google Scholar] [CrossRef]
- Biricik, S.; Khadem, S.K.; Redif, S.; Basu, M. Voltage distortion mitigation in a distributed generation-integrated weak utility network via a self-tuning filter-based dynamic voltage restorer. Electr. Eng. 2018, 100, 1857–1867. [Google Scholar] [CrossRef] [Green Version]
- Biricik, S.; Redif, S.; Özerdem, Ö.C.; Khadem, S.K.; Basu, M. Real-time control of shunt active power filter under distorted grid voltage and unbalanced load condition using self-tuning filter. IET Power Electron. 2014, 7, 1895–1905. [Google Scholar] [CrossRef] [Green Version]
- Rajkumar, K.; Parthiban, P. Grid voltage detection method based on a novel adaptive notch filter for control of transformerless dynamic voltage restorer. In Proceedings of the 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25–26 September 2020; pp. 1–6. [Google Scholar]
- Mellouli, M.S.; Hamouda, M.; Slama, J.B.H.; Al Haddad, K. A Third-order MAF Based QT1-PLL That is Robust against Harmonically Distorted Grid Voltage with Frequency Deviation. IEEE Trans. Energy Convers. 2021, 36, 1600–1613. [Google Scholar] [CrossRef]
- Golestan, S.; Freijedo, F.D.; Vidal, A.; Guerrero, J.M.; Doval-Gandoy, J. A quasi-type-1 phase-locked loop structure. IEEE Trans. Power Electron. 2014, 29, 6264–6270. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; Tir, Z.; Verma, A.K.; Ben Elghali, S.; Benbouzid, M. Quasi Type-1 PLL With Tunable Phase Detector for Unbalanced and Distorted Three-Phase Grid. IEEE Trans. Energy Convers. 2021. [Google Scholar] [CrossRef]
- Wu, C.; Xiong, X.; Taul, M.G.; Blaabjerg, F. On the Equilibrium Points in Three-Phase PLL Based on the d-axis Voltage Normalization. IEEE Trans. Power Electron. 2021, 36, 12146–12150. [Google Scholar] [CrossRef]
- Gautam, S.; Xiao, W.; Lu, D.D.C.; Ahmed, H.; Guerrero, J.M. Development of Frequency-Fixed All-Pass Filter based Single-Phase Phase-Locked Loop. IEEE J. Emerg. Sel. Top. Power Electron. 2021. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M. On the enhancement of generalized integrator-based adaptive filter dynamic tuning range. IEEE Trans. Instrum. Meas. 2020, 69, 7449–7457. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Single-Phase PLLs: A Review of Recent Advances. IEEE Trans. Power Electron. 2017, 32, 9013–9030. [Google Scholar] [CrossRef]
- Omar, A.I.; Aleem, S.H.A.; El-Zahab, E.E.; Algablawy, M.; Ali, Z.M. An improved approach for robust control of dynamic voltage restorer and power quality enhancement using grasshopper optimization algorithm. ISA Trans. 2019, 95, 110–129. [Google Scholar] [CrossRef]
- Li, Y.W.; Blaabjerg, F.; Vilathgamuwa, D.M.; Loh, P.C. Design and comparison of high performance stationary-frame controllers for DVR implementation. IEEE Trans. Power Electron. 2007, 22, 602–612. [Google Scholar] [CrossRef]
- Komurcugil, H.; Biricik, S.; Bayhan, S.; Zhang, Z. Sliding Mode Control: Overview of Its Applications in Power Converters. IEEE Ind. Electron. Mag. 2021, 15, 40–49. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H.; Ahmed, H.; Babaei, E. Super twisting sliding mode control of DVR with frequency-adaptive Brockett oscillator. IEEE Trans. Ind. Electron. 2021, 68, 10730–10739. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H.; Tuyen, N.D.; Basu, M. Protection of Sensitive Loads Using Sliding Mode Controlled Three-Phase DVR With Adaptive Notch Filter. IEEE Trans. Ind. Electron. 2019, 66, 5465–5475. [Google Scholar] [CrossRef]
- Chedjara, Z.; Massoum, A.; Wira, P.; Safa, A.; Gouichiche, A. A fast and robust reference current generation algorithm for three-phase shunt active power filter. Int. J. Power Electron. Drive Syst. 2021, 12, 121–129. [Google Scholar] [CrossRef]
- Sevilmiş, F.; Karaca, H. A fast hybrid PLL with an adaptive all-pass filter under abnormal grid conditions. Electr. Power Syst. Res. 2020, 184, 106303. [Google Scholar] [CrossRef]
- Ramezani, M.; Golestan, S.; Li, S. Non-frequency sensitive all-pass filter based single-phase PLLs. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors UAV. J. Frankl. Inst. 2012, 349, 685–699. [Google Scholar] [CrossRef]


| System and Control Parameters | Values |
|---|---|
| Controller gains | |
| PLL gain | |
| Grid: voltage and frequency | 120 V |
| Grid: impedance | , |
| Transformer turns ratio | 1:1 |
| DC link voltage, | 120 V |
| LC filter | , |
| Sensitive series load |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.; Biricik, S.; Komurcugil, H.; Benbouzid, M. Enhanced Quasi Type-1 PLL-Based Multi-Functional Control of Single-Phase Dynamic Voltage Restorer. Appl. Sci. 2022, 12, 146. https://doi.org/10.3390/app12010146
Ahmed H, Biricik S, Komurcugil H, Benbouzid M. Enhanced Quasi Type-1 PLL-Based Multi-Functional Control of Single-Phase Dynamic Voltage Restorer. Applied Sciences. 2022; 12(1):146. https://doi.org/10.3390/app12010146
Chicago/Turabian StyleAhmed, Hafiz, Samet Biricik, Hasan Komurcugil, and Mohamed Benbouzid. 2022. "Enhanced Quasi Type-1 PLL-Based Multi-Functional Control of Single-Phase Dynamic Voltage Restorer" Applied Sciences 12, no. 1: 146. https://doi.org/10.3390/app12010146
APA StyleAhmed, H., Biricik, S., Komurcugil, H., & Benbouzid, M. (2022). Enhanced Quasi Type-1 PLL-Based Multi-Functional Control of Single-Phase Dynamic Voltage Restorer. Applied Sciences, 12(1), 146. https://doi.org/10.3390/app12010146








