Modeling Hot Deformation of 5005 Aluminum Alloy through Locally Constrained Regression Models with Logarithmic Transformations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Tensile Tests
3. Flow Stress Modeling
3.1. Arrhenius Type Constitutive Equation
3.2. Locally Constrained Regression Model
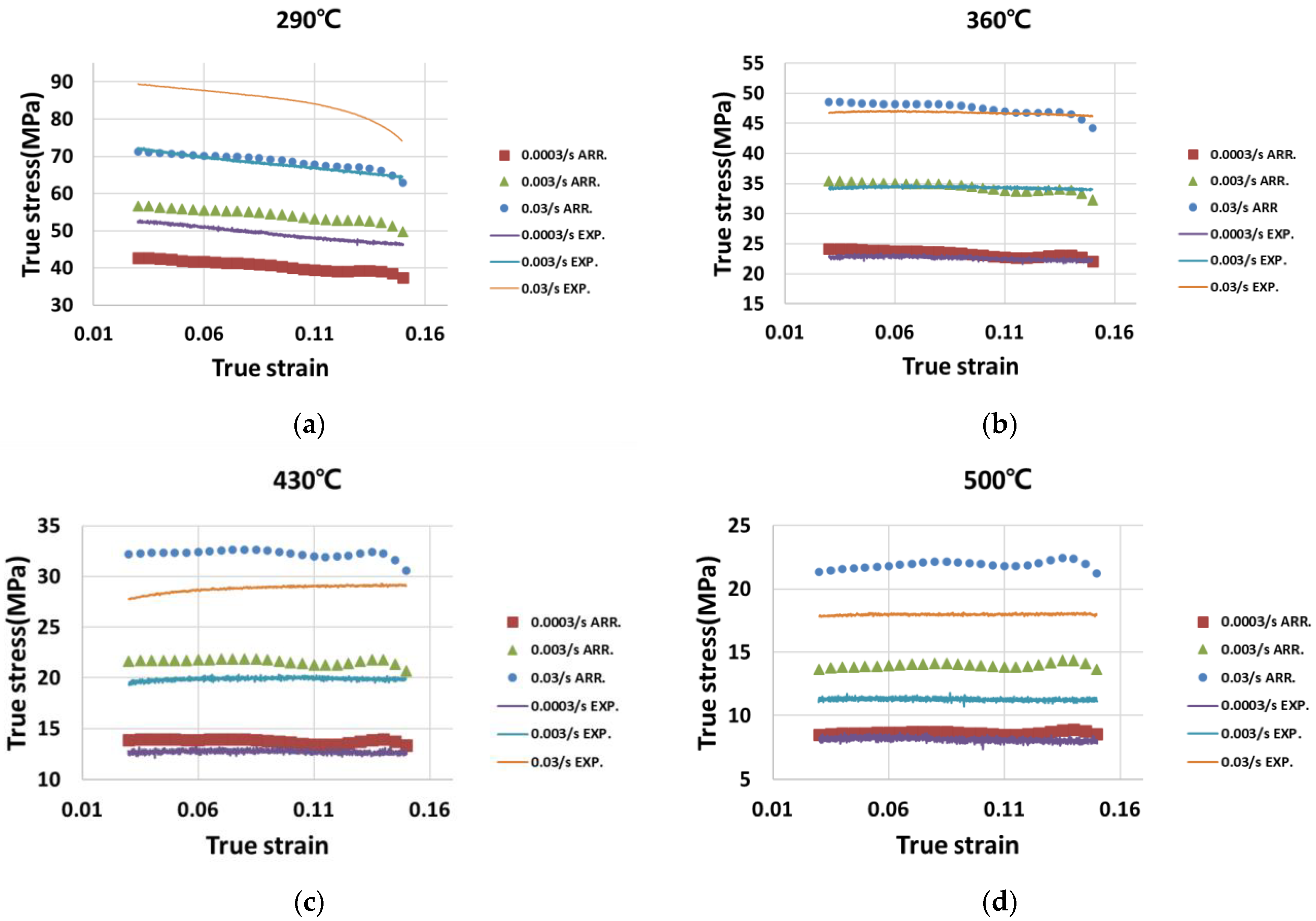
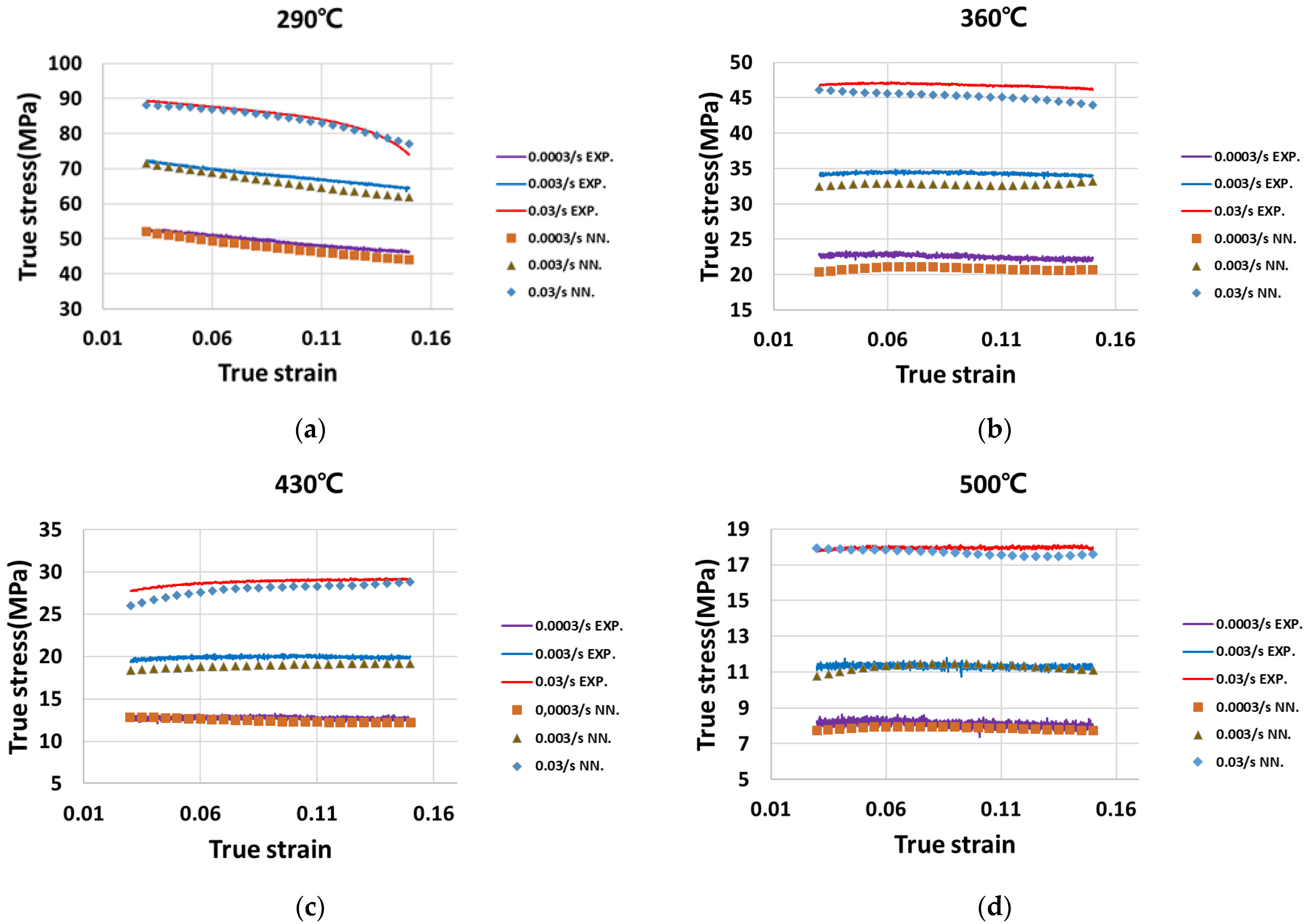
4. Results and Discussion
4.1. Results
4.2. Discussion on the Performances of the Algorithms
5. Conclusions, Limitations, and Future Research
5.1. Conclusions
5.2. Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, R.; Knight, S.P.; Holtz, R.L.; Goswami, R.; Davies, C.H.J.; Birbilis, N. A Survey of Sensitization in 5xxx Series Aluminum Alloys. Corrosion 2016, 72, 144–159. [Google Scholar] [CrossRef]
- Tzeng, Y.-C.; Chen, R.-Y.; Lee, S.-L. Nondestructive Tests on the Effect of Mg Content on the Corrosion and Mechanical Properties of 5000 Series Aluminum Alloys. Mater. Chem. Phys. 2021, 259, 124202. [Google Scholar] [CrossRef]
- Kramer, L.; Phillippi, M.; Tack, W.T.; Wong, C. Locally Reversing Sensitization in 5xxx Aluminum Plate. J. Mater. Eng. Perform. 2012, 21, 1025–1029. [Google Scholar] [CrossRef]
- Miller, W.S.; Zhuang, L.; Bottema, J.; Wittebrood, A.J.; De Smet, P.; Haszler, A.; Vieregge, A. Recent Development in Aluminium Alloys for the Automotive Industry. Mater. Sci. Eng. A 2000, 280, 37–49. [Google Scholar] [CrossRef]
- Scotto D’Antuono, D.; Gaies, J.; Golumbfskie, W.; Taheri, M.L. Direct Measurement of the Effect of Cold Rolling on β Phase Precipitation Kinetics in 5xxx Series Aluminum Alloys. Acta Mater. 2017, 123, 264–271. [Google Scholar] [CrossRef] [Green Version]
- Tang, K.; Zhang, Z.; Tian, J.; Wu, Y.; Jiang, F. Hot Deformation Behavior and Microstructural Evolution of Supersaturated Inconel 783 Superalloy. J. Alloy. Compd. 2021, 860, 158541. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Ren, X.; Xiao, Z.; Zhang, X.; Huang, Y. Flow Stress Prediction of Hastelloy C-276 Alloy Using Modified Zerilli−Armstrong, Johnson−Cook and Arrhenius-Type Constitutive Models. Trans. Nonferrous Met. Soc. China 2020, 30, 3031–3042. [Google Scholar] [CrossRef]
- Ohdar, R.K.; Equbal, A.; Equbal, M.I. Hot Deformation Studies of AISI 1035 Steel Using Thermo Mechanical Simulator. Mater. Today Proc. 2020, 26, 3305–3310. [Google Scholar] [CrossRef]
- Kant Thakur, S.; Harish, L.; Kumar Das, A.; Rath, S.; Pathak, P.; Kumar Jha, B. Hot Deformation Behavior and Processing Map of Nb-V-Ti Micro-Alloyed Steel. Mater. Today Proc. 2020, 28, 1973–1979. [Google Scholar] [CrossRef]
- Quan, G. Artificial Neural Network Modeling to Evaluate the Dynamic Flow Stress of 7050 Aluminum Alloy. J. Mater. Eng. Perform. 2016, 25, 553–564. [Google Scholar] [CrossRef]
- Zhao, J.; Ding, H.; Zhao, W.; Huang, M.; Wei, D.; Jiang, Z. Modelling of the Hot Deformation Behaviour of a Titanium Alloy Using Constitutive Equations and Artificial Neural Network. Comput. Mater. Sci. 2014, 92, 47–56. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Kharmanda, G.; Mahdi, E. Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy. Materials 2019, 12, 2873. [Google Scholar] [CrossRef] [Green Version]
- Mosleh, A.; Mikhaylovskaya, A.; Kotov, A.; Pourcelot, T.; Aksenov, S.; Kwame, J.; Portnoy, V. Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network. Metals 2017, 7, 568. [Google Scholar] [CrossRef] [Green Version]
- Quan, G.-Z.; Zhang, Z.-H.; Zhang, L.; Liu, Q. Numerical Descriptions of Hot Flow Behaviors across β Transus for As-Forged Ti–10V–2Fe–3Al Alloy by LHS-SVR and GA-SVR and Improvement in Forming Simulation Accuracy. Appl. Sci. 2016, 6, 210. [Google Scholar] [CrossRef] [Green Version]
- Quan, G.; Pan, J.; Wang, X. Prediction of the Hot Compressive Deformation Behavior for Superalloy Nimonic 80A by BP-ANN Model. Appl. Sci. 2016, 6, 66. [Google Scholar] [CrossRef] [Green Version]
- Alhassan, A.M.; Wan Zainon, W.M.N. Taylor Bird Swarm Algorithm Based on Deep Belief Network for Heart Disease Di-agnosis. Appl. Sci. 2020, 10, 6626. [Google Scholar] [CrossRef]
- Information on Aluminium 5005—Thyssenkrupp Materials (UK). Available online: https://www.thyssenkrupp-materials.co.uk/aluminium-5005.html (accessed on 15 December 2021).
- Zener, C.; Hollomon, J.H. Effect of Strain Rate upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Eskinat, E.; Johnson, S.H.; Luyben, W.L. Use of Hammerstein Models in Identification of Nonlinear Systems. AIChE J. 1991, 37, 255–268. [Google Scholar] [CrossRef]
- Qin, Y.; Kumon, M.; Furukawa, T. Estimation of a Human-Maneuvered Target Incorporating Human Intention. Sensors 2021, 21, 5316. [Google Scholar] [CrossRef] [PubMed]
- Daliya, V.K.; Ramesh, T.K.; Ko, S.-B. An Optimised Multivariable Regression Model for Predictive Analysis of Diabetic Disease Progression. IEEE Access 2021, 9, 99768–99780. [Google Scholar] [CrossRef]
- Chan, C.-L.; Chen, C.-L.; Ting, H.-W.; Phan, D.-V. An Agile Mortality Prediction Model: Hybrid Logarithm Least-Squares Support Vector Regression with Cautious Random Particle Swarm Optimization. Int. J. Comput. Intell. Syst. 2018, 11, 873–881. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.-W.; Hsu, C.-M. Lightweight Convolutional Neural Networks with Model-Switching Architecture for Multi-Scenario Road Semantic Segmentation. Appl. Sci. 2021, 11, 7424. [Google Scholar] [CrossRef]








| Properties | Melting Temp. | Thermal Conductivity | Thermal Expansion | Tensile Strength | Brinell Hardness |
|---|---|---|---|---|---|
| Values | 655 °C | 201 W/mK | 23.5 × 10−6/K | 145–185 MPa | 47 HB |
| Constant | 5th | 4th | 3rd | 2nd | 1st | 0th |
|---|---|---|---|---|---|---|
| 119,942.697 | −51,904.395 | 9175.732 | −809.63 | 32.563 | 4.198 | |
| 644.172 | −200.608 | 20.968 | −0.566 | −0.017 | 0.034 | |
| 3.7 × 109 | −1.5 × 109 | 2.32 × 108 | −1.7 × 107 | 398,016.905 | 151,749.123 | |
| 4.72 × 1014 | −1.9 × 1014 | 2.71 × 1013 | −1.1 × 1012 | −5.5 × 1010 | 4.58 × 109 |
| Method | 290 °C | 360 °C | 430 °C | 500 °C | Average | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Arrhenius equation | 12.872 | 13.296 | 0.769 | 0.903 | 2.052 | 2.324 | 2.367 | 2.769 | 4.515 | 6.904 |
| NN | 1.448 | 1.594 | 1.621 | 1.653 | 0.73 | 0.831 | 0.238 | 0.286 | 1.009 | 1.229 |
| LCRMs (ours) | 0.525 | 0.818 | 0.133 | 0.169 | 0.145 | 0.183 | 0.105 | 0.127 | 0.227 | 0.432 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.; Song, S.-H. Modeling Hot Deformation of 5005 Aluminum Alloy through Locally Constrained Regression Models with Logarithmic Transformations. Appl. Sci. 2022, 12, 152. https://doi.org/10.3390/app12010152
Cho J, Song S-H. Modeling Hot Deformation of 5005 Aluminum Alloy through Locally Constrained Regression Models with Logarithmic Transformations. Applied Sciences. 2022; 12(1):152. https://doi.org/10.3390/app12010152
Chicago/Turabian StyleCho, Jeongho, and Shin-Hyung Song. 2022. "Modeling Hot Deformation of 5005 Aluminum Alloy through Locally Constrained Regression Models with Logarithmic Transformations" Applied Sciences 12, no. 1: 152. https://doi.org/10.3390/app12010152
APA StyleCho, J., & Song, S. -H. (2022). Modeling Hot Deformation of 5005 Aluminum Alloy through Locally Constrained Regression Models with Logarithmic Transformations. Applied Sciences, 12(1), 152. https://doi.org/10.3390/app12010152







